1 Introduction

The Third Generation Partnership Project Long-Term Evolution (3GPP-LTE) proposes different schemes for mobile broadband access in order to meet the throughput and coverage requirements of next generation cellular networks [1]. Deployment of Relay Stations (RSs) to increase coverage area and/or improve capacity [2] is one of the proposed techniques in long term evolution (LTE). In this paper, we analyze the capacity improvement due to RS deployment and analytically determine the blocking probability to quantify this improvement. Blocking probability corresponds to the probability that a user is denied sevice due to non-availability of sufficient resources in the network.

User who experiences poor signal strength from the base station (BS), requires more resources to meet its rate requirement and a large amount of resources are consumed in serving such users. This leads to an increase in the blocking probability. With RS deployed in the network, the signal to noise ratio (SNR) experienced by these users may improve due to closer proximity of RS and as a result, they may meet their rate requirement with fewer resources. This reduces the blocking probability and improves the system capacity. However, as the radio resources are shared between BS and RS, deployment of RSs introduce additional sources of interference. Therefore, it is significant to study the impact of interference on the blocking probability.

Blocking probability has been used as a performance metric in [3], in which the transmission scheme selection policy (single hop or multi-hop) has been proposed to provide guaranteed target bit error rate (BER) and data rate to a mobile user. Another metric to quantify the performance improvement in a cellular network is Erlang capacity, which is the traffic load in Erlangs supported by the cell while ensuring that the blocking probability remains less than a certain value. There is sufficient work on Erlang capacity and blocking probability in cellular networks [4, 5] and some literature is available on determining the Erlang capacity of cellular orthogonal frequency division multiple access (OFDMA) networks. In [6], the performance of subcarrier allocation in OFDM system has been investigated considering multi-class users. However, in this work, the model assumes such that the subcarriers are released one by one on call termination and not simultaneously, as would happen in practice. The Erlang Loss Model for blocking probability analysis has been suggested in [7] and is proved to be numerically efficient and insensitive to the distribution of call duration. More recently in [8], the OFDM system for blocking probability computation considers both power and subcarrier allocation. Despite the availability of sufficient literature on determining the Erlang capacity and blocking probability in cellular networks including OFDMA networks, limited literature is available on determining the Erlang capacity of relay based cellular OFDMA network [9–11]. In [9], the uplink Erlang capacity of relay-based OFDMA network has been derived considering adaptive modulation and coding supporting both voice and data traffic. In [10], the uplink capacity and spectral efficiency of relay-based cellular networks have been analyzed. The bandwidth distribution between BS and RSs has been determined to ensure that the blocking probability is less than a specific threshold. The impact of number of RSs and their positions on the Erlang capacity is investigated by considering adaptive modulation and coding (AMC) and multiple-input multiple-output (MIMO) transmissions.

In [9] and [10], it is assumed that all users require equal number of resources and the impact of user location, shadowing and interference from neighboring cells on the resource requirement has not been considered. If distinct users of same data rate requirement are present at different locations, they may experience different signal to interference ratio (SIR) and hence require different resources in terms of number of subcarriers to satisfy their data rate requirement. In the queuing literature, the problem of incoming users requiring different number of resources has been addressed in some works. In [12], wide band and narrow band traffic is considered, where no queuing is allowed for narrow band traffic and a finite length queue is provided for wide band traffic. The blocking probability for each traffic class is determined using numerical methods. Similarly, in [13] and [14], the problem of multiple server requirement is analyzed and multidimensional Erlang loss formulas have been derived.

To the best of our knowledge, no literature is available for the computation of blocking probability in relay based cellular OFDMA network where different users of same rate requirement need different subcarriers. In [11], different subcarrier requirement of users has been considered in the blocking probability computations. However, SIR experienced by a user and the distribution of subcarrier requirement were determined using simulations. In [15] (by one of the authors), cumulative distribution function (CDF) of interference is computed analytically. However, blocking probability is not determined.

In this paper, we propose an analytical model to evaluate the performance of a relay based cellular OFDMA network (such as an LTE network) in terms of blocking probability. The distinct feature of our paper is that we consider the impact of user location, shadowing and interference from neighboring cells in our analysis for blocking probability. Specifically, we determine the SIR experienced by a user and probability distribution of the number of subcarriers required. Then, we classify incoming users into different classes based on their subcarrier requirement. We consider the network to be a multi-dimensional system with different classes and model the system states by multi-dimensional Markov chain. In such a system model, the computational complexity is more due to the large state space involving the states of both BS and RS. To reduce this complexity, we propose an approximation where the state space of BS and RS are decoupled. With this simplification, we evaluate the blocking probability of each class in a relay based OFDMA network. This approximation is justified by comparing the analytical results with the simulation results where we do not make such assumption.

The rest of the paper is organized as follows. Section 2 introduces the system model for the downlink of relay based cellular OFDMA network. In Sect. 3, a model to characterize inter-cell interference (ICI) on a mobile station (MS) is presented and the CDFs of ICI on BS–MS, BS–RS and RS–MS transmission links are derived. In Sect. 4, an analytical model is proposed to determine the subcarrier requirement and its probability distribution based on ICI experienced. In Sect. 5, the incoming users are classified into various classes based on their subcarrier requirement. It is also shown that complexity is introduced due to the large size of state space when both BS and RS are considered. Then, an analytical model is developed by considering the state space of BS and RS separately. This model is used to compute the blocking probability for each class of user at BS and RS. Finally, the blocking probability of a relay-based OFDMA network is computed using multi-dimensional Erlang loss formulas [14]. In Sect. 6, the simulation methodology is explained and both analytical and simulation results are discussed. Here, the system performance (in terms of blocking probability) of a non-relay system with that of the relay-based cellular OFDMA system is compared. Finally, Sect. 7 concludes the paper with an insight into the future extensions of the present work.

2 System Model

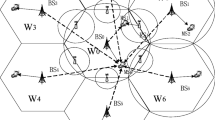
We consider the downlink transmission scenario in a relay-based cellular OFDMA network as shown in Fig. 1. We define the reference cell as a combination of seven sub-cells. The central sub-cell \(H_{0}\) consists of a BS centered at \((0,0)\), while each surrounding sub-cell (i.e. \(H_{1}, \ldots , H_{6}\)) consists of one RS at the centre. For convenience, we approximate the coverage of BS and RS by hexagons as shown in Fig. 1. We define the central sub-cell \((H_{0})\) as base region and the six surrounding sub-cells \((H_{1}, \ldots , H_{6})\) as relay region in every cell. We define a MS (user) present in the reference cell as the target MS. We assume that BS and RS have line of sight (LoS) connection. All RSs are assumed to be amplify-and-forward type relays.

Fig. 1
figure 1

Architecture of relay based cellular OFDMA system

Full size image

We consider universal frequency reuse, i.e. all cells use the same spectrum, which is shared between BS and six RSs. We consider the interference from the first tier of neighboring cells only. We also consider the effect of path loss and lognormal shadowing on the transmitted signal. Let the BS transmit with power \(P\) to a MS located at distance \(d\), then the received power at the MS will be \(Pd^{-\beta }10^{\xi /10}\), where \(\beta \) is path loss exponent and \(\xi \) represents lognormal shadowing on BS–MS link. \(\xi \) is assumed to be a Gaussian random variable with mean 0 and standard deviation \(\sigma \,\hbox {dB}\). Since thermal noise is negligible in an interference-limited reuse-one network, we ignore it in our computations. Note that we do not consider short-term fading as our objective is to evaluate the blocking probability from a long term capacity planning perspective. For the same reason, we do not consider any power control mechanism and assume that BS transmits at fixed power.

In practice, the association of a MS with BS or RS is determined based on SIR. If SIR experienced by a MS from a BS is above threshold, then it will be associated with the BS otherwise it will be associated with a RS. In the present paper however, we consider a model where users present in the BS region are associated with the BS directly and those present in the relay region are associated with the corresponding RS. It is assumed that the users are uniformly distributed in the respective regions of the cell. As explained later in Sect. 5, out of the total call arrivals to the cell, a fraction is assumed to occur in BS region, while the remaining are assumed to have occurred in relay regions.

We assume that there are \(K\) number of subcarriers available in the reference cell, which are shared between BS and six RSs. Each RS and BS are allocated \(K_{RS}\) and \(K_{BS}\) subcarriers respectively, such that \(K = K_{BS} + 6 K_{RS}\). If insufficient number of subcarriers are allocated to RS, then RS will not be able to relay the signals received from BS to MS. On the other hand, if the subcarriers allocated to RSs are more than the required, then there may be an increase in call blocking at the BS. We evaluate the blocking probability for two different values of \(K_{BS}\) and \(K_{RS}\) later in this paper.

In the reference cell, all users have been allocated orthogonal subcarriers and therefore no intra-cell interference exists. However, in a network with universal frequency reuse, users will experience interference from RSs and BSs of neighboring cells. We consider the system to be fully loaded (i.e. all \(K\) subcarriers are in use in all neighboring cells of the first tier of cells). We analyze this interference on BS–MS, BS–RS and RS–MS links and compute their CDFs. Using these CDFs, we determine the probability distribution of the number of subcarriers required on these three links.

We consider the rate requirement to be the same for all users. The blocking probability on each link is calculated and then overall blocking probability for relay based OFDMA network is determined.

3 Inter-Cell Interference Modeling

In this section, we consider a target MS (user) in the reference cell. We analyze the SIR experienced by the target MS on BS–MS link if it is associated with the BS and on BS–RS and RS–MS links, if it is associated with the RS. Then, we compute the CDF of SIR on these links following [15]. For this, we divide the incoming users into two groups,

Group 1: Users present in the base region are associated with the BS directly on BS–MS link. These users are called direct users.

Group 2: Users present in the relay regions are associated with the BS via the corresponding RS on BS–RS and RS–MS links. These users are called hopped users.

Note that we use the terms users and calls interchangeably in this paper.

3.1 SIR on BS–MS, BS–RS and RS–MS Transmission Links

Let \(\gamma _{BS-MS}\), \(\gamma _{BS-RS}\) and \(\gamma _{RS-MS}\) denote SIR on a subcarrier used on BS–MS, BS–RS and RS–MS links respectively. Then we have,

$$\begin{aligned} \gamma _{BS-MS}= & {} \frac{P_{BM} d_{BS-MS}^{-\beta } 10^{\frac{\xi _{BS-MS}}{10}}}{\sum _{i=1}^{N}P_{BM}d_{i BS-MS}^{-\beta } 10^{\frac{\xi _{i BS-MS}}{10}} }, \end{aligned}$$
(1)
$$\begin{aligned} \gamma _{BS-RS}= & {} \frac{P_{BR} d_{BS-RS}^{-\beta } 10^{\frac{\xi _{BS-RS}}{10}}}{\sum _{i=1}^{N}P_{BR} d_{i BS-RS}^{-\beta } 10^{\frac{\xi _{i BS-RS}}{10}} } \end{aligned}$$
(2)

and

$$\begin{aligned} \gamma _{RS-MS} = \frac{P_{RM} d_{RS-MS}^{-\beta } 10^{\frac{\xi _{RS-MS}}{10}}}{\sum _{i=1}^{N}P_{RM} d_{i RS-MS}^{-\beta } 10^{\frac{\xi _{i RS-MS}}{10}} }, \end{aligned}$$
(3)

where,

  • \(P_{BM}\), \(P_{BR}\) and \(P_{RM}\) denote the powers transmitted by BS to the target MS, BS to RS and RS to the target MS respectively.

  • \(d_{BS-MS}\), \(d_{BS-RS}\) and \(d_{RS-MS}\) denote the distances between the BS and the target MS present in the base region, BS and RS (with which the target MS is associated) and RS and the target MS present in any of the relay regions respectively.

  • \(d_{i BS-MS}\), \(d_{i BS-RS}\) and \(d_{i RS-MS}\) denote the distances between ith neighboring BS and the target MS (present in the base region), ith neighboring BS and RS (with which the target MS is associated) and ith neighboring RS and the target MS (present in any of the relay regions) respectively.

  • \(N\) is the number of interferers in the first tier of cells.

  • \(\xi _{BS-MS}\), \(\xi _{BS-RS}\) and \(\xi _{RS-MS}\) represent lognormal shadowing on BS–MS, BS–RS and RS–MS links. Each of them is a Gaussian random variable with mean 0 dB and standard deviations \(\sigma _{BS-MS}\), \(\sigma _{BS-RS}\) and \(\sigma _{RS-MS}\) dB respectively.

  • \(\xi _{i BS-MS}\), \(\xi _{i BS-RS}\) and \(\xi _{i RS-MS}\) represent lognormal shadowing on ith neighboring BS and target MS link, ith neighboring BS and RS link, and ith neighboring RS and target MS link. Each of them is a Gaussian random variable with mean 0 dB and standard deviations \(\sigma _{i BS-MS}\), \(\sigma _{i BS-RS}\) and \(\sigma _{i RS-MS}\) dB respectively.

3.2 CDF of SIR

In this section, we determine the mean and variance of interference to signal ratio \(I_{BS-MS}\) in two steps. In [16–18], it has been argued that the total interference power received from various interferers (in a universal frequency reuse system) can be modeled by lognormal distribution with some mean and variance. We make the same assumption here. Accordingly, we proceed to calculate the mean and variance of \(I_{BS-MS}\).

We rewrite Eq. 1 as,

$$\begin{aligned} \gamma _{BS-MS}= & {} \frac{1}{\sum _{i=1}^{N}\left( \frac{d_{i BS-MS}}{d_{BS-MS}}\right) ^{-\beta } 10^{\frac{\xi _{i BS-MS}-\xi _{BS-MS}}{10}}}= \frac{1}{I_{BS-MS}}. \end{aligned}$$

Step-1 Let \((0,0)\), \((x, y)\) and \((x_{i}, y_{i})\) be the coordinates of BS in the reference cell, target MS in the reference cell and ith interfering BS present in the first tier respectively.

\(I_{BS-MS}\) is grouped into two components, \(B_{i}\hbox {s}\) and \(C_{i}\hbox {s}\) as,

$$\begin{aligned} I_{BS-MS} = \sum _{i=1}^{N}B_{i} C_{i}, \end{aligned}$$
(4)

where, \(B_{i}= \left( \frac{d_{i BS-MS}}{d_{BS-MS}}\right) ^{-\beta }=\left[ \frac{(x-x_{i})^{2}+(y-y_{i})^{2}}{x^{2}+y^{2}}\right] ^{\frac{-\beta }{2}} \) and \(C_{i}=10^{\frac{\xi _{i BS-MS}-\xi _{BS-MS}}{10}}\).

\(B_{i}\) is the ratio of distances and is a function of the position \((x, y)\) of user in the reference cell. The position of target MS in the reference cell is random but the interfering BSs have fixed positions. Therefore, \(d_{i}\hbox {s}\) are correlated and as a result, \(B_{i}\hbox {s}\) are correlated RVs.

\(C_{i}\) is a ratio of two lognormal RVs, shadowing from ith interfering BS to the target MS and shadowing from the serving BS to the target MS. As suggested in [19], it can be approximated by a lognormal RV with mean 0 and variance \((\sigma _{i BS-MS}^{2} + \sigma _{ BS-MS}^{2})\). Thus, all \(C_{i}\hbox {s}\) are lognormal RVs but correlated. Note that lognormal shadowing \(\xi \) is independent of the position of the user. Hence, it is reasonable to also assume for \(B_{i}\) and \(C_{j}\) to be independent for any pair \((i,j)\).

We assume that,

$$E\left[ C_{i}\right] = E\left[ C_{j}\right] \quad \hbox { and} \quad E\left[ C_{i}C_{j}\right] = \hbox {constant},\quad \forall \,i \ne j.$$

The first and second moments of \(I_{BS-MS}\) are determined as,

$$E[I_{BS-MS}] = E\left[ C_{i}\right] E\left[ \sum _{i=1}^{N}B_{i}\right],$$
(5)
$$E\left[ I_{BS-MS}^{2}\right]= E\left[ C_{i}^{2}\right] E\left[ \sum _{i=1}^{N}B_{i}^{2}\right] + E\left[ C_{i}C_{j}\right] \left[ E\left( \sum _{i=1}^{N}B_{i}\right) ^{2} - E\left( \sum _{i=1}^{N}B_{i}^{2}\right) \right].$$
(6)

In Eqs. 5 and 6, computations of \(E[C_{i}]\), \(E[C_{i}^{2}]\) and \(E\left[ \sum _{i=1}^{N}B_{i}\right] \) are straightforward. \(E\left[ \sum _{i=1}^{N}B_{i}\right] ^{2}\) and \(E\left[ \sum _{i=1}^{N}B_{i}^{2}\right] \) are solved as follows,

Since the distances \(d_{i BS-MS}\hbox {s}\) between the target MS and ith interfering fixed BS are correlated, \(E\left[ \sum _{i=1}^{N}B_{i}\right] ^{2}\) can not be separated into a sum of terms. It is computed by averaging over the area as follows,

$$E\left[ \sum _{i=1}^{N}B_{i}\right] ^{2}= \dfrac{2}{3\sqrt{3}} \iint\limits_{x,y\in H_{0}}\left[ \sum _{i=1}^{N} \sqrt{\dfrac{(x-x_{i})^{2}+(y-y_{i})^{2}}{{x^{2}+y^{2}}}}^{ -\beta }\right] ^{2} dx dy.$$
(7)

Now, to compute \(E\left[ \sum _{i=1}^{N}B_{i}^{2}\right] \), expectation is taken over all possible positions \((x, y)\) the target MS can take in the base region. These integrals are evaluated separately for each interfering BS and then summed for all BSs to get \(E\left[ \sum _{i=1}^{N}B_{i}^{2}\right] \), as shown below,

$$\begin{aligned} E\left[ \sum _{i=1}^{N}B_{i}^{2}\right] = \sum _{i=1}^{N}E \left[ B_{i}^{2}\right] = \sum _{i=1}^{N}\frac{2}{3\sqrt{3}} \iint\limits_{x,y\in H_{0}}\left[ \frac{(x-x_{i})^{2}+(y-y_{i})^{2}}{x^{2}+y^{2}}\right] ^{-\beta } dx dy. \end{aligned}$$
(8)

Equations 7 and 8 can be solved numerically for hexagonal geometry.

Step-2 We have obtained first and second moments of \(I_{BS-MS}\) in Step-1 (Eqs. 5, 6). Its distribution can be approximated by lognormal distribution with parameters \((\mu _{I_{BS-MS}},\sigma _{I_{BS-MS}}^{2})\).

In general kth moment can be written as,

$$\begin{aligned} E\left[ I^{k}_{BS-MS}\right] = e^{k \mu _{I_{BS-MS}}+\frac{k^{2}}{2}\sigma ^{2}_{I_{BS-MS}}}. \end{aligned}$$
(9)

Using \(k = 1\) and 2 and on inverting, we obtain,

$$\begin{aligned} \mu _{I_{BS-MS}}= 2 ln E\left[ I_{BS-MS}\right] - \frac{1}{2} ln E\left[ I_{BS-MS}^{2}\right] \end{aligned}$$
(10)

and

$$\begin{aligned} \sigma _{I_{BS-MS}}^{2}= -2 ln E \left[ I_{BS-MS}\right] + ln E \left[ I_{BS-MS}^{2}\right] . \end{aligned}$$
(11)

Using Eqs. 10 and 11, we determine the distribution as,

$$\begin{aligned} F_{\mathbf {I_{\mathbf {BS-MS}}}}(x)= \Phi \left[ \frac{lnx- \mu _{I_{BS-MS}}}{\sigma _{I_{BS-MS}}}\right] ,\quad x > 0. \end{aligned}$$
(12)

Here \(\Phi (.)\) is the standard normal CDF. Note that \(x\) is log-normally distributed.

Similar calculations are performed to obtain the CDF of \(I_{BS-RS}\) and \(I_{RS-MS}\) on BS–RS and RS–MS links as,

$$\begin{aligned} F_{\mathbf {I_{\mathbf {BS-RS}}}}(x)= \Phi \left[ \frac{lnx- \mu _{I_{BS-RS}}}{\sigma _{I_{BS-RS}}}\right] ,\quad x > 0 \end{aligned}$$
(13)

and

$$\begin{aligned} F_{\mathbf {I_{\mathbf {RS-MS}}}}(x)= \Phi \left[ \frac{lnx- \mu _{I_{RS-MS}}}{\sigma _{I_{RS-MS}}}\right] ,\quad x > 0. \end{aligned}$$
(14)

Thus, we have determined the distribution of interference to signal ratio on a subcarrier on the three transmission links, i.e. BS–MS, BS–RS and RS–MS links.

4 Analytical Model to Determine Resource Requirement Based on CDF of SIR

In cellular OFDMA network, an incoming user is allocated a certain number of sub-carriers to satisfy its rate requirement. In our formulation, we consider that all incoming users have the same rate requirement R. Due to different SIR experienced by the users, they will require different number of subcarriers (Table 1).

Table 1 List of notations used in Sects. 4 and 5
Full size table

The objective of BS is to satisfy the rate requirement of each user, by allocating it the requested number of subcarriers which depends upon its experienced SIR. There are \(K_{BS}\) orthogonal subcarriers available at the BS, each of bandwidth W Hz.

Let, \(\gamma ^{m}_{BS-MS}\) be the SIR experienced by a user while using mth subcarrier on BS–MS link. Then, the rate R achieved using M number of subcarriers on BS–MS link is given by,

$$\begin{aligned} R= W \sum _{m=1}^{{M}}log_{2} \left( 1+\gamma ^{m}_{BS-MS}\right) . \end{aligned}$$
(15)

Since no frequency dependent fast fading is considered (Sect. 2), SIR on each subcarrier is same, i.e. \(\gamma ^{1}_{BS-MS}=\gamma ^{2}_{BS-MS} \ldots \gamma ^{M}_{BS-MS} = \gamma _{BS-MS} \), the number of subcarriers (M) required by any user can be expressed as,

$$\begin{aligned} M = \frac{R \cdot log_{10}(2)}{W \cdot log_{10}\left( 1+\gamma _{BS-MS} \right) }. \end{aligned}$$
(16)

Now, we distinguish users based on their subcarrier requirement as follows. We divide the entire interference to signal ratio \(I_{BS-MS}\) (determined in Sect. 3.2) range into \(l+1\) non-overlapping consecutive intervals with boundaries denoted by \(\left\{ I^{r}_{BS-MS}\right\} _{r=1}^{l+1}\). For each new user on BS–MS link, when the received interference to signal ratio \(I_{BS-MS}\) falls in the range \(I_{BS-MS}\in \left[ I^{r}_{BS-MS}, I^{r+1}_{BS-MS}\right] \), then user is considered to be in class r. As r lies in the range \((1,\ldots ,l+1)\) the highest possible class of a user will be \(l\) when \(I_{BS-MS}\) falls in the range \(I_{BS-MS}\in \left[ I^{l}_{BS-MS}, I^{l+1}_{BS-MS}\right] \).

Let \(M^{r}\) denote the number of subcarriers required by the class r user on that link. In the present case, we have \(M^r = r\). Let \(A = \frac{R}{W}log_{10}\left( 2\right) \). Then, Eq. 16 can be re-written as,

$$\begin{aligned} I^{r}_{BS-MS} = \left( 10^{\frac{A}{M^{r}}}-1\right) ^{-1}. \end{aligned}$$
(17)

Note that Eq. 17 is used to determine the interference boundaries by assigning the number of subcarriers \(M^r = 1, 2, \ldots ,l\) to each rth interval \((r = 1,\ldots , l)\). Thus, for each interval \((r = 1, \ldots , l)\) and the assigned number of subcarriers \((M^r = 1, 2,\ldots ,l)\), the interference boundaries are determined.

Let, \({\mathbb {P}}_{BS-MS}\left( {M^{r}}\right) \) denote the probability that an incoming user belongs to class r and requires \(M^{r}\) number of subcarriers on BS–MS link to meet its rate requirement. It is determined as,

$$\begin{aligned} {\mathbb {P}}_{BS-MS} \left( {M^{r}}\right)&= {\mathbb {P}}\left[ I^{r}_{BS-MS}< I_{BS-MS}< I^{r+1}_{BS-MS}\right] \\&= F_{\mathbf {I_{BS-MS}}}\left( I^{r+1}_{BS-MS}\right) - F_{\mathbf {I_{BS-MS}}}\left( I^{r}_{BS-MS}\right) . \end{aligned}$$
(18)

where \(F_{\mathbf {I_{BS-MS}}}\left( I^{r}_{BS-MS}\right) \) is the CDF of interference to signal ratio (Eq. 12) on BS–MS link. Similar calculations are performed to determine the probability that user belongs to class r and requires \(M^r\) subcarriers on BS–RS and RS–MS links. They are denoted by \({\mathbb {P}}_{BS-RS}\left( {M^{r}}\right) \) and \({\mathbb {P}}_{RS-MS}\left( {M^{r}}\right) \) respectively.

5 Analysis of Blocking Probability

For a relay based cellular OFDMA network, we have two types of incoming calls (as mentioned in Sect. 3): direct and hopped calls. Let, \(N_{D}\) and \(N_{H}\) be the number of classes of direct calls and hopped calls respectively. Let, \(n\) and \(h\) denote the class of direct and hopped calls where \(n = 1, \ldots , N_{D} \) and \(h = 1, \ldots , N_{H} \). Let \(M^{n}_{D}\), \(M^{h}_{H BR}\) and \(M^{h}_{H RM}\) denote the number of subcarriers required by class \(n\) of direct calls and class \(h\) of hopped calls on BS–MS, BS–RS and RS–MS links respectively such that, \(M^{h}_{H} = M^{h}_{H BR} + M^{h}_{H RM}\). Note that \(M^{h}_{H}\) denotes the total subcarriers required by the class \(h\) user of the hopped call. Let \( {\mathbb {P}}_{BS-MS}\left( M_{D}^{n}\right) \), \({\mathbb {P}}_{BS-RS}\left( M_{HBR}^{h}\right) \) and \({\mathbb {P}}_{RS-MS}\left( M_{HRM}^{h}\right) \) denote the probability that \(M^{n}_{D}\), \(M^{h}_{H BR}\) and \(M^{h}_{H RM}\) number of subcarriers are required on BS–MS, BS–RS and RS–MS links respectively. These probabilities are evaluated as illustrated in Eq. 18 in Sect. 4.

To admit a direct call, the required number of subcarriers should be available at the BS. However, to accomodate a hopped call, the required number of subcarriers should be available at BS as well as at RS. Thus, a direct call implies the arrival of one call on BS–MS link and a hopped call implies arrival of one call each on BS–RS and RS–MS linkFootnote 1. In this section, we determine the blocking probability of users belonging to direct and hopped calls.

We assume that call arrivals in each cell are Poisson distributed with mean arrival rate \(\lambda \). Let, a fraction of the total call arrivals, say \(f\) be served directly by BS, then the arrival rate of direct calls is \(\lambda _{D} = f\lambda \) and that of hopped calls is \(\lambda _{H} = (1-f) \lambda \). The service times of each class of direct and hopped calls are exponentially distributed with mean \(\frac{1}{\mu }\). From the assumption of uniform distribution of users, hopped calls are equally distributed across the six RSs in the cell. Thus, the arrival rate of hopped calls in the coverage area of each RS is \(\lambda _{H}/6\). Let, \({\mathbb {P}}_{B_{D}}\) and \({\mathbb {P}}_{B_{H}}\) be the blocking probability of direct and hopped calls respectively. Then, the overall call blocking probability is given by,

$$\begin{aligned} {\mathbb {P}}_{B}= f{\mathbb {P}}_{B_{D}}+ (1-f){\mathbb {P}}_{B_{H}}. \end{aligned}$$
(19)

A direct call is blocked if the required number of subcarriers is not available at the BS and a hopped call is blocked if the required number of subcarriers is not available at any of the two i.e. BS or RS. We define the state of the system to be

$$\begin{aligned} {\mathbf {S}} = \left( M^{1}_{D}U^{1}_{D},\ldots ,M^{n}_{D} U^{n}_{D}, \ldots , M^{N_D}_{D} U^{N_{D}}_{D}, M^{1}_{H}U^{1}_{H},\ldots ,M^{h}_{H} U^{h}_{H},\ldots ,M^{N_{H}}_{H} U^{N_{H}}_{H}\right) , \end{aligned}$$
(20)

where \(U^{n}_{D}\) and \(U^{h}_{H}\) are the number of users in nth class of direct calls and hth class of hopped calls respectively.

These system states can be modeled by discrete time \(N_{D}+N_{H}\) dimensional Markov chain. The state space is finite and meets the following constraints-

$$\begin{aligned}&\sum _{n=1}^{N_D} M^{n}_{D}U^{n}_{D}+\sum _{h=1}^{N_{H}} M^{h}_{HBR}U^{h}_{H} + \sum _{h=1}^{N_{H}} M^{h}_{HRM}U^{h}_{H} \le K_{BS}+ 6K_{RS}, \end{aligned}$$
(21)
$$\begin{aligned}&\sum _{n=1}^{N_D} M^{n}_{D}U^{n}_{D}+\sum _{h=1}^{N_{H}} M^{h}_{HBR}U^{h}_{H} \le K_{BS}, \end{aligned}$$
(22)
$$\begin{aligned}&\sum _{h=1}^{N_{H}} M^{h}_{HRM}U^{h}_{H} \le K_{RS}, \quad \forall \,\text {RSs}, \end{aligned}$$
(23)
$$\begin{aligned}&U^{n}_{D} \ge 0 \quad \text {and} \quad U^{h}_{H} \ge 0. \end{aligned}$$
(24)

The constraint in Eq. 21 gives an upper bound on the number of subcarriers available for allocation on the three links. The total number of subcarriers available at the BS and the corresponding RS gives an upper bound on the number of subcarriers that can be used in the system. The number of subcarriers available at the BS gives an upper bound on the number of subcarriers that can be used by direct calls on BS–MS link and hopped calls on BS–RS link (Eq. 22). Similarly, the number of subcarriers available at the RS gives an upper bound on the number of subcarriers that can be used by hopped calls on RS–MS link (Eq. 23). In the system there can be either no user or a finite non-negative number of users on each link (Eq. 24).

Example 1

For illustration, let us consider only one class of each call say, class 2 of direct call (i.e., \(M^{2}_{D}=2\)) and class 3 of hopped call (i.e., \(M^{3}_{H}=3\)). Let \(K_{BS}=10\) and \(K_{RS}=6\). The number of subcarriers for hopped call \((M^{3}_{H}=3)\) is the sum of subcarriers required on BS–RS and RS–MS links. Note that BS–RS and RS–MS links may require either \( M^{3}_{HBR}=1\) and \( M^{3}_{HRM}=2\) or \( M^{3}_{HBR}=2\) and \( M^{3}_{HRM}=1\) depending on the SIR experienced on each link. Thus, there are two possible combinations of subcarrier requirement for a hopped call on BS–RS and RS–MS links i.e. \((1,2)\) and \((2,1)\). Let, \({\mathbb {P}}_{H}\left( M^{3}_{H}\right) \) denote the probability that \(M^{3}_{H}\) number of subcarriers are required by a hopped call. Then we have,

$$\begin{aligned} {\mathbb {P}}_{H}\left( M^{3}_{H}=3\right) = {\mathbb {P}}_{BS-RS}\left( 1\right) {\mathbb {P}}_{RS-MS}\left( 2\right) +{\mathbb {P}}_{BS-RS}\left( 2\right) {\mathbb {P}}_{RS-MS}\left( 1\right) . \end{aligned}$$
(25)

The arrival rates of hopped calls of class \(3\,(\lambda ^{3}_{H}\)) and direct calls of class \(2\,(\lambda ^{2}_{D})\) are given by,

$$\begin{aligned} \lambda ^{3}_{H}= & {} \lambda _{H}{\mathbb {P}}_{H}\left( M^{3}_{H}=3\right) , \\ \lambda ^{2}_{D}= & {} \lambda _{D}{\mathbb {P}}_{BS-MS}\left( M^{2}_{D}=2\right) . \end{aligned}$$
(26)

The states of the system are represented by the two dimensional Markov chain in Fig. 2. Each state corresponds to the number of subcarrier required by direct calls and hopped calls. There are various combinations of subcarriers that may be required on BS–RS and RS–MS links for a hopped call.

Fig. 2
figure 2

Two-dimensional state transition diagram for a system with \(K_{BS}=10\), \(K_{RS}=6\), \(M^{1}_{D}=2\) and \(M^{1}_{H}=3\). Each call has only one class

Full size image

The different combinations of subcarrier requirement for the first row of Markov chain in Fig. 2 denotes the case, when only users of hopped call are present. It is further illustrated in Fig. 3, where the state representation is modified to indicate the number of subcarriers required for hopped calls on BS–RS and RS–MS links distinctly.

Fig. 3
figure 3

Illustration of various possible combinations of the number of subcarriers required on BS–RS and RS–MS links for a hopped call for a system with \(K_{BS}=10\), \(K_{RS}=6\), \(M^{1}_{D}=2\) and \(M^{1}_{H}=3\)

Full size image

At any instant of time, the number of calls present in the system using various combination of subcarriers can be found by traversing a path as shown with dotted lines in Fig. 3. Similar combinations of subcarrier requirement of hopped calls with direct calls present in the system can be obtained for various rows of Markov chain of Fig. 2.

As mentioned in Example 1, when a hopped call with \(M^3_H=3\) arrives in the system, it requires either of the combinations \((1,2)\) or \((2,1)\) subcarriers on BS–RS and RS–MS links. This hopped call is blocked when the required number of subcarriers are unavailable at either BS or RS. Observing the dotted lines in Fig. 3, it becomes clear that after allocating the resources to user 5, BS is left with 1 subcarrier for new allocation on BS–RS link and RS has no subcarriers left for further allocation on RS–MS link and blocking occurs. The notation \((2,1,1,1,1)\) indicates that subcarriers \(2,1,1,1,1\) are being used by different hopped calls on RS–MS link. Similarly, other combinations of states leading to blocking state are shown in Fig. 3. This implies that there can be at most 5 users of hopped calls in this example.

As can be noticed from this example, determining the set of all possible states which satisfy the given constraints for a single class of each call is complex. As the number of classes and the number of subcarriers at BS and RS increase, the size of the state space increases and it becomes very difficult to determine all possible combinations. This complexity is due to two reasons: a) State space consists of the number of subcarriers required for the calls of all classes on all the three links and b) The states on BS–MS and BS–RS links are interrelated because BS has to use the available \(K_{BS}\) subcarriers for allocation to both direct call and hopped calls.

To simplify the computational complexity, we consider the calls served by BS and RS as separate systems as both have distinct set of subcarriers. We also consider that for a hopped call, the required number of subcarriers are allocated by BS on BS–RS link and by RS on RS–MS link. Allocation of subcarriers to a hopped user on BS–RS and RS–MS links by BS and RS separately enables decoupling of the state space of BS and RS. With this consideration, we determine the blocking probability in base and relay regions separately in the following subsections. The sum of blocking probability of calls in base region and relay region is an approximation to the overall blocking probability. We verify the validity of this approximation through Monte-Carlo simulations.

5.1 Blocking for Users present in Relay Region (Hopped Calls)

When a user is in any of the relay regions and experiences SIR \(\gamma _{BS-RS}\) and \(\gamma _{RS-MS}\) on BS–RS and RS–MS link, it requires \(M^{h}_{HBR}\) number of subcarriers with probability \({\mathbb {P}}_{BS-RS}(M^{h}_{HBR})\) and \(M^{h}_{HRM}\) number of subcarriers with probability \({\mathbb {P}}_{RS-MS}(M^{h}_{HRM})\). The availability of subcarriers on both the links i.e. BS–RS and RS–MS links is determined. If subcarriers are available on both the links, \(M^{h}_{HBR}\) and \(M^{h}_{HRM}\) subcarriers are allocated by BS and RS. Otherwise, the incoming user is blocked. In other words, blocking occurs when either \(M^{h}_{HBR}\) number of subcarriers are unavailable on BS–RS link or \(M^{h}_{HRM}\) number of subcarriers are unavailable on RS–MS link.

Let, \({\mathbb {P}}_{B_{HBR}}\) and \({\mathbb {P}}_{B_{HRM}}\) be the blocking probability of hopped call on BS–RS and RS–MS links respectively. Then, the average blocking probability of hopped calls \(({\mathbb {P}}_{B_{H}})\) is given as,

$$\begin{aligned} {\mathbb {P}}_{B_{H}}=1-\left( 1- {\mathbb {P}}_{B_{HBR}}\right) \left( 1-{\mathbb {P}}_{B_{HRM}}\right) . \end{aligned}$$
(27)

In this subsection, we determine \({\mathbb {P}}_{B_{HRM}}\) and in the next subsection we will determine \({\mathbb {P}}_{B_{HBR}}\).

There are \(N_{H}\) classes of hopped calls on RS–MS link, each requiring \(M^{h}_{HRM}\) subcarriers. The arrival rate of each hth class of these calls at RS is \(\lambda ^{h}_{H} = \lambda _{H} {\mathbb {P}}_{RS-MS}(M^{h}_{HRM})\). Let the service time for all classes of call be exponentially distributed with mean service time \(\frac{1}{\mu }\). Then, the offered load for hth class on RS–MS link is \(\rho _{h} = \frac{\lambda ^{h}_{H}}{\mu }\). It is assumed that after completion of a call, the subcarriers are released by the user on both the links and they become available for use at both BS and RS.

We define the state of serving RS as,

$$\begin{aligned} \Omega _{RS} = \left( M^{1}_{HRM}U^{1}_H,M^{2}_{HRM}U^{2}_H,\ldots , M^{h}_{HRM}U^{h}_H,\ldots , M^{N_H}_{HRM}U^{N_H}_H\right) , \end{aligned}$$
(28)

where \(U^{h}_H\) is the number of users of hopped calls of hth class and \(M^{h}_{HRM}\) is the number of subcarriers required by this hopped call of hth class. Any class of hopped call is said to be blocked, when all subcarriers \(K_{RS}\) are in use. Therefore, the states of the system are modeled by \(N_{H}\) dimensional Markov chain. The state space is finite and meets the following constraints-

$$\begin{aligned} \sum _{h=1}^{N_{H}} M^{h}_{HRM}U^{h}_H \le K_{RS}, \quad U^{h}_H \ge 0 \quad \text { and } \quad 1 \le h \le N_{H}. \end{aligned}$$
(29)

Example 2

Let us consider \(K_{RS}=4\) subcarriers and \(N_{H}=2\) classes of hopped users. Let the users require \(M^1_{HRM}=1\) subcarrier with probability \({\mathbb {P}}_{RS-MS}(M^{1}_{HRM})=0.6\) and \(M^2_{HRM}=2\) subcarriers with probability \({\mathbb {P}}_{RS-MS}(M^{2}_{HRM})=0.4\). Thus, the arrival rate of class-1 users is \((\lambda _{H}^{1}) = 0.6\lambda \) and that of class-2 is \((\lambda _{H}^{2}) = 0.4\lambda \). The states of the system are denoted by \((M^{1}_{HRM}U^{1}_H,M^{2}_{HRM}U^{2}_H)\). The state transition diagram is shown in Fig. 4. Under the assumption of statistical equilibrium, the state probabilities are obtained by solving the global balance equations for each state.

Let us consider any four interconnected states in Fig. 4. If the flow in clockwise direction equals the flow in the opposite direction, then the process is said to be reversible [14], which is illustrated below. Let, \(p(M^{1}_{HRM}U^{1}_H,M^{2}_{HRM}U^{2}_H) = p(1,2)\) denotes the state probability, i.e., the probability with which the total number of subcarriers used by class-1 and class-2 users on RS–MS link turn out to be 1 and 2 respectively. Then, from Fig. 4, we have,

Clockwise:

$$\begin{aligned} p(1,2) \cdot \mu \cdot p(1,0)\cdot \lambda _{H}^{1} \cdot p(2,0) \cdot \lambda _{H}^{2} \cdot p(2,2)\cdot 2\mu . \end{aligned}$$

Anticlockwise:

$$\begin{aligned} p(1,2) \cdot \lambda _{H}^{1} \cdot p(2,2)\cdot \mu \cdot p(2,0) \cdot 2\mu \cdot p(1,0)\cdot \lambda _{H}^{2}. \end{aligned}$$
Fig. 4
figure 4

Two-dimensional state transition diagram for a system with \(K_{RS}=4\) and \(N_{H}=2\). Incoming users are divided into two classes

Full size image

If these two expressions are equal, then the process is said to be reversible [14].

We can express any state probability, say \(p(M^{1}_{HRM}U^{1}_H, M^{2}_{HRM}U^{2}_H)\) in terms of \(p(0,0)\) by choosing any path between the two states, \(p(0,0)\) and the state itself, i.e., \(p(M^{1}_{HRM}U^{1}_H, M^{2}_{HRM}U^{2}_H)\) (Kolmogorov’s criteria [21]).

In Fig. 4, \(p(2,2)\) can be obtained by choosing the path: \((0,0)\), \((0,2)\), \((1,2)\) and \((2,2)\), and we obtain the following equation,

$$\begin{aligned} p(2,2)= & {} \frac{1}{2!} \left( \frac{\lambda _{H}^{1}}{\mu }\right) ^2 \cdot \frac{\lambda _{H}^{2}}{\mu } \cdot p(0,0) \\= & {} \frac{(\rho _{1})^{2}}{2!} \cdot \frac{(\rho _{2})^{1}}{1!} \cdot p(0,0). \end{aligned}$$
(30)

Thus, there are two users of class 1 and one user of class 2 and this state probability has product form. Similarly, Kolmogorov’s criteria is applicable to a system with \(N_{H}\) classes, and the state probabilities in \(N_{H}\) dimensional system will have product form [14].

Let, \({\mathbb {P}}_{\Omega _{RS}}\) be the probability that the system is in state \(\Omega _{RS}\). Since all the states are reversible following [14], applying the results from [14], the solution is given in the standard product form as,

$$\begin{aligned} {\mathbb {P}}_{\Omega _{RS}} = \frac{ \prod _{h=1}^{N_{H}} \frac{\rho _h^{U^h_H}}{{U^h_H}!}}{\sum _{\Omega _{RS}} \prod _{h=1}^{N_{H}} \frac{\rho _h^ {U^h_H}}{{U^h_H}!}}. \end{aligned}$$
(31)

Let, \(\Omega _{h}\) be the set of states in which an incoming hopped call on RS–MS link of either class is blocked. It is represented as,

$$\begin{aligned} \Omega _{h} := \left\{ \Omega _{h}\in \Omega _{RS} : \sum _{h=1}^{N_{H}} M^{h}_{HRM}U^{h}_H > K_{RS} \right\} . \end{aligned}$$
(32)

In Fig. 4, the states in which an incoming user of class-1 will be blocked are \(\{(4,0)\), \((2,2)\) and \((0,4)\}\). The sum of the probabilities of these states is equal to the blocking probability for class-1. Similarly, the states in which an incoming user of class-2 will be blocked are \(\{(3,0)\), \((1,2)\) and \((0,4)\}\). The sum of the probabilities of these states is equal to the blocking probability for class-2. The above illustration makes it clear that the blocking probability for any class can be obtained by summing the probabilities of all those states in which an incoming user of that class will be blocked.

In general, for a relay based cellular OFDMA system with \(N_{H}\) classes, the blocking probability for hopped call of hth class on RS–MS link is given by,

$$\begin{aligned} {\mathbb {P}}^{h}_{B_{HRM}}= & {} \sum _{\Omega _{h}}{\mathbb {P}}_{\Omega _{RS}}= \sum _{\Omega _h} \frac{ \prod _{h=1}^{N_{H}} \frac{\rho _h^{U^h_H}}{{U^h_H}!}}{\sum _{\Omega _{RS}} \prod _{h=1}^{N_{H}} \frac{\rho _h^ {U^h_H}}{{U^h_H}!}}. \end{aligned}$$
(33)

The average blocking probability for hopped calls on RS–MS link is given by,

$$\begin{aligned} {\mathbb {P}}_{B_{HRM}} = \sum _{h=1}^{N_{H}}{\mathbb {P}}^{h}_{B_{HRM}} {\mathbb {P}}_{RS-MS}\left( M^{h}_{HRM}\right) . \end{aligned}$$
(34)

In the next sub-section, we determine the blocking probability of direct calls.

5.2 Blocking for Users Present in Base Region (Direct Calls)

When a user is in base region and experiences SIR \(\gamma _{BS-MS}\), it requires \(M^{n}_{D}\) number of subcarriers with probability \({\mathbb {P}}_{BS-MS}(M^{n}_{D})\). The availability of subcarriers is determined at BS. If they are available, then \(M^{n}_{D}\) subcarriers are allocated by the BS. However \(K_{BS}\) subcarriers are also shared by hth class of hopped call on BS–RS link, each of which requires \(M^{h}_{HBR}\) subcarriers. Thus, there are \(N_{D}\) and \(N_{H}\) classes of direct calls on BS–MS link and hopped calls on BS–RS link respectively. The arrival rate of nth class of direct calls is \(\lambda ^{n}_{D}=\lambda _{D}{\mathbb {P}}_{BS-MS}(M^{n}_{D})\) and hth class of hopped calls is \(\lambda ^{h}_{HBR}=\lambda _{H}{\mathbb {P}}_{BS-RS}(M^{h}_{HBR})\).

We define the state of BS as,

$$\begin{aligned} \Omega _{BS} = \left( M^{1}_{D}U^{1}_{D},M^{2}_{D}U^{2}_{D},\ldots , M^{N_{D}}_{D} U^{N_{D}}_{D}, M^{1}_{HBR}U^{1}_{H},M^{2}_{HBR}U^{2}_{H},\ldots , M^{N_{H}}_{HBR} U^{N_{H}}_{H}\right) , \end{aligned}$$
(35)

where \(U^{n}_{D}\) is the number of direct users of nth class and \(U^{h}_{H}\) is the number of hopped users of hth class. If the number of subcarriers required by any class of direct call and hopped call on BS–RS link is same, then for BS both the calls belong to the same class, irrespective of whether it is a direct or a hopped call. Thus, the state of BS can be modified as, \(\Omega _{BS} = (M^{m}_{BS}U^{m}_{BS})\) where \(m = 1,\ldots ,\, \max (N_{D},N_{H})\), denoting the class of users arriving at the BS. \(M^{m}_{BS}\) denotes the subcarrier required by mth class user and \(U^{m}_{BS}\) denotes the number of users of mth class arriving at the BS.

It is possible that some hopped calls get the required number of subcarriers on BS–RS link but not on RS–MS link. This is accounted by multiplying \(\lambda _{H}\) by a discount factor \(1-{\mathbb {P}}_{B_{HRM}}\). Let, the arrival rate of all calls at the BS be \(\lambda _{BS}\). Then, the arrival rate of class m call at BS will be, \(\lambda _{BS}^{m}=\lambda _{D}^{m} + (1-{\mathbb {P}}_{B_{HRM}}^{m})\lambda _{H}^{m}\). The service time for all classes of calls at BS is exponentially distributed with mean service time \(\frac{1}{\mu }\). Then, the offered load for class m call at BS is \(\rho _{m} = \frac{\lambda _{BS}^{m}}{\mu }\).

Any class of calls (direct or hopped calls) at BS is said to be blocked, when all subcarriers \(K_{BS}\) are in use. Therefore, the states of the system are represented by \(\max (N_{D},N_{H})\) dimensional Markov chain. The state space is finite and the constraints to be met are,

$$\begin{aligned} \sum _{m=1}^{\max (N_D,N_H)} M^{m}_{BS}U^{m}_{BS} \le K_{BS},\quad U^{m}_{BS} \ge 0, \quad 1 \le m \le \max (N_{D},N_{H}). \end{aligned}$$
(36)

Let, \({\mathbb {P}}_{\Omega _{BS}}\) be the probability that the system is in state \(\Omega _{BS}\). Since all the states are reversible [14], applying the results from [14], the solution is given in the product form as,

$$\begin{aligned} {\mathbb {P}}_{\Omega _{BS}} = \frac{\prod _{m=1}^{\max (N_{D},N_{H})}\frac{(\rho _{m})^{U^{m}_{BS}}}{U^{m}_{BS}!}}{\sum _{\Omega _{BS}}\prod _{m=1}^{\max (N_{D},N_{H})}\frac{(\rho _{m})^{U^{m}_{BS}}}{U^{m}_{BS}!}}. \end{aligned}$$
(37)

Let, \(\Omega _{m}\) be the set of those states in which an incoming direct call or hopped call at BS of any class is blocked. It is represented as,

$$\begin{aligned} \Omega _{m} := \left\{ \Omega _{m} \in \Omega _{BS}: \sum _{m=1}^{\max (N_D,N_H)} M^{m}_{BS}U^{m}_{BS} > K_{BS}\right\} . \end{aligned}$$
(38)

Therefore, the blocking probability for mth class user at BS is given by,

$$\begin{aligned} {\mathbb {P}}^{m}_{B_{BS}}= & {} \sum _{\Omega _{m}}{\mathbb {P}}_{\Omega _{BS}} \\= & {} \sum _{\Omega _m}\frac{ \prod _{m=1}^{\max (N_{D},N_{H})} \frac{(\rho _{m})^{U^{m}_{BS}}}{U^{m}_{BS}!}}{\sum _{\Omega _{BS}} \prod _{m=1}^{\max (N_{D},N_{H})} \frac{(\rho _{m})^{U^{m}_{BS}}}{U^{m}_{BS}!}}. \end{aligned}$$
(39)

The average blocking probability for direct calls on BS–MS link \(({\mathbb {P}}_{B_{D}})\) and hopped calls on BS–RS link \(({\mathbb {P}}_{B_{HBR}})\) is given by,

$$\begin{aligned} {\mathbb {P}}_{B_{D}}= & {} \sum _{m=1}^{N_{D}}{\mathbb {P}}^{m}_{B_{BS}} {\mathbb {P}}_{BS-MS}(M^{m}_{D}), \\ {\mathbb {P}}_{B_{HBR}}= & {} \sum _{m=1}^{N_{H}}{\mathbb {P}}^{m}_{B_{BS}} {\mathbb {P}}_{BS-RS}(M^{m}_{HBR}). \end{aligned}$$
(40)

Thus, from Eqs. 19, 27, 34 and 40, we can determine the overall blocking probability of the system.

6 Results and Discussions

6.1 Comparison of Analytical and Simulation Results

In this section, we illustrate the results based on the analytical models developed in the previous sections and present validation of the analytical results using Monte-Carlo simulations. We consider the downlink of relay assisted OFDMA network. The values of system parameters chosen for the analysis are as per the LTE standard [22] and are given in Table 2. We perform the analysis considering four rate requirement—64, 128, 256 and 1024 Kbps.

Table 2 Parameters for numerical analysis
Full size table

The simulation procedure consists of modeling a snapshot of location of users (calls), their arrival and departure times in the reference cell as well as neighboring cells. The user can be located either in the base region or relay region of a cell. We generate a fraction \((f)\) of the total calls in the base region and remaining in the relay region. The call arrivals are Poisson distributed with rate \(\lambda \) and holding times are exponentially distributed with mean \(\frac{1}{\mu }\) in all cells. Available subcarriers \(K\) are shared between BS and six RSs.

For every new call arrival, we check the association of user with base region or relay region. Based on this association, a call is termed as direct call or hopped call. Accordingly, we evaluate the SIR experienced by that call on BS–MS link (or BS–RS and RS–MS links). We consider the random subcarrier allocation scheme on all the three transmission links. For a direct (hopped) call on BS–MS link (BS–RS and RS–MS links), one subcarrier is randomly chosen from the available subcarriers, i.e., the unused subcarriers from the total of \(K_{BS}\) for BS and \(K_{RS}\) for RS. Then, it is checked whether the user’s rate requirement is satisfied, that is whether \(\log _{2}(1+\gamma _{BS-MS})\) for that subcarrier is greater than or equal to the required rate \((R_{req})\). If not, BS or RS continues to add randomly chosen subcarriers until the total achievable rate becomes greater or equal to \(R_{req}\). If the available set of subcarriers can not meet the rate requirement, the call is blocked. Note that a hopped call is blocked if the required number of subcarriers is not available on either of the links. We consider that the set of allocated subcarriers to the user is utilized for the entire duration of the call. After the completion of call, the subcarriers are released by the user and they become available for use simultaneously at both BS and RS. At this point, the processing of one snapshot is complete and another snapshot is continued. Simulation is performed over such 10,000 independent snapshots. From these simulations, we determine the probability distribution of the number of subcarriers required on each of the links.

Figures 5 and 6 illustrate the probability of number of subcarriers required (evaluated in Eq. 18) for four different data rates on BS–MS and BS–RS link respectively. It is the probability of a call belonging to a certain class. The probability of a call belonging to lower class is more on BS–RS link due to line of sight path and lesser impact of shadowing. From these two figures, we observe that the number of subcarriers required changes with the change in rate requirement (R). For lower R, less number of subcarriers are required and therefore, majority of users will belong to lower classes. For example, in Fig. 5, for \(R=64\) Kbps, the probability of a call belonging to a class between 1 and 15 is non-zero, and the probability of a call belonging to higher classes is close to zero. Similarly, for high R, say \(R=1024\) kbps, there are effectively no users that require less number of subcarriers.

Fig. 5
figure 5

Probability of the number of subcarriers required (i.e. class) for varying rate requirements on BS–MS link (subcarrier \(\hbox {BW} = 15\,\hbox {KHz}\))

Full size image
Fig. 6
figure 6

Probability of the number of subcarriers required (i.e. class) for varying rate requirements on BS–RS link (subcarrier \(\hbox {BW} = 15\,\hbox {KHz}\))

Full size image

Figures 7 and 8 illustrate the impact of rate requirement on the blocking probability (evaluated in Eq. 19). We consider two cases: (1) \(K_{BS}=480\) and \(K_{RS}=30\) and (2) \(K_{BS}=240\) and \(K_{RS}=15\). This corresponds to subcarrier bandwidth of 15 and 30 KHz respectively. We observe that increasing the subcarrier bandwidth results in an increase in the blocking probability. It is because when the subcarrier bandwidth is more, the total number of subcarriers available in the system reduces. In this case, even though a user may meet its rate requirement with fewer number of subcarriers, the overall blocking probability is likely to increase. Similar observation can be made from Fig. 9 where the blocking probability is computed for three different subcarrier bandwidth, 15, 30 and 60 KHz, for fixed rate requirement of 1024 Kbps.

Fig. 7
figure 7

Impact of rate requirement on blocking probability when subcarrier \(\hbox {BW} = 15\,\hbox {KHz}\) (number of classes for \(256\,\hbox {Kbps} = 15\), number of classes for 512 and \(1024\,\hbox {Kbps} = 31\))

Full size image
Fig. 8
figure 8

Impact of rate requirement on blocking probability when subcarrier \(\hbox {BW} = 30\,\hbox {KHz}\) (number of classes for \(256\,\hbox {Kbps} = 15\), number of classes for 512 and \(1024\,\hbox {Kbps} = 31\))

Full size image
Fig. 9
figure 9

Variation in blocking probability with change in subcarrier BW for a given rate requirement =1024 Kbps and number of classes =31

Full size image

From Figs. 7 and 8, we also observe that irrespective of the subcarrier bandwidth, the blocking probability is influenced by the rate requirement of users. As the rate requirement of users increases, they will require more number of subcarriers and therefore, blocking probability increases. For the simulations, we count the number of times an incoming call is blocked and plot the blocking probability of the system. We observe a good agreement between analytical and simulation results.

As an intuitive insight, when the subcarrier bandwidth is high, the blocking probability is influenced by the number of users belonging to lower classes and higher classes. If majority of users belong to lower classes, then the subcarrier bandwidth will result in an allocation which will be much more than their requirement, leading to an inefficient resource utilization and hence, increase in blocking probability. On the other hand, if majority of users belong to higher classes, then they will quench their resource requirement in fewer resources and blocking probability is likely to reduce. However, in general when the probability that a user belongs to a higher or a lower class (i.e., the number of subcarriers required by user of a class is more or less) is equal, an increase in the subcarrier bandwidth will reduce the number of resources available in the system and hence there will be an increase in the blocking probability.

6.2 Comparison of Non-relay System with Relay-Based OFDMA Network Through Simulations

Figure 10a, b illustrates the impact of rate requirement on blocking probability for two cases: cellular OFDMA network without and with relays for subcarrier bandwidth of 15 KHz, i.e., \(K_{BS}=480\) and \(K_{RS}=30\). There are two common observations in both figures. First, as the arrival rate increases, there is an increase in the blocking probability. Second, for the same arrival rate, number of subcarrier required is more when the data rate is high compared to the case when data rate is low. We understand that the increase in number of subcarriers required directly impacts the blocking probability. However, this difference in blocking probability for different data rates is not very evident when the arrival rates are low. Comparing the two results, we observe that when arrival rate is low and data rate is high, blocking probability in relay-based system is greater than that of the non-relay system. This happens because of the resource partitioning between BS and RS. The impact of using relays to reduce the blocking probability is more noticeable when arrival rates increase, as is evident from the figures for mean arrival rate >70. This demonstrates that relay deployment decreases the blocking probability when arrival rates are high and hence improves the capacity. We also observe that in relay based cellular OFDMA systems, for higher arrival rate and higher rate requirements such as, 1024 Kbps, the blocking probability is reduced by only 10 %. However, for higher arrival rate and lower rate requirements, such as 512 Kbps, the blocking probability reduces by about 50 %. We also observe that there is a close match between the Monte-Carlo simulation and analytical results in case of relay-based OFDMA system.

Fig. 10
figure 10

Blocking probability versus mean arrival rate for various rate requirements a without relays and b with relays in a cellular OFDMA system. a Blocking probability for non-relay cellular OFDMA system. b Blocking probability for relay based cellular OFDMA system

Full size image

Note that due to delay tolerant characteristic, data calls can be queued (delayed) and can be analyzed in terms of waiting time probability, i.e., the probability that a queued user gets service within the maximum acceptable waiting time. Thus, blocking probability analysis using Erlang loss model can not be applied for data calls. Following standard queuing theory, it is known that very small blocking probability in Erlang loss model can also achieve small delay in equivalent Erlang delay model. It is due to this fact, analysis for voice calls at higher rates is also applicable for data calls of higher rate services such as, video downloads, video streaming, multimedia conferencing, on-line gaming etc. In general, blocking probability for voice traffic \(({\mathbb {P}}_B)\) and waiting time probability for data traffic (\(\mathbb {P_D}\)) are related as follows,

$$\begin{aligned} {\mathbb {P}}_D = {\mathbb {P}}_B \frac{K}{K-\rho }, \, K > \rho \end{aligned}$$
(41)

where, \(K\) is the number of resources (subcarriers) available in the system and \(\rho \) is the offered traffic. This implies that the waiting time probability is greater than blocking probability by a factor of \(\frac{K}{K-\rho }\). The determination of blocking probability of voice calls for higher data rates may be helpful in the determination of waiting time probability of data calls. Therefore, we have performed the blocking probability analysis of voice calls for rate requirements as 256, 512 and 1024 Kbps.

7 Conclusions and Future Work

In cellular OFDMA networks, in order to meet the same rate requirement, the number of subcarriers required is different for different users (due to differences in their locations and experienced SIR) on various links. Therefore traditional methods of blocking probability computation cannot be used directly. We have proposed an analytical model to evaluate blocking probability for relay based cellular OFDMA networks. The CDF of SIR is determined to compute the probability distribution of subcarriers required on the three transmission links. The incoming users are classified into different classes based on the number of subcarriers they require. We have modelled such a system by a multi-dimensional Markov chain. The effects of subcarrier bandwidth (W) and rate requirement (R) on the blocking probability are analyzed. We have also analyzed the effect of rate requirement on the definition of class and number of classes.

We have considered six relays per cell in our system model, with their locations fixed in the cell. However, the optimal location of RSs can impact the system performance in terms of improving cellular coverage or network capacity. One of the author’s work [23] considers the optimal relay placement problem in the context of maximizing the cellular coverage. The optimal relay positioning to maximize capacity and reduce blocking probability can be investigated as future work. Though we do not consider multi-service traffic where each class of users has a different rate requirement, our analysis can be extended to such a scenario.