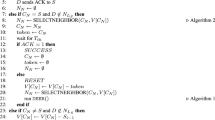1 Introduction

A wireless sensor network (WSN) is consisted of very tiny sensor nodes which are spread out in a specific geographical area. This network is usually used in monitoring or surveillance applications. Each sensor node collects information from its surrounding environment and forwards it to one or several sink nodes in a single or multi hop way. In such networks, each of the sensor nodes is powered by a very tiny battery and usually due to utilizing of these networks in hazardous or out of reach environments, replacing node batteries would be rarely possible. So the main problem in these networks is that sensor nodes can operate for a long duration of time by such limited batteries. This issue has guided current studies toward methods to increase or, in optimum case, maximize the network lifetime in WSNs. Since the definition of network lifetime will completely depend on the network application, often there is no unified definition for the lifetime of a sensor network. In most of the studies, the lifetime of a sensor network is considered the time duration in which the first node of the network is de-energized [1, 2]. In some others, the network lifetime is considered the time duration in which a certain percentage of network nodes are deactivated [3]. In other studies, lifetime network is defined the time duration in which the coverage area of sensor network for gathering and reporting data is reduced to the given threshold level [4]. In a common sensor node, the battery energy is consumed by different parts of the sensor node. But the most energy consumed is related to the communicational subsystem of each node [5]. In this subsystem, four processes including sending data, receiving data, idle listening (IL) for receiving data and sleeping are done. These activities will be effective on the other energy wasting factors like collision and overhearing. Thus the way of performing the above quadruplet activities will be intensely influential on the lifetime of each node and hence overall network lifetime. Based on this fact, lifetime extension techniques in sensor networks can be divided into two main branches: energy efficient routing methods and duty cycle scheduling techniques.

In the first branch, the proper assignment of different routes of network for sending and receiving data, and in the second branch suitable timing mechanism related to the processes of IL and sleeping are considered in order to access the most efficiency of energy. Many methods have been suggested for lifetime maximization of sensor networks based on the energy efficient routing methods which are common as maximum lifetime routing problem. The issue related to maximum lifetime routing problem has been pioneered by Chang and Tassiulas [1] and modeled as a mathematical linear programming problem. In this method, authors have used a centralized modeling method based on calculating the flow rate of data on the connecting links of sensor nodes as independent optimizing parameters. They have assumed the network lifetime as the time duration in which the first node of the network runs out of energy. Madan and Lall [6] were the first researchers who presented a pure distributed classic solution to this problem. In both of methods presented in [1, 6], it has been assumed that all of the data communication among the nodes is performed in multi hop way and there is no direct link between sensor nodes and the sink nodes. But this assumption will cause lack of energy balance in the network nodes and usually the closer nodes to the sink deactivate sooner than the other ones. Thus the network lifetime is often limited to the lifetime of closer nodes to the sink. To prevent this deficiency, in [3] the issue of lifetime maximization, based on energy balance has been presented by utilizing both single and multi hop transmission policies. This issue has been formulated by an integer linear programming problem and also a distributed protocol named distributed energy balance routing (DEBR) has been presented to practical implementing the scheme. In DEBR protocol, it has been allowed to each node to choose its route toward the sink node by a neighboring node as a data relay node or directly. This choice has been performed based on a specific criterion of the energy cost.

In the second branch of researches, increasing lifetime of the sensor network has been carried out by duty cycle scheduling techniques. Duty cycle scheduling is defined as determining time durations of waking and sleeping of a sensor node. The foundation of all methods of extending the lifetime based on duty cycle scheduling, is reducing the time of activity of a sensor node or in other words, increasing the time of its sleeping; when neither node receives any data nor sends it. In fact, at this time sensor node waiting for receiving data ought to keep its receiver on and listen to the radio channel. This situation is well known as IL mode. But this procedure will cause a lot of energy wastage in a sensor node. Because the experiments have shown that the amount of energy consumed in IL mode, is nearly equal to energy consumed in receiving data mode [5]. The duty cycle scheduling techniques can be divided into two main categories, including synchronous and asynchronous methods [5]. In synchronous methods, it is assumed that sensor nodes in their communicational routes are aware of their sleeping and waking time durations of each other. Synchronizing the network nodes especially in large scales imposes heavy signaling load on the network. On the contrary in asynchronous techniques, duty cycle scheduling of nodes is performed independent of each other; so handling these methods is easier to implement than synchronous ones. However they may be positioned in lower level in terms of energy efficiency and lifetime. Anastasi et al. [7] have suggested a new synchronous protocol for duty cycle scheduling named adaptive staggered sleep protocol (ASLEEP) in order to extend the lifetime of a data gathering tree based WSN. ASLEEP adjusts dynamically the sleep time duration of nodes based on some specific network parameters like traffic rate. In [8] a synchronous MAC protocol named S-MAC designed specifically for a sensor network has been suggested to improve the efficiency of traditional CSMA/CA MAC protocol. In S-MAC to reduce the IL time, periodical listening and sleeping has been used for duty cycle scheduling of each sensor node. In S-MAC protocol, in order to synchronizing the nodes, they exchange a certain packet named SYNC. In [9] an asynchronous MAC protocol called B-MAC using a preamble along data packet has been suggested for reducing IL time duration of nodes. In [10] the issue of asynchronous duty cycle scheduling has been presented and formulated with two main objectives including lifetime maximization and overall power consumption minimization.

In each of the aforementioned researches, extending or maximizing the network lifetime is done by focusing on any of the energy efficient routing or duty cycle scheduling branches; while considering both of these techniques jointly can be numbered as prosperous method to extend or maximize the network lifetime. Kartal et al. [11] have presented a lifetime maximization issue based on joint routing and duty cycle scheduling in WSNs and modeled the issue as a linear programming problem. In that research it has been assumed that there exists an underlying synchronized duty cycle scheduling mechanism. Also it has been supposed that all of the sensor nodes operate with the same duty cycle, but as the authors have mentioned, it is obvious that this assumption cannot guarantee the maximum lifetime in the network. In [12] also an issue named joint routing and sleep scheduling problem for lifetime maximization in sensor network has been presented. In [12], it has been assumed that sensor nodes are independent of each other in setting their sleeping time duration. Despite the advantages of both methods presented in [11, 12], they have a main drawback. In the both presented issues, it has been assumed that data transmitting of all nodes toward the sink is only performed in multi hop way. But this policy will cause lack of energy balance in the nodes and early deactivating of closer nodes to the sink.

In this paper, a novel energy balance based lifetime maximization issue in WSNs employing joint routing and asynchronous duty cycle scheduling techniques is introduced which is called as EB-JRADCS problem. To model the EB-JRADCS problem a new asynchronous MAC protocol utilizing flooding of RTS and random sending of CTS named FRTS–RCTS is proposed. This protocol leads to new constraints called flow sharing (FS) constraints that joint the network lifetime maximization parameters including flow rate of information on any route and duty cycle of nodes. In fact in EB-JRADCS issue, three approaches will be considered. First, duty cycle scheduling of each node will be done in an asynchronous manner. Second, routing and duty cycle scheduling mechanisms are performed jointly. It means both of them are considered as the factors of lifetime maximization problem simultaneously. Third, lifetime maximization based on energy balance will occur in the network; so for this sake, sensor nodes are able to send their data into the sink nodes either in single hop or multi hop way. In this paper, first we show that EB-JRADCS problem can be expressed as a standard signomial geometric programming (SGP) problem. Due to the complexity of solving the achieved problem, first it is converted into a simpler problem by relaxing FS constraints from equal to unequal form. Also because of inherent non-convexity of the problem, we use a convexification method which has been presented in recent literature [13] in order to solve the problem and calculate overall optimum network lifetime.

The rest of the paper is organized as follows. In Sect. 2 after introducing the system model and assumptions, we will illustrate the new asynchronous FRTS–RCTS protocol and resulted FS constraints in detail. Then we compute energy constraints according to precise computations of energy consumption in each node based on proposed protocol and subsequently describe the way of formulating EB-JRADCS problem based on all of the obtained constraints. In Sect. 3 by defining a SGP problem, we will show that EB-JRDCS problem is easily convertible to a SGP problem and then we will briefly present the procedure of solving the problem. Also in this section, we will show that the problem can be converted into a simpler problem by relaxing FS constraints from equal to unequal form. In Sect. 4 simulation results including maximum network lifetime under various scenarios, and also flow rate of information and duty cycle of nodes on a given scenario will be presented. Eventually in Sect. 5 we will conclude the paper.

2 System Model, Assumptions and EB-JRADCS Problem Formulation

Consider a WSN where V is the set of all sensor nodes. N sensor nodes are uniformly distributed and fixed in a specific region. Also, M sink nodes are placed in different locations of this area. Each sensor node contains primary battery energy E i and generates fixed data rate of g i . Also it has been assumed that sensor nodes have ability of adjusting their transmission power level based on their own distance to the target node. Each sensor node forwards its generated information, either directly to the sink or to one of its neighbors as a data relaying node. In the network consisted of multiple sinks, in the condition of directly sending of information to the sink, data is sent to the nearest sink. To avoid data collision in directly sending case, we assume that sending data is done on a separate channel. It is clear that the number of neighbors of each node will completely depend on its transmitting power level, as by increasing power transmission level of each node, more nodes as adjacent nodes or in other words relaying nodes will be covered. Now consider that each node covers communicational radius R by sending specific power level in its neighborhood. Later we will investigate the effect of changing radius R or equivalently changing power transmission level on the network lifetime. The set of neighbors of a sensor node like node i in coverage radius R is shown by \( N_{i}^{R} . \) If r ij denotes the rate of transmitting data from node i to j and S i represents the nearest sink to node i, then flow conservation constraints will be shown as follows:

$$ \mathop \sum \limits_{{ j \in N_{i}^{R} + \left\{ {S_{i} } \right\}}} r_{ij} = \mathop \sum \limits_{{k:i \in N_{k}^{R} }} r_{ki} + g_{i} ,\quad \forall i \in V $$
(1)

Equation 1 shows that the sum of outgoing data rate from any node involving outgoing data rate toward neighbors and outgoing data rate directly to the sink node is equal to incoming data rate from nodes which node i is their neighbor plus data generated by node i itself. In fact, since all generated data should be sent to the sink nodes, the incoming and outgoing data rate at a sensor is the same.

2.1 FRTS–RCTS Protocol and Flow Sharing (FS) Constraints

In this section, by designing a new asynchronous MAC protocol named FRTS–RCTS, it is shown that lifetime maximization parameters, including flow rate of information on any route and duty cycle of nodes are jointed via new constraints named FS constraints. In traditional asynchronous MAC protocol called CSMA/CA, duty cycle scheduling in order to reduce energy consumption is not supported. Hence, each sensor node in order to make a connection with another node, just forwards RTS packet toward it. Then to overcome hidden terminal problem the receiver node sends CTS packet in response to the transmitter node. To support duty cycle scheduling in the proposed protocol, the procedure of CSMA/CA protocol is modified in both stages of RTS and CTS transmissions. It should be noted that the fundamental idea in designing the new protocol is independence of duty cycle of nodes from each other. To this end, first a clear definition of duty cycle should be presented. Duty cycle of a node can be defined as the ratio of its activity time duration to a given fixed time duration called duty cycle period. In each duty cycle period a sensor node performs some operations like data sending, data receiving and IL in its waking time and during the remaining time of the period goes to sleep mode for saving its battery energy. In the sleep mode, the sensor node deactivates all of its communicational equipment whether transmitter or receiver, so that the energy consumption in this situation would be negligible. Since in WSNs due to low traffic rate, the time relating to sending and receiving data in comparison to the time of IL is too small, usually the duty cycle of a node can be considered as the ratio of IL time to the duty cycle period. In this paper we utilize this principle for calculating of node duty cycle. By considering this assumption, in the following we will illustrate the procedure of FRTS–RCTS protocol in detail.

If a sensor node like j, the neighbor of node i, works with a given duty cycle denoted by dc j and node i in an arbitrary moment, sends a RTS packet to this node, the probability of that node j be in IL mode is dc j . Now when node i, needs to send a data packet to the sink node, due to the lack of awareness of its waking neighbors, first it sends the RTS packet toward its neighbors in flooding way in a given radius R. The set of neighbors of sensor node i in coverage radius R is shown by \( N_{i}^{R} \) and the number of them is denoted by \( \left| {N_{i}^{R} } \right|. \) Also the set of waking and sleeping neighbors of node i is represented by \( WN_{i}^{R} \) and \( SN_{i}^{R} \) respectively. Now in terms of waking or sleeping modes of neighbors of node i, FRTS–RCTS protocol works exactly after sending RTS, as one of the two following different cases:

2.1.1 FRTS–RCTS Protocol: Case 1

Among all neighbors of node i, k neighbors are awake or in other words in IL mode. In this case, all of these neighbors receive sent RTS packet from node i. In this condition any of these neighbors can send CTS packet in response to the received RTS packet. But by sending CTS packet immediately after receiving RTS, by at least two neighbors, collision will be occurred. To overcome this obstacle, FRTS–RCTS protocol acts in two main phases which is called CTS random scheduling (CRS) phase and data scheduling (DS) phase. In CRS phase, the transmitter node i, forms a time slotted window consisted of \( \left| {N_{i}^{R} } \right| \) slots. In fact each of the slots is considered for receiving one of the sending CTS packets. Thus the time duration of each slot in this window is equal to the time duration needed to receive one CTS packet. The transmitter node along RTS packet sends a random and uniform sequence of numbers between 1 and \( \left| {N_{i}^{R} } \right| \) such that each of the numbers corresponds to one of the neighbors. In other words to each of the neighbors whether awake or asleep, one random number is assigned. In fact, each random number specifies a slot number for receiving CTS packets from the neighbors. Each waking neighbor that has received the RTS packet ought to send CTS packet in its specified slot number. To prevent energy wastage, each waking neighbor goes to sleep mode upon receiving RTS packet and its own slot number. Then it awakes in the assigned time slot and sends its CTS packet and goes to sleep mode again until the time of receiving data that will be happened in DS phase. In contrast, the RTS transmitter means node i, listens to the radio channel until receiving the first CTS packet from its neighbors.

When the first CTS packet is received from a neighbor in nth slot of CRS phase, to avoid collision between data packet and probably the remaining CTS packets from other waking neighbors and also minimize the energy wastage in node i, this node goes to sleep mode and postpones sending its data packet at least as much as \( |N_{i}^{R} | - n \) time slots. After \( \left| {N_{i}^{R} } \right| \) time slots, CRS phase is finished. After the end of CRS phase, DS phase is started. In this phase a time slotted window consisted of \( \left| {N_{i}^{R} } \right| \) slots is used similarly. Because if sending data is done immediately after CRS phase, then data overhearing will be accrued by other senders of CTS. This operation causes extra energy wastage in the CTS senders, because other senders of CTS packet are waiting to receive data packet too. Each slot is consisted of two parts in this phase. The first part is used for sending data packet from transmitter to receiver and the second part is used for sending ACK packet from receiver to transmitter conversely. In DS phase, if data transmitter node has been received the first CTS packet by a node like j in nth slot of CRS phase, so it will send data packet in nth slot of DS phase for node j too. To minimize energy wastage in this phase also, the transmitter node just awakes in slot of sending data. Also in this phase, overhearing never occurs by any other CTS senders, because all CTS senders awake only in the same slot of DS phase that is corresponding to their own specified CTS slot. In fact, the node which has sent its CTS packet later ought to check available carrier of the channel in its own data time slot only. In this situation, if the carrier is not heard, the node goes back to sleep mode again. In Fig. 1, the timing related to FRTS–RCTS protocol in the case 1 has been shown. In this figure white color is used for showing node sleeping mode. According to the Fig. 1, it has been assumed that transmitter node has ten neighbors and at the moment of RTS sending, only two neighbors, means neighbors 1 and 2 are active or in idle listing mode. Also it is supposed that assigned CTS random slots are the 7th and 4th slots for node 1 and 2 respectively which has been determined by node i. Therefore these nodes send CTS packet in the given time slots and the node 2 which has sent CTS packet sooner than node 1, will be chosen as data receiver node. Hence after the end of CRS phase, data packet will be sent to the chosen node means node 2 in the 4th slot of DS phase. This node also, awakes in the 4th time slot of DS phase and receives the sent data packet. Also node 1, which has sent CTS packet in 7th slot, awakes to receive the data packet in 7th slot of DS phase; but by checking the channel and lack of carrier existence, goes to sleep mode again. As it is seen in the Fig. 1, to prevent energy wastage of transmitter node, it goes to sleep mode immediately after receiving the first CTS packet in CRS phase until the moment of data transmitting in DS phase.

Fig. 1
figure 1

FRTS–RCTS protocol timing (case 1)

Full size image

Now based on the illustrated FRTS–RCTS protocol procedure, we can calculate the probability of receiving a data packet by one of the neighbors of node i like j. If the set of waking neighbors of node i, including j in radius R is denoted by \( WN_{i}^{j} \) and the number of them are represented by \( \left| {WN_{i}^{j} } \right|, \) then the probability of receiving a data packet by node j is:

$$ p\left( {r = j \left| { WN_{i}^{j} } \right.} \right) = \frac{1}{{\left| {WN_{i}^{j} } \right|}} ,\quad WN_{i}^{j} \subseteq N_{i}^{R} $$
(2)

In fact due to the random and uniform assignment of slot numbers to all neighbors, the probability of sending the first CTS packet and consequently, data receiving by any of the neighbors will be the same. But due to independence of duty cycle of nodes the probability that the set of waking nodes including node j be \( WN_{i}^{j} , \) would be calculated as follows:

$$ p\left( {WN_{i}^{j} } \right) = \mathop \prod \limits_{{k \in WN_{i}^{j} }} dc_{k} \mathop \prod \limits_{{k \in SN_{i}^{j} }} \left( {1 - dc_{k} } \right),\quad WN_{i}^{j} \cup SN_{i}^{j} = N_{i}^{R} $$
(3)

In (3), \( SN_{i}^{R} \) represents the set of sleeping neighbors of node i. Finally, by using total probability and conditional probability law, the probability of receiving a data packet by one of the neighbors of node i like j denoted by p(r = j) is:

$$ \begin{aligned} p\left( {r = j} \right) & = \mathop \sum \limits_{{ WN_{i}^{j} \subseteq N_{i}^{R} }} p\left( {r = j \left| { WN_{i}^{j} } \right.} \right) p\left( {WN_{i}^{j} } \right) \\ & = \mathop \sum \limits_{{ WN_{i}^{j} \subseteq N_{i}^{R} }} \frac{1}{{\left| {WN_{i}^{j} } \right|}}\mathop \prod \limits_{{k \in WN_{i}^{j} }} dc_{k} \mathop \prod \limits_{{k \in SN_{i}^{j} }} \left( {1 - dc_{k} } \right) \\ \end{aligned} $$
(4)

In fact in (4) the summation operator is done on the all of the possible subsets of \( N_{i}^{R} \) including j.

2.1.2 FRTS–RCTS Protocol: Case 2

All of the neighbors of node i are in sleep mode. In fact in this case, \( WN_{i}^{R} \) is an empty set or in other words \( SN_{i}^{j} \) is equal to \( N_{i}^{R} \). In this situation, node i after sending RTS packet and waiting duration of time equal to \( \left| {N_{i}^{R} } \right| \) time slots, by increasing its transmitter power level according to its distance to the nearest sink and switching to the second channel, after sending RTS packet to the sink node directly and receiving the corresponding CTS packet, sends data packet to the sink node. In Fig. 2 the protocol timing related to this case have been shown. The probability of receiving a data packet by the sink node that is sent by node i denoted by p(r = S i ) is:

$$ p\left( {r = S_{i} } \right) = p\left( {WN_{i}^{j} = {\emptyset }} \right) = p\left( {SN_{i}^{j} = N_{i}^{R} } \right) = \mathop \prod \limits_{{k \in N_{i}^{R} }} (1 - dc_{k} ) $$
(5)
Fig. 2
figure 2

FRTS–RCTS protocol timing (case 2)

Full size image

In (5), S i represents the nearest sink to node i. Now according to the two possible cases in the proposed protocol, in sending each data packet by transmitter node i, either one of the members of \( N_{i}^{R} \) like j with probability of p(r = j) would be as a data relay node or the nearest sink with probability of p(r = S i ) would be as the receiver. Given that the sum of all the probabilities in a random event is equal to 1, we have:

$$ \left[ {\mathop \sum \limits_{{j \subseteq N_{i}^{R} }} \mathop \sum \limits_{{ WN_{i}^{j} \subseteq N_{i}^{R} }} \frac{1}{{\left| {WN_{i}^{j} } \right|}}\mathop \prod \limits_{{k \in WN_{i}^{j} }} dc_{k} \mathop \prod \limits_{{k \in SN_{i}^{j} }} \left( {1 - dc_{k} } \right)} \right] + \mathop \prod \limits_{{k \in N_{i}^{R} }} (1 - dc_{k} ) = 1 $$
(6)

Equation 6 will be used in Sect. 3 to simplify the EB-JRDCS problem.

Now consider that the network, works for a long duration of time T. If during this time, node i sends R i data packets, then the number of sent packets for all of the neighbors and also the sink node will be written as follows:

$$ R_{i} = \mathop \sum \limits_{{j \in N_{i}^{R} }} R_{ij} + R_{{iS_{i} }} $$
(7)

In (7) R ij is all of the outgoing packets from node i to j and \( R_{{iS_{i} }} \) is all of outgoing packets from node i to the sink S i . So it can be said that the ratio of all the outgoing packets from sensor node i to j, to the total number of outgoing packets from node i, is equal to the probability of successful receiving data by node j and similarly, the ratio of all the outgoing packets from node i to the sink S i , to the total number of outgoing packets from node i, is equal to probability of successful receiving data by the sink S i , so we can write:

$$ \frac{{R_{ij} }}{{R_{i} }} = p(r = j) $$
(8)
$$ \frac{{R_{{iS_{i} }} }}{{R_{i} }} = p(r = S_{i} ) $$
(9)

If sending all packets by node i, happens in the time duration of T, by dividing numerator and denominator of fractions in the left side hand of (8) and (9) to T and using (4) and (5) we have:

$$ r_{ij} = \left[ {\mathop \sum \limits_{{ WN_{i}^{j} \subseteq N_{i}^{R} }} \frac{1}{{\left| {WN_{i}^{j} } \right|}}\mathop \prod \limits_{{k \in WN_{i}^{j} }} dc_{k} \mathop \prod \limits_{{k \in SN_{i}^{j} }} (1 - dc_{k} )} \right].\mathop \sum \limits_{{j \in N_{i}^{R} + \left\{ {S_{i} } \right\}}} r_{ij} $$
(10)
$$ r_{{iS_{i} }} = \left[ { \mathop \prod \limits_{{k \in N_{i}^{R} }} (1 - dc_{k} )} \right]. \mathop \sum \limits_{{j \in N_{i}^{R} + \left\{ {S_{i} } \right\}}} r_{ij} $$
(11)

In the above equations or constraints in other words, the share of outgoing data flow rate to any of neighbors or to the sink node, in proportion to the total amount of outgoing data flow rate by node i, is calculated. So that’s why we have named these equations as FS constraints. Also as it is seen, data flow rates on any route and duty cycle of nodes are tightly jointed by these constraints.

2.2 Energy Consumption Model

In each sensor node, data sending, data receiving and IL operations are the major factors of energy consumption. As other operations like sensing or information processing can be considered as negligible factors from this point of view. We use the basic model which is presented in [14] for energy consumption modeling in sending and receiving data statuses. According to this model, the energy required to send one unit of data from node i to j can be determined as follows:

$$ E_{t}^{ij} = e_{elec} + e_{amp} (d_{ij} )^{\beta } $$
(12)

where e elec and e amp are fixed coefficients depending on energy consumption of electronic equipment and transmitter amplifier module of sensor node respectively. Also d ij is the Euclidean distance between node i and j and β is the path loss exponent which is typically in the range of 2–6, depending on the environment. In the case of receiving data, energy consumption of each node is fixed as follows:

$$ E_{r} = e_{elec} $$
(13)

Finally in IL mode the amount of energy consumption is dependent on the radio module of sensor node. In respect to nothingness of energy wastage in sleep mode, it has been ignored in this paper. According to the above mentioned model, in the next part we will compute the amount of energy consumption based on the proposed FRTS–RCTS protocol.

2.3 Energy Consumption Computation in FRTS–RCTS Protocol

Based on the Fig. 1, the energy consumed by each node like i, in sending one data packet to a neighbor node like j, is consisted of energy consumption of sending one RTS packet in radius R \( (E_{t\_RTS}^{R} ), \) energy consumption of waiting time to receive the first CTS packet from a neighbor \( (E_{w\_CTS}^{i} ), \) energy consumption of receiving one CTS packet \( (E_{r\_CTS} ), \) energy consumption of sending one data packet to node j \( (E_{t\_DATA}^{ij} ) \) and finally energy consumption to receive the ACK packet \( (E_{r\_ACK}). \) So the energy consumption of node i, to send a data packet to a neighbor like j, without considering energy consumed when being in IL mode to receive the first CTS packet denoted by \( E_{t}^{ij} \) will be calculated as follows:

$$ E_{t}^{ij} = E_{t\_RTS}^{R} + E_{r\_CTS} + E_{t\_DATA}^{ij} + E_{r\_ACK} $$
(14)

For simplicity, energy consumed during IL mode to receive the first CTS packet will be computed separately. According to FRTS–RCTS protocol in case 2, if any CTS packet is not received after the end of CRS phase, transmitter node by adjusting its transmitting power level sends RTS packet to the nearest sink. In this situation, the energy consumption of node i, to send a data packet to the sink, without considering energy consumed when it is waiting to receive the first CTS packet, denoted by \( E_{t}^{{iS_{i} }} \) will be calculated as follows:

$$ E_{t}^{{iS_{i} }} = E_{t\_RTS}^{R} + E_{t\_RTS}^{{iS_{i} }} + E_{r\_CTS} + E_{t\_DATA}^{{iS_{i} }} + E_{r\_ACK} $$
(15)

In (15), the energy consumption of sending RTS packet and sending data packet from node i to sink S i are denoted by \( E_{t - RTS}^{{iS_{i} }} \) and \( E_{t - DATA}^{{iS_{i} }} \) respectively. If the rate of outgoing data from node i to j, including a neighbor or sink S i is represented by r ij , therefore the average consumed power of node i for sending data denoted by \( P_{t}^{i} \) would be as follows:

$$ P_{t}^{i} = \mathop \sum \limits_{{j \in N_{i}^{R} + \left\{ {S_{i} } \right\}}} E_{t}^{ij} \cdot r_{ij} $$
(16)

Now we calculate the energy consumption related to waiting time during IL mode to receive the first CTS packet. When each node like i, wants to send a data packet, first it sends the RTS packet to its neighbors in radius R in flooding way. In this case the number of waking neighbors can be a number between 0 and \( N_{i}^{R} . \) Consider at the moment of sending RTS packet, the number of waking neighbors is k. In this situation, based on the protocol FRTS–RCTS in case 1, transmitter node i sends a random sequence of numbers 1 to \( N_{i}^{R} \) to all of its neighbors such that each of the random numbers is assigned to one of the neighbors. Since the transmitter node chooses the first CTS transmitter as the receiver of the data packet, we can consider the average of the receiving slot numbers as the receiving slot number of CTS packet on the whole working time of the network. Assume that X is a random variable used for showing the slot number in which the first CTS packet is received by node i. So based on different values of k the following cases would be occurred:

  1. 1.

    None of the neighbors are awake. In this case, the transmitter node does not receive any CTS packet during the CRS phase which is the time duration equivalent to \( \left| {N_{i}^{R} } \right| \) time slots. So, the amount of waiting time would be equal to \( \left| {N_{i}^{R} } \right| \) time slots.

  2. 2.

    Among \( \left| {N_{i}^{R} } \right| \) neighbors, only one neighbor is awake. In this case, it is clear that the random variable X is a uniform random variable in the range of 1–\( \left| {N_{i}^{R} } \right| \) and its average value will be calculated as follows:

    $$ E_{1} \left[ X \right] = \mathop \sum \limits_{n = 1}^{{\left| {N_{i}^{R} } \right|}} n \cdot p\left( {X = n} \right) = \mathop \sum \limits_{n = 1}^{{\left| {N_{i}^{R} } \right|}} n \cdot \frac{1}{{\left| {N_{i}^{R} } \right|}} = \frac{{\left| {N_{i}^{R} } \right| + 1}}{2} $$
    (17)

    • In (17), \( E_{1} [X] \) has been used to show the expected value of random variable X when there is only 1 waking neighbor.

  3. 3.

    Among \( \left| {N_{i}^{R} } \right| \) neighbors, k ≥ 2 neighbors are awake. In this situation, the random variable X takes one of the numbers between 1 and \( \left| {N_{i}^{R} } \right| - k + 1. \) In this case the probability that among k waking neighbors, CTS packet is received in the first slot of CRS phase can be computed as follows:

    $$ p\left( {X = 1} \right) = \frac{{\left( {\left| {N_{i}^{R} } \right| - 1} \right) \cdot \left( {\left| {N_{i}^{R} } \right| - 2} \right) \ldots \left( {\left| {N_{i}^{R} } \right| - k + 1} \right) \cdot k}}{{\left( {\begin{array}{*{20}c} {\left| {N_{i}^{R} } \right|} \\ k \\ \end{array} } \right) \cdot k!}},\quad k \ge 2 $$
    (18)

Also the probability that among k waking neighbors, CTS packet is received in the second slot of CRS phase can be computed as follows:

$$ p\left( {X = 2} \right) = \frac{{\left( {\left| {N_{i}^{R} } \right| - 2} \right) \cdot \left( {\left| {N_{i}^{R} } \right| - 3} \right) \ldots \left( {\left| {N_{i}^{R} } \right| - k} \right) \cdot k}}{{\left( {\begin{array}{*{20}c} {\left| {N_{i}^{R} } \right|} \\ k \\ \end{array} } \right) \cdot k!}} ,\quad k \ge 2 $$
(19)

And generally, the probability that among k waking neighbors, CTS packet is received in the nth slot of CRS phase can be written as follows:

$$ \begin{aligned} p\left( {X = n} \right) & = \frac{{\left( {\left| {N_{i}^{R} } \right| - n} \right) \cdot \left( {\left| {N_{i}^{R} } \right| - n - 1} \right) \ldots \left( {\left| {N_{i}^{R} } \right| - k + 2 - n} \right) \cdot k}}{{\left( {\begin{array}{*{20}c} {\left| {N_{i}^{R} } \right|} \\ k \\ \end{array} } \right) \cdot k!}} \\ & = \frac{{\left( {\left| {N_{i}^{R} } \right| - n - m} \right)}}{{ \left( {\begin{array}{*{20}c} {\left| {N_{i}^{R} } \right|} \\ k \\ \end{array} } \right) \cdot \left( {k - 1} \right)!}},\quad k \ge 2 \\ \end{aligned} $$
(20)

Hence, the average of the receiving slot numbers will be calculated as follows:

$$ \begin{aligned} E_{k} \left[ X \right] & = \mathop \sum \limits_{n = 1}^{{\left| {N_{i}^{R} } \right| - k + 1}} n \cdot p\left( {X = n} \right) \\ & = \mathop \sum \limits_{n = 1}^{{\left| {N_{i}^{R} } \right| - k + 1}} n \cdot \frac{{\left( {\left| {N_{i}^{R} } \right| - n - m} \right)}}{{ \left( {\begin{array}{*{20}c} {\left| {N_{i}^{R} } \right|} \\ k \\ \end{array} } \right) \cdot \left( {k - 1} \right)!}},\quad k \ge 2 \\ \end{aligned} $$
(21)

If the time duration of each slot in CRS phase is denoted by t s , the amount of waiting time for receiving the first CTS packet, in terms of all values k, represented by CRT as a function of variables \( N_{i}^{R} \) and k will be computed as follows:

$$ CRT\left( {N_{i}^{R} , k} \right) = \left\{ {\begin{array}{*{20}l} {\left| {N_{i}^{R} } \right| \cdot t_{s} } \hfill & {k = 0} \hfill \\ {\left( {E_{k} \left[ X \right] - 1} \right) \cdot t_{s} } \hfill & {k \ge 1} \hfill \\ \end{array} } \right. $$
(22)

In (22), function \( CRT(N_{i}^{R} , k) \) computes waiting time for receiving the first CTS packet of node i containing \( N_{i}^{R} \) neighbors witch k of them are awake. Let \( \Omega_{i}^{k} \) be a k-member subset of \( N_{i}^{R} . \) The probability that among \( \left| {N_{i}^{R} } \right| \) neighbors, only the neighbors belonging to \( \Omega_{i}^{k} \) are awake at the sending moment of RTS denoted by \( p(\Omega_{i}^{k} ) \) is as follows:

$$ p\left( {\Omega_{i}^{k} } \right) = \mathop \prod \limits_{{k \in \Omega_{i}^{k} }} dc_{k} \mathop \prod \limits_{{k \in N_{i}^{R} - \Omega_{i}^{k} }} \left( {1 - dc_{k} } \right) $$
(23)

If the average consumed power of each node in IL mode is P IL , according to (23), the energy consumption of node i, in the waiting time of receiving the first CTS packet from its neighbors will be calculated as follows:

$$ E_{w\_CTS}^{i} = \mathop \sum \limits_{k = 0}^{{\left| {N_{i}^{R} } \right|}} CRT\left( {N_{i}^{R} , k} \right) \cdot \mathop \sum \limits_{{\Omega_{i}^{k} \subseteq N_{i}^{R} }} \left[ {\mathop \prod \limits_{{k \in \Omega_{i}^{k} }} dc_{k} \mathop \prod \limits_{{k \in N_{i}^{R} - \Omega_{i}^{k} }} (1 - dc_{k} )} \right] \cdot P_{IL} $$
(24)

Finally, the average consumed power of node i in the waiting time for receiving the first CTS packet from its neighbors in terms of data rate denoted by \( P_{w - CTS}^{i} \) will be calculated as follows:

$$ P_{w - CTS}^{i} = \left( {\mathop \sum \limits_{k = 0}^{{\left| {N_{i}^{R} } \right|}} CRT\left( {N_{i}^{R} , k} \right) \cdot \mathop \sum \limits_{{\Omega_{i}^{k} \subseteq N_{i}^{R} }} \left[ {\mathop \prod \limits_{{ k \in \Omega_{i}^{k} }} dc_{k} \mathop \prod \limits_{{k \in N_{i}^{R} - \Omega_{i}^{k} }} \left( {1 - dc_{k} } \right)} \right] \cdot P_{IL} } \right) \cdot \mathop \sum \limits_{{j \in N_{i}^{R} + \left\{ {S_{i} } \right\}}} r_{ij} $$
(25)

In data receiving mode, if the receiver node not to be the first transmitter of CTS packet, thus won’t receive any data packet in its corresponding time slot in DS Phase. The only energy consumption in this case is the energy consumed due to the hearing carrier signal in the channel at very short duration of time, which will be negligible. But, if a receiver node like k is the first transmitter of CTS packet, the energy consumption of node i is including energy consumed due to receiving a data packet from node k and consumed energy related to sending ACK packet. So we have:

$$ E_{r\_DATA}^{ki} = E_{r\_DATA} + E_{t\_ACK}^{ik} $$
(26)

If data receiving rate of node i from each node like k is r ki , thus the average consumed power of node i in receiving data mode denoted by \( P_{r\_DATA}^{i} \) will be computed as follows:

$$ P_{r\_DATA}^{i} = \mathop \sum \limits_{{k:i \in N_{i}^{R} }} E_{r\_DATA}^{ki} \cdot r_{ki} $$
(27)

If a node like i receives a RTS packet, two possible cases would be occurred. Either node i will be the first transmitter of CTS packet or not. It is obvious that in both cases, it will send CTS packet to the transmitter. So, either in the first or second case, energy consumption denoted by \( E_{r\_RTS,t\_CTS}^{ik} \) would be computed as follows:

$$ E_{r\_RTS,t\_CTS}^{ik} = E_{r\_RTS} + E_{t\_CTS}^{ik} $$
(28)

If sending data rate of every node like k, which node i is one of its neighbors, to all of its neighbors is denoted by \( \sum\nolimits_{{j \in N_{k}^{R} }} {r_{kj} } \) and node i works with duty cycle dc i , therefore the share of receiving rate of RTS packets from node k to i denoted by \( S_{r\_CTS}^{ki} \) would be computed as follows:

$$ S_{r\_CTS}^{ki} = dc_{i} \cdot \mathop \sum \limits_{{j \in N_{k}^{R} }} r_{kj} $$
(29)

So the average consumed power of node i in receiving RTS packets from node k and sending CTS packets to it which is denoted by \( P_{r\_RTS,t\_CTS}^{ik} \) would be calculated as follows:

$$ P_{r\_RTS,t\_CTS}^{ik} = E_{r\_RTS,t\_CTS}^{ik} \cdot S_{r\_CTS}^{ki} $$
(30)

Thus using (29) and (30), the average consumed power of node i in receiving all RTS packets from all of the neighbors that node i is their neighbor and sending all CTS packets to them denoted by \( P_{r\_RTS,t\_CTS}^{i} \) would be calculated as follows:

$$ \begin{aligned} P_{r\_RTS,t\_CTS}^{i} & = \mathop \sum \limits_{{k:i \in N_{k}^{R} }} P_{r\_RTS,t\_CTS}^{ik} = \mathop \sum \limits_{{k:i \in N_{k}^{R} }} E_{r\_RTS,t\_CTS}^{ik} \cdot dc_{i} \cdot \mathop \sum \limits_{{j \in N_{k}^{R} }} r_{kj} \\ & = dc_{i} \cdot \mathop \sum \limits_{{k:i \in N_{k}^{R} }} E_{r\_RTS,t\_CTS}^{ik} \cdot \mathop \sum \limits_{{j \in N_{k}^{R} }} r_{kj} \\ \end{aligned} $$
(31)

In IL mode also, in which sensor node i listens to the radio channel, in order to receive any RTS packet, if it works with duty cycle of dc i , its average consumed power will be as follows:

$$ P_{IL}^{i} = P_{IL} \cdot dc_{i} $$
(32)

Finally, using Eqs. (16), (25), (27), (31) and (32) the average consumed power of each node like i denoted by \( \bar{P}_{i}^{cons} \) would be calculated as follows:

$$ \begin{aligned} \bar{P}_{i}^{cons} & = \mathop \sum \limits_{{j \in N_{i}^{R} + \left\{ {S_{i} } \right\}}} E_{t}^{ij} \cdot r_{ij} + \left( {\mathop \sum \limits_{k = 0}^{{\left| {N_{i}^{R} } \right|}} CRT\left( {N_{i}^{R} , k} \right) \cdot \mathop \sum \limits_{{\Omega_{i}^{k} \subseteq N_{i}^{R} }} \left[ {\mathop \prod \limits_{{k \in \Omega_{i}^{k} }} dc_{k} \mathop \prod \limits_{{k \in N_{i}^{R} - \Omega_{i}^{k} }} \left( {1 - dc_{k} } \right)} \right] \cdot P_{IL} } \right) \cdot \mathop \sum \limits_{{j \in N_{i}^{R} + \left\{ {S_{i} } \right\}}} r_{ij} \\ & \quad + dc_{i} \cdot \sum\limits_{{k:i \in N_{k}^{R} }} {E_{r\_RTS,t\_CTS}^{ik} \cdot \mathop \sum \limits_{{j \in N_{k}^{R} }} r_{kj} + \mathop \sum \limits_{{k:i \in N_{i}^{R} }} E_{r\_DATA}^{ki} \cdot r_{ki} + P_{IL} \cdot dc_{i} } \\ \end{aligned} $$
(33)

2.4 EB-JRADCS Problem

In this section EB-JRADCS problem is constructed based on all of the above obtained constraints. If node i works in a time duration T i and its initial battery energy is E i , its energy constraint under a given flow rate \( \varvec{R}^{i} = \left\{ {r_{ij} } \right\} \) and duty cycle dc i will be written as follows:

$$ \bar{P}_{i}^{cons} \cdot T_{i} \left( {\varvec{R}^{i} ,dc_{i} } \right) \le E_{i} $$
(34)

Now, let us define the network lifetime as the minimum lifetime over all nodes, i.e.,

$$ T_{net} = \mathop {\hbox{min} }\limits_{i \in V} T_{i} \left( {\varvec{R}^{i} ,dc_{i} } \right) $$
(35)

Our goal is to compute the flow data rates and duty cycle of all nodes such that the network lifetime is maximized. This maximization is carried out definitely by considering three aforementioned constraints including flow conservation constrains, FS constrains and energy constrains calculated in (1), (10), (11) and (33). Thus the EB-JRADCS maximization problem can be written as follows:

$$ \begin{aligned} & maximize\left( {\mathop {\hbox{min} }\limits_{i \in V} T_{i} \left( {\varvec{R}^{i} ,dc_{i} } \right)} \right)\mathop \sum \limits_{{ j \in N_{i}^{R} + \left\{ {S_{i} } \right\}}} r_{ij} - \mathop \sum \limits_{{k:i \in N_{k}^{R} }} r_{ki} = g_{i} ,\quad \forall i \in V \\ &\quad \left[ {\mathop \sum \limits_{{j \in N_{i}^{R} + \left\{ {S_{i} } \right\}}} E_{t}^{ij} .r_{ij} + \left( {\mathop \sum \limits_{k = 0}^{{\left| {N_{i}^{R} } \right|}} CRT\left( {N_{i}^{R} , k} \right) \cdot \mathop \sum \limits_{{\Omega_{i}^{k} \subseteq N_{i}^{R} }} \left[ {\mathop \prod \limits_{{ {\text{k}} \in \Omega_{i}^{k} }} dc_{k} \mathop \prod \limits_{{{\text{k}} \in N_{i}^{R} - \Omega_{i}^{k} }} \left( {1 - dc_{k} } \right)} \right] \cdot P_{IL} } \right)} \right.. \mathop \sum \limits_{{j \in N_{i}^{R} + \left\{ {S_{i} } \right\}}} r_{ij} \\ & \quad \left. { +\,dc_{i} \cdot \mathop \sum \limits_{{k:i \in N_{k}^{R} }} E_{r\_RTS,t\_CTS}^{ik} .\mathop \sum \limits_{{j \in N_{k}^{R} }} r_{kj} + \mathop \sum \limits_{{k:i \in N_{i}^{R} }} E_{r\_DATA}^{ki} \cdot r_{ki} + P_{IL} \cdot dc_{i} } \right] \cdot T_{i} \left( {\varvec{R}^{\varvec{i}} ,dc_{i} } \right) \le E_{i} \\ & r_{ij} = \left[ {\mathop \sum \limits_{{ WN_{i}^{j} \subseteq N_{i}^{R} }} \frac{1}{{\left| {WN_{i}^{j} } \right|}}\mathop \prod \limits_{{{\text{k}} \in WN_{i}^{j} }} dc_{k} \mathop \prod \limits_{{{\text{k}} \in SN_{i}^{j} }} \left( {1 - dc_{k} } \right)} \right] \cdot \mathop \sum \limits_{{j \in N_{i}^{R} + \left\{ {S_{i} } \right\}}} r_{ij} \\ & r_{{iS_{i} }} = \left[ { \mathop \prod \limits_{{{\text{k}} \in N_{i}^{R} }} \left( {1 - dc_{k} } \right)} \right] \cdot \mathop \sum \limits_{{j \in N_{i}^{R} + \left\{ {S_{i} } \right\}}} r_{ij} \\ \end{aligned} $$
(36)

Problem (36) is a max–min problem which can be rewritten as a maximization problem as follows:

$$ \begin{aligned} & maximize(T)\mathop \sum \limits_{{ j \in N_{i}^{R} + \left\{ {S_{i} } \right\}}} r_{ij} - \mathop \sum \limits_{{k:i \in N_{k}^{R} }} r_{ki} = g_{i} ,\quad \forall i \in V \\ & \quad \left[ {\mathop \sum \limits_{{j \in N_{i}^{R} + \left\{ {S_{i} } \right\}}} E_{t}^{ij} .r_{ij} + \left( {\mathop \sum \limits_{k = 0}^{{\left| {N_{i}^{R} } \right|}} CRT\left( {N_{i}^{R} , k} \right) \cdot \mathop \sum \limits_{{\Omega_{i}^{k} \subseteq N_{i}^{R} }} \left[ {\mathop \prod \limits_{{{\text{k}} \in \Omega_{i}^{k} }} dc_{k} \mathop \prod \limits_{{{\text{k}} \in N_{i}^{R} - \Omega_{i}^{k} }} \left( {1 - dc_{k} } \right)} \right] \cdot P_{IL} } \right)} \right.. \mathop \sum \limits_{{j \in N_{i}^{R} + \left\{ {S_{i} } \right\}}} r_{ij} \\ & \quad \left. { +\,dc_{i} \cdot \mathop \sum \limits_{{k:i \in N_{k}^{R} }} E_{r\_RTS,t\_CTS}^{ik} .\mathop \sum \limits_{{j \in N_{k}^{R} }} r_{kj} + \mathop \sum \limits_{{k:i \in N_{i}^{R} }} E_{r\_DATA}^{ki} \cdot r_{ki} + P_{IL} \cdot dc_{i} } \right] \cdot T \le E_{i} \\ & r_{ij} = \left[ {\mathop \sum \limits_{{ WN_{i}^{j} \subseteq N_{i}^{R} }} \frac{1}{{\left| {WN_{i}^{j} } \right|}}\mathop \prod \limits_{{{\text{k}} \in WN_{i}^{j} }} dc_{k} \mathop \prod \limits_{{{\text{k}} \in SN_{i}^{j} }} \left( {1 - dc_{k} } \right)} \right] \cdot \mathop \sum \limits_{{j \in N_{i}^{R} + \left\{ {S_{i} } \right\}}} r_{ij} \\ & r_{{iS_{i} }} = \left[ { \mathop \prod \limits_{{{\text{k}} \in N_{i}^{R} }} \left( {1 - dc_{k} } \right)} \right] \cdot \mathop \sum \limits_{{j \in N_{i}^{R} + \left\{ {S_{i} } \right\}}} r_{ij} \\ \end{aligned} $$
(37)

In the next section we present the procedure of solving the EB-JRADCS problem.

3 Solving the EB-JRADCS Problem

It is clear that problem (37) is a highly nonlinear and non-convex problem generally. To solve this problem, first we try to conform it to one of the classic non-linear programming problems. To this end, first some primary preliminaries and definitions adopted from [13] are introduced in the beginning of this section.

Definition 1

Afunction M(x) is monomial if

$$ M(x) = a \cdot \mathop \prod \limits_{k = 1}^{n} x_{k}^{{\alpha_{k} }} $$
(38)

where a is a nonnegative constant coefficient and exponential constants \( \alpha_{k} \) are real numbers.

Definition 2

A function P(x) is posynomial if

$$ P(x) = \mathop \sum \limits_{i} M(x) $$
(39)

where the functions M i (x) are arbitrary monomial functions.

Definition 3

A function \( \varPhi (x) \) is called signomial if it is in the same form as a posynomial function except that multiplicative constant coefficients can be negative.

Definition 4: Signomial Geometric Programming (SGP) Problem

A signomial geometric programming (SGP) problem is an optimization problem of the form:

$$ \left\{ {\begin{array}{*{20}l} {min} \hfill & {\varPhi_{0} (x)} \hfill \\ {\varPhi_{i} \left( x \right) \le 1,} \hfill & {\forall i = 1, \ldots , p} \hfill \\ {\varPhi_{i} \left( x \right) = 1,} \hfill & {\forall i = p + 1, \,p + 2 , \ldots ,q} \hfill \\ \end{array} } \right. $$
(40)

where function \( \varPhi_{i} (x) \) is signomial for all of the values \( i \in [0,q] \). In special case, if \( \varPhi_{i} (x) \) is posynomial for \( i \in [0,p] \) and monomial for \( i \in [p + 1,q], \) the SGP problem is well known as standard geometric programming (GP) problem. In [15] it has been shown that a GP problem can be turned into an equivalent convex optimization problem and thus solved efficiently. But a SGP problem, in general, is an intrinsically intractable NP-hard problem and difficult to solve for global optimality. In [13, 16] two new methods have been introduced and presented in order to solve SGP problem. According to the above definitions, we can easily conform the EB-JRADCS problem into a SGP problem with replacing variable T by q −1. Since at this problem objective function is posynomial and the constraints are as signomial functions. In the following we briefly illustrate the procedure of solving a SGP problem in the special case of posynomial objective function according to the method presented in [13]. The interested readers are referred to [13] for further details on solving the problem in general form and convergence proof. At this method, the signomial constraints should be converted into the standard constraints usable in a GP problem. Since the procedure of converting unequal signomail constraint is different from the equal one, at two the following parts the procedures are described briefly.

3.1 Uunequal Signomial Constraints Conversion

Since in the standard GP problem, unequal constraints are posynomial, therefore unequal signomail constraints in SGP problem should be converted into posynomial terms. To this end, it is clear that a signomial function \( \varPhi_{i} (x) \) can be written as the difference of two posynomials \( \varPhi_{i}^{ + } (x) \) and \( \varPhi_{i}^{ - } (x) \) as follows:

$$ \varPhi_{i} (x) = \varPhi_{i}^{ + } (x) - \varPhi_{i}^{ - } (x) $$
(41)

In this case, unequal signomial \( \varPhi_{i} (x) \le 1 \) can be written as follows:

$$ \frac{{\varPhi_{i}^{ + } (x)}}{{1 + \varPhi_{i}^{ - } (x)}} \le 1 $$
(42)

Now to convert the left hand side of (42) into posymonial function the denominator of the fraction is approximated to a monomial function. For this purpose, consider a posynomial function as \( P(x) = \sum\nolimits_{k} {M_{k} (x)} \) in which functions M k (x) are monomial terms. The required monomial approximation can be calculated using the following arithmetic–geometric mean inequality [17].

$$ g(x) \ge \hat{g}(x) = \mathop \prod \limits_{k} \left( {\frac{{u_{k} (x)}}{{\alpha_{k} (x_{0} )}}} \right)^{{\alpha_{k} (x_{0} )}} $$
(43)

where parameters \( \alpha_{k} (x_{0} ) \) can be computed as follows:

$$ \alpha_{k} (x_{0} ) = \frac{{u_{k} (x_{0} )}}{{g(x_{0} )}} \quad \forall k $$
(44)

where x 0 is a positive and fixed point. It has been shown in [17] that the approximation of (43) is the best local monomial approximation of P(x) near x 0. Finally by applying the described monomial approximation to denominator of constraint (42), the constraint will be transformed into a posynomial function.

3.2 Equal Signomial Constraints Conversion

To convert equal signomial constraint as \( \varPhi_{i} (x) = 1 \) into a standard constraint useable in GP problem, by using (41) two inequality constraints are constructed as follows:

$$ \left\{ {\begin{array}{*{20}l} {\frac{{\varPhi_{i}^{ + } (x)}}{{1 + \varPhi_{i}^{ - } (x)}} \le 1} \hfill \\ {\frac{{\varPhi_{i}^{ + } (x)}}{{1 + \varPhi_{i}^{ - } (x)}} \ge s_{i}^{ - 1} ,\quad s_{i} \ge 1} \hfill \\ \end{array} } \right. $$
(45)

Or equivalently:

$$ \left\{ {\begin{array}{*{20}l} {\frac{{\varPhi_{i}^{ + } (x)}}{{1 + \varPhi_{i}^{ - } (x)}} \le 1} \hfill \\ {\frac{{\left( {1 + \varPhi_{i}^{ - } (x)} \right) \cdot s_{i}^{ - 1} }}{{\varPhi_{i}^{ + } (x)}} \le 1,\quad s_{i} \ge 1} \hfill \\ \end{array} } \right. $$
(46)

In the inequalities (45) and (46), s i is an auxiliary variable. As s i approaches to 1, inequalities (46) will approach to equality and so \( \varPhi_{i} (x) \) will approaches to 1. To accomplish this approach, all variables s i is added to objective function as penalty term. Thus the new objective function can be rewritten as follows:

$$ \varPhi_{0} (x) + \mathop \sum \limits_{i} w_{i} \cdot s_{i} $$
(47)

By using this policy when objective function is minimized s i is forced to approach to 1 for all values i.

In (47), w i > 0 are weighting coefficients with sufficiently large values. As it is seen, in the case of existence of any equality constraint, the converting process is more complicated than inequality one and according to [13], the rate of convergence will be slow.

Now, two unequal constraints in (46), based on what described in Sect. 3.1 are transformed into unequal posynomial constraints which are allowable expressions in GP problem. In fact this process is performed by means of converting the denominators of two unequal constraints into their equivalent monomials. Finally, after converting all unequal and equal signomial constraints, a standard GP problem is obtained which can be solved efficiently. Then in order to compute the global optimum solution, an iterative algorithm is used which has been introduced in [13]. It has been proven that the proposed iterative algorithm converges to the global optimum solution. Before presenting the algorithm, first we return to our problem and describe the procedure of converting it into the standard problem that will be solvable by this algorithm. In EB-JRADCS problem, flow conservation constraints and FS constraints are equal signomial constraints. So, according to Sect. 3.2 the constrains most be converted into equivalent approximate posynomial constraints. This procedure is almost easy for flow conservation constraints but because of being long terms in FS constraints the converting process would be quite complex. Also as it mentioned above, the rate of algorithm convergence will be so slow. In the following theorem, we show that these constraints can be relaxed to unequal form without any effect on the problem solution.

Theorem 1

In EB-JRADCS problem, if equal constraints related to FS constraints are transformed into unequal constraints, the solution of the problem would not change.

Proof

To prove Theorem 1, first we state and prove the following lemma.

Lemma 1

Suppose that x i are non-negative variables and a i are non-negative coefficients for all of the values \( i = 1,2, \ldots ,N \) such that a i  ≤ 1 and two following expressions hold.

$$ x_{i} \ge a_{i} \cdot \mathop \sum \limits_{n = 1}^{N} x_{n} \quad and \quad \mathop \sum \limits_{i = 1}^{N} a_{i} = 1 $$
(48)

Then it can be concluded that for all of the values \( i = 1,2, \ldots ,N, \) the following equalities hold:

$$ x_{i} = a_{i} \cdot \mathop \sum \limits_{n = 1}^{N} x_{n} $$
(49)

To prove this lemma, we can use reductive ad absurdum. So let us consider the equality (49) is not true for only \( i = j,\,j \in [1,N], \) Hence according to the assumption of the lemma we have:

$$ x_{i} = a_{i} \cdot \mathop \sum \limits_{n = 1}^{N} x_{n} \quad \forall i = 1,2, \ldots ,N\quad and\quad i \ne j\quad and\quad x_{j} > a_{j} \cdot \mathop \sum \limits_{n = 1}^{N} x_{n} $$
(50)

So we have:

$$ x_{1} = a_{1} \cdot \mathop \sum \limits_{n = 1}^{N} x_{n} ,\quad x_{2} = a_{2} \cdot \mathop \sum \limits_{n = 1}^{N} x_{n} , \ldots ,x_{j} > a_{j} \cdot \mathop \sum \limits_{n = 1}^{N} x_{n} , \ldots , x_{N} = a_{N} \cdot \mathop \sum \limits_{n = 1}^{N} x_{n} $$
(51)

By adding all of the terms in the both sides of the relations in (51), we conclude:

$$ \mathop \sum \limits_{i = 1}^{N} x_{i} > \mathop \sum \limits_{i = 1}^{N} a_{i} . \mathop \sum \limits_{n = 1}^{N} x_{n} \Rightarrow 0 > 0 $$
(52)

But as it is seen the above resulted inequality leads to contradiction. Hence the assumption (50) is wrong and (49) will be true for all of the values \( i = 1,2, \ldots ,N. \).

Now to prove Theorem 1, we define coefficients a j as follows:

$$ a_{j} = \left\{ {\begin{array}{*{20}l} {\mathop \sum \limits_{{ WN_{i}^{j} \subseteq N_{i}^{R} }} \frac{1}{{\left| {WN_{i}^{j} } \right|}}\mathop \prod \limits_{{{\text{k}} \in WN_{i}^{j} }} dc_{k} \mathop \prod \limits_{{{\text{k}} \in SN_{i}^{j} }} \left( {1 - dc_{k} } \right)} \hfill & {j \in N_{i}^{R} } \hfill \\ {\mathop \prod \limits_{{{\text{k}} \in N_{i}^{R} }} (1 - dc_{k} )} \hfill & { j = S_{i} } \hfill \\ \end{array} } \right. $$
(53)

But according to (6) we have:

$$ \mathop \sum \limits_{{j \in N_{i}^{R} + \left\{ {S_{i} } \right\}}}^{N} a_{j} = 1 $$
(54)

Now by applying the result of Lemma 1 and using (10) and (11), Theorem 1 is proved and so it concludes two bellow constraints:

$$ r_{ij}^{ - 1} \cdot \left[ {\mathop \sum \limits_{{ WN_{i}^{j} \subseteq N_{i}^{R} }} \frac{1}{{\left| {WN_{i}^{j} } \right|}}\mathop \prod \limits_{{{\text{k}} \in WN_{i}^{j} }} dc_{k} \mathop \prod \limits_{{{\text{k}} \in SN_{i}^{j} }} \left( {1 - dc_{k} } \right)} \right] \cdot \mathop \sum \limits_{{j \in N_{i}^{R} + \left\{ {S_{i} } \right\}}} r_{ij} \le 1 $$
(55)
$$ r_{{iS_{i} }}^{ - 1} \cdot \left[ {\mathop \prod \limits_{{{\text{k}} \in N_{i}^{R} }} \left( {1 - dc_{k} } \right)} \right] \cdot \mathop \sum \limits_{{j \in N_{i}^{R} + \left\{ {S_{i} } \right\}}} r_{ij} \le 1 $$
(56)

Now, using (55) and (56), in the EB-JRADCS Problem, energy constraints and FS constraints are as unequal signomial constraints which must be converted into posymonials. But due to largeness of these constraints, this process will be complicated even in the network with a few nodes. To solve this complication, we use a small variable changing in these constraints called off cycle (oc) as oc = 1 − dc. This only will add following auxiliary equal constraints to the problem.

$$ dc_{i} + oc_{i} = 1 \quad \forall i \in V $$
(57)

By applying this variable changing, FS constraints and also energy constraints are converted into posynomial and thus don’t need any extra converting. The only required conversion to solve the problem is converting equal flow conservation constraints and described auxiliary constraints in (57) into their approximate equivalences as has been illustrated in Sect. 3.2. In order to convert flow conservation constraints we can write:

$$ \begin{aligned} & \begin{array}{*{20}c} {\sum\nolimits_{{j \in N_{i}^{R} }} {r_{ij} } } \\ {\overline{{g_{i} + \sum\nolimits_{{k:i \in N_{k}^{R} }} {r_{ki} } }} } \\ \end{array} \le 1,\quad \forall i \in V \Rightarrow \begin{array}{*{20}c} {\sum\nolimits_{{j \in N_{i}^{R} }} {r_{ij} } } \\ {\overline{{\left( {\frac{{g_{i} }}{{\alpha_{0} }}} \right)^{{\alpha_{0} }} .\prod\nolimits_{{k:i \in N_{k}^{R} }} {\left( {\frac{{r_{ki} }}{{\alpha_{ki} }}} \right)}^{{\alpha_{ki} }} }} } \\ \end{array} \le 1 \\ & \frac{{\left( {g_{i} + \sum\nolimits_{{k:i \in N_{k}^{R} }} {r_{ki} } } \right) \cdot s^{ - 1} }}{{\sum\nolimits_{{j \in N_{i}^{R} }} {r_{ij} } }},\quad \forall i \in V \Rightarrow \frac{{\left( {g_{i} + \sum\nolimits_{{k:i \in N_{k}^{R} }} {r_{ki} } } \right) \cdot s^{ - 1} }}{{\prod\nolimits_{{j \in N_{i}^{R} }} {\left( {\frac{{r_{ij} }}{{\beta_{ij} }}} \right)} }} \le 1 \\ \end{aligned} $$
(58)

Such that α 0, α ki and β ij would be calculated as follows:

$$ \begin{aligned} \alpha_{0} & = g_{i} \left/\left( {g_{i} + \mathop \sum \limits_{{k:i \in N_{k}^{R} }} r_{ki}^{(m)} } \right)\right.,\quad \alpha_{ki} = r_{ki}^{(m)} \left/\left( {g_{i} + \mathop \sum \limits_{{k:i \in N_{k}^{R} }} r_{ki}^{(m)} } \right)\right., \\ \beta_{ij} & = r_{ij}^{(m)} \left/\left( {\mathop \sum \limits_{{j \in N_{i}^{R} }} r_{ij}^{(m)} } \right)\right. \\ \end{aligned} $$
(59)

Similarly, to convert auxiliary constraints in (57), we have:

$$ dc_{i} + oc_{i} \le 1\quad \forall i \in V $$
(60)
$$ \frac{{z_{i}^{ - 1} }}{{dc_{i} + oc_{i} }} \le 1 \quad \forall i \in V \Rightarrow \frac{{z_{i}^{ - 1} }}{{\left( {\frac{{dc_{i} }}{{\gamma_{i}^{1} }}} \right)^{{\gamma_{i}^{1} }} \cdot \left( {\frac{{oc_{i} }}{{\gamma_{i}^{2} }}} \right)^{{\gamma_{i}^{2} }} }} \le 1 $$
(61)

Such that \( \gamma_{i}^{1} \) and \( \gamma_{i}^{2} \) would be calculated as:

$$ \gamma_{i}^{1} = dc_{i}^{(m)} \left/\left( {dc_{i}^{(m)} + oc_{i}^{(m)} } \right)\right. ,\quad \gamma_{i}^{2} = oc_{i}^{(m)} \left/\left( {dc_{i}^{(m)} + oc_{i}^{(m)} } \right)\right. $$
(62)

In (59) and (62), \( r_{ki}^{(m)} (\forall k) , r_{ij}^{(m)} (\forall j) , dc_{i}^{(m)} \) and \( oc_{i}^{(m)} \) are given values that will be described later. Also s i and z i are auxiliary variables that will add to objective function as penalty terms.

Finally, EB-JRADCS problem for a given m will be rewritten as follows:

$$ \begin{aligned} & minimize\,\,q + \mathop \sum \limits_{i = 1}^{N} w_{i}^{(m)} \cdot s_{i} + u_{i}^{(m)} \cdot z_{i} \\ & \alpha_{0} = g_{i} \left/\left( {g_{i} + \mathop \sum \limits_{{k:i \in N_{k}^{R} }} r_{ki}^{(m)} } \right)\right.,\quad \alpha_{ki} = r_{ki}^{(m)} \left/\left( {g_{i} + \mathop \sum \limits_{{k:i \in N_{k}^{R} }} r_{ki}^{(m)} } \right)\right.,\quad \beta_{ij} = r_{ij}^{(m)} \left/\left( {\mathop \sum \limits_{{j \in N_{i}^{R} }} r_{ij}^{(m)} } \right)\right. \\ & \begin{array}{*{20}c} {\sum\nolimits_{{j \in N_{i}^{R} }} {r_{ij} } } \\ {\overline{{\left( {\frac{{g_{i} }}{{\alpha_{0} }}} \right)^{{\alpha_{0} }} \cdot \prod\nolimits_{{k:i \in N_{k}^{R} }} {\left( {\frac{{r_{ki} }}{{\beta_{ki} }}} \right)}^{{\alpha_{ki} }} }} } \\ \end{array} \le 1,\quad \frac{{\left( {g_{i} + \sum\nolimits_{{k:i \in N_{k}^{R} }} {r_{ki} } } \right) \cdot s^{ - 1} }}{{\prod\nolimits_{{j \in N_{i}^{R} }} {\left( {\frac{{r_{ij} }}{{\beta_{ij} }}} \right)}^{{\beta_{ij} }} }} \le 1 \quad \forall i \in V \\ & \frac{1}{{E_{i} }}\left[ {\mathop \sum \limits_{{j \in N_{i}^{R} + \left\{ {S_{i} } \right\}}} E_{t}^{ij} \cdot r_{ij} + \left( {\mathop \sum \limits_{k = 0}^{{\left| {N_{i}^{R} } \right|}} CRT\left( {N_{i}^{R} , k} \right) \cdot \mathop \sum \limits_{{\Omega_{i}^{k} \subseteq N_{i}^{R} }} \left[ {\mathop \prod \limits_{{ {\text{k}} \in \Omega_{i}^{k} }} dc_{k} \mathop \prod \limits_{{{\text{k}} \in N_{i}^{R} - \Omega_{i}^{k} }} oc_{k} } \right] \cdot P_{IL} } \right) \cdot \mathop \sum \limits_{{j \in N_{i}^{R} + \left\{ {S_{i} } \right\}}} r_{ij} } \right. \\ & \quad \left. { +\,dc_{i} \cdot \mathop \sum \limits_{{k:i \in N_{k}^{R} }} E_{{r_{RTS} ,t\_CTS}}^{ik} \cdot \mathop \sum \limits_{{j \in N_{k}^{R} }} r_{kj} + \mathop \sum \limits_{{k:i \in N_{i}^{R} }} E_{r\_DATA}^{ki} \cdot r_{ki} + P_{IL} \cdot dc_{i} } \right] \cdot q^{ - 1} \le 1\quad \forall i \in V \\ & r_{ij}^{ - 1} \cdot \left[ {\mathop \sum \limits_{{ WN_{i}^{j} \subseteq N_{i}^{R} }} \frac{1}{{\left| {WN_{i}^{j} } \right|}}\mathop \prod \limits_{{{\text{k}} \in WN_{i}^{j} }} dc_{k} \mathop \prod \limits_{{{\text{k}} \in SN_{i}^{j} }} oc_{k} } \right] \cdot \mathop \sum \limits_{{j \in N_{i}^{R} + \left\{ {S_{i} } \right\}}} r_{ij} \le 1\quad \forall i \in V \\ & r_{{iS_{i} }}^{ - 1} \cdot \left[ { \mathop \prod \limits_{{{\text{k}} \in N_{i}^{R} }} oc_{k} } \right] \cdot \mathop \sum \limits_{{j \in N_{i}^{R} + \left\{ {S_{i} } \right\}}} r_{ij} \le 1\quad \forall i \in V \\ & \gamma_{i}^{1} = dc_{i}^{(m)} \left/\left( {dc_{i}^{(m)} + oc_{i}^{(m)} } \right)\right. ,\quad \gamma_{i}^{2} = oc_{i}^{(m)} \left/\left( {dc_{i}^{(m)} + oc_{i}^{(m)} } \right)\right. \quad \forall i \in V \\ & dc_{i} + oc_{i} \le 1,\quad \frac{{z_{i}^{ - 1} }}{{\left( {\frac{{dc_{i} }}{{\gamma_{i}^{1} }}} \right)^{{\gamma_{i}^{1} }} \cdot \left( {\frac{{oc_{i} }}{{\gamma_{i}^{2} }}} \right)^{{\gamma_{i}^{2} }} }} \le 1 \quad \forall i \in V \\ & s_{i} \ge 1,\quad z_{i} \ge 1\quad \forall i \in V \\ \end{aligned} $$
(63)

Now we use iterative algorithm described in [13] and conform it to solve our problem. The steps of the adapted algorithm are given bellow:

Step 0

Set iteration counter m = 0. Choose initial feasible values for the variables \( r_{ij}^{(0)} , \) \( dc_{i}^{(0)} \) and \( oc_{i}^{(0)} . \) For this purpose, one solution can be obtained by simply solving the simultaneous nonlinear Eqs. (1), (10) and (11). Also give initial weights \( w_{i}^{(0)} , u_{i}^{(0)} \) and solution accuracy \( \varepsilon > 0. \)

Step 1

At the mth iteration, obtain all of the constraints in (63) with the given \( r_{ij}^{(m - 1)} \), \( dc_{i}^{(m - 1)} \) and \( oc_{i}^{(m - 1)} \).

Step 2

Solve the standard GP problem (63) to compute \( r_{ij}^{(m)} \), \( dc_{i}^{(m)} \) and \( oc_{i}^{(m)} \) with weighting coefficients \( w_{i}^{(m - 1)} , u_{i}^{(m - 1)} \).

Step 3

If the expressions \( \left| {r_{ij}^{(m)} - r_{ij}^{(m - 1)} } \right| \le \varepsilon \), \( \left| {dc_{i}^{(m)} - dc_{i}^{(m - 1)} } \right| \le \varepsilon \) and \( \left| {oc_{i}^{(m)} - oc_{i}^{(m - 1)} } \right| \le \varepsilon \) are satisfied \( \forall i \in V \) and \( j \in N_{i}^{R} \) then stop the algorithm, else go to Step 4.

Step 4

Update the weighting coefficients \( w_{i}^{(m)} , u_{i}^{(m)} \) with \( w_{i}^{(m)} = W(w_{i}^{(m - 1)} ) \), \( u_{i}^{(m)} = U(u_{i}^{(m - 1)} ) \); where W and U are monotonically increasing functions of \( w_{i}^{(m - 1)} \) and \( u_{i}^{(m - 1)} \) respectively. Set m = m + 1 and return to Step 1.

4 Simulation and Numerical Results

To simulate and evaluate this problem, we consider a sensor network including ten sensor nodes distributed in a square area of 200 m by 200 m. Also it is assumed that two sink nodes have been located at two separate positions of the area such that each sensor node is able to communicate at least with one of the sink nodes directly. We suppose that each sensor node has 3 V AA batteries with 2000 mAh capacity. All sensor nodes generate same and fixed data rate. The parameter settings for the simulation have been listed in Table 1. The parameters related to energy consumption have been selected similar to [18] based on Motes. To solve the problem (63) in each iteration, we use MATLAB based solver GPPLAB designed by Mutapcic et al. [19]. In Fig. 3, the configuration of the assumed network considering RTS flooding radius of 80 m has been shown. In this figure, each solid line shows a route between two sensor nodes or a route between one sensor node and the sink node which is in RTS flooding radius of the sensor node. Also each dash line shows a direct route between a sensor node and its nearest sink node which is not in its RTS flooding radius. It is clear that all of the obtained constraints in EB-JRADCS problem are quite dependent on RTS flooding radius. In the first experiment, we investigate that how the mentioned iterative algorithm converges to the optimum solution for a given RTS flooding radius. To this end, data generation rate is considered to be 0.001 packet/s and RTS flooding radius is assumed to be 80 m. In Fig. 4 the optimum solution of EB-JRADCS problem means maximum network lifetime versus iteration number has been shown. As it is observed, the solution of the problem converges to its optimum level after 31 iterations. In the second experiment, we evaluate the effect of data generation rate on the network lifetime. In Fig. 5 the calculated maximum network lifetime versus various data generation rates from 0.001 to 0.1 packet/second and fixed RTS flooding radius of 80 m has been shown. As expected, by increasing data generation rate, network lifetime will decrease. Finally in the third experiment, we investigate the effect of changing RTS flooding radius on the maximum network lifetime. In Fig. 6, the network lifetime versus RTS flooding radius in the range of 60–120 m has been shown. As it is observed, first, the network lifetime increases by increasing RTS flooding radius until it reaches to its maximum level at radius 89 m and then by more increasing RTS flooding radius, network lifetime reduces. We can illustrate the reason of this result in the fact that by increasing RTS flooding radius, consumed energy for sending RTS packets will start to increase, but on the other hand less sensor nodes ought to be awake to receive RTS packets and so duty cycle of them will reduce. Hence this reduction overcomes to increasing energy consumed due to increasing RTS flooding radius until a threshold level. After the threshold level this procedure will be occurred conversely. It means when RTS flooding radius increases more than the threshold level, the energy consumed due to this increasing will dominate to energy consumed due to duty cycle of nodes. In Fig. 7, the network configuration in the case of RTS flooding radius of 89 m has been shown.

Table 1 Parameter settings [18]
Full size table
Fig. 3
figure 3

Sensor network configuration with RTS flooding radius of 80 m

Full size image
Fig. 4
figure 4

Convergence of network lifetime to its maximum value

Full size image
Fig. 5
figure 5

Network lifetime versus data generation rate

Full size image
Fig. 6
figure 6

Network lifetime versus RTS flooding radius

Full size image
Fig. 7
figure 7

Sensor network configuration with RTS flooding radius of 89 m

Full size image

In Table 2, the obtained flow rate of data packets, duty cycle of sensor nodes and remaining energy at the ending of network lifetime in the case of RTS flooding radius of 89 m and data generation rate of 0.001 packet/s has been shown. As it is seen, under the achieved flow rates and duty cycles, the amount of remaining energy in all of the sensor nodes has been equal to zero. It means that consumed energy has been balanced in all of the sensor nodes. In other words all of the nodes in the network run out of energy exactly at the same time equal to maximum network lifetime.

Table 2 Flow rate of data packets on all routes, duty cycle of sensor nodes and their remaining energy
Full size table

5 Conclusion

In this paper, the issue of lifetime maximization in WSNs based on Energy Balance, employing Joint routing and asynchronous duty cycle scheduling (EB-JRADCS) techniques was introduced. This problem was modeled based on a new asynchronous MAC protocol named FRTS–RCTS. This protocol was the modified version of traditional CSMA/CA protocol which supported the duty cycle scheduling mechanism. With the aid of the proposed protocol new constraints named as FS constraints, were found which jointed network lifetime maximization parameters including flow rate of information on any route and duty cycle of nodes. Also the precise computation of energy consumption based on the FRTS–RCTS protocol was accomplished. With the small change of a parameter in the formulated EB-JRADCS problem, it was converted into the SGP problem and due to the complexity of solving the resulted problem, first it was transformed into a simpler problem by relaxing FS constraints from equal to unequal form. Then the simplified problem was solved utilizing a specific convexification method and the global optimum solution of the network lifetime was evaluated under various scenarios. The simulation results verified that under achieved flow rates and duty cycles, the amount of remaining energy in all of the sensor nodes had been equal to zero. In other words, the consumed energy had been balanced in all of the sensor nodes. The achieved optimum solution can be used as a benchmark for evaluating and comparing distributed and heuristic methods that aim to increase the network lifetime. In the future work we are going to find a heuristic distributed algorithm that will use only some local information to adjust duty cycle of nodes which in turn will lead to calculation of data flow rates in all of the routes based on found FS constraints in this paper.