Research on multi-service slice resource allocation over licensed and unlicensed bands

Abstract

Cognitive radio is known to be an important technology to overcome the shortage of spectrum resources, and the resource allocation problem of multi-service multi-carrier slice in 5G system has remained a challenge. In this paper, a multi-leader multi-follower Stackelberg game is designed to analyze the interaction between operators and users over licensed and unlicensed bands. Further, we verify the impact of users’ dynamic throughput allocation ratio on Nash equilibrium (NE) in the game. The game is divided into two independent subgames: licensed band and unlicensed band games. A simplified Vickrey-Clarke-Groves algorithm is designed in the former sub-game to ensure the fairness of user transmission. In the latter, an interference price is set to protect the transmission performance of primary users in unlicensed band. By predicting the actions of other players, optimal prices or spectrum and power demands are set in a non-cooperative way. We prove the existence of NE solution in the Stackelberg game and design dynamic distributed algorithms for operators and users to achieve NE. Simulation results show the effectiveness of our proposed resource management schemes based on Stackelberg game. Compared to other Stackelberg models, our scheme provides users with high-quality services and provides a guidance on pricing strategies for operators.

1 Introduction

In the era of rapid development of information, a large number of users transmit through radio bands [1]. As a scarce communication resource, the traditional spectrum allocation strategies adopt fixed frequency allocation, which divide the required spectrum resources into fixed bands and allocate them to licensed users [2]. Due to the explosive growth of information and new applications, the existing wireless communication applications have occupied most of the available radio frequency bands, and the frequency bands that can be allocated to these emerging applications are less and less, while most of the licensed spectrum is in the state of extremely low utilization, resulting in the waste of spectrum resources [3]. How to achieve an efficient allocation of resources under the condition of limited spectrum resources is one of the urgent problems to be solved in today’s wireless communication technology. Network slicing and cognitive radio (CR) are regarded as two key technologies to solve the problems of spectrum resource shortage and low spectrum utilization [4], which can combine multiple spectrum resources for communication transmission and use unlicensed spectrum to overcome the shortage of spectrum resources. Network slicing provides flexible customized service and CR provides a prominent solution for the shortage on spectrum. Combining spectrum sharing technology with resource allocation of different systems is an important means to achieve effective and rational utilization of 5G system resources.

There have been some existing works on spectrum sharing and channel coexistence of different systems.

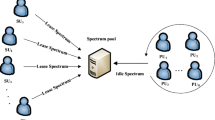
First, the spectrum sharing method is the first problem to be solved in unlicensed bands. The transmission of secondary users (SUs) in the unlicensed bands will affect the transmission of primary users (PUs). If the interference of SUs cannot be effectively controlled, the transmission quality of PUs will be seriously affected [5]. Spectrum sharing can be achieved by shared spectrum pools, Non-Orthogonal Multiple Access (NOMA), spectrum leasing [6,7,8,9], etc. Using multi-priority sequences and queuing theory to formulate an admission framework is an effective way to achieve dynamic resource management and interference control [10,11,12,13,14,15].Furthermore, setting interference price for SUs has become an effective resource management method to compensate the PUs [16,17,18,19]. Generally, the PUs set interference price, and SUs pay the interference price for channel occupancy. In this way, the interference to the PU can be reduced and the performance of spectrum sharing can be optimized.

Secondly, how to allocate the licensed and unlicensed spectrum resources for SUs is the next problem to be solved. The different resource allocation strategies of users will greatly affect the channels’ communication efficiency and users’ experience. There are some existing works on resource allocation in licensed and unlicensed bands [20,21,22,23,24], including dynamic duty ratio, water-filling algorithm, estimation of spectrum occupancy, etc. These solutions improve system fairness and system capacity in cognitive networks. As an optimization theory that studies the behavioral decision-making among multiple participants, game theory plays an important role in the complex network environment. The multi-objective resource optimization schemes of operators and users were proposed based on game theory, including Stackelberg game, alliance game, bargaining game [25,26,27,28,29], etc. These solutions improve system performance with limited channel information.

In 5G/6G networks, network virtualization technology and slicing technology are widely used. Multiple mobile network operators share infrastructure networks, including licensed and unlicensed spectrum resources. However, in this multi-operator multi-slice network, the problem of spectrum resource allocation has not been well resolved. In multi-operator scenarios, game theory is a better way to solve the competition and allocation of wireless resources. To the best of our knowledge, there are no solutions for this problem. We construct the network model and prove the interactive impact of the dynamic allocation of resources between licensed and unlicensed bands, especially how to maximize the users’ revenue when selecting two bands simultaneously. A solution based on the Stackelberg game is proposed to solve the problems of interference price and user resource allocation in cognitive networks.

The main contributions of this paper are as follows:

• 1) A multi-operator multi-service slices network model in the licensed and unlicensed bands is constructed. We investigate the spectrum resource allocation mechanism of multi-operator in the licensed band, the power control mechanism in the unlicensed band, and the dynamic throughput allocation mechanism of multi-service users. We formulate the resource allocation problem as the multi-leader multi-follower Stackelberg game to solve the problem.

• 2) For the problem of resource allocation in cognitive networks, the simplified Vickrey-Clarke-Groves (VCG) algorithm and interference pricing strategy are used to reduce interference to PU and improve users’ service quality. The theory based on Stackelberg game analyses the interactions between operators and users, which can prove that the game exists Nash equilibrium.

• 3) Distributed dynamic update algorithms are developed to achieve Nash equilibrium in the multi-operator and multi-user scenarios, including the operators’ interference price setting and the users’ power and spectrum allocation. The revenue of operators and transmission rates of users are improved.

The rest of the paper is organized as follows. In Sect. 2, we discuss the system model. Section 3 is problem formulation. Section 4 discusses the solution to the problem. Section 5 is the simulation evaluation. Finally, we summarize our work in Sect. 6.

Table 1 Notations and symbols

2 System model

2.1 Network model

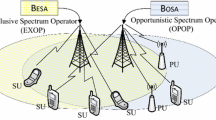
We consider the underlay CR network shown in Fig. 1 : M operators serve N users in the coverage area. The advantage of the underlay mode is that it does not need to collect much channel information of users. We assume that there is a common unlicensed band in the base station deployment coverage of operator i, $\forall i \in \varvec{M} = \left\{ {1,2, \ldots \ldots ,M} \right\}$. Users can use the operator’s licensed band spectrum and the public unlicensed band spectrum for communication. It is assumed that operators support L types of service slices in both licensed and unlicensed bands, which can be cut dynamically to meet the needs of different types of services by customized aggregation slice. The service type is represented by l, $l \in \varvec{L} = \left\{ {1,2, \ldots \ldots ,L} \right\}$. The spectral bandwidth of type L service slice owned by operator i is $B_i^{\left( l \right) }$. User j, $\forall j \in \varvec{N} = \left\{ {1,2, \ldots \ldots ,N} \right\}$, selfishly consider their own benefits, and obtain communication resources from licensed and unlicensed bands to support communication services. We further divide users from the perspective of operators and business types, $\forall j \in$ $\varvec{N_{i,l}}$ is a set of spectrum slicing service users that operator i provides class l service. If user j fails to gain enough resources from the licensed band or wants to gain higher profit from the throughput, user j will also look for spectrum resources in the unlicensed spectrum to improve its service quality. A summary of key notations and symbols is given in Table 1.

Fig. 1

System architecture of the network

We assume that users share the licensed band by OFDMA and will not interfere with each other [18, 29, 30]. When operator i broadcasts the unit spectrum slice price $\rho _i^{\left( l \right) }\;$ for supporting service l, user j purchases spectrum resources through competition to support transmission requirements.

If the users are not satisfied with the services in the licensed band or want to further improve their economic benefits, they can choose to set the transmission power in the unlicensed bands for transmission, as shown in Fig. 2. Assuming that N users have the right to access unlicensed band. In the unlicensed band, all operators use the public spectrum pool in the unlicensed band and compete with other operators with distributed access points. In order to ensure the isolation of services, we assume that all operators have agreed that there are L mutually isolated sub-bands in the unlicensed band for unlicensed band services, and each sub-band corresponds to a type of user’s service.

Fig. 2

Resource allocation of user

2.2 Licensed band

In the licensed band, we use the simplified Vickrey-Clarke-Groves algorithm to set the penalty mechanism, that is, assuming that when the user j, $j \in {N_{i,l}}$ reports the spectrum proportion requirement as$\{ a_{i,1}^{\left( l \right) },a_{i,2}^{\left( l \right) }, \ldots \ldots ,a_{i,{N_{i,l}}}^{\left( l \right) }\},$ the actual allocated spectrum slice bandwidth is $\left\{ {\frac{{a_{i,1}^{\left( l \right) }}}{{\mathop \sum \nolimits _{j \in {N_{i,l}}} a_{i,j}^{\left( l \right) }}}B_i^{\left( l \right) },\frac{{a_{i,2}^{\left( l \right) }}}{{\mathop \sum \nolimits _{j \in {N_{i,l}}} a_{i,j}^{\left( l \right) }}}B_i^{\left( l \right) }, \ldots \ldots ,\frac{{a_{i,{N_{i,l}}}^{\left( l \right) }}}{{\mathop \sum \nolimits _{j \in {N_{i,l}}} a_{i,j}^{\left( l \right) }}}B_i^{\left( l \right) }} \right\},$ and the revenue set to be paid to operator i is still $\{ \rho _i^{\left( l \right) }a_{i,1}^{\left( l \right) }B_i^{\left( l \right) },\rho _i^{\left( l \right) }a_{i,2}^{\left( l \right) }B_i^{\left( l \right) }, \ldots \ldots ,\rho _i^{\left( l \right) }a_{i,{N_{i,l}}}^{\left( l \right) }B_i^{\left( l \right) }\}$. In this way, users can be encouraged to report the proportion of spectrum demand based on actual demand. Otherwise, false reporting of a higher proportion will lead to higher payment [31]. Meanwhile, operators will get less revenue when setting unreasonably high price. When the VCG algorithm and Stackelberg model are combined, the operator can give its own optimal price by predicting the user’s optimal response to reach an equilibrium solution.

2.3 Unlicensed band

In order to ensure the transmission quality of the primary users in the unlicensed band, all users use the method of listen before talk (LBT) for channel monitoring. For the users served by different operators, if they transmit in the same unlicensed band in the way of underlay, they will interfere with each other and affect the transmission of the primary users in the unlicensed band. Because the high transmission power of each user will strongly interfere with the transmission of other secondary users in the same sub-band, then affect the transmission quality of the whole unlicensed band. Therefore, we use the interference price ${r_i}$ to constrain the profit between the transmission power and channel revenue of users [16,17,18,19]. In a non-cooperative way, each operator i assigns its own transmission interference price ${r_i}$ to manage the unlicensed band according to the behavior of other operators and the response of users. When users want to use unlicensed band for service transmission, they need to pay interference prices to each operator i according to the transmission power.

For operator i , high interference price ${r_i}$ will reduce the willingness of users to transmit in the unlicensed band, and the operators may not charge any interference revenue brought by the unlicensed band. At the same time, low interference price ${r_i}$ will cause users to strongly interfere in the unlicensed band and affect the communication quality of all users in unlicensed band.

For users, after observed the price $\rho _i^{\left( l \right) }$ and interference price ${r_i}$ given by operators, they need to choose the appropriate spectrum proportion requirement $a_{i,j}^{\left( l \right) }\;$ in licensed band and transmission power ${p_j}$ in the unlicensed band to make fair and efficient use with other users. Therefore, users need to consider the response of other users, determine the most appropriate spectrum allocation scheme and transmit power, maximize the transmission revenue under the constraints of minimum throughput and maximum transmit power.

2.4 Revenue setting

Assumed that at the beginning of each time slot, operator i will determine its own unit licensed spectrum price $\rho _i^{\left( l \right) }$ and the unit unlicensed interference price ${r_i}$ in a non-cooperative way. Therefore, the revenue of operator i in the licensed band is:

$$\begin{aligned} {W_{i,a}} = \;\mathop \sum \limits _{l = 1}^L \mathop \sum \limits _{j \in {N_{i,l}}} \rho _i^{\left( l \right) }a_{i,j}^{\left( l \right) }B_i^{\left( l \right) } \end{aligned}$$

(1)

where $a_{i,j}^{\left( l \right) }$ is the proportion of spectrum demand of support service l purchased for user j, $B_i^{\left( l \right) }$ is the total bandwidth allocated for operator i to support service l in licensed band. Supposed that in the unlicensed band, the transmission power set by user j is $p_j$, then the revenue of operator i in unlicensed band is:

$$\begin{aligned} {W_{i,b}} = \;\mathop \sum \limits _{l = 1}^L r_i^{\left( l \right) }\mathop \sum \limits _{k = 1}^M \mathop \sum \limits _{j \in {N_{k,l}}} {g_j}{p_j} \end{aligned}$$

(2)

where ${g_j}$ is the transmission gain of user j in the unlicensed sub-band, $r_i^{\left( l \right) }$ is the interference price paid to operator i.

Total revenue of operator i in licensed and unlicensed bands:

$$\begin{aligned} {W_i} = {W_{i,a}} + {W_{i,b}} \end{aligned}$$

(3)

After each operator announced the unit spectrum slice price $\rho _i^{\left( l \right) }$ and interference price ${r_i}$, each user will compete for spectrum resources according to their own choice. We establish and solve the game by using non-cooperative complete information game. The user comprehensively measures the cost of licensed and unlicensed bands, and aggregates the two bands to meet their throughput standards.

Thus, the revenue of user j in the licensed band is:

$$\begin{aligned} U_{j,a}^{\left( l \right) } = {\gamma _j}\frac{{a_{i,j}^{\left( l \right) }}}{{\mathop \sum \nolimits _{j \in {N_{i,l}}} a_{i,j}^{\left( l \right) }}}B_i^{\left( l \right) }{R_{i,j}} - \rho _i^{\left( l \right) }a_{i,j}^{\left( l \right) }B_i^{\left( l \right) } \end{aligned}$$

(4)

where ${\gamma _j}$ is the profit coefficient of user j, ${\gamma _j}\frac{{a_{i,j}^{\left( l \right) }}}{{\mathop \sum \nolimits _{j \in {N_{i,l}}} a_{i,j}^{\left( l \right) }}}B_i^{\left( l \right) }{R_{i,j}}$ is the revenue for the purchase of $\frac{{a_{i,j}^{\left( l \right) }}}{{\mathop \sum \nolimits _{j \in {N_{i,l}}} a_{i,j}^{\left( l \right) }}}B_i^{\left( l \right) }$ bandwidth for spectrum transmission, $\rho _i^{\left( l \right) }a_{i,j}^{\left( l \right) }B_i^{\left( l \right) }$ is the interference price paid to operator i. ${R_{i,j}}$ is the Spectrum efficiency from user j to base station i in licensed band. Users purchase spectrum through OFDMA in license band. When ${p_{j}}$ is given, ${R_{i,j}}$ is a constant parameter.

The revenue of user j in the unlicensed band is:

$$\begin{aligned} U_{j,b}^{\left( l \right) } = {\gamma _j}B_u^{\left( l \right) }R_j^U - \mathop \sum \limits _{i = 1}^M r_i^{\left( l \right) }{g_j}{p_j} \end{aligned}$$

(5)

where $B_u^{\left( l \right) }$ is the unlicensed bandwidth for service l, $R_j^U$ is the spectrum efficiency in unlicensed band for users, $\;R_j^U = {\log _2}\left( {1 + \frac{{{p_j}{g_j}}}{{{p_{ - j}}{g_{ - j}} + {z_j}}}} \right)$. ${z_j}$ is the interference of primary user to user j in the unlicensed band. $\;{p_{ - j}}{g_{ - j}} = \mathop \sum \limits _{k = 1}^M \mathop \sum \limits _{z \in {N_{k,l}}} {p_z}{g_z} - {p_j}{g_j}$ is the interference of other users in the unlicensed band for user j. ${\gamma _j}B_u^{\left( l \right) }{R_j}$ is the profit that user j can get by choosing to transmit in unlicensed band and $\mathop \sum \limits _{i = 1}^M r_i^{\left( l \right) }{g_j}{p_j}$ is the sum of interference price to be paid to each operator for users to choose to transmit in unlicensed band.

Thus, the total revenue of user j in licensed and unlicensed band is:

$$\begin{aligned} {U_j} = {U_{j,a}} + {U_{j,b}} \end{aligned}$$

(6)

3 Problem formulation

In this section, we use the Stackelberg game to describe the problem mathematically. The advantage of the Stackelberg model is that operators can maximize their own revenue by predicting the users’ strategies, and users may maximize their own revenue by predicting the reaction of other participants according to the prices given by the operators. In the network, we introduce a distributed spectrum controller (SC) to serve each operator. A communication interface is defined between spectrum controllers of operators. Operators can exchange information and negotiate spectrum sharing rules to share spectrum resources fairly and effectively. Due to the competitive relationship between operators, operators will not be willing to exchange more detailed sensitive information. Therefore, some fuzzy information can be transmitted between operators, obtained through the statistics of all the base station information under each operator’s spectrum controller. Operators can forecast and analyze the information independently and give their slice price and interference price.

We abstract the game between operators and users as a multi-leader multi-follower Stackelberg game. In this game, the set $\varvec{M}$ as the set of leaders. Each operator uses the information collected by SC to predict the price strategy of other operators and the possible purchase strategy of users, independently gives its multi-service slice price and interference price. Therefore, the problems of operator i are as :

Leader:

$$\begin{aligned} \begin{aligned} Max\;\; {W_i}( \rho _i,r_i,\varvec{r_{ - i}^*},\varvec{a^*},\varvec{p^*})&= {W_{i,a}} + {W_{i,b}}\;,\;\forall i \in \varvec{M} \\ s.t. \;\;0 \le p_j^*&\le {p^{max}}\;,\;\forall j \in \varvec{N};\\ \varvec{{r^*}}&\ge 0;\\ \varvec{{\rho _i}}&\ge \varvec{0};\\ \varvec{1} \varvec{\ge {a^*}}&\ge \varvec{0}; \end{aligned} \end{aligned}$$

(7)

In the above formula, constraint 1 means that the transmission power of any user in unlicensed band should have a lower bound of 0 and an upper bound of ${p^{max}}$. Constraint 2 represents the interference price $\varvec{r^*} = \left\{ {{r_1},{r_2}, \ldots \ldots ,{r_n}} \right\}$ is non-negative. Constraint 3 means that the price setting is non-negative. Constraint 4 indicates that the spectrum demand ratio of each user is between 0 and 1. $\varvec{{\rho _i}} = \left\{ {\rho _i^{\left( 1 \right) },\rho _i^{\left( 2 \right) }, \ldots \ldots ,\rho _i^{\left( l \right) }} \right\}$ is the set of unit slice price given by operator i, $\varvec{r_{ - i}^*}$ is the set of interference prices predicted by other operators except operator i, $\varvec{a^*}$ is the set of responses predicted by operator i to the purchase quantities of licensed band of users, and $\varvec{p^*}$ is the set of responses predicted by operator i to the transmission power in unlicensed band of users.

Each operator i will determine its own non-cooperative ${r_i}$ and send to the distributed SC, and then the SC sends the channel information and price information to users. After obtaining the channel information and price information, each user gives the quantities of slices purchased and the transmission power of unlicensed band according to its own demand and the reaction of other users. Therefore, the problem of user i is as follows:

Follower:

$$\begin{aligned} \begin{aligned} Max\;\;{U_j}( {{p_j},{a_j},\varvec{\rho _i^\mathrm{{*}}},\varvec{{r^*}},\varvec{p_{ - j}^*},\varvec{a_{ - j}^*}} )&= {U_{j,a}} + {U_{j,b}}\;,\;\forall j \in \varvec{N};\\ s.t.\;\; 0 \le {p_j} \le {p^{max}}\;&,\;\forall l \in \varvec{L};\\ \frac{{a_{i,j}^{\left( l \right) }}}{{\mathop \sum \nolimits _{j \in {N_{i,l}}} a_{i,j}^{\left( l \right) }}}B_i^{\left( l \right) }{R_{i,j}}&+ B_u^{\left( l \right) }{R_j^U} \ge {\eta _j}; \end{aligned} \end{aligned}$$

(8)

In the above formula, constraint 1 means that the transmission power of user j in unlicensed band should have a lower bound of 0 and an upper bound of ${p^{max}}$; Constraint 2 means that the total throughput obtained in licensed and unlicensed bands should meet the minimum standard of throughput. $\varvec{a_{ - j}^*}$ is the predicted purchase quantity set of other users except user j, $\varvec{\rho _i^\mathrm{{*}}}$ is the set of slice prices set by operators, $\varvec{p_{ - j}^*}$ is the set of unlicensed band transmission power choices of other users predicted by user j, and $\varvec{{r^\mathrm{{*}}}}$ is the set of interference prices set by operators. In the following sections, the problem will be analyzed by using backward induction. We decompose constraint 2 into two sub-constraints $\frac{{a_{i,j}^{\left( l \right) }}}{{\mathop \sum \nolimits _{j \in {N_{i,l}}} a_{i,j}^{\left( l \right) }}}B_i^{\left( l \right) }{R_{i,j}} \ge {\theta _j}{\eta _j}$ and $B_u^{\left( l \right) }R_j^U \ge \left( {1 - {\theta _j}} \right) {\eta _j}$ to solve the problem. The above sub-constraints represent the minimum throughput of users in the licensed and unlicensed bands, and ${\theta _j}$ will be solved and discussed in the solution and simulation part. Considering the slice price and interference price set by all operators, we first discuss the strategy of users. Then, by predicting the best behavior of users, we design the spectrum allocation and power allocation scheme, and propose the corresponding non-cooperative strategy to maximize the utility of operators and users.

Therefore, we decompose the above game into two independent sub-games, obtain the sub-game-perfect equilibrium of the sub-games corresponding to the revenue of the licensed and unlicensed bands, respectively, and prove that the subgame-perfect equilibrium solutions are the global Nash equilibrium solutions. The sub-game 1 is as follows:

Leader 1:

$$\begin{aligned} \begin{aligned} Max\;\;{W_{i,a}}&( {{\rho _i},\varvec{{a^*}}} )\;,\;\forall i \in \varvec{M}; \\ s.t.\;\; {\rho _i}&\ge \varvec{0};\\ \varvec{1} \varvec{\ge {a^*}}&\ge \varvec{0}; \end{aligned} \end{aligned}$$

(9)

Follower 1:

$$\begin{aligned} \begin{aligned} Max\;\;{U_{j,a}}&( {{a_j},\varvec{a_{ - j}^*},\varvec{{\rho _i}^*}} )\;,\;\forall i \in \varvec{M},\forall j \in \varvec{N},\forall l \in \varvec{L}; \\ s.t.\;\;&\frac{{a_{i,j}^{\left( l \right) }}}{{\mathop \sum \nolimits _{j \in {N_{i,l}}} a_{i,j}^{\left( l \right) }}}B_i^{\left( l \right) }{R_{i,j}} \ge {\theta _j}{\eta _j};\\&\varvec{1} \varvec{\ge {a^*}} \ge \varvec{0}; \end{aligned} \end{aligned}$$

(10)

The sub-game 2 of unlicensed band is as follows:

Leader 2:

$$\begin{aligned} \begin{aligned} Max\;\;&{W_{i,b}}( {{r_i},\varvec{r_{ - i}^*},\varvec{{p^*}}} )\;,\;\forall i \in \varvec{M}; \\ s.t.\;\;&0 \le {p_j} \le {p^{max}}\;,\;\forall j \in \varvec{N};\\&\varvec{{\rho _i}} \ge \varvec{0}; \end{aligned} \end{aligned}$$

(11)

Follower 2:

$$\begin{aligned} \begin{aligned} Max\;\;&{U_{j,b}}( {{p_j},\varvec{{r^*}},\varvec{p_{ - j}^*}} )\;,\;\forall j \in \varvec{N}; \\ s.t.\;\;&0 \le {p_j} \le {p^{max}}\;,\;\forall j \in \varvec{N};\\&B_u^{\left( l \right) }R_j^U \ge \left( {1 - {\theta _j}} \right) {\eta _j}\;,\;\forall l \in \varvec{L}; \end{aligned} \end{aligned}$$

(12)

4 Game solution

Lemma 1

Debreu-Fan-Glicksberg theorem, in a strategic non-cooperative game $\varvec{G}$ , if for $\forall i\in$ $\varvec{N}$, $\varvec{{S_i}}$ is a compact convex set, ${u_i}\left( \varvec{S} \right)$ is a continuous function in the policy space, and with respect to $\varvec{{S_i}}$ is quasi concave, then $\varvec{G}$ has at least one pure strategy Nash equilibrium [32,33,34].

Theorem 1

There is a subgame-perfect equilibrium solution in sub-game 1, $\mathrm{{\;}}{\varvec{a^\mathrm{{*}}}} = \left\{ {a_{i,1}^{\left( l \right) \mathrm{{*}}},a_{i,2}^{\left( l \right) \mathrm{{*}}}, \ldots \ldots ,a_{i,{N_{i,l}}}^{\left( l \right) \mathrm{{*}}}} \right\}$ and for $\forall j \in {N_{i,l}}$, $\forall a_{i,j}^{\left( l \right) \mathrm{{'}}} \in \varvec{a}$ ,we have ${U_{j,a}}\left( {a_{i,j}^{\left( l \right) \mathrm{{*}}},\varvec{a_{ - j}^\mathrm{{*}}},\varvec{{\rho _i}^\mathrm{{*}}}} \right) \ge {U_{j,a}}\left( {a_{i,j}^{\left( l \right) \mathrm{{'}}},\varvec{a_{-j}^\mathrm{{*}}},\varvec{{\rho _i}^\mathrm{{*}}}} \right)$ ,where $a_{i,j}^{\left( l \right) \mathrm{{'}}}$ represents the Non-Nash-equilibrium solution of user j.

The proof of Theorem 1 is shown in APPENDIX A. We get a set of Nash equilibrium (Stackelberg equilibrium) solutions as:

$$\begin{aligned} \;\rho _i^{\left( l \right) *}= & {} \frac{{{{(\mathop \sum \nolimits _{j \in {N_{i,l}}} \sqrt{{\gamma _j}{R_{i,j}}{a_{ - j}}} )}^2}}}{{4{{\left( {{N_{i,l}} - 1} \right) }^2}{{\left( {{a_j} + {a_{ - j}}} \right) }^2}}}\;,\;\forall i \in \varvec{N},\forall j \in \varvec{N_{i,l}}; \end{aligned}$$

(13)

$$\begin{aligned} \;a_{i,j}^{\left( l \right) **}= & {} min\left\{ {max}\left\{ {a_{i,j}^{\left( l \right) *},\frac{{{\theta _j}{\eta _j}{a_{ - j}}}}{{B_i^{\left( l \right) }{R_{i,j}} - {\theta _j}{\eta _j}}}} \right\} ,1 \right\} \end{aligned}$$

(14)

It is concluded that there is at least one sub-game-perfect equilibrium solution in sub-game 1 by Lemma1. The Nash equilibrium solutions show that the operators’ spectrum prices in the licensed band are functions of the number of users’ channel gain, and the spectrum prices are functions of users’ choices. The users’ optimal choices are related to their own channel gain and other users’ choices, and its lower limit is constrained by the throughput allocation ratio.

So far, the problem of sub-game 1 has been solved. Next, we will solve the problem of sub-game 2.

Theorem 2

There is a subgame-perfect equilibrium solution in sub-game 2, ${\varvec{{p^*}} = \left\{ {p_1^*,p_2^*, \ldots \ldots ,p_j^*} \right\} }$ and for ${\forall j \in \varvec{{N_{i,l}}}}$, ${\forall p_j^{'} \in \varvec{p}}$, we have ${{U_{j,b}}\left( {p_j^*,\varvec{{r^*}},\varvec{p_{ - j}^*}} \right) \ge {U_{j,b}}\left( {p_j^{'},\varvec{{r^*}},\varvec{p_{ - j}^*}} \right) }$, where ${p_j^{'}}$ represents the Non-Nash-equilibrium solution of user j.

The proof of Theorem 2 is shown in APPENDIX B. A set of Nash equilibrium (Stackelberg equilibrium) solutions is obtained as:

$$\begin{aligned} r_i^{\left( l \right) *}= & {} max\left\{ {\sqrt{\frac{{r_{ - i}^{\left( l \right) }\mathop \sum \nolimits _{k = 1}^M \;\mathop \sum \nolimits _{j \in {N_{k,l}}} {\gamma _j}B_u^{\left( l \right) }}}{{\mathop \sum \nolimits _{k = 1}^M \;\mathop \sum \nolimits _{j \in {N_{k,l}}} \left( {{z_j} + {p_{ - j}}{g_{ - j}}} \right) }}} - r_{ - i}^{\left( l \right) },0} \right\} \end{aligned}$$

(15)

$$\begin{aligned} \;p_j^{**}= & {} max\left\{ p_j^{*},\frac{{{z_j} + {p_{ - j}}{g_{ - j}}}}{{{g_j}}}{e^{\frac{{\left( {1 - {\theta _j}} \right) {\eta _j}}}{{B_u^{\left( l \right) }}}}} - \frac{{{z_j} + {p_{ - j}}{g_{ - j}}}}{{{g_j}}} \right\} ^{-} \end{aligned}$$

(16)

where ${\left( x \right) ^ - } = \mathrm{{min}}\left\{ {x,p^{max}} \right\}$.

The Nash equilibrium solution shows that the operator’s Nash interference price in the unlicensed band is related to the user’s transmit power and channel gain, and is affected by the interference prices of other operators. The user’s Nash power selection is related to the interference prices and users’ channel gain. The throughput allocation ratio constrains its lower limit.

It is concluded that there is at least one refined Nash equilibrium solution in sub-game 2 by Lemma 1. In practice, the operator’s equilibrium solution is related to the interference price strategy of other operators, and the user’s strategy is related to the profit ratio of other users. Without knowing the strategy of others, each user only obtains some information about the resource allocation of others through the historical information of the game, each player uses the distributed dynamic algorithm DDS-U and DDS-O to adjust its proposed prices and choices. The algorithm slowly converges to Nash equilibrium.

Algorithm DDS-U is a strategy for users to dynamically adjust their choices. When there is at less one operator to adjust the price, the user will select ${\Delta _1}$ and ${\Delta _2}$ as the adjustment step. Then updating ${\theta _j}$ through Algorithm 3. The user obtains a new iterative solution by calculating the revenue between adding/subtracting the adjustment step and the original strategy. Because we have proved that the user’s choice is a convex function, the optimized result is closer to the Nash equilibrium solution.

Algorithm DDS-O is a strategy for operators to dynamically adjust their choices. Similar to Algorithm 1, when at least one user’s choice changes, the operator will select ${\Delta _3}$ and ${\Delta _4}$ as the adjustment step. The operator obtains a new iterative solution by calculating the revenue between adding/subtracting the adjustment step and the original strategy. Because we have proved that the operator’s choice is a convex function, the optimized result is closer to the Nash equilibrium solution.

Corollary 1

$\left( {\rho _i^{\left( l \right) \mathrm{{*}}},a_{i,j}^{\left( l \right) \mathrm{{**}}},r_i^{\left( l \right) \mathrm{{*}}},p_j^\mathrm{{**}}} \right)$ is the refined Nash equilibrium solution of the Stackelberg game for the resource allocation problem.

Proof

From Theorem 1 and Theorem 2, we derive $\left( {\rho _i^{\left( l \right) \mathrm{{*}}},a_{i,j}^{\left( l \right) \mathrm{{**}}}} \right)$ is the subgame-perfect equilibrium solution of sub-game 1, $\left( {r_i^{\left( l \right) \mathrm{{*}}},p_j^\mathrm{{**}}} \right)$ is the subgame-perfect equilibrium solution of sub-game 2. Given the $\theta _j$, sub-game 1 and sub-game 2 are completely independent sub-games, so the subgame-perfect equilibrium solutions of the two sub-games is the Nash equilibrium solutions as well as Stackelberg equilibrium solutions of the total game [35], operators and users have no motivation to deviate from the point $\left( {\rho _i^{\left( l \right) \mathrm{{*}}},a_{i,j}^{\left( l \right) \mathrm{{**}}},r_i^{\left( l \right) \mathrm{{*}}},p_j^\mathrm{{**}}} \right)$, which proves Corollary 1. $\square$

Theorem 3

For each user, there is at least one optimal throughput allocation ratio to maximize their own revenue.

Fig. 3

The feasible region of game

Proof

As shown in the Fig. 3, $\;\overline{AB}$ is the upper bound of feasible region of the game, $\overline{CD}$ is the Nash equilibrium solution of the game, $\overline{EF}$ represents the lower bound of the game due to throughput allocation. We hope that by adjusting the throughput allocation factor to change the situation of $\overline{EF}$, $\overline{CD}$ can belong to the scope of ABFE and constitutes a feasible region of the game. Otherwise, users can not achieve Nash equilibrium, and can only achieve the sub-optimal solution to meet the throughput requirements. $\square$

From $a_{i,j}^{\left( l \right) \mathrm{{**}}}$ and $p_j^{\mathrm{{**}}},$ when $\frac{{a_{i,j}^{\left( l \right) }}}{{{\eta _j}\mathop \sum \nolimits _{z \in {N_{i,l}}} a_{i,z}^{\left( l \right) }}}B_i^{\left( l \right) }{R_{i,j}} \ge {\theta _j} \ge 1 - \frac{{B_u^{\left( l \right) }{R_j}}}{{{\eta _j}}},$ the user’s revenue is only related to the upper limit or Nash equilibrium solution, and is not related to ${\theta _j}$.

Because $f\left( {{\theta _j}} \right) = \frac{{{\theta _j}{\eta _j}{a_{ - j}}}}{{B_i^{\left( l \right) }{R_{i,j}} - {\theta _j}{\eta _j}}}$ is a monotone increasing function, $g\left( {{\theta _j}} \right) = \frac{{{z_j} + {p_{ - j}}{g_{ - j}}}}{{{g_j}}}{e^{\frac{{\left( {1 - {\theta _j}} \right) {\eta _j}}}{{B_u^{\left( l \right) }}}}} - \frac{{{z_j} + {p_{ - j}}{g_{ - j}}}}{{{g_j}}}$ is a monotone decreasing function. From the user utility function and its concavity and convexity, we can see that, when $\frac{{a_{i,j}^{\left( l \right) }}}{{{\eta _j}\mathop \sum \nolimits _{z \in {N_{i,l}}} a_{i,z}^{\left( l \right) }}}B_i^{\left( l \right) }{R_{i,j}} \ge {\theta _j}$ and ${\theta _j} \le 1 - \frac{{B_u^{\left( l \right) }{R_j}}}{{{\eta _j}}}$ , increase ${\theta _j}$ to ${\theta _j}^\mathrm{{'}} = \frac{{a_{i,j}^{\left( l \right) }}}{{{\eta _j}\mathop \sum \nolimits _{z \in {N_{i,l}}} a_{i,z}^{\left( l \right) }}}B_i^{\left( l \right) }{R_{i,j}}$ , we have ${U_j}\left( {\theta _j^\mathrm{{'}}} \right) \ge {U_j}\left( {{\theta _j}} \right)$ . When $\frac{{a_{i,j}^{\left( l \right) }}}{{{\eta _j}\mathop \sum \nolimits _{z \in {N_{i,l}}} a_{i,z}^{\left( l \right) }}}B_i^{\left( l \right) }{R_{i,j}} \le {\theta _j}$ and ${\theta _j} \ge 1 - \frac{{B_u^{\left( l \right) }{R_j}}}{{{\eta _j}}}$ , decreasing ${\theta _j}$ to $\theta _j^{\mathrm{{''}}} = \frac{{a_{i,j}^{\left( l \right) }}}{{{\eta _j}\mathop \sum \nolimits _{z \in {N_{i,l}}} a_{i,z}^{\left( l \right) }}}B_i^{\left( l \right) }{R_{i,j}}$ we have ${U_j}\left( {\theta _j^{\mathrm{{''}}}} \right) \ge {U_j}\left( {{\theta _j}} \right)$.

If $\frac{{a_{i,j}^{\left( l \right) }}}{{{\eta _j}\mathop \sum \nolimits _{z \in {N_{i,l}}} a_{i,z}^{\left( l \right) }}}B_i^{\left( l \right) }{R_{i,j}} \le {\theta _j} \le 1 - \frac{{B_u^{\left( l \right) }{R_j}}}{{{\eta _j}}}$ establish, and $a_{i,j}^{\left( l \right) \mathrm{{*}}} \ne 1, p_j^\mathrm{{*}} \ne {p^{max}}$ , the revenue depends on ${\theta _j}$ , the revenue function is ${U_j}\left( {{\theta _j}} \right) = {\gamma _j}{\eta _j} - \frac{{\rho _i^{\left( l \right) }B_i^{\left( l \right) }{a_{ - j}}{\eta _j}{\theta _j}}}{{B_i^{\left( l \right) }{R_{i,j}} - {\eta _j}{\theta _j}}} - \mathop \sum \limits _{k = 1}^M r_k^{\left( l \right) }{h_j}\left[ {\frac{{{z_j}}}{{{g_j}}}{e^{\frac{{\left( {1 - {\theta _j}} \right) {\eta _j}}}{{B_u^{\left( l \right) }}}}} - \frac{{{z_j}}}{{{g_j}}}} \right]$ Then we have $\frac{{\partial {U_j}}}{{\partial {\theta _j}}} = \frac{{\rho _i^{\left( l \right) }B_i^{\left( l \right) 2}{a_{ - j}}{\eta _j}{R_{i,j}}}}{{{{\left( {B_i^{\left( l \right) }{R_{i,j}} - {\eta _j}{\theta _j}} \right) }^2}}} + \mathop \sum \limits _{k = 1}^M r_k^{\left( l \right) }{h_j}\frac{{{z_j}{\eta _j}}}{{{g_j}B_i^{\left( l \right) }}}{e^{\frac{{\left( {1 - {\theta _j}} \right) {\eta _j}}}{{B_u^{\left( l \right) }}}}}$ and $\frac{{\partial {U_j}}}{{\partial {\theta _j}}} \ge 0$.

Thus, we have proved Theorem 3. We use distributed algorithm DDS-R to get the best choice of $\theta _j$. The stability of the Algorithm 1 and Algorithm 2 is discussed in [31, 36]. The complexity of gradient descent is related to the value of initial value and step, and we analyze these two parameters in the experimental part. In order to represent the above three algorithms better, we use the flow chart (see Fig. 4) to represent the distributed iterative process. Because operators and users use distributed algorithms to game prices and resources, compared to centralized algorithms, our algorithms are no need for additional information overhead between operators, operators and users give their own strategies in a distributed way.

Fig. 4

Flow chart of distributed algorithm

Table 2 Experimental parameters

5 Simulation and evaluation

We will verify the rationality of the model in MATLAB. The basic simulation parameters are shown in Table 2. The basic model includes three mobile network operators. Each MNO has two types of services, high throughput and low throughput corresponds to eMBB and URLLC slices [37], and five users support this kind of service transmission. The unit of d in the loss function is km. Licensed band for each operator and the unlicensed spectrum pool are both set as 30MHz. In the simulation, we first verify the convergence of the distributed algorithm and analyze the two convergence cases. Then, the influence of the number of users and the profit coefficient on the model’s performance are analyzed, and the situation beyond the user carrying capacity is shown. Finally, we verify the influence of primary user interference on secondary users’ choice in unlicensed band, and prove the rationality of the model by comparing the improved Stackelberg model with other Stackelberg models.

Fig. 5

Results of MNO iteration and user iteration

Figure 5(a) and (b) show the changes of the two service prices and total revenue of the three MNOs with the number of iterations. After the initial price is set and iterated, all operators adjust the unit price of their licensed band by predicting the user’s purchase quantity until the price and revenue do not change. At this time, the operators reach the Nash equilibrium state, and the price reaches the Nash equilibrium solution or the lower bound solution of the throughput requirement. Furthermore, we choose the iteration status of a single operator in the unlicensed band for analysis [1, 2, 14, 20, 38]. The choice of MNO will eventually iterate to the Nash equilibrium solution or fluctuate near the Nash equilibrium solution. The fluctuation curve of the interference price of unlicensed band of a single MNO on the equilibrium is shown in Fig. 5(c). Setting the initial value closer to the equilibrium value will result in fewer iterations. Increasing the step value can approach the Nash equilibrium solution faster. But when the value of step is too large, the value will fluctuate around the equilibrium value, and it will take more iterations to stabilize. This phenomenon is more obvious when the initial value is far from the equilibrium value, so steps and initial values need to be adjusted according to experience and calculation.

Fig. 6

Results of users’ need between different profit ratios

As shown in Fig. 6, service 1 represents high throughput service users and service 2 represents low throughput service users. Figure 6(a) shows the consistency of the average demand ratio of the two types of service users in the licensed band. The results show that users have almost the same interest in the requirements of the licensed band when only the throughput is limited and the user revenue coefficient and other parameters are consistent. According to Fig. 7(a), users choose to adjust the throughput allocation coefficient to ensure the revenue of the licensed band and the size of the spectrum.

Figure 6(a) also shows that when the number of users increases, the user’s demand for the licensed band first increases and then decreases. Because when the number of users increases, users first consider increasing their own proportion of spectrum to obtain enough spectrum. At this time, users will choose a higher proportion of spectrum than their actual needs, therefore reducing part of the revenue to obtain enough spectrum. When the number of users increases to overload, due to too many competing users, even if they declare a higher proportion of spectrum, they only get a small amount of spectrum, so users choose to reduce their spectrum demand proportion after the game. The spectrum demand proportion of users with low profit ratio is always lower than that of users with high profit ratio.

Figure 6(b) shows the difference in average power configuration between the two types of service users in the unlicensed band. The results show that when the number of users increases within a reasonable range, service 1 have higher throughput requirements and they are configured with higher transmission power in the unlicensed band. With the increase of users’ quantity, the interference of users of similar services to other users in the unlicensed band increases, and users need to configure higher power to meet the throughput requirements. For service 2 with low throughput requirements, when they can obtain enough throughput in the licensed band, the power configuration in the unlicensed band only affects their revenue. Therefore, within a reasonable number of users, service 2 will choose to reduce the transmission power to maximize their revenue due to the increased interference from other users and interference costs in the unlicensed band. When the number of users increases to the overload range, both services choose to increase the transmission power to ensure their own throughput requirements until they reach the upper limit of transmission power. The users with a low profit ratio always keep lower transmission power than those with a high profit ratio.

Fig. 7

Results of users’ need between different services

Figure 7(a) shows the difference in throughput allocation coefficient ${\theta _j}$ between the two types of service users. Combined with the analysis in Fig. 6(a), high throughput users choose to place a higher proportion of throughput requirements in the unlicensed band. In contrast, low throughput users prefer to use the licensed band to meet their throughput requirements, and use the unlicensed band as a means to improve revenue. When the number of users is at a highly competitive level, the high throughput users set the unlicensed band power as the upper threshold, which can only relieve the throughput pressure by improving the throughput allocation of the licensed band. In fact, it cannot meet the throughput requirements of the licensed band, which is beyond the feasible region of Nash equilibrium solution. Meanwhile, low throughput users reduce the throughput allocation of licensed band due to the increased competition of licensed band, and achieve the throughput requirement by increasing the power of unlicensed band.

Figure 7(b) shows the impact of interference from unlicensed primary users on two types of users. When the interference of primary users increases, the power allocation of low throughput users will decrease slowly, while the power allocation of high throughput users will increase slowly. It is because using the non-cooperative game theory, users give their power allocation requirements in a distributed way, and there is no information to distinguish whether the source of interference increase is primary users or other secondary users. Therefore, it shows the same phenomenon and reason as Fig. 6(b).

Fig. 8

Results between different Stackelberg models

We choose two algorithms as benchmark schemes. H. Zhang et al. [18] proposed the Strategy Of operators in LTE-U(SOO), which is non-cooperative Stackelberg strategies without dynamic allocation of licensed bands and DDS-R of users. We choose SOO as benchmark algorithm 1. We choose non-cooperative strategies as benchmark algorithm 2 ,which is non-cooperative Stackelberg strategies without dynamic allocation of both licensed and unlicensed bands. We compare our DDS with the two algorithms. The simulation results are shown in Fig. 8. The horizontal axis represents the number of users in each MNO’s services. The vertical axis represents the ratio of the throughput obtained by users to the minimum required throughput. It can be seen that when the number of users increases, the throughput satisfaction rate of different types of users in the proposed Stackelberg model is always better than other two algorithms, which realizes more reasonable resource allocation and can accommodate more users in the same system to ensure the transmission quality. Through the users’ DDS-R, the interference caused by users in the unlicensed band is reduced, and higher throughput is obtained. When users’ choices can’t achieve the feasible region of Nash equilibrium solution, they can still get sub-optimal solutions by DDS-R. The results show that, compared with algorithm 1, the users’ transfer rate increased by an average of 0.7583 times. Compared with algorithm 2, the users’ transmission rate is increased by an average of 1.078 times.

Fig. 9

Results of unlicensed revenue between different models

Figure 9 shows the comparison between algorithm 1 and our algorithms in the MNO revenue of unlicensed band. When the number of users is small, the two algorithms achieve the similar benefits. When the number of users increases and the competition is greater, DDS can achieve better results in unlicensed bands because it can adjust resource allocation through user dynamic strategies. The resource allocation of MNO is reflected in the revenue higher than model 1. The results show that compared with algorithm 1, the unlicensed band revenue of MNO increased by an average of 0.0842 times.

6 Conclusion

The spectrum allocation method of multiple operators in the licensed band, the power control method in the unlicensed band and the dynamic throughput allocation method of multi-service users are studied in this paper, so as to achieve more reasonable resource allocation and control the interference in the unlicensed band.

A multi-leader multi-follower Stackelberg model is established in this paper. We propose a simplified VCG mechanism in the licensed band, an interference price mechanism in the unlicensed band, and a dynamic throughput allocation mechanism in the follower stage. Each player can independently and selfishly consider their own revenue and maximize the revenue. Simulation results show that the improved model can improve the rationality of user resource allocation and the utility of operators.

Appendices

Appendix A: The Proof of Theorem 1

Proof

The pure policy set of users is concave, closed and bounded. The second partial derivative is as follows:

$$\begin{aligned} \frac{{\partial U_{j,a}^2}}{{{\partial ^2}a_{i,j}^{\left( l \right) }}} = \frac{{ - 2{\gamma _j}{a_{ - j}}}}{{{{\left( {{a_j} + {a_{ - j}}} \right) }^3}}}B_i^{\left( l \right) }{R_{i,j}} < 0 \end{aligned}$$

(A1)

where ${a_{ - j}} = \mathop \sum \limits _{z \in {N_{i,l}}} a_{i,z}^{\left( l \right) } - a_{i,j}^{\left( l \right) }$. The function is always less than zero in the domain of definition, which satisfies the definition of concave function. There is the second order partial derivative:

$$\begin{aligned} \frac{{\partial U_{j,a}^2}}{{{\partial ^2}{a_{ - j}}}} = \frac{{2{\gamma _j}B_i^{\left( l \right) }{R_{i,j}}}}{{{{\left( {{a_j} + {a_{ - j}}} \right) }^3}}} > 0 \end{aligned}$$

(A2)

The function is always greater than zero in the domain of definition, which satisfies the definition of convex function. Theorem 1 shows that there is at least one pure strategy Nash equilibrium in sub-game 1.

From $\frac{{\partial {U_{j,a}}}}{{\partial {a_j}}} = 0$, we get $a_{i,j}^{\left( l \right) *} = \sqrt{\frac{{{\gamma _j}{R_{i,j}}{a_{ - j}}}}{{\rho _i^{\left( l \right) }}}} - {a_{ - j}}$. Substitute $a_{i,j}^{\left( l \right) *}$ into the function of Leader1,

$$\begin{aligned} {W_{i,a}} = \;\mathop \sum \limits _{l = 1}^L \mathop \sum \limits _{j \in {N_{i,l}}} \rho _i^{\left( l \right) }\left( {\sqrt{\frac{{{\gamma _j}{R_{i,j}}{a_{ - j}}}}{{\rho _i^{\left( l \right) }}}} - {a_{ - j}}} \right) B_i^{\left( l \right) } \end{aligned}$$

(A3)

There is the second order partial derivative:

$$\begin{aligned} \frac{{\partial W_{i,a}^2}}{{{\partial ^2}\rho _i^{\left( l \right) }}} = \;\mathop \sum \limits _{j \in {N_{i,l}}} \frac{{\sqrt{{\gamma _j}{R_{i,j}}{a_{ - j}}} }}{{ - 4\sqrt{\rho {{_i^{\left( l \right) }}^3}} }} < 0 \end{aligned}$$

(A4)

The function is always less than zero in the domain of definition, which satisfies the definition of concave function. From $\frac{{\partial {W_{i,a}}}}{{\partial \rho _i^{\left( l \right) }}}$, we get $\rho _i^{\left( l \right) *} = \frac{{{{(\mathop \sum \nolimits _{j \in {N_{i,l}}} \sqrt{{\gamma _j}{R_{i,j}}{a_{ - j}}} )}^2}}}{{4{{\left( {{N_{i,l}} - 1} \right) }^2}{{\left( {{a_j} + {a_{ - j}}} \right) }^2}}}$.

Lemma 1 shows the basic conditions for the existence of Nash equilibrium. We have proved that sub-game 1 satisfies the conditions of Lemma 1and obtained a unique set of equilibrium solutions. A set of Nash equilibrium solutions is obtained as:

$$\begin{aligned} \;\rho _i^{\left( l \right) *}= & {} \frac{{{{(\mathop \sum \nolimits _{j \in {N_{i,l}}} \sqrt{{\gamma _j}{R_{i,j}}{a_{ - j}}} )}^2}}}{{4{{\left( {{N_{i,l}} - 1} \right) }^2}{{\left( {{a_j} + {a_{ - j}}} \right) }^2}}}\;,\;\forall i \in \varvec{N},\forall j \in \varvec{N_{i,l}}; \end{aligned}$$

(A5)

$$\begin{aligned} \;a_{i,j}^{\left( l \right) **}= & {} min\left\{ {max}\left\{ {a_{i,j}^{\left( l \right) *},\frac{{{\theta _j}{\eta _j}{a_{ - j}}}}{{B_i^{\left( l \right) }{R_{i,j}} - {\theta _j}{\eta _j}}}} \right\} ,1 \right\} \end{aligned}$$

(A6)

$\square$

Appendix B: The Proof of Theorem 2

Proof

The pure policy set of users is concave, closed and bounded. The second partial derivative is as follows:

$$\begin{aligned} \mathrm{{\;}}\frac{{\partial U_{j,b}^2}}{{{\partial ^2}{p_j}}} = \frac{{ - {\gamma _j}g_j^2}}{{{{\left( {{z_j} + \mathop \sum \nolimits _{k = 1}^M \mathop \sum \nolimits _{z \in {N_{k,l}}} {p_z}{g_z}} \right) }^2}}}B_u^{\left( l \right) } < 0 \end{aligned}$$

(B7)

The function is always greater than zero in the domain of definition, which satisfies the definition of convex function. From $\frac{{\partial {U_{j,b}}}}{{\partial {p_j}}} = 0$, we get $p_j^\mathrm{{*}} = \frac{{{\gamma _j}B_u^{\left( l \right) }}}{{{g_j}\mathop \sum \nolimits _{k = 1}^M r_k^{\left( l \right) }}} - \frac{{{z_j} + {p_{ - j}}{g_{ - j}}}}{{{g_j}}}$. Substitute $p_j^\mathrm{{*}}$ into the function of Leader2:

$$\begin{aligned} {W_{i,b}} = \;\mathop \sum \limits _{l = 1}^L r_i^{\left( l \right) }\left[ {\frac{{B_u^{\left( l \right) }\mathop \sum \nolimits _{k = 1}^M \;\mathop \sum \nolimits _{j \in {N_{k,l}}} {\gamma _j}}}{{\mathop \sum \nolimits _{k = 1}^M r_k^{\left( l \right) }}} - \mathop \sum \limits _{k = 1}^M \;\mathop \sum \limits _{j \in {N_{k,l}}} \left( {{z_j} + {p_{ - j}}{g_{ - j}}} \right) } \right] \end{aligned}$$

(B8)

There is the second order partial derivative:

$$\begin{aligned} \frac{{\partial W_{i,b}^2}}{{{\partial ^2}r_i^{\left( l \right) }}} = \frac{{ - r_{ - i}^{\left( l \right) }\mathop \sum \nolimits _{k = 1}^M \;\mathop \sum \nolimits _{j \in {N_{k,l}}} {\gamma _j}B_u^{\left( l \right) }}}{{{{\left( {r_i^{\left( l \right) } + r_{ - i}^{\left( l \right) }} \right) }^3}}} < 0 \end{aligned}$$

(B9)

where $r_{ - i}^{\left( l \right) } = \mathop \sum \limits _{k = 1}^M r_k^{\left( l \right) } - r_i^{\left( l \right) }$. The function is always less than zero in the domain of definition, which satisfies the definition of concave function. From $\frac{{\partial {W_{i,b}}}}{{\partial r_i^{\left( l \right) }}} = 0$, we get $r_i^{\left( l \right) *} = \sqrt{\frac{{r_{ - i}^{\left( l \right) }\mathop \sum \nolimits _{k = 1}^M \;\mathop \sum \nolimits _{j \in {N_{k,l}}} {\gamma _j}B_u^{\left( l \right) }}}{{\mathop \sum \nolimits _{k = 1}^M \;\mathop \sum \nolimits _{j \in {N_{k,l}}} \left( {{z_j} + {p_{ - j}}{g_{ - j}}} \right) }}} - r_{ - i}^{\left( l \right) }$.

Lemma 1 shows the basic conditions for the existence of Nash equilibrium. We have proved that sub-game 2 satisfies the conditions of Lemma 1 and obtained a unique set of equilibrium solutions. A set of Nash equilibrium solutions is obtained as:

$$\begin{aligned} r_i^{\left( l \right) *}= & {} max\left\{ {\sqrt{\frac{{r_{ - i}^{\left( l \right) }\mathop \sum \nolimits _{k = 1}^M \;\mathop \sum \nolimits _{j \in {N_{k,l}}} {\gamma _j}B_u^{\left( l \right) }}}{{\mathop \sum \nolimits _{k = 1}^M \;\mathop \sum \nolimits _{j \in {N_{k,l}}} \left( {{z_j} + {p_{ - j}}{g_{ - j}}} \right) }}} - r_{ - i}^{\left( l \right) },0} \right\} \end{aligned}$$

(B10)

$$\begin{aligned} \;p_j^{**}= & {} max\left\{ p_j^{*},\frac{{{z_j} + {p_{ - j}}{g_{ - j}}}}{{{g_j}}}{e^{\frac{{\left( {1 - {\theta _j}} \right) {\eta _j}}}{{B_u^{\left( l \right) }}}}} - \frac{{{z_j} + {p_{ - j}}{g_{ - j}}}}{{{g_j}}} \right\} ^{-} \end{aligned}$$

(B11)

where ${\left( x \right) ^ - } = \mathrm{{min}}\left\{ {x,p^{max}} \right\}$. $\square$