1 Introduction

Higher data rates in cellular networks can be achieved by deploying small cells over the existing macrocells that share the same frequency band with macrocells. Small cells like femtocells can be considered as a promising solution to enhance system capacity [1]. FBSs are small, short-range, and low-power access points that are located at the center of the considered area to serve the FUE [2]. By keeping the transmitter and receiver close to each other as in femtocell, data rate in cellular networks increases [3]. D2D communication, which has been recently a subject of intensive research, uses this property. In D2D communication, Tx and Rx communicate in the direct link without communicating through any BS [4]. The coexistence of macrocells, femtocells, and D2D communications leads to HetNet [5].

Due to spectrum scarcity, spectrum sharing is more preferable rather than spectrum dedicating between femtocells, macrocells, and D2D communications. However, in the case of spectrum sharing, the major problem is the intra- and inter-cell interferences. One technique, which was introduced to solve this issue, is FFR. In FFR scheme, the whole frequency band and cell coverage area are partitioned into several non-overlapping parts, and each part is allocated to each region. The orthogonality of allocated resources in FFR structure reduces both the co-channel and cross-channel interferences [6]. Also, introducing new technologies has led to the hidden cost of increasing energy consumption. Therefore, it is important to develop new approaches for communicating and networking that result in lower energy consumption and interference [7,8,9]. Using FFR structure for new technologies increases the overall spectral efficiency (i.e., throughput) and the energy efficiency of network [5].

There are a few works that introduced efficient FFR structures for the co-existence of D2D communication with femto-macrocell network and considered different resource allocation and power control strategies. In [10], the coexistence of D2D communication with macrocells was considered, where different frequency sub-bands were assigned to DUE and MUE in FFR structure and the interference was alleviated by power control. Although this method reduces the interference, from the EE point of view it is not appropriate. In [11], an optimization problem was used for attaining the optimal macro-dedicated, shared, and femto-dedicated spectrum portions in FFR structure and the overall system capacity was maximized. However, the introduced FFR structure is not spectrally efficient since the whole spectrum is not reused by femtocell and macrocell simultaneously.

The resource allocation method presented in [12] maximizes the SE of femtocell network while guarantying the minimum QoS requirement of MUE. In [13], the weighted sum rate optimization was applied to D2D communication that shares multiple RBs with macrocell network, where an overall system capacity improvement was obtained. In [14] a traffic load based resource allocation is considered for D2D communication. In [15], resource and power allocation and mode selection were investigated for D2D communication coexisting with femto-macrocell network. In the reuse mode, geometric vertex search approach is used to solve power allocation problem. In the dedicated mode, RB allocation problem was considered to maximize the throughput by considering the maximum transmit power constraint; however, it is notable that this method is not energy efficient. In [16], soft frequency reuse cellular network is considered and EE optimization problem is applied to the network. In [17, 18], the EE of network is enhanced by using network coding. In [19], an EE-based routing algorithm considering load balancing is introduced. The authors in [20] investigated an optimal routing strategy based on EE maximization for medical applications. In [21], the maximum EE in the uplink mode is obtained by optimizing the location and coverage range of relay stations. In [22], an auction-based model is used for optimal relay selection considering EE optimization.

The works in [12, 13, 15] maximize SE without considering energy consumption, which may be efficient for MBS and FBS, since the power supply of MBS and FBS can be attained by many resources. However, as the limited battery life of UE is more important [23, 24], considering energy efficient RB allocation for DUE is more critical. The tradeoff between SE and EE was considered in [25] in which an algorithm for optimizing the EE of each D2D and MUE was utilized and RB allocation was ignored. In [26], the authors considered FFR-based RB allocation scheme in HetNet for both macrocell and picocell tiers and applied the optimization problem of maximizing EE to find the optimal RB and power allocation.

In [5], EE-based resource optimization problem was performed on D2D communication in HetNets. The problem was solved by a non-cooperative game. According to this game, each D2D Tx selects the power and RBs in a way that its EE with the constraint on the QoS requirement of other tiers, is improved. However, the performance improvement of MUE and FUE is not taken into account. Also, the authors did not use FFR-based resource allocation, which can lead to interference reduction and performance improvement.

In the this study, to reduce the interference we propose an efficient FFR structure with directional antennas for macrocell network in the presence of femtocells and D2D communications. In the proposed FFR structure, the coverage of macrocell consists of cell-center and cell-edge areas, where for each tier of each area, different frequency sub-band is allocated. In the proposed scheme, the frequency resources assigned to MUE, FUE, and DUE in each region are orthogonal to reduce both intra- and inter-cell interferences, leading to EE improvement. Due to the power limitation of DUE, we also present an energy-efficient resource allocation algorithm to maximize the EE of each DUE with the constraints on SE and transmit power of DUE. Further, we present power control algorithms to optimize the SEs of MUE and FUE. The optimization problems can be efficiently solved by non-cooperative game [25] in which each UE independently maximizes its own EE in D2D mode as well as the SEs of FBS and MBS. We also present mathematical analysis of SE distribution. Thus, the main contributions of this paper include three parts: a) resource allocation for D2D communication underlaying HetNets, b) mathematical analysis of SE, and c) EE and SE-based optimization problems for power allocation. The results indicate that the proposed FFR structure enhances system performance. We also show that EE-based D2D optimization problem and SE-based femtocell and macrocell optimization problems are the best optimization schemes. The fast convergence of the iterative algorithms is demonstrated through computer simulation. Finally, we study the tradeoff between EE and SE of the proposed structure.

The rest of this paper is organized as follows. The proposed resource allocation method and spectrum partitioning scheme are explained in Section II. Section III develops the introduced optimization problems. Simulation results and performance evaluation are presented in Section IV. Finally, Section V concludes the paper.

2 Proposed resource allocation scheme

In this section, we explain the proposed FFR structure and RB allocation for each tier of HetNet.

2.1 Resource allocation to macrocell network

In HetNets with D2D communications, in order to obtain high SE, the available spectrum should be used by macrocell, femtocell, and D2D communications simultaneously. Also, it has been reported that using directional antennas instead of omnidirectional antennas in MBS increases the SE [27]. Another way for improving SE is to use FFR structure, in which the whole cell is divided into two inner and outer regions. Omnidirectional antennas are utilized for the inner region and three or six directional antennas are used for the outer region [6]. We propose a new RB allocation scheme based on the FFR structure in which the whole bandwidth is used in each macrocell, femtocell, and D2D of HetNet that results in frequency reuse factor equal to one. Also, communications in all modes (i.e., macrocell, femtocell, and D2D) in a specific region use different resources to reduce the cross tier interference.

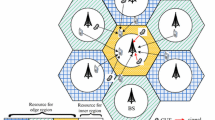
Two layers of the proposed FFR-based macrocell network are demonstrated in Fig. 1a. As shown in Fig. 1b, the whole bandwidth is divided into four sub-bands F1, F2, F3, and F4. Sub-band F1 is allocated to MUE in the inner region, which is served by an omnidirectional antenna. On the other hand, sub-bands F2, F3, and F4 are assigned to MUE in different zones of the outer region that are served by three 120° directional antennas (sectors). The number of resources for each sub-band is determined based on the number of users in each zone.

Fig. 1
figure 1

The structure of macrocell network. a Two layers of macrocell network with allocated sub-bands and b spectrum partitioning into four sub-bands

Full size image

It is assumed that the locations of MUE, FUE, and DUE are mutually independent random variables with uniform distribution in each cell. Hence, the PDF of the location of users in the polar coordinates \((r,\theta )\) can be written as [28]:

$$f(r,\theta ) = f(r)f(\theta )$$
(1)

where

$$f(r) = \frac{{2\,\left( {r - R_{0} } \right)}}{{\left( {R_{m} - R_{0} } \right)^{2} }}; \,\quad R_{0} \le r < R_{m}$$
(2)
$$f(\theta ) = \frac{1}{2\pi } ; { }\quad - \pi \le \theta < \pi$$
(3)

where r, Rm, and R0 denote the distance of user from the origin, the radius of macrocell coverage area and the minimum possible distance of user from the MBS (which is set to 40 meters in this research), respectively [6]. Since the coverage of both inner and outer regions is the whole range \([ - \pi ,\,\,\pi )\), the number of users in the inner and outer regions only depends on r. Therefore, the number of RBs assigned to the inner and outer regions is evaluated through the CDF of MUE distance from the origin where its PDF is shown in (2). If there are totally \(N_{RB}^{{total}}\) RBs, the number of RBs assigned to the inner region of macrocell, i.e., the number of RBs belonging to F1, is calculated as

$$N_{RB}^{in} = N_{RB}^{total} \int_{{R_{0} }}^{{R_{{th}} }} {f(r)\,dr} = N_{RB}^{total} \left( {\frac{{R_{th} - R_{0} }}{{R_{m} - R_{0} }}} \right)^{2}$$
(4)

where Rth denotes the radius of inner region. Consequently, the number of RBs assigned to the outer region (i.e., the number of RBs belonging to F2, F3, and F4) will be as follows

$$N_{RB}^{out} = N_{RB}^{total} - N_{RB}^{in} = N_{RB}^{total} \left( {1 - \left( {\frac{{R_{th} - R_{0} }}{{R_{m} - R_{0} }}} \right)^{2} } \right)$$
(5)

Since all sectors in the outer region have the same coverage area, the number of RBs allocated to each sector, i.e., each of the sub-bands F2, F3, and F4, in the outer region of macrocell (\(N_{RB}^{scr,out}\)) will be equal to \(N_{RB}^{scr,out} = N_{RB}^{out} /3\). In order to achieve the orthogonality between the RBs of different tiers, the same number of RBs in each sub-band of macrocell network should be allocated to femtocell and D2D networks.

2.2 Proposed resource allocation to femtocell network

In this part, we explain the proposed resource allocation structure for femtocells in the proposed FFR structure. It is assumed that the location of FBSs follows the SPPP distribution with the intensity \(\lambda_{F}\) [29]. In order to reduce the cross-tier interference from femtocell network to macrocell network and D2D communication, the RBs allocated to femtocells should be orthogonal to the RBs assigned to macrocell and D2D communication. As shown in Fig. 2, sub-bands F2, F3, and F4 are allocated to the FUE of inner region while the sub-band F1 is assigned to the outer region. To reduce the interference of femtocells in the cell edge on the neighbor cells that use the same resources, we propose to partition the sub-band F1 into three equal sub-bands F1,1, F1,2, and F1,3. The number of RBs allocated to the sub-bands F1,1, F1,2, and F1,3 (\(N_{RB}^{scr,in}\)) is equal to \(N_{RB}^{scr,in} = N_{RB}^{in} /3\). In this way, the distance between the femtocells that use the same RBs, increases.

Fig. 2
figure 2

Proposed resource allocation to femtocell network, a two layers of femtocell network along with the allocated sub-bands and b spectrum partitioning

Full size image

2.3 Resource allocation to D2D network

To avoid the severe interference from D2D communication on macrocell, femtocell communications, and vice versa, frequency resources allocated to macrocell and femtocell should be different from those assigned to D2D communications in each region. Thus, DUE in locations near to the MBS cannot use the resources of sub-band F1. As shown in Fig. 3, sub-bands F2, F3, and F4 are allocated to DUE in the inner region.

Fig. 3
figure 3

Two layers of D2D network along with allocated sub-bands to D2D communications [6]

Full size image

Furthermore, the assigned sub-bands to D2D communication should be different from those allocated to the femtocell. As shown in Fig. 3, the sub-band F1 is divided into three parts F1,1, F1,2, and F1,3 like femtocell sub-bands in the outer region, but the way that the sub-bands F1,1, F1,2, and F1,3 are allocated to D2D communications is different from that of the femtocell and thus the interference is reduced.

2.4 Interference analysis

In this study, we consider downlink scenario of HetNet.

  1. 1.

    Interference analysis of MUE.

Figure 4 shows different sources of interference in the proposed HetNet, which are explained in details in the following. FBS and D2D Tx use omnidirectional antennas, thus the direct link between MUE in the inner region and MBS (link 1 in Fig. 4a) receives interference from FBS and D2D Txs in the outer region (links 2 and 3 in Fig. 4a). Also, the direct link between MUE in the outer region and MBS (link 1 in Fig. 4b) interferes with FBS and D2D Txs in the inner region (links 2 and 3 in Fig. 4b).

Fig. 4
figure 4

Direct and interfering links in the proposed resource allocation scheme a sub-band F1, b sub-bands F2, F3, and F4

Full size image
  1. 2.

    Interference analysis of FUE and DUE.

The allocated resources to FUE and DUE in the inner region of each sector are the same as those assigned to MUE in outer region of other sectors and transmission directions of sectors do not overlap with each other. Consequently, the direct link between D2D Tx and D2D Rx (link 6 in Fig. 4b) and direct link between FBS and FUE in the inner region (link 4 in Fig. 4b) do not interfere with MBS. Furthermore, since FBSs use omnidirectional antennas, FBSs in the neighbor sector of inner region interfere with the D2D Rx in the inner region (link 7 in Fig. 4b) and the D2D Tx in the inner region interferes with the FUE in the neighbor sector of inner region (link 5 in Fig. 4b).

The direct link between D2D Tx and D2D Rx in the outer region (link 7 in Fig. 4a) of a specific sector interferes with MBS and FBSs in the outer region of other sectors (links 8 and 9 in Fig. 4a). Since MBS, FBS, and D2D Tx use omnidirectional antennas for transmission in the sub-band F1, the FUE in the outer region (link 4 in Fig. 4a) receives interference from MBS and D2D Tx (links 5 and 6 in Fig. 4a).

3 Proposed optimization problems

In this section, we present mathematical analysis for SE distribution and non-cooperative power allocation algorithm. Our goal is to maximize EE by finding the transmit power of DUE. We also aim to maximize the SEs of MUE and FUE and then analyze the convergence of our optimization algorithms.

3.1 SINR of MUE, FUE, and D2D Rx in different regions

The received power, \(P_{R}\), (or received interference) of each user can be calculated as

$$P_{R} = P_{T} \,H\,\varPsi \,L^{{ - 1}}$$
(6)

where \(P_{T}\), H, \(\varPsi\), and L denote the transmit power, channel power gain, lognormal shadowing, and path loss, respectively. We represent all of the mentioned channel impairments with the channel coefficient \(K = {\text{H}}\,\varPsi \,L^{ - 1}\); therefore, \(P_{R} = P_{T} \,K\).

Suppose that there are NF FBSs and ND D2D communications co-channel with MUE in the cth RB of the inner region. The SINR of MUE in the cth RB of inner region (\(\gamma_{mi}^{c}\)) is formulated as

$$\gamma_{mi}^{c} = \frac{{P_{TM}^{c} \, K_{m}^{c} }}{{\sigma_{N}^{2} + \sum\nolimits_{j = 1}^{{N_{F} }} {P_{TF}^{j,c} \;K_{fm}^{j,c} } + \sum\nolimits_{l = 1}^{{N_{D} }} {P_{TD}^{l,c} \, K_{dm}^{l,c} } + I_{mi} }}$$
(7)

where \(P_{TM}^{{c}}\), \(P_{TF}^{j,c}\), and \(P_{TD}^{l,c}\) denote the transmit powers of MBS, jth FBS, and lth D2D Tx in the cth RB, respectively. The direct channel coefficient from MBS to MUE is shown by \(K_{m}^{c} .\)

Also, the interfering channel coefficient from the jth FBS to MUE is shown by \(K_{fm}^{{j,c}}\) while the interfering channel coefficient from the lth D2D Tx to MUE is denoted by \(K_{dm}^{l,c}\). Further, \(\sigma_{N}^{2}\) is the noise power. \(I_{mm}^{c}\), \(I_{fm}^{c}\), and \(I_{dm}^{c}\) indicate the co-channel interferences from MBSs, FBSs, and D2D Txs of the upper layers to MUE, respectively, and \(I_{mi} = I_{mm}^{c} + I_{fm}^{c} + I_{dm}^{c}\).

Similarly, the SINR of MUE in the kth RB of outer region (\(\gamma_{mo}^{{k}}\)) can be written as

$$\gamma_{mo}^{{k}} = \frac{{P_{TM}^{k} \, K_{m}^{k} }}{{\sigma_{N}^{2} + \sum\nolimits_{j = 1}^{{N_{F} }} {P_{TF}^{j,k} \;K_{fm}^{j,k} } + \sum\nolimits_{l = 1}^{{N_{D} }} {P_{TD}^{l,k} \, K_{dm}^{l,k} } + I_{mo} }}$$
(8)

where \(I_{mo} = I_{mm}^{k} + I_{fm}^{k} + I_{dm}^{k}\). Similar expression can be obtained for the SINR of FUE of the nth FBS that uses the kth RB in the inner region as follows

$$\gamma_{fi}^{n,k} = \frac{{P_{TF}^{n,k} \, K_{f}^{n,k} }}{{\sigma_{N}^{2} + \sum\nolimits_{j = 1\;j \ne n}^{{N_{F} }} {P_{TF}^{j,k} \, K_{ff}^{j,n,k} } + \sum\nolimits_{l = 1}^{{N_{D} }} {P_{TD}^{l,k} \, K_{df}^{l,n,k} } + I_{fi} }}$$
(9)

where \(K_{f}^{{n,k}}\) denotes the direct channel coefficient from the nth FBS to its associated FUE in the kth RB, \(K_{ff}^{j,n,k}\) represents the interfering channel coefficient from the jth FBS to the associated FUE of the nth FBS in the kth RB, \(K_{df}^{l,n,k}\) indicates the interfering channel coefficient from the lth D2D pair to associated FUE of the nth FBS in the kth RB, and \(I_{fi} = I_{mf}^{n,k} + I_{ff}^{n,k} + I_{df}^{n,k}\).

For FUE of the nth FBS that uses the cth RB in outer region, we obtain the SINR as below

$$\gamma_{fo}^{n,c} = \frac{{P_{TF}^{n,c} \, K_{f}^{n,c} }}{{\sigma_{N}^{2} { + }P_{TM}^{c} \,K_{mf}^{n,c} { + }\sum\nolimits_{j = 1\;j \ne n}^{{N_{F} }} {P_{TF}^{j,c} \,K_{ff}^{j,n,c} } { + }\sum\nolimits_{l = 1}^{{N_{D} }} {P_{TD}^{l,c} \,K_{df}^{l,n,c} } { + }I_{fo} }}$$
(10)

where \(K_{f}^{{n,c}}\) is the direct channel coefficient from the nth FBS to its associated FUE in the cth RB. \(K_{mf}^{n,c}\) denotes the interfering channel coefficient from the MBS to the associated FUE of the nth FBS in the cth RB. \(K_{ff}^{j,n,c}\) represents the interfering channel coefficient from the jth FBS to the associated FUE of the nth FBS in the cth RB. \(K_{df}^{{l,n,c}}\) indicates the interfering channel coefficient from the lth D2D pair to the associated FUE of the nth FBS in the cth RB, and \(I_{fo} = I_{mf}^{n,c} + I_{ff}^{n,c} + I_{df}^{n,c}\).

The SINR of Rx of the nth D2D pair operating in the kth RB of inner region (\(\gamma_{di}^{n,k}\)) is calculated as

$$\gamma_{di}^{n,k} = \frac{{P_{TD}^{n,k} \, K_{d}^{n,k} }}{{\sigma_{N}^{2} + \sum\limits_{j = 1}^{{N_{F} }} {P_{TF}^{j,k} \, K_{fd}^{j,n,k} } + \sum\limits_{\begin{subarray}{l} l = 1 \\ l \ne n \end{subarray} }^{{N_{D} }} {P_{TD}^{l,k} \, K_{dd}^{l,n,k} } + I_{di} }}$$
(11)

where \(K_{d}^{n,k}\) denotes the coefficient of direct channel from Tx of the nth D2D pair to its Rx in the kth RB. \(K_{fd}^{j,n,k}\) represents the interfering channel coefficient from the jth FBS to the Rx of the nth D2D pair in the kth RB. \(K_{dd}^{l,n,k}\) is the interfering channel coefficient from the Tx of the lth D2D pair to the Rx of the nth D2D pair in the kth RB, and \(I_{di} = I_{md}^{n,k} + I_{fd}^{n,k} + I_{dd}^{n,k}\).

Similarly, the SINR of Rx of the nth D2D pair operating in the cth RB in outer region \((\gamma_{do}^{n,c} )\) is computed as

$$\gamma_{do}^{n,c} = \frac{{P_{TD}^{n,c} \, K_{d}^{n,c} }}{{\sigma_{N}^{2} + P_{TM}^{c} \,K_{md}^{n,c} + \sum\limits_{j = 1}^{{N_{F} }} {P_{TF}^{j,c} \,K_{fd}^{j,n,c} } + \sum\limits_{\begin{subarray}{l} l = 1 \\ l \ne n \end{subarray} }^{{N_{D} }} {P_{TD}^{l,c} \,K_{dd}^{l,n,c} } + I_{do} }}$$
(12)

where \(K_{md}^{n,c}\) indicates the interfering channel coefficient from the MBS to the Rx of the nth D2D pair operating in the cth RB, and \(I_{do} = I_{md}^{n,c} + I_{fd}^{n,c} + I_{fd}^{n,c}\).

Considering \(\gamma\) as the SINR of UE, its SE or throughput, R, is obtained as

$$R = \log_{2} \left( {1 + \gamma } \right)\;{\text{bits/sec/Hz}}$$
(13)

3.2 Mathematical analysis of SE distribution

In this part, we calculate the PDF of SE of each user in every location. According to (6), PR is the multiplication of exponential and lognormal random variables which can be modeled as another lognormal random variable [27], i.e., \(P_{R} \sim\;LN\left( {\mu_{s} ,\sigma_{s}^{2} } \right)\), where \(\sigma_{s}^{2} = \zeta \left( {\sigma_{dB}^{2} + 5.57^{2} } \right)\), and \(\zeta = 0.1\ln \,(10)\) is the scaling factor. The interference has the same distribution with \(\mu_{i} = \zeta \left( {\mu_{dB} - 2.5} \right) + \ln \left( {{{P_{T} } \mathord{\left/ {\vphantom {{P_{T} } {L_{i} }}} \right. \kern-0pt} {L_{i} }}} \right)\) and \(\, \sigma_{i}^{2} = \zeta \left( {\sigma_{dB}^{2} + 5.57^{2} } \right)\). For simplicity, we only consider the macro-femto and macro-D2D cross-tier interferences in the coverage of central macrocell and neglect the effect of thermal noise and interferences from the macrocells of upper layers [6]. Therefore, SE can be calculated as \(\log_{2} \left( {1 + \left( {S/I} \right)} \right) = \log_{2} \left( {(I + S)/I} \right),\) where S and I represent RSS and interference, respectively. We need to calculate the PDF of \(\left( {(I + S)/I} \right)\) in which the numerator and denumerator are the sum of independent and different lognormal random variables. We use LSN distribution [30] to approximate the sum of lognormal random variables, which is represented with \(LSN\left( {\lambda ,\varepsilon ,\omega^{2} } \right)\) where \(\lambda\), \(\varepsilon\), and \(\omega^{2}\) are the skewness, mean, and variance, respectively. In [30], it has been shown that the LSN distribution leads to a tight approximation of the sum of lognormal distributions. According to [30], the LSN optimal parameters are calculated as follows

$$\frac{{\sum\nolimits_{i = 1}^{N} {e^{{2\mu_{i} }} e^{{\sigma_{i}^{2} }} \left( {e^{{\sigma_{i}^{2} }} - 1} \right)} }}{{\left( {\sum\nolimits_{i = 1}^{N} {e^{{\mu_{i} }} e^{{{{\sigma_{i}^{2} } \mathord{\left/ {\vphantom {{\sigma_{i}^{2} } 2}} \right. \kern-0pt} 2}}} } } \right)^{2} }} = e^{{\sum\nolimits_{i = 1}^{{\frac{{1 + \lambda^{2} }}{N}}} {\sigma_{i}^{ - 2} } }} \frac{{\phi \left( {2{\lambda \mathord{\left/ {\vphantom {\lambda {\sqrt {\sum\nolimits_{i = 1}^{N} {\sigma_{i}^{ - 2} } } }}} \right. \kern-0pt} {\sqrt {\sum\nolimits_{i = 1}^{N} {\sigma_{i}^{ - 2} } } }}} \right)}}{{2\phi^{2} \left( {{\lambda \mathord{\left/ {\vphantom {\lambda {\sqrt {\sum\nolimits_{i = 1}^{N} {\sigma_{i}^{ - 2} } } }}} \right. \kern-0pt} {\sqrt {\sum\nolimits_{i = 1}^{N} {\sigma_{i}^{ - 2} } } }}} \right)}} - 1$$
(14)

where \(\phi (x) = \int_{ - \infty }^{x} {\varphi (\xi )\,d\xi }\) and \(\varphi (x) = \frac{{e^{{{{ - x^{2} } \mathord{\left/ {\vphantom {{ - x^{2} } 2}} \right. \kern-0pt} 2}}} }}{{\sqrt {2\pi } }}.\)\(\lambda_{opt}\) is calculated by solving the nonlinear Eq. (14). Also, \(\varepsilon_{opt}\) and \(\omega_{opt}\) are obtained as [30]:

$$\omega_{opt} = \sqrt {{{\left( {1 + \lambda_{opt}^{2} } \right)} \mathord{\left/ {\vphantom {{\left( {1 + \lambda_{opt}^{2} } \right)} {\sum\limits_{i = 1}^{N} {\sigma_{i}^{ - 2} } }}} \right. \kern-0pt} {\sum\limits_{i = 1}^{N} {\sigma_{i}^{ - 2} } }}}$$
(15)
$$\varepsilon_{opt} = \ln \left( {\sum\limits_{i = 1}^{N} {e^{{\mu_{i} }} e^{{{{\sigma_{i}^{2} } \mathord{\left/ {\vphantom {{\sigma_{i}^{2} } 2}} \right. \kern-0pt} 2}}} } } \right) - \frac{{\omega_{opt}^{2} }}{2} - \ln \left( {\phi \left( {{{\lambda_{opt} } \mathord{\left/ {\vphantom {{\lambda_{opt} } {\sqrt {\sum\limits_{i = 1}^{N} {\sigma_{i}^{ - 2} } } }}} \right. \kern-0pt} {\sqrt {\sum\limits_{i = 1}^{N} {\sigma_{i}^{ - 2} } } }}} \right)} \right)$$
(16)

Using the above equations, the sum of lognormal variables in numerator and denumerator can be approximated as \(LSN\left( {\lambda_{num} ,\varepsilon_{num} ,\omega_{num} } \right)\) and \(LSN\left( {\lambda_{den} ,\varepsilon_{den} ,\omega_{den} } \right),\) respectively. Now, the outage probability of SE, which is defined as the probability of SE being lower than a threshold value \((R_{th} ),\) is obtained as

$$\begin{aligned} &\Pr \left( {R \le R_{th} } \right) = \Pr \left( {\log_{2} \left( {\frac{I + S}{I}} \right) \le R_{th} } \right) \hfill \\ &\quad = \Pr \left( {\left[ {\frac{1}{\ln (2)}\ln \left( {I + S} \right) - \frac{1}{\ln (2)}\ln \left( I \right)} \right] \le \ln \left( {R_{th} } \right)} \right) \hfill \\ \end{aligned}$$
(17)

where \(\ln (I + S) - \ln (I)\) is SN with distribution \(SN\left( {\lambda_{1} ,\varepsilon_{1} ,\omega_{1} } \right)\) [30]. According to [30], the parameters of SN are obtained from the parameters of LSN and the outage probability of SE is calculated through the SN approximation. The SN distribution is formulated as follows [30]:

$$f_{R} \left( {\left. R \right|r,\theta } \right) = \frac{2}{{\omega_{1} }}\varphi \left( {\frac{{R - \varepsilon_{1} }}{{\omega_{1} }}} \right)\phi \left( {\lambda_{1} \frac{{R - \varepsilon_{1} }}{{\omega_{1} }}} \right)$$
(18)

Since the distributions of radius and angle of user location are independent, their joint PDF noting (2) and (3) is

$$f\left( {r,\theta } \right) = f\left( r \right)f\left( \theta \right) = \frac{{\left( {r - R_{0} } \right)}}{{\pi \left( {R_{m} - R_{0} } \right)^{2} }}$$
(19)

From (18) and (19), the joint distribution of SE and user location can be obtained as

$$\begin{aligned} & f\left( {R,r,\theta } \right) = f_{R} \left( {\left. R \right|r,\theta } \right)f\left( {r,\theta } \right) \\ & \quad = \frac{{2\left( {r - R_{0} } \right)}}{{\pi \omega_{1} \left( {R_{m} - R_{0} } \right)^{2} }}\varphi \left( {\frac{{R - \varepsilon_{1} }}{{\omega_{1} }}} \right)\phi \left( {\lambda_{1} \frac{{R - \varepsilon_{1} }}{{\omega_{1} }}} \right) \\ \end{aligned}$$
(20)

The PDF of SE can be obtained by integrating (20) over the ranges of \(r\) and \(\theta\) as follows

$$\begin{aligned} & f_{R} (R) = \int_{{R_{0} }}^{{R_{m} }} {\int_{0}^{2\pi } {f\left( {R,r,\theta } \right)dr\,d\theta } } \\ & \quad = \int_{{R_{0} }}^{R} {\int_{0}^{2\pi } {\frac{{2\left( {r - R_{0} } \right)}}{{\pi \omega_{1} \left( {R_{m} - R_{0} } \right)^{2} }}\varphi \left( {\frac{{R - \varepsilon_{1} }}{{\omega_{1} }}} \right)\phi \left( {\lambda_{1} \frac{{R - \varepsilon_{1} }}{{\omega_{1} }}} \right)dr\,d\theta } } \\ \end{aligned}$$
(21)

3.3 EE maximization problem

The EE utility function of D2D pair is defined as the ratio of SE to the sum power consumption, which consists of transmit power of D2D Txs and circuit power. As mentioned before, there are ND D2D communications in each RB. It is assumed that D2D Tx and Rx have the same circuit power, hence their sum is denoted as 2Pcir [15]. The EEs of DUE in the cth RB in outer region (sub-band F1) and the kth RB in inner region (sub-bands F2, F3, F4) are calculated respectively as

$$U_{EE,o}^{c} = \frac{{\sum\nolimits_{l = 1}^{{N_{D} }} {R_{do}^{l,c} \left( {P_{TD}^{l,c} } \right)} }}{{\sum\nolimits_{l = 1}^{{N_{D} }} {P_{T,do}^{l,c} } + 2P_{cir} }}$$
(22)
$$U_{EE,i}^{k} = \frac{{\sum\nolimits_{l = 1}^{{N_{D} }} {R_{di}^{l,k} \left( {P_{TD}^{l,k} } \right)} }}{{\sum\nolimits_{l = 1}^{{N_{D} }} {P_{TD}^{l,k} } + 2P_{cir} }}$$
(23)

where \(R_{do}^{l,c}\) represents SE of the lth DUE in the cth RB in outer region, and \(R_{di}^{l,k}\) denotes SE of the lth DUE in the kth RB in inner region. Then, the EE maximization problems with the constraint on minimum rate requirement and transmit power in the outer and inner regions are respectively given by

$$P_{TD,o}^{ * ,c} = \mathop {\arg {\max} }\nolimits_{{P_{TD}^{{l,c}} }} \,\,\frac{{\sum\nolimits_{l = 1}^{{N_{D} }} {R_{do}^{l,c} \left( {P_{TD}^{l,c} } \right)} }}{{\sum\nolimits_{l = 1}^{{N_{D} }} {P_{TD}^{l,c} } + 2P_{cir} }}$$
$$\begin{aligned} {\text{subject to: }}R_{do}^{l,c} \left( {P_{TD}^{l,c} } \right) \ge R_{d}^{\hbox{min} } \hfill \\ \, 0 \le \sum\limits_{l = 1}^{{N_{D} }} {P_{TD}^{l,c} } \le P_{TD}^{{\max} } \hfill \\ \end{aligned}$$
(24)
$$P_{TD,i}^{ * ,k} = \mathop {\arg {\max} }\nolimits_{{P_{TD}^{l,k} }} \,\,\frac{{\sum\nolimits_{l = 1}^{{N_{D} }} {R_{di}^{l,k} \left( {P_{TD}^{l,k} } \right)} }}{{\sum\nolimits_{l = 1}^{{N_{D} }} {P_{TD}^{l,k} } + 2P_{cir} }}$$
$$\begin{aligned} {\text{subject to: }}R_{di}^{l,k} \left( {P_{TD}^{l,k} } \right) \ge R_{d}^{\hbox{min} } \hfill \\ \, 0 \le \sum\limits_{l = 1}^{{N_{D} }} {P_{TD}^{l,k} } \le P_{TD}^{{\max} } \hfill \\ \end{aligned}$$
(25)

The EE optimization problems in (24) and (25) are non-convex optimization ones, which are difficult to solve. The Lemma in [25] (see Appendix) proves that by incrementing the value of \(P_{TD}^{n,c}\), \(U_{EE,o}^{c}\) first increases and then decreases. Therefore, \(U_{EE,o}^{c}\) is quasi-concave.

It is shown in [31] that a non-convex optimization problem can be transformed into a concave one by applying nonlinear fractional programming. For a distributed resource allocation, the EE problem for DUE is defined as follows [32]

$$q_{do}^{l * } = {\max} \frac{{R_{do}^{l,c} \left( {P_{TD}^{l,c} } \right)}}{{P_{TD}^{l,c} + 2P_{cir} }} = \frac{{R_{do}^{l,c} \left( {P_{TD,o}^{ * ,c} } \right)}}{{P_{TD,o}^{ * ,c} + 2P_{cir} }}$$
(26)

where \(P_{TD,o}^{ * ,c}\) is the optimal power of DUE in the outer region. The same expression can be considered for DUE in the inner region. In [25], the following theorem is proved.

Theorem 1

The condition for Eq. (26) to be achievable is

$$\begin{aligned} &R_{do}^{l,c} \left( {P_{TD}^{l,c} } \right) - q_{do}^{l * } \left( {P_{TD}^{l,c} + 2P_{cir} } \right) \hfill \\ &\quad= R_{do}^{l,c} \left( {P_{T,do}^{r * } } \right) - q_{do}^{r * } \left( {P_{TD,o}^{ * ,c} + 2P_{cir} } \right) = 0 \hfill \\ \end{aligned}$$
(27)

Similarly, for DUE in the inner region, the same condition is proved. Consequently, the problem in (24) is transformed into the subtractive form as

$$P_{TD,o}^{*,c} = \mathop {\arg {\max} }\limits_{{P_{TD}^{l,c} }} \, \left( {R_{do}^{l,c} \left( {P_{TD}^{l,c} } \right) - q_{do}^{l,c} \left( {P_{TD}^{l,c} + 2P_{cir} } \right)} \right)$$
$$\begin{aligned} {\text{subject to: }}\,\,\,\,\,\,\,R_{do}^{l,c} \left( {P_{TD}^{l,c} } \right) \ge R_{d}^{\hbox{min} } \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,0 \le P_{TD}^{l,c} \le P_{TD}^{{\max} } \hfill \\ \end{aligned}$$
(28)

We use Dinkelbach iterative algorithm [31] (explained below) to solve (28) by considering small initial value for \(q_{do}^{r}\).

Since the transformed optimization problems are now concave, the KKT is applied to (28) to solve EE maximization problem. The Lagrangian of (28) can be written as follows

$$\begin{aligned} L_{do} \left( {P_{TD}^{{l,c}} ,\alpha_{do}^{l} ,\beta_{do}^{{l}} } \right) = R_{do}^{{l,c}} \left( {P_{TD}^{{l,c}} } \right) - q_{do}^{l} \left( {P_{TD}^{{l,c}} + 2P_{cir} } \right) \hfill \\ + \,\alpha_{do}^{l} \left( {R_{do}^{{l}} \left( {P_{TD}^{{l,c}} } \right) - R_{d}^{{\hbox{min} }} } \right) - \beta_{do}^{{l}} \left( {P_{TD}^{{l,c}} - P_{TD}^{{{\max} }} } \right) \hfill \\ \end{aligned}$$
(29)

where \(\alpha_{do}^{{l}}\) and \(\beta_{do}^{{l}}\) are the Lagrangian multipliers of constraints on the SE and transmit power, respectively.

The dual decomposition of (29) is shown by (30). Equation (30) consists of two sub-problems: maximizing (29) to find the optimal transmit power and then minimizing to find the optimum Lagrange multipliers as

$$\mathop { \hbox{min} }\limits_{{\left( {\alpha_{do}^{l} \ge 0\,,\,\,\beta_{do}^{{l}} \ge 0} \right)}} \, \mathop {{\max} }\limits_{{\left( {P_{TD}^{{l,c}} } \right)}} \left( {L_{do} \left( {P_{TD}^{{l}} ,\alpha_{do}^{{l}} ,\beta_{do}^{{l}} } \right)} \right)$$
(30)

By taking the first derivative of (29) and setting it to zero, \(\frac{{\partial L_{do} }}{{\partial P_{TD}^{{l}} }} = 0\), the optimum value of \(P_{TD}^{{l,c}}\) can be obtained as

$$P_{TD,o}^{ * ,c} = \left[ {\frac{{1 + \alpha_{do}^{{l}} }}{{\ln (2)\left( {q_{do}^{{l}} + \beta_{do}^{{l}} } \right)}}} \right. - \frac{1}{{K_{d}^{n,c} }}\left. {\left( {\sigma_{N}^{2} { + }P_{TM}^{{c}} K_{md}^{{nc}} + \sum\limits_{j = 1}^{{N_{F} }} {P_{TF}^{{j,c}} \,K_{fd}^{{j,n,c}} } + \sum\limits_{\begin{subarray}{l} l = 1 \\ l \ne r \end{subarray} }^{{N_{D} }} {P_{TD}^{{l,c}} K_{dd}^{{l,n,c}} } + I_{do} } \right)} \right]^{ + }$$
(31)

where \(I_{do} = I_{md}^{n,c} + I_{fd}^{n,c} + I_{fd}^{n,c}\) and \(\left[ x \right]^{ + } = {\max} \{ 0,\,\,x\} .\) The Lagrangian multipliers of minimization problem can be found by gradient method as [33, 34]

$$\frac{{\partial L_{do} }}{{\partial \alpha_{do}^{\,l} }} = R_{do}^{\,l,c} \left( {P_{TD}^{{l,c}} } \right) - R_{d}^{\hbox{min} }$$
(32)
$$\frac{{\partial L_{do} }}{{\partial \beta_{do}^{{l}} }} = P_{TD}^{{l,c}} - P_{TD}^{{{\max} }}$$
(33)

Therefore, the updated Lagrangian multipliers are calculated as

$$\alpha_{do}^{l} \left( {i + 1} \right) = \left[ {\alpha_{do}^{l} (i) - \mu_{{\alpha_{do} }}^{l} (i)\left( {R_{do}^{{l,c}} \left( {P_{TD,o}^{ * ,c} } \right) - R_{d}^{\hbox{min} } } \right)} \right]^{ + }$$
(34)
$$\beta_{do}^{l} \left( {i + 1} \right) = \left[ {\beta_{do}^{{l}} (i) + \mu_{{\beta_{do} }}^{{l}} (i)\left( {P_{TD,o}^{ * ,c} - P_{TD}^{{\max} } } \right)} \right]^{ + }$$
(35)

where \(i\) is the iteration index, \(\mu_{{\,\alpha_{do} }}^{\,l} (i)\) and \(\mu_{{\,\beta_{do} }}^{\,l} (i)\) are positive step sizes, which have to be chosen in a way that a balance between optimality and convergence speed is obtained. The solution is summarized in Algorithm 1, in which \(I_{max}\) is the maximum number of iterations and \(\varepsilon\) is the maximum tolerance. The algorithm continues until the condition \(R_{do}^{{l,c}} \left( {P_{TD}^{{l,c}} \left( i \right)} \right) - q_{do}^{{l}} \left( i \right)\left( {P_{TD}^{{l,c}} \left( i \right) + 2P_{cir} } \right) \le \varepsilon\) is satisfied. Similarly, the same algorithm can be applied to DUE in inner region.

To prove the efficiency of the iterative algorithm for EE optimization problem, the following Theorem is presented. Theorem2: The applied EE optimization problem provides optimum EE. The proof of theorem 2 is given in [25].

figure e

3.4 SE optimization

Here, we study SE optimization problem in order to maximize the SEs of macrocell and femtocell networks. We model it as a non-cooperative game to overcome the problem of vast overhead, in which each UE independently maximizes its own SE [25]. Thus, the problems of SE maximization of macrocell and femtocell networks with the constraints on user transmit power and minimum QoS requirement in the sub-band F1 are respectively formulated as

$$P_{TM}^{*} = \mathop {\arg {\max} }\limits_{{P_{TM}^{{c}} }} \, R_{mi}^{c} \left( {P_{TM}^{c} } \right)$$
$$\begin{aligned} {\text{subject to: }}R_{mi}^{c} \left( {P_{TM}^{c} } \right) \ge R_{m}^{\hbox{min} } ; \, \hfill \\ \, 0 \le P_{TM}^{c} \le P_{TM}^{{\max} } ; \hfill \\ \end{aligned}$$
(36)

and

$$P_{TF}^{*} = \mathop {\arg {\max} }\limits_{{P_{TF}^{j,c} }} \, \sum\limits_{j = 1}^{{N_{F} }} {R_{fo}^{j,c} \left( {P_{TF}^{j,c} } \right)}$$
$$\begin{aligned} {\text{subject to: }}R_{fo}^{n} \left( {P_{TF}^{n} } \right) \ge R_{f}^{\hbox{min} } \, \hfill \\ \, \,0 \le P_{TF}^{j} \le P_{TF}^{{\max} } \hfill \\ \end{aligned}$$
(37)

where \(P_{TM}^{*}\) and \(P_{TF}^{*}\) denote the optimal transmit powers of MBS and FBS, respectively.

SE optimization problem can be formulated for sub-bands F2, F3, and F4 in similar manner. As mentioned in [35], SE maximization is a non-convex optimization problem and it is a NP-hard problem, thus obtaining the optimal solution is difficult. We can conclude from the concave characteristic of (36) and (37) that the optimal values of these functions occur at edge points [36, 37]. By considering the worst case from the aspect of interference, the non-convex problem is transformed into an optimization problem with only one variable. If the goal is macrocell SE maximization, we consider maximum transmit power levels for FBS and D2D, and if the aim is femtocell SE maximization, we consider maximum transmit power levels for MBS and D2D.

We utilize a gradient-based iterative solution for the objective functions described in (36) and (37). In this way, the updated values of transmit powers at the \((i + 1)\) th iteration for each MUE and FUE and variable step-size will be respectively as follows [13]

$$P_{TM}^{{c}} \left( {i + 1} \right) = P_{TM}^{{c}} \left( i \right) + \left( {\tau \left( i \right) \times R_{mi}^{{c}} \left( i \right)} \right)$$
(38)
$$P_{TF}^{n,c} \left( {i + 1} \right) = P_{TF}^{n,c} \left( i \right) + \left( {\tau \left( i \right) \times R_{fo}^{n,c} \left( i \right)} \right)$$
(39)
$$\tau \left( {i + 1} \right) = \tau \left( 1 \right){{\left( {1 + d} \right)} \mathord{\left/ {\vphantom {{\left( {1 + d} \right)} {\left( {i + d} \right)}}} \right. \kern-0pt} {\left( {i + d} \right)}}$$
(40)

where \(d\) is a fixed positive number [13]. The solution is summarized in Algorithm 2, where \(I_{{\max} }\) is the maximum number of iterations and \(\varepsilon\) is the maximum tolerance. The algorithm continues until at least one of the conditions \(\left( {P_{TM}^{c} \left( i \right) - P_{TM}^{c} \left( {i - 1} \right)} \right) < \varepsilon ,\; \, \left( {P_{TM}^{c} \left( i \right) \le P_{TM}^{{\max} } } \right)\), or \(i \le I_{{\max} }\) is satisfied.

figure f

4 Performance evaluation

In this section, we assess downlink performance of the proposed resource allocation scheme, and EE and SE optimization problems for three-tier HetNet. In the considered macrocell, FBSs are distributed according to SPPP with the intensity \(\lambda_{F}\) and users are distributed uniformly in the coverage area of the considered cell. Also, it is assumed that in each RB, there are three DUEs, three FUEs, and one MUE. The simulation parameters are provided in Table 1, which are adopted from [6, 21, 38,39,40].

Table 1 The values of parameters used in simulations
Full size table

4.1 EE and SE performance analysis

The CDFs of transmit powers of MUE, FUE, and DUE in different sub-bands are illustrated in Fig. 5 for different optimization problems. As shown in Figs. 5a and 5b, the optimal solutions for transmit powers of MUE and FUE in SE optimization problem are obtained in the range of minimum possible values, while in EE optimization problem, the optimal solution includes whole possible transmit powers. This is due to the high transmission powers of FBS and MBS, which lead to high interference compared to D2D network. Therefore, to achieve the maximum value of SE, the power should be lower. According to Fig. 5c, the transmit power of DUE for SE optimization falls in near the maximum possible value, while for EE optimization problem, it includes the values in the whole range of transmit power. This is due to the fact that the range of transmission power of D2D is low, thus low interference on DUE is expected. Consequently, the maximum value of SE is obtained by increasing the transmission power of D2D. Actually, the value of consumed power is more important in EE optimization problem than the SE case, therefore all optimum values of power in EE optimization problem occur in minimum values based on (22) and (23).

Fig. 5
figure 5

CDFs of transmit powers in different optimizations, a MUE, b FUE and c DUE

Full size image

The CDFs of SEs of MUE, FUE, and DUE obtained via different optimization problems are depicted in Fig. 6. As shown in Figs. 6a and 6b, the SE of MUE and FUE obtained from SE optimization outperforms the SE obtained from EE optimization. However, the contradictory results are obtained for DUE in all sub-bands. It is clear from Fig. 5c that the obtained optimal power from EE optimization problem is lower than that of SE optimization problem while the achieved SE in EE optimization is better than the SE optimization problem. The results indicate the efficiency of using EE optimization for DUE and SE optimization for MUE and FUE. Moreover, Fig. 7 compares the CDF of SE of the proposed method with that of [25]. We observe that the proposed method has better performance.

Fig. 6
figure 6

CDF of SE in different optimizations, a MUE, b FUE and c DUE

Full size image
Fig. 7
figure 7

Comparison of SE of the proposed method with that of [25]

Full size image

4.2 Convergence analysis

The convergence speed of SE optimization problem is illustrated in Fig. 8. The normalized average SE was achieved by averaging 1000 simulation results and then normalizing to the maximum value. It is observed that the SEs of MUE and FUE converge approximately after two and four iterations, respectively. This fast convergence shows the effectiveness of SE optimization problem.

Fig. 8
figure 8

Convergence speed of proposed SE optimization problem

Full size image

Similarly, the convergence speed of normalized EE is demonstrated in Fig. 9. The results show that EE converges after five iterations, which indicates the efficiency of EE optimization problem.

Fig. 9
figure 9

Convergence speed of proposed EE optimization problem

Full size image

4.3 EE and SE tradeoff

Here, we present the tradeoff between EE and SE for D2D network in the proposed method and compare it with the method of [25]. The results of Fig. 10 verify the effectiveness of the proposed structure in term of EE. It is observed that as the minimum SE requirement increases, EE increases until it reaches the optimal point, then the decrease in EE occurs. The reason is that, when the minimum SE requirement is high, the EE optimization problem must lead to an optimal solution that fulfills the minimum SE requirement. In the method of [25], the inefficiency of network structure leads to a low EE and drop of EE in lower values of minimum SE requirement compared to the proposed network.

Fig. 10
figure 10

Tradeoff between EE and SE for D2D network

Full size image

5 Conclusion and future works

Although D2D communication underlying HetNet increases the capacity of the overall system, it causes high interference and consequently degrades system performance. In order to overcome the problem, we proposed efficient FFR structures for D2D, femtocell, and macrocell. The proposed FFR structures provide good performance for all communication modes by allocating resources to each communication mode orthogonally in each region. Furthermore, the performances of the proposed structures are improved by applying different optimization problems. We considered EE optimization for the D2D user because of battery limitation. The result confirmed that considering EE optimization for D2D and SE optimization for FUE and MUE lead to efficient solutions. Moreover, using the proposed structure and optimization problems, the tradeoff between SE and EE is improved significantly compared with other work.

For future studies, we propose to apply mode selection scheme among D2D, femto, and macrocell considering EE maximization of network. We also propose to use adaptive resource allocation based on the distribution of users in each tier. Finally, D2D clustering can be utilized to enhance the performance.