1 Introduction

A typical wireless sensor network (WSN) [1] is composed of a large set of inexpensive sensors with sensing, processing and communication capabilities. These sensors, when deployed in large numbers in a sensor field, can self-organize into an ad hoc network [2]. Wireless sensor networks (WSNs) have been widely used in a variety of applications for monitoring and surveillance purpose, such as environmental monitoring [3], natural disaster relief [4], biomedical health monitoring [5], smart home [6] and military target tracking [7]. As WSNs are usually battery-driven, limited battery energy is a crucial problem and battery life is a vital factor on which the sensor node’s lifetime strongly depends on [8]. Mostly, two schemes are adopted to extend battery life. One scheme is to charge the battery with the natural energy such as wind, tide and sun; the other is to find a high efficient way to manage the energy consumption. As the main way to prolong network lifetime, the second scheme is widely studied recently and has been a hotspot [9].

In WSNs, usually one or more powerful base stations (BSs) are deployed over a large area for the purpose of collecting data from sensor nodes [10, 11]. Since most nodes should not directly transmit data to BS due to their limited energy capacity, a reasonable routing protocol is necessary to manage the energy consumption efficiently and prolong the network lifetime effectively [12]. To date, many relevant routing protocols based on energy consideration have been put forward. And these protocols can be divided into two categories [11, 13]: flat routing [14–16] and hierarchical routing [17–19]. In flat routing, such as Sensor Protocols for Information via Negotiation (SPIN) [14], Minimum Cost Forwarding Algorithm (MCFA) [15] and Directed Diffusion (DD) [16], all nodes have the same functionalities and behave according to the same rules (i.e., generating and forwarding the data) [13]. These flat routing protocols are relatively effective in small-scale networks. However, they are not suitable for large-scale networks, since the form of flooding is usually used for data transmission that needs more data processing and bandwidth usage [11]. Hierarchical routing, also known as clustering, such as LEACH [17], PEGASIS [18] and HEED [19], has obtained a good scalability and received extensive attentions [20–23]. It is implemented by selecting a fraction of nodes as cluster heads (CHs) and carrying out reasonable classification for all nodes [24]. CHs can aggregate the data collected by the cluster members and transmit it to BS, thus the energy consumption of the majority of nodes has been reduced.

Game theory is a branch of applied mathematics and often used to analyze the problem of rational individual decision in conflict situations [25]. In recent years, it has been widely applied to WSNs and brought new insights [25–28] for routing, coverage optimization, resource allocation, network security, etc. When designing cluster-based routing protocols for WSNs, sensor nodes can be regarded as rational individuals who have freedom to decide whether to be CHs according to their own interests [29, 30]. On the one hand, each node in the network tends to avoid being a cluster head (CH) to preserve energy. But on the other hand, it needs to provide the required services. This conflict makes game theory very useful to achieve a trade-off between minimizing the energy consumption and providing required services effectively [28]. In [29], game theory is firstly used to analyze the clustering problem for WSNs. A protocol named CROSS is proposed based on the theory. Each node is modeled as a player, and it can get an equilibrium probability by playing a clustering game with all other players in the network. And then, each node self-decides whether to be a CH based on this equilibrium probability. However, it is not realistic that CROSS assumes each player can exchange messages with all other players, since longer communication distance leads to much more interference and nodes usually have limited communication ability. Later, a localized game theoretical clustering algorithm (LGCA) [30] is put forward. Each player only exchanges information with the players in a close neighbor. Though LGCA is more practical than CROSS in real networks, there are still many aspects not concerned, such as residual energy, node degree and distance to BS. In this paper, by using game theory, we will further analyze the clustering problem to let each node achieve a better trade-off between minimizing energy consumption and providing required service effectively. And our main contributions are listed as follows:

  • We present a clustering protocol named Hybrid, Game Theory based and Distributed clustering (HGTD) based on game theory. Each node gets an equilibrium probability by playing a localized clustering game, and it decides whether to be a CH according to the equilibrium probability that can make its payoff keep equilibrium.

  • We specifically define the payoff for each node when choosing different strategies in the clustering game, and both node degree and distance to BS are considered. Under our definition of payoff, we calculate the equilibrium probability based on game theory for each node, and a good trade-off can be achieved between minimizing energy consumption and providing required services effectively.

  • We propose an iterative algorithm to select the final CHs from the potential CHs for the purpose of avoiding the case that more than one CH occurs in a close proximity. Moreover, residual energy and the number of neighboring potential CHs are both considered to assure that the potential CHs with more energy and fewer neighboring potential CHs have priority to be final CHs. Our iterative algorithm can effectively balance the energy consumption among nodes, and we further prove that it can terminate in finite iterations.

  • We prove our protocol outperforms LEACH, CROSS and LGCA by extensive simulations.

The rest of this paper is organized as follows: Sect. 2 summarizes the related works on clustering problem. Section 3 gives an overview of LGCA, a brief introduction and some important observations on LGCA are included. The system model is given in Sect. 4. And some theoretical analyses about the clustering game are shown in Sect. 5. The detail of our proposed protocol is shown in Sect. 6. And Sect. 7 gives the simulations and results analyses. Finally, we conclude this paper in Sect. 8.

2 Related works

Clustering protocols for WSNs have been widely addressed [17–19, 31–33]. Heinzelman et al. [17] proposed a famous clustering protocol named low-energy adaptive clustering hierarchy (LEACH). All nodes are randomly self-selected to be CHs, and a mechanism is adopted to ensure that each node will be the CH once within an elaborately designed time interval. Consequently, all nodes almost take turns to be CHs, and the energy consumption is well distributed among nodes. But the random rotation mechanism leads to an uneven distribution of the CHs. Moreover, the residual energy is not concerned in LEACH, which results in premature death of a part of nodes. And later, a centralized version of LEACH called LEACH-C was proposed in [31]. Each node no longer decides to be CH independently, and all CHs are selected by the BS. Since BS holds the global knowledge of the network by collecting all sensors’ information, it can make a better decision and plan. The results show that LEACH-C achieves a longer network lifetime compared with LEACH. However, LEACH-C is not suitable for large-scale networks as it needs to maintain the global knowledge in each round.

A chain-based clustering protocol named PEGASIS was proposed in [18]. A single chain is formed based on nodes’ physical location by using a greedy algorithm. In the chain, every node only receives data from or transmits the fused data to its close neighbor. Only one CH is selected to forward the data to BS, and all nodes become the CH in turns. Thus, the average energy consumed by each node is reduced in every round. Compared with LEACH, PEGASIS has improved the network lifetime. But it has increased the time delay as the chain is too long, then it can’t be applied on real-time systems.

Another famous clustering protocol named HEED was proposed in [19]. CHs are periodically selected according to a hybrid of the residual energy of node, the proximity of node to its neighbors and node degree. Thus, nodes with more residual energy have a bigger probability to be CHs and join clusters to minimize the communication cost. HEED is completely distributed, energy-efficient and has proved to obtain a better performance than LEACH. But it is prone to produce “isolated node” (the node which is not covered by a CH) or “isolated CH” (the CH which has no member nodes).

The concept of social welfare was introduced in [32], and a protocol named PARPEW was proposed. The tentative CHs are determined by a random mechanism. Each normal node selects the nearest tentative CH to join cluster. To select the final CHs, both the residual energy of node and the distance matrix are considered to predict energy welfare by using a social welfare function. And the final CH is selected within each cluster to acquire the largest energy welfare of the cluster. Correspondingly, both the energy efficiency and energy balance are achieved within each cluster. However, the forming of clusters has adopted a random mechanism that results in an uneven distribution of clusters.

Bajaber and Awan [33], proposed a novel protocol called ECOMP for forming clusters and determining the appropriate routings. A bidirectional ring structure among the sensor nodes is formed within every cluster. And each sensor node receives data from its previous neighbor, aggregates this with its own data and then forwards it to the next neighbor on the ring. The data finally arrives at a cluster sender node. Each cluster sender transmits the data to BS using single-hop or multi-hop communication with its neighbor CHs. ECOMP has reduced the energy consumption of CHs, since a CH doesn’t need to perform any data aggregating tasks. And the data transmission distance of a sensor node is well reduced as it only needs to transmit data to its next close neighbor on the ring. However, to establish the ring structure in ECOMP, all nodes need to exchange information with BS and obtain the location with GPS that needs much extra cost.

Based on game theory, a protocol named CROSS was proposed in [29]. Each node is modeled as a game player, and it plays the clustering game with other players to decide whether to be a CH. On the one hand, a sensor node tends to avoid being the CH to save energy. But on the other hand, it also needs to provide the required services. To keep the benefit equilibrium when selecting different strategies, each node adopts the mixed strategy in the game. And at the end of the game, each node gets an equilibrium probability to be CH. However, it is not realistic that CROSS assumes all nodes can communicate with each other in the network. And the game is played by all nodes simultaneously leads to an extremely small equilibrium probability. Hence, CROSS needs to be further improved.

3 Overview of LGCA

To address the problems occurred in CROSS, a protocol named LGCA was proposed in [30]. In this section, we will briefly introduce the protocol LGCA, and then we give our observations on it.

3.1 A brief introduction to LGCA

LGCA assumes that the maximum power level is large enough for each node to transmit data to BS. And for the sake of preserving energy, only when a node is selected as a CH, it will transmit data at this maximum power level, otherwise, it keeps its power at a particular level which corresponding to a communication radius R. Each node is modeled as a player, who can exchange messages with its neighbors which are defined as the nodes within its communication radius R (excluding this node itself). Let Nb(i) denote the set consisting of the neighbors of node i, it can be expressed as follows:

$$Nb\left( i \right) = \left\{ {k\left| {dis(i,k) \le R,\quad k \ne i} \right.} \right\}$$
(1)

where dis(i, k) is the distance between node i and k; and R is the communication radius of each node.

By playing a localized clustering game with the neighbors, each node selfishly decides whether to be a CH. For any node i, its clustering game model can be defined as follows:

$$CG = \left\langle {N, S,U} \right\rangle$$
(2)

where N is the set of players including node i itself and its neighbors; S = {S j | j∈N} is the set of players’ strategies. U = {U j | j∈N} is the set of players’ utility functions.

In pure strategies, the strategy space of each player includes two choices: declaring to be a CH (D) and not declaring to be a CH (ND). Regarding payoffs, if a player chooses the strategy ND, then if no other neighbor chooses the strategy D, its payoff will be zero since it will be unable to transmit its data to BS. If at least one other neighbor chooses the strategy D, its payoff will be v which is the amount of gain for successfully transmitting the data to BS. Finally, if the player chooses the strategy D, its payoff for successfully transmitting data v will be reduced by an amount c which is the overhead of becoming a CH. So, in this case the final payoff will be v–c. Hence, the utility function of any player i can be expressed as follows:

$$U_{i} = \left\{ \begin{aligned} &0,\text{ }\quad if\text{ }S_{j} = ND,\text{ }\forall j \in N \hfill \\ & v - c,\text{ }\quad if\text{ }S_{i} = D \hfill \\ & v,\text{ }\quad if\text{ }S_{i} = ND\text{ }{\text{and }}\exists j \in N\text{ }s.t.\text{ }S_{j} = D \hfill \\ \end{aligned} \right.$$
(3)

Letting p i be the probability that player i chooses the strategy D. According to the theorem 1 in [29], a symmetrical mixed strategies Nash Equilibrium exists, and the equilibrium probability p i is described as:

$$p_{i} = 1 - (w)^{{1/\left| {Nb(i)} \right|}}$$
(4)

where w = c/v < 1; |Nb(i)| is the number of elements in set Nb(i) which consists of the neighbors of player i.

By using the above game theoretical analysis, a repeated clustering game in terms of rounds is defined in LGCA. In the first round, each node acts as a player. It plays its own clustering game and meanwhile joins their neighbors’ games. As each node can only exchange messages with its neighbors, it considers that the participants of its own clustering game consist of itself and its neighbors. And then, by playing its own game each node gets an equilibrium probability, based on which it decides whether to be a CH. For any node i, its equilibrium probability can be calculated by Eq. (4). As a result, some nodes successfully declare themselves as CHs.

To avoid the situation that more than one node happens to be the CH in a close proximity, a contention procedure is carried out by utilizing CSMA/CA (Carrier Sense Multiple Access with Collision Avoidance) mechanism. A potential CH who first contends for the physical media will immediately declare itself to be a final CH. Once hearing the declaration, other potential CHs will give up their own declarations and return to the normal state.

For the purpose of distributing the energy consumption among nodes, a localized zero probability rule (ZPR) [30] is adopted. These nodes that have served as CHs in the first round will not join any games in the second round, and their probabilities to be CH will be set to zero. For the node having not yet served as a CH in the first round, it will replay its own game in the second round. And it considers that the participants of its own game consist of itself and the neighbors having not served as CHs in the first round. And then, for any node i, if it has not served as a CH in the first round, its equilibrium probability in the second round will be updated as follows:

$$p_{i} = 1 - {\text{w}}^{{1/\left| {Ncur(i)} \right|}}$$
(5)

where |Ncur(i)| is the number of elements in set Ncur(i) which consists of player i’s neighbors that have not served as CHs in the first round.

In general, for a node having already served as the CH, it will not join any games in the following rounds. And it will reset to the initialization state when all its neighbors have also served as CHs.

3.2 Our observations on LGCA

In LGCA, each node decides whether to be a CH according to an equilibrium probability achieved by playing its own localized clustering game. LGCA is completely distributed and easy to be extended. But there are still many aspects need to be further studied.

First, the parameter v and c are not specific enough, and LGCA assumes each node has the same value of parameter v and c that is not very reasonable.

Second, many parameters which are important for improving the performance of the protocol are not concerned, such as residual energy, node degree and distance to BS.

Third, once a node becomes a CH, its probability to be CH will be set to zero until all its neighbors have also served as CHs. Thus, for each node, its probability to be CH is not strictly in accordance with its equilibrium probability. And it can’t keep its payoff at the equilibrium state all the time.

Finally, the using of final CHs competition mechanism makes the result tend to be random in nature. And it will be more effective if some more powerful (such as more residual energy) potential CHs have higher priority to be final CHs.

Based on LGCA and our observations on it, we will devote to present a more energy-efficient clustering protocol that can achieve a better trade-off between minimizing the energy consumption and providing required services effectively.

4 System model

4.1 Network model

As shown in Fig. 1, the two-layer structure of the network [33] is adopted in this paper. The cluster members in the bottom layer collect data from the sensor field, and transmit the data to their CHs in the top layer. CHs aggregate the data and forward it to the BS.

Fig. 1
figure 1

Two-layer structure of the network

Full size image

For the development of our protocol, we make some assumptions about the sensor nodes as follows:

  • Each node has a unique ID which is used to identify the data source;

  • These sensor nodes, once deployed in the sensor field, their locations will not change again;

  • All nodes have the same battery energy which can not be recharged, and the BS has no energy limitations;

  • Each node can adjust its transmission power according to the distance to the destination.

4.2 Radio model

The radio model [17] adopted in this paper is shown in Fig. 2.

Fig. 2
figure 2

Radio model

Full size image

The energy spent to transmit a k-bit packet to the destination can be calculated as follows [24, 31, 34, 35]:

$$E_{Tx} (k,d) = \left\{ \begin{aligned} kE_{elec} + k\varepsilon_{fs} d^{2} ,\quad d < d_{0} \hfill \\ kE_{elec} + k\varepsilon_{amp} d^{4} ,\quad d > d_{0} \hfill \\ \end{aligned} \right.$$
(6)

Here, E elec is the energy spent by the transmitter or receiver circuitry; ε fs and ε amp are the amplifier characteristic constants corresponding to the free-space propagation model and the two-ray ground reflection model respectively; d is the distance between transmitter and receiver; d 0 is the distance threshold [34] which is used to distinguish that two kinds of path loss model, \(d_{0} = \sqrt {{\raise0.5ex\hbox{$\scriptstyle {\varepsilon_{fs} }$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {\varepsilon_{amp} }$}}}\).

The energy consumed by the receiver for the data packet of k bits is expressed as follows [35]:

$$E_{Rx} (k) = kE_{elec} + kE_{DA}$$
(7)

where E DA is the energy consumed by the CH for aggregating a one-bit packet.

5 Theoretical analyses

In this section, we will theoretically analyze the cost and payoff of a node when choosing different strategies to be a CH or not. And then, by taking into account of node degree and distance to BS, we recalculate the equilibrium probability for each node to get a better trade-off between minimizing energy consumption and providing required services effectively.

5.1 Analyses on the cost and payoff

As the concrete expressions of parameter v and c are not further studied in LGCA, it assumes each node has the same value of parameter v and c that is not very reasonable.

For a sensor node, if selected as a CH, the amount of energy consumed by it is closely related to its node degree and distance to BS. A bigger node degree will leads to more amount of energy consumption since it will process and forward the data for more non-cluster head nodes within its close neighbor. Thus, a CH with bigger node degree can gain fewer payoffs than the one with smaller node degree. Furthermore, a CH with longer distance to BS can also gain fewer payoffs than the one with shorter distance, since it will consume more energy to transmit the data for a longer distance.

Based on the analyses above, we specifically define the payoff of a node as the ratio of the number of packets that can be successfully delivered to BS to the amount of energy consumed to provide the required services.

5.2 Calculating the equilibrium probability

We use the same definition of neighbors and assumptions about the power level of nodes as those used in LGCA that have been shown above. We define node degree Dr as the number of node’s neighbors (excluding this node itself).

For a node i, if it selects the strategy ND when playing its own clustering game, and if at least one other node selects the strategy D within its close neighbor, its payoff v i can be calculated by

$$v_{i} = \frac{L}{{Ecm_{i} }}.$$
(8)

where L is the size of data packet collected by each sensor node per round and Ecm i is the energy consumed by node i to transmit the packet to its corresponding CH.

If node i chooses the strategy D, its payoff v i -c i can be expressed as follows:

$$v_{i} - c_{i} = \frac{{\left( {Dr_{i} + 1} \right)L}}{{Ech_{i} }}$$
(9)

where c i is the overhead of becoming a CH for node i; Dr i is the degree of node i and Ech i is the energy consumed by node i when serving as a CH.

Based on Eqs. (8) and (9), we can compute c i as follows:

$$c_{i} = \frac{L}{{Ecm_{i} }} - \frac{{\left( {Dr_{i} { + }1} \right)L}}{{Ech_{i} }}$$
(10)

Let w i  = c i /v i , we have the following equation:

$$w_{i} = 1 - \frac{{\left( {Dr_{i} + 1} \right)Ecm_{i} }}{{Ech_{i} }}$$
(11)

In Eq. (11), Ech i /(Dr i  + 1) denotes the average energy consumed by node i when acting as a CH for receiving, aggregating and forwarding the data collected by one cluster member. To avoid the case that w i may be a negative value, we introduce a parameter w min . And then, w i can be reformulated as follows:

$$w_{i} = \hbox{max} \left( {w_{\hbox{min} } ,1 - \frac{{\left( {Dr_{i} + 1} \right)Ecm_{i} }}{{Ech_{i} }}} \right)$$
(12)

Thus, according to Eq. (4), we can calculate the equilibrium probability of player i as follows:

$$p_{i} { = }1 - (w_{i} )^{{1/\left| {Nb\left( i \right)} \right|}}$$
(13)

where |Nb(i)| is the number of neighbors of player i. Actually, p i  is the average equilibrium probability of all players within communication radius R of player i.

However, when playing its own clustering game, node i can’t calculate the value of v i since it can’t determine which one will be its own CH if it chooses strategy ND. That is, the value of Ecm i can’t be calculated before the end of the clustering game. And then, we will set the value of Ecm i to approximately be the average amount of energy consumed by a non-cluster head node to transmit its data to its corresponding CH. If we adopt free-space propagation model for the intra-cluster communication, we can calculate Ecm i as follows:

$$Ecm_{i} = LE_{elec} + L\varepsilon_{fs} d_{toCH}^{2}$$
(14)

where L is the size of data packet collected by each sensor node per round and d toCH is the average distance to CH for a non-cluster head node.

We assume only one CH will be selected within a close neighbor with radius R. Then the average radius of each cluster is equal to R. And by using the same way adopted in [31], the average distance to CH d toCH for a non-cluster head node can be calculated by

$$d_{toCH} = \int\limits_{\theta = 0}^{2\pi } {\int\limits_{r = 0}^{R} {\rho \left( {r,\theta } \right)r^{2} drd\theta } } \text{ }.$$
(15)

Here, ρ is the density of nodes. If nodes are uniformly deployed in the sensor field, we can calculate ρ(r, θ) as follows [31]:

$$\rho \left( {r,\theta } \right) = \frac{1}{{\pi R^{2} }}$$
(16)

Based on Eqs. (15) and (16), d toCH can be recomputed as follows:

$$d_{toCH} = \frac{2}{3}R$$
(17)

Then, we can recalculate Ecm i as follows:

$$Ecm_{i} = LE_{elec} + \frac{4}{9}L\varepsilon_{fs} R^{2}$$
(18)

Regarding Ech i , it also can’t be determined before the end of the clustering game, we can set its value to approximately be the amount of energy consumed by a CH to receive, aggregate and forward the data collected by all its neighbors. If we adopt two-ray ground reflection model for the data transmission from a CH to BS, we have the following equation:

$$Ech_{i} = Dr_{i} LE_{elec} + \left( {Dr_{i} + 1} \right)LE_{DA} + L\varepsilon_{amp} \left( {d_{i}^{toBS} } \right)^{4}$$
(19)

where Dr i is the node degree of player i; E DA is the energy consumed for aggregating a one-bit data packet and d toBS i is the distance to BS of player i, which can be got by measuring the received signal strength when BS initially broadcasts the “Start” message.

As a result, the concrete value of equilibrium probability for each node can be computed according to Eqs. (12), (13), (18) and (19).

6 Our proposed protocol

In this section, we will first describe the detail of our proposed protocol which we call it as Hybrid, Game Theory based and Distributed clustering (HGTD). And then we give several observations on it.

Figure 3 gives the procedures of our protocol, which consists of an initialization phase and many repeated rounds that can be further divided into set-up phase and steady-state phase.

Fig. 3
figure 3

Time line denoting the procedures of HGTD

Full size image

In the initialization phase, the main task for each node includes localized information collecting and calculating the distance to BS. First, BS broadcasts “Start” message and we suppose this message can be received by all nodes. Then each node calculates its distance to BS according to the received signal strength, and broadcasts “Hello” message to its neighbors within radius R. Finally, each node knows all its neighbors by recording the “Hello” messages transmitted by the nodes within radius R into its own storage.

Regarding the set-up phase, it includes three sub phases: tentative CHs selection, final CHs election and clusters formation. And we will discuss the detail of these three sub phases later.

In the steady-state phase, based on the topology formed in the set-up phase, every non-cluster head node collects data from the sensor field and transmits the data to the CH at its own time slot. And each CH aggregates the data collected by its member nodes and forwards it to BS.

6.1 Tentative CHs selection

In tentative CHs selection sub phase, each node acts as a player and will play several clustering games which include its own one and its neighbors’. And by playing its own clustering game, each node self-decides whether to be a CH according to its equilibrium probability.

In each round, for any node i, it first calculates its equilibrium probability. If there are no dead neighbor nodes that have exhausted their energy, it calculates the equilibrium probability according to Eq. (13); otherwise, it calculates the equilibrium probability as follows:

$$p_{i} = 1 - (w_{i} )^{{1/\left( {\left| {Nb\left( i \right)} \right| - \left| {Nd\left( i \right)} \right|} \right)}}$$
(20)

where Nb(i) is the neighbors of node i; Nd(i) is the set consisting of the dead neighbors of node i and |Nd(i)| is the number of elements in set Nd(i).

And then, node i will randomly choose a number within range (0, 1). If this random number is smaller than its equilibrium probability, it will be selected as a CH. To avoid the case that more than one CH occurs within a close neighbor, a sensor node successfully self-decided to be a CH will keep the CH state tentatively (tentative CH) and will further compete for the final CH in the final CHs election sub phase. By broadcasting the tentative CH selection message “CH_msg1” (including node ID, CH status and node’s Cost which we define it as the amount of energy that has been consumed at present) with communication radius R and receiving this kind of messages, each tentative CH will know its neighbor tentative CHs. Let S TCH denote the set consisting of all tentative CHs in the network. For any tentative CH node i, the set of its neighbor tentative CHs can be calculated by

$$N_{TCH} \left( i \right) = \left\{ {j\left| {j \in Nb\left( i \right)\text{ }and\text{ }j \in S_{TCH} } \right.} \right\}\text{ }.$$
(21)

where Nb(i) is the neighbors of node i.

6.2 Final CHs election

As more than one tentative CH selected in the previous sub phase may occur in a close neighbor, which leads to the uneven distribution of CHs. The final CHs election sub phase is introduced to avoid this problem. In addition, if a tentative CH with less energy is elected to be the final CH, the network lifetime may be weakened. And if a tentative CH with more neighboring tentative CHs is elected to be the final CH, more tentative CHs will lose this chance to be the final CHs that may result in the uneven coverage of the sensor field. Thus, it is more effective that the tentative CHs with more residual energy and less neighbor tentative CHs have bigger probability to be the final CHs.

For any tentative CH i, if it has no neighbor tentative CHs, that is, the set N TCH (i) is empty, it will be a final CH automatically and broadcast the final CH election message “CH_msg2” (including node ID, CH status and node degree Dr) within radius R. If set N TCH (i) is not empty, several iterations will be executed by tentative CH i for the election of the final CH. And its maximum number of iterations can be calculated as follows:

$$n_{\hbox{max} } (i) = \left| {N_{TCH} (i)} \right| + 2$$
(22)

where N TCH (i) is the set consisting of the neighbor tentative CHs of node i (excluding node i itself); |N TCH (i)| is the number of elements in set N TCH (i).

For the description of the iteration process, we record S iter as the set consisting of the tentative CHs which need several iterations to compete for the final CHs. And S iter can be expressed as follows:

$$S_{iter} = \left\{ {j\left| {j \in S_{TCH} \text{ }and\text{ }N_{TCH} (j) \ne \emptyset } \right.} \right\}$$
(23)

where S TCH is the set consisting of all tentative CHs and N TCH (j) is the set consisting of the neighbor tentative CHs of node j.

In the first iteration, as each node in set S iter is still the tentative CH, it selects its own CH (my_CH) to be the one with the lowest Cost within radius R (including itself). The nodes which select themselves as their own CHs will broadcast the message “CH_msg1” within radius R and be the tentative CHs in the next iteration, the other nodes in set S iter will return to the state of normal node.

For any node i in set S iter , it continues the iteration process until it has received the message “CH_msg2” or completed n max (i) iterations in total. And during any iteration k, 1 < k < n max (i), node i selects its own CH with the lowest Cost from the tentative CHs within radius R. If it selects itself as its own CH or has no neighbor CHs, it will be tentative CH in next iteration and broadcast message “CH_msg1” within radius R. During the iteration n max (i), if node i is the tentative CH with the lowest Cost within radius R or has no neighbor CHs, it will be the final CH and broadcast message “CH_msg2” within radius R.

After a node in set S iter completes its iteration process, if it is not a final CH and still have not received the message “CH_msg2”, it will be a final CH and broadcast message “CH_msg2” within radius R.

The pseudo-code of this sub phase for any node i is shown in Algorithm 1.

figure f

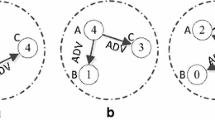
An example of several tentative CHs to show the neighbor relationship is given in Fig. 4. Where node A, B, C, D, and E are tentative CHs selected in the former sub phase, and the nodes connected by the solid line are neighbors.

Fig. 4
figure 4

An example of several tentative CHs to show the neighbor relationship

Full size image

The results of the iteration process for each node in Fig. 4 are shown in Table 1. Node E is the first one to complete the iteration process and has priority to become the final CH, since it has the least number of neighboring tentative CHs. As node C has the lowest Cost, it is selected as the tentative CH in each time of the iteration and be the final CH at last. Node D receives the final CH election message sent by E and then exits the iteration process early. And there is no more than one final CH in a close proximity.

Table 1 The results of all iterations
Full size table

6.3 Clusters formation

After all final CHs have been determined, the normal node which has neighboring final CHs will choose the one with the smallest node degree to join cluster. The join message join_cluster (including node’s residual energy Eres) is broadcasted by each normal node within radius R, and it will be received by the corresponding CH and the nodes which have no neighboring CHs. The node with no neighboring CHs will select a relay with the maximum residual energy among its neighbors to join the corresponding cluster. Each CH creates a schedule and broadcasts it to its member nodes.

6.4 Analyses of HGTD

Several observations of HGTD are discussed as follows:

Observation 1:

Our protocol is completely distributed. Each node runs for the CH within its close neighbor and each non-cluster head node selects its own CH or relay node among its neighbors.

Observation 2:

By playing its own clustering game, each node gets its equilibrium probability. And the node with bigger node degree or longer distance to BS has smaller equilibrium probability, which makes it achieve a good trade-off between energy consumption and providing the required services effectively.

Observation 3:

In the final CHs election sub phase, the tentative CHs with fewer neighboring tentative CHs become final CHs with higher priority, which makes the sensor field be widely covered. And if a tentative CH have the fewest neighboring tentative CHs among its neighbor tentative CHs, it will be a final CH without doubt.

Observation 4:

In the final CHs election sub phase, the tentative CHs with more residual energy have priority to become final CHs, which makes the energy consumption among nodes be well balanced. If a tentative CH has the most residual energy among its neighboring tentative CHs, it will be a final CH without doubt.

Observation 5:

The final CHs election process terminates in finite iterations.

Proof:

According to Eq. (22), the maximum times of iteration for a tentative CH is limited by the number of its neighbor tentative CHs. Let ρ be the node density and we assume nodes are uniformly deployed in the sensor field. For a tentative CH, its average number of neighbor tentative CHs (excluding itself) can be calculated by

$$n_{nbr} \,= \, p\left( {\rho \pi {\text{R}}^{2} - 1} \right)\text{ }.$$
(24)

where p is the average equilibrium probability of a sensor node and R is the communication radius of a sensor node.

Based on Eqs. (22) and (24), the average times of the iteration for a tentative CH can be expressed as follows:

$$n_{iter} \,= \,n_{nbr} + 2$$
(25)

The resulting n iter  = 7 for p = 0.05, ρ = 1 node/50 m2 and R = 40 m.

Observation 6:

The probability that two nodes in each other’s neighborhood are both final CHs is small.

Proof:

As only tentative CHs have opportunity to become final CHs, assume that any two neighboring tentative CHs are expressed as s 1 and s 2 respectively. And the number of neighbor tentative CHs for node s 1 and s 2 are N 1 and N 2, the maximum number of iteration are N 1 + 2 and N 2 + 2 respectively. Consider the following worst case scenario: s 1 and s 2 have fewer times of iteration than their other neighbor tentative CHs, thus no final CHs will occur before they complete the iteration process. And under this scenario, three cases may occur during the iteration process:

Case 1:

N 1 = N 2 = 1. In this case, as s 1 and s 2 have no other neighboring tentative CHs, the one with less Cost will be the final CH. It is impossible that s 1 and s 2 are both final CHs in this case.

Case 2:

N 1 ≠ N 2. Without loss of generality, we assume N 1 < N 2. In this case, s 1 will be elected to be the final CH before s 2. Thus, s 2 will receive a final CH message from s 1 and give up to become the final CH.

Case 3:

N 1 = N 2 ≥ 2. In this case, s 1 and s 2 will be final CHs simultaneously if the following two conditions are satisfied: First, both s 1 and s 2 select their other neighbor CHs as their own CHs in the N 1 + 1st iteration; second, both s 1 and s 2 have no neighboring CHs in the N 1 + 2nd iteration. Assume p nbr represents the probability that s 1 and s 2 be the final CHs simultaneously, and it could be approximately calculated by

$$p_{nbr} { = }\left( {\frac{{N_{1} - 1}}{{N_{1} }}\left( \frac{1}{2} \right)^{{N_{1} }} } \right)^{2} .$$
(26)

The resulting p nbr  = 0.0156 for N 1 = N 2 = 2, and p nbr  = 0.0069 for N 1 = N 2 = 3. The resulting p nbr rapidly decreases as N 1 increases.

7 Simulations and results analyses

In this section, we will first set the value of parameters used in the simulations and give the simulation model. And then we will show the simulation results and evaluate the performance by analyzing these results.

7.1 Simulation model

We simulate the sensor field by a rectangular area with size S, and nodes are randomly deployed with density ρ. BS is placed outside the sensing field. In our protocol, the communication radius of each node is R and only one CH will be selected within an area with radius R. that is, the radius of a cluster is equal to R. Let n CH-opt denote the optimal number of clusters in the network. Then the average area of a cluster can be expressed as S/n CH-opt . Thus, the communication radius R can be calculated by

$$R = \sqrt {\frac{S}{{\pi n_{{CH{ - }opt}} }}} \text{ }\text{.}$$
(27)

Adopting the similar methods as those in [31], we can get n CH-opt by minimizing the total energy in the network, which is

$$n_{{CH{ - }opt}} \,=\, \frac{{\sqrt {\rho S} }}{{\sqrt {2\pi } }}\sqrt {\frac{{\varepsilon_{fs} }}{{\varepsilon_{amp} }}} \frac{\sqrt S }{{d_{toBS}^{2} }}\text{ }\text{.}$$
(28)

Here, d toBS is the average distance to BS. We simply compute d toBS as follows:

$$d_{toBS} = \frac{{\left( {d_{toBS}^{\hbox{min} } + d_{toBS}^{\hbox{max} } } \right)}}{2}$$
(29)

Here, \(d_{toBS}^{\hbox{min} }\) is the minimum value of distance to BS and \(d_{toBS}^{\hbox{min} }\) is the maximum value of distance to BS. And they can be determined before the deployment of the sensor nodes.

We will evaluate the performance of our protocol by comparing it with LEACH, CROSS and LGCA. The expected percentage of CHs in LEACH is set to be 5 %. And the predefined parameter w in CROSS and LGCA is computed as follows:

$$w = \sum\limits_{i = 1}^{n} {w_{i} }$$
(30)

where n is the total number of sensor nodes and w i is the value calculated by Eq. (12).

The values of other parameters used throughout the simulations are given in Table 2.

Table 2 Simulation parameters
Full size table

We will evaluate the performance of our protocol under the followed two situations:

First, for several different sizes S (L × W m2) of the network, we compare our protocol with LEACH, CROSS and LGCA under the case that the communication radius R in our protocol and LGCA is calculated by Eq. (27). And these values of S are 50 × 100, 100 × 100, 100 × 150, 150 × 150, 150 × 200 and 200 × 200 m2 respectively. The position of BS is (L/2, W + 50), and the node density ρ is 1 node/50 m2.

Second, for several different values of communication radius R, we compare our protocol with LEACH, CROSS and LGCA under the case that the network size S is equal to 50 × 50 m2. The position of BS is (25, 125) and node density ρ is 1 node/25 m2.

7.2 Results analyses

Network lifetime is the most important evaluation criterion for clustering protocols, and it is defined as the lifespan of the node who first depletes its energy in the network. Figure 5 is a comparison of network lifetime among LEACH, CROSS, LGCA and HGTD for several different sizes S of the network.

Fig. 5
figure 5

The comparison of network lifetime among LEACH, CROSS, LGCA and HGTD for several sizes of the network

Full size image

It is clear from Fig. 5 that in terms of the network lifetime, HGTD outperforms LEACH, CROSS and LGCA in all cases of S. In addition, the curves of all the four protocols have a downward trend when S increases. This is because the distance to BS increases with the increase of S. And LGCA has a shorter network lifetime than CROSS when S is smaller, but the opposite is true when S becomes bigger than 1.5 × 103 m2. This phenomenon indicates that LGCA is more suitable than CROSS in large-scale networks.

Figure 6 is a comparison of rounds until 10 % of nodes die among LEACH, CROSS, LGCA and HGTD for several sizes of the network. And HGTD still outperforms LEACH, CROSS and LGCA in all cases of S.

Fig. 6
figure 6

The comparison of rounds until 10 percent of nodes die among LEACH, CROSS, LGCA and HGTD for several sizes of the network

Full size image

The network lifetime is a very important metric for the performance evaluation of clustering protocols, since it gives the moment when nodes begin to die. And the lifespan of the last dead node is also important. Figure 7 shows the comparison of rounds until the last node dies among LEACH, CROSS, LGCA and HGTD for several sizes of the network.

Fig. 7
figure 7

The comparison of rounds until the last node dies among LEACH, CROSS, LGCA and HGTD for several sizes of the network

Full size image

Although the network lifetime of HGTD is longer than CROSS and LGCA, the opposite is true about the rounds until the last node dies as shown in Fig. 7. This is because HGTD has a higher energy consumption rate when nodes begin to die. And Fig. 7 also shows that the rounds until the last node dies for all the four protocols decrease with the increase of network size S.

Figure 8 shows the difference of average number of clusters per round among LEACH, CROSS, LGCA and HGTD for several sizes of the network.

Fig. 8
figure 8

Average number of clusters per round among LEACH, CROSS, LGCA and HGTD for several sizes of the network

Full size image

From this figure, we can see that the average number of clusters in LEACH rapidly increases with the increase of network size S. This is because the total number of sensor nodes rapidly increases with the increase of S and the expected number of clusters in LEACH is set to be a fixed value 5 %. The average number of clusters in CROSS is relatively stable, this is because that on the one hand, a sensor node, once selected as a CH, will not be a CH until all other nodes in the network have also served as CHs. And on the other hand, as shown in Fig. 9, the value of predefined parameter w changes within a small range when S increases. And the average number of clusters in LGCA and HGTD increases slowly when S increases. This is because that although the total number of sensor nodes increases with the increase of S, the cluster radius which is equal to the communication radius R also increases as shown in Fig. 10. And to some extent, the increase of parameter w has reduced the increase rate of the number of clusters.

Fig. 9
figure 9

Values of parameter w predefined in CROSS and LGCA for several sizes of the network

Full size image
Fig. 10
figure 10

Values of communication radius R predefined in LGCA and HGTD for several sizes of the network

Full size image

And from Fig. 8, we also find that the average number of clusters in HGTD is slightly larger than that in LGCA, this is because a sensor node in LGCA, once selected as a CH, will not be a CH until all its neighbors have also served as CHs. But in HGTD, every sensor node has the chance to be a CH in each round.

To show the performance of our protocol in more detail, Fig. 11 gives the number of nodes alive in each round for LEACH, CROSS, LGCA and HGTD when S = 1  ×  104 m2.

Fig. 11
figure 11

Number of nodes alive versus rounds for LEACH, CROSS, LGCA and HGTD when S = 1 × 104 m2

Full size image

Figure 11 shows HGTD has the shortest time interval from the round of the first node dead to the round of the last node dead. And conversely, LGCA has the longest time interval. This indicates that the energy consumption among nodes is well balanced in HGTD but not in LGCA. A sensor node in LGCA, once selected as a CH, will not be a CH until all its neighbors have also served as CHs. This can result in that a sensor node with more neighbors has less chance to be a CH. Thus, the energy consumption among nodes can’t be well balanced in LGCA.

Figure 12 gives the comparison of network lifetime among LEACH, CROSS, LGCA and HGTD when S = 2.5 × 103 m2 for several values of communication radius R.

Fig. 12
figure 12

The comparison of network lifetime among LEACH, CROSS, LGCA and HGTD when S = 2.5 × 103 m2 for several values of communication radius R

Full size image

From Fig. 12, we can see that our protocol outperforms LEACH, CROSS and LGCA for all cases of R. Furthermore, the network lifetime of LGCA is longer than CROSS when R is equal to 50 or 40 m, and the opposite is true when R is equal to 30 or 20 m. This is because that a node in LGCA almost can communicate with all other nodes in the network when R is equal to 50 or 40 m. Under this case, almost each node has the same number of neighbors. But when R is equal to 30 or 20 m, a big difference of the number of neighbors will occur among the nodes in the network due to the uneven distribution of the nodes. Thus, as aforementioned, the energy consumption among nodes can’t be well balanced in LGCA.

8 Conclusions

In this paper, based on game theory, we present a clustering protocol called HGTD (Hybrid, Game Theory based and Distributed clustering) to reduce the energy consumption and enhance the network lifetime.

First, we define the payoff for each node when choosing different strategies to be a CH or not, and both node degree and distance to BS are considered. And then, under this definition of payoff, we calculate the equilibrium probability to be CH for each node based on game theory. The nodes with longer distance to BS or bigger node degree have smaller probability to be CHs that can achieve a good trade-off between minimizing energy consumption and providing the required services effectively. At last, to avoid the case that more than one CH occurs in a close proximity, we present an iterative algorithm to select final CHs from the potential CHs. And a hybrid of residual energy and the number of neighboring potential CHs is considered to effectively distribute the energy consumption among nodes. And we further prove that our iterative algorithm terminates in finite iterations.

Through extensive simulations, we verify that compared with LEACH, CROSS and LGCA, our protocol has reduced the energy dissipation effectively and achieved the longest network lifetime under the cases of different network sizes and different communication radiuses.