Chain-based barrier coverage in WSNs: toward identifying and repairing weak zones

Abstract

Barrier coverage constructs a sensing barrier for detecting intruders crossing a belt region. Recent studies mostly focus on efficient algorithms to guarantee barrier coverage, with little consideration on the collaboration between individual nodes. Observing that in many situations, sensors naturally fall into several clusters (or components), for example when the sensors are deployed uniformly at random with a relatively low density, or when random sensors go down as a result of energy exhaustion, we propose to use chain as a basic scheduling unit for sensing and communication. A chain is a set of sensors whose sensing areas overlap with each other, and it can be extracted from a cluster. We present a distributed algorithm, named BARRIER, to provide barrier coverage with a low communication overhead for the wireless sensor networks (WSNs). The algorithm is able to detect weak zones that are often found in an initial deployment of a WSN, and repair them by adding an appropriate number of sensors. Theoretic analysis and simulations show that, compared with a representative previous algorithm, BARRIER significantly reduces the communication overhead and reparation cost in terms of number of sensors.

1 Introduction

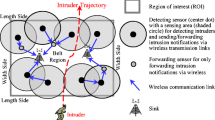
One of the surveillance applications in the Wireless Sensor Networks (WSNs) is to detect intruders crossing a belt region. This application is called barrier coverage [3, 4, 9, 15]. Different types of coverage are needed for various applications: full coverage covers the whole region, trap coverage [5] allows coverage on the holes with bounded diameter in a region, and barrier coverage focuses on detecting intruders that attempt to cross a sensor field [13]. Barrier coverage can provide sensor barriers to detect whether there are intruders across the boundaries of crucial infrastructures, such as battlefields, country borders, and coast lines [11, 17].

There are two types of barrier coverage [9]: weak barrier coverage and strong barrier coverage. Weak barrier coverage can only detect the intruder crossing a region at orthogonal crossing paths while strong barrier coverage can detect an arbitrary trajectory. Yang et al. [18] proposed a heuristic algorithm to provide weak barrier coverage with a minimum number of sensors under a probabilistic sensing model. Other researchers have concentrated on strong barrier coverage problems, such as how to achieve barrier coverage with high probability when sensors are deployed randomly [9], how to measure and guarantee the quality of barrier coverage [4, 5, 8], how to achieve barrier coverage with a long lifetime [6, 10], how to construct sensor barriers to detect intruders crossing a randomly deployed sensor network in a rectangular area [11], and how to deploy sensors to obtain effective barrier coverage [14, 18, 19]. Besides, random deployment is widely-used when the researchers in [3–5, 9, 11, 17] study barrier coverage problem.

Fig. 1

Weak and strong barrier coverages

Most previous studies have considered individual node as the unit for sensing and communication. We argue that this can incur a high communication cost, especially when the number of sensors is large (e.g., thousands). To improve message efficiency, we propose a method called BARRIER, motivated by the observation that in many situations, sensor nodes fall into clusters (or components, see Fig. 1). This can be a consequence that results from an initial deployment following a somewhat random distribution. For example, in an aircraft-led deployment [14], sensors are scattered from the air over a specified region or along a given path, naturally producing a fairly random (e.g., Poisson) node distribution. When the node density is not high enough, network disconnection may happen and clusters emerge. Even when the nodes are regularly placed in the beginning, as time goes on, random errors (e.g., energy depletion) that result in a non-uniform/random coverage layout may occur, still giving rise to clusters. Given the popular practice with random distribution [1, 11] and the typical operational error patterns found in WSNs, we believe that the existence of clusters will stay as a common case in WSNs, and it is this that justifies our optimization.

The BARRIER algorithm uses chain [14] as the scheduling unit for sensing and communication. A chain is a set of sensors crossing the deployed field with the sensing areas of adjacent sensors overlapping with each other. Fig. 1 shows an example with three chains. Similar to [4, 5], we assume there are base stations at certain places of the belt region so that every node can communicate with its neighbors and at least one gateway. Chains can be extracted from a cluster. Given a chain, two sensors are selected to be delegates that take the responsibility of communication and computations for the chain. Two delegates of a chain can cooperate with the delegates of another chain within communication range, denoted by $r_c$. Compared with traditional methods using individual node as the unit for sensing and communication, our chain-based approach can significantly reduce communication overhead, thereby prolonging the lifetime of WSNs. We also present novel strategies to identify and repair weak zones for both weak and strong barrier coverages. As it turns out, BARRIER requires much fewer sensors than other reparation methods.

The rest of this paper is organized as follows. In Sect. 2, we discuss the related works on barrier coverage. Section 3 describes the network model. We describe the theoretic background of identifying and repairing weak zones in Sects. 4 and  5, respectively. In Sect. 6, a novel algorithm is presented to guarantee the quality of barrier coverage. Performance study and results analysis are shown in Sect. 7. Finally, we give the conclusion and our future work in Sect. 8.

2 Related work

Barrier coverage problem has been extensively studied in [4, 5, 7, 10, 11, 14, 18, 19]. A centralized optimal algorithm using sleep-wakeup model is proposed in [10] to achieve globally strong barrier coverage. An efficient algorithm in [11], called Divide-and-Conquer, constructs node-disjoint barriers between the left and right boundaries of a region under special conditions. The authors in [14, 18, 19] assume that the sensors are line-based deployed by aircrafts, and show that the deployment strategy has considerable impact on the effectiveness of constructing strong barrier coverage. Yang et al. [18] adopt the probabilistic sensing model and present a distributed algorithm to minimize the number of sensors while guaranteeing weak barrier coverage.

k -barrier coverage is first proposed in [9]. It means that any path crossing the belt region is covered by at least k sensors. This concept is generalized to L-local k-barrier coverage by [3], whose goal is to guarantee that the detection of intrusion’s trajectory is confined within a slice (of length L) of a belt region.

Recent studies which are close to our work include [4, 5, 9]. A network can provide strong k-barrier coverage if and only if there exist k node-disjoint barriers between the left and right boundaries of a region [9]. The authors in [4, 5] propose distributed algorithms to measure and guarantee the quality of strong barrier coverage at a given required quality $Q^{*}$. They consider two types of weak zones in a network: non- k -barrier covered zones which are not strongly k-barrier covered, and critical k -barrier covered zones which are strongly k-barrier covered but may fail to detect certain arbitrary crossing paths whose trajectories are not completely inside their areas. Besides, they claim that a critical k-barrier covered zone should be repaired if its length is less than $Q^{*}$.

They define the actual quality of strong barrier coverage, denoted as $Q_{k}$, as follows. $Q_{k}$ = $\max${L: the belt region is L-local k-barrier covered}. $Q_{k}=-1$ if there exists at least one non-k-barrier covered zone in the belt region. Otherwise, $Q_{k}$ equals to the minimum length of the critical k-barrier covered zones.

For each weak zone Z, they create an extended zone $Z'\supset Z$ with additional length $\delta$ on both the left and right sides of Z, where $\delta =Q^{*}$ for each non-k-barrier covered zone and $\delta =Q^{*}-L$ for each critical k-barrier covered zone of length L. This strategy may not be precise and requires more sensors than the network actually needs. The required quality $Q^{*}$ can affect both the number of critical k-barrier covered zones and the number of sensors needed to repair the network.

In this paper we discuss both weak and strong barrier coverages by considering the chains in wireless sensor networks as sensing and communication units. By first identifying weak zones independent of $Q^{*}$ in a sensor network, we aim to reduce communication overhead and the number of sensors required for reparation.

3 Network model

Sensors are deployed in a belt region [4], with two of its boundaries parallel to each other and the other two orthogonal to the parallel ones. We assume that sensors are static and have no mobility capability after deployment. Each sensor can only detect an intruder’s movement if the intruder is within the sensor’s sensing area. The sensing area of a sensor is a continuous area surrounding its center (not necessarily a disk). In addition, two sensors are said to be neighbors if their sensing areas overlap with each other. We summarize the notations in Table 1.

Table 1 Summary of used important symbols

A cluster is a set of sensors which can communicate with each other via routing between neighbors. A unit cluster contains a single sensor. Likewise a unit chain contains a single sensor. A cluster can be decomposed into several chains under certain conditions, as will be detailed in Sect. 6. Note that all chains are node-disjoint.

Fig. 2

An example of clusters, chains, orthogonal lines and zones. Chains are linked by blue lines. Cluster 2 can be decomposed into chain $B_{1}$ and $B_{2}$. Zone Z can be covered by chain $B_{1}$ (Color figure online)

The two sensors at the ends of a chain are called left and right end sensors respectively. The leftmost (resp. rightmost) orthogonal line of a chain is an orthogonal line with the smallest (resp. biggest) horizontal coordinate (denoted as V) which is tangent to the sensing area of the left (right) end sensor. We denote the leftmost and rightmost orthogonal lines, left and right end sensors of a chain A as ll(A), rl(A), ls(A) and rs(A), respectively. Chain B is said to be on the left (resp. right) of chain A if $V_{ll(B)}\le V_{ll(A)}$ (resp. $V_{rl(B)}\ge V_{rl(A)}$). In particular, we use two virtual chains, $C_{s}$ and $C_{t}$, to represent the left and right boundaries of a belt region, see Fig. 2 for example.

A Zone, denoted as Z, is a slice of the belt region. Two of its edges coincide with the parallel boundaries of the belt region while the other two are orthogonal to the parallel boundaries [4]. Let ll(Z)(rl(Z)) be the orthogonal line $l_{l}$($l_{r}$) on the left (right) side of Z. Let $ll(Z)=l_{l}$ , $rl(Z)=l_{r}$ be $Z=Z(l_{l},l_{r})$. $L_{Z}$ is the length of Z. For zone $Z_{1}$ and $Z_{2}$, we define $Z_{1}\subset Z_{2}$ if $V_{ll(Z_{2}})\le V_{ll(Z_{1}})$ and $V_{rl(Z_{1})}\le V_{rl(Z_{2}})$ hold. Furthermore, zone Z is said to be covered by chain A if $V_{ll(A)}\le V_{ll(Z)}$ and $V_{rl(Z)}\le V_{rl(A)}$. This can be given by $Z\subset Z_{A}=Z(ll(A),rl(A))$.

4 Weak zones identification

In this section, we describe several definitions used in this paper, followed by a number of metrics to identify weak zones for both weak and strong barrier coverages.

A crossing path is k -barrier covered if it can be detected by at least k sensors. A zone is said to provide weak/strong k-barrier coverage if the arbitrary orthogonal/arbitrary crossing path through the belt region is k-barrier covered [4, 5, 9]. Obviously, weak k-barrier coverage is a special case of strong k-barrier coverage, because orthogonal crossing paths is a special case of crossing paths. Fig. 1 gives an illustration of weak and strong 1-barrier coverages. The following lemma leads to an important relationship between a chain and barrier coverage.

Lemma 1

Chain A can provide strong 1-barrier coverages for any zone Z it covers.

Proof

Any arbitrary crossing path through $Z_{A}=Z(ll(A),$ rl(A)) can be detected by at least one sensor in chain A, and thus chain A can provide strong 1-barrier coverage in zone $Z_{A}$. If zone Z can be covered by chain A, then $Z\subset Z_{A}$. Hence, chain A can provide strong 1-barrier coverage for zone Z. $\square$

An implication of Lemma 1 is that a zone is strongly k-barrier covered if it can be covered by k chains in the belt region.

4.1 Weak k-barrier coverage

We mainly focus on the leftmost and rightmost orthogonal lines of chains in the belt region. First we introduce the concept of chain-boundary zone, and then provide theoretical analysis for measuring the quality of weak barrier coverage.

A chain-boundary zone is defined as follows. Denote $S_{L}$ as the set of all the leftmost and rightmost orthogonal lines of chains (including two virtual chains, $C_{s}$ and $C_{t}$ ) in a belt region. Let $l_{0}$, $l_{1}$ ,...,$l_{n}$ be the lines from left to right (i.e.,$V_{l_{0}}\le ...\le V_{l_{i}}\le ...\le V_{l_{n}}$) in $S_{L}$($1\le i\le n$). We define the zone between $l_{i-1}$ and $l_{i}$ as a chain-boundary zone (see Fig. 3 for instance), denoted by $Zn(l_{i-1},l_{i})$ and $Zn(l_{i-1},l_{i})=Z(l_{i-1},l_{i})$. Accordingly, $l_{i-1}$ and $l_{i}$ are the neighboring orthogonal lines in $S_{L}$, and no other leftmost or rightmost orthogonal line exists between them. Note that a belt region can be seen as a set of continuous chain-boundary zones.

Fig. 3

Chain-boundary zones

The following lemma describes the weak/strong barrier coverage problem in a chain-boundary zone.

Lemma 2

A chain-boundary zone $Zn(l_{i-1},l_{i})$ is weakly k -barrier covered if and only if it is strongly k -barrier covered.

Proof

(Sufficiency) Immediate from definitions.

(Necessity) Suppose an orthogonal crossing path throu-gh $Zn(l_{i-1},l_{i})$ can be detected by at least one sensor of chain A. $V_{l_{i-1}} \le V_{ll(A)} \le V_{l_{i}}$, $V_{l_{i-1}} \le V_{rl(A)} \le V_{l_{i}}$ or $V_{l_{i-1}} \le V_{ll(A)} \le V_{ll(A)} \le V_{l_{i}}$ contradicts that $Zn(l_{i-1},l_{i})$ is a chain-boundary zone, for no other leftmost or rightmost orthogonal line of certain chain exists between $l_{i-1}$ and $l_{i}$, so $V_{ll(A)} \le V_{l_{i-1}} \le V_{l_{i}} \le V_{rl(A)}$. Thus, $Zn(l_{i-1},l_{i})\subset Z(ll(A),rl(A))$, which means chain A can provide strong 1-barrier coverage for zone $Zn(l_{i-1},l_{i})$ (Lemma 1). Furthermore, if $Zn(l_{i-1},l_{i})$ is weakly k-barrier covered, there exist at least k barriers that provide strong 1-barrier coverage for $Zn(l_{i-1},l_{i})$ respectively. So $Zn(l_{i-1},l_{i})$ can be strongly k-barrier covered. See Fig. 4 for illustration. $\square$

Fig. 4

Illustration of Lemma 2

The following lemma reveals the relationship between weak k-barrier coverage in a belt region and that in chain-boundary zones.

Lemma 3

The belt region can provide weak k -barrier coverage if and only if all chain-boundary zones in the belt region are weakly or strongly k -barrier covered.

Proof

(Sufficiency) A belt region can be seen as a set of continuous chain-boundary zones. If all chain-boundary zones in the belt region are weakly or strongly k-barrier covered, then all the orthogonal crossing paths through the belt region are k-barrier covered; thus, the belt region can provide weak k-barrier coverage.

(Necessity) If a belt region can provide weak k-barrier coverage, then all the orthogonal crossing paths through the whole belt region are k-barrier covered; all orthogonal crossing paths in each chain-boundary zone are k-barrier covered, so all the chain-boundary zones in the belt region can be weakly k-barrier covered. And all chain-boundary zones are strongly k-barrier covered (Lemma 2). $\square$

Theorem 1

$Q_{k}\ne -1$ if and only if the belt region can provide weak k -barrier coverage.

Proof

If a belt region can provide weak k-barrier coverage, then all the chain-boundary zones are strongly k-barrier covered, which means $L>0$. Hence, $Q_{k}\ne -1$. Conversely, if $Q_{k}\ne -1$, all chain-boundary zones are weak (strong) k-barrier covered because $L>0$. Thus, the belt region can provide weak k-barrier coverage (Lemma 3). $\square$

4.2 Strong k-barrier coverage

In this section we discuss how to construct k node-disjoint barriers between the left and right boundaries for strong k-barrier coverage in a belt region. First, we introduce two important concepts.

A zone between two chains is described as follows. For any chains, for example chain A and B, in a belt region, if $V_{ll(A)}\le V_{rl(B)}$, we denote Zn(A, B) as zone between chain A and B, where $ll(Zn(A,B))=ll(A)$ and $rl(Zn(A,B))=rl(B)$ (see illustration in Fig. 5). From the definition we know that $Zn(A,B)=Z(ll(A),rl(B))$.

The concept of critical k -barrier covered zone was introduced in [4, 5]. We make a small modification to it as the zone between two chains instead of that between two sensors [4]. Critical k-barrier covered zone is an important concept for strong k-barrier coverage. First, it is a strongly k-barrier covered zone; however, it may not detect certain arbitrary crossing paths whose trajectories are not completely inside its area (see the green crossing path in Fig. 5). Second, for a belt region that can provide weak k-barrier coverage ($Q_{k}\ne -1$), if all the critical k-barrier covered zones are repaired, then strong k-barrier coverage can be guaranteed. We have a lemma similar to Lemma 4.6 in [4] as follows.

Lemma 4

Zn(A, B) is a critical k -barrier covered zone if Zn(A, B), $Zn(A',B)$ and $Zn(A,B')$ are strongly k -barrier covered while $Zn(A',B')$ is not, where chain A and chain B share no orthogonal line with the left or right boundary of the belt region, and $A'$ is the nearest chain on the left of A while $B'$ is the nearest chain on the right of B (see Fig. 5).

Fig. 5

Zn(A, B) is a critical 1-barrier covered zone. Zn(A, B), $Zn(A',B)$ and $Zn(A,B')$ are strongly 1-barrier covered while $Zn(A',B')$ is not

We illustrate the role of critical k-barrier covered zone in Lemma 2 based on Lemma 4. We can also use it to identify all the critical k-barrier covered zones in a belt region.

Theorem 2

If Zn(A, B) is a critical k -barrier covered zone, and let $S_{B_{left}}$ be the set of chains in the belt region except chains A, B, $A'$ and $B'$, then.

(1) :

If $Zn(A',B)$ can be covered by chain i in $S_{B_{left}}$, the same hold for $Zn(A,B')$ and $Zn(A',B')$; if $Zn(A,B')$ can be covered by chain i in $S_{B_{left}}$, the same hold for $Zn(A',B)$ and $Zn(A',B')$.

(2):

$Zn(A',B)$, $Zn(A,B')$ and $Zn(A',B')$ are covered by $k-1$ same chains in $S_{B_{left}}$.

(3):

$Zn(A',B)$ can be covered by chain B if $V_{ll(B)}<V_{ll(B')}$.

(4):

$Zn(A,B')$ can be covered by chain A if $V_{ll(A')}<V_{ll(A)}$.

Proof

(1) Suppose $Zn(A',B)$ can be covered by chain i in $S_{B_{left}}$, then $V_{ll(i)}\le V_{ll(A')}\le V_{rl(B)}\le V_{rl(i)}$. Furthermore, $B'$ is the nearest chain on the right of B and $B \not \in S_{B_{left}}$, so chain i must be on the right of chain $B'$, i.e., $V_{rl(B')}\le V_{rl(i)}$. Thus, $V_{ll(i)}\le V_{ll(A')}\le V_{rl(B')}\le V_{rl(i)}$, which means $Zn(A',B')$ can be covered by chain i. $Zn(A,B')\subset Zn(A',B')$, so it is also covered by chain i. A similar conclusion can be deduced when $Zn(A,B')$ is covered by chain $i \in S_{B_{left}}$.

(2)–(4) Suppose $Zn(A',B)$ is covered by at least k chains in $S_{B_{left}}$, then $Zn(A',B')$ is also covered by at least k chains in $S_{B_{left}}$ according to conclusion (1), then $Zn(A',B')$ is strongly k-barrier covered, which contradicts Lemma 4. Therefore Zn(A, B), $Zn(A,B')$ and $Zn(A',B')$ can be covered by at most $k-1$ chains in $S_{B_{left}}$.

At the same time, both $Zn\!(\!A'\!,\!B\!)$ and $Zn\!(\!A\!,\!B'\!)\!$ are strongly k-barrier covered. Thus, $Zn\!(\!A'\!,\!B\!)\!$ or $Zn\!(\!A\!,\!B'\!)\!$ should be covered by at least one chain of A, B, $A'$ and $B'$. Zn(A, B) is a critical k-barrier covered zone, so $V_{ll(A')}\le V_{ll(A)}\le V_{rl(B)}\le V_{rl(B')}$.

Suppose $Zn(A',B)$ is covered by chain A, then $V_{ll(A)}$ $\le V_{ll(A')}\le V_{rl(B)}\le V_{rl(A)}$, and chain A must be on the left of chain $B'$ for $B'$ is the nearest chain of B on its right, i.e., $V_{rl(B')}\le V_{rl(A)}$. So $V_{ll(A)}\le V_{ll(A')}\le V_{rl(B)}\le V_{rl(B')}\le V_{rl(A)}$, then $Zn(A',B')$ can also be covered by barrier A. Similar conclusions can be obtained by considering $Zn(A',B)$ is covered by chain $A'$ or $B'$.

If $Zn(A',B)$ can be covered by chain B, then $V_{ll(B)}\le V_{ll(A')}\le V_{rl(B)}\le V_{rl(B')}$. If $V_{rl(B)}< V_{rl(B')}$, then $Zn(A',B')$ is not covered by chain B. Otherwise, it is.

As mentioned above, both $Zn(A',B)$, $Zn(A,B')$ and $Zn(A',B')$ are covered by at most $k-1$ chains in $S_{B_{left}}$. If $Zn(A',B)$($Zn(A,B')$) is covered by one or more chains in A(B), $A'$ and $B'$, so is $Zn(A',B')$. In such a case, $Zn(A',B)$($Zn(A,B')$) is strongly k-barrier covered if and only if it can be covered by $k-1$ chains in $S_{B_{left}}$ and chain B(A), which satisfies the conditions described in Lemma 4 that Zn(A, B) is a critical k-barrier covered zone. Furthermore, such $k-1$ chains by which $Zn(A',B)$, $Zn(A,B')$ and $Zn(A',B')$ are covered in $S_{B_{left}}$ are the same (conclusion (1)). Similar conclusion can be obtained by considering $Zn(A,B')$. $\square$

The following lemma, along with Lemma 2, will be used when we repair critical k-barrier covered zones for strong k-barrier coverage in a belt region.

Lemma 5

No critical k -barrier covered zone $Zn(\!A_1 \!,\! B_1\!)\!$ exists inside $Z(ll(\!A'\!)\!,ll(\!A\!))$, or $Z(\!rl(\!B\!)\!,rl(\!B'\!))\!$ if $Zn(A,\!B)\!$ is a critical k -barrier covered zone.

Proof

Let $A_{1}^{'}$ be the nearest chain on the left of $A_{1}$, $B_{1}^{'}$ be the nearest chain on the right of $B_{1}$. If $Zn(A_{1},B_{1})$ exists inside $Z(ll(A'),ll(A))$, then $V_{ll(A')}\le V_{ll(A_{1})}\le V_{ll(B_{1})}\le V_{ll(A)}$. $V_{ll(A_{1})}\le V_{ll(A')}$, for $A'$ is the nearest chain on the left of A. And $V_{ll(A_{1}^{'})}\le V_{ll(A_{1})}$, for $A_{1}^{'}$ is the nearest chain on the left of $A_{1}$. Thus, $V_{ll(A_{1}^{'})}=V_{ll(A_{1})}=V_{ll(A')}$. We consider the three following cases.

• (1) If $V_{rl(B_{1}^{'})}\le V_{rl(B)}$, then $V_{ll(A_{1}^{'})}=V_{ll(A')}\le V_{rl(B_{1}^{'})}\le V_{rl(B)}$, so $Zn(A_{1}^{'},B_{1}^{'})$ can also be strongly k-barrier covered because $Zn(A_{1}^{'},B_{1}^{'})\subset Zn(A',B)$ and $Zn(A',B)$ is strongly k-barrier covered, which is a contraction.

• (2) If $V_{rl(B)}\le V_{rl(B_{1}^{'})}< V_{rl(B')}$, this condition contradicts that $B'$ is the nearest chain on the right of B.

• (3) If $V_{rl(B')} \le V_{rl(B_{1}^{'})}$, then $V_{ll(A_{1})}\!=\!V_{ll(A')} \le V_{rl(B)} \le V_{rl(B_{1}^{'})}$. Hence, $Zn(A',B')$ can also be k-barrier covered because $Zn(A',B')\!\subset \! Zn(A_{1},B_{1}^{'})$ and $Zn(A_{1},B_{1}^{'})$ is strongly k-barrier covered, which is also a contraction.

Therefore, no critical k-barrier covered zone can exist inside $Z(ll(A'),ll(A))$. Similar conclusion can be deduced for $Z(rl(B),rl(B'))$. $\square$

4.3 Identifying all the weak zones

If sensors deployed in a belt region are to provide weak k-barrier coverage, we just identify all the chain-boundary zones that are not k-barrier covered according to Lemma 2, and such zones are usually called non- k -barrier covered zones [4]. If a belt region needs to be strongly k-barrier covered, we should identify both the non-k-barrier covered zones and critical k-barrier covered zones by applying Lemma 2.

5 Repairing weak zones

In this section, we propose strategies for repairing the weak zones in a belt region, achieving weak and strong k-barrier coverages.

5.1 Dealing with weak k-barrier coverage

A belt region cannot provide weak k-barrier coverage if there is at least one non-k-barrier covered zone inside. We give the strategy of guaranteeing weak k-barrier coverage in a belt region:

Lemma 6

Let $Z_{i}$ be a non- k -barrier covered zone, and $Z_{i}$ is $k_{i}$ -barrier covered, where $1\le i\le p$, $k_{i}<k$ and p is the number of non- k -barrier covered zones in a belt region. If we add $k-k_{i}$ chains to each $Z_{i}$, and for each chain $C_{repair}$ added to $Z_{i}$ s.t., $V_{ll(C_{repair})}=V_{ll(Z_{i})}$ and $V_{rl(C_{repair})}=V_{rl(Z_{i})}$, then, the belt region can provide weak k -barrier coverage after all non- k -barrier covered zones are repaired.

Proof

For each non-k-barrier covered zone $Z_{i}$, it is initially $k_{i}$-barrier covered, i.e., covered by $k_{i}$ barriers. If $k-k_{i}$ new barriers that for each barrier $V_{ll(C_{repair})}=V_{ll(Z_{i})}$ and $V_{rl(C_{repair})}=V_{rl(Z_{i})}$ are added to $Z_{i}$, then $Z_{i}$ can be covered by k barriers. Therefore, $Z_{i}$ is weakly/str-ongly k-barrier covered (Lemma 2). If all the non-k-barrier covered zones are weak/strongly k-barrier covered, the belt region can provide weak k-barrier coverage (Lemma 3). $\square$

Figure 6 gives an example of repairing a belt region for weak k-barrier coverage.

Fig. 6

Example of repairing a belt region for weak k-barrier coverage (No non-1-barrier covered zone for $k=1$. Two non-2-barrier covered zones $Zn(l_{0},l_{1})$ and $Zn(l_{4},l_{5})$ for $k=2$. Four non-3-barrier covered zones $Zn(l_{0},l_{1})$, $Zn(l_{1},l_{2})$, $Zn(l_{3},l_{4})$ and $Zn(l_{4},l_{5})$ for $k=3$)

5.2 Dealing with strong k-barrier coverage

As mentioned earlier, there are two types of weak zones for reparation, that is, non-k-barrier covered zones and critical k-barrier zones, and each non-k-barrier covered zone is a chain-boundary zone. Suppose there are p non-k-barrier covered zones and q critical k-barrier covered zones in the belt region. Let $Z_{i}$($1\le i\le p$ ) be a non-k-barrier covered zone, so $Z_{i}=Zn(l_{j-1},l_{j})$($1\le j\le n$), where n is the number of the leftmost and rightmost orthogonal lines of all the chains (including two virtual chains) in the belt region. The strategy which guarantees strong k-barrier coverage is elaborated in the following lemma.

Lemma 7

We construct k node-disjoint barriers between the left and right boundaries of a belt region as follows.

(1) :

For a chain-boundary zone $Zn(l_{j-1},l_{j})$ that is $k_{j}$ -barrier covered ($k_{j}<k$),

(a) :

if $1\le j<n$, add $k-k_{j}$ new chains to $Zn(l_{j-1},l_{j})$ s.t. $Z(l_{0},l_{j})$ is strongly k-barrier covered, and $Z(l_{0},l_{j+1})$ is strongly $k_{j+1}$-barrier covered.

(b) :

if $j=n$, add $k-k_{n}$ new chains to $Zn(l_{n-1},l_{n})$ s.t. $Z(l_{0},l_{n})$ (is strongly) k -barrier covered.

(2) :

For each critical k -barrier zone $Zn(A,B)=Z(l_{t},l_{s})$ ($s\ge t+1$), we add a new chain to it s.t. chain A and chain B become one chain, then $Z(l_{0},rl(B'))$ is strongly k -barrier covered.

Proof

We utilize the induction to prove this lemma. Zone $Z(l_{0},l_{j})$ ($1\le j\le n$) is strongly k-barrier covered if it is covered by k barriers. If $Z(l_{0},l_{n})$ is strongly k-barrier covered, then the whole belt region is strongly k-barrier covered, where $l_{0}$ and $l_{n}$ are the left and right boundaries of the belt region respectively.

• (1) For $j=1$, $Zn(l_{0},l_{1})$ cannot be critically k-barrier covered according to Lemma 4. If $Zn(l_{0},l_{1})$ is strongly k-barrier covered, so is $Z(l_{0},l_{1})$($Zn(l_{0},l_{1})\!=\!Z(l_{0},l_{1})$). Otherwise, we add $k\!-\!k_{1}$ new chains to $Zn(l_{0},l_{1})$, and make it that $Z(l_{0},l_{1})$ is strongly k-barrier covered and $Z(l_{0},l_{2})$ is strongly $k_{2}$-barrier covered. If $k_{2}\!<\!k$, go to (2).

• (2) For any $j=t$ ($1\le t<n$), assume $Z(l_{0},l_{t})$ is already strongly k-barrier covered.

  • (a) If $Zn(l_{t},l_{t+1})$ is a non-k-barrier covered zone, we add $k-k_{t+1}$ new chains to $Zn(l_{t},l_{t+1})$ and make it that $Z(l_{0},l_{t+1})$ is strongly k-barrier covered and $Z(l_{0},l_{t+2})$ is strongly $k_{t+2}$-barrier covered (if $t+2<n$).

  • (b) If $Z(l_{t},l_{s})=Zn(A,B)$ ($s\ge t+1$) is a critical k-barrier covered zone, no critical k-barrier covered zone exists inside $Z(ll(A'),ll(A))$ (Lemma 5), thus no chains will be added to $Zn(A',B)$ in order to make $Z(l_{0},l_{s})=Z(l_{0},rl(B))$ strongly k-barrier covered. On the other hand, $Z(l_{0},ll(A'))$ is strongly k-barrier covered, because $Z(l_{0},ll(A'))\subset Z(l_{0},ll(A))=Z(l_{0},l_{t}))$ and $Z(l_{0},l_{t})=Z(l_{0},ll(A))$ is already strongly k-barrier covered. Hence, each of the k chains $Zn(A',B)$ which are initially covered by, now becomes part of each of k reconstructed barriers that now $Z(l_{0},ll(A))$ is covered by. Thus, $Z(l_{0},rl(B))=Z(l_{0},l_{s})$ is strongly k-barrier covered and $Z(l_{0},rl(B'))$ is strongly $k\!-\!1$-barrier covered, for $Zn(A',B)$ and $Zn(A,B')$ are covered by $k-1$ same chains according to Lemma 2 (the former can be covered by chain B rather than chain A, while the latter is just opposite). Hence, if we add a new chain to Zn(A, B) and make it that chain A and chain B become one chain, then $Zn(A',B)$ and $Zn(A,B')$ are covered by k same chains. Therefore in such a case, $Z(l_{0},rl(B'))$ can also be a strongly k-barrier covered zone.

• (3) For $j=n$, $Z(l_{0},l_{n-1})$ is already strongly k-barrier covered. If $Zn(l_{n-1},l_{n})$ is a strongly k-barrier covered zone, $Z(l_{0},l_{n})$ can be strongly k-barrier covered. Otherwise, we add $k-k_{n}$ new chains to $Zn(l_{n-1},l_{n})$ and make it that $Z(l_{0},l_{n})$ is strongly k-barrier covered. Hence, the whole region is strongly k-barrier covered.

$\square$

As described in Lemma 7, the basic idea of guaranteeing strong k-barrier coverage in a belt region is to construct k chains that cover zone $Z(l_{0},l_{j})$ ($1\le j\le n$)) by adding adequate number of chains to it with j increasing. For each non-k-barrier covered zone $Zn(l_{j-1},l_{j})$, we should guarantee not only $Z(l_{0},l_{j})$ is strongly k-barrier covered but also $Z(l_{0},l_{j+1})$ is strongly $k_{j+1}$-barrier covered when we repair it. While for each critical k-barrier covered zone Zn(A, B), $Z(l_{0},rl(B))$ is already strongly k-barrier covered after the weak zones in $Z(l_{0},ll(A'))$ have been repaired. And a chain, which is added to Zn(A, B) to make it that chain A and chain B become one chain, is to guarantee $Z(l_{0},ll(B'))$ is strongly k-barrier covered, see Fig. 7 for instance.

Fig. 7

Example of repairing a belt region for strong k-barrier coverage(Two critical 1-barrier covered zones Zn(B, A) and Zn(C, B) for $k=1$. Two non-2-barrier covered zones $Zn(l_{0},l_{1})$, $Zn(l_{4},l_{5})$ and one critical 2-barrier covered zone Zn(A, C) for $k=2$. Four non-3-barrier covered zones $Zn(l_{0},l_{1})$, $Zn(l_{1},l_{2})$, $Zn(l_{3},l_{4})$ and $Zn(l_{4},l_{5})$ for $k=3$)

6 Distributed algorithm

We present a distributed algorithm here. A set of weak zones will be obtained after we perform the algorithm. Once such weak zones are repaired, weak or strong k-barrier coverage can be guaranteed in the belt region. Note that if the set of weak zones is empty, the algorithm stops.

Some assumptions are made here. First, each sensor in the belt region has a unique ID. Second, each chain selects two sensors, its left and right end sensors, as its delegates, and the two delegates cooperate with each other in sensing and communication. Third, there are certain base stations in a belt region, and the delegate sensors can communicate with at least one of them. The base stations can communicate with each other, so we assume that there is a single base station in belt region for simplicity.

6.1 The BARRIER algorithm

In BARRIER, a report R contains the following information that represents a weak zone in its header: $\texttt{<Left-SensorID }$, RightSensorID, LeftCoordinate, RightCoordinate, ${{\bar{\texttt{k }}}>}$. Let $Z(l_{l},l_{r}), r \ge l+1$, be a weak zone and it is ${\bar{k}}$-barrier covered. LeftSensorID (RightSensorID) is the ID of the left or right end sensor which only has one intersection point with $l_{l}$($l_{r}$) of certain chain. LeftCoordinate = $V_{l_{l}}$ and RightCoordinate = $V_{l_{r}}$. If $\bar{k}<k$, $Z(l_{l},l_{r})$ is a non-k-barrier covered zone; otherwise, it is a critical k-barrier covered zone. Furthermore, if $Z(l_{l},l_{r})=Zn(rl(A),?)$, the base station updates it as $Zn(rl(A),l''')$, where $l'''$ is actually the nearest leftmost or rightmost orthogonal line of certain chain on the right of rl(A), after all the chains send their reports to the base station.

Note that if no chain exists in $Zn(l_{0},l_{1})$ ($l_{0}$ is the left boundary of the belt region), the base station should add $Zn(l_{0},l_{1})$ to non-k-barrier covered zones set $S_{non}$ because no reports from the chains will contain such information.

At the end of BARRIER, the weak zones needed to be repaired are contained in $S_{non}$ and $S_{critical}$ (for weak k-barrier coverage is just $S_{non}$). We can utilize the lemmas in Sect. 5 to repair the weak zones in order to guarantee weak or strong k-barrier coverage in a belt region.

6.2 Time complexity

Let s be the number of sensors, a be the maximum number of neighbors of any sensor, b be the number of chains and c be the maximum number of chains in any zones with length of $r_c$ in the belt region. For part 1 of BARRIER, the chain extraction runs in $O(k\cdot s\cdot a)$ time. Whether a zone is a k-barrier covered zone or a critical one can be determined in O(c) time. Thus, for part 2, identifying all the weak zones can be completed in $O(b\cdot c)$ time. Finally, updating $Q_{k}$, $S_{non}$ and $S_{critical}$ can be finished in O(b) time. Hence, the total running time of BARRIER is $\max \{O(k\cdot s\cdot a),O(b\cdot c)\}$.

7 Performance evaluation

In this section, we choose the GUARANTEE [4] algorithm as representative of the works [4, 5, 9] which are close to BARRIER to make comparison. We present simulation results and analysis of the performance comparison between the BARRIER and GUARANTEE algorithms for strong barrier coverage in a belt region. For fair comparison with [4], we set $r_c=Q^*+r_{max}$.

We adopt the widely-used random sensor deployment [1–5, 9, 11, 12, 16] in our simulations: sensors are randomly deployed in a belt region of dimension 500m * 200m; the sensing radius $r_{\max }$ of each sensor is 30m and $k=1$. A total of 1000 experiments are run for each scenario.

7.1 Number of weak zones

First we study the performance of the GUARANTEE and BARRIER on identifying the two types of weak zones. We set the required quality $Q^{*}=200m$, and vary the number of sensors in a belt region from 200 to 1000. The results in Fig. 8 show that both GUARANTEE and BARRIER are capable of identifying two types of weak zones.

Fig. 8

Comparison of identifying weak zones

7.2 Number of messages

According to the complexity analysis in [4], GUARANTEE needs $O(k^{2}\cdot s\cdot n\cdot \log n)$ messages, where n is the maximum number of sensors in any zone with length of $Q^{*}+r_{\max }$. The number of messages BARRIER needed is only $\max \{O(k\cdot s\cdot a),O(b\cdot c)\}$, which is lower than that of GUARANTEE($a\ll n$ when s is big enough). The comparison of the number of messages transmitted is shown in Fig. 9.

Fig. 9

Comparison of message number($Q^{*}$=200m)

7.3 Effect of required quality Q ^*

In GUARANTEE, a critical k-barrier covered zone is a weak zone if its length is less than $Q^{*}$. Thus, GUARANTEE may fail to report some critical weak zones if $Q^{*}$ is not big enough. An example is shown in Fig. 10, in which GUARANTEE fails to report the critical 1-barrier covered zone if $Q^{*}<L_{Zn(A,B)}$. However, BARRIER can always report all the critical weak zones because it is independent of $Q^{*}$ when identifying critical k-barrier covered zones. We set the number of sensors to 400 and the area of the belt region to 500m * 200m, and vary $Q^{*}$ from 60m to 360m. From the results presented in Fig. 11, we can see that GUARANTEE performs well in identifying the critical weak zones only when $Q^{*}$ is no less than 180m; as a comparison, BARRIER is not affected at all.

Fig. 10

Zn(A, B) is a critical 1-barrier covered zone ($A'=B$,$B'=A$) but algorithm GUARANTEE fails to report if $Q^{*}<L_{Zn(A,B)}$

Fig. 11

Comparison of reporting critical weak zones

7.4 Number of repaired / newly added sensors

Even though GUARANTEE can identify all the weak zones when $Q^{*}$ is appropriate, it uses more sensors to repair the weak zones than BARRIER. According to Lemma 6 in [4], for each weak zone Z, the authors use an extended zone $Z'$ ($Z'\supset Z$) by a length of $\delta$ on both left and right sides ($\delta =Q^{*}$ for each non-k-barrier covered zone, and $\delta =Q^{*}-L$ for each critical k-barrier covered zone of length L). In this paper, we apply the approach described in Lemma 7 to repair the weak zones using deterministic deployment. Suppose the belt region initially contains 1500 sensors and meets the required quality $Q^{*}$. We vary the number of active sensors from 200 to 1000. The results in Fig. 12 show that BARRIER significantly reduces the number of added sensors compared with GUARANTEE.

Fig. 12

Comparison of repairing the weak zones

7.5 Effect of quasi-UDG model

Finally, we conduct experiments under a different radio model—Quasi-UDG model. We set $\alpha = 0.9$. That is, a link exists between two nodes if the distance between the two nodes is smaller than 0.1 times of radio range with the probability of 1.0; a link does not exist between two nodes when the distance between two nodes is larger than than 1.9 times of radio range. Besides, a link between two nodes exists with the probability of $p = 0.8$ if the distance of the two nodes is between 0.2 and 1.8 times of radio range.

Figure 13 shows the results of comparison of identifying weak zones under Quasi-UDQ model. We find that, similar to Fig. 8(a), the numbers of non-k-barrier covered zones using the two algorithms are nearly the same. As for the number of critical k-barrier covered zones, again, our algorithm outperforms GUARANTEE, similar to the results shown in Fig. 8(b). It is noted that the number of critical k-barrier covered zones shown in Fig. 13 is considerably larger than that shown in Fig. 13. The reason is that the Quasi-UDG exhibits more randomness than the typical one, and thus this leads to more variable node connectivity, more clustered network, and hence more chains.

Fig. 13

Comparison of identifying weak zones

8 Conclusion

In this paper, we use chain instead of individual sensor as sensing and communication unit when we identify all weak zones in a belt region. The algorithm we propose can greatly reduce the communication overhead. Based on extensive analysis, several strategies are presented to guarantee weak and strong barrier coverages in a belt region. We identify all the critical k-barrier covered zones for strong barrier coverage and the performance is independent of required quality $Q^{*}$, and the number of sensors required to repair a belt region is significantly reduced.

In the future, we will design algorithms to extract chains from a cluster and also extend the algorithm to guarantee weak and strong barrier coverages in a probabilistic sensing model [16, 18].