1 Introduction

This paper is part one of a 2 paper series. In this paper, a detailed literature review on the concept and the technical aspects of previous work and the methodology related to both papers is presented. Data preparation and flood frequency analysis results are described here and the results of reliability analysis are discussed in Part 2.

Coastal flooding also has negative impacts on infrastructures and structures located close to the coastline, such as wastewater treatment plants (WWTP), by inundating them, which lead to extensive damages. In order to alleviate the inundation-related damages to coastal infrastructures, best management practices (BMPs) as adaptive hazard mitigation approaches are widely applied by means of structural and non-structural methods to prevent coastal flooding and improve the way in which the society responds to these extreme events. Karamouz et al. 2016 highlighted these challenges and developed a flood damage estimator package to quantify a variety of financial impacts of coastal flooding.

Wahl et al. (2015) and Nguyen et al. (2018) have performed a coastal flood frequency analysis where non-stationarity through observed trends have been identified for storm surge and rainfall measured in 30 tide gauges. Thus, the non-stationarity of climatic and hydrological events are necessary to be analyzed (Salas and Obeysekera 2014). The non-stationary likelihood of flooding is characterized by estimating the given distribution parameters in terms of a specific covariate (e.g., time). Generally, the non-stationarity response of extremes is addressed through time-dependent distribution parameters coupled with linear or non-linear trends (El Adlouni et al. 2007; Agilan and Umamahesh 2017; Cheng et al. 2014; Cheng and AghaKouchak 2015; Zhang et al. 2015). Generalized Extreme Value (GEV) is an approach for simulation of hydrological and climatic responses, where time is selected as the covariate to provide a vigorous physical implication corresponding to changes in the flood time series (Boettle et al. 2013; Salas and Obeysekera 2014). Three methods of Maximum likelihood estimation (MLE) (Zhang et al. 2017), L-moments (Hosking 1990), and Bayesian inference-based (Cheng et al. 2014) are utilized to fit the parameters to GEV distribution in the flood frequency analysis. The two former methods obtain a single value without considering inherent uncertainty in the parameter estimation for extreme value analysis (Luke et al. 2017), while the latter method provides a tool to approximate the posterior distribution of non-stationary methods accounting for built-in uncertainties (Renard et al. 2013). The Bayesian inference method is based on the integration of the Differential Evolution (DE) approach and Monte Carlo Markov Chain (MCMC) modeling, namely Differential Evolution Markov Chain (DE-MC) algorithm. This method provides a robust method for estimation of the posterior distribution of extreme marginal values. The readers are referred to Cheng et al. 2014 for further details, where the Bayesian inference method is applied to estimate the extreme value of annual temperature. This study however applies this technique, perhaps for the first time, to analyze the extreme surge events.

When storm surge coincides with heavy rainfall over inland areas, it is important to understanding their complex interplay that may exacerbate the impact of flooding (Karamouz et al. 2015). In a few studies, copula model has been employed to identify the appropriate correlation structure between joint events. Lian et al. (2013) and Xu et al. (2014) have used a copula-based model to study the tidal level and rainfall effects and their corresponding joint probability on flood hazard in a coastal urban area. Their analysis illustrated that a strong correlation between tidal level and rainfall has existed. They highlighted that the presence of statistical correlation between these two mechanisms aggravates the flood risk. Wahl et al. (2015) evaluated the joint likelihood of storm surge and heavy rainfall through a copula model to understand the probability of these joint events in the US. The results demonstrated an increasing correlation between storm surge and heavy rainfall.

While extensive literature review is carried out on the effect of BMP incorporation flood risk management, there is little known about the concurrent effects of rainfall and surge in determining flood design values and allowing the analyst/decision maker to look at the tradeoffs. This has been realized and attended to in this study. The importance of selecting a rainfall station that correlates better with a surge station has been also realized. Furthermore, the non-stationary copula approach is employed to approximate the joint probability of storm surge and rainfall events. This study utilizes a DE-MC algorithm (Bayesian inference-based approach) to estimate the marginal probability of storm surge and rainfall events for parameter estimation. In order to quantify the resulting uncertainty in flood reliability of WWTPs located in the coastal regions, the intrinsic variations in certain reliability-related factors (criteria) are measured by randomly generating values within their range of variations. Finally, the concept of Margin of Safety (MOS) is utilized to calculate the flood reliability of WWTP through applying a probabilistic approach to an MCDM based load-resistance concept.

This paper is organized as follows. In the next section, the concept and the methodology for Part 1 and Part 2 papers are presented. Then, the statistical analysis and flood frequency for univariate and bivariate rainfall and surge data with details explanation of parameter estimations are discussed for the Bronx Borough in New York City. Finally, a summary and conclusion existed.

2 Methodology

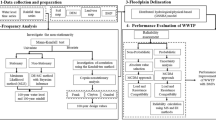
Figure 1 outlines the proposed framework for estimating the marginal and joint probability of climatic and hydrological extremes, and quantifying the flood reliability with a load-resistance approach. In the first step, the water level and rainfall time series along with the physical characteristics of watershed as the input parameters to the hydrologic model are obtained. The second step carries out a trend detection in observational extremes with regard to time. Univariate and bivariate flood frequency analyses are performed to estimate the extreme values of surge and rainfall. In the third step, a probabilistic-based reliability measure is described to evaluate the WWTP performance. A companion paper (Karamouz et.al (…)) presents the proposed framework validation, where the utilization of coastal protection strategies in terms of best management practices leads to significant improvement of flood reliability in Hunts Point WWTP located in New York City.

Fig. 1
figure 1

Proposed framework for flood reliability of coastal infrastructure/WWTP (Karamouz et al. (…)_Part 2)

Full size image

2.1 Concept – Coastal Flood Inundation Attributes

The pertaining concepts in this study consist of attributes of joint non-stationary statistical and frequency analysis of rainfall and surge; flood remediation design values; load and resistance interplays; flood modeling and mitigation strategies; and reliability quantification and BMPs performance. The four steps, presented in Fig. 1, outlines how these attributes are interplaying and where the hydrologic distributed modeling could simulate a real world problem. Hydrologic and hydraulic analysis is performed using gridded surface subsurface hydrologic analysis (GSSHA) that is explained in detail in the paper in Part 2.

2.2 Non-Stationary Extreme Value Analysis

The presence of trends has been detected in the extremes of observational data through the Mann-Kendall test (Kendall 1975; Mann 1945). This study assumed the significance level to be 0.05, which is commonly used in hydrological studies (Zhang et al. 2004). From a design perspective, the design value in the present and future could be different if non-stationarity is considered (Salas et al. 2018). In a stationary analysis, the extreme values for the same return period are assumed to remain constant. But, in non-stationary frequency analysis, the time variation of flood values for a given return period is considered. This analysis is divided into two sections of univariate and bivariate. In the univariate section, two methods of differential Markov chain Bayesian-based (DE-MC with Bayesian inference) and maximum likelihood (MLE) are applied for parameter estimation. In the bivariate analysis, the MLE method considering the stationary time windows is used and compared with the L-moment method by reassessing the work of Mohammadi (2019).

2.2.1 Univariate Flood Frequency

After the detection of the non-stationarity conditions and identifying a suitable time-dependent distribution model (GEV distribution in this study), the parameters for each variable time series are quantified. The method of parameter estimation of MLE, which is popular for its simplicity, is extended for non-stationary applications (Agilan and Umamahesh 2017). L-moment method provides an individual point estimate of the parameters. These methods have a drawback, according to Luke et al. (2017), of neglecting the uncertainty analysis of parameter estimates. Conversely, the Bayesian inference approach allows us to estimate the distribution parameters under non-stationary condition, while the inherent uncertainty of data is taken into account. Bayesian inference is utilized based on the Differential Evolution Markov Chain (DE-MC) framework through the integration of the Differential Evolution (DE) approach and Bayesian-based Markov Chain Monte Carlo (MCMC) method, to develop a robust estimation of posterior parameter distribution. This study employs the Non-stationary Extreme Value Analysis (NEVA) software package developed by Cheng et al. (2014) for estimating the return periods and hazards of climatic extremes through application of Bayesian inference approach.

In a non-stationary approach, the distribution function parameters would vary with respect to time. The cumulative distribution function of the GEV (φ) for an independent variable (x) such as storm surge can be expressed as (Coles et al. 2001):

$$ \varphi (x)=\exp \left\{-{\left(1+\xi (t)\left(\frac{x-\mu (t)}{\sigma (t)}\right)\right)}^{\frac{-1}{\xi (t)}}\right\}.\left(1+\xi (t)\left(\frac{x-\mu (t)}{\sigma (t)}\right)\right)>0 $$
(1)

According to Eq. (1) among the GEV parameters, the location parameter is assumed to be a linear function of time (μ(t) = μ0 + μ1.t). The scale(σ) and shape (ξ) parameters remain unchanged since modeling of temporal variations in σ and ξ parameters need long-term observational data according to Cheng et al. (2014).

To estimate the parameters of GEV distribution, NEVA incorporates a Bayesian technique under the non-stationary assumption. The prior distribution and observation vector (\( \overrightarrow{y}={\left({y}_t\right)}_{t=1:{N}_t} \)) are used in the posterior distribution of parameters θ(μ, σ, ξ). Nt is the number of observations in the observation vector \( \overrightarrow{y} \). For all parameters, the prior distributions are considered independent. Then the Bayes theorem under the non-stationary condition can be expressed by Eq. (2) and Eq. (3).

$$ p\left(\theta |\overrightarrow{y}\right)\ \alpha\ p\left(\overrightarrow{y}|\theta \right)\ p\left(\theta \right)=\prod \limits_{N_t}p\left({y}_t|\theta \right)p\left(\theta \right) $$
(2)
$$ p\left(\overrightarrow{y}|\beta, x\right)=\prod \limits_{N_t}p\left({y}_t|\beta, x(t)\right) $$
(3)

where β can be any of the parameters (μ1,μ0,σ,ξ) in non-stationarity, θ can take any parameters of (μ, σ, ξ) in stationarity, and x(t) indicates the set of covariate values in the non-stationary analysis. The resultant posterior distributions \( p\left(\theta |\overrightarrow{y}\right) \) and \( p\left(\beta |\overrightarrow{y},x\right) \) give information about parameters in stationarity (θ) or non-stationarity (β) analysis. Given the DE-MC, the Differential Evolution algorithm is employed to perform a global optimization of the parameter over the location parameter.

Return periods of extremes have been computed in NEVA software using the GEV distribution, as shown in Eq. (4). Return level (qp) is defined in terms of return period T.

$$ {q}_p=\mu +\raisebox{1ex}{$\sigma $}\!\left/ \!\raisebox{-1ex}{$\xi $}\right.\times \left(\frac{1}{{\left(-\ln \left(1-\left(\frac{1}{T}\right)\right)\right)}^{\xi }}-1\right) $$
(4)

where T is the reciprocal of (1-p). For further details, readers are referred to Cheng et al. (2014). In the following section, the joint effect of rainfall and surge are described that are then compared with the univariate condition for selecting the best design values.

2.2.2 Bivariate Flood Frequency

In most of the hydrological events, more than one event could take place, so it is realistic to analyze all of them in the frequency analysis. The joint probability distribution function is also defined as the copula function. For non-stationary analysis, data are separated into time windows in the sequential order with n data and n-1 overlap. The data of each time window is considered stationary. The length of these time windows is determined large enough to satisfy the stationary assumption and providing a good fit for the copula function. Also, in this part, the MLE method is used for parameter estimation. The generator parameter (θ) of selected Archimedean copulas (Clayton, Frank, and Gumbel) is calculated based on the relation between the Kendall-tau coefficient and copula parameter (Bender et al. 2014). In this study Kendall-tau coefficient (τ) is estimated as follows:

$$ \tau =\frac{nc- nd}{\frac{1}{2}n\left(n-1\right)} $$
(5)

where n is the number of observaion data, nc is the number of concordant pairs and nd is the number of discordant pairs. A copula function with the productive function of φ: (0,1) → (0.∞) belongs to the Archimedean copula family. The general function of the one-parameter Archimedean copula is expressed as follow:

$$ {C}_{\theta}\left(u.\nu \right)={\varphi}^{-1}\left[\varphi (u)+\varphi \left(\nu \right)\right] $$
(6)

where θ is the generator parameter. For Archimedean copula, the relation between the copula parameter and Kendall-tau coefficient is defined as:

$$ \tau =4{\int}_0^1\frac{\phi (t)}{\phi^{\prime }(t)} dt+1\kern1.75em ,t=u,v\kern2.25em $$
(7)

where ϕ(t) is the copula generator and ϕ′(t) is its first derivation. After estimating θ in each time window, the better type of copula is recognized by Root Mean Square Error (RMSE) (McElroy 1967). The joint distribution of rainfall and surge is obtained using best copula function.

The MLE method is utilized to approximate the parameters of GEV distribution under time window stationary conditions. For parameter estimation, the likelihood function is evaluated to select the parameters that produce the maximum occurrence probability of extreme events. The likelihood function applied to the GEV distribution is determined using Eq. (8).

$$ L\left(\mu, \sigma, \xi\ \right)=\frac{1}{n}{\prod}_{i=1}^n\kern0.33em \ln \left[f\left({x}_1\right)\right] $$
(8)

where L is the probability function corresponding to the GEV approximating the distribution of rainfall.

The values of μ, σ, ξ are obtained by setting the partial derivatives of probability function respect to each GEV parameter (μ, or σ, or ξ) equal to zero, as shown in Eq. (9).

$$ \frac{\partial L\left(\mu, \sigma, \xi \right)}{\partial \mu }=\frac{\partial L\left(\mu, \sigma, \xi \right)}{\partial \sigma }=\frac{\partial L\left(\mu, \sigma, \xi \right)}{\partial \xi }=0 $$
(9)

L moment parameter estimation details are not given as it was not selected as the preferred option in this study. Please refer to Bender et al. (2014) and Mohammadi (2019).

2.3 Flood Remediation Design Values

To obtain an appropriate design value, the joint return period (TX. Y) is calculated using the bivariate copula function and marginal CDF (i.e. FX for Surge and FY for Rainfall) as follows:

$$ {T}_{X,Y}=\frac{1}{1-{F}_X(x)-{F}_y(y)+C\left({F}_X(x).{F}_y(y)\right)} $$
(10)

where TX. Y is the inverse of the probability that X and Y exceed the values of x and y, respectively. These joint variables of x (i.e. Surge) and y (i.e. Rainfall) for a specific return period are plotted, which are called joint exceedance probability-isolines. Owing to various possible combinations of design values, it is important to consider the best design value based on the highest joint probability density. To be on a conservative side, an envelope as an extrapolation curve can also be drawn, which is independent of time window ending year and allows selection of design values for different purposes with some build in safety factors.

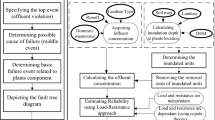
2.4 Load and Resistance Interplays

In basic engineering design, load and resistance have a well-understood stature that has formed many theoretical and practical principles and applications. The failure of an infrastructure (i.e. a WWTP) occurs when the resistance of the infrastructure cannot withstand external load during flood implying that the system is no longer functional. Resistance criteria include the physical and operational capacity of the plant to resist changes to its normal operation due to flooding pressure, while the load criteria account for the intensity of the design flood. The details of criteria and sub-criteria associated with load and resistance are explained in Part 2. In this study, the weight and values associated with each sub-criterion are applied to an MCDM approach named preference ranking organization method for enrichment evaluation (PROMETHEE) to calculate the reliability of the WWTP. Further information on detailed information of PROMETHEE method can be found in (Balali et al. 2014).

2.5 Flood Modeling and Mitigation Strategies

The first step to delineate floodplain is hydrologic distributed modeling of flood events. Hydrologic and hydraulic analysis is performed using gridded surface subsurface hydrologic analysis (GSSHA) model. This model is a module of the WMS developed by the US Army Corps of Engineers. GSSHA is utilized by the integration of a GIS-based rainfall-runoff and flood routing model to represent in-depth details of the characteristics of a watershed (land-use and soil type) and associated spatial variability.

The mitigation strategies are investigated in terms of BMPs that could resist, store, and delay the process of flood routing. See the companion paper, Karamouz et al. (…) Part 2, for more details.

2.6 Reliability Quantification and BMPs Performance

The performance of infrastructure is assessed by quantifying reliability in a load-resistance approach. In this study, load and resistance account for the intensity of a flood and potential carrying capacity of a plant to deal with flood. The mitigation strategies are investigated and the reliability has been assessed after implementing the strategies in a Margin of safety framework proposed by Tung and Mays (1981) and Mays (2019). The reliability index can be calculated as normal deviate of the ratio of the mean and standard deviation of the MOS when the independent load and resistance values along with resulting MOS maintain a normal distribution.This is the main focus of Part 2 paper.

3 Case Study

The procedures outlined in this study were employed to detect the possible design values for assessing the reliability of the Hunts Point WWTP in Bronx, NY as highlighted in Fig. 2. This plant treat wastewater for more than half-million people resided at the northeast side of the Bronx county. The primary aim of this study is to thoroughly analyze how the incorporation of BMPs leads to increasing the flood reliability of coastal infrastructures, thereby decreasing the catastrophic effects of coastal floods on urban areas. The locations of rainfall and surge stations, as well as Hunts Point WWTP in the Bronx, are shown in Fig.2.

Fig. 2
figure 2

Coastline map of Bronx along with locations of Hunts Point WWT plant, surge and rainfall stations

Full size image

3.1 Data Collection

To assess the risk of joint high-impact flooding and find the design parameters of water-level time series and rainfall from joint probability analysis. Here, time series of maximum annual surge data recorded at Kings Point/Willets Point stations, along with annual maximum rainfall data recorded at LaGuardia airport and Central Park stations are used to perform flood frequency analysis (Table 1). The dependence between storm surge and rainfall at both rainfall stations is investigated to see the spatial and temporal variability of rainfall data in the study area. The data is obtained from the National Oceanic and Atmospheric Administration (NOAA). A DEM of 10 m resolution (USDA 2018), land-use and soil type are used in GSSHA model to illustrate inundation depth in the Plant’s sewershed. A resampled 30 m DEM is used to bring the model run time to a manageable time of about 2 h with an Intel i7, 3600 GHZ Processor computer. Land-use and soil type maps indicate the characteristics of the area. The flow at the interface between coastline and floodplain area is calculated using Manning’s formula and water level at the shoreline. The overland Manning’s roughness coefficient was assigned to a land-use index map based on the USGS Chesapeake Bay Watershed Land Cover Data Series (Phillips and Tadayon 2006). More details on the model setting and sewershed characteristics are presended in Part 2.

Table 1 Characteristics and recorded time for surge and rainfall stations
Full size table

4 Results and Discussions

In this section, after selecting the appropriate rainfall station, the result of non-stationary frequency analysis is presented. Then the parameters of a bivariate joint probability distribution are estimated so the probability of simultaneous occurrence of extreme events can be investigated. In the second part, a set of coastal protection strategies is employed based on the characteristics and spatial constraints of each neighborhood.

Attempts have been made to identify the suitable rainfall stations by assessing the correlation between the rainfall data obtained from stations within a radius of 20 km around the WWTP and storm surge data. In each year, the maximum annual storm surge is selected. Afterward, the extreme value for rainfall and surge is used for simulating the flood inundation.

In order to investigate the correlation between time series of data, a comparison has been made between the correlation of storm surge and rainfall of LaGuardia station and the correlation of surge and rainfall of Central Park station. The main reasons for choosing these two stations are that the LaGuardia station is the closest station to the study area, and the Central Park station is the widely used station for rainfall measurement. The correlation between the rainfall and surge are assessed for 50-year moving time windows (see the section on Bivariate Flood Frequency Analysis). The variation of τ coefficients from two rainfall stations of LaGuardia and Central Park are shown in Fig. 3 (a) and (b), respectively, where a decrease in τ is observed for both stations and for time windows ending at more recent years. As shown, the correlation between the time series of observed data of surge and rainfall is greater when LaGuardia station is used specially for time window ending at 2017. The reason is due to the proximity of LaGuardia station and storm surge stations.

Fig. 3
figure 3

Time dependent Kendall’s τ of annual maximum flood surge and corresponding rainfall derived with a 50-year moving time window ending 2017 a) LaGuardia station b) Central Park station

Full size image

4.1 Flood Frequency Analysis

The existence of stationarity in storm surge and rainfall time series are investigated by the Mann-Kendall test with a significance level of 0.05. The null hypothesis, H0 is assumed to be valid when no significant trend is observed between the two data time series (i.e., Z > Zα/2, where Z is the test statistics for the Mann-Kendall test).

It is shown in Table 2 that the results of the Mann-Kendall test reject the null hypothesis, where the p value is less than 0.05. However, the rainfall data is stationarity as the null hypothesis is accepted (the p values is higher than 0.05). Owing to the fact that the flooding mechanism is dominated by a destructive storm surge event in coastal regions, non-stationarity in storm surge data is a dominating factor.

Table 2 Result of the Mann-Kendall test applied to storm surge and rainfall data (1940–2017)
Full size table

4.1.1 Univariate Flood Frequency Analysis

The GEV parameters are estimated through the Bayesian and MLE approaches in order to perform extreme value analysis of 100-year storm surge and rainfall under non-stationary and stationary assumptions, respectively. Using NEVA package (Cheng et al. 2014), the GEV distribution parameters for storm surge are inferred under non-stationary condition by considering the location parameter (μ) be linearly dependent on time covariant, while the scale (σ) and shape (k) parameters remain unchanged, as outlined in Table 3. For rainfall, the GEV distribution parameters are assumed to be independent of time covariant.

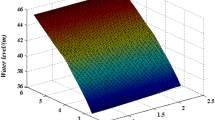
Table 3 The quantification of GEV Parameters for the time period of 1940–2017
Full size table

The storm surge and rainfall versus the time covariate are shown in Fig. 4(a) and(b), respectively, where the probability of occurrence is considered as 0.01. Using GEV distribution, the extreme value analysis of hydrological data is performed to obtain the design values of storm surge and rainfall. Since the surge data is non-stationary and the location parameter of GEV distribution is linearly time-dependent, then according to the Eq. 4 the extreme value of surge is time-dependent. The year 2017 is selected because it is the last record for this study. It is concluded that the storm surge and rainfall corresponding to a 100-year event in the time window ending in year 2017 are 2.91 m and 161 mm.

Fig. 4
figure 4

a 100-year surge under the non-stationary assumption at Kings Point/Willets Point stations from 1940 to 2017, b 100-year rainfall under the stationary assumption at LaGuardia station from 1940 to 2017

Full size image

4.1.2 Bivariate Flood Frequency Analysis

In this study, the time-dependent surge parameter of the marginal distribution and the time-dependent copula parameter (θ) are obtained to assess the temporal variation of the joint probabilities of this joint event. To employ the non-stationary joint probability distribution, all observational data from 1940 to 2017 are divided into sequential time window with n data and n-1 overlaps. Each time window is assumed to show a stationary behavior. For this purpose, a time window length of 50 years (50-year moving window (resemble moving average setup) is chosen to provide an estimation of copula parameters. It should be noted that the observed surge and rainfall data of year 2012 associated with the Superstorm Sandy is excluded in this part of analysis because it lowers the cross-correlation. It should be noted that in univariate analysis Sandy data is included. The results show that in a vast majority of time windows, the Gumbel copula yields to the lowest RMSE values. For fitting the GEV parameters to a moving time window, MLE parameter estimation method is utilized to quantify the joint distributions of storm surge and rainfall. The results obtained from utilizing MLE are compared to those obtained by L-moment parameter estimation. Mohammadi’s (2019) work has been reassessed as he utilized a similar approach for a different case study, using L-moment in the same region. The time-dependent isolines curves from L-moment and MLE methods are shown in Figs. 5 and 6. These curves begin for time windows ending 1990 to 2017 (the 50-year time window starting with 1940–1990 window and extending to 1967–2017 window). The selection of the station could change according to the priorities and criteria of the decision makers. Two time series of observational rainfall data recorded in stations of Central Park (Fig. 5(b) and Fig. 6(b)) and LaGuardia airport (Figs. 5(a) and 6(a)) are utilized to determine the suitable design values. According to the results, the diagrams have many fluctuations around the diagrams associated with the stationary frequency analysis (solid black curve). Each curve demonstrates the likelihood of joint occurrence of storm surge and rainfall variables associated with a return period of 100 years. Also, it could be used by the decision makers to choose a design value among the different combination of surge and rainfall.

Fig. 5
figure 5

Joint 100-year flood design values -isoline curves for 50 year time windows based on L-moment parameter estimation (a) LaGuardia station (b) Central Park station

Full size image
Fig. 6
figure 6

Joint 100-year flood design values -isoline curves for 50 year time windows based on MLE parameter estimation (a) LaGuardia station (b) Central Park station

Full size image

An enveloped trade-off curve is drawn to provide the most suitable design values independent of the ending year of the time windows. A line across the maximum curvature of the diagrams is defined as the line of highest joint PDFs. The year 2017 (last year of data in this study) is regarded as the main record in this analysis, which fluctuates between minimum and maximum design values. As can be seen in Figs. 5b and 6b for the Cental park station, design values based on MLE parameter estimation tend to yield slightly higher values of surge and rainfall than L-moment. Furthermore, the stationary curve falls in the middle of isoline curves using MLE whereas in L-moment it is close to the lower side. But for La Gardia it is the oposite.On the other hand, for LaGuardia, MLE is slightly lower at the rainfall extreme ends than L-moment (Figs. 5a and 6a). But as for surge in LaGaurdia the difference is insignificant. Besides, applying the same method (L-moment or MLE), it is shown that the rainfall variation and design value (100-year flood) associated with the Central Park station are higher compared to the LaGuardia station. The central Park station results could be used for designing infrastructures near that station and when rainfall is the primary concern in the city. Near water fronts, LaGuardia seems to be a better station to choose.

Here, two scenarios are defined to compare the extreme values obtained from L-moment and MLE methods. Two data points located at the two tails of the 2017 joint exceedance curve are acquired, as shown in Fig. 6. For selection of these points, two thresholds are proposed. The extreme surge event co-occurs with a rainfall event of 50 mm, whereas the extreme rainfall event co-occurs with a surge event of 1 m. The threshold values along with the corresponding rainfall and surge values in Central Park and LaGuardia stations are shown in Table 4. Due to coastal flood surges, the Hunts Point WWTP is most likely to be exposed to co-occurring events of extreme surge and moderate rainfall. It is worth mentioning that providing the joint exceedance isolines of othe ending years as well as the envelope trade-off curve allows the decision-makers to choose alternative design flood values based on their needs and preferences.

Table 4 100 year design values obtained based on rainfall or surge controlled design options for the time window ending year 2017
Full size table

For the rest this study, the LaGuardia station is selected as the rainfall station due to higher correlation (kendall-tau) with surge station as explained earlier and less conservative rainfall design value.

Once the 100-year surge and rainfall design values are obtained, the water level hydrograph is used as an input into the hydrological model to estimate the inundation depth in the sewershed. In Part 2, a surge with the 100-year return period is obtained using the hydrograph of Hurricane Irene as the reference flood scenario according to Karamouz et al. (2017).

In the companion paper, a combination of two flood management practices including one levee and two constructed wetlands, are employed. These flood hazard mitigation strategies are selected based on the availability of coastline space and natural settings. The results of the MCDM based reliability quantification of Margin of Safety before and after implementing BMPs are also presented that shows some remarkable improvement.

5 Summary and Conclusion

The frequent occurrence of extreme hydrologic events in coastal areas justifies the necessity of evaluating the performance of critical infrastructures, including the wastewater treatment plants in order to find appropriate mitigation strategies for improving their performance. Due to the increased co-occurrence probability of inland rainfall and storm surge in low-lying coastal areas, knowing the likelihood of joint occurrence of these two phenomena is of paramount importance. Also, it has been observed that the frequency and severity of the floods have been intensified. These joint events have exacerbated the impact of flooding and resulted in widespread damages and loss of human life. In this study, the hydrograph of surge and hyetograph of rainfall are developed. Surge data is limited so the closest station of Kings/Willets point. For rainfall, two stations have been selected and LaGuardia station was found more suitable with much higher correlation with the surge station. Results of data analysis show the surge data to be non-stationary and rainfall data to be stationary. To obtain the extreme values of rainfall and surge in the 100-year flood, the GEV distribution is applied. In order to estimate the GEV parameters, different parameter estimation methods are used. The Maximum likelihood method (MLE) for stationary analysis and Differential Evaluation Markov chain Bayesian-based for non-stationary analysis are used. In the non-stationary bivariate flood frequency analysis, the MLE method, along with sequential stationary time windows are applied to estimate the GEV parameters. In addition, different copula models are applied for joint distribution analysis of surge and rainfall, and Gumbel copula function is selected for time windows. A series of trade-off curve of rainfall and surge are developed for each time window. In copula non-stationary 100-year flood analysis, the design value for the year of 2017, according to the trade-off curves, is determined and used for the rest of the analysis in part 2.

In the companion paper (Part 2), the application of the concepts and the proposed methodology are utilized to set the strategies in order to quantify reliability attributes. The framework presented in this paper is applicable to other coastal watersheds and could be a platform for some pressing issues in coastal preparedness with some implications on design criteria of coastal infrastructure.