1 Introduction

The operation of a reservoir system is generally complex as it involves many variables, a large number of constraints and multiple objectives (Qin et al. 2010). Although simulation models and optimization tools can be used to derive the detailed release policies for each time step of reservoir system (Yeh 1985), a more desirable approach for real-time operation is to optimize operation rules (Karamouz and Houck 1982; Chen et al. 2007). The operation rules can be presented in the form of graphs or tables and define the desired reservoir release or output during each period as a function of water levels, the time of year and inflows. Therefore, giving an optimization operational rule can provide a more practical and reliable guidance to reservoir system operators in the current period. There are two main ways to get such operational rules. One way is to generate optimal input-output patterns by running optimization model first and then extract the release rules using data mining methods (Wei and Hsu 2009; Zhang et al. 2015). Another way is to optimize the rule curves or rule tables directly by optimization algorithm within the constraints (Zhou et al. 2015). This paper focuses on the second way.

Flood disaster is one of the most damaging natural disasters and it usually causes a large amount of economic losses (Cutter et al. 2015). New tactics are needed to help boost flood control. Flood control models have been developed over the past several decades (Marien et al. 1994; Needham et al. 2000; Jia et al. 2016). In addition to flood control requirement, many investigators consider water conservation purposes like hydropower generation and water supply during flood season (Ding et al. 2015). These objectives are often conflict with flood control objective, since flood control requires a certain amount of empty storage for minifying the flood peaks while water conservation requires more remaining storage for hydropower generation or water supply purpose. The problems with multiple conflicting objectives is called multi-objective optimization problems (MOPs). During the past decades, various multi-objective evolutionary algorithms (MOEAs) based on Pareto dominance have been proposed like Multi-objective Genetic Algorithm (MOGA) (Fonseca and Fleming 1993), the Improved Strength Pareto Evolutionary Algorithm (SPEA2) (Zitzler et al. 2001), Nondominated Sorting Genetic Algorithm II (NSGA-II) (Deb et al. 2002), Multi-objective Particle Swarm Optimization (MOPSO) (Coello and Becerra 2004) and Multi-objective Evolutionary Algorithm based on Decomposition (MOEA/D) (Zhang and Li 2007). With the development of MOEAs, more and more researchers have begun to apply MOEAs in multipurpose reservoir operation problems and get good achievements (Reddy and Kumar 2006; Baltar and Fontane 2008; Qin et al. 2010).

In this paper, a multi-objective cultured evolutionary evolution based on decomposition (MOCEA/D) is proposed to optimizing the hierarchical flood operation rules (HFORs) with 4 objectives during flood season. Major contributions are outlined as follows:

  1. 1)

    The HFORs is proposed for flood resources utilization, which mainly focus on small and medium floods. Different HFORs trend to different tradeoffs of flood control objectives and water conservation objectives.

  2. 2)

    A mathematical model with 4 objectives is formulated, which contains upstream flood control objective, downstream flood control objective, power generation objective and navigation objective.

  3. 3)

    A new MOEA named MOCEA/D is proposed. The algorithm combines the advantages of Cultural Algorithm (CA) (Reynolds 1994) and MOEA/D and shows its high performance when solve some well-known test functions.

  4. 4)

    MOCEA/D is applied to solve the multi-objective HFORs optimization problem: a case study of Three Gorges Project (TGP).

The rest of the paper is organized as follows: section 2 introduces the HFORs and formulates the multi-objective mathematical model. Section 3 describes MOCEA/D in detail. Section 4 applies MOCEA/D to a practical HFORs optimization problem and analyzes the experimental results. Section 5 concludes this work.

2 HFORs and Mathematical Model

This section first introduces the general form of HFORs, then formulates the mathematical model with multi-objectives and several constraints.

2.1 HFORs

The operational rules are usually presented in the form of graphs or tables, define the desired reservoir release as a function of existing storage volumes, the date time of year, and inflows. In HFORs, water level and expected inflow are taken into consideration for then function. The water level and inflow can be divided into different interval Zi ∈ [Zil, Ziu], Ij ∈ [Ijl, Iju], Zi and Ij denote the i-th hierarchical water level and j-th hierarchical inflow, l and u represent the lower and upper bound of the interval. The general HFORs can be express as a function as follow:

$$ {R}_{ij}=f\left({Z}_i,{I}_j\right) $$
(1)

Where Rij is the desired reservoir release under the i-th hierarchical water level and j-th hierarchical inflow.

2.2 Objective Function

The target of this study is to obtain optimal HFORs for regulating small and medium floods, in which many objectives and constraints should be considered. The objectives are expressed as follows:

Flood control objectives: generally, there are two goals for reservoir flood control: reducing flood disaster in the downstream flood protection area and flood control requirement for reservoir area. Considering these two goals, the two objectives of flood control are expressed as follows.

$$ \min {F}_1=\underset{\forall t=1,2,...,T}{\min}\left\{\max \left({Z}_t\right)\right\} $$
(2)
$$ \min {F}_2=\underset{\forall t=1,2,...,T}{\min}\left\{\max \left({R}_t\right)\right\} $$
(3)

Where T is the number of periods; Rt is the discharge volume of the t-th period; Zt is the upstream water level of the reservoir during the t-th period.

Maximizing hydropower generation of the reservoir system:

$$ \max {F}_3=\sum \limits_{t=1}^T{N}_t\varDelta t=\sum \limits_{t=1}^TA{H}_t{q}_t\varDelta t $$
(4)

Where Nt is power output of the t-th period; Δt is the operation interval; A is the power production coefficient of the hydropower plant; Ht is net head of the t-th period and qt is the release passing turbines of the t-th period.

Maximum guarantee rate of navigation:

$$ \max {F}_4=\frac{1}{T}\sum \limits_{t=1}^T{f}_n\left({R}_t\right) $$
(5)

Where fn() is the function of navigation guarantee rate, which is related to discharge volume Rt.

2.3 Constraints

The optimization is subject to the following constraints:

  1. (1)

    Water balance constraint:

$$ {S}_t={S}_{t-1}+{I}_t-{R}_t $$
(6)

Where St is the reservoir storage of the t-th period; It and Qt are the reservoir inflow and discharge volume during t-th period, respectively.

  1. (2)

    Water level constraint:

$$ {Z}_t^{\mathrm{min}}\le {Z}_t\le {Z}_t^{\mathrm{max}} $$
(7)

Where Ztmin is minimum limit of upstream water level during the t-th period, Ztmax is the maximum limit of upstream water level during the t-th period.

  1. (3)

    Water release capacity constraint:

$$ {R}_t\le {R}_{\mathrm{max}}\left({Z}_t^{avg}\right) $$
(8)

Where Ztavg is the average upstream water level of the t-th period, Rmax(Ztavg) is the release ability function of Ztavg.

  1. (4)

    Discharge volume constraint:

$$ {R}_t^{\mathrm{min}}\le {R}_t\le {R}_t^{\mathrm{max}},t\in \left[1,T\right] $$
(9)

Where Rtmin and Rtmax are the minimum and maximum limit of discharge volume during the t-th period..

  1. (5)

    Power-generation limits:

$$ {N}_t^{\mathrm{min}}\le {N}_t\le {N}_t^{\mathrm{max}} $$
(10)

Where Ntmin and Ntmax are the minimum and maximum limit of power output during the t-th period.

3 Multi-Objective Cultured Evolutionary Algorithm Based on Decomposition

In this section, the MOCEA/D is described in detail, which incorporate the advantages of CA and MOEA/D. Firstly, some basic concepts related to MOEA/D and CA are provided, then the major procedures of MOCEA/D are described in detail, at last it performance is verified by using some benchmark test problems.

3.1 Background

3.1.1 Deposition for Multi-Objective Optimization

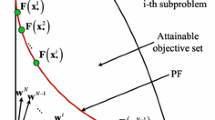
MOEA/D requires a decomposition approach for converting approximation of a MOP into a number of single objective optimization problems. The 3 most commonly used decomposition approaches are weighted sum, weighted Tchebycheff, and boundary intersection approaches. In this paper, we use the penalty-based boundary intersection (PBI) approach. The i-th subproblem is defined as:

$$ \operatorname{minimize}\;{g}^{pbi}\left(x|{\lambda}^i,{z}^{\ast}\right)={d}_1^i+\theta {d}_2^i $$
(11)

subject to x ∈ Ω.

Where:

$$ {d}_1^i=\left\Vert {\left(F(x)-{z}^{\ast}\right)}^T{\lambda}^i\right\Vert /\left\Vert {\lambda}^i\right\Vert $$
(12)
$$ {d}_2^i=\left\Vert F(x)-{z}^{\ast }-\left({d}_1^i/\left\Vert {\lambda}^i\right\Vert \right){\lambda}^i\right\Vert $$
(13)

\( {\lambda}^i={\left({\lambda}_1^i,\dots, {\lambda}_m^i\right)}^T \) is a weight vector for the i-th subproblem, i.e.,\( {\lambda}_j^i\ge 0 \) for allj = 1, …, mand\( {\sum}_{j=1}^m{\lambda}_j^i=1 \); \( {z}^{\ast }={\left({z}_1^{\ast },\dots, {z}_m^{\ast}\right)}^T \)is the reference point, i.e., \( {z}_i^{\ast }=\min \left\{{f}_i(x)|x\in \varOmega \right\} \)for each i = 1,…, m; Ω is the decision space; θ (>0) is a preset penalty parameter; ‖ ⋅ ‖ denotes the Euclidean distance.

3.1.2 Cultural Algorithm

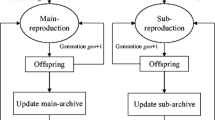
CA is a technique that add domain knowledge to improve the performance of evolutionary algorithms (Renfrew 1994). The main features of CA are population space and belief space. Population space consists of a set of individuals, which will be updated according to some evolutionary algorithms (Reynolds 1994; Landa Becerra and Coello 2006). Belief space contains different kinds of knowledge, which can be learned from the evolutionary process. After that, the knowledge will be used to guide the evolutionary process in population space. The key technology of CA is how to define the knowledge in the belief space and how to guide the operators of the evolutionary algorithm. In this paper, we define two knowledge structures and use MOEA/D as the population space of CA.

3.2 Proposed Algorithm: MOCEA/D

3.2.1 Framework of MOCEA/D

The framework of MOCEA/D is presented in Algorithm 1. First, the weight vectors are generated by (Das and Dennis 1998) systematic approach. Then, the neighborhood index set, population, archive set, and the evolutionary parameters of MOCEA/D are initialized by initialization procedure. In the main while-loop, for each subproblem, a new offspring is generated according to the reproduction procedure. After reproduction, the parent solution and evolutionary parameters will be updated according to the comparison mechanisms in step 11. Finally, the belief space is updated following the new population space. In the following sections, the major procedures of RSEA are described in detail.

figure a

3.2.2 Belief Space

Two kinds of knowledge is proposed in MOCEA/D: situational knowledge and normative knowledge.

  1. 1)

    Situational knowledge: it consists of a series of non-inferior solutions named archive set, which represent the best solutions obtained from the population space. After the evolution of each generation, it need to find all non-dominated individuals from this generation and add them into situational knowledge. Then, a truncation operation is applied to reduce archive set if its size exceeds NQ, NQ is the predefined size of archive set. The truncation operator we employ is similar with the truncation operator in SPEA2, which sort the solutions by the distance to the k-th nearest data point (Zitzler et al. 2001)

This situational knowledge can influence the mating and update pool of MOCEA/D in Algorithm 1, step 8. On the one hand, the Archive set contains the best elites of the entire evolutionary which can give more useful information for reproduction procedure. On the other hand, the situational knowledge has its own truncation operator, which can maintain the diversity of the archive set. Therefore, the offspring will have a low probability of falling into local optimum.

  1. 2)

    Normative knowledge: it consists of N groups of evolutionary algorithm parameters, N is equal to the size of population. In this paper, MOCEA/D use DE as the evolutionary algorithm, which contains parameters F and CR. To choose suitable parameters adaptively, we use the belief space to dynamically update the parameters to improve the performance of the algorithm.

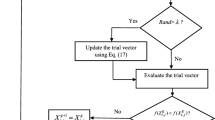
First, all parameters F and CR are set randomly within a reasonable range, each set of parameters Fi and CRi corresponds to subproblem i. Before the DE operator of the i-th sub-problem, new parameters are generated as follow

$$ F=\Big\{{\displaystyle \begin{array}{l}{F}_{\mathrm{min}}+\mathit{\operatorname{ran}}{d}_1\left(\right)\cdot \left({F}_{\mathrm{max}}-{F}_{\mathrm{min}}\right)\kern0.24em \mathit{\operatorname{ran}}{d}_2\left(\right)<{\tau}_1\\ {}{F}_i\kern4.199998em otherwise\end{array}} $$
(14)
$$ CR=\Big\{{\displaystyle \begin{array}{l}C{R}_{\mathrm{min}}+\mathit{\operatorname{ran}}{d}_3\left(\right)\cdot \left(C{R}_{\mathrm{max}}-C{R}_{\mathrm{min}}\right)\kern0.24em \mathit{\operatorname{ran}}{d}_4\left(\right)<{\tau}_2\\ {}C{R}_i\kern4.679997em otherwise\end{array}} $$
(15)

Where rand1–4() are four mutually independent random numbers between 0 and 1. Fmin and Fmax are the minimum and maximum values of F. CRmin and CRmax are the minimum and maximum values of CR. τ1 and τ2 are the threshold values between 0 and 1. According to our experiment, Fmin and Fmax are set as 0 and 1, CRmin and CRmax are set as 0 and 1, τ1 = τ2 = 0.01.

Then, the offspring solution xc is generated by a classic DE (DE/rand/1/bin) (Storn and Price 1997) with the new parameters F and CR. And the parameter of k-th subproblem Fk and CRk will be updated as F and CR follow the offspring, in Algorithm 2 step 6 and step 10.

3.2.3 Update Procedure and Constraint Handling

In the original MOEA/D, the comparison of two solutions is entirely based on the decomposition approach like PBI. This single way of evaluation may loss some elite during the evolutionary process. MOCEA/D combines dominance relations with PBI approach to improve the update procedure. When the offspring xc is compared with parent solution p, the dominance relations of the two solutions is measured first. If xc dominate p, then the solution p is replaced by the offspring xc; otherwise, the solution p is kept; if neither of them is dominated by the each other, then we compare them according to the PBI value.

As for constrained problems, a simple scheme is used, which modify the definition of domination between two solutions i and j. After checking their constraints, if 1) solution i is feasible and solution j is not, 2) solutions i and j are both infeasible, but solution i has a smaller overall constrains violation, 3) solutions i and j are feasible and solution i dominates j, it said that solution i is constrained-dominate the solution j. The update procedure is presented in Algorithm 2.

figure b

3.3 Test Suites and Experimental Results

3.3.1 Benchmark Problems and Performance Metrics

To demonstrate the performance of MOCEA/D, DTLZ1 to DTLZ4 (Deb et al. 2005) are used for our experimental studies. The number of objectives for each benchmark problem are varies from 3 to 8. As recommended in reference (Deb and Jain 2014), the number of variables are (m + k − 1), where m is the number of objectives and k = 5 for DTLZ1, while k = 10 for DTLZ2, DTLZ3, and DTLZ4.

To measure both the convergence and diversity of the Pareto-optimal set, the inverse generational distance (IGD) metric (Deb and Jain 2014) is used. Let P* be a set of uniformly distributed points along the Pareto Front (PF). A is the final nondominated solutions set obtained by an algorithm. The IGD value of A is computed as:

$$ IGD\left(A,{P}^{\ast}\right)=\frac{1}{\mid {P}^{\ast}\mid}\sum \limits_{i=1}^{\mid {P}^{\ast}\mid}\underset{j=1}{\overset{\mid A\mid }{\min }}d\left({p}_i,{a}_j\right) $$
(16)

Where d(pi, aj) = ‖pi − aj‖2. The lower value of IDG(A, P∗) means the algorithm obtains a better solutions set A.

3.3.2 Results and Discussion

To verify MOCEA/D, three evolutionary algorithms, including NSGA-III, MOEA/D-SBX, and MOEA/D-DE are considered for comparisons. For each algorithm, 20 independently run is applied on each problem. And the termination is a predefined number of generation for each run, listed in Table 1. The parameter settings for comparisons algorithms NSGA-III, MOEA/D-SBX, and MOEA/D-DE are according to the reference (Deb and Jain 2014). The parameters of MOCEA/D are the same as MOEA/D-DE.

Table 1 Best, median and worst IGD values obtained by MOCEA/D, NSGA-III, MOEA/D-SBX and MOEA/D-DE on m-objective DTLZ1–4 problems. Best performance is shown in bold
Full size table

Table 1 presents the best, median and worst IGD values obtained by MOCEA/D, NSGA-III, MOEA/D-SBX and MOEA/D-DE on m-objective DTLZ1–4 problems. As shown in Table 1, MOCEA/D performs slightly better for DTLZ1, DTLZ3 and DTLZ4 than other algorithms. For DTLZ2 problems, the performance of MOEA/D-SBX is better than MOCEA/D. But the performances of MOCEA/D is better than MOEA/D-DE and are similar to NSGA-III. Figure 1 shows the nondominated solutions obtained by MOCEA/D for the three-objective DTLZ1 to DTLZ4. It can be seen that the solutions are get close to the PF and also get a uniform distribution on the whole PF.

Fig. 1
figure 1

Obtained solutions by MOCEA/D for DTLZ1 to DTLZ4. (Dots are the solutions, the grid is the true PF of each problem)

Full size image

4 Case Study: Multi-Objective HFORs Optimization for TGP

The TGP, with the largest installed hydro power capacity in the world, is located in the Yangtze River. The normal water level is 175 m, the total reservoir storage capacity is 39.3 billion m3. The flood control limit level is 145 m and the flood control storage capacity is 22.15 billion m3. Installation capacity and firm power output of it are 22,500 and 4990 MW respectively.

4.1 Flood control indicators

For flood control, TGP have to not only minify the flood peaks for downstream areas but also control the water level for preventing potential major flood and dam safety. Different flood control tasks map to different thresholds of discharge value and water level. The flood control indicators with corresponding discharge value and water level are summarize as follow:

  1. 1)

    To keep the flood control limit level, discharge value should equal to inflow, water level should be controlled as 145 m;

  2. 2)

    For the safety of Chenglingji station, discharge value should less than 40,000 m3/s, water level should under 171 m;

  3. 3)

    For the warning water level of Shashi station (43 m, 44.5 m and 45 m), discharge value should less than 45,000 m3/s, 55,000 m3/s, 61,000 m3/s respectively, water level should under 171 m;

  4. 4)

    To keep the streamflow of Zhicheng station less than 80,000 m3/s, discharge value should less than 76,000 m3/s respectively, water level should under 175 m;

  5. 5)

    For dam safety, water level should under 175 m.

4.2 Guarantee rate of navigation

For navigation rule, the ship locks will not allow navigation when the discharge volume of the Three Gorges Reservoir is greater than 45,000 m3/s. Moreover, when the discharge volume is between 25,000 to 45,000 m3/s, TGP will restrict the navigation according to the different size of the ships’ power. When the discharge volume is between 3200 to 25,000 m3/s, ships of all sizes can pass through the ship locks. The navigation standard is shown in Table 2.

Table 2 The Navigation Standard of TGP
Full size table

According to the actual navigable ship classification statistics from 2003 to 2013: ships with power less than 200 kW accounted for 16.49%, 200 ~ 270 kW accounted for 21.60%, 270 ~ 368 kW accounted for 26.49%, 368 ~ 440 kW accounted for 16.79%, and 440 ~ 630 kW accounted for 7.19%, 11.46% of the ships with a power of more than 630 kW. Assuming that the proportions of the ascending (passing through the ship locks from downstream to upstream) and descending (passing through the ship locks from upstream to downstream) ships are the same, the mapping relation between the discharge volume of the TGP and the guarantee rate of the navigation can be established.

4.3 HFORs for TGP

According to the general HFORs and flood control indicators for TGP. This section proposes the HFORs for TGP, presented in Table 3. It mainly focus on small and medium floods and ensure the discharge volume of TGP less than 55000m3/s (upper bound of X1~29). The water level of TGP must be lower than 171 m for the potential major flood. When the water level is higher than 171 m, TGP should discharge according original designed rules. As is shown in Table 3, the decision variables X1~X29 denote discharge volume Rij. The bound of every decision variable is set as [3, 5.5] (104 m3/s). In addition to the constraints expressed in section 2, the HFORs are generated follow the regulation that∀j Rij ≤ Ri + 1, j, ∀i Rij ≤ Ri, j + 1 and all the decision variables are divisible by 100 m3/s.

Table 3 HFORs table for TGP
Full size table

The simulation model of the HFORs is executed according to the following step: (1) Get the current inflow It and water level Zt of TGP. (2) Find the desire discharge volume Rt according to the HFORs. (3) Calculate the water level of next time Zt-1. If Zt-1 is less than the minimum limit of water level or larger than the maximum limit of water level, set Zt-1 as the limit values and update the discharge volume Rt.

4.4 Results and Discussion

MOCEA/D is applied to optimize the HFORs for TGP with four objectives. A total of 130 years (From 1882 to 2011) historical daily streamflow during flood season (From June 11 to October 31, 143 days) of Yichang station is used as inflow of TGP in the simulation. The starting regulation level for every year is 145 m. The population space is composed of N = 120 individuals, and the belief space can accommodate up to NQ = 60 individuals, the maximum number of generations GenNum is set to 500.

4.4.1 Results of the Application

Tables 4 presents the obtained non-dominated schemes of HFORs for TGP, the 4 objectives of every scheme max water level, max discharge volume, power generation and navigation rate are listed. All solutions satisfy the flood control constraints: maximum water levels are lower than 171 m and maximum discharge volumes are less than 5.5 × 104 m3/s. From Table 4 we can see that, the average maximum water levels are in the range that from 145.8 (Scheme 1) to 158.8 m (Scheme 60). The average maximum discharge volumes are decreased from 49,096 (Scheme 1) to 42,319 m3/s (Scheme 40). The average annual power generation are in the range from 533.3 (Scheme 1) to 588.6 (Scheme 60) × 108 kWh, which means Scheme 60 can increase the average annual power generation by 10.37%. The average navigation rate can be optimized to 80.2% (Scheme 55), which the average navigation rate of original designed rule is 77.8% (Scheme 1).

Table 4 Non-dominated operation schemes of HFORs
Full size table

The HFORs can be expressed as a three-dimensional chart like Fig. 2. The HFROs chart can visually give the discharge volume values with different water levels and inflows. In the figures, the coordinate axis in X direction stand for different inflow hierarchies, Y direction stand for different water level hierarchies and Z direction represent the target discharge volumes optimized.

Fig. 2
figure 2

The HFORs chart of Scheme 30, 40, 47, 60

Full size image

4.4.2 Results Analysis and Discussion

To give a more detail analysis of the trade-offs of four objective, a matrix of scatterplots is shown in Fig. 3. From the plots, a negative correlation can be seen between the upstream flood control objective and downstream flood control objective. The reason is that too much concern about downstream flood control (lower discharge volumes) will lead to a high water level, which may be harmful to upstream flood control. The power generation has a strong correlation with upstream flood control objective. Because higher water level will lead high head, which makes power plant generate more electricity. The navigation rate is weakly related to the other three objectives, which means that a scheme with both high navigation rate and high power generation can be found, like Scheme 55.

Fig. 3
figure 3

MOCEA/D solutions are shown using scatterplot matrices of 4 objectives

Full size image

Two typical years with large floods are chosen from 130 years for the verification. The first year is 1954, which has the largest average inflow 34,000m3/s during the flood season and its flood peak is 66,100m3/s, almost a 1% frequency flood. The second year is 1981, which has the largest flood peak 71,100m3/s and its average inflow is 29,800m3/s. Figures 4 and 5 shows the water level and discharge processes of five typical schemes with two flood situations. It can be seen from the figures that Scheme 1 minify the discharge to 55,000m3/s only when the inflow is larger than 55,000m3/s or the water level is higher than 145 m. This way can maximize the protection of upstream safety, but the power generation will be limited because of the low water level. The 30-th scheme, the 40-th scheme, the 47-th scheme, and the 60-th scheme not only hold back large flood but also hold back small and medium flood that the inflow is less than 55,000m3/s. In these schemes, more flood resources are used for power generation while the small discharge volume values will helpful for navigation.

Fig. 4
figure 4

Discharge processes and water lever processes of a Scheme 1, b Scheme 30, c Scheme 40, d Scheme 47, and e Scheme 60 for the flood in 1954; f water lever process of different schemes for the flood in 1954

Full size image
Fig. 5
figure 5

Discharge processes and water lever processes of a Scheme 1, b Scheme 30, c Scheme 40, d Scheme 47, and e Scheme 60 for the flood in 1981; f water lever process of different schemes for the flood in 1981

Full size image

5 Conclusions

This paper proposes the HFORs and establishes a mathematical model with four objectives. A novel multi-objective optimization algorithm MOCEA/D is proposed to solve the problem. MOCEA/D combines the advantages of decomposition technology and CA and shows its high performance in some benchmark problems. Then, MOCEA/D is applied to a case study—HFORs for TGP. The experimental results show that MOCEA/D obtains a uniform non-dominated schemes set, which can improve the power generation and navigation rate as much as possible under the premise of ensuring flood control safety.

The HFROs define the current target releases based on the current water level and inflows, it is point out that a reliable inflow forecast can be useful for water recourse management (Liu et al. 2018). Future work includes extending the hierarchical flood operation rule for multi-reservoir systems and considering the inflow forecast to guide the target discharge volume.