1 Introduction

Water resources optimization is increasingly being recognized as a strategic issue (Hossain and El-Shafie 2013; Wen et al. 2018). The water resources optimization model can produce an optimal solution to the decision-making problems in water resources system management. Methods previously implemented into single-objective optimization of water resources systems include linear (Ding et al. 2018) or nonlinear programing (Ahmad et al. 2014), dynamic programming (Zhang et al. 2017) and artificial neural networks (Yu et al. 2015). Recently, evolutionary algorithms (EAs), such as genetic algorithm, particle swarm optimization algorithm, differential evolution (DE) algorithm have been successfully used for solving various water resources optimization problems because of their population-based nature, non-continuous and non-convex objective space, and ease of implementation (Maier et al. 2014; Tayfur 2017).

However, water resources optimization problems have become more complex than ever before, especially when it comes to the water resources systems designed for multi-purposes, such as water supply, flood control, power generation, and irrigation (Wen et al. 2016). A multi-objective optimization model was proposed to improve the operational effectiveness of water resources systems for trade-offing the benefits of their usage (Scola et al. 2014). Traditional multi-objective optimization techniques (weighting and E-constraint) generally transform a multi-objective problem into a single-objective one and then solve with classical optimization algorithms (Guo et al. 2018; Karamouz et al. 2007). However, these methods can only generate one solution, and can become difficult to satisfy inputting reasonable bounds for all objectives. To overcome these problems, EAs based on Pareto theory, better known as multi-objective evolutionary algorithms (MOEAs) (Arshi et al. 2014) have been developed, e.g., non-dominated sorting genetic algorithm (NSGA-II) and multi-objective particle swarm optimization algorithm (MOPSO). These algorithms have been successfully applied to optimize water resource systems (Fallah-Mehdipour et al. 2011; Li et al. 2010; Lopez-Ibanez et al. 2005), which can find a set of non-dominated solutions without the need to convert the multi-objective problem into the single-objective one. In recent years, researchers have attempted to develop novel multi-objective algorithms in the field of water resource management, and achieved various degrees of success (Liu et al. 2012; Makaremi et al. 2017; Siew et al. 2016). Results indicate the modified multi-objective algorithm is a one of crucial methods to optimize the water resources systems. There are still some serious challenges in the operation and management of water resources systems (Sun et al. 2016), therefore it is necessary to develop new multi-objective algorithms for complex water resource management.

Shuffled frog leaping algorithm (SFLA) is a new meta-heuristic population-based EAs inspired by natural memetics (Eusuff et al. 2006), which has only a few parameters, but fast calculation speed and excellent global search capability. SFLA has been successfully applied to solve many optimization problems, such as production scheduling (Yenisey and Yagmahan 2014), water resource distribution (Pazoki et al. 2016), and vehicle routing (Luo and Liu 2014). However, SFLA can easily fall into local minima and has slow convergence in later stage of the evolution and poor calculation accuracy (Sun et al. 2016). Thus, through combination with other optimization algorithms, SFLA has been developed as new algorithms to overcome its shortcomings such as chaos-based SFLA (Li et al. 2008) and hybrid PSO-SFLA (Orouji et al. 2013). Meanwhile, researchers began to extend SFLA to multi-objective problems and proposed the multi-objective SFLA (MOSFLA) based on Pareto theory. Li et al. (2010) presented a MOSFLA incorporating an archiving strategy based on self-adaptive niche method. Rahimi-Vahed et al. (2009) established a hybrid MOSFLA based on SFLA and Bacteria Optimization for solving the Mixed-Model Assembly Line sequencing problem. Gao and Cao (2012) applied the theory of membrane computing and quantum computing to MOSFLA. The above MOSFLA have been tested on several benchmark functions that present their better performance to many optimization problems than some multi-objective algorithms like NSGA-II.

DE algorithm (Storn and Price 1997) is a population-based stochastic search technique with applications in many fields, such as pattern recognition (Ilonen et al. 2003), dynamic systems (Angira and Santosh 2007), and folded laminated composite plates (Le-Anh et al. 2015). Chaos is a general phenomenon in nonlinear systems with some special characteristics (Cheng et al. 2008). It has such a high sensitivity that even a tiny change of the initial condition can lead to a dramatic change of the system.

Based on the efficiency of SFLA, DE algorithm and Chaos, considering few published work to deal with multi-objective optimization problems by using MOSFLA in the field of water resource systems, we propose a novel algorithm named as multi-objective differential evolution-chaos shuffled frog leaping algorithm (MODE-CSFLA). The novel MOSFLA initializes a population by Chaos and replaces the local update of SFLA with stochastic search technique of DE algorithm. Moreover, an external archive with dynamic updating mechanism is implemented to improve the diversity of Pareto solutions in MODE-CSFLA. Then, the proposed algorithm is verified using five mathematical benchmark problems compared with that of NSGA-II and MOPSO. At last, MODE-CSFLA is used to solve the multi-objective optimal water resources allocation model of the East Route of the South-to-North Water Transfer (E-SNWT) Project in the normal, dry, and extremely dry conditions.

2 Methodology

2.1 Chaos

The chaotic sequence (Zhu et al. 2017) can usually be produced by the following one-dimensional logistic map:

$$ {x}_{i+1}=\mu {x}_i\left(1-{x}_i\right) $$
(1)

where xi is the range of the random chaotic variable, xi ∈ (0, 1), i = 0, 1, 2…; and μ is a control parameter,μ ∈ (0, 4]. In this paper,x0 ∉ {0.25, 0.5, 0.75}andμ = 4.

2.2 Shuffled Frog Leaping Algorithm

SFLA is a meta-heuristic optimization method that mimics the memetic evolution of a group of frogs while seeking for the location that has the maximum amount of available food (Khosroshahi et al. 2015). It consists of a set of interacting population of virtual frogs partitioned into different groups referred to as memeplexes. The different memeplexes are considered as different cultures of frogs, each frog performing a local search. Within each memeplex, the individual frog holds ideas that can be influenced by the ideas of other frogs, and these ideas can evolve through a process of memetic evolution. After a defined number of memetic evolution iterations, ideas are passed among memeplexes in a shuffling process.

2.3 Novel Differential Evolution Algorithm

DE algorithm uses mutation, crossover, and selection operators at each generation to move its population toward the global optimum (Zhao et al. 2016). Here, some novelties on each operator were proposed to improve the searching ability of DE algorithm.

  1. (1)

    Mutation

For each target vector xi, the traditional mutation operation is used to generate a mutant vector vi using Eq.2:

$$ {v}_i(t)={x}_{i1}(t)+F\times \left({x}_{i2}(t)-{x}_{i3}(t)\right) $$
(2)

where xi1(t), xi2(t) and xi3(t) are the three vectors selected randomly from sub-population, i1 ≠ i2 ≠ i3,i = 1, 2, …, M,M is the number of each sub-population; t is the current time of sub-population iterations; F is the mutation scale factor, which is a positive constant, F ∈ (0, 2).

Some measures were proposed on Eq.2 to improve the local searching ability of DE algorithm, as shown in Eq.3.

$$ {v}_i(t)={x}_{best}(t)+F\times \left({x}_{i_1}(t)-{x}_{i_2}(t)\right) $$
(3)

where xbest(t) is the best individual of sub-population.

As the mutant vector vi(t) varies significantly with F, a dynamic change strategy of Fwas proposed to reduce the variance of F with increasing global iteration times, as shown in Eq.4:

$$ F={F}_{\mathrm{max}}-\frac{i\left({F}_{\mathrm{max}}-{F}_{\mathrm{min}}\right)}{Ngen} $$
(4)

where Fmax = 0.75, Fmin = 0.37and Ngen is the times of global iteration, i = 1, 2, ⋯, Ngen.

  1. (2)

    Crossover

Following the mutation operation, a trial vector uij is generated from the mutant vector vij(t) and its target vector xij(t) using a crossover operation. In this study, the binomial crossover was used, as shown in Eq.5:

$$ {u}_{ij}=\left\{\begin{array}{l}{v}_{ij}(t), if\ \mathit{\operatorname{rand}}1\le CR\ or\ j=\mathit{\operatorname{rand}}2\\ {}{x}_{ij}(t), if\ \mathit{\operatorname{rand}}1> CR\ or\ j\ne \operatorname{rand}2\end{array}\right. $$
(5)

where rand1 is a uniform random number, rand1 ∈ [0, 1].CR is the crossover rate, CR ∈ [0, 1]. D is the dimension of the optimization problem, j = 1, 2, …, D.rand2 is a integer randomly selected from {1, 2, 3, …, D}. rand2 is used to ensure the difference between the trial vector and the target vector so as to increase the efficiency of evolution.

CR determines the effect of mutant vector. If CR is large, uij mainly obtained from vij(t) can reduce the convergence speed; on the contrary, uij mostly from the xij(t) can led to the prematurity of the algorithm. A dynamic change strategy of CRwas proposed to overcome this drawback, as shown in Eq.6.

$$ CR={CR}_{\mathrm{max}}-\frac{i\left({CR}_{\mathrm{max}}-{CR}_{\mathrm{min}}\right)}{Ngen} $$
(6)

where CRmax = 0.3 and CRmin = 0.1.

  1. (3)

    Selection

In this part, there is a competition between each target vector xij(t) and its trial vector uij. For maximization problems, the selection operation can be expressed as Eq.7:

$$ {x}_i\left(t+1\right)=\left\{\begin{array}{l}{u}_i(t)\kern0.75em if\ f\left({u}_i(t)\ \right)>f\left({x}_i(t)\ \right)\\ {}{x}_i(t)\kern0.75em if\ f\left({u}_i(t)\ \right)\le f\left({x}_i(t)\ \right)\ \end{array}\right. $$
(7)

where f is the fitness value, and xi(t + 1)is used as a parent vector in the next generation.

2.4 External Archive with Dynamic Updating Mechanism

Here, an external archive with dynamic updating mechanism (Modiri-Delshad and Rahim 2016) is used to save and update the non-dominated solutions. The dynamic updating mechanism consists of two basic operations: the analog binary crossover method and the dynamic crowding distance calculation.

  1. (1)

    Analog binary crossover

The analog binary crossover method can increase the number of individuals who meet the defined requirements if there are not enough individuals in EA. It is based on the principle of the binary string of single-point crossover, in which chromosome is expressed in real number string and two parent individuals cross to generate new individuals, as shown in Eq.8:

$$ {\displaystyle \begin{array}{l}{x}_{1,k}=\frac{1}{2}\left[\left(1-{\beta}_k\right){p}_{1,k}+\left(1+{\beta}_k\right){p}_{2,k}\right]\\ {}{x}_{2,k}=\frac{1}{2}\left[\left(1+{\beta}_k\right){p}_{1,k}+\left(1-{\beta}_k\right){p}_{2,k}\right]\end{array}} $$
(8)

where xi, k is the kth variable of the ith individual; pi, k is the kth variable of parent individuals; βk is a random variable of the kth variable, βk ≥ 0specifically, and βk can be presented in Eq.9:

$$ \beta (u)=\left\{\begin{array}{l}{(2u)}^{\frac{1}{1+{\eta}_c}}\kern3.5em u\le 0.5\\ {}{\left[\frac{1}{2\left(1-u\right)}\right]}^{\frac{1}{1+{\eta}_c}}\kern1.5em u>0.5\end{array}\right. $$
(9)

where u is a random number, u ∈ (0, 1); and ηc is the cross distribution index, ηc ≥ 0.

  1. (2)

    Crowding distance

The crowding distance is a quality measure for the Pareto front distribution. A solution with a larger crowding distance is located in a less crowded region, and thus it has more potential to be exploited in terms of the population diversity. Solutions with a short crowding distance could be removed, while solutions with a larger crowding distance are preferred (Xiang and Zhou 2015). The crowding distance for the ith solution of the Pareto front can be calculated from Eq.10:

$$ P{\left[i\right]}_{dis}=\sum \limits_{k=1}^M\left({f}_k\left(i+1\right)-{f}_k\left(i-1\right)\right) $$
(10)

where P[i]dis is the crowding distance of the ith solution with its two neighbors; fk(i + 1) and fk(i − 1) are the i + 1thand i − 1th solution of the kth objective function, respectively; and M is the number of objective functions, k = 1, 2, …, M;

2.5 Multi-Objective Differential Evolution-Chaos Shuffled Frog Leaping Algorithm

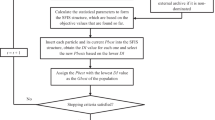
Initializing a population by Chaos can overcome the shortcoming of uneven distributed initial population in optimization problem. Meanwhile, replacing the local update of SFLA with stochastic search technique of NDE algorithm can improve the search ability of SFLA. Meanwhile, EA with dynamic updating mechanism can improve the diversity of Pareto solutions in multi-objective algorithm. Thus, MODE-CSFLA was proposed here by coupling SFLA, NDE algorithm and Chaos together based on the EA theory, aiming to improve multi-objective optimization performance. The detailed process of MODE-CSFLA shown in Fig.1 is summarized as follows:

  1. Step 1.

    Define objective function and specify parameters of the algorithm.

Fig. 1
figure 1

The flowchart of MODE-CSFLA

Full size image
$$ opt\kern0.5em F(x)=\left\{{f}_1(x),{f}_2(x),\cdots, {f}_n(x)\right\} $$
(11)
$$ s.t\kern0.5em x\in G(x) $$
(12)

where F(x) is objective function set; fn(x) is the objective function; n is the number of the objective function; x is the decision variable; G(x) is the constraint set. The parameters involved in MODE-CSFLA include the dimension of the optimization problem D, the size of population Npop, the size of sub-population Nsub, the times of global iterations Ngen, the times of sub-population iterations Nk, the size of external archive NEA, the maximum and minimum crossover probabilities Pcmax and Pcmin, and the maximum and minimum mutation probabilities Pmmax and Pmmin.

  1. Step 2.

    Initialize a population based on Chaos.

Generate an initial vector x0 at random and the chaotic variables xi can be obtained from Eq.1. Then, apply xi to the variance ranges of optimization variables by Eq.13:

$$ W{\hbox{'}}_i={W}_{i,\min }+\left({W}_{i,\max }-{W}_{i,\min}\right)\ast {x}_i $$
(13)

where Wi, max and Wi, min are the ith variance ranges of optimization variables; W'i is the ith value of the optimization variable.

  1. Step 3.

    Update EA based on dynamic updating mechanism;

  2. (1)

    Calculate the objective function values of each individual and sort the solutions in EA according to the value of each objective function, and save the non-dominated solutions;

  3. (2)

    Check the numbers of the non-dominated sets (Nnds) in EA. If Nnds > NEA, perform Step (3), otherwise, increase the number of individuals to meet the defined requirements in EA using the analog binary crossover method.

  4. (3)

    Computer the crowding distance of each solution for the non-dominated sets using Eq.10, and remove solutions with the smallest crowding distance. An infinite distance value is assigned to the boundary solution.

  5. Step 4.

    Global optimal operation by SFLA and local optimal operation by the NDE algorithm;

  6. (1)

    Divide the whole population into sub population and search the dominated solutions (WDS) of each sub population.

  7. (2)

    Update WDS based on NDE algorithm.

  8. (3)

    Compare the new solutions (WNS) with WDS, and define the updated solutions (WUS).

    Decision for \( WUS=\left\{\begin{array}{l} WNS\kern1.5em if\ \mathrm{WNS}\ \mathrm{can}\ \mathrm{dominate}\ WDS\ \\ {} WDS\kern1.25em if\ \mathrm{WNS}\ \mathrm{can}\ \mathrm{not}\ \mathrm{dominate}\ WDS\ \end{array}\right. \).

  9. (4)

    Save the non-dominated solutions from WUS. And for dominated solutions: Repeat (2) and (3) until the times of sub-population iteration Nk is satisfied and apply the non-dominated solutions in EA to replace WDS in each sub population.

  10. (5)

    Shuffle the sub population to the whole population.

  11. Step 5.

    Check the stopping criteria.

Repeat Step2 until the times of population iteration Ngen is reached. Finally, export the optimal Pareto solutions.

The Multi-objective optimization algorithm aims to achieve two objectives: one is that the obtained exact non-dominated solution set (PFkonw) should quickly approach the real non-dominated solution set (PFtrue), and the other one is that PFkonwshould be evenly distributed in PFtrue. In this paper, MODE-CSFLA is firstly applied to solve the five mathematical benchmark problems (ZDT1, ZDT2, ZDT3, ZDT4, and ZDT6) (Zitzler et al. 2000). Meanwhile, generational distance metric (γ) and diversity metric (Δ) are used to evaluate the performance of the algorithm (Fonseca et al. 2003).

3 Case Study

3.1 Study Area and Data

The E-SNWT Project is constructed to mitigate water shortage in Northern China. Water from the Yangtze River is pumped by many pumping stations, and then flows along the Grand Canal in Jiangsu Province, through a tunnel under the Yellow River and down an aqueduct to reservoirs in Shandong Province. In this study, we focus on the project in Jiangsu Province (32°15′-34°30’ N, 117°00′-119°45′ E), as shown in Fig.2. This project involves three lakes (Hongze (HZ) Lake, Luoma (LM) Lake and Nansi (NS) Lake) and twelve pumping stations. The three lakes are presented in Table 1. The twelve pumping stations can be categorized into six cascaded groups, as shown in Table 2. The water is used for agricultural, industrial and domestic purposes through hundreds of sluices along the canal. Water users can be categorized into six groups based on their locations. The schematic diagram of the E-SNWT Project is shown in Fig.2.

Fig. 2
figure 2

The location and schematic diagram of the E-SNWT Project

Full size image
Table 1 The features of the three lakes in the E-SNWT Project
Full size table
Table 2 The features of the pumping station groups in the E-SNWT Project
Full size table

The other parameters are the same as in the benchmark problems. Based on the cumulative distribution function fitting analysis of the annual runoff data for 60 years, three typical hydrological years with a probability of 50%, 75 and 95% were selected to represent normal (1971.6–1972.5), dry (1958.6–1959.5), and extremely dry (1959.6–1960.5) conditions, respectively.

3.2 Optimal Water Resources Allocation Model for the E-SNWT Project

The optimal water resources allocation model for the E-SNWT Project includes objective functions and constraints. The optimization model is at a monthly time step. The pumpage of each pumping station group is set as the decision variable.

  1. (1)

    Objective functions

The objective functions here are to minimize the total pumpage and to maximize the water supply rate (defined as the ratio of total supply to total demands), which can be expressed as:

$$ Obj1=\min \sum \limits_{t=1}^T\sum \limits_{m=1}^M WP\left(m,t\right) $$
(14)
$$ Obj2=\max \frac{\sum \limits_{t=1}^T\sum \limits_{n=1}^N WR\left(n,t\right)}{\sum \limits_{t=1}^T\sum \limits_{n=1}^N WN\left(n,t\right)} $$
(15)

where Obj1 and Obj2 are the total pumpage (m3) and the water supply rate (%), respectively; T is the total number of allocation periods, T = 12. N is the total number of water users, N = 6. M is the total number of pumping station groups, M = 6. WP(m,t) is the pumpage of the mth pumping station group at time stept, m = 1,2,...M.WR(n,t) and WN(n,t) are the water supply and water requirement of the nth water user at time step t, respectively, t = 1,2,...,T, n = 1,2,...,N.

  1. (2)

    Constraints

There are four main constraints, as follows.

  1. 1)

    Water balance constraint

$$ V\left(i,t+1\right)=V\left(i,t\right)+ PI\left(i,t\right)+ PR\left(i+1,t\right)- WS\left(i,t\right)-W\left(i,t\right)- PR\left(i,t\right) $$
(16)

where V(i, t) is the water storage of the ith lake at time step t, m3. PI(i, t) + PR(i + 1, t) are the inflow and outflow of the ith lake at time step t, m3, respectively. W(i, t) is the water supply of the ith lake at time step t, m3. WS(i, t) − W(i, t) are the water pumpage from and into the ith lake at time step t, m3, respectively.

  1. 2)

    Pumping capacity constraint

$$ 0\le WS\left(i,t\right)\le {WS}_{\mathrm{max}}\left(i,t\right)0\le WI\left(i,t\right)\le {WI}_{\mathrm{max}}\left(i,t\right) $$
(17)

where WSmax(i, t) and WImax(i, t) are the maximum pumping capacity of the pumping station group of the ith lake at time stept, m3.

  1. 3)

    Lake level constraint

$$ {L}_{\mathrm{min}}\left(i,t\right)\le L\left(i,t\right)\le {L}_{\mathrm{max}}\left(i,t\right) $$
(18)

where Lmin(i, t) and Lmax(i, t) are the minimum and maximum level boundary of the ith lake at time step t, m, respectively.

  1. 4)

    Minimum lake level for water diversion

Generally, water pumping will be stopped if the lake level is lower than the minimum level for water diversion (shown in Table 1).

4 Results and Discussion

4.1 Results of Mathematical Benchmark Problems

The algorithms were performed in Matlab. MODE-CSFLA was coded in 4 function files (one main function, and three sub-functions) with only 402 lines of code. The decision variables are coded by real values. In this study, MODE-CSFLA, NSGA-II and MOPSO were applied to solve the five mathematical benchmark problems. The simulations times, Npop, Ngen and NEA of the three algorithms are 20, 100, 1000 and 50, respectively. Pcmax and Pcmin of MODE-CSFLA are 1 and 0.75, and Pmmax and Pmmin are 1 and 0.80, respectively. Nsub and Nk of MODE-CSFLA are 5 and 15, respectively.

Fig.3 shows the comparison between the Pareto solutions of MODE-CSFLA and the real Pareto front for benchmark problems. It is evident that the Pareto solutions of MODE-CSFLA are evenly distributed and agree well with the real Pareto front for all ZDT problems.

Fig. 3
figure 3

The Pareto solutions of MODE-CSFLA and the real Pareto front for benchmark problems: (a) ZDT1, (b)ZDT2, (c) ZDT3, (d) ZDT4, and (e) ZDT6

Full size image

Table 3 lists the mean and variance of the convergence index (λ) and diversity index (Δ) for the five benchmark problems. It shows that MODE-CSFLA performs best in solving ZDT1, ZDT2, ZDT3 and ZDT4, as indicated by the minimum mean and variance value of λ. However, for ZDT6, the mean λ of MODE-CSFLA is slightly higher than that of MOPSO (0.003 vs. 0.000), while the variance of λ is zero. MODE-CSFLA presents the minimum mean and variance value of Δ for the five benchmark problems. The variance of Δ is close to zero except for ZTD4. These results indicate that the EA with dynamic updating mechanism can improve the diversity of Pareto solutions. Compared with NSGA-II and MOPSO, MODE-CSFLA can better handle the convex or non-convex multi-modal optimization problems with discontinuous or non-uniform distribution of the target space However, MODE-CSFLA improves accuracy in solving complex multi-objective optimization problems with sacrificing computational speed. It takes MODE-CSFLA about 92.378 s to perform one test problem, which is 5 and 0.4 times lower than NSGA-II and MOPSO, respectively.

Table 3 The mean and variance of the convergence and diversity metric for the five benchmark problems using NSGA-II, MOPSO and MODE-CSFLA
Full size table

4.2 Multi-Objective Optimal Water Resources Allocation of the E-SNWT Project

The model was solved by MODE-CSFLA, NSGA-II and MOPSO, based on which the optimal water resources allocation strategy was proposed for the E-SNWT Project. Two single-objective optimal allocation models regarding Obj1 and Obj2 were also solved by SFLA and MODE-CSFLA, respectively. Npop, Ngen and NEA of NSGA-II, MOPSO and MODE-CSFLA are 200, 10,000 and 100, respectively. Nsub of MODE-CSFLA is 20. Fig. 4 shows the multi-objective model solved by MODE-CSFLA, NSGA-II and MOPSO, and the single-objective model solved by SFLA and MODE-CSFLA under the three conditions. It can be seen that the solutions space of the three multi-objective algorithms is more extensive than that of SFLA. The results in all multi-objective algorithms can dominate those derived by SFLA for single-objective models.

Fig. 4
figure 4

Pareto solutions of the multi-objective model optimized by MODE-CSFLA, NSGA-II, and MOPSO and single-objective model optimized by SFLA and MODE-CSFLA in (a) normal, (b) dry, and (c) extremely dry years.

Full size image

The boxplot of the total pumpage and water supply rate optimized by NSGA-II, MOPSO and MODE-CSFLA is shown in Fig.5. Under normal and dry conditions, the total pumpage optimized by MODE-CSFLA is 20.95–33.73% higher than that optimized by NSGA-II and MOPSO; while the water supply rate optimized by MODE-CSFLA is 0.13–39.05% higher. Therefore, MODE-CSFLA can produce more reasonable solutions than NSGA-II and MOPSO. Under extremely dry conditions, NSGA-II and MOPSO can produce a wider range of Pareto solutions than MODE-CSFLA. However, these solutions are dominated by that obtained by MODE-CSFLA. Besides, the solutions obtained from MOPSO appear to be unevenly distributed at the front of the Pareto curve, while that obtained by MODE-CSFLA are more uniformly distributed.

Fig. 5
figure 5

Boxplots of Pareto solutions optimized by the three multi-objective algorithms in normal, dry and extremely dry years: (a) total pumpage and (b) water supply rate

Full size image

The comparison between the closet solutions of MODE-CSFLA interpolated from the Pareto solutions (a1, a2; b1, b2; c1, c3 in Fig.4) and SFLA for the single-objective optimal allocation models Obj1 and Obj2 is shown in Table 4 and Table 5. Compared with SFLA, MODE-CSFLA can result in a 29.39, 27.47 and 22.55% increase in water supply when the single objective is to minimize the water pumpage (Obj1); and a 41.01, 39.63 and 30.94% decrease in total pumpage when the single objective is to maximize the water supply (Obj2), in the normal, dry, and extremely dry scenarios, respectively.

Table 4 Results optimized by MODE-CSFLA and SFLA for Obj1 in normal, dry, and extremely dry years
Full size table
Table 5 Results optimized by MODE-CSFLA and SFLA for Obj2 in normal, dry, and extremely dry years
Full size table

Table 4 presents the total pumpage and water supply for Obj1 optimized by MODE-CSFLA and SFLA in normal, dry and extremely dry years, respectively. It shows that the total pumpage of BJ and HH group is increased by 8.20–22.78 108m3; while water pumped by HS, PZ, TL and HL group is reduced by 8.60–22.90 108m3 after optimization by MODE-CSFLA. More water supplied for YZ and HZ Users leads to the improvement of the water supply rate for the whole study area. However, there are negative values of water supply for some users, because water is pumped to meet their upstream users.

Table 5 shows the total pumpage and water supply for Obj2 optimized by MODE-CSFLA and SFLA under all scenarios. In this case, MODE-CSFLA results in a decrease in the total pumpage of each pumping station group by 1.29–53.62 108 m3, indicating that MODE-CSFLA can make better use of natural inflow to meet the model requirements. Compared with Obj1, the total pumpage is increased by 38.51–52.90% to meet the needs of water supply, and there are less negative water supply values under all hydrological conditions.

5 Summary and Conclusions

A novel multi-objective algorithm, MODE-CSFLA, was proposed in this study for water resources system optimization. The novel MOSFLA initialized a population by Chaos and replaced the local update of SFLA with stochastic search technique of DE algorithm. Moreover, EA with dynamic updating mechanism was implemented to improve the diversity of Pareto solutions in MODE-CSFLA. The performance of MODE-CSFLA in solving benchmark problems was presented compared with NSGA-II and MOPSO. At last, MODE-CSFLA was used to solve the optimal allocation model of water resources in the E-SNWT Project in the normal, dry, and extremely dry conditions. Experimental results show that MODE-CSFLA can overcome the shortcomings of uneven distributes initial population, easily falling into local minima and early convergence in SFLA, and improve the diversity of Pareto solutions. Thus, it has the potential to be used for solving complex optimization problems of water resources systems.