Impact of Hydrological Uncertainty on Water Management Decisions

Abstract

This study focuses on the analysis of uncertainties in hydrologic series and their impact on water resources management decisions. The methodology is based on Monte Carlo simulation, where relevant parameters on the rainfall-runoff processes of a hydrologic model were sampled from suitable probability distributions in order to analyse the probability distribution of output variables in a water resources system model. The procedure was applied to three water resources systems in the Duero basin (Spain). Results showed that the performances of the water resources systems are very sensitive to uncertainties in the model input. The deviation from the reliabilities or cumulated supply deficits obtained in the water resources systems compared to the reference inflows was much larger when the perturbations were unfavourable than when they were favourable. This suggests that the uncertainty analysis may have important implications when using these performance measures of the water resources system in decision making, particularly in dry years. The uncertainty on hydrologic variables may change dramatically our assessment of the performance of a water resources system and thus hydrologic inputs should be evaluated with extreme care.

1 Introduction

Ensuring adequate water supply and management to support human development while sustaining healthy and functioning ecosystems is becoming increasingly complex, particularly in regions characterized by water scarcity and unfavourable projections due to climate change (Iglesias et al. 2007; Poff et al. 2015). For the purposes of planning and design, system managers usually assume that the hydrological processes in a specific basin can be described as stationary (WWAP 2012). Nowadays, it is largely accepted that nonstationary climate factors need to be considered for long-term planning, with increasing interest on accounting for climate change uncertainties (Mastrandrea et al. 2010; Hall et al. 2012). Climate change could cause a decline in the amount of water available for supply, particularly in the dry season if lower average rainfall coincides with higher temperatures (Murphy et al. 2009). Water demand may also be sensitive to climate variability (Parker and Wilby 2013). Water resources planners, system managers and socio-economic policy-makers must deal with changes in land use, urbanization, precipitation, temperature, evaporation, groundwater, runoff, demands, policies, among others (Folke et al. 2004; Hamilton and Keim 2009; WWAP 2012). Thus, the inclusion of these non-stationarity considerations for water planning and management is challenging.

Water resources management models simulate the operation of water resources systems under the application of certain management strategies. Model results are frequently summarized in terms of performance indices that are evaluated by decision makers to identify the most adequate strategy (e.g.: Hsu et al. 2004). Simonovic (2009) presented two new paradigms for shaping tools for water resources systems management: the first focused on the complexity of the water resources domain and the complexity of the modelling tools, and the second was related to the availability of data and the time and space variability of the variables affecting the uncertainty in water management decisions. Although system managers are well aware that model results are uncertain, a sensitivity analysis on hydrological input to water resources management models is seldom made while linking important decisions to model results. However, some studies showed that an analysis of uncertainties could be critical for water system performances (e.g. Steinschneider et al. 2014). Water systems are usually analysed for current and future scenarios. For current scenarios, most planning decisions are based on historic naturalized streamflow series that are obtained either from flow-gauge observations or rainfall and temperature measurements with a rainfall-runoff model assuming stationarity. The uncertainty associated to this hypothesis is usually neglected. In addition, the on-site measurements have an uncertainty that is seldom taken into consideration (Westerberg et al. 2016).

Several studies have analysed the uncertainty of future river flows stemming from both climate and hydrologic model uncertainties. Some authors conclude that hydrologic model uncertainties are much less significant than those originating from climate change (Prudhomme and Davies 2009; Chen et al. 2011). However Steinschneider et al. (2014) suggested that this conclusion can in part be attributed to the small sample sizes used. It is common to link the prediction of Global and/or Regional Climate Models with hydrological models to address changing flow regimes. This approach, however, presents important sources of uncertainty on account of the difficulties that climate models have in representing precipitation and streamflow (Leith and Chandler 2010; González-Zeas et al. 2012; Bardossy and Pegram 2012). In addition, many studies require important computational efforts for assessing climate change impacts on water resource systems. Even considering several hydrological models and climate projections, different estimations of streamflow can be carried out, but with large uncertainty (Nazemi and Wheater 2014).

It is widely known that the error and uncertainty can be propagated from one modelling domain to another (Dunn et al. 2012; Nazemi and Wheater 2014). Many authors (Fowler et al. 2007; Nazemi and Wheater 2014; Steinschneider et al. 2014) agree on the need to analyse how the propagation of the uncertainties affects water resource system performances. Such studies in this field have been rarely made. Although most studies mainly focused on short-term decision-making timescales (Yao and Georgakakos 2001; Alemu et al. 2011), a few interesting studies including long-term analyses can be found. For example Steinschneider et al. (2014) showed that the integrated effects of parametric and residual error uncertainty in a conceptual hydrologic model can have relevant implications when analysing water resources system performance. Meanwhile, Nazemi and Wheater (2014) showed that the response of the water resources system to the uncertainty in the generated inflow regime depends on the system state, flow condition and the component of interest, and might be different during the wet and dry years.

In this paper we present a sensitivity analysis experiment carried out in three water resources systems in the Duero basin (central Spain). The objective is to assess the impact of different sources of uncertainty on the width of the confidence interval for some hydrological variables and to propagate this uncertainty through water resources management models to assess its impact on performance indices commonly used for decision making.

2 Materials and Methods

The methodology of analysis was based on a Monte Carlo simulation approach. The process was divided in two steps. In the first step uncertainty on hydrologic variables was characterized through the analysis of uncertainty propagation in a stochastic rainfall-runoff model of the region under analysis. In the second step, uncertainty on river flows was propagated through water resources simulation models of the three systems. A general conceptual framework of the methodology proposed is presented in Fig. 1.

Fig. 1

General scheme of the methodology proposed

2.1 Case Studies

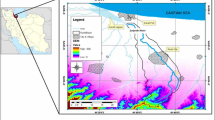
The stochastic rainfall-runoff model was applied to the Spanish Duero basin (with a total area of 78,859 km²) in the west region of mainland Spain (Fig. 2). The model was based on the analysis of the rainfall-runoff process as described by the results of the SIMPA model (Estrela and Quintas 1996; Alvarez et al. 2004). SIMPA is a deterministic distributed rainfall-runoff model that operates on a grid of 1 km² resolution at the monthly time scale. This model is computationally intensive and not adequate to perform Monte Carlo analyses. For this reason, a stochastic model of the rainfall-runoff process was built for the Duero basin based on the results obtained with the SIMPA model over the period October 1940 to September 2011 (70 years). Available hydrologic variables were precipitation (P, in mm), temperature (T, in °C), potential evapo-transpiration (PET, in mm), actual evapo-transpiration (AET, in mm), soil storage (S, in mm) and total runoff (R, in mm).

Fig. 2

Location of the Duero basin and main characteristics of the three water resources systems considered in this study; a Adaja-Cega; b Pisuerga – Carrión; c Tormes. Filled arrows: inflows to the system, rectangles: demands (I.D. = irrigation demand, U.D. = urban demand), triangles: reservoirs, circles: junction nodes and arrows: streams

The water resources simulation model was applied to three systems in the Duero basin: Adaja-Cega, Pisuerga-Carrion and Tormes. Monthly streamflow series in different points distributed across the Duero basin were only available for the period October 1940 to September 1996, since they correspond to an earlier version of the SIMPA model than that used for the hydroclimatic series. The most relevant demands, irrigation and urban supply were considered in all systems. The main characteristics of the water resources systems are presented in Fig. 2 and Table 1.

Table 1 Characteristics of the water resources systems considered in this study

2.2 Uncertainty in the Rainfall-Runoff Model

The rainfall-runoff process in the Duero basin was characterized through a stochastic model. The formulation and calibration of the model are described as follows.

2.2.1 Formulation of the Stochastic Rainfall-Runoff Model

The stochastic model for the rainfall-runoff process was based on the observed relationship between precipitation and runoff at the annual time scale. The model had one input variable: precipitation (P), one state variable: soil storage (S), two output variables: runoff (R) and actual evapotranspiration (AET) and three random forcing variables (ε_t for runoff, γ_t for AET and δ_t for soil storage). The observed precipitation series was fitted to a parametric distribution function. The proposed model equations are the following:

$$ {R}_t=a\cdot {e}^{b{P}_t}+{\varepsilon}_t $$

(1)

$$ AE{T}_t=c\left({P}_t-{R}_t\right)+d+{\gamma}_t $$

(2)

$$ {S}_t={S}_{t-1}+e\left({P}_t-{R}_t-AE{T}_t\right)+f+{\delta}_t $$

(3)

where R_t is runoff, P_t is precipitation, AET_t is actual evapotranspiration and S_t is soil storage, all in year t. ε _t , γ _t and δ _t are uncorrelated random processes normally distributed. Model parameters a, b, c, d, e, f and mean and variance of the processesε _t , γ _t and δ _t were estimated using the data produced by the SIMPA model.

2.2.2 Uncertainty Propagation through the Rainfall-Runoff Relationship

In order to characterize different sources of uncertainty the uncertainty propagation through the rainfall-runoff model was analysed under four hypotheses: 1) observed input, 2) random input with deterministic parameters, 3) random input with random parameters and 4) random input with random parameters and random model coefficients.

• 1. Observed Input

We analysed uncertainty propagation through model variables considering the observed rainfall in the basin during the historic period 1940–2011. In this case, variability was only due to the random noise of the model (ε _t , γ _t and δ _t ).

• 2. Random Input with Deterministic Parameters

Uncertainty propagation was analysed considering stochastic precipitation forcing with constant mean and standard deviation, equal to the mean and standard deviation of the observed precipitation series in the basin. In this step we introduce additional variability due to the stochastic nature of precipitation.

• 3. Random Input with Random Parameters

In this case we considered that the mean and standard deviation of the precipitation series were themselves random variables. In each realization we obtained the value of the precipitation mean and standard deviation sampling from their respective distributions. The mean of the precipitation realizations was assumed to be a random variable distributed as a Student t with n-1 degrees of freedom, with mean equal to the sample mean, μ, and standard deviation equal to$\frac{s}{\sqrt{n}}$, where s is the sample standard deviation and n is the sample size, 70 years (Norusis 2011). The variance of the precipitation realizations was assumed to be a random variable distributed as a Chi-Squared with n-1 degrees of freedom, with mean equal to the sample variance, s ², and standard deviation equal to $\frac{2{s}^4}{n-1}$(Knight 1999).

• 4. Random Input with Random Parameters and Random Model

Finally we accounted for the fact that model parameters (a, b, c, d, e and f) were also random variables estimated through data fitting. In the case of linear regression the properties of the probability distribution of model parameters can be known through the mean and standard deviation of the residuals as they follow a Student t distribution (Janke and Tinsley 2005). The following model was applied to sample from the probability distribution of parameters:

$$ {p}_i=E\left[{p}_i\right]-{\sigma}_i\cdot {t}_{n-2} $$

(4)

where p_i is model parameter i obtained in the regression y' _i  = gx _i  + h, E[p_i] is the expected value of the parameter, σ_i is the standard deviation of parameter i and t _n-2 is a Student t distribution with n-2 degrees of freedom.

For the slope coefficient, g, σ_m is:

$$ {\sigma}_m=\sqrt{\frac{\frac{1}{n-2}{\displaystyle \sum_{i=1}^n{\left(y{\hbox{'}}_i-{y}_i\right)}^2}}{{\displaystyle \sum_{i=1}^n{\left({x}_i-\overline{x}\right)}^2}}} $$

(5)

For the independent term, h, σ_n is:

$$ {\sigma}_n={\sigma}_m\sqrt{\frac{1}{n}{\displaystyle \sum_{i=1}^n{\left({x}_i\right)}^2}} $$

(6)

1000 realizations were generated sampling the regression coefficients on the models from their corresponding probability distributions. The Runoff equation was transformed into its linear form in order to characterize the variability of the parameters:

$$ {R}_t=a\cdot {e}^{b{P}_t} $$

(7)

was transformed into

$$ \ln \left({R}_t\right)=b{P}_t+a $$

(8)

2.3 Uncertainty in the Water Resources Model

The analysis of the uncertainty in the water resources model was performed by propagating the uncertainty obtained for the runoff variable in the previous section. The scales of analysis of the rainfall-runoff model and the water resources model were different: annual time step for the entire Duero basin and monthly time step applied to the local study cases. We first present the methodology for downscaling the results obtained in the rainfall-runoff model to the scale of analysis of the water resources model, and afterwards we present the water resources model and the performance indices.

2.3.1 Downscaling of Runoff Uncertainty

The downscaling of runoff uncertainty was performed by perturbing the available SIMPA runoff time series that were input to each water resources model at the points of interest. The perturbation was carried out by altering the mean and the coefficient of variation of the series in the same manner as it was obtained in the 1000 realizations performed in Section 2.2.2.

• 1. Perturbation of the Mean

$$ \varDelta \mu =\frac{\mu_p-{\mu}_r}{\mu_r} $$

(9)

• 2. Perturbation of the Standard Deviation

$$ \varDelta \sigma =\frac{\sigma_p-{\sigma}_r}{\sigma_r} $$

(10)

where μ is the mean of the series and σ is the standard deviation. The sub-index r stands for the reference series and the sub-index p stands for the perturbed series. The values of the perturbations were obtained from the 1000 series generated in each of the four experiments performed in Section 2.2.2. The perturbation was carried out by applying the algorithm presented by Chavez-Jimenez et al. (2013).

2.3.2 Water Resources Model

The analysis of the water resources systems was performed by applying the Water Availability and Adaptation Policy Analysis (WAAPA) model (Garrote et al. 2015). WAAPA is a model that simulates reservoir operation in a water resources system. Basic components of WAAPA are reservoirs, inflows and demands. These components are linked to nodes of the river network. WAAPA allows the simulation of reservoir operation and the computation of supply to demands from an individual reservoir or from a system of reservoirs accounting for ecological flows and evaporation losses. From the time series of supply volumes, supply reliability can be computed according to different criteria.

The WAAPA model was run for the three systems under the four hypotheses analysed in Section 2.2.2. For each case a total of 1000 realizations were performed, each one with input time series perturbed according to the methodology described above. Model results were summarized by analysing the variation of the system reservoir storage and an objective function Z (Rossi et al. 2011). The objective function tries to avoid catastrophic deficits, when only a small fraction of demand is supplied, by squaring the standardized monthly deficit:

$$ Z={\displaystyle \sum_{t=1}^T{\displaystyle \sum_{k=1}^K{\beta}_k{D}_k^{m(t)}{\left(\frac{S_k^{m(t)}-{D}_k^{m(t)}}{D_k^{m(t)}}\right)}^2}} $$

(11)

where K is the number of demand types in the system, β_k is the weighting coefficient for deficits incurred in demand type k, D^m(t) _k is the required supply volume to demand of type k in time t and S^m(t) _k is the actual supplied volume to demand type k in time t. Lower Z objective function values imply better performance for a given water resources system.

In addition to the objective function, we analysed the effect of inflow variability on several performance indices: a) Total urban demand deficit, in hm³; b) Total irrigation demand deficit, in hm³, c) Urban demand monthly time reliability, in %, assuming that a month was considered to fail if supply was less than 90 % of monthly urban demand, and d) Irrigation demand monthly time reliability, in %, assuming that a month was considered to fail if supply was less than 50 % of monthly irrigation demand.

3 Results and Discussion

In this section we first show the equation for the input process (precipitation), the rainfall-runoff model configuration and the uncertainty propagation applied to the case studies. Afterwards, we present the water resources model results and the analysis for the different hypothesis analysed.

3.1 Precipitation Characterization and Rainfall-Runoff Model Parameters Determination

The precipitation sample had an annual mean of 613.77 mm and a standard deviation of 120.52 mm. Annual rainfall showed no autocorrelation (not shown in this study). The rainfall variable was fitted to a lognormal distribution. The log of precipitation had a mean of 2.7796 and its standard deviation was 0.0867 (p-value of the Kolmogorov-Smirnov test (KS) = 0.62). Thus the proposed stochastic equation for the input process was:

$$ {P}_t={10}^{N{\left(2.7796,0.0867\right)}_t} $$

(12)

The models proposed for runoff and actual evapotranspiration presented R(Alvarez et al. 2004) values of 0.89 and 0.97, respectively. In addition normally distributed functions for the residuals were calculated presenting both a p-value of 0.98 according to the Kolmogorov-Smirnov test (KS) with means of 0.46 and 0.009, and small variances (24.13 and 8.67) compared to the mean of the estimated value (163 and 457 mm/year)). The above results show the goodness of fit of the proposed model. The R(Alvarez et al. 2004) for the model equation of variation of soil storage was 0.34. While all other model variables refer to average values over the year, soil storage is evaluated at end of the hydrological year (for the month of September). Since this is the driest month of the year it presents very small values which are difficult to observe (mean of 0.0 mm/year). Variations of delta storage (that could improve or worsen significantly the R(Alvarez et al. 2004) coefficient) generally correspond to small absolute values and they are not relevant for other model results.

Hence, we adopted the following rainfall-runoff model equations:

$$ {R}_t=16.357\cdot {e}^{\frac{P_t}{278}}+N{\left(0,24.13\right)}_t $$

(13)

$$ AE{T}_t=0.8667\left({P}_t-{R}_t\right)+66.371+N{\left(0,8.67\right)}_t $$

(14)

$$ {S}_t={S}_{t-1}+0.4268\left({P}_t-{R}_t-AE{T}_t\right)+2.6719+N{\left(0,6.82\right)}_t $$

(15)

3.2 Uncertainty Propagation of Rainfall-Runoff Relationship

The uncertainty propagation through the rainfall-runoff model was analysed under the four hypotheses. For each one, 1000 realizations were generated by sampling the regression coefficients on the models from their corresponding probability distributions. The results are presented in Table 2 and Fig. 3. Table 2 shows the 90 % confidence intervals of mean values and standard deviations of model variables. Figure 3 shows the probability distribution of the mean and standard deviation of model variables obtained with 1000 realizations of 70 years each.

Table 2 90 % confidence interval of model variables

Fig. 3

Probability distribution of the mean (left) and standard deviation (right) of model variables obtained in the four hypotheses. a, b Precipitation mean (mm); c, d Runoff mean (mm); e, f Actual Evapotranspiration mean (mm); g, h Soil Storage mean (mm). Obs: observed input, Det: random input with deterministic parameters, Rand: random input with random parameters and Mod: random input with random parameters and random model

As expected, the width of the confidence interval grew as we introduced more variability in the input (precipitation, Fig. 3a) and in the rainfall-runoff model (Fig. 3c). However, in the last step the increase was relatively moderate, which suggests that this may be the limiting case. Soil storage was the variable with the largest uncertainty in the mean (Fig. 3g), while runoff showed the largest uncertainty in the standard deviation (Fig. 3d). Uncertainty of soil storage was several times larger than the mean (which was close to zero, Fig. 3g). On the other hand, the width of the confidence interval of runoff was approximately 30 % of the mean (Fig. 3c).

It should be noted that there are still many sources of uncertainty that have not been taken into consideration in this study like, for instance, the possible non-stationarity of precipitation, the measurement error for the precipitation, the uncertainty associated to the spatial interpolation of rainfall or the actual differences between the SIMPA model and reality. These sources of uncertainty would probably increase the width of the confidence intervals for all variables.

3.3 Uncertainty in the Water Resources Model

First, we present the results and discussion of the time evolution of relevant variables during the simulation for the hypothesis named observed rainfall. Results are summarized by analysing the system reservoir storage variation, and the objective function value. Second, we analyse the effect of inflow variability on the water systems performance indices and the objective function proposed in Section 2.3.2.

3.3.1 Evolution of Relevant Variables for the Observed Rainfall

Figure 4 presents the results of the time evolution of the reservoir storage and the cumulative value of the objective function for the observed rainfall. The available reference time series covered the period 1940–1996. The plots show the time evolution of the variable for the 1000 realizations (in grey) compared to the time evolution of the variable for the reference inflow time series (in black, Fig. 4b, d and f). To allow comparisons, the objective function series were normalized by the objective function value for the reference time series at the end of the simulation. In general, it can be seen that the variability of the reservoir storage volume is less than 10 % for all three systems (it is barely visible in the plots, Fig. 4a, c and e). This is due to the fact that the time sequence of the years in the reference inflow was conserved in the perturbed inflows (e.g., dry years in the reference inflow corresponded to dry years in the perturbed inflows) and the processes of filling and emptying the reservoirs were relatively fast. The reasons for the different behaviours of the systems may be found in their characteristics: mean annual flow, reservoir storage, total demand or number of scarcity periods experienced by each system. The reservoirs of the Adaja-Cega system were full most of the time, and only four scarcity periods occurred during the simulation (Fig. 4a), while the Pisuerga-Carrión system presented a much higher number of scarcity periods (a total of 13, Fig. 4c). The Tormes system presented an intermediate number of scarcity periods leading to demand deficits: 9 (Fig. 4e). If we assume that the effect of inflow variability during one single scarcity period is constant, the higher the number of scarcity periods the less relative effect when deficits are summed up over the year. Results agree with Nazemi and Wheater (2014) who found that the relative inflow uncertainty spreads more at the system outlet during the wet years.

Fig. 4

(Left) Ensemble results of reservoir storage (reservoir storage =1 means that the reservoir is at the 100 % of its operative capacity) and (Right) cumulative value of the objective function obtained in the hypothesis of observed input. a, b: Adaja-Cega; c, d Pisuerga-Carrion; e, f: Tormes

3.3.2 Performance of the Analysed Systems

Figure 5 and Table 3 show the results obtained in the three systems for the urban and irrigation demand deficits for all cases analysed. The plots show the probability distribution of the variables compared to the values obtained in the reference condition (vertical dashed grey line). Table 3 presents a summary of results of the uncertainty analyses which shows the 90 % confidence intervals for the objective function values and urban and irrigation demands deficit in the three systems analysed. The results reproduced the effects already discussed: the sensitivity to uncertainty in inflows is larger for the Adaja-Cega system, which is the one showing the best overall volume reliability (Fig. 5a and b), and smaller for the Pisuerga-Carrión system, which is the one showing the worst overall reliability (Fig. 5c and d). The simulations performed with the inflows corresponding to the case with observed precipitation showed a range of 27.08 for the objective function value (90 % confidence interval) while those performed with the cases that corresponded to random precipitation showed ranges of 84.01 (Det), 108.18 (Rand) and 116.33 (Mod) (Table 3). As expected, the width of the confidence interval grew as we introduced more variability in the inflows.

Fig. 5

(Left) Probability distribution of the deficit for urban and (Right) irrigation demands obtained in the four hypotheses. Obs: observed input, Det: random input with deterministic parameters, Rand: random input with random parameters and Mod: random input with random parameters and random model. a, b Adaja-Cega; c, d Pisuerga-Carrion; e, f Tormes

Table 3 90 % confidence intervals for the objective function values and urban and irrigation demand deficits in the three systems analysed for all cases analysed: observed precipitation (Obs), random precipitation with deterministic parameters (Det), random precipitation with random parameters (Rand) and random precipitation and model parameters (Mod)

The results of time reliability for urban and irrigation demands in the three systems are presented in Fig. 6. It shows the probability distribution of demand reliability, expressed as time reliability, for all cases analysed. Time reliabilities were smaller than volume reliabilities for urban demands, while they were larger for irrigation demands. This was due to the fact that the threshold of acceptability were very different in both cases, 90 % for the urban demand and 50 % for the irrigation demand. As discussed before, it was apparent that the system with best reliability (Adaja-Cega) showed the greatest sensitivity (Fig. 6a and b). The sensitivity also appeared to be larger for irrigation demand than for urban demand. This may be due to the fact that urban demand was assumed a priority, and hence it was generally satisfied first. Consequently, the assumed priorities for supplying the different demands could condition the results. The assumption of considering urban demand as a priority compared with the irrigation demand is usually adopted for most of the national and regional water management institutions.

Fig. 6

(Left) Probability distribution of time reliability for urban and (Right) irrigation demands obtained in the four hypotheses. Obs: observed input, Det: random input with deterministic parameters, Rand: random input with random parameters and Mod: random input with random parameters and random model. a, b Adaja-Cega; c, d Pisuerga-Carrion; e, f Tormes

We also see in Fig. 5 and Fig. 6 that the effect of uncertainty on the output systems performance was highly skewed. The deviation from the reliabilities or deficits obtained with the reference inflows was much larger when the perturbations were unfavourable than when they were favourable. This fact may have important implications when using these performance measures of the water resources system in decision making.

4 Conclusions

Results show that the uncertainty on hydrologic variables may change dramatically our assessment of the performance of a water resources system and thus extreme care must be taken when evaluating hydrologic inputs. This is certainly relevant in the case of analysis of climate change impacts, since uncertainty on future hydrologic scenarios is particularly large. Specifically, in this study:

• We propose a methodology of analysis based on a Monte Carlo simulation approach. The process was divided in two steps. In the first step uncertainty on hydrologic variables was characterized through the analysis of uncertainty propagation in a stochastic rainfall-runoff model. In the second step, uncertainty on river flows was propagated through water resources simulation models of different systems. The methodology allows assessing the influence of the uncertainty of climate forcing on water resources systems models used for water management decisions.

• This methodology is directly applicable to the analysis of the influence of the uncertainty of different climate change models on water resources systems performances.

• The width of the confidence interval (90 %) of the rainfall-runoff model grows as we introduce more variability in the input (precipitation series) and in the rainfall-runoff model. However, the increase is relatively moderate for the extreme hypotheses (named Rand and Mod), which suggests the existence of a limiting case.

• The width of the confidence interval (90 %) of the water resources system model performance grows as we introduce more variability in the input (runoff series).

• The relative inflow uncertainty (runoff series) spreads more at the system outlet during the wet years.

• The water resources system with better volume reliability shows the greatest sensitivity to uncertainty propagation.

• The sensitivity to uncertainty propagation appears to be larger for irrigation than for urban demands (assuming urban demand as a priority)

• The deviation from the reliabilities or cumulated deficits from the water resources systems compared to the reference inflows is much larger when the perturbations are unfavourable than when they are favourable. This suggests that the uncertainty analysis may have important implications when using these performance measures of the water resources system in decision making, particularly in dry years.

It should be noted that the methodology and analysis is based on limited case studies and need to be extended to other systems in order to validate the conclusions presented in this study.