1 Introduction

The forecasting and estimating future streamflows are very important for many of the activities associated with planning and operation of the components of a water resource system such as operation of water infrastructures, flood mitigation, dam planning, operation of water reservoirs, distribution of drinking water and planning for navigation. Therefore, forecasting of river flows can be considered as one of the main research topics in hydrology (Awchi 2014).

Traditionally, the autoregressive moving average (ARMA) models have been widely used for forecasting water resources time-series (Maier and Dandy 2000). The main disadvantage of these models is assuming linear relationships among variables. In the real world, however, streamflow pattern is highly nonlinear and non-stationary (Hsu et al. 1995). Nonlinear model such as least square support vector regression (LSSVR), which is suited to complex nonlinear problems, is needed for the analysis of real world temporal data.

In the last decades, the application of artificial intelligence has received much attention in water resources (Kisi 2006, 2007; Guven 2009; Guven and Talu 2010; Kumar et al. 2011; Mustafa et al. 2012; Sanikhani and Kisi 2012; Awchi 2014). Recently, the support vector regression (SVR) has been widely used in solving hydrologic problems (Sivapragasam et al. 2001; Vapnik et al. 1997; McNamara et al. 2005; Awad et al. 2007; Kaheil et al. 2008; Kisi and Cimen 2009; Chen et al. 2010; He et al. 2014). Sivapragasam et al. (2001) used SVR for forecasting rainfall and runoff. The SVR was successfully employed to forecast flood stage by Liong and Sivapragasam (2002), to develop rating curves at three gauging stations in Washington by Sivapragasam and Muttil (2005), to predict water level fluctuations of Lake Erie by Khan and Coulibaly (2006), to forecast long-term discharges by Lin et al. (2006), to predict daily sediments in natural rivers by Cimen (2008), to model daily potential evapotranspiration by Kisi and Cimen (2009), to downscale the daily precipitations by Chen et al. (2010), to predict daily streamflows with weather and climate inputs by Rasouli et al. (2012), to forecast daily dam water levels by Hipni et al. (2013), to improve forecast of annual rainfall-runoffs by Wang et al. (2013), and to forecast daily river flows in the semiarid mountain region by He et al. (2014). The major disadvantage of the SVR method is its higher computational burden for the constrained optimization problems. This drawback of the SVR has been overcome by LSSVR method, which solves linear equations instead of a quadratic programming problem (Wang and Hu 2005). LSSVR has been successfully applied to solve different problems in engineering (Tao et al. 2008; Huang et al. 2009; Deng and Yeh 2010; Pahasa and Ngamroo 2011; Shokrollahi et al. 2013; Kamari et al. 2014; Hemmati-Sarapardeh et al. 2014). Tao et al. (2008) used LSSVR for prediction of bearing raceways super finishing. Huang et al. (2009) predicted effluent parameters of wastewater treatment plant based on LSSVR. Deng and Yeh (2010) applied LSSVR to the airframe wing-box structural design cost estimation. Pahasa and Ngamroo (2011) used LSSVR for power system stabilization by SMES. Shokrollahi et al. (2013) predicted CO2-reservoir oil minimum miscibility pressure using LSSVR. Kamari et al. (2014) used LSSVR for efficient screening of enhanced oil recovery and prediction of economic analysis. Hemmati-Sarapardeh et al. (2014) determined the reservoir oil viscosity using LSSVR approach. However, there are limited studies in the literature related to application of LSSVR in water resources (Guo et al. 2011; Hwang et al. 2012; Kisi 2012, 2013; Okkan and Serbes 2013). Guo et al. (2011) used LSSVR for prediction of reference evapotranspiration and found promising results. Hwang et al. (2012) forecasted daily water demand and daily inflows by using LSSVR method and compared with neural networks (NN) and multiple linear regression (MLR) models. They indicated that the LSSVR performed better than the NN and MLR methods. Kisi (2012) modeled discharge-sediment relationship by LSSVR and compared with NN and sediment rating curve (SRC) models. The results showed that the proposed model gave better accuracy than the NN and SRC. Kisi (2013) applied LSSVR for modeling daily reference evapotranspiration and compared with feed forward NN and empirical models. He showed that LSSVR model performed better than the NN and other models. Okkan and Serbes (2013) used and proposed LSSVR with wavelet in reservoir inflow modeling. Despite the reported success of employing LSSVR in numerous studies, to the best of our knowledge the capability of LSSVR has not yet been examined in terms of streamflow forecasting.

In the last decades, adaptive neuro-fuzzy (ANFIS) method has also been successfully applied in water resources (Chen et al. 2006; Kisi 2006; Yarar et al. 2009; Kisi et al. 2012; Rezaeianzadeh et al. 2014; Sharma et al. 2015) The ANFIS was successfully employed to forecast flood by Chen et al. (2006); to model daily pan evaporation by Kisi (2006); to estimate level changes of Lake Beysehir by Yarar et al. (2009); to forecast daily intermittent streamflows by Kisi et al. (2012); to forecast flood flows of Khosrow Shirin watershed located in the Fars Province of Iran by Rezaeianzadeh et al. (2014); and to simulate streamflows in El Nino Southern Oscillation (ENSO)-affected watershed by Sharma et al. (2015). In the ANFIS related literature, the grid partition (GP) method were generally used for training. The GP method, however, uses many fuzzy rules and many parameters to be optimized which makes it unsuitable for many input variables (Chen and Gao 2012). Therefore, in the present study, the fuzzy c-means clustering (FCM) was used instead of GP. To the best of the authors’ knowledge, no research work has yet been published on the forecasting of monthly streamflows using adaptive neuro-fuzzy embedded fuzzy c-means clustering (ANFIS-FCM) method.

The study aims to investigate the ability of LSSVR and ANFIS-FCM methods in monthly streamflow forecasting and estimation. The effect of periodicity on forecasting performance of the LSSVR and ANFIS-FCM models was also investigated. The LSSVR and ANFIS-FCM techniques were also used to estimate monthly flows of Bitlis Stream using the data of Garzan Stream. The term forecasting is used here for the model applications where the input and output data belonging to the same river station in the study. The term estimation is used when input and output data belong to different stations.

2 Least Square Support Vector Regression

SVR as one of the most efficient and powerful learning machines has been much attended during the last few years (Suykens and Vandewalle 1999; Awad et al. 2007; Kisi and Cimen 2009; Chen et al. 2010; He et al. 2014). Any function can be expressed by SVR in the following format (Suykens et al. 2002) as

$$ f(X)={w}^T\varphi (X)+b $$
(1)

where w shows the m-dimensional weight vector, φ is the mapping function and b is the bias term. Vapnik proposed minimization of the cost function \( \frac{1}{2}{w}^T+c{\displaystyle {\sum}_{i=1}^M\left({\xi}_k-{\xi}_k^{*}\right)} \) to calculate w and b (Suykens et al. 2002). This cost function is subjected to the following constraints:

$$ \left\{\begin{array}{ll}{y}_k-{w}^T\varphi \left({x}_k\right)-b\le \varepsilon +{\xi}_k,\hfill & k=1,2,\dots, M\hfill \\ {}{w}^T\varphi \left({x}_k\right)+b-{y}_k\le \varepsilon +{\xi}_{{}_k}^{*}\hfill & k=1,2,\dots, M\hfill \\ {}{\xi}_k-{\xi}_{{}_k}^{*}\ge 0,\hfill & k=1,2,\dots, M\hfill \end{array}\right. $$
(2)

Where x k and y k indicate the kth input and output data, respectively; ε stands for the fixed precision of the function approximation; ξ k and ξ * k are the two slack variables. The tuning parameter, c of the SVR controls the amount of deviation from the interested ε. As a matter of fact, one of the tuning parameters of the SVM is c. To minimize the cost function and its constraints, the Lagrangian of this problem should be used (Suykens et al. 2002):

$$ L\left(a,{a}^{*}\right)=-\frac{1}{2}{\displaystyle {\sum}_{k,l=1}^M\left({a}_k - {a}_k^{*}\right)}\left({a}_l-{a}_l^{*}\right)K\left({x}_k,{x}_l\right)-\upvarepsilon {\displaystyle {\sum}_{k=1}^M\left({a}_k - {a}_k^{*}\right)}+{\displaystyle {\sum}_{k=1}^M{y}_k\left({a}_k - {a}_k^{*}\right)} $$
(3)
$$ {\displaystyle {\sum}_{k=1}^M\left({a}_k-{a}_k^{*}\right)}=0,\ {a}_k,{a}_k^{*}\in \left[0,c\right] $$
(4)
$$ K\left({x}_k,{x}_l\right)=\varphi {\left({x}_k\right)}^T\varphi \left({x}_l\right),\kern0.24em k=1,2,\dots, \mathrm{N} $$
(5)

Where a k and a * k are Lagrangian multipliers. The final form of the SVR can be obtained as (Esfahani et al. 2015)

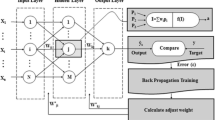
$$ f(x)={\displaystyle {\sum}_{k,l=1}^M\left({a}_k-{a}_k^{*}\right)}K\left(x,{x}_k\right)+b $$
(6)

A quadratic programming problem is solved in order to solve the above problem and determine a k , a * k and and b, which is considerably difficult. For improving the original SVR method, Suykens and Vandewalle (1999) proposed the least square modification of the SVR (LSSVR). The LSSVR originated from SVR is a powerful technique for solving non-linear problems, classification, function and density estimation (Kumar and Kar 2009). Figure 1 shows the procedure of LSSVR. The cost function of the LSSVR is

Fig. 1
figure 1

LSSVR and ANFIS models for streamflow forecasting

Full size image
$$ minJ\left(w,e\right)=\frac{1}{2}{w}^Tw+\frac{\gamma }{2}{\displaystyle {\sum}_{i=1}^M{e}_i^2} $$
(7)

that subject to following constraints

$$ \begin{array}{ll}{y}_i={w}^T\varphi \left({x}_i\right)+b+{e}_i\hfill & \left(i=1,2,\dots, M\right)\hfill \end{array} $$
(8)

where γ is the regularization constant and e i is the training error for x i .

To derive solutions w and e, the Lagrange Multiplier optimal programming method is applied to solve Eq. (7); the objective function can be obtained by changing the constraint problem into an unconstraint problem. The Lagrange function L can be given as

$$ L\left(w,b,e,\propto \right)=J\left(w,e\right)-{\displaystyle {\sum}_{i=1}^M{a}_i\left\{{w}^T\varphi \left({x}_i\right)+b+{e}_i-{y}_{i\ }\right\}} $$
(9)

where a i denotes Lagrange multipliers.

According to the Karush-Kuhn-Tucker (KKT) conditions (Flecher 1987), the optimal conditions can be derived after taking the partial derivatives of Eq. (9) with respect to w, b, e and a, respectively as

$$ \left\{\begin{array}{l}w={\displaystyle {\sum}_{i=1}^m{a}_i\varphi \left({x}_i\right)}\hfill \\ {}{\displaystyle {\sum}_{i=1}^m{a}_i=0}\hfill \\ {}{a}_i=\gamma {e}_i\hfill \\ {}{w}^T\varphi \left({x}_i\right)+b+{e}_i-{y}_i=0\hfill \end{array}\right. $$
(10)

After elimination of e i and w, the linear equations are obtained as

$$ \left[\begin{array}{cc}\hfill 0\hfill & \hfill -{Y}^T\hfill \\ {}\hfill Y\hfill & \hfill Z{Z}^T+I/\gamma \hfill \end{array}\right]\left[\begin{array}{c}\hfill b\hfill \\ {}\hfill a\hfill \end{array}\right]=\left[\begin{array}{c}\hfill 0\hfill \\ {}\hfill 1\hfill \end{array}\right] $$
(11)

where Y = y 1, …, y m , Z = φ(x 1)T y 1, …, φ(x m )T y m , I = [1, …, 1], a = [a 1, …, a l ].

Kernel function can be defined as K(x, x i ) = φ(x)T φ(x i ), i = 1, …, M, according to the Mercer’s condition. Thus, the LSSVR becomes

$$ f(x)={\displaystyle {\sum}_{i=1}^m{a}_iK\left(x,{x}_i\right)+b} $$
(12)

The RBF kernel function, commonly used in regression problems, was used in this study. It can be defined as

$$ K\left(x,{x}_i\right)= exp\left(-{\left\Vert x-{x}_i\right\Vert}^2/2{\sigma}^2\right) $$
(13)

LSSVR has two tuning parameters, γ and σ 2 which are obtained by minimization of the deviation of the LSSVR model from measured values (Shu-gang et al. 2008).

3 Adaptive Neuro-Fuzzy Inference System

ANFIS, first introduced by Jang (1993), is a universal approximator and is capable of approximating any real continuous function on a compact set. ANFIS has a structure composed of a number of nodes connected to each other through directional links. Each node is characterized by a node function consists of fixed or adjustable parameters (Jang et al. 1997).

As an example, for a fuzzy inference system (FIS) having three inputs x, y and z and one output f, the rule base contains two fuzzy if-then rules of Takagi and Sugeno’s type can expressed as

$$ \mathrm{Rule}\ 1:\ \mathrm{If}\kern0.2em x\kern0.2em \mathrm{is}\kern0.2em {A}_1,y\kern0.2em \mathrm{is}\kern0.2em {B}_1\kern0.2em \mathrm{and}\kern0.2em z\kern0.2em \mathrm{is}\kern0.2em {C}_1\kern0.2em \mathrm{then}\kern0.2em {f}_1={p}_1x+{q}_1y+{r}_1z+{s}_1 $$
(14)
$$ \mathrm{Rule}\ 2:\ \mathrm{If}x\kern0.2em \mathrm{is}\kern0.2em {A}_2,\kern0.2em y\kern0.2em \mathrm{is}\kern0.2em {B}_2\kern0.2em \mathrm{and}\kern0.2em z\kern0.2em \mathrm{is}\kern0.2em {C}_2\kern0.2em \mathrm{then}\kern0.2em {f}_2={p}_2x+{q}_2y+{r}_2z+{s}_2 $$
(15)

Here f 1 and f 2 indicate the output function of rule 1 and rule 2, respectively. The ANFIS structure is shown in Fig. 1. The node functions in each layer are described below.

Every square node i in layer 1 is an adaptive node with a node function O l,i  = φA i (x), for i = 1, 2 where x is the input to the ith node and A i is a linguistic label (such as “small” or “big”) associated with this node function. O l , i is the membership function (MF) of a fuzzy set A (e.g., A 1 , A 2 , B 1 , B 2 , C 1 , C 2 ) and it specifies the degree to which the given input x satisfies the quantifier A i . φA i (x) is usually chosen to be Gaussian function with maximum equal to 1 and minimum equal to 0 as

$$ \varphi {A}_i(x)= \exp \left(-{\left(\frac{x-{a}_i}{b_i}\right)}^2\right) $$
(16)

where {a i, b i } is the parameter set. Parameters of this layer are called as premise parameters. Every circle node in layer 2 is labelled Π which multiply the incoming signals and sends the product out. For instance, w i  = φA i (x)φB i (y)φC i (z), i = 1, 2. The output of each node indicates the firing strength of a rule. Every circle node in layer 3 is labelled N. Here the ratio of the ith rule’s firing strength to the sum of all rules’ firing strengths is calculated by ith node as

$$ {\overset{\_\_}{w}}_i=\frac{w_i}{w_1+{w}_2},\kern0.84em i = 1,\ 2. $$
(17)

Every square node in layer 4 has a node function \( {O}_{4,i}={\overset{\_\_}{w}}_i{f}_i={\overset{\_\_}{w}}_i\left({p}_ix+{q}_iy+{r}_iz+{s}_i\right) \) where \( {\overset{\_\_}{w}}_i \) is the output of layer 3, and {p i , q i , r i , s i } is the parameter set. Each parameter of this layer is called as consequent parameters. The single circle node in layer 5 is labelled Σ calculates the final output as the summation of all incoming signals

$$ {O}_{5,i}={\displaystyle \sum_{i=1}{\overset{\_\_}{w}}_i{f}_i}=\frac{{\displaystyle \sum_i{w}_i{f}_i}}{{\displaystyle \sum_i{w}_i}} $$
(18)

Thus, an ANFIS network have been constructed which is functionally equivalent to a first-order Sugeno FIS. ANFIS method use linear or constant functions for the output. Detailed information for ANFIS can be obtained from Jang (1993).

In the present study, ANFIS with fuzzy c-means clustering (ANFIS-FCM) were applied. In the FCM method, the data points are grouped by measuring the potential of data points in the feature space. The mountain clustering method is used for estimating number of clusters and the cluster centers (Chiu 1994; Cobaner 2011). The fuzzy c-means clustering (FCM) is a modification of the K-means algorithm which owns some limitations and may not work appropriately with big data set. The FCM minimizes intra cluster variance (Ayvaza et al. 2007) and comprises grouping of data by means of the clustering algorithm. In FCM, the distance or objective squared error function is minimized.

4 Case Studies

In this study, the monthly streamflow data from two stations, Besiri Station (No: 2603) on the Garzan Stream and the Baykan Station (No: 2610) on the Bitlis Stream, in the Firat-Dicle Basin of Turkey were used. Figure 2 illustrates the location of the stations. The drainage areas at these sites are 2450 km2 for Besiri and 636 km2 for Baykan. The observed data are 30 years (360 months) long with an observation period between 1965 and 1994 for both stations. The observed data obtained from the report of the Turkish General Directorate of Electrical Power Resources Survey and Development Administration are for hydrologic years, i.e., the first month of the year is October and the last month of the year is September.

Fig. 2
figure 2

The Besiri (2603) and Baykan (2610) stations on rivers Garzan and Bitlis (Sanikhani and Kisi 2012)

Full size image

In the present study, cross validation method was applied and whole data were divided into four training/testing parts to get effective modeling. In all the applications, three parts were used in training and remaining one part in testing. In each application, test part was changed and thus four different applications were employed. The statistical properties of each data set used in the study are given in Table 1 for the both stations. The observed monthly streamflows show high positive skewness (Csx = 1.75 and 2.29). The auto-correlations are quite low showing low persistence (e.g., r1 = 0.607, r2 = 0.152, r3 = 0.102). The auto-correlations of Baykan Station are generally higher than those of the Besiri Station.

Table 1 The monthly statistical parameters of data set for Besiri and Baykan stations
Full size table

5 Application

In the first part of the study, the LSSVR and ANFIS-FCM models were tested in 1-month ahead streamflow forecasting and results were compared with ARMA models. Three input combinations based on current and preceding monthly streamflow values were evaluated. Let assume that the Qt represents the flow at time t, the input combinations evaluated in the study are; (i) Qt, (ii) Qt, Qt-1, (iii) Qt, Qt-1 and Qt-2. The models were evaluated with respect to root mean square errors (RMSE), mean absolute errors (MAE) and determination coefficient (R2) statistics for each input combination. The RMSE and MAE can be expressed as

$$ RMSE=\sqrt{\frac{1}{N}{\displaystyle \sum_{i=1}^N}{\left({Q}_{i,o}-{Q}_{i,f}\right)}^2} $$
(19)
$$ MAE=\frac{1}{N}{\displaystyle {\sum}_{i=1}^N\left|{Q}_{i,o}-{Q}_{i,f}\right|} $$
(20)

where N is the number of data, Q i,o is the observed discharge values and Q i,f is the model’s forecast.

For each input combination, cross validation method was employed by dividing data into four sets. Different parameters were tried for each LSSVR model and the optimal ones that gave the minimum RMSE error in test period were obtained. The parameters of the optimal LSSVR models for each input combination are provided in Table 2. In this table, M1 indicates model 1 and (0.2, 0.8) shows the regularization constant and width of the RBF kernel, respectively. Various regularization constants and RBF kernels were tried for the LSSVR models. As an example, the variation of test RMSE vs regularization constant and RBF kernel for the M1 model comprising input Qt (input combination i) is shown in Fig. 3 for the Besiri Station. The test results of the best LSSVR models are given for the Besiri Station in Table 3. It is clear from the table that both LSSVR and ANFIS-FCM models give different forecasts for different data sets. According to the average performance of the models, the LSSVR and ANFIS-FCM models comprising current and one previous flow values (input combination ii) perform better than the other models. The input combination (iii) seems to be slightly worse than the input combination (ii) for the both methods. It is clear that the LSSVR and ANFIS-FCM models give the worst results for the M2 data set. The reason behind this may be the fact that the maximum streamflow value of the testing data set (xmax = 354 m3/s) is higher than that of the training data set (see Table 1). This implies that the trained LSSVR and ANFIS-FCM models face difficulties in making extrapolation in high values in the case of M2. The best LSSVR model was obtained for the M1 and input combination (iii) while the best ANFIS-FCM model was obtained for the M3and input combination (iii). Table 3 clearly indicates that the LSSVR models generally perform better than the ANFIS-FCM models in 1-month ahead streamflow forecasting.

Table 2 The parameters of the optimal LSSVR models for each combination – Besiri and Baykan stations
Full size table
Fig. 3
figure 3

The variation of test RMSE vs regularization constant and RBF kernel for the LSSVR model – input combination (i) and M1 data set of Besiri station

Full size image
Table 3 Comparison of the LSSVR and ANFIS-FCM models - Besiri Station
Full size table

Table 4 shows the test results of the best LSSVR and ANFIS-FCM models for the Baykan Station. According to the average performance of the models, the LSSVR models give similar results for the input combinations (ii) and (iii) and they have better accuracies than the input combination (i). The ANFIS-FCM models, however, have similar accuracy for the input combinations (i) and (iii) and they perform worse than the input combination (ii). Similar to the Besiri, the LSSVR models give the worst results for the M2 data set while the worst forecasts of the ANFIS-FCM models were obtained for the M2 data set, followed by M2. Here, also the maximum streamflow value of the testing data set (xmax = 126 m3/s) is higher than those of the training data set (see Table 1). This confirms the extrapolation difficulties of the LSSVR models for this data set. Here also the best LSSVR model was obtained for the M1 and input combination (iii). The ANFIS-FCM model, however, gave its best forecasts for the M1 and input combination (ii). It is clear from the Table 4 that the LSSVR models generally have better accuracy than the ANFIS-FCM in 1-month ahead streamflow forecasting. Comparison of Tables 3 and 4 clearly shows that the LSSVR and ANFIS-FCM models are more successful in Besiri Station than the Baykan. The reason of this may be the higher auto-correlations of the Baykan Station in relative to the Besiri.

Table 4 Comparison of the LSSVR and ANFIS-FCM models - Baykan Station
Full size table

Different ARMA models were also tested by using same data sets and the optimal ones that gave the minimum RMSE were selected. The results are given in Table 5 for the Besiri and Baykan stations. In Besiri Station, it should be noted that the ARMA model also gave its worst results for the M2 data set similar to the LSSVR and ANFIS-FCM. Comparison of Tables 3 and 5 clearly indicates that the LSSVR and ANFIS-FCM models perform better than the ARMA model for all the data sets. For the Baykan Station, also the worst forecasts were obtained from the M2 model while the M1 model was found to be the best. Comparison of ARMA, LSSVR and ANFIS-FCM models (Tables 4 and 5) shows that the LSSVR and ANFIS-FCM models have better accuracy than the ARMA in monthly streamflow forecasting. The average RMSE accuracy of the ARMA models was increased by 15.6–12.4 % using LSSVR models for the Besiri and Baykan stations, respectively.

Table 5 Comparison of the ARMA models
Full size table

In this part of the study, the periodicity effect was also investigated by adding a component α which takes values between 1 and 12 according to the month of the year to be forecast into each input combination. The test results of the periodic LSSVR models are provided in Table 6 for the both stations. According to the average performance of the models, the periodic LSSVR models provide similar accuracy for the different input combinations. Similar to the previous application, the periodic LSSVR model has the worst forecasts for the M2 data set while the M1 model is found to be the best for the Besiri Station. Comparison of Tables 3 and 6 reveals that adding periodic component into input combinations significantly increases the LSSVR model accuracy. The average RMSE accuracies of the ARMA and LSSVR models were respectively increased by 25.9–12.2 % using periodic LSSVR models for the Besiri Station. The observed and forecasted monthly streamflows by the LSSVR, periodic LSSVR (P-LSSVR), ANFIS-FCM and ARMA for the M1 data set are shown in Fig. 4 in the form of scatterplot. It is clear from the scatterplots that the fit line coefficients a and b (assume that the fit line equation is y = ax + b) of the P-LSSVR model are respectively closer to the 1 and 0 with a higher R2 value than those of the LSSVR, ANFIS-FCM and ARMA models. In Baykan Station, according to the average accuracy of the models, the periodic LSSVR models provide almost same performance for the input combinations (i) and (iii). Input combination (ii) has slightly better accuracy than the other combinations for the. Here also the periodic LSSVR model has the best forecasts for the M1 data set while the M2 model was found to be the worst. Comparison of Tables 4 and 6 clearly indicates that the LSSVR model accuracy significantly increases by adding periodic component into inputs. The average RMSE accuracy of the ARMA and LSSVR models was respectively increased by 21–9.9 % using periodic LSSVR models for the Baykan Station. Figure 5 illustrates the observed and forecasted monthly streamflows by the LSSVR, periodic LSSVR (P-LSSVR), ANFIS-FCM and ARMA for the M1 data. Similar to the Besiri Station, here also the P-LSSVR forecasts are closer to the observed streamflows than those of the LSSVR, ANFIS-FCM and ARMA. LSSVR and ANFIS-FCM models also perform better than the ARMA model.

Table 6 Comparison of the periodic LSSVR models
Full size table
Fig. 4
figure 4

The observed and forecasted streamflows by the LSSVR, P-LSSVR, ANFIS-FCM and ARMA models for the M1 data set - Besiri station

Full size image
Fig. 5
figure 5

The observed and forecasted streamflows by the LSSVR, P-LSSVR, ANFIS-FCM and ARMA models for the M1 data set - Baykan station

Full size image

In the second part of the study, the ability of the LSSVR and ANFIS-FCM models was tested in streamflow estimation using data from nearby stream. The streamflow estimation using nearby stream’s data is an important issue since the downstream or upstream data are missing for many rivers. In this case, the streamflow data of the nearby streams can be used to estimate the missing streamflow data. It should be noted that the Besiri and Baykan stations have drainage basins with similar hydrological characteristics. The data of the Besiri Station were used to estimate monthly streamflows of the Baykan Station. In this application, also cross validation method was employed by dividing data into four parts. The four input combinations were tried as (i) Qt, (ii) Qt, Qt-1, (iii) Qt, Qt-1, Qt-2, and (iv) Qt, Qt-1, Qt-2, Qt-3. The output is the current flow, Qt of the Baykan Station. The optimal regularization constant and RBF kernel values obtained by using trial and error method are given in Table 7 for each data set and each input combination. The test results of the LSSVR and ANFIS-FCM models are provided in Table 8. According to the average performance of the models, the best accuracy of the LSSVR models was obtained from M1 data set while the M4 gave the worst estimates. For the ANFIS-FCM, however, the best accuracy was obtained for the M3 data set while the M4 gave the worst estimates. It is clear from the table that the LSSVR models gave better estimates than the ANFIS-FCM models in cross station application. The observed and estimated flows by LSSVR and ANFIS-FCM models for each data set are shown in Fig. 6. It is clearly seen from the figure that both LSSVR and ANFIS-FCM models closely estimate streamflow data of Baykan Station by using the data of Besiri Station especially for the M1, M2 and M3 data sets. The superior accuracy of the LSSVR models to the ANFIS-DCM models is obviously seen from the figüre.

Table 7 The parameters of the optimal LSSVR models in cross-station application
Full size table
Table 8 Comparison of the LSSVR and ANFIS-FCM models in estimating monthly river flows of the Baykan Station by using the data of Besiri Station
Full size table
Fig. 6
figure 6

The streamflow estimates of the Baykan Station by LSSVR and ANFIS-FCM using the data of Besiri station

Full size image

6 Conclusions

In the present study, the ability of LSSVR and ANFIS-FCM models in forecasting and estimation of monthly streamflows was investigated. In the first part of the study, the LSSVR and ANFIS-FCM models were tested in 1-month ahead streamflow by using data from two stations, Besiri Station on Garzan Stream and Baykan Station on Bitlis Stream, in Dicle Basin of Turkey. Cross validation method was also employed in the applications. The LSSVR and ANFIS-FCM forecasts were compared with those of the ARMA models. Both models were found to be better than the ARMA in 1-month ahead streamflow forecasting. The LSSVR model reduced the average RMSE value with respect to the ARMA model by 15.6 and 12.4 % for the Besiri and Baykan stations, respectively. The effect of periodicity component on forecasting ability of the LSSVR models was also examined. It was found that adding periodicity into the model inputs significantly improved the LSSVR accuracy in forecasting. The average RMSE accuracies of the LSSVR models were increased by 12.2 and 9.9 % using periodic LSSVR models for the Besiri and Baykan stations, respectively. The second part of the study focused on testing the accuracy of the LSSVR and ANFIS-FCM models in streamflow estimation using data from nearby stream. The results indicated that the LSSVR performed better than the ANFIS-FCM and could be successfully used in estimating monthly streamflows by using nearby station data.