1 Introduction

Coastal aquifers are a valuable source of freshwater, which is particularly at risk due to its proximity to seawater. In addition, quite large water requirements usually appear in coastal areas due to high population density. Unless properly managed, a coastal aquifer will be destroyed (salinized) by sea water intrusion within a rather short period (Bear 2004). The primary detrimental effects of seawater intrusion are reduction in the available freshwater storage volume and contamination of production wells, whereby less than 1 % of seawater renders freshwater unfit for drinking (Werner et al. 2013).

The measures that can be taken to protect or restore aquifers from seawater intrusion are, among others, the control of pumping, the reallocation of pumping sites and the promotion of natural and artificial recharge. A useful tool for evaluating the effectiveness of these measures is mathematical modelling. Mathematical models have appeared in literature during the last decades, and range from simple (steady flow) analytical solutions to complex numerical solutions of unsteady flow. A clear distinction between the approaches used in several solutions depends on considering freshwater and seawater as immiscible or miscible fluids. In the former case, the assumption of a sharp interface between freshwater and seawater is adopted, and finite element solutions were presented by Wilson and Sa da Costa (1982) and Voss (1984), among others. When the two fluids are considered miscible, on the other hand, the variable density flow approach is used, and applying the finite element method, solutions presented by Segol et al. (1975), Frind (1982) and Voss and Souza (1987) in a two-dimensional flow field and by Huyakorn et al. (1987), Kolditz et al. (1998) and Doulgeris (2005) in a three-dimensional flow field. Popular numerical codes, commercial or freely available, for simulating seawater intrusion are reviewed by Werner et al. (2013).

A common issue in coastal aquifer management is to find the maximum pumping rate without observing an increase of salt concentration in pumped water. Mantoglou et al. (2004) applied a numerical model based on the sharp interface and the Ghyben-Herzberg approximation, which can handle aquifers of complex shapes and non-uniform distribution of surface recharge and hydraulic conductivity, to investigate the efficiency of two optimization methods. Katsifarakis and Petala (2006) presented a model which combines the genetic algorithms as the optimization tool and the boundary element method for the simulation of groundwater flow. Sreekanth and Datta (2011) evaluated genetic programming as a potential surrogate modelling tool and compared the advantages and disadvantages with the neural network based surrogate modelling approach. Kourakos and Mantoglou (2011) proposed a management plan for the island of Santorini that is formulated in a multi-objective, optimization framework, where simultaneous minimization of economic and environmental costs is desired. In the above cases, the optimization of coastal aquifer management is achieved by combining an optimization and a flow simulation model. A simulation model runs many times through a process which is dictated by an optimization model in order to find the optimal solution. Thus, the overall computational procedure is usually quite demanding in processing power and a simple, steady flow model or a surrogate model is chosen in most cases as the simulation model, which provides solutions in a reasonable computational time. However, the adoption of a simplified approach may be insufficient to simulate the seawater intrusion process, especially when pumping wells form a three-dimensional groundwater flow field and a transition zone between freshwater and seawater which cannot be ignored.

This paper presents a three-dimensional variable density flow model for the simulation of seawater intrusion and reviews the optimum pumping rate suggested by a two-dimensional constant density flow to illustrate the necessity of a three-dimensional variable density flow model for the management of pumping in coastal aquifers. The variable density model is verified against two and three dimensional benchmarks problems and is applied to a heterogeneous coastal aquifer to study the effects of a) the pumping rate, b) the salinity of freshwater inflow and c) the thickness of the aquifer on the degradation of pumped water quality through wells in certain locations. Model results show that seawater intrusion into coastal aquifers may exist even for an optimum pumping scheme solution based on a simple two-dimensional flow model. Therefore, the application of the variable density flow model is necessary to adequately determine the use of each well depending on the pumping rate combined with the quality of freshwater inflow and the aquifer thickness.

2 Governing Equations

The governing equations of seawater intrusion in coastal aquifers, using the variable density flow approach, results from the continuity fluid equation and the continuity mass equation of a conservative substance. Furthermore, a generalized form of Darcy’s law is used to calculate the fluid velocities and an equation of state correlates the fluid density and the substance concentration.

The partial differential equation of the variable density fluid flow in porous media can be written as (Bear 1999):

$$ \nabla \cdot \left[\boldsymbol{K}\cdot \left(\nabla \mathrm{h}+{\upbeta}_{\mathrm{c}}^{\prime}\mathrm{c}\nabla \mathrm{z}\right)\right]={\mathrm{S}}_{\mathrm{S}}\frac{\partial \mathrm{h}}{\partial \mathrm{t}}+\mathrm{n}{\upbeta}_{\mathrm{c}}^{\prime}\frac{\partial \mathrm{c}}{\partial \mathrm{t}}+\frac{1}{\uprho_0}{\displaystyle \sum_{\left(\mathrm{m}\right)}\uprho \kern0.28em {\mathrm{Q}}_{\mathrm{m}}\left({\mathbf{x}}_{\mathrm{m}},\mathrm{t}\right)\kern0.28em \updelta}\left(\mathbf{x}-{\mathbf{x}}_{\mathrm{m}}\right) $$
(1)

where h is the reference hydraulic head, c is the relative concentration, Κ is the tensor of hydraulic conductivity, SS is the specific storage, βc΄ is the coefficient of density difference with concentration, n is the porosity, Qm(xm,t) is the pumping rate at point xm, δ(x-xm) is the Dirac delta at point xm, ρ and ρ0 are the density of water and freshwater, respectively, z is the distance from the datum and t is the time.

The reference hydraulic head, h, is associated with the density of freshwater and the coefficient β ′c , which can be referred as the density difference factor, are given by:

$$ \mathrm{h}=\frac{\mathrm{p}}{\uprho_0\mathrm{g}}+\mathrm{z} $$
(2)
$$ {\upbeta}_{\mathrm{c}}^{\prime }=\frac{1}{\uprho_0}\frac{\partial \uprho}{\partial \mathrm{c}} $$
(3)

where p is the fluid pressure and g is the gravitational acceleration. The hydraulic conductivity tensor and the specific storage of the aquifer are given with respect to the density by:

$$ \boldsymbol{K}=\frac{\uprho\ \mathrm{g}\ \boldsymbol{k}}{\upmu} $$
(4)
$$ {\mathrm{S}}_{\mathrm{S}}=\uprho\ \mathrm{g}\left[\left(1-\mathrm{n}\right)\upalpha +\mathrm{n}\ \upbeta \right] $$
(5)

where k is the tensor of porous medium permeability, μ is the fluid’s dynamic viscosity, and α and β are coefficients of soil and water compressibility, respectively.

The relative, dimensionless, concentration of total dissolved salts in water varies from 0 to 1 and is given by:

$$ \mathrm{c}=\frac{\overline{\mathrm{c}}-{\mathrm{c}}_0}{{\mathrm{c}}_{\mathrm{s}}-{\mathrm{c}}_0} $$
(6)

where \( \overline{\mathrm{c}} \)is the concentration of salts in water and cs and c0 are the concentration of salts in seawater and freshwater, respectively, in mg/l.

The advection–dispersion equation governing solute transport in porous media can be written as (Bear 1999):

$$ \nabla \cdot \left(\boldsymbol{D}\cdot \nabla \mathrm{c}\right)={\mathrm{W}}_{\mathrm{c}}\left(\frac{\partial \mathrm{c}}{\partial \mathrm{t}}+\boldsymbol{V}\cdot \nabla \mathrm{c}\right) $$
(7)

where D = n D h and Wc is a factor given by:

$$ {\mathrm{W}}_{\mathrm{c}}=\left[1-\frac{\uprho_0}{\uprho}{\upbeta}_{\mathrm{c}}^{\prime}\left(\frac{{\mathrm{c}}_0}{{\mathrm{c}}_{\mathrm{s}}\hbox{-} {\mathrm{c}}_0}+\mathrm{c}\right)\right]\mathrm{n} $$
(8)

The velocity tensor, V, for variable density flow can be expressed by Darcy’s law as:

$$ \boldsymbol{V}=-\frac{\uprho_0}{\uprho\ \mathrm{n}}\boldsymbol{K}\cdot \left(\nabla \mathrm{h}+{\upbeta}_{\mathrm{c}}^{\prime}\mathrm{c}\nabla \mathrm{z}\right) $$
(9)

and the tensor of hydrodynamic dispersion coefficient, D h , for an isotropic porous medium can be expressed in indicial notation (Bear 1979):

$$ {\left({\mathrm{D}}_{\mathrm{h}}\right)}_{\mathrm{i},\mathrm{j}}={\mathrm{D}}_{\mathrm{i},\mathrm{j}}^{\prime }+{\left({\mathrm{D}}_{\mathrm{m}}\right)}_{\mathrm{i},\mathrm{j}}={\upalpha}_{\mathrm{T}}\;\overline{\mathrm{V}}\ {\updelta}_{\mathrm{i},\mathrm{j}}+\left({\upalpha}_{\mathrm{L}}-{\upalpha}_{\mathrm{T}}\right)\frac{{\mathrm{V}}_{\mathrm{i}}\cdot {\mathrm{V}}_{\mathrm{j}}}{\overline{\mathrm{V}}}+{\mathrm{D}}_{\mathrm{m}}^{*}\;{\mathrm{T}}_{\mathrm{i},\mathrm{j}}\;{\updelta}_{\mathrm{i},\mathrm{j}} $$
(10)

where αL and αT are the longitudinal and the transverse dispersivities of the porous medium, respectively, \( \overline{\mathrm{V}} \)is the magnitude of average fluid velocity, D ∗m is the molecular diffusion coefficient, Τi,j is the tortuosity of the porous medium and δi,j is the Kronecker delta.

The fluid density variation is affected mainly by the substance concentration and the fluid temperature and less by fluid pressure (Holzbecher 1998). Under isothermal conditions, the equation of state that expresses the relationship between the density and the concentration is satisfactorily approximated by a linear relationship as:

$$ \uprho ={\uprho}_0\left(1+{\upbeta}_{\mathrm{c}}^{\prime}\mathrm{c}\right) $$
(11)

3 Numerical Approach

The governing Eqs. 1 and 7 constitute a nonlinear coupled set of partial differential equations that have to be solved for hydraulic head, h, and concentration, c, by numerical methods. The Galerkin finite element method was applied and the flow area was discretized by linear hexahedral elements, while the time was discretized by a finite difference scheme. Furthermore, the diagonalization of the mass matrix (also known as lumped mass matrix) was applied, according to which the nodal values of the dependant variable time derivative are calculated as mean derivative values of the whole flow area, which is a procedure to avoid convergence and stability problems (Frind 1982). Based on the above assumptions, Eq. 1 can be written in matrix form as (Doulgeris 2005):

$$ \left({\uptheta}_{\mathrm{h}}{\mathrm{A}}_{\mathrm{I},\mathrm{J}}+\frac{1}{\varDelta \mathrm{t}}{\mathrm{B}}_{\mathrm{I},\mathrm{J}}\right){\mathrm{h}}_{\mathrm{J}}^{\mathrm{k}+1}=\left(-\left(1-{\uptheta}_{\mathrm{h}}\right){\mathrm{A}}_{\mathrm{I},\mathrm{J}}+\frac{1}{\varDelta \mathrm{t}}{\mathrm{B}}_{\mathrm{I},\mathrm{J}}\right){\mathrm{h}}_{\mathrm{J}}^{\mathrm{k}}-{\uptheta}_{\mathrm{h}}{\Gamma}_{\mathrm{I}}^{\mathrm{k}+1}-\left(1-{\uptheta}_{\mathrm{h}}\right){\Gamma}_{\mathrm{I}}^{\mathrm{k}}+{\Delta}_{\mathrm{I}} $$
(12)

where I, J are the indexes of nodes, hJ are the head nodal values, Δt is the time step, k is the time index and θh (∈[0,1]) is the weighting factor for the finite difference scheme of time discretization. Matrices A, Β, Γ and Δ are given by:

$$ {\mathrm{A}}_{\mathrm{I},\mathrm{J}}={\displaystyle \sum_{\mathrm{e}}{\mathrm{A}}_{\mathrm{I},\mathrm{J}}^{\mathrm{e}}}={\displaystyle \sum_{\mathrm{e}}{\displaystyle \underset{{\mathrm{U}}^{\mathrm{e}}}{\int }{\mathrm{K}}_{\mathrm{i},\mathrm{j}}\frac{\partial {\mathrm{N}}_{\mathrm{I}}}{\partial {\mathrm{x}}_{\mathrm{i}}}\frac{\partial {\mathrm{N}}_{\mathrm{J}}}{\partial {\mathrm{x}}_{\mathrm{j}}}\mathrm{d}\mathrm{U}}} $$
(13a)
$$ {\mathrm{B}}_{\mathrm{I},\mathrm{J}}={\displaystyle \sum_{\mathrm{e}}{\mathrm{B}}_{\mathrm{I},\mathrm{J}}^{\mathrm{e}}}={\displaystyle \sum_{\mathrm{e}}{\displaystyle \underset{{\mathrm{U}}^{\mathrm{e}}}{\int }{\mathrm{S}}_{\mathrm{S}}{\mathrm{N}}_{\mathrm{I}}^{\prime}\mathrm{d}\mathrm{U}}} $$
(13b)
$$ {\Gamma}_{\mathrm{I}}={\displaystyle \sum_{\mathrm{e}}{\Gamma}_{\mathrm{I}}^{\mathrm{e}}}={\displaystyle \sum_{\mathrm{e}}{\displaystyle \underset{{\mathrm{U}}^{\mathrm{e}}}{\int }}}\left(\frac{\mathrm{n}{\upbeta}_{\mathrm{c}}^{\prime }}{\Delta \mathrm{t}}{\mathrm{N}}_{\mathrm{I}}{\mathrm{N}}_{\mathrm{J}}\left({\mathrm{c}}_{\mathrm{J}}^{\mathrm{k}+1}-{\mathrm{c}}_{\mathrm{J}}^{\mathrm{k}}\right)+{\upbeta}_{\mathrm{c}}^{\prime }{\mathrm{K}}_{\mathrm{i},\mathrm{j}}{\mathrm{N}}_{\mathrm{J}}{\mathrm{c}}_{\mathrm{J}}\frac{\partial {\mathrm{N}}_{\mathrm{I}}}{\partial {\mathrm{x}}_{\mathrm{i}}}{\upeta}_{\mathrm{j}}+{\mathrm{N}}_{\mathrm{I}}\frac{\uprho}{\uprho_0}{\mathrm{Q}}_{\mathrm{I}}\right)\mathrm{d}\mathrm{U} $$
(13c)
$$ {\Delta}_{\mathrm{I}}={\displaystyle \sum_{\mathrm{e}}{\Delta}_{\mathrm{I}}^{\mathrm{e}}}={\displaystyle \sum_{\mathrm{e}}{\displaystyle \underset{{\mathrm{R}}^{\mathrm{e}}}{\int }{\mathrm{N}}_{\mathrm{i}}{\mathrm{q}}_{\mathrm{n}}\mathrm{d}\mathrm{R}}} $$
(13d)

where N ′I  = Ν I when I = J and N ′I  = 0 when I ≠ J, N are the shape functions, Ue is the volume and Re is the boundary of element e, qn is the inflow discharge per surface unit perpendicular to boundary Re, cJ is the concentration, ηj = 1 in the direction of gravity and ηj = 0 in the horizontal directions.

Similarly, Eq. 7 can be written in matrix form as (Doulgeris 2005):

$$ \left({\uptheta}_{\mathrm{c}}{\mathrm{A}}_{\mathrm{I},\mathrm{J}}^{\prime }+\frac{1}{\varDelta \mathrm{t}}{\mathrm{B}}_{\mathrm{I},\mathrm{J}}^{\prime}\right){\mathrm{c}}_{\mathrm{J}}^{\mathrm{k}+1}=\left(-\left(1-{\uptheta}_{\mathrm{c}}\right){\mathrm{A}}_{\mathrm{I},\mathrm{J}}^{\prime }+\frac{1}{\varDelta \mathrm{t}}{\mathrm{B}}_{\mathrm{I},\mathrm{J}}^{\prime}\right){\mathrm{c}}_{\mathrm{J}}^{\mathrm{k}}+{\varGamma}_{\mathrm{I}}^{\prime } $$
(14)

where

$$ {\mathrm{A}}_{\mathrm{I},\mathrm{J}}^{\prime }={\displaystyle \sum_{\mathrm{e}}{\mathrm{A}}_{\mathrm{I},\mathrm{J}}^{\prime \operatorname{e}}}={\displaystyle \sum_{\mathrm{e}}{\displaystyle \underset{{\mathrm{U}}^{\mathrm{e}}}{\int}\left({\mathrm{D}}_{\mathrm{i},\mathrm{j}}\frac{\partial {\mathrm{N}}_{\mathrm{I}}}{\partial {\mathrm{x}}_{\mathrm{i}}}\frac{\partial {\mathrm{N}}_{\mathrm{J}}}{\partial {\mathrm{x}}_{\mathrm{j}}}+{\mathrm{WcV}}_{\mathrm{I}}{\mathrm{N}}_{\mathrm{I}}\frac{\partial {\mathrm{N}}_{\mathrm{J}}}{\partial {\mathrm{x}}_{\mathrm{i}}}\right)\mathrm{d}\mathrm{U}}} $$
(15a)
$$ {\mathrm{B}}_{\mathrm{I},\mathrm{J}}^{\prime }={\displaystyle \sum_{\mathrm{e}}{{\mathrm{B}}^{\prime}}_{\mathrm{I},\mathrm{J}}^{\mathrm{e}}}={\displaystyle \sum_{\mathrm{e}}{\displaystyle \underset{{\mathrm{U}}^{\mathrm{e}}}{\int }{\mathrm{W}}_{\mathrm{c}}{\mathrm{N}}_{\mathrm{I}}^{\prime}\mathrm{d}\mathrm{U}}} $$
(15b)
$$ {\varGamma}_{\mathrm{I}}^{\prime }={\displaystyle \sum_{\mathrm{e}}{\varGamma}_{\mathrm{I}}^{\prime \mathrm{e}}}={\displaystyle \sum_{\mathrm{e}}\Big[{\displaystyle \underset{{\mathrm{R}}^{\mathrm{e}}}{\int }{\mathrm{N}}_{\mathrm{i}}\left({\mathrm{D}}_{\mathrm{i},\mathrm{j}}\frac{\partial \mathrm{c}}{\partial {\mathrm{x}}_{\mathrm{j}}}\right){n}_i\mathrm{d}\mathrm{R}}} $$
(15c)

The values of θh and θc were taken equal to unit, i.e. a fully implicit finite difference scheme of time discretization was used, which resulted in a quick convergence of the solution.

The application of the finite element method to the velocity Eq. 9 leads to:

$$ {\mathrm{A}}_{\mathrm{I},\mathrm{J}}^{\prime \prime }{\mathrm{V}}_{\mathrm{J}}^{\mathrm{k}+1}={\mathrm{B}}_{\mathrm{I},\mathrm{J}}^{\prime \prime } $$
(16)

where

$$ {\mathrm{A}}_{\mathrm{I},\mathrm{J}}^{\prime \prime }={\displaystyle \sum_{\mathrm{e}}{\mathrm{A}}_{\mathrm{I},\mathrm{J}}^{\prime \prime \mathrm{e}}}={\displaystyle \sum_{\mathrm{e}}{\displaystyle \underset{{\mathrm{U}}^{\mathrm{e}}}{\int }{\mathrm{N}}_{\mathrm{I}}{\mathrm{N}}_{\mathrm{J}}\mathrm{d}\mathrm{U}}} $$
(17a)
$$ {\mathrm{B}}_{\mathrm{I},\mathrm{J}}^{\prime \prime }={\displaystyle \sum_{\mathrm{e}}{\mathrm{B}}_{\mathrm{I},\mathrm{J}}^{\prime \prime \mathrm{e}}}={\displaystyle \sum_{\mathrm{e}}{\displaystyle \underset{{\mathrm{U}}^{\mathrm{e}}}{\int }-\frac{\uprho_0}{\uprho n}{\mathrm{N}}_{\mathrm{J}}\left({\mathrm{K}}_{\mathrm{i},\mathrm{j}}\left(\frac{\partial {\mathrm{N}}_{\mathrm{J}}}{\partial {\mathrm{x}}_{\mathrm{j}}}{\mathrm{h}}_{\mathrm{J}}^{\mathrm{k}+1}+{\upbeta}_{\mathrm{c}}^{\prime }{\mathrm{N}}_{\mathrm{J}}{\mathrm{c}}_{\mathrm{J}}^{\mathrm{k}+1}{\upeta}_{\mathrm{j}}\right)\right)}}\mathrm{d}\mathrm{U} $$
(17b)

The integrals of terms of Eqs. 12, 14 and 16 were numerically calculated using the Gauss-Legendre method. It should be noted that matrices A and Α΄΄ are symmetric and the matrix form solution of (12) and (16) was based on the Cholesky decomposition, while Α΄ is a non-symmetric matrix and for the solution of (14) an LU decomposition was used. The non-linearity of (14), due to the velocity tensor V and the Wc terms, was overcome by an iterative process and the convergence was speeded up by the prediction of concentration in the next time step by using a linear relationship such as:

$$ {\mathrm{c}}^{\mathrm{k}+1}={\mathrm{c}}^{\mathrm{k}}+\left({\mathrm{c}}^{\mathrm{k}}\hbox{-} {\mathrm{c}}^{\mathrm{k}\hbox{-} 1}\right)\frac{\Delta {\mathrm{t}}^{\mathrm{k}}}{\Delta {\mathrm{t}}^{\mathrm{k}\hbox{-} 1}} $$
(18)

The iterative process was based on the method of successive substitutions to solve the system of flow, velocity and transport equations for h, V and c. Specifically, we follow a usual solution procedure, which is to decouple the problem by first solving the flow equation, then calculating the velocity field, and finally solving the transport equation. This three-step sequence is repeated until convergence is achieved. This approach, known as the Picard scheme, has been successfully employed in cases of saturated/unsaturated flow problems, variable density flow problems and multiphase flow problems. A detailed discussion of the advantages and restrictions of this procedure in non-linear problems of flow and transport equations could be found in Putti and Paniconi (1995).

4 Verification of the Model

The model verified successfully against other numerical solutions in two common 2D variable-density flow problems, the Henry seawater intrusion problem and the Elder salt convection problem, and against experimental results of the 3D saltpool (case 1) problem.

The Henry problem consists of a homogeneous isotropic aquifer that is recharged on one side (e.g. right) by a freshwater influx and is exposed on the other side to a body of seawater. The transient simulation of the system results to a steady-state equilibrium and takes the form of a seawater wedge intruding in the lower part of the aquifer. The present solution is consistent with existing solutions (Frind 1982, Croucher and O’Sullivan 1995) in terms of the shape of the interface. More specifically, it creates a slightly advanced seawater wedge at the bottom of the aquifer compared to Frind’s solution, and is very close to the solution of Croucher and O’Sullivan (1995), except for the upper portion of the seaward side which is not considered a freshwater outflow boundary in their solution. Croucher and O’Sullivan (1995) used a very dense network of 33,153 nodes while Frind (1982) and the present solution used element size of 10 × 10 m (231 nodes).

The Elder problem consists of a vertical section of a homogeneous and isotropic porous medium. A source with constant unit concentration is applied in a centre portion along the top boundary while zero concentration is held at the bottom boundary. The solute enters the pure water initially by diffusion, the fluid density increases and a circulation process begins induced by density differences. The present solution is compared with the solution of Kolditz et al. (1998). A low density mesh consisting of 44 elements in horizontal and 25 elements in vertical direction is used in the present solution and obtained similar results with Kolditz et al. (1998) solution for a denser mesh (132 × 75 elements). Using our model and denser meshes (128 × 32 and 256 × 64), the concentration pattern is analogue to that of the solution of 44 × 25 elements. Similar results to our solution have been presented by Ackerer et al. (1999) using a sparse mesh and the mixed hybrid finite element method.

The saltpool experimental set-up (Oswald and Kinzelbach 2004) consists of a cubic container filled with a homogeneous porous medium. Initially, a horizontal saltwater layer exists below freshwater. The cube is recharged with freshwater through a hole on a top corner and brackish water discharges through an outflow hole located on the diagonal top corner. In order to fit the model results with the experimental data, we have modified some of the parameters (hydraulic conductivity, porosity and traverse dispersivity) following Johannsen et al. (2002). When the flow area was discretized with 7,200 hexahedra elements (8,619 nodes), the simulated breakthrough curve at the outflow hole is compared satisfactorily with the experimental data. In lower density meshes, the breakthrough curve is overestimated by the present model.

5 Applications

5.1 Problem Description

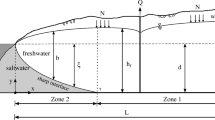
The three-dimensional variable density flow model is applied to a hypothetical confined coastal aquifer, of rather irregular shape, shown in Fig. 1. The coastline is in contact with the aquifer at the AB boundary and freshwater inflows into the aquifer through the DE boundary. The aquifer bears two zones of hydraulic conductivity and water is pumped via two wells, W1 and W2.

Fig. 1
figure 1

Horizontal section of the aquifer

Full size image

The aquifer in Fig. 1 has been studied by Petala (2004) and Katsifarakis and Petala (2006) by using an optimization model in conjunction with a 2D flow model. The optimization code is based on genetic algorithms while the flow is simulated as two-dimensional steady-state flow of a constant density fluid applying the boundary element method. Their objective was to find the maximum groundwater extraction rate without seawater entering the pumping wells, i.e. the salts concentration in pumped water should be 0 % of seawater. Seawater intrusion in pumping wells is checked by the fluid velocity direction at the coastline, assuming that, under steady-state conditions, if seawater inflows into the aquifer it will ultimately reach the wells. The outcome of their work was that the maximum pumping rates are Q1 = 31 l/s and Q2 = 38 l/s in W1 and W2, respectively, and increasing either Q1 or Q2 by 1 l/s leads to seawater intrusion into the wells.

The application of the three-dimensional variable density flow model requires to adjust some of the model parameters of the two-dimensional model. For example, the aquifer transmissivity should be replaced with the aquifer thickness and the hydraulic conductivity. Also, the density of seawater and freshwater should be taken into account, as well as the solute transport equation parameters. The main parameters of the variable density flow model used in this study are given in Table 1.

Table 1 Parameters of the three-dimensional variable density flow model
Full size table

Boundary conditions concern both the flow equation and the transport equation. The freshwater inflow into the aquifer exists through the vertical surface on DE boundary, in which a constant value of hydraulic head (h = 50 m) and a constant concentration of freshwater (c = 0) are assumed. The upper and bottom boundary of the aquifer are considered impermeable, as well as the BCD and EFA boundaries. Boundary condition in coastline (AB) requires considering a typical vertical section of the aquifer, like BB΄DD΄, as shown in Fig. 2. Seawater level is on the same level with the upper boundary of the aquifer and is assumed to be the reference datum. Reference hydraulic head is h = 0 m in the upper point of the BB΄ boundary and is increasing as moving towards to the bottom of the aquifer due to density difference and according to the relationship h = HSEA + β ′c (HSEA ‐ z), where HSEA is the sea level. Concentration of salts at the BB΄ boundary is assumed to be that of seawater (c = 1), apart from the upper portion of the boundary which is considered as freshwater outflow boundary and a second-type boundary condition is applied, namely ∂c/∂n = 0, where n denotes the normal to the boundary. The freshwater outflow boundary is not known a priori and it may vary with time, but it can be estimated based on the velocity distribution on the boundary (Doulgeris and Zissis 2005). If the velocity direction is towards the interior of the aquifer then at these nodes the concentration is c = 1 and the remaining portion of the BB΄ boundary is the freshwater outflow boundary. Pumping of wells W1 and W2 was applied to the whole aquifer thickness and concentration of salts in pumped water is taken as the average concentration at the computational nodes of the well.

Fig. 2
figure 2

Vertical section of the aquifer

Full size image

A non-uniform mesh consists of 23,680 elements used for the discretization of the flow area. Most of the elements are in the 1st aquifer zone, i.e. close to the coastline and in the vicinity of wells, where the higher gradients of hydraulic head and concentration are expected. The size of the elements in the x-direction varies from 25 to 29 m, in the y-direction from 19 to 65 m and is 4 m in the z- direction.

The transient flow solution reaches an equilibrium state which is defined here by a variation of the dependent variables of less than 10−3 in a time step. The time step varies, depending on the convergence speed of the solution, from 10 days at the start of the simulation to 120 days at later times and close to equilibrium.

5.2 Results and Discussion

5.2.1 Effect of Dispersion Coefficient and Pumping Rate

Table 2 presents the relative concentration of salts in pumped water assuming that the pumping rates are those suggested by the two-dimensional constant density flow model, namely Q1 = 31 l/s and Q2 = 38 l/s. Three values of hydrodynamic dispersivity were used, considering the same value for longitudinal and transverse dispersivity, i.e. αL = αT. Results show that in all cases salts intrude into the wells; concentration in water of W2 is close to 1 % of seawater and is 1.5 to 3.5 times higher compared to the concentration of W1. Also, it is worth a mention that the increase of dispersivity results in the increase of salts concentration in W1 and the decrease in W2.

Table 2 Relative concentration of salts in pumped water for different values of dispersivity (pumping discharge: Q1 = 31 l/s and Q2 = 38 l/s)
Full size table

Distribution of salts in the cross-section area of W1 is shown in Fig. 3. If the value of dispersivity increases the slope of isoconcentration lines decreases, and more specifically, for the higher dispersivity there are small changes in concentration with depth, while for the lower dispersivity a well-shaped wedge of seawater exists. Figure 4 shows the distribution of salts at the bottom of the aquifer. Seawater intrusion is mainly advanced in the area of wells, and the distance of the impermeable boundary from the wells affects the distribution of salts and subsequently the salts concentration in pumped water.

Fig. 3
figure 3

Family of isoconcentration lines in the cross-section area of well W1 at equilibrium

Full size image
Fig. 4
figure 4

Family of isoconcentration at the bottom of the aquifer at equilibrium

Full size image

Table 3 presents the relative concentration of salts in pumped water for different sets of pumping discharges and a dispersivity value equal to 2.5 m. Salts concentration are approximately 10 times higher in W1 and 5 times higher in W2 for an increase of pumping discharge by 10 %.

Table 3 Relative concentration of salts in pumped water for various pumping discharges (dispersivity: αL = αT = 2.5 m)
Full size table

5.2.2 Salinity of Freshwater Inflow and Aquifer Thickness Impact

It is hard to evaluate the relative concentration of salts to the suitability of water for the various uses, such as water supply, irrigation etc., and in order to do it, the salinity of seawater and freshwater needs to be known, where the salinity is expressed as the concentration of total dissolved solids (TDS) in mg/l. Although seawater does not contain the same amount of salts everywhere and values from 8,000 mg/l to 40,000 mg/l have been recorded, in most of the cases varies from 33,000 to 37,000 mg/l. Therefore, we consider here cs = 35,000 mg/l as a representative value for seawater salinity. For freshwater salinity we consider four cases. In the first case, characterised as the “ideal“, freshwater does not contain salts at all, i.e. c0 = 0 mg/l, while in the other cases we assume that freshwater contains a small quantity of salts, namely 100, 200 or 300 mg/l. Although freshwater could be influenced by many environmental and anthropogenic factors (e.g. geology of the area, disposal of wastes, irrigation) and higher values of salinity may exist, we consider freshwater of low salinity to show that even in this case degradation of pumped water could not be avoided.

Table 4 presents the salinity of pumped water using Eq. 6 and data of Table 3. In the ideal case, water salinity in wells is at low level and below the threshold value of drinking water (~500 mg/l) except for the case of higher pumping discharges. For the other cases, where salts exist in freshwater, we notice a considerable increase in the salinity of pumped water. For example, when freshwater salinity is equal to 300 mg/l, a common value for bottled water, the concentration of salts in pumped water always exceeds the threshold value of drinking water, except for the lower pumping discharge of W1. However, even for the higher salinity values given in Table 4, the water could be used to irrigate some salt tolerant crops.

Table 4 Concentration of salts, mg/l, in pumped water for various freshwater salt concentrations
Full size table

From the above analysis of results given in Table 4, it is clear that the maximum (optimum) pumping discharges are directly dependent on the concentration of salts in freshwater and the water salinity threshold of water use. Assuming that the salinity in water should not exceed 500 mg/l, then in the “ideal” case (c0 = 0 mg/l), the maximum pumping discharges could be higher than those suggested by the two-dimensional constant density flow model (31 and 38 l/s), even higher than 32 and 39 l/s. If salts exist in freshwater, e.g. 200 mg/l, water in W1 could be used for water supply even if pumping discharge is 32 l/s, but the discharge of 39 l/s in W2 should be used for another use.

In results presented up to now, it was considered that the aquifer thickness was equal to 40 m. We examined two other cases, to increase and decrease the aquifer thickness by 20 %, while keeping in any case the same value of aquifer transmissivity in order to be comparable with the two dimensional solution. The concentration of salts in pumped water is given in Table 5; for a greater aquifer thickness, the concentration of salts increased considerably. This could be explained by the head boundary condition in the coastline, h = HSEA + β ′c (HSEA ‐ z), where due to the density difference a higher value of head at the bottom of the aquifer is calculated for a greater aquifer thickness. Therefore, as the aquifer thickness is decreased, the solution of 3D variable density flow model approaches the solution of 2D constant density flow model.

Table 5 Concentration of salts, mg/l, in pumped water for different aquifer thickness (pumping discharge: Q1 = 31 l/s and Q2 = 38 l/s)
Full size table

5.2.3 Rearrange Pumping Discharge for Minimizing the Total Withdraw Salinity

As mentioned before, the two-dimensional constant density flow model suggested that pumping discharge should be Q1 = 31 l/s and Q2 = 38 l/s, in order to avoid seawater intrusion into the wells. Assuming that the total discharge remains unchanged, we check different sets of pumping discharge and calculate the total concentration of salts in pumped water from the relationship (c1Q1 + c2Q2)/(Q1 + Q2); results are given in Table 6. Bearing in mind that in any case the total pumping discharge is 69 l/s, we assume that the best solution is to pump Q1 = 32 l/s and Q2 = 37 l/s, at which the total concentration of salts in pumped water is less, for each one of the freshwater salt concentration examined.

Table 6 Total concentration of salts, mg/l, in pumped water for various pumping discharges
Full size table

6 Conclusions

Coastal aquifers are subject to seawater intrusion and numerical simulation is a useful tool for groundwater exploitation and management. The optimization of pumping is usually achieved by using a simple groundwater flow model due to the high computational demand of the optimization procedure. However, adopting a simplified approach to groundwater flow simulation although it is useful is not adequate. The three-dimensional variable density flow model developed in this paper applied to review such an optimization solution based on a steady state two-dimensional flow model.

The application of the variable density flow model allows to approach the physical phenomenon of seawater intrusion in more detail compared to a simple two-dimensional constant density flow model, and furthermore to assess the concentration of salts in pumped water and consequently to assign the use of water in each well. Even for an optimum solution (maximum pumping rate) estimated by a simple model, it was found by the application of the 3D variable density model that, for the local conditions of the hypothetical case study, the water quality in pumped water degraded due to seawater intrusion into the aquifer. Additionally, the variable density flow model is capable of estimating the distribution of salinity in aquifer.

The salts concentration in pumped water strongly depends on the salts concentration in seawater and freshwater. Applying the variable density flow model we showed that, for the aquifer of the hypothetical case study, if the concentration of salts in freshwater increases the concentration of salts in pumped water also increases significantly. Thus, for a given value of salts concentration in freshwater the pumped water could be used for water supply, whilst for a greater value of salts concentration in freshwater the pumped water could be allocated for other uses.

In a simple two-dimensional model, the aquifer transmissivity is a model parameter, while the corresponding parameters for the three-dimensional model are hydraulic conductivity and aquifer thickness. The application of the three-dimensional model shows that for a greater aquifer thickness, while the aquifer transmissivity is considered the same, the concentration of salts in pumped water increased.

Two-dimensional steady-state ground water flow models are commonly used in optimization of pumping in coastal aquifers, due to reasonable processing power they require in the whole procedure, but they may be insufficient to simulate seawater intrusion process. Nevertheless, the use of simple optimization models is particularly useful because in conjunction with a 3D variable density model can lead to safer solutions.