1 Introduction

Multi-Gbps LDPC decoding has become an essential requirement for contemporary digital communication standards, such as the 5G New Radio [1, 2], IEEE 802.11n/ac/ax (WiFi) [3], and IEEE 802.11ad (WiGig) [4], among others. The design of high-throughput LDPC decoders is typically constrained by strict requirements on power consumption, operating clock frequency, physical area, and memory bandwidth. Power consumption of an LDPC decoder increases with throughput, especially if delivered at high clock speeds. Parallel decoders with many cores are bulky and require high memory bandwidth in order to sustain high throughput, which again leads to excessive power consumption. Hence, relying purely on high clock frequencies or explicit parallel replication of decoder cores to boost throughput, are rarely viable approaches when designing communication modules for modern industry-grade system-on-chips (SoCs).

It is well known that hardware architectures operating at lower clock speeds consume less power, and therefore, are highly desirable for embedded SoC applications. Such SoCs typically operate in a clock speed range of 200-300 MHz, in order to meet the power budget and to close timing across all process, voltage, and temperature (PVT) corners in modern CMOS process technologies [5]. With such constraints on clock speed, improving the energy efficiency of multi-Gbps LDPC decoders for embedded applications becomes an even more challenging task.

An alternative and complementary approach to pure architectural or circuit-level optimizations that a designer can pursue is algorithmic in nature, targeting the iterative nature of the LDPC decoding schedule itself. Fast-converging LDPC decoding simultaneously enables low-power and high-throughput VLSI implementation by reducing the number of decoding iterations required for convergence. The reduction in the number of iterations decreases processing latency, leading to a higher decoder throughput at lower clock speed. Fast-convergence also minimizes power consumption because of the reduction in the number of computations performed.

The LDPC decoding schedule, as originally proposed by Gallager in [6], and later rediscovered in [7], is a flooding schedule that operates by passing messages iteratively back and forth between nodes on a bipartite graph. In each iteration, only nodes in the same partition are allowed to fire and pass messages to their neighboring nodes in the other partition. Variations to this flooding or standard message-passing (SMP) schedule later emerged in the literature. The most notable of which are the serial LDPC decoding schedules [8, 9] that are known to converge in half the number of decoding iterations compared with the flooding schedule.

Based on whether the row order or the column order of the parity-check matrix is followed when scheduling node operations, serial decoding is further divided into two types: row message-passing (RMP) [8] and column message-passing (CMP) [9]. In the RMP schedule, decoding starts from a check node, and message computations are immediately sent back to their neighboring variable nodes. This process is repeated serially for all the check nodes. A turbo-decoding schedule for LDPC decoding, based on RMP, was first proposed in [8, 10], and further analyzed in [11]. On the other hand, in CMP, decoding starts in reverse order compared to RMP, following the order of variable nodes; messages at check nodes that are connected to a particular variable node are processed and immediately exchanged with that variable node [9, 12]. Serial decoders, in general, provide faster convergence without incurring any significant complexity overhead, i.e., the number of computations stays almost the same in one iteration of RMP and CMP as that in SMP. Memory efficiency is an additional advantage of serial decoders; they require significantly lower memory than SMP [8, 10].

To further accelerate the convergence rate of serial decoding schedules, several approaches that determine the best processing order of variable nodes or check nodes for serial decoders have emerged in the literature. A maximum mutual-information-increase based schedule is presented in [13]. The schedule predicts the next message to be updated based on the mutual-information increase, which is used as a metric to improve convergence speed. Similarly, in [14], a column-weight-based fixed schedule that processes variable nodes by following the high-to-low column-weight order for irregular LDPC codes is investigated. Informed fixed scheduling (IFS), which finds the best order that ensures the maximum number of updated messages is utilized within a single iteration, is introduced in [15]. These schedules, however, attain marginal improvement in convergence speed over the original serial decoding schedules.

The informed dynamic scheduling (IDS) strategy is introduced in [16]. The scheme employs residual belief propagation (RBP), and updates only those nodes that correspond to the maximum residuals of the check-nodes messages. Although RBP achieves faster convergence than existing decoding schedules, its decoding performance after convergence is even worse than the flooding or serial schedules [16]. Node-wise RBP (NWRBP) is also introduced in [16] to address the “greediness” of the RBP. Motivated by the IDS approach, several techniques with alternative message selecting and updating methods, have been presented in the literature. Examples include the silent-variable-node-free (SVNF) scheduling [17], the dynamic-silent-variable-node-free (D-SVNF) [18], the tabu search-based dynamic scheduling (TSDS) [19], and the two-reliability-metrics based RBP (TRM-TVRBP) scheduling [20]. These fast-decoding schedules accelerate the convergence rate of LDPC decoding, but the added cost of computing the residuals and the required search operations is far from trivial in VLSI implementations. This high computational cost explains the reason why no VLSI implementations of theses schedules, to the best of authors’ knowledge, have been reported in the literature so far.

The interlaced column-row message-passing (ICRMP) schedule also speeds up the convergence of an LDPC decoder by a factor of two, in comparison with other serial decoding schedules [21]. However, the number of clock cycles it takes ICRMP to complete one decoding iteration is proportional to the number of ones in the associated sparse parity-check matrix (SPCM). This relatively high number of clock cycles limits the ICRMP in meeting the high-throughput and low-latency requirements of contemporary LDPC decoding.

Motivated by the above shortcomings of existing decoding schedules, we propose in this work a fast-converging LDPC decoding schedule with hardware-friendly features that are amenable for efficient implementation. The target is to attain multi-Gbps LDPC decoding throughput with improved energy-efficiency, while operating at a maximum clock frequency of 200 MHz. To this end, the contributions of this work are the following:

  • A fast-converging LDPC decoding schedule, dubbed fast column message-passing (FCMP), is proposed and investigated. The schedule converges in half the number of iterations than the RMP and CMP serial decoding schedules. The computational complexity of the FCMP schedule is significantly lower than other RBP-based fast-decoding schedules. It can also be implemented with similar processing elements used in existing LDPC decoder architectures, without the need for complex logic to support any search criteria used in other fast-converging schemes in the literature.

  • Complexity and convergence analyses of the proposed FCMP schedule are carried out and used to compare with other existing LDPC decoding schedules. The convergence rate of the proposed schedule is verified using two analytical methods: by plotting EXIT charts, and by using density-evolution by Gaussian approximation tool.

  • An FCMP-based LDPC decoder architecture, implementing the IEEE 802.11ad (WiGig) LDPC codes, is proposed. The decoder achieves a decoding performance comparable to state-of-the-art architectures, using a maximum number of iterations of only 2. This allows the architecture to achieve a multi-Gbps throughput with very high-energy efficiency.

  • The proposed FCMP based decoder architecture is synthesized using the TSMC 40 nm and the TSMC 65 nm CMOS technology nodes. The synthesized architecture achieves a throughput of 8.4 Gbps while operating at a clock frequency of 200 MHz. The architecture synthesized using the 40 nm technology node consumes 72 mW of power. This results in an energy-efficiency of 8.6 pJ/bit, which is the highest energy-efficiency of an IEEE 802.11ad LDPC decoder reported in the literature.

The rest of the paper is organized as follows. Background material related to exiting decoding schedules, check-node computations, and density evolution by Gaussian approximation, is presented in Section 2. The proposed schedule is introduced in Section 3. Complexity analysis is carried out in Section 4, while convergence analysis is presented in Section 5. The proposed architecture for the FCMP schedule is presented and elaborated in Section 6. Finally, simulation and VLSI synthesis results are reported in Section 7. Section 8 concludes the paper.

2 Background and Related Work

This section briefly summarizes RMP and CMP LDPC decoding, hardware implementation of LDPC codes, and the method of density-evolution to evaluate the convergence behavior of LDPC decoding schedules.

2.1 Row Message-Passing (RMP) Schedule

Consider an LDPC code, and let G(V ∪ C,E) denote its associated bipartite graph G with vertex set V, as variable nodes, vertex set C, as check nodes, and an edge set E, connecting the vertices. Let Pv be the log-likelihood ratio (LLR) of variable-node v, Lcv represent the message sent from check-node c to variable-node v, and Qvc be the message sent from variable-node v to check-node c. The RMP schedule, updates the variable nodes and check nodes as follows:

  • Initialize all variable and check node messages as

    $$ P_{v}^{(0)} = \mathsf{LLR}[v],\quad \forall v \in \mathsf{G}. $$
    (1)

  • Update all check-node messages at iteration k ≥ 1 as

    $$ Q_{vc}^{(k)} = P_{v}^{(k)}-L_{cv}^{(k-1)} $$
    (2)
    $$ L_{cv}^{(k)} = {{{\varPsi}}}^{-1} \Big({\sum}_{v^{\prime}\in\mathsf{R}[c]\backslash{v}}{{{\varPsi}}}\left( \left|{Q_{v^{\prime}c}^{(k)}}\right| \right)\Big),\quad \forall c \in \mathsf{G}, $$
    (3)

    where \({{{\varPsi }}}(x)\triangleq 0.5 \log (\tanh (x/2))={{{\varPsi }}}^{-1}(x)\) and R[c] denotes the set of dc variable nodes connected to check-node c. Here \(L_{cv}^{(0)}=0\), if none of the check-nodes is updated.

    • Update all variable nodes, connected to c, as

      $$ \begin{array}{@{}rcl@{}} R_{vc}^{(k)} &=& P_{v}^{(k)}-L_{cv}^{(k-1)}, \end{array} $$
      (4)
      $$ \begin{array}{@{}rcl@{}} P_{v}^{(k)} &=& R_{vc}^{(k)} +L_{cv}^{(k)}, \quad \forall v \in \mathsf{R}[c]. \end{array} $$
      (5)

  • Decision making in the final iteration is made by hard decisions based on the signs of the LLR values in Eq. 5.

Theoretically, Eqs. 2 and 4 should give identical results. However, for pipelined implementations, the two equations become different because the messages involved in the update process get delayed by the pipeline depth.

2.2 Column Message-Passing (CMP) Schedule

After the initialization step in Eq. 1, CMP follows the order of variable nodes. The check nodes in the neighboring set of a variable node send their updated messages to the variable node after updating their messages using Eqs. 2 and 3. This process of evaluating each variable node by collecting updated messages from its neighboring set of check nodes, is repeated for all variable nodes in the bipartite graph G in one iteration. Decision making in the final iteration is performed by evaluating (5), as in RMP. CMP is also named as shuffled iterative decoding in the literature [9].

2.3 Check-Node Computations

Several low-complexity variants of Eq. 3 have emerged in the literature because the hardware implementation of Eq. 3 is not straightforward [22]. The most widely used is the offset min-sum approximation, which is given as [23,24,25]:

$$ \begin{array}{@{}rcl@{}} L_{cv}^{(k)} &=& \max\left\{ \left( \min_{v^{\prime} \in \mathsf{R}[c] \backslash{v}} |Q_{v^{\prime}c}^{(k-1)}|\right) - \beta, 0 \right\}\\&& {\prod}_{v^{\prime} \in \mathsf{R}[c] \backslash{v}}\text{sign}(Q_{v^{\prime}c}^{(k-1)}) \end{array} $$
(6)

where β is a correction factor determined empirically. If \(\min \limits _{1}\), \(\min \limits _{2}\) are the magnitudes of the first and second minima among the inputs of the check node, and if vm1 is the index of the first minimum magnitude, then Eq. 6 can equivalently be written as:

$$ L_{cv}^{(k)} = \begin{cases} \max(\min_{2} - \beta,0) {\prod}_{v^{\prime} \in \mathsf{R}[c] \backslash{v}}\text{sign}(Q_{v^{\prime}c}^{(k-1)}) &{v=v_{m1}}, \\ \max(\min_{1} - \beta,0) {\prod}_{v^{\prime} \in \mathsf{R}[c] \backslash{v}} \text{sign}(Q_{v^{\prime}c}^{(k-1)}) &{\text{otherwise}}. \end{cases} $$
(7)

Here the sign of each input, \({\text {sign}}(Q_{v^{\prime }c})\), is a single bit, so their product is accomplished by just taking the Exclusive-OR (XOR) of all the bits.

2.4 Hardware Implementation of Serial LDPC Decoders

Quasi-Cyclic (QC-LDPC) LDPC codes [26] have been adopted for present and future communication standards. (QC-LDPC) LDPC codes are defined by a base-SPCM and an expansion factor. Several RMP-based QC-LDPC decoder architectures have emerged in the literature [8, 23, 25, 27], and a block diagram of a single-frame based QC-LDPC decoder architecture is shown in Figure 1. The LLRMemory stores LLR values of Eq. 5, while the CNMem stores Lcv messages of Eq. 3 in Figure 1. The SPCM stores the base SPCM, while the CheckNodeUnits implement (6). The BarrelShifters and Rev.BarrelShifters, in the CN2VN and VN2CN blocks, implement rotations and their reverse operations, required for QC-LDPC codes. The number of instantiated Adder, Subtractor, and CheckNodeUnit blocks is equal to the expansion factor of a QC-LDPC code. This exploits the structure of QC-LDPC codes in order to support the throughput demands of multi-Gbps LDPC decoding.

Figure 1
figure 1

Block diagram of a single-frame RMP based QC-LDPC decoder architecture.

Full size image

2.5 Density Evolution by Gaussian Approximation

The method of density evolution by Gaussian approximation is a mathematical tool used to investigate the behavior of iterative message-passing decoding algorithms. It essentially approximates the probability densities of the exchanged messages as Gaussian. Density evolution with Gaussian approximation can be explained as follows. Assume that variable-node messages and check-node messages are modeled as Gaussian random variables, with means mv and mc, respectively. The way these means get updated with every iteration k, will be tracked using the variables \( m_{v}^{(k)}\) and \(m_{c}^{(k)}\). By considering the flooding schedule for regular LDPC codes, these means get updated at iteration k ≥ 1 according to the following rules [28]:

$$ \begin{array}{@{}rcl@{}} m_{v}^{(k)} &=& m_{co} + (d_{v}-1)m_{c}^{(k-1)} \end{array} $$
(8)
$$ \begin{array}{@{}rcl@{}} m_{c}^{(k)} &=& \phi^{-1}\!\bigl(1 - \bigl[1 - \phi\bigl(m_{co} + (d_{v} - 1)m_{c}^{(k-1)}\bigr)\bigr]^{d_{c}-1}\bigr), \end{array} $$
(9)

where mco is the initial mean, \(m_{c}^{(0)} = 0\), and

$$ \phi(x) = \begin{cases} 1-\tfrac{1}{\sqrt{4\pi x}}{\int}_{\mathbb{R}} \tanh{\left( \tfrac{u}{2}\right)} e^{-\frac{(u-x)^{2}}{4x}} du &{\text{if}~ x>0}, \\ 1 &{\text{if}~ x=0}. \end{cases} $$

For small x, say x < 10, the following approximation of ϕ(x) is typically used [28]:

$$ \phi(x) \approx e^{-0.4527x^{0.86}+0.0218},~ 0<x<10. $$
(10)

3 Proposed FCMP Schedule

For the purpose of hardware implementation of LDPC decoders, check-node processing is significantly simplified using the “min-sum” approximation [22]. In the min-sum approximation, each check node identifies the first and second minimum magnitudes among its inputs, and the check- node outputs are then generated by combining these minima with their corresponding signs, which are determined separately. The min-sum approximation simplifies the check-node processing for RMP, where each row of the SPCM directly corresponds to a check node. For CMP, however, complexity reduction is not significant. Several techniques have emerged in the literature to leverage the benefits of the min-sum based check-node processing for the CMP, but the benefits come at the expense of potential degradation in decoding performance [29,30,31,32].

In the CMP schedule, each check node in the neighboring set of a given variable node determines two minima, and the message propagated by each check node to that variable node is determined using these minima. The same minima, however, can be used to determine messages for the other variable nodes, which are in the neighboring sets of the check nodes being processed. The proposed FCMP schedule relies on the messages that could be generated for other variable nodes using the already determined minima, instead of applying existing complexity reduction techniques [30, 31] in the CMP schedule. This potential utilization of the check-node outputs creates an advantage in terms of convergence speed, in contrast to the loss in decoding performance incurred by applying the complexity reduction techniques.

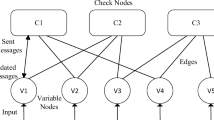
Motivated by the above observation, the FCMP schedule is proposed in this paper. The FCMP schedule propagates messages to all neighboring variable nodes of a check node, instead of just to the variable node, for which the check node is processed, as is the case in CMP. Referring to Figure 2, the process starts by considering the first variable-node v1 and updating it using the messages from check-nodes c1 and c3; processing up to this point is similar to CMP. Next comes the part which makes FCMP different than the CMP, and essentially amplifies its convergence speed. Check-nodes c1 and c3 also propagate the messages to their neighboring variable nodes, other than v1, and these variable nodes also get updated. This additional processing has minimal impact on the overall complexity of the CMP schedule, as shown by the complexity analysis in Section 4. The processing order of the proposed FCMP schedule is depicted in Figure 2 for the first variable node. In Figure 2, the solid lines correspond to edges that take part in the update process. Variables vij represents the edge connecting the i th check node to its j th neighboring variable node. For example, v13 is the connection of the first check node to its third neighboring variable node.

Figure 2
figure 2

The proposed FCMP schedule for variable-node v1. The check-nodes c1 and c3, connected to v1, not only update v1 but also their complete neighboring sets of variable nodes.

Full size image

The process of propagating newly generated messages at the check nodes to all connected variable nodes completes a sub-cycle (or sub-iteration) of information exchange that started from the first variable node and concluded at some set of variable nodes, depending on the structure of the SPCM. A similar sub-cycle is repeated for each other variable node. Processing all variable nodes concludes one iteration. Hence, the number of sub-cycles equals the number of variable nodes of the associated SPCM.

In summary, one sub-iteration of the proposed FCMP schedule, for a particular variable node, processes all check nodes connected to that variable node and propagates the check-node messages to their neighboring-sets of variable nodes in a parallel fashion. The number of sub-iterations equals the number of variable nodes constitutes one iteration of FCMP. One iteration of the FCMP requires dc − 1 times more XOR operations and dc − 1 times more addition operations, compared to the CMP, with dc being the check-node degree.

The proposed FCMP schedule is, thus, an optimization of the CMP schedule that improves the decoding throughput of a CMP-based decoder by accelerating its convergence speed, rather than being solely a complexity reduction technique applied to simplify the CMP hardware implementation [30, 31]. The FCMP schedule retains the standard min-sum approximation [33] for check-node processing, in order to avoid any loss in decoding performance incurred by other simpler approximations to check-node messages, and relies on modifying the CMP schedule to accelerate the convergence speed.

The pseudo-code of the proposed FCMP schedule is summarized in Algorithm 1. In the pseudo-code, \(d_{v_{j}}\) represents the degree of j th variable node, and ci denotes the i th neighboring check node to the variable-node vj. The parallel loop of FCMP, demarcated by a bounding box in the pseudo-code, reduces the critical path delay by processing the check nodes connected to a particular variable node in parallel.

figure a

4 Complexity Analysis

In this section, the computational complexities of the CMP and the proposed FCMP schedules are analyzed and compared with other LDPC decoding schedules. In what follows, we assume an irregular LDPC code whose bipartite graph includes Nv variable nodes, and Nc check nodes. We also assume that the average degree of variable nodes is dv, and that of check nodes is dc. The total number of edges in the graph is proportional to E = Nv × dv = Nc × dc.

4.1 Computational Complexity of CMP

In CMP, decoding starts from a variable node, and each of its connected check nodes computes a message to send to the variable node. For message computation, each check node determines two minima from among the inputs, applies offset correction, and determines the sign of each output by XOR-ing the sign bits of the input messages. Each of the connected check nodes then sends its message to the variable node, and these messages are accumulated and get added to the channel LLR value. So the processing of one variable node involves dv XOR operations and dv addition operations at the variable node, along with the operations to determine the two minima and apply offset correction. The process is repeated for all the Nv variable nodes. If Vc and Cc are the number of variable-node to check-node (V2C) operations and check-node to variable-node (C2V) computations, respectively, then for a single iteration, Vc and Cc are given by the following equations:

$$ \begin{array}{@{}rcl@{}} V_{\text{c}} &=& N_{v} \times d_{v} = E, \end{array} $$
(11)
$$ \begin{array}{@{}rcl@{}} C_{\text{c}} &=& N_{v} \times d_{v} \times (X + 2 \times M) = E, \end{array} $$
(12)

In Eq. 12, X represents the XOR operation count, while M corresponds to the operation count of computing a single minimum with the offset correction. Since X + 2 × M is considered a single C2V computation, therefore, Cc = E.

4.2 Computational Complexity of FCMP

For the FCMP schedule, messages computed at check nodes, connected to a particular variable node, are further propagated to their neighboring variable nodes, as illustrated in Figure 2. Compared to CMP, this incurs additional computational costs at the check nodes and at the variable nodes. For each check node connected to the variable node being processed, the operation of determining the two minima stays the same, but each check node has to perform now dc XOR operations to determine the signs of their output messages. Since the number of connected check nodes to each variable node is dv, then dv × dc XOR operations are required to complete the processing of one variable node. Similarly, at the variable nodes side, dv × dc variable nodes in total are updated using addition operations. This process is repeated for all Nv variable nodes. If Vf and Cf are the number of V2C and C2V computations of the FCMP, respectively, then for a single iteration, Vf and Cf are given by the following equations:

$$ \begin{array}{@{}rcl@{}} V_{\text{f}} &=& N_{v} \times d_{v} \times d_{c}= d_{c}\times E, \end{array} $$
(13)
$$ \begin{array}{@{}rcl@{}} C_{\text{f}} &=& N_{v} \times d_{v} \times (d_{c}\times X + 2 \times M). \end{array} $$
(14)

By comparing (11) with (13), and (12) with (14), it is evident that the FCMP requires dc times additions at the variable nodes, compared to the CMP schedule. Also, the number of XOR operations is multiplied by the same factor at the check-nodes side. However, addition and XOR are considered simple operations compared to the complexity of determining the first two minima among a set of messages. Crucially, the number of these operations is the same for the CMP and FCMP schedules. For practical purposes, this additional computational cost is considered moderate, compared to the more costly search and residual-computations operations introduced by other RBP-based fast-converging LDPC decoding schedules proposed in the literature.

From a power perspective, the power consumption of a decoder is directly related to the number of computations involved during node processing, the number of iterations required for convergence at a given SNR, and other circuit-level factors such as clock frequency and switching activity. For the proposed FCMP decoder, the additional number of computations required to complete a decoding iteration is moderate, compared to a decoding iteration of a CMP decoder. So, keeping other factors constant, including the number of iterations, the increase in power consumption of the proposed decoder is moderate as per the moderate increase of the computations. However, the proposed FCMP schedule does significantly better. It converges in almost half the number of iterations compared to CMP and RMP. So the power consumption drops proportionally with the reduction in the number of iterations required for convergence.

4.3 Complexity Comparison

The computational complexities of various LDPC decoding schedules, along with the proposed FCMP schedule, are summarized in Table 1. In the last column of the table, r(v) denotes the number of operations required to calculate the variable-node residuals. The comparison of the complexities reveals that the proposed FCMP schedule, along with the CMP, RMP, and ICRMP schedules, does not introduce any costly search operations nor any costly node-residual operations. In contrast, both FCMP and ICRMP schedules incur a moderate increase in complexity, over RMP and CMP schedules. The rest of the fast-converging schedules, NWRBP, SVNF, TSDS, TRM-TVRBP, and RM-RBP, introduce costly search and residual operations. To the best of the authors’ knowledge, these operations are the main reason why no VLSI implementations of LDPC decoders based on such schedules have appeared in the literature so far. Finally, the computational complexities of the FCMP and ICRMP schedules are the same. However, the proposed FCMP schedule processes the neighboring sets of check nodes in parallel rather than serially, which crucially enables the FCMP to achieve a higher throughput than ICRMP.

Table 1 Computational complexities of different LDPC decoding schedules
Full size table

5 Convergence Analysis

Convergence analysis of the proposed FCMP schedule is carried out using two methods: 1) Extrinsic information transfer (EXIT) charts, and 2) the evolution of the mean of Gaussian-approximated message-densities of the nodes.

5.1 Convergence Analysis using EXIT Charts

EXIT charts are used to analyze the convergence performance of iterative decoders [34]. For the purposes of EXIT chart analysis, this section uses the notation of [35], which defines IA and IE as the average mutual information between the transmitted bits and the a priori LLRs, and between the transmitted bits and the extrinsic LLRs, respectively. An approximation of the mutual information between the transmitted bits xn and the LLR value L(xn), using the time average, is given as [36]:

$$ \small I(x_{n})\approx{1-\frac{1}{N}{{\sum}_{n=1}^{N}{\log_{2}\big(1+e^{-x_{n} \cdot L(x_{n})}\big)}}}. $$
(15)

To plot EXIT charts, the approximated mutual information is determined after every iteration, for a variable-node decoder (VND) and a check-node decoder (CND). The corresponding EXIT charts of CMP and the proposed FCMP-based decoding are shown in Figures 3 and 4, respectively. The EXIT charts reveal that the transfer of extrinsic information for the proposed FCMP schedule is much faster than that of CMP. In fact, the FCMP converges in half the number of iterations than the CMP; the FCMP requires 7 iterations to converge, while CMP requires 14.

Figure 3
figure 3

EXIT chart of CMP decoding for WiFi LDPC codes, rate 1/2, block-length 1944, at Eb/N0 = 1.2 dB.

Full size image
Figure 4
figure 4

EXIT chart of proposed FCMP decoding, for the same LDPC codes and Eb/N0 as in Figure 3.

Full size image

5.2 Convergence Analysis by Gaussian Approximation

Convergence analysis of message-passing schedules can also be performed by tracking the mean-evolution of Gaussian-approximated message densities of variable and check nodes. The means of the node messages of a fast converging schedule evolve rapidly in comparison with slow-converging schedules. The convergence speed of a serial LDPC decoding schedule is analyzed in [37] using this method by partitioning the check nodes. To verify the convergence behavior of the proposed FCMP and to compare it with the CMP, the equations that update the means of Gaussian-approximated messages for the CMP and the FCMP schedules are derived in this section by modifying (8) and (9).

In the CMP schedule, every update of the variable node receives messages from the check nodes. A portion of these messages are updated in the current iteration, and the rest are updated from the previous iteration. Let p1 and p2 be the probabilities of the number of check-node messages updated in the previous iteration and the current iteration, respectively, where p1 + p2 = 1. The total number of check-node messages for a particular variable node is dv. Therefore, the expected number of neighboring check-node messages to a variable node that depend on the previous iteration is p1 × dv. Similarly, the expected number of neighboring check-node messages to a variable node that depend on the current iteration is p2 × dv. The higher the number of messages that depend on the current iteration (i.e., higher p2), the faster the evolution of the means of messages is. The means of the variable-node messages \(\overline {m}_{v}^{(k)}\) and the check-node messages \(\overline {m}_{c}^{(k)}\) for the CMP at the k th iteration are given by:

$$ \begin{array}{@{}rcl@{}} \overline{m}_{v}^{(k)}\!&=&\! m_{co} + p_{1}\times (d_{v} - 1)\!\times\! \overline{m}_{c}^{(k-1)} + p_{2}\times (d_{v} - 1)\!\times\! \overline{m}_{c}^{(k)} \end{array} $$
(16)
$$ \begin{array}{@{}rcl@{}} \overline{m}_{c}^{(k)}\!&=&\!\phi^{-1}\left( 1 - \left[1 - \phi\left( m_{co} + p_{1}\!\times\! (d_{v} - 1)\!\times\! \overline{m}_{c}^{(k-1)}\right.\right.\right.\\ &&\left.\left.\left.\qquad\qquad\qquad\qquad+p_{2}\!\times\! (d_{v} - 1)\!\times\!\overline{m}_{c}^{(k)}\right) \right]^{d_{c}-1}\right). \end{array} $$
(17)

Other quantities and initial conditions are similar to Eqs. 8–9. Here p1 and p2 depend on the processing order of variable nodes. For instance, for the first variable node in the processing schedule, all check nodes connected to the variable node perform computations that depend on messages from the previous iteration. Since no variable nodes are updated yet, hence p1 = 1 and p2 = 0. For the second variable node in the processing schedule, the check nodes, common in the neighboring sets of the first and second variable nodes, get updated during the processing of the first variable node and, therefore, depend on the current iteration and contribute to p2. The rest of the neighboring check nodes of the second variable node depend on the previous iteration, and therefore contribute to p1. As processing proceeds, the check nodes connected to a given variable node perform computations that depend more on the input messages of the current iteration rather than the previous iteration. In this way, p1 continues to decrease and p2 continues to increase, with the actual final values of p1 and p2 depend on the structure of the SPCM. For the last variable node in the processing schedule, p1 = 0 and p2 = 1 since all the nodes have now been updated.

For the FCMP schedule, each check node connected to a given variable node, not only updates that variable node but also the remaining dc − 1 variable nodes. Therefore, for a variable node, the probability of getting a check-node message whose computations are based on the current iteration is multiplied by dc − 1. Hence, by using the same p1 and p2 as defined above for CMP, the means of the variable-node messages \(\overline {\overline {m}}_{v}^{(k)}\) and the check-node messages \(\overline {\overline {m}}_{c}^{(k)}\) for k th iteration of the FCMP are updated as:

$$ \begin{array}{@{}rcl@{}} \overline{\overline{m}}_{v}^{(k)} &=& m_{co} + \frac{p_{1}\times (d_{v}-1)\times \overline{\overline{m}}_{c}^{(k-1)}}{p_{1} + p_{2}\times d_{c}}\\ && + \frac{p_{2}\times d_{c}\times (d_{v}-1)\times \overline{\overline{m}}_{c}^{(k)}}{p_{1} + p_{2}\times d_{c}} \end{array} $$
(18)
$$ \begin{array}{@{}rcl@{}} \overline{\overline{m}}_{c}^{(k)} &=& \phi^{-1}\Big(1-\big[1-\phi(m_{co}+\frac{p_{1}\times (d_{v}-1)\times\overline{\overline{m}}_{c}^{(k-1)}}{p_{1}+p_{2}\times d_{c}}\\ && +\frac{p_{2}\times d_{c}\times (d_{v}-1)\times\overline{\overline{m}}_{c}^{(k)}}{p_{1}+p_{2}\times d_{c}})\big]^{d_{c}-1}\Big) \end{array} $$
(19)

By considering a check node with different values of p2 (and therefore different p1), the mean evolution of the node-message versus the number of iterations is plotted in Figure 5. The figure shows that the evolution of the means of the FCMP (plotted in red) is faster than the CMP. In general, different values of p1 and p2 for each node result in different mean evolution curves. The overall convergence speed of the schedule depends on the overall effect of all the mean evolution curves. Here p1 and p2, for a given variable node, are determined by considering the LDPC graph and figuring out the fractions of check-node messages connected to the variable node that depend on the previous and the current iteration, respectively.

Figure 5
figure 5

Comparison of mean evolution of check-node messages of a (3,6) regular LDPC code using the CMP and the proposed FCMP schedule.

Full size image

6 Proposed FCMP Decoder Architecture

An LDPC decoder architecture based on the proposed FCMP schedule is presented in this section. The decoder supports IEEE 802.11ad LDPC codes [4]. The block diagram of the proposed FCMP decoder architecture is shown in Figure 8. The architecture replicates the processing units, in comparison with Figure 1, by a factor of 4, which is the maximum column-degree of the base SPCM of IEEE 802.11ad as defined in [4]. The processing units are replicated by 4 in order to process the neighboring set of check nodes of a particular variable node in a single clock cycle, as required in FCMP. The number of memory modules is doubled in order to store the messages of two frames instead of a single frame, as in Figure 1. The memory modules are modified in order to support the reading and writing of messages to and from multiple blocks of processing units instead of a single block. The decoder architecture is pipelined to enable the processing of the two frames simultaneously without any idle cycles.

In the subsections below, we elaborate on the design space exploration phase and discuss the details of the pipeline and its main processing blocks. We end the section with a discussion on the fixed-point decoding performance of the proposed architecture.

6.1 Design Space Exploration

The design space of the proposed architecture is explored for appropriate selection of the correction-factor β used in Eq. 7, the number of quantization bits for LLRMem (QL), the number of quantization bits for CheckNodeUnits (QC), and the maximum number of iterations \(I_{\max \limits }\). The values of QL = 7, QC = 5, β = 1, and \(I_{\max \limits }=2\) are determined empirically. By comparing Figures 6 and 7, it is evident that the loss in decoding performance is not significant in reducing \(I_{\max \limits }=5\) to \(I_{\max \limits }=2\), compared to the increase in throughput that is achieved by capping \(I_{\max \limits }\) to 2. Therefore \(I_{\max \limits }=2\) is chosen for the proposed architecture (Figure 8).

Figure 6
figure 6

Fixed-point decoding performance of the proposed FCMP architecture for IEEE 802.11ad (WiGig), with QL = 7, QC = 5, and \(I_{\max \limits }=5\). Solid and dotted lines represent BERs and FERs, respectively.

Full size image
Figure 7
figure 7

Fixed-point decoding performance of the proposed FCMP architecture for IEEE 802.11ad (WiGig), with QL = 7, QC = 5, \(I_{\max \limits }=2\). Solid and dotted lines represent BERs and FERs, respectively.

Full size image

6.2 Pipelining

Pipelining the architecture of an LDPC decoder significantly affects the convergence speed, area, and throughput of the decoder. A single-frame based pipelining alters the decoding schedule by delaying the updates of messages, and consequently, slows down the decoding convergence. Therefore, a double-frame based pipelined architecture, with a pipeline depth of 2, is proposed and implemented in this paper. The two pipeline stages of the datapath are balanced by introducing pipeline registers deep inside the CNUs, as shown in Figure 10. The pipeline diagram illustrating the processing stages of the decoder for the two frames is shown in Figure 9. In the first pipeline stage, messages are read from the memories, processed in VN2CN block, and then forwarded to the first stage of the CNUs. In the second pipeline stage, messages are processed in the second stage of the CNUs, forwarded to CN2VN block, and written back to the memories. The VN2CN and CN2VN blocks consist of adders, subtractors, barrel shifter, and reverse barrel shifters, as shown in Figure 8.

Figure 8
figure 8

Block diagram of the FCMP decoder architecture. The decoder is pipelined to process two frames compliant with IEEE 802.11ad LDPC codes.

Full size image
Figure 9
figure 9

Pipeline diagram illustrating the processing stages of the proposed decoder for the two frames. The processing stages correspond to Figure 8.

Full size image

6.3 Check Node Unit (CNU)

The datapath of the CNU is pipelined to balance the two pipeline stages of the proposed decoder architecture. The block diagram of the CNU is shown in Figure 10. Pipelining enables idle-cycle-free processing of two-frames simultaneously. For IEEE 802.11 ad (WiGig), the maximum degree of a check node is 16. Hence the number of inputs of each CNU is also 16. Each block of CheckNodeUnits is composed of 42 such CNUs. A total of 4 blocks of CNUs are used in the proposed architecture, as shown in Figure 8.

Figure 10
figure 10

Block diagram of a single pipelined Check Node Unit.

Full size image

6.4 Check-Node Memory

The Check-Node (CN) Memory block of the decoder is a multi-port memory. Figure 11 shows the internal organization of this memory block. The memory stores the magnitudes of first and second minima, as well as the signs and indices of the check-node messages required to regenerate the check-node outputs using Eq. 7. The WriteCircuitry in Figure 11 enables the memory locations for writing, while the ReadCircuitry is a network of multiplexers that selects and generates the required check-node outputs. The number of inputs and outputs of the CN Memory block is shown as 4, in order to emphasize the fact that the memory stores and generates messages for 4 blocks of CNUs in a single clock cycle. The CN Memory saves check-nodes messages, and by referring (7), it is evident that the check-nodes messages comprise of first and second minima and the index of the first minimum. A memory also requires the address of a location to complete the corresponding read or write operation. Therefore, each of the input buses further consists of wires for minima, signs, indices, and addresses of the check-node messages.

6.5 Decoding Performance

The fixed-point decoding performance of the proposed FCMP-architecture, targeted for IEEE 802.11ad (WiGig), is plotted in Figure 7. The design parameters QL = 7, QC = 5, β = 1, and \(I_{\max \limits }=2\) have been determined during the design exploration phase. By considering Figure 7, it is evident that the proposed architecture converges to a BER value of 10− 6 at Eb/N0 = 3.3, 3.6, 4.0, and 4.8, for code rates 1/2, 5/8, 3/4, and 13/16, respectively. The architecture presented in [38], for example, achieves a BER value of 10− 6 at Eb/N0 = 4.6, 4.6, 5.0, and 5.4, for code rates 1/2, 5/8, 3/4, and 13/16, respectively, while operating at 202 MHz and running for \(I_{\max \limits }=10\) decoding iterations. Therefore, the proposed architecture based on the FCMP schedule achieves a better decoding performance and higher energy efficiency than [38].

7 Simulation and VLSI Synthesis Results

7.1 Simulation Results

The potential advantages of the proposed schedule in terms of convergence speed, BER performance, and FER performance are assessed by simulating the RMP, CMP, ICRMP, RBP-based, and the proposed FCMP decoding schedules. BER and FER curves, as well as the corresponding convergence speed in terms of the number of iterations taken by the schedules to converge, are simulated and plotted. Randomly generated LDPC codes, IEEE 802.11ad (WiGig) LDPC codes, IEEE 802.11n/ac (WiFi) LDPC codes, and IEEE 802.16e (WiMAX) LDPC codes are considered, while fixing the maximum number of iterations. The comparison of the proposed FCMP schedule with the RMP, CMP, ICRMP is shown in Figures 12, 13 and 14. As is evident from the plots, the fast convergence rate of the FCMP, along with ICRMP, in comparison with RMP and CMP, is verified consistently throughout these simulations. The plots reveal that the proposed FCMP schedule requires a slightly higher number of iterations than ICRMP; however, the overall throughput of the FCMP is higher than that of the ICRMP, as explained in Section 4. The comparisons of the proposed FCMP schedule with RBP-based fast-decoding schedules, using BER and FER plots against Eb/N0 and the maximum number of iterations, are shown in Figures 15, 16, 17, 18, 19 and 20. The comparisons reveal that the proposed FCMP schedule achieves the same decoding and convergence performance as the RBP-based schedule, although the computational complexity of the proposed FCMP schedule is significantly lower. This crucial advantage enables a multi-Gbps low-power VLSI implementation of an FCMP-based decoder.

Figure 11
figure 11

Block diagram of Check-Node (CN) memory.

Full size image
Figure 12
figure 12

Comparison of the proposed FCMP schedule with the ICRMP, CMP and RMP, for randomly generated LDPC codes with rate = 1/2,dv = 3,dc = 6,Nv = 2000, and \(I_{\max \limits } = 100\): (a) Floating-point bit error rate (b) Iterations count.

Full size image
Figure 13
figure 13

Comparison of the proposed FCMP schedule with the ICRMP, CMP and RMP, for IEEE 802.11ad (WiGig), rate = 1/2 LDPC codes with \(I_{\max \limits } = 100\): (a) Floating-point bit error rate (b) Iterations count.

Full size image
Figure 14
figure 14

Comparison of the proposed FCMP schedule with the ICRMP, CMP and RMP, for IEEE 802.11n/ac (WiFi), rate = 1/2 LDPC codes with \(I_{\max \limits } = 100\): (a) Floating-point bit error rate (b) Iterations count.

Full size image
Figure 15
figure 15

Floating-point BER comparison of the proposed FCMP and other schedules, for IEEE 802.16e LDPC codes, rate = 1/2, block-length 576, with \(I_{\max \limits } = 5\).

Full size image
Figure 16
figure 16

Floating-point FER comparison of the proposed FCMP and other schedules, for IEEE 802.16e LDPC codes, rate = 1/2, block-length 576, with \(I_{\max \limits } = 5\).

Full size image
Figure 17
figure 17

Comparison of BER vs. number of iterations for IEEE 802.16e LDPC codes, rate 1/2, block-length 576, at Eb/N0 = 3.0 dB.

Full size image
Figure 18
figure 18

Comparison of BER vs. number of iterations for IEEE 802.16e LDPC codes, rate 1/2, block-length 576, at Eb/N0 = 2.5 dB.

Full size image
Figure 19
figure 19

Comparison of BER vs. number of iterations for IEEE 802.16e LDPC codes, rate 1/2, block-length 1152, at Eb/N0 = 2.2 dB.

Full size image
Figure 20
figure 20

Comparison of frame-error-rate vs. number of iterations for WiFi LDPC codes, rate 1/2, block-length 1296, at Eb/N0 = 2.25 dB.

Full size image

7.2 VLSI Synthesis Results

The proposed hardware architecture of the FCMP schedule for IEEE 802.11 ad LDPC codes, shown in Figure 8, is synthesized using the TSMC 40 nm 65 nm CMOS processes, for a target clock frequency of 200 MHz. The throughput of the decoder, 𝜃, is calculated as:

$$ \theta = \frac{F_{L} \times N_{F}}{I_{\max} \times C } \times f_{\mathrm{c}\mathrm{l}\mathrm{k}}. $$
(20)

Here, FL is the frame-length, NF is the number of frames, \(I_{\max \limits }\) is the maximum number of iterations, C is the number of cycles to complete one decoding iteration, and fclk is the clock frequency. For the proposed architecture, \(F_{L}=672, N_{F}=2, I_{\max \limits }=2, C=16\), and fclk = 200MHz, which result in a throughput of 8.4 Gpbs. The latency η of the proposed architecture is calculated as:

$$ \eta = \frac{I_{\max} \times C}{f_{\mathrm{c}\mathrm{l}\mathrm{k}} } . $$
(21)

By using the same values as in Eq. 20, the latency η of the decoder turns out to be 0.16 μ s. For the proposed architecture, it is possible to shorten the critical path even further, and thus a higher throughput can be achieved by increasing the clock speed. However, a realistic clock speed of an LDPC decoder should be constrained around 200 MHz to support practical SoC integration of intellectual property (IP) cores with other signal processing blocks in a digital baseband processor [38]. The synthesis results of the proposed architecture using both the CMOS processes are summarized in Table 2.

7.3 Comparison with State-of-the-Art

A comparison of the VLSI synthesis results of the proposed architecture with state-of-the-art is summarized in Table 3. Dennard’s scaling rules are used to compare the results of different process nodes [39]. If RT and ST are the reference and scaled technologies, then the scaled area, As, and scaled throughput, Ts, are obtained from the reference area, Ar, and reference throughput, Tr, as follows:

$$ As=Ar\times\left( \frac{S_{T}}{R_{T}}\right)^{2}, $$
(22)
$$ Ts=Tr\times\frac{R_{T}}{S_{T}}. $$
(23)

This work synthesizes the proposed architecture both for 40 nm and 65 nm technologies, and Dennard’s scaling rules do not apply very well below 40nm technology, therefore, there was no need of using these scaling rules for comparison in this paper. The comparison of results in Table 3 reveals that the proposed architecture consumes the least power compared to the corresponding state-of-the-art implementations using 40 nm and 65 nm technology nodes. The power consumption of the 40 nm implementation of the proposed architecture is even less than the state-of-the-art implementations using 28 nm. Thus, the proposed decoder consumes the least power while achieving a throughput that is comparable with other architectures. Owing to this minimal power consumption feature while maintaining a comparable throughput, the proposed FCMP schedule and its decoder architecture attain the best-reported energy efficiency of 8.6 pJ/bit for LDPC codes compliant with the IEEE 802.11ad standard.

The throughput of the proposed architecture can be further increased by simply increasing the clock frequency. For instance, in [40], a higher throughput is achieved by increasing the clock frequency, but this leads to excessive power consumption. Also, such a high clock speed of 720 MHz is not desirable in industry-grade communication/networking SoCs. Thus, the real parameter to consider is not just the throughput, but rather the energy efficiency (i.e., power-to-throughput ratio). The energy efficiency of the decoder in this work is almost double that of [40]. Specifically, the proposed architecture consumes significantly less power because of its ability to converge in fewer iterations to achieve a specific FER/BER at a given Eb/N0. The switching activity of a decoder, and consequently, the power consumption, is directly related to the number of iterations required for convergence.

Table 2 Synthesis results
Full size table

The area of the proposed architecture is larger than other designs, which is a direct consequence of replicating the processing units and decoding the two frames simultaneously. However, the additional area does not offset the energy efficiency benefits of the FCMP schedule and its architecture. In fact, the additional area indirectly causes a reduction in the overall power consumption by enabling the implementation of the FCMP schedule, which cuts the number of the iterations required for convergence. The real motivation of this work is to address the energy efficiency problem of multi-Gbps LDPC decoders, and this is adequately treated with the proposed fast converging schedule and its architecture.

Table 3 Comparison of proposed decoder with state-of-the-art
Full size table

8 Conclusion

A low-latency and energy-efficient multi-Gbps fast column message-passing LDPC decoding schedule, which converges in a reduced number of iterations compared to existing serial decoding schedules, has been presented and investigated. It has been verified that the proposed FCMP schedule achieves fast-decoding performance with reduced computational complexity, compared with other schedules in the literature. For a specific throughput, FCMP consumes less power to achieve the target BER at a given SNR. The advantages of FCMP have been demonstrated through convergence analysis, throughput analysis, complexity analysis, and BER and FER comparisons using empirical simulations of random LDPC codes, IEEE 802.11ad (WiGig) LDPC codes, IEEE 802.11n/ac (WiFi) LDPC codes, and IEEE 802.16e (WiMAX) LDPC codes. Through complexity analysis, it has also been shown that the added cost for FCMP is more addition operations at variable nodes and XOR operations at check nodes, compared to existing serial decoding schedules. Finally, an FCMP-based decoder architecture, targeting IEEE 802.11ad (WiGig) LDPC codes, has been proposed. The architecture is pipelined and optimized to process two frames simultaneously. VLSI synthesis results, using the TSMC 40 nm CMOS process, have revealed that the decoder achieves an energy efficiency of 8.6 pJ/bit while operating at 8.4 Gbps, which is the best-reported energy-efficiency of a WiGig LDPC decoder.