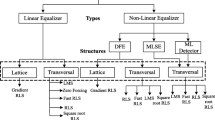
Abstract
In this paper, we propose an efficient architectural design for Adaptive Decision Feedback Equalizer (ADFE) for high-speed reliable data transmission through wired as well as wireless communication channels to minimize Inter Symbol Interference (ISI). High hardware cost of the system makes an urge to redesign it in order to minimize overall circuit complexity and cost. Realization of CORDIC based pipelined ADFE architecture using reformulated LMS algorithm has not only reduced multipliers in its feed forward path, the flexibility and modularity of the components makes it possible for easy implementation also. The realization results area efficient, high speed and throughput with good convergence. The efficacy of the proposed equalizer is corroborated with MATLAB simulations for mitigation of severe channel distortion arise due to ISI in high speed communication systems.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In digital communication, high operating speed of adaptive equalizer is being demanded to cater high speed reliable data transmission over wired or wireless channel. But the transmitted data are often distorted due to non-linearity of channel response. The amount of distortion also varies with respect to time-varying nature of the operating channel. Due to the deviation of channel frequency response, both tails of the transmitted pulse will interfere with the neighboring pulses creating an Inter Symbol Interference (ISI) which may lead to erroneous decision by escalating the probability of error in detection process. To overcome this problem an Adaptive Decision Feedback Equalizer (ADFE) at the receiver with a transfer function which is essentially inverse of the channel transfer function is capable to eliminate ISI.The performance of non-linear ADFE is better on a channel with spectral nulls in their frequency response characteristics than the linear equalizer which introduces significant amount of additive noise present in the received signal by introducing a large gain [1, 2].
In this paper, a pipelined CORDIC architecture has been used as a main processing element of the design. Since last few decades, a tremendous inclination among the researchers toward the implementation of CORDIC algorithm [3] in various applications of digital signal processing arena had been witnessed [4, 5]. The modularity, compatibility, pipelinability, numerical stability and efficiency in generation of trigonometric and hyperbolic function have made the CORDIC algorithm suitable for implementation of fast Fourier transform (FFT), discrete Fourier transform (DFT), adaptive lattice filter, and many more applications [6–8]. In this paper, an adaptive transversal filter has been designed with a pipelined CORDIC unit as a core processing element in the equalizer for filtering and filters weight updating. Unlike the conventional LMS algorithm, the rotational angles rather than the tap weights are updated directly. The most popular and highly robust Least Mean Squared (LMS) algorithm [9] has been efficiently mapped to obtain trigonometric form of LMS algorithm which facilitates in incorporating CORDIC processing element to participate in filtering as well as weight updating operations of the Feed Forward Filter (FFF) of the ADFE. Due to trivial bit length, decision feedback loop (DFL) has been simplified with general purpose multiplier to reduce complexity of the Feedback Filter (FBF). The proposed architecture uses CORDIC blocks instead of multipliers in the FFF and hence is more efficient in terms of internal numerical errors and power consumption.
2 Related Work
Adaptive Decision Feedback Equalizer (ADFE) is widely used equalization technique for radar, antenna beam forming, digital communication systems, wireless video telephony, magnetic storage and many more applications [10, 11]. Wide variants of ADFE are available in the literature [12–14]. However, pipeline design of ADFE is known to be a difficult task for high speed applications. It is well known fact that the clock rate is limited by DFL. The quantizer and adaptive feedback loop in ADFE makes it difficult for design of pipelined architecture. Therefore, previously published works mostly have used parallelism technique for its design [15, 16]. These architectures are inherited by incorrect initialization which leads to degraded performances along with huge hardware overhead as it transforms serial algorithm into equivalent pipelined algorithm. Shanbag et al. [17] and Yang et al. [18] has tried to reduce hardware overhead although it suffers from performance degradation in terms of output signal-to-noise ratio (SNR) and the rate of convergence.
VLSI implementation of ADFE as well as its performance in high-speed communication systems has become an ardent requirement. Reformulated trigonometric LMS (TLMS) algorithm based transversal filter using CORDIC processing unit has been proposed in [19]. Later on transform domain equalization technique using CORDIC was proposed [20]. In this paper, we have used two transversal filters namely feed forward filter (FFF) and feedback filter (FBF). In FFF CORDIC element has been used whereas, in FBF trivial multipliers have been used. Throughout the architecture, pipeline design technique has been used to reduce hardware complexity and to obtain high throughput for high speed applications. The modular design of multiplier has been incorporated to avoid place and route problem during physical layout. The combination of modified booth encoding (MBE) techniques [21, 22] along with partial product reduction schemes [23–25] have facilitated in reduction of overall latency of the design to a single adder which has been implemented with carry look-ahead adder (CLA). This kind of design not only facilitates in easy implementation on FPGA device, but also reduces complexity significantly as compared to multiplier and accumulator (MAC) based design. It has been observed that during digital conversion of input analog signals with limited number of bits of ADC, sampling at Nyquist rate disturbs the amplitude and phase response curve of equalizer. Again, finite word-length, round-off noise or overflow in MAC based transversal filter creates huge instability within the system. The effects of quantization noise continuously gets accumulated due to its feedback path resulting in severe instability. The CORDIC processing element has been used by optimizing the quantization error [26] and to facilitate easy implementation of the equalizer for digital signal processing application. The simulation results for convergence behavior under various step sizes and its ability to generate inverse transfer function in severe channel mismatched situation have been adequately analyzed.
The rest of the paper is organized as follows. In the next section, we review the simple LMS algorithm and subsequently mapped into trigonometric form. In section 4, CORDIC algorithm has been revisited and corresponding pipelined architecture is implemented. Section 5 deals with the design of pipelined Adaptive Decision Feedback Equalizer along with explanation of associated components used with the design. Performance analysis of proposed design and discussion part of the paper is accommodated section 6 and finally, conclusions are presented in section 7.
3 Trigonometric Mapping of LMS Algorithm
The LMS algorithm is one of the simplest as well as robust adaptive algorithms available in literature. We would like to reformulate LMS in trigonometric form for our design. Let the FIR filter is linear discrete time filter x(n) and d(n) are input and desired output sequence of the FIR filter (Fig. 1).
Let w and x(n) are filter coefficient and input vector of N-tap filter,
The output signal of the adaptive filter, y(n), can be computed as the inner product of w(n) and x(n).
The error signal e(n) is expressed as the difference between the desired response d(n) and the filter output y(n), i.e.,
The weight vector is updated iteratively in such manner that the mean-square error (MSE) is minimized.
where R ≡ E[x(n)x T(n)] is the input auto-correlation matrix and p ≡ E[x(n)d(n)] is the cross-correlation vector.
Solving the Eq. (5b), the gradient first term is zero and overall ∇ w ε becomes
Solving for ∇ w ε = 0, the optimal weights of a FIR filter can be derived as
The straightforward application of w opt = R −1 p to calculate the optimum filter weight (w opt ) is not of practical use. The computer burden corresponding to the matrix inversion can be evaluated from the number of complex multiplications, which is proportional to N 3. Hence, it is not compatible with the constraint of real-time operations. To avoid these complexities, steepest descent search method can be used for the design. The expression for steepest descent search method can be written for n-th index as
Putting the value of R and p in Eq. (8), we get the simplest LMS algorithm in the following form:
The pipelined implementation of the above mentioned conventional LMS algorithm is difficult as it does not support pipelined implementation due to its recursive behavior. That is why delayed LMS (DLMS) algorithm has been used for easy implementation. If L numbers of pipelined stages are used in the design, the error signal e(n) becomes available after adaptation delay for architecture of L cycles. The error in DLMS algorithm corresponds to (n ‐ L)th iteration for updating current filter weight in place of recent most error. Therefore, the iterative equation of delayed LMS algorithm can be expressed as:
Since our proposed architecture uses CORDIC as a main processing element for weight updating, the iterative Eq. (9) is required modification in terms of angle. Let the tap weight w k be
w k satisfies,−A k ≤ w k ≤ + A k , and maps uniquely to a θ k in the interval \( \left[-\frac{\pi }{2},+\frac{\pi }{2}\right] \). The function sinθ k is a monotonically increasing continuous function of θ k , as it lies within [\( -\frac{\pi }{2}\le {\theta}_k\le +\frac{\pi }{2} \)], i.e. \( \frac{\partial \varepsilon }{\partial {\theta}_k} \) has the same sign as that of \( \frac{\partial \varepsilon }{\partial {w}_k} \) everywhere within the hypercube resulting in local minima or maxima less MSE. Using the Eq. (11), we can show the variation of error w.r.t angle variation as follows:
Or
Here Δ is N × N diagonal matrix whose k-th term can be given by:
Using the Eq. (6) and (13), we get the following
With replacing p and R by x(n)d(n) and x(n)x T(n) in Eq. (14), we get the trigonometric form of LMS algorithm as
But the input as well as desired signals to real communication channels is complex in nature and the filter tap weights are also complex. Therefore, we can write filter tap as:
Where w kr = sin θ kr and w ki = sin θ ki .
Again, Eq. (12) can be modified to
The complex trigonometric form of LMS algorithm with real and imaginary form can be shown separately as angle update equation,
where \( {e}^{*}(n)=d(n)-{\displaystyle \sum_{k=0}^{N-1}}\left( \sin {\theta}_{kr}-j \sin {\theta}_{ki}\right)x\left(n-k\right) \).
The above form of LMS algorithm can be realized using CORDIC processing element. The sinusoidal term generated by CORDIC can be utilized for filtering as well as updating filter coefficients in the equalizer.
4 CORDIC Processing Element
4.1 CORDIC Algorithm:
Rotation of a vector p 0 = [x 0 y 0] in 2-dimensional space (shown in Fig. 2) through an angle θ with n number of sequence of elementary rotations to get a final vector p n = [x n y n ] can be accomplished by using a corresponding matrix product p n = R rot . p 0, where R rot is represented as rotation matrix:
The rotation matrix R rot in (20) can be written after factoring out the cosine term as:
where, K = [(1 + tan2 θ)−1/2] is called scale-factor and \( {\mathbf{R}}_c=\left[\begin{array}{cc}\hfill 1\hfill & \hfill - \tan \theta \hfill \\ {}\hfill \tan \theta \hfill & \hfill 1\hfill \end{array}\right] \)is a pseudo-rotation matrix. During these elementary operations, the vector p 0 = [x 0 y 0] changes its magnitude only by amount of scale-factor, K = [(1 + tan2 θ)−1/2], to obtain pseudo rotated vector
The CORDIC algorithm decomposes the desired rotation angle into the weighted sum of a set of consecutive micro rotation and these micro rotations are based on sequence of elementary angles, α i = arctan (2−i).Therefore, tanα i = 2−i can be easily implemented on hardware by right shifting through i. CORDIC achieves a desired rotational angle θ by performing a sequence of micro rotations through angle α i which can be represented as:
The rotation matrix at i-th iteration for a specific angle α i is given by:
where scale-factor,
\( K=\underset{i=0}{\overset{n-1}{\varPi }}{K}_i=\underset{i=0}{\overset{n-1}{\varPi }}1/\sqrt{\Big(1+{2}^{-2i}}\Big) \) and pseudo-rotation matrix
Since the scale-factor decreases monotonically irrespective of direction of micro rotation, it finally converges to ≅1.6467605. Therefore, it would be better to scale the final output by K instead of scaling during each micro rotation to maintain correct phase at the output. The scaling free CORDIC iterations are given by:
For specific angle α i , the iterative equations can be shown as,
4.2 Implementation of Pipelined CORDIC:
In Pipelined CORDIC architecture, a number of rotational modules are incorporated and each module is responsible for one elementary rotation. The modules are cascaded through intermediate latches (Fig. 3). Every stage within the pipelined CORDIC architecture, only adder/subtractor is used. The shift operations are hardwired using permanent oblique bus connections to perform multiplications by 2−i as shown in Fig. 4. The pre-computed values of i-th iteration angle α i required at each module can be generated through required sequence of binary data within V cc and G nd using trivial hardware arrangements. The delay is adjusted by using proper bit-length in the shift register. In the design of CORDIC module, adders and subtracters contribute the critical path. Since carry propagation delay in full adders is the source of delay, Carry Save Adder (CSA) [27, 28] was the obvious choice for the design. The use of these adders reduces the stage delay significantly. With the pipelining architecture, the propagation delay of the multiplier is the total delay of a single adder. So ultimately the throughput of the architecture is increased significantly as the throughput is given by: “1/(delay due to a single adder)”. If an iterative implementation of the CORDIC is used, the processor would take several clock cycles to give output for a given input. But in the pipelined architecture, each pipeline stage takes exactly one clock cycle to pass one output.
It is very important in our design to keep the rotation angles within −π/2 ≤ θ i ≤ + π/2 for utilization of CORDIC in design of equalizer in updating weights and filtering purpose utilizing sine/cosine data. The quadrants can be transformed by using first two MSB bits. If required rotation angle falls either in second quadrant (π/2 ≤ θ i ≤ + π) or in third quadrant (−π ≤ θ i ≤ − π/2), addition/subtraction of π with the θ i will facilitate to transform to fall within fourth or first quadrant respectively through complementing corresponding MSBs. The transformation of angles in different quadrant has been illustrated in Fig. 5.
We now discuss the hardware and time complexities of the proposed design and our design can be compared with various types of CORDIC architectures including the basic one which is discussed in [30, Fig. 2]. Unlike the proposed design, the conventional and few other designs available in the literatures uses adders, resisters, barrel shifters and MUX. It has been seen that shifting operations using barrel-shifter for maximum of S shifts for word-length L can be implemented by ⌈log2(S + 1⌉ stages of 2:1 MUX. Few designs have used ROM memory to store arctan angles as well as control signals for CORDIC operations. Therefore, the hardware complexity of the design also increases with increase in required word-length which leads to maximum number of shift operations for the design. We have compared our design with the other published work [29] in respect of clock period, throughput, latency and area which have been shown in Table 1 and Table 2 using TSMC 90-nm library.
5 Architecture of ADFE
The adaptive decision feedback equalizer consists of feed forward filter (FFF) and feedback filter (FBF) and equalized signal is generated from the sum of the outputs of both the filter. The feed forward filter (FFF) in our design is a linear transversal filter which is implemented with a finite duration impulse response (FIR) filter with adjustable coefficients. The decisions made on the equalizer signal are fedback via a second transversal filter as shown in Fig. 6. If the detected symbols are stationary, then the ISI contributed by these symbols can be cancelled exactly by subtracting past symbol values with appropriate weight from the equalizer output [30]. But channel response may not be same always. Therefore, the forward and feedback filter should adjust its coefficients simultaneously [31] to counter the variation in channel response by minimizing the mean square error (MSE). At initial operation, the coefficients of the equalizer are needed to be adjusted as per the channel response and therefore, a known sequence of symbols named as training sequence is transmitted through the desired channel for this purpose. The design uses pipelined CORDIC unit as a main processing element. In circular rotation mode, CORDIC unit generates sinθ and cosθ which are the main ingredients for filtering and weight updating respectively in the proposed design as derived in Eq. (18, 19) [32].
The pipelined technique has been adopted throughout the architecture to implement delayed version of trigonometric form of LMS algorithm in FFF and simple delayed LMS (DLMS) for FBF. The reason behind that is the inputs to the FBF are the transmitted symbols whose bit lengths are very small and hardware required for multiplication is trivial. But it is not the case for FFF filter. Adaptation delay in FFF naturally more as compared to FBF. The μ f and μ b are the step sizes used to compute the weight update term of FFF and FBF respectively to synchronize the error output. The filtering process in ADFE has been explained briefly with the help of architecture shown in Fig. 7. The FF and FB filter uses equal number of taps (N). The FIFO F 1, pipelined CORDIC processing unit and accumulator unit constitute the FF filter. On the other hand, FB filter consist of FIFO F 2, multiplier and FIFO F 4. Synchronization is essential within FF and FB filter and therefore, FIFO F 1 and F 2 has been employed for proper sequencing of input data to FF and FB filter. N number of input samples are circulated through the FIFO F 1 and F 2 at primary clock cycles. The new input samples are introduced after every (N + 1) primary clock cycles by flipping the multiplexer MUX 1 and MUX 2. The FIFO F 3 and F 5 has been employed for proper sequencing of intermediate results required for angle and weight updating respectively. MUX 3 is being used to add desired signal for training of the equalizer. The architecture gives its output at every (N + 1) primary clock periods. The primary clock is responsible for loading of data into different latches and the maximum frequency of primary clock, f PMax , is totally dependent on propagation delay of the critical path of the design. In our design, the critical path is equal to propagation delay of single adder. The real part of input signals to the basic filtering block has been considered and processing elements are used in the filtering blocks engaged in corresponding operations only. x(n) and v(n) are the input signals for FF and FB filter respectively. Whereas, w(n) and θ are the weight and angle updating signals are being used in the process. The computed result of present samples being processed are stored in FIFO F 1 and in FIFO F 2 of respective FF and FB filters before arrival of next sample on which similar process is to be carried out. To achieve high speed operation of the design, the computations on input signals are carried out simultaneously in FF and FB sections sothat the final outcome can be retrieved at every system clock cycle. Hence, on subsequent clock cycles, filter output come out and repeated processes continue.
The pipelined multiplier we have used in the design is Modified Booth encoding (MBE) algorithm based design which has been widely used in implementation due to its efficiency in reduction of partial products by half. The presented multiplication operations are performed using three steps [33]. All the partial products are generated in first step. For this purpose, popular MBE scheme has been employed and has not been discussed in detail in this design. The second step deals with reduction of all partial products in parallel structure using 4-to-2 adder. The third step uses fast adder named Carry Look-Ahead (CLA) to add the two numbers obtained from second stage to generate final product. The reduction of partial products using 4-to-2 adder has been shown in Fig. 8 (a). There are four 4-to-2 adder have been used to accommodate 16 partial product generated from the input coming from CORDIC as well as error generator circuits. Each 4-to-2 adder receives four inputs and gives two outputs in terms of sum and carry. The adder cell consists of carry generator which receives three inputs from previous adder cell and a parity generator which generates a control signal for the two MUXes to be selected. The expended architecture of the adder has been shown in Fig. 8 (b).
The multiplier has been synthesized on Xilinx 13.4 using target device spartan 3E xc3s250e-5-pq208. The resource utilization summary has been shown in Table 3 .
6 Performance Analysis and Discussion
It is well known that pipelined CORDIC itself has got good convergence property which has been efficiently used in this application. Exact convergence analysis of proposed architecture using trigonometric LMS algorithm is not possible due to presence of nonlinearity of the filter as well as angle update equation. Using the iteration error generated in the equalizer, approximate convergence studies have been carried out. The channel system function has been considered for simulation is H(z),
The input sequence to the channel is considered to be white Gaussian with corresponding unity variance. The channel noise is modeled as additive Gaussian noise process. The equalizer delay is set at 10. 11-tap adaptive filter with centre placed at 6-th tap has been taken for simulation studies. The tap weights are initialized to zero. The step size (μ) which is the guiding force for fast or slow conversion of the system is appropriately taken care. If μ ≤ 0.002 the convergent speed of the algorithm will be very slow and too large μ can cause instability. The simulation for convergence performance of ADFE consists of MATLAB simulated outcome in terms of learning curves of the design at μ = 0.003 and μ = 0.012 has been shown in Fig. 9 and Fig. 10 respectively.
The proposed design has been tested using randomly generated signal as an input for the equalizer which is to be used in mismatched channel. The equalization of mismatched channel has been shown in Fig. 11 (a) whereas, Figure 11(b) shows the equalizer response which is essentially inverse of the given channel response. Again MATLAB simulation of the proposed design and the corresponding ideal ADFE has been simulated and compared considering the decision error plots against number of iterations. The Fig. 12 shows that the proposed architecture gives good convergence result. The proposed design starts converging at iteration number 29 and finally it is fully converged at iteration 33. The ideal ADFE converges at iteration number 21.
The pipelined design of ADFE faces difficulty while implementing on the hardware due to its huge resource utilization. Though hardware utilization of pipelined architecture available in the literature is limited, we have tried to compare our design with the available pipelined design [17, 18] in the Table 4.
The proposed architecture has been coded in Verilog HDL and synthesized it using Cadence design tool. TSMC 90-nm CMOS library have been used for synthesis of the design. The area consumed by the hardware is 384,376 sq.um. Again, timing analysis shows that the delay produced by the design is 4.715 ns which lead to the operating speed of 212.09 MHz. The power consumptions of the proposed hardware have been tested with the same technology file at different operating frequencies and the results are shown in Table 5.
7 Conclusion
This paper presents realization of CORDIC based adaptive feedback equalizer using reformulated LMS algorithm in mitigating severe Inter Symbol Interference (ISI) in wire as well as wireless communication systems. The use of pipelined CORDIC computational architecture replaces few multipliers and makes pipelined implementation of adaptive DFE realizable on the chip. For better convergence, numbers of micro-rotations and internal word-length has been optimized at the micro-level that not only increases the speed of operation, the decision error also minimized greatly. Again, optimization in quantization noise in CORDIC which is the main processing element in feed forward filter reduces instability in the performance of design as the system never get the quantization noise to accumulate in the feedback system. Therefore, proposed design achieves high degree of computational accuracy facilitating better application in channel equalization where ISI is severe. The convergence result shows the suitability of the design in real-time applications.
References
Farhang-Boroujeny, B. (2013). Adaptive filters: theory and applications. John Wiley & Sons.
R. Mishra, A. Mandal, (2012). Coordinate rotation algorithm based non-linear Adaptive Decision Feedback Equalizer, In IEEE 2012 9th International Multi-Conference on Systems, Signals and Devices (SSD), pp. 1–5
Volder, J. E. (1959). The CORDIC trigonometric computing technique. IRE Transactions on Electronic Computers, EC-8, 330–334.
Hu, Y. H. (1992). CORDIC-based VLSI architectures for digital signal processing. IEEE Signal Processing Magazine, 9(3), 16–35.
Meher, P. K., et al. (2009). 50 years of CORDIC: algorithms, architectures, and applications. IEEE Transactions on Circuits and Systems I: Regular Papers, 56(9), 1893–1907.
Banerjee, A., Dhar, A. S., & Banerjee, S. (2001). FPGA realization of a CORDIC based FFT processor for biomedical signal processing. Microprocessors and Microsystems, 25(3), 131–142.
Hu, Y. H., & Liao, H. E. (1992). CALF: a CORDIC adaptive lattice filter. IEEE Transactions on Signal Processing, 40(4), 990–993.
Angarita, F., Canet, M. J., Sansaloni, T., Perez-Pascual, A., & Valls, J. (2008). Efficient mapping of CORDIC algorithm for OFDM-based WLAN. Journal of Signal Processing Systems, 52(2), 181–191.
S. S. Haykin, (2008). Adaptive filter theory, 4 ed., Pearson Education India.
Sung, W., Ahn, Y., & Hwang, E. (2005). VLSI implementation of an adaptive equalizer for ATSC digital TV receivers. Journal of VLSI signal processing systems for signal, image and video technology, 40(3), 301–310.
Chen, S., Hanzo, L., & Livingstone, A. (2006). MBER space-time decision feedback equalization assisted multiuser detection for multiple antenna aided SDMA systems. IEEE Transactions on Signal Processing, 54(8), 3090–3098.
Chakraborty, M., & Pervin, S. (2003). Pipelining the adaptive decision feedback equalizer with zero latency. Signal Processing, 83(12), 2675–2681.
Shaik, R. A., & Chakraborty, M. (2013). A block floating point treatment to finite precision realization of the adaptive decision feedback equalizer. Signal Processing, 93(5), 1162–1171.
Magarini, M., Barletta, L., & Spalvieri, A. (2012). Efficient computation of the feedback filter for the hybrid decision feedback equalizer in highly dispersive channels. IEEE Transactions on Wireless Communications, 11(6), 2245–2253.
Raghunath, K. J., & Parhi, K. K. (1993). Parallel adaptive decision feedback equalizers. IEEE Transactions on Signal Processing, 41(5), 1956–1961.
Gatherer, A., & Meng, T. H. (1993). A robust adaptive parallel DFE using extended LMS. IEEE Transactions on Signal Processing, 41(2), 1000–1005.
Shanbhag, N. R., & Parhi, K. K. (1995). Pipelined adaptive DFE architectures using relaxed look-ahead. IEEE Transactions on Signal Processing, 43(6), 1368–1385.
Yang, M. D., Wu, A. Y., & Lai, J. T. (2004). Fast convergent pipelined adaptive DFE architecture using post-cursor processing filter technique. IEEE Transactions on Circuits and Systems II: Express Briefs, 51(2), 57–60.
Chakraborty, M., Dhar, A. S., & Lee, M. H. (2005). A trigonometric formulation of the LMS algorithm for realisation of pipelined CORDIC. IEEE Trans. Circuits and Systems, 52(9), 530–534.
Banerjee, A., & Dhar, A. S. (2013). Pipelined VLSI architecture using CORDIC for transform domain equalizer. Journal of Signal Processing Systems, 70(1), 39–48.
Wu, A., Ng, C. K., & Tang, K. C. (1998). Modified booth pipelined multiplication. Electronics Letters, 34(12), 1179–1180.
Waters, R. S., & Swartzlander, E. E. (2010). A reduced complexity wallace multiplier reduction. IEEE Transactions on Computers, 59(8), 1134–1137.
Kornerup, P. (2005). Reviewing 4-to-2 adders for multi-operand addition. Journal of VLSI signal processing systems for signal, image and video technology, 40(1), 143–152.
Galbi, D., et al. (1990). U.S. Patent No. 4,901,270. Washington, DC: U.S. Patent and Trademark Office.
Kuang, S.-R., Wang, J.-P., & Guo, C.-Y. (2009). Modified booth multipliers with a regular partial product array. IEEE Transactions on Circuits and Systems II: Express Briefs, 56(5), 404–408.
Hu, Y. (1992). The Quantization Effects of the CORDIC Algorithm. IEEE Transactions on Signal Processing, 40(4), 834–844.
Biswas, D., & Maharatna, K. (2015). A CORDIC-Based Low-Power Statistical Feature Computation Engine for WSN Applications. Circuits, Systems, and Signal Processing, 1–18. doi:10.1007/s00034-015-0041-5.
Noll, T. G. (1991). Carry-save architectures for high-speed digital signal processing. Journal of VLSI signal processing systems for signal, image and video technology, 3(1–2), 121–140.
Meher, P. K., & Park, S. Y. (2013). CORDIC designs for fixed angle of rotation. IEEE Transactions on Very Large Scale Integration (VLSI) Systems, 21(2), 217–228.
Lin, Y. C., Jou, S. J., & Shiue, M. T. (2012). High throughput concurrent lookahead adaptive decision feedback equalizer. IET Circuits, Devices and Systems, 6(1), 52–62.
Sailer, T., & Tröster, G. (2003). An Efficient VLSI Architecture for Computing Decision Feedback Equalizer Coefficients from the Channel State Information. Journal of VLSI signal processing systems for signal, image and video technology, 35(1), 91–103.
Chakraborty, M., Dhar, A. S., & Pervin, S. (2001). CORDIC realization of the transversal adaptive filter using a trigonometric LMS algorithm. In proceedings of 2001 IEEE International Conference on Acoustics, Speech, and Signal Processing, 2001 (ICASSP'01), (2), 1225–1228.
Mandal, A., Mishra, R., Kaushik, B. K., & Rizvi, N. Z. (2015). Design of LMS Adaptive Radar Detector for Non-homogeneous Interferences, IETE Technical Review. doi:10.1080/02564602.2015.1093436.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Mandal, A., Mishra, R. Design of Complex Non-Linear Adaptive Equalizer in Mitigating Severe Intersymbol Interferences. J Sign Process Syst 84, 225–236 (2016). https://doi.org/10.1007/s11265-015-1047-8
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11265-015-1047-8