1 Introduction

Significant effects on chemical equilibrium in small closed (“nanoconfined”, NC) reaction mixtures (NCECE) were predicted by us first for the reaction \({A_2}+{B_2} \Leftrightarrow 2AB\) in the framework of the statistical-mechanics partition-function based methodology [1]. Generally, the effect involves distinct enhancement of the equilibrium constant in the case of exothermic reactions. Later, a pronounced NCECE induced enhancement was evaluated for nucleotide dimerization within molecular cages taking into account hydrogen-bonding energy variations under pyridine vs. aqueous environments [2]. It can be noted that nanoconfinement can alter also the intrinsic properties of water [3,4,5,6], which can somewhat affect the overall reaction energy, but probably cannot change significantly the basic NCECE effect. Our subsequent work, dealing with nanoconfined nitrogen hydrogenation steps on the Ru(0001) surface [7] and taking into account DFT-computed energies of the adsorbed species, predicted again pronounced deviations from the thermodynamic limit (TL) of the corresponding macroscopic system. Just recently, we reported about enhanced dimerization of two Ir atoms inside the core of Pd–Ir nanoparticles (NPs) using simple (uniform) energetics [8]. All these addition reaction studies employed the (ideal) lattice-gas model (LGM) [1], whereas this work deals also with a non-lattice model (NLM) applied to both NC addition and dimerization reactions (e.g., between solutes or gaseous molecules), as well as with Ir subsurface dimerization within the LGM using improved energetics.

It can be noted that the pioneering approach of Hill to “thermodynamics of small systems” [9] considered isomerization (unimolecular) reactions only, thus overlooking the NCECE, which starts to be relevant in the case of bimolecular reactions. A review of Hill’s theory and of more recent, sometimes controversial ideas on “nanothermodynamics” was given later by Garcia-Morales et al. [10]. It should be further noted that the term “confinement” is often applied to systems that are actually open and/or contain huge number of molecules, such as reactions within carbon pores in equilibrium with a gas phase [11], and often the focus is on effects of pore walls and geometry [12] (e.g., slit and cylindrical nanopores). This situation is successfully treated by the reaction ensemble Monte Carlo method (RxMC) [13] and DFT energetics. To avoid ambiguity, it should be stressed that the NCECE can occur only in small closed (“nanoconfined”) systems that contain very limited number of molecules (typically up to ~ 10). It originates from the inherent reduction in the number of reactant–product mixed microstates in such systems [1, 2]. In other words, the corresponding entropy of mixing, which in macroscopic systems facilitates the backward reaction, is diminished under NC, and is expected even to vanish in the extreme case of a reaction, e.g., addition reactions, involving only two reactant molecules, so the forward reaction can go to completion. In a first approximation, this entropic effect is independent of the shape/geometry of the reaction mixture volume (“nanospace”), except for possible effects of surface adsorption and of the solvent on the reaction energy, as mentioned above [2, 7]. NCECE effects generally diminish with increased nanospace size, while in the case of reactions preserving the overall number of molecules such volume effects are absent [1, 2].

The NCECE phenomenon should be relevant to several advanced routes for the synthesis of encapsulated organic molecules, metallic or inorganic nanoclusters, and other nanoscale structures, as well as to reactions inside pores, droplets or nanoalloys. Yet, it appears that a comprehensive recognition of the NCECE strict nanoconfinement conditions for its potentially practical implications, as well as its entropic origin and theoretical importance, are still lacking. For example, the NCECE was referred to in recent studies of synthesis of colloidal silver nanoparticles [14, 15] and AgBiSe2 nanowires [16], although the nanoconfined necessary conditions probably were not met. A recent work by Szymanski et al. [17] is particularly relevant in the context of part of the present article. While our partition-function based methodology seems to be preferred for studies of nanoconfined equilibrated reaction systems, that study used a kinetics-based approach, namely, numerical integration of stochastic master equations [18,19,20] and Monte Carlo simulations [21]. While it reaffirmed the effect and reproduced the enhanced equilibrium constant under nanoconfinement, \({K^{NC}}\), and its proportionality under certain conditions to the squared value of the thermodynamic \({K^{TL}}\) predicted by us before [1], that work neither referred to the entropic origin of the phenomenon, nor to our above-mentioned pertinent original studies [1, 2, 7, 22]. Furthermore, here we refer not only to the remarkable NCECE manifestations in exergonic reactions, but also to the less common and almost unexplored endergonic ones. The present straightforward approach that includes rather simple formulations and computations can furnish also fluctuations in concentrations and reaction extent.

Various other factors were attributed before to the increased reactivity in nanospaces, such as the above-mentioned geometrical constrains preorganizing encapsulated molecules toward the transition state, preferential guest–host (interfacial) interactions, including selective adsorption on pore walls, and (increased) effective concentrations or density [11, 23]. Full verification of the NCECE, including its apparent dominance over the above alternative confinement effects (e.g., of energetics origin), was reported by us for ssDNA hybridization [22] based on previous experimental data (single-molecule fluorescence from labeled DNA confined inside nanofabricated chambers in aqueous solution [24]). These unambiguous results can serve as a case study that justifies focusing on the role of the smallness of fully confined (i.e., “closed”) molecular mixtures as inducing a dominant entropic effect. While in other cases the dominance of one effect or the other can depend on the particular system properties, experimental observations can help to identify the dominant effect. In particular, it appears that the NCECE should be much more system-size dependent than other, e.g., energetic contributions, but according to the previous and present studies (see below) only for a system consisting of quite small numbers of reacting molecules, beyond which the effect should actually disappear.

The article is organized in three main parts, namely, statistical-mechanical derivations using the NLM and LGM followed by pertinent computation results, and ending with the introduction of quite distinctive NCECE effects predicted for Pd–Ir nanoparticles. Regarding the latter, the strong Pd tendency to segregate at the alloy surface (according to Ref. [25] and results below), makes the core a natural confined nanospace for Ir dimerization [8]. In addition to the above-mentioned energetically equivalent intra-core sites (energetics1) [8], a more realistic approach is employed (energetics2) that takes into account coordination dependent bond energy variations (CBEV), introduced by us earlier [26]. Thus, the nearest-neighbor (NN) elemental bond-energy variations of Pd and Ir are derived for surface–subsurface (and intra-surface) bonds employing DFT computed surface energies [27]. These variations are found to play a significant role in the energy of dimerization and its specific subsurface sites. On the other hand, elastic effects on the near-surface energetics and compositions are neglected here because of the very small difference (~ 1%) in atomic radii between the two elements.

It is worth noting that Pd–Ir nanoparticles are efficient catalysts, e.g., in promoting preferential oxidation of CO in the presence of excess H2 in proton exchange membrane fuel cells [28,29,30], in the selective hydrogenation of benzonitrile [31], and in tetralin hydroconversion, which is key to reducing particulate emissions arising from the combustion of diesel fuel [32, 33]. The results presented in Sect. 3 suggest that the NCECE and CBEV effects are likely to have some impact on Pd–Ir NP catalytic activities.

2 Statistical–Mechanical Derivation: NC Addition and Dimerization Reactions

2.1 Non-Lattice Model

The case of \(A+B \Leftrightarrow C\) chemical equilibrium, involving initially very limited stoichiometric numbers (\({n_0}\)) of solute (or gas) \(A\) and \(B\) molecules nano-confined in volume \(V\) in contact with a thermal reservoir, has been chosen for modeling. The pertinent equilibrium-constant and reaction-extent are compared to the TL macroscopic-system values for the same initial reactant molarities. In order to obtain \(K_{{NLM}}^{{NC}} \equiv [C]/([A][B])\) the average numbers of reactant and product molecules per unit volume have to be computed. The theoretical assessment of the NCECE for the addition reaction starts from the canonical-ensemble partition-function given for any \({n_0}\) by,

$$Q_{{NLM}}^{{add}}=\sum\limits_{{{n_C}=0}}^{{{n_0}}} {\frac{{q_{A}^{{{n_0} - {n_C}}}}}{{({n_0} - {n_C})!}}\frac{{q_{B}^{{{n_0} - {n_C}}}}}{{({n_0} - {n_C})!}}\frac{{q_{C}^{{{n_C}}}}}{{{n_C}!}}\exp [ - ({n_C} - {n_0})\Delta E/kT]} ,$$
(1)

where \({q_X}\) (\(X=A,\,B,\,C\)) denotes the molecular partition function, and \(\Delta E\) = reaction energy (per product molecule). After omitting a microstate-independent prefactor that does not affect computations of average properties Eq. 1 becomes,

$$Q_{{NLM}}^{{add}}=\sum\limits_{{{n_C}=0}}^{{{n_0}}} {\frac{1}{{{{[({n_0} - {n_C})!]}^2}{n_C}!}}{{\left[ {\frac{{{q_C}}}{{{q_A}{q_B}}}\exp ( - \Delta E/kT)} \right]}^{{n_C}}}} .$$
(2)

Considering first the TL case of very large \({n_0}\), the maximal term in the partition function is highly dominant, and it corresponds to the condition, \(\frac{{n_{C}^{{TL}}}}{{{{(n_{0}^{{TL}} - n_{C}^{{TL}})}^2}}}=\frac{{{q_C}}}{{{q_A}{q_B}}}\exp ( - \Delta E/kT)\). Furthermore, \({{n_{C}^{{TL}}} \mathord{\left/ {\vphantom {{n_{C}^{{TL}}} {{{\left( {n_{0}^{{TL}} - n_{C}^{{TL}}} \right)}^2}}}} \right. \kern-0pt} {{{\left( {n_{0}^{{TL}} - n_{C}^{{TL}}} \right)}^2}}}={{{K^{TL}}} \mathord{\left/ {\vphantom {{{K^{TL}}} {{{10}^3}V{N_{Av}}}}} \right. \kern-0pt} {{{10}^3}V{N_{Av}}}}\) (Avogadro’s number, \({N_{Av}}\), and the factor 103 corresponding to the conversion of cubic meters to liters, appear since the equilibrium constant is defined in terms of molarities), so the latter term can be substituted into Eq. 2 brackets giving,

$$Q_{{NLM}}^{{add}}=\sum\limits_{{{n_C}=0}}^{{{n_0}}} {\frac{1}{{{{[({n_0} - {n_C})!]}^2}{n_C}!}}{{\left( {\frac{{K_{{NLM}}^{{TL}}}}{{{{10}^3}V{N_{Av}}}}} \right)}^{{n_C}}}} ,$$
(3)

Any average value characterizing the system can be obtained using the partition function, such as the average numbers of reactant and product molecules (\(\overline {{{n_A}}}\), \(\overline {{{n_B}}}\), \(\overline {{{n_C}}}\)), yielding the NC equilibrium constant \(\left( {K_{{NLM}}^{{NC}}={{\overline {{{n_C}}} {{10}^3}V{N_{Av}}} \mathord{\left/ {\vphantom {{\overline {{{n_C}}} {{10}^3}V{N_{Av}}} {\overline {{{n_A}}} \times \overline {{{n_B}}} }}} \right. \kern-0pt} {\overline {{{n_A}}} \times \overline {{{n_B}}} }}} \right)\), the NC reaction extent \(\left( {{\xi ^{NC}}=\overline {{{n_C}}} /{n_0}} \right)\) and the equilibrated system energy \({E^{NC}}={\xi ^{NC}}{n_0}\Delta E\) (with respect to the initial pure-reactant state). Likewise, the NC thermal fluctuations in terms of the variance, \(\sigma _{C}^{2} \equiv \overline {{{{(\Delta {n_C})}^2}}} =\overline {{n_{C}^{2}}} - {(\overline {{{n_C}}} )^2}\), \(\sigma _{\xi }^{2}=\sigma _{C}^{2}/n_{0}^{2}\) and \(\sigma _{E}^{2}=\sigma _{\xi }^{2}n_{0}^{2}\Delta {E^2}\), can be obtained. It can be noted that the latter equation together with the known relation between heat-capacity and fluctuations in energy, \({C_V}=\sigma _{E}^{2}/k{T^2}\), leads to \(\sigma _{\xi }^{2}=k{T^2}{C_V}/n_{0}^{2}\Delta {E^2}\), and since \(C_{V}^{{TL}} \propto {n_0}\), the standard-deviation \({\sigma _\xi }\) should be proportional to \(1/\sqrt {{n_0}}\) for large enough \({n_0}\).

The dimerization reaction \(M+M \Leftrightarrow D\) can be treated similarly. The reaction involves initially \(2{n_0}\) monomers \(M\), which can form \({n_0}\) dimers \(D\) at the most. Taking into account that the numbers of dimers and monomers are related by \({n_M}=2({n_0} - {n_D})\), the derived canonical-ensemble partition-function is somewhat similar to \(Q_{{NLM}}^{{add}}\) (Eq. 3),

$$Q_{{NLM}}^{{dim}}=\sum\limits_{{{n_D}=0}}^{{{n_0}}} {\frac{1}{{[2({n_0} - {n_D})]!}}\frac{1}{{{n_D}!}}{{\left( {\frac{{K_{{NLM}}^{{TL}}}}{{{{10}^3}V{N_{Av}}}}} \right)}^{{n_D}}}} .$$
(4)

Again, starting from this \(Q\) all characteristics of the system can be calculated including the reaction extent, \({\xi ^{NC}}=\overline {{{n_D}}} /{n_0}\) and the equilibrium constant, \(K_{{NLM}}^{{NC}} \equiv [D]/{[M]^2}\).

2.2 Lattice-Gas Via Non-Lattice Model

While the NLM is appropriate for NCECE exploration for nanoconfined gas (e.g., in closed pores) or solute molecules (e.g., in droplets), the case of solid solutions such as crystalline alloy nanoparticles requires derivation in the LGM. Thus, the dimerization of only two impurity M atoms inside S–M nanoparticles was studied by us previously [8] assuming energetically uniform (equivalent) intra-core sites (energetics1). The latter assumption can be plausible as a first approximation, since each impurity atom residing in the core have similar NN surroundings. The corresponding partition-function was given by us previously [8],

$$Q_{{LGM}}^{{dim}}=\left[ {\frac{{n(n - 1)}}{2} - n^{\prime}} \right]\exp \,(\Delta E/kT)+n^{\prime},$$
(5)

where \(n\) denotes the number of intra-core atomic sites and \(n^{\prime}\) corresponds to the number of dimer locations, namely, NN pair bonds. \(Q_{{LGM}}^{{dim}}\) readily yields the reaction extent, namely, the probability of dimer formation, \({\xi ^{NC}}=n^{\prime}/Q_{{LGM}}^{{dim}}\).

Concentrations of M atoms and D dimers are related to the reaction extent as \({c_M}=c_{M}^{{\hbox{max} }}(1 - {\xi ^{NC}})\) and \({c_D}=c_{D}^{{\hbox{max} }}{\xi ^{NC}}\), where \(c_{M}^{{\hbox{max} }}=2/n\) and \(c_{D}^{{\hbox{max} }}=1/n^{\prime}\). Since the lattice-gas chemical-potential depends on \({c \mathord{\left/ {\vphantom {c {1 - c}}} \right. \kern-0pt} {1 - c}}\) [34], the dimerization equilibrium constant is given by, \(K_{{LGM}}^{{NC}}={{{c_D}/(1 - {c_D})} \mathord{\left/ {\vphantom {{{c_D}/(1 - {c_D})} {{{[{c_M}/(1 - {c_M})]}^2}}}} \right. \kern-0pt} {{{[{c_M}/(1 - {c_M})]}^2}}}\), that can be approximated by \({{{c_D}} \mathord{\left/ {\vphantom {{{c_D}} {c_{M}^{2}}}} \right. \kern-0pt} {c_{M}^{2}}}\) in medium-large dilute NPs (\({c_M},{c_D}<<1\)). The computed data will be compared to the thermodynamic-limit equilibrium-constant corresponding to very large number of impurity atoms in a macroscopic lattice, \(K_{{LGM}}^{{TL}} \approx \exp ( - \Delta E/kT)\). Likewise, for a given initial M concentration, the NC reaction extent, \({\xi ^{NC}}\), can be compared with \({\xi ^{TL}}\) related to \(K_{{LGM}}^{{TL}}\).

In a first attempt to correlate LGM predictions with those of the NLM, M and D LGM concentrations should be expressed by molarities, \([M]={{{c_M}n} \mathord{\left/ {\vphantom {{{c_M}n} {{{10}^3}V{N_{Av}}}}} \right. \kern-0pt} {{{10}^3}V{N_{Av}}}}\) and \([D]={{{c_D}n^{\prime}} \mathord{\left/ {\vphantom {{{c_D}n^{\prime}} {{{10}^3}V{N_{Av}}}}} \right. \kern-0pt} {{{10}^3}V{N_{Av}}}}\), respectively. Taking into account that \(n^{\prime}/n=6\) in a macroscopic fcc lattice, the TL equilibrium constant to be substituted into the NLM partition function (\(Q_{{NLM}}^{{dim}}\)) reads \(K_{{NLM}}^{{TL}}={[D]^{TL}}/{({[M]^{TL}})^2}=6 \times {10^3}V_{{S}}^{{TL}}{N_{Av}}K_{{LGM}}^{{TL}}\), where \(V_{{S}}^{{TL}}\) denotes the volume per S atom (estimated via the density and the atomic weight). Another input parameter is the NC volume, \(V\) (to be used in the NLM) that somewhat exceeds \(nV_{{S}}^{{TL}}\). In particular, since the number of sites per unit volume, \(n/V\) (vs. \(1/V_{{S}}^{{TL}}\)), decreases with the average number of neighbors per site as \(\frac{{n/V}}{{1/V_{{S}}^{{TL}}}}=\frac{{2n^{\prime}/n}}{{12}}\), the volume reads \(\frac{6}{{n^{\prime}/n}}\,nV_{{S}}^{{TL}}\). By substitution of these expressions for \(K_{{NLM}}^{{TL}}\) and \(V\), the NLM partition function (4) is obtained in terms of the lattice characteristics \(n\), \(n^{\prime}\) and \(K_{{LGM}}^{{TL}}\) (without explicit dependence on the NC volume),

$$Q_{{NLM}}^{{dim}}=\sum\limits_{{{n_D}=0}}^{{{n_0}}} {\frac{1}{{[2({n_0} - {n_D})]!}}\frac{1}{{{n_D}!}}{{\left( {\frac{{n^{\prime}}}{{{n^2}}}K_{{LGM}}^{{TL}}} \right)}^{{n_D}}}} .$$
(6)

This yields \(\xi _{{NLM}}^{{NC}}\) and \(K_{{NLM}}^{{NC}}\) (for any number of dimers in dilute NP) aimed to replace the n0 > 1 unachievable \(\xi _{{LGM}}^{{NC}}\) and \(K_{{LGM}}^{{NC}}\).

3 Results and Discussion

3.1 General Addition Reaction (NLM)

The results for a stoichiometric \(A+B \Leftrightarrow C\) reaction are presented for both exergonic (\({K^{TL}}>1\)) and for endergonic (\({K^{TL}}<1\)) reactions, but the more important exergonic case is highlighted. Plots of \({K^{NC}}\equiv{K^{NC}_{NLM}}\) computed as function of system size for three \({K^{TL}}\) values (Fig. 1a) show NCECE-induced significant enhancement of \({K^{NC}}\) relative to \({K^{TL}}\) only for quite small sizes (\({n_0}<10\)), and it increases with \({K^{TL}}\). The NCECE-induced increase of the equilibrium constant is reflected in a corresponding decrease of the residual equilibrium fraction of reactant molecules, \((1 - \xi )\), which is more pronounced for smaller system sizes (Fig. 1b). While substantial NCECE-induced variations, \(\Delta \xi \equiv {\xi ^{NC}} - {\xi ^{TL}}\), correspond in many cases to intermediate values of the equilibrium constant when both \({\xi ^{NC}}\) and \({\xi ^{TL}}\) are not too close to the limits (0 or 1), only the ratio of the diminished \((1 - {\xi ^{NC}})\) to \((1 - {\xi ^{TL}})\) is significant for the present case of a large equilibrium constant, \({K^{TL}}={10^6}\) L/mol, as can be seen in Fig. 1b (this can be important when trace residual concentrations play a role in nanoscale properties).

Fig. 1
figure 1

The NCECE effect computed in the NLM. a NC equilibrium constants versus the initial number of reactant molecules \({n_0}\), (constant molarity \({[A]_0}={[B]_0}=\)1 mol/L) for the marked values of the macroscopic TL equilibrium constant. b Residual equilibrium fraction of reactant molecules versus initial molar concentration for three system sizes (\({K^{TL}}={10^6}\) L/mol). The partition-function based plots accurately match reported kinetics-approach results [17] (second plot from the top in a and b)

Full size image

Plots of \(\ln {K^{NC}}\) versus \(\ln {K^{TL}}\) reflect distinctly the increasing NCECE effects in smaller size systems (Fig. 2a). In accordance with our previous LGM-based predictions [1], in the case of exergonic reactions \(\ln {K^{NC}}\) exhibits a doubled slope compared to \(\ln {K^{TL}}\) that results in highly enhanced values, especially at the lower temperature range when the bimolecular association of \(A\) and \(B\) molecules prevails, particularly for the smallest system (\({n_0}=1\)). Even near \({K^{TL}}=1\) the relative enhancement obtained for \({K^{NC}}\) is about 100% in magnitude (Fig. 2a inset). On the other hand, for endergonic addition reactions the effect becomes minor, and starting from \(\ln {K^{TL}} \approx - 1\) it gradually vanishes at lower temperatures when the system-size independent unimolecular dissociation prevails (as we showed before for endothermic reactions, NCECE is meaningful only if the sum of the product stoichiometric coefficients of the elementary reaction exceeds one [1]). Likewise, the reaction extent exhibits NCECE-induced enhancement (\(\Delta \xi\)) primarily in the exergonic case (Fig. 2b). As noted above, it is maximal in the range where the equilibrium constant is not too large (i.e., \(T\) is not too low), otherwise both \({\xi ^{NC}}\) and \({\xi ^{TL}}\) approach the upper limit (\(=1\)), so \(\Delta \xi \to 0\). Furthermore, the maximal standard-deviation of the reaction extent (\({\sigma _\xi }\), or its fluctuations, \(\sigma _{\xi }^{2}\)) corresponds to a high-\(T\) quite uniform distribution over microstates, and consistently decreases for larger system sizes (Fig. 2b). This maximal value obeys the dependence predicted above, namely, it is proportional to the reciprocal of the square root of the initial number of reacting molecules, \({n_0}\).

Fig. 2
figure 2

The NCECE effect for exergonic and endergonic addition reactions (NLM). a Equilibrium constants and b extents for \(A+B \Leftrightarrow C\) reaction (blue lines) versus \(\ln {K^{TL}}\) computed for the marked initial number of reactant molecule pairs (constant molarity \({[A]_0}={[B]_0}=\)1 mol/L). The corresponding standard-deviation of the reaction extent is given by red lines. The value of \(\ln {K^{TL}}\) can be considered as linearly related to (i) the inverse temperature of a given reaction, or (ii) energies of different reactions at a given temperature

Full size image

3.2 Addition Versus Dimerization (NLM)

It is instructive to compare these addition reaction predictions with the NCECE effects computed for \(M+M \Leftrightarrow D\) dimerization reactions (Fig. 3a). First, the dimers exhibit larger extents (even in the TL), namely, enhanced stability related to diminished mixing entropy involving two chemical species, compared to three in the case of the addition reaction (Fig. 3b). Secondly, as can be seen, a crossing between the NC and TL curves is predicted only for the dimerization. In particular, NCECE-induced dimerization enhancement takes place mostly in the exergonic region and an inverse NCECE in the endergonic region. The latter effect, mentioned briefly in our LGM-based modeling of \({A_2}+{B_2} \Leftrightarrow 2AB\) [1], is attributed to the abundance of reactant–product mixed microstates corresponding to intermediate \({\xi ^{TL}}\) values (maximal TL mixing entropy appears at \({\xi ^{TL}} \approx 0.39\), Fig. 3b). Thus, for high \({\xi ^{TL}}\) this facilitates the backward dissociation reaction (leading to ordinary NCECE in the exergonic region), whereas for relatively small \({\xi ^{TL}}\) the forward reaction is promoted compared to the NC systems in which the number of reactant–product microstates is limited or even vanishes, so the dissociation comparatively prevails (inverse NCECE in the endergonic region). For the same reason, the \({\xi ^{TL}}\) temperature variations are more gradual compared to those of the \({\xi ^{NC}}\). On the other hand, in the case of \(A+B \Leftrightarrow C\) the forward reaction is hardly promoted by the TL mixing entropy, since the latter is significant even at zero reaction extent and mostly decreases with \({\xi ^{TL}}\) increase (its maximum corresponds to \({\xi ^{TL}} \approx 0.14\), Fig. 3b). An additional factor opposes the inverse NCECE and further enhances the ordinary effect (with respect to the TL), unlike the dimerization case (Fig. 3c). Thus, while in the latter every monomer can associate with every other monomer independently of the system size, in the stoichiometric addition reaction the fraction of \(A+B\) molecular pairs available for association decreases with size increase, since nonreacting \(A+A\) and \(B+B\) pairs appear. Namely, in the TL a certain molecule (e.g., \(A\)) can react with only half of the other molecules (i.e., \(B\)), unlike with the total amount of molecules in the case of dimerization or in the case of the smallest addition system (single A + single B).

Fig. 3
figure 3

a Extent under nanoconfinement as function of the thermodynamic limit equilibrium constant computed for dimerization (blue lines) and addition (black lines) reactions (the latter is given in Fig. 2b). The initial numbers of reactant molecule pairs are marked (constant molarity \({[M]_0}=\)2 mol/L versus \({[A]_0}={[B]_0}=\)1 mol/L). b Entropy of mixing calculated for the two reactions by using the thermodynamic-limit ideal-gas formula (\(\propto - \sum {{x_i}\ln } {x_i}\)). c The NCECE-induced variations of the reaction extent, \(\Delta \xi \equiv {\xi ^{NC}} - {\xi ^{TL}}\). Note the inverse effect in the case of endergonic dimerization versus nearly no effect in the case of the endergonic addition reaction

Full size image

3.3 Application to Ir Dimerization

Intra-core dimerization of a single Ir atomic pair was studied using the above-mentioned two energetics models, namely, energetically equivalent intra-core sites (energetics1), and the more accurate energetics2 that takes into account surface effects via coordination dependent bond-energy variations (CBEV).

3.3.1 Energetics1

For Ir atoms in the fcc Pd core (each surrounded by 12 NN Pd atoms) the energy of the intra-core \(2Ir \Leftrightarrow I{r_2}\) reaction equals twice the bulk Effective-Pair-Interaction (EPI), \(\Delta {E_1}=2V'=({w^{PdPd}}+{w^{IrIr}} - 2{w^{PdIr}}) \approx - 74\) meV, as derived from DFT-computed low-temperature formation enthalpy [35]. According to the computations, below a certain temperature the equilibrium constant corresponding to dimerization of one pair of impurity atoms is enhanced and the \(\ln {K^{NC}}\) slopes are twice larger than the TL slope (Fig. 4a), just as in the case of the addition reaction (Fig. 2a). As noted above, this slope doubling is characteristic of nanoconfined bimolecular reactions [1]. At temperatures above the crossing of the \(\ln {K^{NC}}\) curves with the \(\ln {K^{TL}}\) line the introduced “inverse-NCECE” effect is manifested. Likewise, the extent of nanoconfined dimerization is enhanced at temperatures below the crossing, whereas at higher temperatures the effect is reversed (Fig. 4b). Moreover, plots obtained by the non-lattice and lattice-gas models are quite close in the case of 55-atom and almost coincide for the 309-atom NP cores (in even larger NPs the difference practically disappears, Fig. 4a). The somewhat higher LGM versus NLM extent obtained for the smaller core seems to be due to geometrical factors, namely, this core contains quite a large fraction of nearest-neighbor site pairs, whereas in the NLM the concept of nearest-neighbors is irrelevant in the present context. Employing the NLM facilitates dimerization modeling for several pairs of impurity atoms (Fig. 4c) avoiding tedious LGM combinatorial computations. As can be seen, in the case of four pair dimerization the NCECE almost disappears, especially the inverse effect.

Fig. 4
figure 4

a The temperature dependence of the dimerization equilibrium “constants” (energetics1) for two Ir atoms in 55 and 309-atom (size magic-numbers) cores of cuboctahedral Pd–Ir NPs, b the corresponding NC dimerization extents (the TL curves correspond to the same \(c_{M}^{{\hbox{max} }}\) and \(c_{D}^{{\hbox{max} }}\) values as for the NC), and c the extent for larger numbers of Ir pairs in 55-atom core. The NLM and LGM predictions are shown by magenta and blue lines, respectively, and the thermodynamic limit (TL) by black dashed lines

Full size image

3.3.2 Energetics2

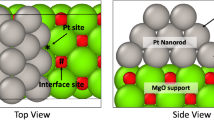
According to the CBEV model introduced by us earlier [26], the energy of a near-surface NN \(m - n\) elemental bond is typically amplified relative to the bulk pair bond-energy \({w_b}\) by a coordination-related contribution, \({w_{mn}}={w_b}+\delta {w_{mn}}\). In the present work the coordination dependence of \(\delta {w_{mn}}\) as six-term polynomial functions [26] is extracted from DFT derived bulk energies and surface-energy anisotropies of pure Pd and Ir [27]. The reasonable accuracy of this two-layer model was revealed before by comparison to direct DFT computations of Pt–Pd NPs [26, 36], as well as to near surface compositional profiles measured for Pt0.25Rh0.75(111) [26, 37]. According to Fig. 5a and Table 1 surface–subsurface bonds exhibit the expected general tendency of increased strengthening for lower coordinations. Furthermore, all bond energy variations of Ir are larger than the respective Pd variations, and the difference \(\Delta \delta w\) also increases for lower coordinations. Therefore, Ir being the element with larger \(\delta {w_{mn}}\) tends to enrich the subsurface [26], especially at subvertexes (sv, 5 NNs) and subedges (se, 7 NNs). All relevant surface–subsurface bonds are hetero-atomic and their energies are found using the elemental bonds by \({w^{PdIr}}=({w^{PdPd}}+{w^{IrIr}} - 2{V'^{CBEV}})/2\), where \({V'^{CBEV}}\) denotes the corresponding coordination-dependent EPIs that are expected to increase relative to the bulk value as \({V'^{(111)}}={V'^{(100)}}=1.5\,V'\) and \({V'^{edge}}={V'^{vert}}=2\,V'\) [38]. Thus, by straightforward adding NN bond energies (Table 1) the energetically most favorable sites obtained for a single Ir impurity atom are indeed the 12 subvertexes and next are the subedges. Most favorable for Ir2 dimers are the 48 subvertex–subedge bonds with the corresponding dimerization geometry schematically illustrated in Fig. 5b. As given in Table 1, the reaction \(2I{r^{sv}} \Leftrightarrow Ir_{2}^{{sv - se}}\) is less exothermic than \(I{r^{sv}}+I{r^{se}} \Leftrightarrow Ir_{2}^{{sv - se}}\) \((\Delta {E^{sv - sv}}>\Delta {E^{sv - se}})\).

Fig. 5
figure 5

a The dependence of surface–subsurface elemental bond-energy variations, relative to the bulk bonding, on the number of pair missing bonds, as extracted from DFT-computed surface energies. The larger variations for Ir send it to subsurface sites below the surface-segregated Pd. b Illustration of \(2I{r^{sv}} \Leftrightarrow Ir_{2}^{{sv - se}}\) equilibrated dimerization at energetically preferred subsurface sites of Pd surface-segregated 561-atom Pd–Ir cuboctahedron

Full size image
Table 1 Summary of derived energies related to Pd–Ir cuboctahedron energetics2 model
Full size table

In order to compute the dimerization extent as function of temperature the partition function is used,

$$Q_{{LGM,CBEV}}^{{dim}}=\frac{{{n^{sv}}({n^{sv}} - 1)}}{2}\exp (\Delta {E^{sv - sv}}/kT)+({n^{sv}}{n^{se}} - n{'^{sv - se}})\exp (\Delta {E^{sv - se}}/kT)+n{'^{sv - se}},$$

where the three contributions correspond to arrangements of (i) two Ir atoms on subvertexes, (ii) one Ir atom on subvertex and the second on subedge, and (iii) subvertex–subedge dimer. The extent (probability) of dimer formation is given readily by,

$${\xi _{e2}}=n{'^{sv - se}}/Q_{{LGM,CBEV}}^{{dim}}.$$

Similarly to the modeling with energetics1, \({\xi _{e2}}\) decreases (i.e., \(I{r_2}\) dissociates) with temperature and with the increase of the NP size (Fig. 6). Furthermore, the CBEV-induced diminishing of available nanospace compared to the entire core in the case of the uniform energetics1 model amplifies the NCECE. This entropy-related “nanospace size effect” [2] is better reflected in curves of normalized extra dimerization, \(\Delta \xi' \equiv( {\xi _{e2}}/{\xi _{e1}} - 1)\times100\), exhibiting a steeper rise with temperature for larger NP sizes (Fig. 6, inset). (Since the role of entropy generally decreases at lower temperatures, both \({\xi _{e1}}\) and \({\xi _{e2}}\) approach the same maximal value (Fig. 6), so \(\Delta \xi'\) gets smaller). In particular, this trend is associated with the different dependence of the number of subedge sites on size (“energetics2 nanospace”) versus the dependence of the total number of core sites (“energetics1 nanospace”), i.e., they are approximately proportional to the NP radius \(r\) and to \({r^3}\), respectively. Hence, the latter nanospace grows more significantly with size, resulting in larger \(\Delta \xi'\) values. It can be noted that \(Ir\) entropy-driven (equilibrium) eventual desegregation (following \(I{r_2}\) dissociation) should take place at quite high temperatures (segregation energies are given in Table 1), and is expected to strengthen with the NP size increase. Clearly, the \(Ir\) core and additional subsurface sites have to be included in computations of the NCECE full temperature-dependence. This somewhat more complex situation is beyond the scope of this work, yet it seems that the extent values for the coupled equilibria would be intermediate between the two energetics curves (solid and dashed, Fig. 6).

Fig. 6
figure 6

Comparison of dimerization reaction extents computed in the LGM with the CBEV inequivalent site energetics (energetics2, solid lines) versus equivalent site energetics (energetics1, dashed lines) for 309-atom (magenta), 561-atom (blue) and 923-atom (green) cores of Pd cuboctahedral NPs with two Ir impurities. Inset: The relative magnitude of the two model dimerization extents, \(\Delta \xi' =({\xi _{e2}}/{\xi _{e1}} - 1)\times100\)

Full size image

4 Conclusions

The Statistical–mechanical modeling of intrinsic nano-confinement effects on equilibrated reactions (NCECE) introduced by us before is expanded in this article to the following main novel issues:

  1. (i)

    Derivation of the effect using a non-lattice model (NLM) and computations for general addition reactions;

  2. (ii)

    NLM-based derivation for dimerization reactions and comparison to NCECE effects predicted for addition reactions;

  3. (iii)

    Modeling of Ir dimerization at subsurface sites of dilute Pd–Ir nanoparticles using the lattice gas model (LGM) with improved surface–subsurface bond energetics (compared to the previous use of uniform core energetics).

Regarding the first two issues enhancement of the equilibrium constant and extent is predicted for exergonic reactions, whereas the NCECE is diminished for endergonic reactions and even inverse effects can take place in the case of dimerization. The NLM can reproduce quite accurately the NCECE effects obtained by the LGM with uniform core energetics, especially in medium-large NPs exceeding few hundreds of atoms. Furthermore, by avoiding tedious LGM combinatorial computations the NLM facilitates studies of dimerization in case of any number of impurity atoms compared to the case of only one pair of Ir atoms studied by the LGM. Using the latter, the enhancement effect increases under the more elaborate coordination-dependent bond energetics, since the CBEV diminishes the actual reaction nanospace, namely, it makes the subsurface edges and vertexes energetically most preferable for solute Ir atoms and dimers. Pd–Ir model NPs (cuboctahedrons) have been chosen as a model system because of the strong Pd surface segregation tendency forming a confined nanospace for Ir dimerization. Moreover, the predicted subsurface dimerization enhancement due to the NCECE can be relevant to alloy NP catalytic properties, e.g., due to possible reactivity modifying ligand effects such as bandwidth changes via hybridization of d-states of surface atoms with subsurface atoms [39]. In this context it can be noted that the previously reported formation of Cu/Pt(111) near-surface alloy (subsurface Cu) enabled tuning the activity for oxygen electroreduction (up to 8 times increase!) [40]. Likewise, it should be emphasized again that the CBEV effect by sending Ir atoms (and Ir2) to populate the NP subsurface, is expected to affect the reactivity of Pd–Ir NPs used as catalysts. A distinct NCECE effect can be anticipated also in certain catalytic reaction steps taking place on NP surface as a nanoconfined space (e.g., Refs. [2, 7]), but only under strict experimental conditions (local equilibrium, small number of molecules, etc.). Finally, modeling of extensive dimerization or even phase-separation transitions anticipated for Pd–Ir NPs with significantly higher Ir content is planned for the near future.