1 Introduction

Interest in thermal convection in rotating porous media is increasing in theoretical and experimental engineering studies and thermal science. Detailed analysis of various aspects of thermal convection has been documented by Getling (1998), Drazin and Reid (2004), Chandrasekhar (2013), and Joseph (2013). Venezian (1969) first studied the effect of temperature modulation on the onset of convection in a horizontal viscous fluid layer. The author observed, employing a series perturbation expansion for the physical quantities in terms of the amplitude of oscillations, that the onset of convection could be advanced or delayed by varying the in-phase or out-of-phase modulation of the critical temperature compared to an unmodulated system. Through a linear analysis, Rosenblat and Herbert (1970) estimated that large oscillations result in the periodicity criteria led to instability at low frequencies. Gershuni et al. (1970) studied the equilibrium stability of a horizontal fluid layer in the presence of a periodically time-varying temperature gradient. Rosenblat and Tanaka (1971) used the Galerkin method to study the effect of temperature modulation on the onset of convection. Floquet theory, which transforms a periodic system into a traditional linear system with a real constant coefficient, was employed to discuss the system’s stability. Caltagirone (1976) investigated the effect of modulated wall temperature on thermal instability in a fluid-saturated porous layer. Chhuon and Caltagirone (1979) investigated the effect of thermal modulation on the system’s stability through experimental and theoretical analyses employing the Floquet theory. Donnelly (1964) was the first to study the thermal instability of a rotating fluid layer under rotational speed modulation using a free surface perturbation method. The author calculated the shift in the critical Rayleigh number and found that the system could be destabilized or stabilized by adjusting modulation frequency appropriately when tangential stress and normal velocity are zero on the surface.

Malashetty and Swamy (2007) observed that symmetric modulation destabilizes the system at low frequencies, but the system gets stabilized at medium and high frequencies for a rotating fluid layer subjected to temperature modulation. In addition, they reported that asymmetric modulation stabilizes convection at all frequencies. The authors also found that the effects of rotation and thermal modulation disappear at high frequencies, regardless of the type of thermal modulation. The effects of gravitational and temperature modulation on rotating stationary Rayleigh-Bénard convection have been studied by Bhadauria et al. (2012) using the Ginzburg-Landau amplitude equation. The authors found that the Rossby number (defined in terms of the Prandtl number and Taylor number) destabilized the system. Moreover, they concluded that similar to an externally applied transverse magnetic field, rotation can also be used as an external means to understand the effect on the convection mechanism by comparing their results with those obtained by Siddheshwar et al. (2012) for magneto-convection. More studies that investigate the impact the rotation on thermal instability in a porous medium have been carried out by Vadasz (1996a, b, 1998), Vadasz and Govender (2001), Desaive et al. (2002), Govender (2003), and Straughan (2001).

Most previous studies considered that the heat transfer in the fluid-saturated porous materials occur under local thermal equilibrium (LTE) condition, where the temperature of both fluid and solid phases are identical. A single energy equation models the temperature profile in the case of LTE. Horton and Rogers (1945) and Lapwood (1948) independently studied the Darcy-Bénard convection considering the LTE model. However, when the solid phase has a different temperature from the saturating fluid, the heat transfer in the medium occurs under local thermal non-equilibrium (LTNE) conditions. The LTNE effect can be determined using an additional energy equation that quantifies the heat distribution within the solid matrix of the porous structure separated from the fluid phase. LTNE effect was first introduced by Anzelius (1926) and Schumann (1929), which used two different temperature fields of solid and fluid phases. These equations use simple linear source/sink terms, allowing local heat transfer between the phases. Later, several authors considered LTNE effects while investigating the stability of convective flow in a porous medium (see, e.g., Banu and Rees (2002), Vafai and Amiri (1998), Malashetty et al. (2005, 2007), Nield and Kuznetsov (2001), Quintard et al. (1997), Rees (2010), Rees and Pop (1999)). Heat exchangers (Luo et al. (2003)), drying of iron ore pellets (Ljung and Lundstrom (2008)), and geothermal energy extraction (Rees et al. 2008) are some of the examples where it is necessary to adopt the LTNE Model. Melt segregation from the deeper Earth to the upper crust or hydrothermal fluid flow in sedimentary basins are important examples of two-phase flows in which the assumption of local thermal equilibrium is violated in geoscientific studies (Stevenson 1989; Rubin 1998).

Recently, Bansal and Suthar (2022) performed a linear stability analysis to study the effect of thermal modulation on the onset of Darcy-Bénard convection using the LTNE model. To the best of our knowledge, such a study does not exist which investigates the effect of thermal modulation on the onset of Darcy-Bénard convection in a rotating porous medium using the LTNE model. Two-phase energy equations are used to model the temperature profile in the solid and fluid phases that lack thermal equilibrium. A sinusoidal function has been considered to modulate the walls’ temperatures. To obtain the results for the following two cases: (a) when the boundary temperatures are modulated in phase, (b) when the modulation is out of phase. A linear stability analysis is performed, assuming modulation amplitude to be infinitesimal and discussing the effect of parameters, such as \(\alpha\), \(\gamma\), \(\omega\), \(\phi\), H, \(\text {Va}\), and \(\text {Ta}\) on the stability of the system. The results of the present paper can be used to study the onset of convection in the building of thermal insulators, oil reservoir modelling, geothermal energy utilization, and nuclear waste disposal where the fluid flows through a porous medium and is subjected to the earth’s rotation.

2 Mathematical formulation

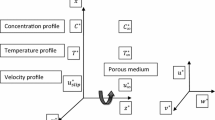
In this study, the coordinate frame (x, y, z) is assumed such that the z-axis is in the vertically upward direction and origin lies on the lower boundary. A Newtonian fluid-saturated horizontal porous layer confined between two infinite extent parallel planes at \(z = 0\) and \(z = d\), heated from below and cooled from above in a time-periodic manner, is considered. Gravitational force is acting in the vertically downward direction. It is assumed that fluid and porous matrix have not attained the local thermal equilibrium and thus a two-field temperature model is used. We consider the modulated boundary temperatures as given by Venezian (1969).

$$\begin{aligned} T_{s} = T_{f} = {\left\{ \begin{array}{ll} T_{0} + \frac{1}{2} \Delta T [1+ \epsilon \cos (\omega t)] &{} ~~~ \text { at}~~~~ z=0,\\ T_{0} - \frac{1}{2}\Delta T [1- \epsilon \cos (\omega t + \phi )] &{} ~~~~\text {at}~~~~z=d, \end{array}\right. } \end{aligned}$$
(2.1)

where \(T_{0}\) is some fluid reference temperature, and \(T_{s}\) and \(T_{f}\) are the solid- and fluid-phase temperatures. \(\epsilon\) and \(\omega\) represents amplitude and frequency of modulation, respectively, and \(\phi\) is the phase angle.

The porous layer is assumed to rotate about the z-axis with an angular velocity, \(\varvec{\Omega } = (0, 0, \Omega )\). The extended Darcy law, which includes the Coriolis and time derivative terms, is used for the momentum equation. To keep the problem analytical tractable we assume the boundaries to be stress-free and isothermal. Under these postulations, the system of equations that govern the fluid motion for the rotating porous layer with LTNE conditions are

$$\begin{aligned}{} & {} \nabla \cdot {\textbf{u}}=0, \end{aligned}$$
(2.2)
$$\begin{aligned}{} & {} \dfrac{\rho _{0}}{\delta } \dfrac{\partial {\textbf{u}}}{\partial t} + \dfrac{2 \rho _{0}}{\delta }{\varvec{\Omega }} \times {\textbf{u}} = -\nabla p - \dfrac{\mu }{K} {\textbf{u}} + \rho (T_{f}){{\textbf {g}}}, \end{aligned}$$
(2.3)
$$\begin{aligned}{} & {} (1- \delta ) (\rho _{0} c)_{s} \dfrac{\partial T_{s}}{\partial t} = (1- \delta ) k_{s} \nabla ^{2} T_{s} - h(T_{s}-T_{f}), \end{aligned}$$
(2.4a)
$$\begin{aligned}{} & {} \delta (\rho _{0} c)_{f} \dfrac{\partial T_{f}}{\partial t} + (\rho _{0} c)_{f} {\textbf{u}}\cdot \nabla T_{f} = \delta k_{f} \nabla ^{2} T_{f} + h(T_{s}-T_{f}), \end{aligned}$$
(2.4b)

where \(\rho (T_{f})\) is given by,

$$\begin{aligned} \rho (T_{f}) = \rho _{0f}[1- \beta (T_{f}-T_{0})], \end{aligned}$$
(2.5)

so that the fluid’s reference density, \(\rho _{0f} =\rho _{f}(T_{0})\).

In the above Eqs. (2.2–2.5), the symbols \({\textbf{u}} = (u, v, w)\) denote the velocity, \(k_{f}\) thermal conductivity, \(\mu\) viscosity, p pressure, and \(\beta\) thermal expansion coefficient of fluid. Further, K represents the permeability and \(\delta\) porosity of the porous medium. \(( \rho _{0}c)_{s}\) and \(( \rho _{0}c)_{f}\) denote the volumetric heat capacity of solid and fluid, respectively. h represents the interphase heat transfer coefficient and \(k_{s}\) thermal conductivity of the solid phase. The physical configuration of the system is illustrated in Fig.1.

Fig. 1
figure 1

Schematic diagram

Full size image

The governing equations are made dimensionless using the following transformation

$$\begin{aligned} {\textbf{r}}_{*}&= \dfrac{ {\textbf{r}}}{d},&\mathbf {u_{*}}&= \dfrac{(\rho _{0} c)_{f} d}{\delta k_{f}} {\textbf{u}},&t_{*}&= \dfrac{k_{f}}{(\rho _{0} c)_{f}d^2} t,&p_{*}&= \dfrac{(\rho _{0} c)_{f} K}{\delta \mu k_{f}} p , \end{aligned}$$
(2.6)
$$\begin{aligned} \omega _{*}&= \dfrac{(\rho _{0} c)_{f}}{k_{f}} d^2\omega ,&\rho _{f*}&= \dfrac{\rho _f - \rho _{0f}}{\rho _{0}},&\theta _{s*}&= \dfrac{T_{s} - T_{0}}{\Delta T},&\theta _{f*}&= \dfrac{T_{f} - T_{0}}{\Delta T}, \end{aligned}$$
(2.7)

where the non-dimensional quantities are denoted with a subscript \(*\).

The resulting non-dimensional system of equations that governs the motion (after dropping the asterisk) can be expressed as

$$\begin{aligned}{} & {} \left( 1+\frac{1}{\text {Va}} \dfrac{\partial }{\partial t} \right) \nabla ^{2} \psi -\sqrt{\text {Ta}} \dfrac{\partial v}{\partial z} + Ra \dfrac{\partial \theta _{f}}{\partial x} = 0, \end{aligned}$$
(2.8)
$$\begin{aligned}{} & {} \left( 1+\frac{1}{\text {Va}} \dfrac{\partial }{\partial t} \right) \dfrac{\partial v}{\partial z} + \sqrt{\text {Ta}} \dfrac{\partial ^{2} \psi }{\partial ^{2} z} = 0, \end{aligned}$$
(2.9)
$$\begin{aligned}{} & {} \alpha \dfrac{\partial \theta _{s}}{\partial t} -\nabla ^{2} \theta _{s} + \gamma H (\theta _{s} - \theta _{f}) = 0, \end{aligned}$$
(2.10)
$$\begin{aligned}{} & {} \dfrac{\partial \theta _{f}}{\partial t} -\nabla ^{2} \theta _{f} - H (\theta _{s} - \theta _{f}) = \dfrac{\partial (\psi ,\theta _{f})}{\partial (x,z)}, \end{aligned}$$
(2.11)

where we introduced stream function \(\psi\), such that \(u = \psi _{z}\) and \(w=-\psi _{x}\).

The corresponding non-dimensionalized boundary conditions are

$$\begin{aligned} \theta _{s} = \theta _{f} = {\left\{ \begin{array}{ll} \frac{1}{2} [1+ \epsilon \cos (\omega t)] &{} ~~~~ \text { at}~~~~ z=0,\\ - \frac{1}{2} [1- \epsilon \cos (\omega t + \phi )] &{} ~~~~\text {at}~~~~z=1, \end{array}\right. } \end{aligned}$$
(2.12)

where \(\nabla ^{2} \equiv \dfrac{\partial ^{2}}{\partial x^{2}} + \dfrac{\partial ^{2}}{\partial z^{2}}\) and the non-dimensional parameters are

$$\begin{aligned} \text {Va}&= \dfrac{\delta Pr}{Da}~~~~\text {(Vadasz number)},\\ Pr&= \dfrac{\mu }{\rho _{0} k_{f}}~~~\text {(Prandtl number)},\\ Da&= \dfrac{K}{d^{2}}~~~\text {(Darcy's number)},\\ \text {Ra}&= \dfrac{\rho g \beta \Delta T K d }{\delta \mu \kappa _{f}}~~~\text {(Darcy-Rayleigh number)},\\ \text {Ta}&= \left( \dfrac{2 \Omega K }{\delta \mu }\right) ^{2}~~~\text {(Darcy-Taylor number)},\\ \alpha&= \dfrac{(\rho _{0} c)_{s}}{(\rho _{0} c)_{f}}\dfrac{k_{f}}{k_{s}} = \dfrac{\kappa _{f}}{\kappa _{s}}~~~\text {(diffusivity ratio)},\\ \gamma&= \dfrac{\delta k_{f}}{(1-\delta )k_{s}}~~~\text {(porosity-modified conductivity ratio)},\\ H&= \dfrac{h d^{2}}{\delta k_{f}}~~~\text {(scaled interphase heat transfer coefficient)}. \end{aligned}$$

Note that these above non-dimensionalized parameters hold when \(0< \delta < 1\). The quantities in the basic state, which is considered quiescent, are given by

$$\begin{aligned} \psi _{b} = 0, \,\,\,\,\,\ \theta _{s} = \theta _{sb}(z,t), \,\,\,\,\,\ \theta _{f} = \theta _{fb}(z,t). \end{aligned}$$

Temperatures of the basic state of solid, \(\theta _{sb}\), and fluid-phases, \(\theta _{fb}\) satisfy the equations:

$$\begin{aligned}{} & {} \alpha \dfrac{\partial \theta _{sb}}{\partial t} =\dfrac{\partial ^{2} \theta _{sb}}{\partial ^{2} z} - \gamma H (\theta _{sb} - \theta _{fb}), \end{aligned}$$
(2.13)
$$\begin{aligned}{} & {} \dfrac{\partial \theta _{fb}}{\partial t} =\dfrac{\partial ^{2} \theta _{fb}}{\partial ^{2} z} + H (\theta _{sb} - \theta _{fb}) , \end{aligned}$$
(2.14)

where the quantities with subscript b represent the basic state.

We shall need the temperature field \(\theta _{fb}\), which consists of the sum of a steady and an unsteady temperature field, i.e., oscillating part \(\epsilon F(z,t)\). Subject to the boundary conditions (2.12), we obtain the quiescent state solution in the form

$$\begin{aligned} \theta _{fb}(z,t) = \frac{1}{2}(1-2z) +\epsilon F(z,t), \end{aligned}$$
(2.15)

where

$$\begin{aligned} F(z,t) = \frac{1}{2}\left[ f(z) e^{i \omega t} + {\bar{f}}(z) e^{-i \omega t}\right] , \end{aligned}$$
(2.16)

with

$$\begin{aligned}{} & {} f(z)= A(\lambda _{1},\lambda _{2},z) +A(\lambda _{2},\lambda _{1},z),\end{aligned}$$
(2.17)
$$\begin{aligned}{} & {} A(\lambda _{1},\lambda _{2},z)= \dfrac{1}{2 \sinh (\lambda _{1})}\dfrac{(\lambda _{2}^{2} + i \omega )}{(\lambda _{2}^{2} - \lambda _{1}^{2})} \left[ e^{- i \phi } \sinh (\lambda _{1} z) + \sinh (\lambda _{1}(1-z))\right] , \end{aligned}$$
(2.18)
$$\begin{aligned}{} & {} \quad \lambda _{1}^{2} = \frac{-X - \sqrt{X^{2} +4(i \omega H(\alpha + \gamma ) + \alpha \omega ^{2} )}}{2}, \end{aligned}$$
(2.19a)
$$\begin{aligned}{} & {} \lambda _{2}^{2} = \frac{-X+ \sqrt{(X^{2} +4(i \omega H(\alpha + \gamma ) + \alpha \omega ^{2} )}}{2}, \end{aligned}$$
(2.19b)

and

$$\begin{aligned} X=(-(1+\gamma )H + i \omega (1+\alpha ) ). \end{aligned}$$
(2.19c)

Also, the solution for \(\theta _{sb}\) can be obtained from Eq. (2.14), excluding the case when  H = 0 (Banu and Rees (2002)). In the next section, we obtain the governing equations for the perturbed quantities and perform linear stability analysis.

3 Stability analysis

We assume finite amplitude perturbation on the quiescent basic state in the form:

$$\begin{aligned} \psi = 0 + \psi ',~~~~~~v = 0 + v',~~~~~~\theta _{s} = \theta _{sb} + \theta _{s}',~~~~~~\theta _{f}=\theta _{fb} + \theta _{f}', \end{aligned}$$
(3.1)

where prime indicates the infinitesimal perturbed quantities. Hence, we obtain

$$\begin{aligned}{} & {} \left( 1 + \frac{1}{\text {Va}}\frac{\partial }{\partial t}\right) \nabla ^{2} \psi ' -\sqrt{\text {Ta}} \dfrac{\partial v'}{\partial z} + Ra \dfrac{\partial \theta _{f}'}{\partial x} = 0, \end{aligned}$$
(3.2a)
$$\begin{aligned}{} & {} \left( 1+\frac{1}{\text {Va}} \dfrac{\partial }{\partial t} \right) \dfrac{\partial v'}{\partial z} + \sqrt{\text {Ta}}\dfrac{\partial ^{2} \psi '}{\partial ^{2} z} = 0, \end{aligned}$$
(3.2b)
$$\begin{aligned}{} & {} \left( \alpha \frac{\partial }{\partial t} - \nabla ^{2} + H \gamma \right) \theta _{s}' -H \gamma \theta _{f}'=0, \end{aligned}$$
(3.2c)
$$\begin{aligned}{} & {} \left( \frac{\partial }{\partial t} - \nabla ^{2} + H\right) \theta _{f}' - H \theta _{s}' - \frac{\partial \psi '}{\partial x}\frac{\partial \theta _{fb}}{\partial z} - \frac{\partial (\psi ' , \theta _{f}' )}{\partial (x,z)} = 0 , \end{aligned}$$
(3.2d)

and the following perturbed boundary conditions are

$$\begin{aligned} \psi ' = 0,~~~~~~ v' = 0,~~~~~~ \theta _{s}' = 0,~~~~~~ \theta _{f}' = 0~~~~~~ \hbox { at}~~~\ z = 0,1. \end{aligned}$$

On simplifying Eqs. (3.2a) and (3.2b), we get

$$\begin{aligned} \left( 1 + \frac{1}{\text {Va}}\frac{\partial }{\partial t}\right) ^{2}\nabla ^{2} \psi ' +\text {Ta}\dfrac{\partial ^{2} \psi '}{\partial z^{2}} + Ra \left( 1 + \frac{1}{\text {Va}}\frac{\partial }{\partial t}\right) \dfrac{\partial \theta _{f}'}{\partial x} = 0. \end{aligned}$$
(3.3)

To proceed with the linear analysis, we seek the periodic solution as

$$\begin{aligned} \begin{aligned} \psi '(x,z,t)&= \Psi (z,t) \sin (a x) ,\\ \theta _{s}'(x,z,t)&= \Theta _{s}(z,t) \cos (a x),\\ \theta _{f}'(x,z,t)&= \Theta _{f}(z,t) \cos (a x), \end{aligned} \end{aligned}$$
(3.4)

where a is the horizontal wavenumber. On substitution of Eq. (3.4) in the system (3.2a–3.2c), with nonlinear terms omitted, we get

$$\begin{aligned}{} & {} \left[ \left( 1 + \frac{1}{\text {Va}}\frac{\partial }{\partial t}\right) ^{2}(D^{2} - a^{2}) + \text {Ta}D^{2}\right] \Psi - a Ra \left( 1 + \frac{1}{\text {Va}}\frac{\partial }{\partial t}\right) \Theta _{f} = 0, \end{aligned}$$
(3.5a)
$$\begin{aligned}{} & {} \left( \alpha \frac{\partial }{\partial t} - (D^{2} - a^{2}) + H \gamma \right) \Theta _{s} -H \gamma \Theta _{f}=0, \end{aligned}$$
(3.5b)
$$\begin{aligned}{} & {} \left( \frac{\partial }{\partial t} - (D^{2} - a^{2}) + H\right) \Theta _{f} - H \Theta _{s} - a \Psi D \Theta _{fb}= 0, \end{aligned}$$
(3.5c)

where \(D \equiv \frac{\partial }{\partial z}\). Before solving the above system of equations, it is apt to mention that the corresponding unmodulated problem has been investigated by Malashetty et al. (2007). The authors report the possibility of oscillatory convection by considering small values of the Vadasz number (denoted by \(\text {Pr}_{D}\) in Malashetty et al. 2007). The typical values of the Vadasz number must be large for a Darcy porous layer saturated by a compressible Newtonian fluid (Vadasz 1998). Thus, an analysis of results reported by (Malashetty et al. (2007) Sec.III(B), one can readily observe that the preferred mode of convection in the unmodulated case is stationary (corresponding to zero growth rate). Since we have assumed that the modulation amplitude is infinitesimal thus, the dynamics of the modulated system should be quite similar to that without modulation. Therefore, we consider the stationary convection mode the preferred one, even for the modulated problem. Following Suthar et al. (2016), Bansal and Suthar (2022), we make the assumption about the regular perturbation expansion for Ra, \(\Psi\), \(\Theta _{s}\), and \(\Theta _{f}\) in terms of modulation amplitude as follows:

$$\begin{aligned}{} & {} Ra = Ra^{(0)} + \epsilon ^{2} Ra^{(2)} + \cdots, \end{aligned}$$
(3.6)
$$\begin{aligned}{} & {} \Psi (z,t) = \Psi _{\circ }(z) +\frac{1}{2} \left[ \Psi _{1}(z) e^{i \omega t} + {\bar{\Psi }}_{1}(z) e^{-i \omega t} \right] , \end{aligned}$$
(3.7)
$$\begin{aligned}{} & {} \Theta _{s} (z,t) = \Theta _{s\circ }(z) +\frac{1}{2} \left[ \Theta _{s1}(z) e^{i \omega t} + {\bar{\Theta }}_{s1}(z) e^{-i \omega t} \right] , \end{aligned}$$
(3.8)
$$\begin{aligned}{} & {} \Theta _{f} (z,t) = \Theta _{f\circ }(z) +\frac{1}{2} \left[ \Theta _{f1}(z) e^{i \omega t} + {\bar{\Theta }}_{f1}(z) e^{-i \omega t} \right] , \end{aligned}$$
(3.9)

where

$$\begin{aligned}{} & {} \Psi _{\circ }(z) = \Psi _{\circ }^{(0)} + \epsilon ^{2} \Psi _{\circ }^{(2)} + \cdots, ~~~~~~~~~~\Psi _{1} = \epsilon \Psi _{1}^{(1)} + \cdots, \\{} & {} \Theta _{s\circ }(z) = \Theta _{s\circ }^{(0)} + \epsilon ^{2} \Theta _{s\circ }^{(2)} + \cdots,~~~~~~~~ \Theta _{s1} = \epsilon \Theta _{s1}^{(1)} + \cdots, \\{} & {} \Theta _{f\circ }(z) = \Theta _{f\circ }^{(0)} + \epsilon ^{2} \Theta _{f\circ }^{(2)} + \cdots,~~~~~~~~ \Theta _{f1} = \epsilon \Theta _{f1}^{(1)} + \cdots. \end{aligned}$$

Substituting Eqs. (3.6–3.9) into Eqs. (3.5a–3.5b) and equating various powers of \(\epsilon\), we obtain the following different order systems:

Zeroth Order

$$\begin{aligned}{} & {} \begin{bmatrix} (1+\text {Ta}) D^{2} - a^{2} &{} 0&{} -a Ra^{(0)} \\ 0 &{} - H \gamma &{} H \gamma - D^{2} + a^{2}\\ a &{} H - D^{2} + a^{2} &{} - H \end{bmatrix} \begin{bmatrix} \Psi _{\circ }^{(0)} \\ \Theta _{s\circ }^{(0)} \\ \Theta _{f\circ }^{(0)} \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ 0 \end{bmatrix}, \nonumber \\{} & {} ~~~~~~~~ \Psi _{\circ }^{(0)} = \Theta _{s\circ }^{(0)} = \Theta _{f\circ }^{(0)} = 0 ~~~~~~~~\hbox { at} ~~~~~\ z = 0,1. \end{aligned}$$
(3.11)

First Order

$$\begin{aligned}{} & {} \begin{bmatrix} \left( 1 + \frac{i \omega }{\text {Va}}\right) ^{2}(D^{2} - a^{2} ) + \text {Ta}D^{2} &{} 0 &{} -a\left( 1 + \frac{i \omega }{\text {Va}}\right) Ra^{(0)} \\ 0 &{} - H \gamma &{} i \alpha \omega + H \gamma - D^{2} + a^{2}\\ a &{} i \omega + H - D^{2} + a^{2} &{} - H \end{bmatrix} \begin{bmatrix} \Psi _{1}^{(1)} \\ \Theta _{s1}^{(1)}\\ \Theta _{f1}^{(1)} \end{bmatrix} \nonumber \\{} & {} \quad = \begin{bmatrix} 0 \\ 0 \\ {\mathcal {R}} \end{bmatrix} \nonumber \\{} & {} \quad \Psi _{1}^{(1)} = \Theta _{s1}^{(1)} = \Theta _{f1}^{(1)} = 0 ~~~~~~~~\hbox { at}\ z = 0,1. \end{aligned}$$
(3.12)

Second Order

$$\begin{aligned}{} & {} \begin{bmatrix} (1+\text {Ta}) D^{2} - a^{2} &{} 0 &{} -a Ra^{(0)} \\ 0 &{} - H \gamma &{} H \gamma - D^{2} + a^{2}\\ a &{} H - D^{2} + a^{2} &{} - H \end{bmatrix} \begin{bmatrix} \Psi _{\circ }^{(2)} \\ \Theta _{s\circ }^{(2)} \\ \Theta _{f\circ }^{(2)} \end{bmatrix} \nonumber \\{} & {} \quad = \begin{bmatrix} {\mathcal {R}}_{1} \\ 0 \\ {\mathcal {R}}_{2} \end{bmatrix} \nonumber \\{} & {} \Psi _{\circ }^{(2)} = \Theta _{s\circ }^{(2)} = \Theta _{f\circ }^{(2)} = 0 ~~~~~~~~\hbox { at}\ z = 0,1. \end{aligned}$$
(3.13)

In the above systems (3.11–3.13):

\(\quad {\mathcal {R}} = a\Psi _{\circ }^{(0)} f_{1}(z),~~~~~~~~~~~~\) \({\mathcal {R}}_{1} = a Ra^{(2)} \Theta _{f \circ }^{(0)},~~~~~~~~~~~\text {and} ~~~~~~~~~~~~\) \({\mathcal {R}}_{2} = \dfrac{a}{4} [\Psi _{1}^{(1)} {\bar{f}}_{1}(z) + {\bar{\Psi }}_{1}^{(1)} f_{1}(z) ]\).

An eigenvalue of the zeroth-order system (3.11) is given by

$$\begin{aligned} Ra^{(0)} = \dfrac{(\pi ^{2} + a^{2})(\pi ^{2}(1+\text {Ta}) + a^{2})}{a^{2}}\left[ \dfrac{(\pi ^{2} + a^{2}) + H(1 + \gamma )}{(\pi ^{2} + a^{2} + \gamma H)}\right] , \end{aligned}$$
(3.14)

with the corresponding eigenfunctions

$$\begin{aligned}{} & {} \Psi _{\circ }^{(0)} = A \sin (\pi z), ~~~~~~ \Theta _{s\circ }^{(0)} = -\dfrac{ \gamma H ((1+ \text {Ta})\pi ^{2} + a^{2}) }{a Ra^{(0)}(\pi ^{2} + a^{2} + \gamma H)} A \sin (\pi z),\nonumber \\{} & {} \quad ~~~~~~\Theta _{f\circ }^{(0)} = -\dfrac{((1+\text {Ta})\pi ^{2} + a^{2}) }{a Ra^{(0)}} A \sin (\pi z). \end{aligned}$$
(3.15)

The above expression (3.14) is the same as the one reported by Malashetty et al. (2007) for the unmodulated case. Further, we proceed to find shift \(Ra_{c}^{(2)}\) in the critical Rayleigh number. To obtain \(Ra_{c}^{(2)}\), we apply standard Fredholm solvability condition to the second-order self-adjoint system, and on rearranging, we get

$$\begin{aligned} Ra_{c}^{(2)} = \dfrac{Ra^{(0)}}{2}\left[ \dfrac{\displaystyle \int _{0}^{1}\Theta _{f\circ }^{(0)} \left[ {\bar{f}}_{1}(z)\Psi _{1}^{(1)} + f_{1}(z){\bar{\Psi }}_{1}^{(1)}\right] dz}{\displaystyle \int _{0}^{1}\Theta _{f\circ }^{(0)}\Psi _{\circ }^{(0)}dz}\right] . \end{aligned}$$
(3.16)

Note that to calculate \(Ra_{c}^{(2)}\), using Eq. (3.16), we analytically solve the first-order system by eliminating \(\Theta _{f1}^{(1)}\) and \(\Theta _{s1}^{(1)}\) from it and obtain a single equation in \(\Psi _{1}^{(1)}\),

$$\begin{aligned} \begin{aligned}&\left\{ \left[ \left( 1+\frac{i \omega }{\text {Va}}\right) ^{2}{\mathcal {L}}_{1}+\text {Ta}D^{2}\right] [{\mathcal {L}}_{2}{\mathcal {L}}_{3} - \gamma H^{2}] + Ra^{(0)} a^{2} \left( 1+\frac{i \omega }{\text {Va}}\right) {\mathcal {L}}_{2}\right\} \Psi _{1}^{(1)} \\&= Ra^{(0)}a^{2} \left( 1+\frac{i \omega }{\text {Va}}\right) {\mathcal {L}}_{2} \Psi _{\circ }^{(0)} f_{1}(z), \end{aligned} \end{aligned}$$
(3.17)

where

$$\begin{aligned} {\mathcal {L}}_{1}&\equiv D^{2} - a^{2},\\ {\mathcal {L}}_{2}&\equiv i \alpha \omega - D^{2} + a^{2} + \gamma H,\\ {\mathcal {L}}_{3}&\equiv i \omega - D^{2} + a^{2} + H. \end{aligned}$$

The boundary conditions for solving Eq. (3.17) are

$$\begin{aligned} \Psi _{1}^{(1)} = D^{2}\Psi _{1}^{(1)} = D^{4}\Psi _{1}^{(1)} = 0 ~~~~~~~~\hbox { at}~~~~~\ z = 0,1 . \end{aligned}$$
(3.18)

where the boundary conditions on \(D^{4}\Psi _{1}^{(1)}\) have been obtained by eliminating \(\Theta _{f1}^{(1)}\) from the first and third equations of the system (3.12). We make a brief remark regarding the choice of idealized boundary conditions in this investigation to obtain analytical results for the problem under consideration. This choice makes our analysis exact and trustworthy. However, it is well-known that an analytical or numerical analysis of a similar problem with different (realistic) boundary conditions will yield qualitatively similar results. The sixth-order differential equation (3.17) can be solved analytically using the built-in function DSolve in Mathematica. The results obtained for the present study are discussed in the following section.

4 Results and discussion

In the present article, we perform a linear stability analysis to investigate the effect of rotation and time-varying temperature field on the onset of convection in a horizontal Darcy porous layer under the local thermal non-equilibrium conditions. The results are obtained analytically by assuming the modulation amplitude to be infinitesimally small and using it as a perturbation parameter in a regular series perturbation method to expand the physical quantities. It converts the system of governing equations to several systems of different orders that are analyzed individually using matrix differential operator theory. The zeroth order system provides a stationary Rayleigh number of the unmodulated case as its eigenvalue. To calculate correction in critical Rayleigh number, \(\it{R}a_c^{(2)}\), we apply Fredholm’s alternative on the second-order self-adjoint system and obtain \(\it{R}a_c^{(2)}\) as its eigenvalue. Under the modulated boundary temperature, the critical Rayleigh number is given by

$$\begin{aligned} Ra_c = Ra_c^{(0)} + \epsilon ^2 Ra_{c}^{(2)}. \end{aligned}$$
(4.1)

The effectiveness of temperature modulation depends on the phase angle, \(\phi\), and modulation frequency, \(\omega\). We consider the results for two types of wall temperature oscillating mechanisms: symmetric (when \(\phi = 0\)) and asymmetric (when \(\phi \ne 0\)) wall temperature modulation. Since our main aim is to understand the combined effect of rotation and temperature modulation using the LTNE model, thus the main governing parameters are Taylor number (\(\text {Ta}\)), porosity-modified conductivity ratio (\(\gamma\)), and interphase heat transfer coefficient (H), along with phase angle (\(\phi\)) and modulation frequency (\(\omega\)). So, we compute the expression for the correction in the critical Darcy-Rayleigh number as a function of \(\alpha\), \(\gamma\), \(\omega\), \(\phi\), \(\text {Va}\), \(\text {Ta}\), and H. To discuss the effect of these parameters on the system’s stability, we need to fix their values, keeping in mind the large parametric space for the present problem. Considering the experimentally realizable values of the parameters, we choose \(\omega =20\), \(\text {Va} = 1000\), \(\alpha =0.4\), \(\gamma = 0.4\), \(\text {Ta}= 25\), and \(H =100\) as constant fixed values of these parameters, i.e., unless mentioned, the parametric values hereafter are those mentioned above.

Fig. 2
figure 2

Variation in \(Ra_{c}^{(2)}\) with \(\phi\) for different values of \(\alpha\), \(\gamma\), H, \(\omega\), and \(\text {Ta}\)

Full size image

Fig.2 reports the effect of \(\phi\) for the different parametric values of \(\alpha\), \(\gamma\), H, \(\omega\), and \(\text {Ta}\) on \(Ra_{c}^{(2)}\) with \(\phi\). The variation of \(Ra_{c}^{(2)}\) for different values of diffusivity ratio, \(\alpha\) with all other parameters kept fixed is illustrated in fig. 2a. It is observed that \(Ra_{c}^{(2)}\) decreases with an increase in \(\alpha\). Since the increasing value of \(\alpha\) leads to high fluid-phase thermal diffusivity compared to solid-phase and thus increases the heat transfer in fluid-phase, which results in an advanced onset of instability. Fig. 2b displays the effect of \(\gamma\) on \(Ra_{c}^{(2)}\) with \(\phi\). It can be observed that on increasing \(\gamma\), the modulation effect decreases. However, the effect of \(\phi\) magnifies for a small value of \(\gamma\) because a dense porous medium leads to the inhibition of flow in the medium, which results in unequal penetration of the unsteady component of the temperature field into the thermal boundary layer for all the intensities of symmetric heating at the boundaries. However, for a large value of \(\gamma\) ( \(\gamma >1\)), slight variation is observed in the value of \(Ra_{c}^{(2)}\) for the entire \(\phi\)- interval \([0,\pi ]\), as reported by Bansal and Suthar (2022). Fig. 2c, d presents the non-monotonic effect of H on \(Ra_{c}^{(2)}\) with \(\phi\). It can be observed that for the set of chosen parametric values, \(Ra_c^{(2)}\) value decreases with an increase in H, and for H > 250, its value again starts increasing. However, in Fig. 2d, a reverse effect is observed near \(\phi = \pi\), i.e., \(Ra_c^{(2)}\) value increases with an increase in the value of H, and the system becomes more stabilized. On further increasing the value of H, i.e., H > 250, the system’s stability reduces. From this, it can be concluded that the modulation effect in a rotating porous layer is important when \(\gamma\) is small, and H takes moderate values. In Fig. 2e, it can be observed that \(Ra_{c}^{(2)}\) value decreases with an increase in modulation frequency, \(\omega\), and for higher values of \(\omega\), its value again starts increasing, and the curve gets flattened. This is because, for large values of \(\omega\), the unsteady component of the temperature field is confined only to a narrow region near the walls. However, for small values of \(\omega\), the disturbances grow to a sufficient size so that the inertia effect becomes important, resulting in an unstable equilibrium state. It can also be observed that the system has a stabilizing effect near \(\phi = \pi\) for all values of modulation frequency. Fig. 2f illustrates the effect of \(\text {Ta}\) on the correction Rayleigh number, \(Ra_{c}^{(2)}\), with the phase angle, \(\phi\). It can be observed that on increasing \(\text {Ta}\), the modulation effect also increases. Since an increase in \(\text {Ta}\) corresponds to an increase in rotation’s influence on the convective system. Thus Ta increases the onset threshold value for all the intensities of symmetric heating at the boundaries.

Fig. 3
figure 3

Variation in \(Ra_{c}^{(2)}\) with \(\phi\) for different cases

Full size image

Considering Fig. 3, which corresponds to the variation in \(Ra_c^{(2)}/ Ra^{(0)}\) with phase angle \(\phi\) for different cases. It can be observed that while assuming a porous layer under local thermal equilibrium (LTE), the effect of temperature modulation is suppressed in the presence of rotation. However, for the porous layer under local thermal nonequilibrium (LTNE), the effect of temperature modulation is magnified in the presence of rotation.

Fig. 4
figure 4

Variation in \(Ra_{c}^{(2)}\) with \(\omega\) for different values of \(\gamma\), H and \(\text {Ta}\) for in-phase modulation(\(\phi = 0\)) and out-phase modulation(\(\phi = \pi\))

Full size image

Fig. 4 corresponds to the plots of variation in correction Darcy-Rayleigh number \(Ra_c^{(2)}\) with the frequency of modulation \(\omega\) to depict the effects of \(\gamma\), H, and \(\text {Ta}\). Fig. 4a illustrates the effect of \(\gamma\) on \(Ra_c^{(2)}\) with \(\omega\) when the boundary walls are modulated in phase. It is observed that \(Ra_c^{(2)}\) is negative over a range of modulation frequencies, indicating that the in-phase modulation always advances the onset of convection compared to the unmodulated system. However, at a low value of modulation frequency, on increasing the value of \(\gamma\), the negative value of \(Ra_c^{(2)}\) decreases, and hence the instability of the system reduces. Further, the value of \(Ra_c^{(2)}\) decreases with increasing \(\omega\). In Fig. 4b, we observe that, in the case of asymmetric modulation, on increasing the value of porosity-modified conductivity ratio, \(\gamma\), the \(Ra_c^{(2)}\) value decreases therefore the stability of the system decreases. The plots in Fig. 4a, b reiterate the similar effect of \(\gamma\) that has been reported in Banu and Rees (2002). Fig. 4c demonstrates the effect of H on the correction Rayleigh number with the modulation frequency for in-phase modulation. An increase in the value of H increases the system’s instability. As a result, the convection sets in earlier at a low modulation frequency value. However, the value of \(Ra_c^{(2)}\) decreases with the increasing value of \(\omega\). In contrast, the opposite effect of the inter-phase heat transfer coefficient is observed for out-phase temperature modulation through fig.4(d), i.e., at the low modulation frequency, the system’s stability also increases by increasing the value of H. Hence, there is a delay in the onset of convection. Further, at large values of modulation frequency, the system tends to stabilize. Fig. 4e, f presents the correction Rayleigh number with the modulation frequency \(\omega\) for in-phase and out-phase modulation, respectively. In Fig. 4e, in the presence of in-phase modulation, for a given value of \(\omega\), \(Ra_c^{(2)}\) negatively increases with an increase in Ta, indicating that rotation’s increasing effect destabilizes the system by enhancing the onset of convection. However, for large values of \(\omega\), the effect of Ta on the system disappears as \(Ra_c^{(2)} \rightarrow 0\). Fig. 4f demonstrates the effect of Ta on \(Ra_c^{(2)}\), in the case of out-phase modulation, with modulation frequency. It can be observed that, for the small modulation frequency values, the system’s stability is enhanced by increasing the value of the Darcy-Taylor number. Thus, the out-phase temperature modulation delays convection for a specific range of values of \(\omega\). However, this stabilizing effect disappears for moderate and high values of modulation frequency.

Fig. 5
figure 5

Variation in \(Ra_{c}^{(2)}\) with \(\omega\) for different cases for a in-phase modulation(\(\phi = 0\)) and b out-phase modulation(\(\phi = \pi\))

Full size image

Fig. 5a, b presents the effect of thermal modulation and rotation on the correction Rayleigh number with the modulation frequency under both thermal equilibrium and non-equilibrium for in-phase and out-phase modulation. Fig. 5a illustrates the effect of symmetric modulation. This plot shows that the temperature modulation combined with the rotation maximizes instability at a lower frequency. In contrast, at higher values of modulation frequency, this instability effect disappears. Fig. 5b displays the effect when the modulation is asymmetric. It can be observed that temperature modulation has a minimum impact in the absence of rotation. In contrast, in the presence of rotation, the maximum effect occurs when the fluid and solid phases are not in thermal equilibrium. It can also be noted that for moderate values of modulation frequency, \(Ra_{c}^{(2)}\) becomes negative, indicating that out-phase temperature modulation is destabilizing for a certain range of modulation frequencies. However, at low and high values of modulation frequency, it has a stabilizing effect.

It is worth mentioning that, in all the plots of asymmetric modulation, the maximum stabilization occurs at low modulation frequencies. It is also noted from all the plots of LTE and LTNE that the effect of temperature modulation is more significant in the presence of rotation as compared to its absence.

5 Conclusions

The effect of time-periodic boundary temperatures and rotation on the onset of Darcy-Bénard convection using a local thermal non-equilibrium model has been studied. A linear stability analysis is performed, using matrix differential operator theory, to obtain onset threshold limit analytically for the stationary convection. Based on the discussion reported in the previous section, the following conclusions are drawn:

  1. 1.

    On increasing the value of the diffusivity ratio, the modulated temperature’s effect is enhanced in the case of in-phase modulation. In contrast, the opposite effect is observed in the case of out-phase modulation.

  2. 2.

    With an increase in the porosity-modified conductivity ratio, the effect of thermal modulation reduces in both symmetric and asymmetric modulation.

  3. 3.

    The interphase heat transfer coefficient enhances the effect of temperature modulation in both symmetric and asymmetric modulation. A similar effect is observed for the Darcy-Taylor number.

  4. 4.

    The symmetric modulation destabilizes the system for small and large frequency values of modulations, while a stabilizing effect is observed for moderate values of \(\omega\).

  5. 5.

    The asymmetric modulation stabilizes the system at a low frequency while destabilizes the system at moderate and high values of modulation frequency.

  6. 6.

    The effect of rotation is to enhance the effect of thermal modulation. However, the effect of both temperature modulation and rotation is more significant in LTNE problems.