1 Introduction

Microfluidic systems have made significant contributions to the fields of chemistry (Demello 2006), biology (Anderson et al. 2000), drug delivery (Dittrich and Manz 2006; Khetani and Bhatia 2008; Chen et al. 2018), stirred vessel (Tian et al. 2004), etc., in recent years. Compared with macro-devices, micro-devices have significant advantages such as high surface-to-volume ratio, less reagent consumption, high sensitivity, excellent transportability and lower cost (Manz et al. 1990). Microfluidic systems include devices such as micro-valves, micromixers, micro-pumps, micro-filters, and micro-needles (Lee et al. 2005; Wang and Lee 2005; Lee et al. 2008); however, micromixers comprise an important subset of this category. One of the main functions intended for micromixers is their capacity to mix different reactants, especially the high-level reactions, which is an incommutable characteristic of microfluids.

Mixing time and mixing quality are two important factors in micromixers (Dong-Ku Kang et al. 2014; Nguyen and Zhigang 2004). Small characteristic length of geometry and low velocity of the flow lead to a low Reynolds regime for the fluid flow in micromixers (\({\text{Re}} \ll 100\)). In other words, the created flow is laminar and is not followed by a turbulent regime; accordingly, in the mixing process, molecular diffusion is the predominant mechanism (Jahn et al. 2010). On the other hand, if the mixing process is carried out based on the molecular diffusion, the mixing time increases, which, in turn, leads to a reduction in mixing quality (Beebe et al. 2002). Micromixers, based on the mechanism of operation, are generally classified into two distinct categories: passive and active micromixers (Demello 2006). Passive micromixers do not require any external sources for mixing during the process. Accordingly, geometrical parameters (Cortes-Quiroz et al. 2010; Aoki and Mae 2006; Stroock et al. 2002; Ansari et al. 2012), injection (Veenstra et al. 1999), flow recombination (Chen et al. 2016; Lee et al. 2016), etc., are the most important factors which improve the performance of passive micromixers. On the other hand, in active mixers, an external source such as magnetic field, ultrasonic vibrations, electro-kinetic, and micro-impeller or stirrer is employed to enhance the mixing performance (Kumar et al. 2011). The complexity of manufacturing and integration of microfluidic systems are two problems associated with active micromixers; however, active micromixers have higher efficiency, in comparison with passive micromixers and, thus, merit scholarly attention. Niu et al. Niu and Lee (2003) investigated chaotic mixing process in micro multiple side channels. In that study, fluids could be mixed by pumping them through the sides of the channel. Zhu and Kim (1998) experimentally studied mixing process based on the thermal bubble agitation mechanism. They used thermal bubbles to generate oscillatory flow that increases the efficiency of mixing process. Lu et al. Liang-Hsuan et al. (2002) designed and fabricated a micromixer with a rotating magnetic field. They concluded that increasing the stirring speed increases the mixing index. An et al. (2006) simulated the mixing process in a microchannel numerically. They examined the impact of the oscillatory and rotational stirrers on the mixing process by defining a new mixing index for periodic and unsteady flows. They found that the performance of a micromixer is a function of Reynolds number and rotational and oscillation speeds of stirrers. Shamsoddini et al. (2014) examined mixing process in a microchannel with straight and cross-shaped stirrers, using a Lagrangian particle-based method. Their results indicated that the cross-shaped stirrer is more effective than the straight stirrer. Kim et al. (2007) simulated numerically the mixing process in microchannels with different arrangements of circular cylinder and an oscillating stirrer. They found that the combination of circular cylinder and stirrer brings about higher performance, compared with the other models. Abdolahzadeh et al. (2019) numerically investigated the mixing process of non-Newtonian fluids in circular and elliptical chambers, using the method of smoothed particle hydrodynamics (SPH). The results indicated that if the time considered for mixing is limited (i.e., a certain degree of homogeneity for mixing samples in a limited time), choosing a suitable type of vessel is crucial. The same authors (Abdolahzadeh et al. 2021) also examined the thermal effects of stir bars in circular and elliptical micromixer chambers. Their results indicated that the elliptical micromixers were more effective than the circular types. Ng and Ng (2013) simulated the mixing process in a cylindrical chamber with a plate impeller, using the moving particle semi-implicit (MPS) method. They concluded that, in comparison with the other modes, the unsteady mixing process with smaller amplitude of oscillating stirrer has better performance.

Taken together, the review of literature above suggests that, hitherto, numerous experimental and numerical studies have been carried out into the effect of boundary types of microchannels on the characteristics of mixing process in passive micromixers. As for active micromixers, however, to the best of our knowledge, all previous studies invariably focused on such factors such as dimensionless parameters, Reynolds number, Péclet number, Strouhal number, and the type of moving objects such as stirrer in the straight channels. Furthermore, the effect of geometry types of channels on the improvement of mixing process is clearly under-researched. Accordingly, the present study primarily seeks to compare the mixing process in active micromixers with sinusoidal wavy- and straight-walled channels.

The paper is organized as follows: first, the physical models for the problem under consideration are introduced. Subsequently, the governing equations and the numerical method are described. This is followed by the results and the discussion related to the simulation of mixing behavior in different active micromixers. Finally, an overall conclusion is drawn.

2 Physical Models Description

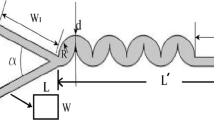
Schematic of physical models to investigate the mixing process in microchannels with stir bar, sinusoidal wave, and straight boundaries is shown in Fig. 1.

Fig. 1
figure 1

Schematic of physical models of micromixers

Full size image

As shown in this figure, the physical dimensions of all channels are introduced according to a unit length, UL, width of microchannel, H, length of microchannel, L, length of stir bar, D, thickness of stir bar, t, X-position of center of stir bar from channel inlet, \(L_{s}\), the length of sinusoidal wavy wall, \(L_{w}\), and X-position of starting sinusoidal wavy wall, \(X_{s}\). The stir bar oscillates rotationally with the amplitude of \(\beta _{0}=45^{\circ }\) in each microchannel to mix Newtonian fluids. It is assumed that the ratio of depth to the width of the channels is considerable. There are some experimental studies indicating that the mixing process can be investigated two-dimensionally in microchannel models (Gobby et al. 2001; Erickson and Li 2002). Therefore, the problem is considered two-dimensional in the present study. The two fluids to be mixed have the same density and viscosity but different concentrations, \(C_{0}\) and \(C_{1}\), at the inlet of microchannels. Two different sinusoidal wavy-walled channels are chosen and are called active-raccoon and active-serpentine micromixers (Fig. 1). As the figure shows, the difference between the two geometries has to do with the phase shifting of top and bottom walls. In other words, the phase shifting for active-raccoon and active-serpentine micromixers is \(0^{\circ }\) and \(180^{\circ }\), respectively. The sinusoidal wavy profile of the top and bottom walls of the active-raccoon micromixer is calculated, using the following functions, respectively:

$$\begin{aligned} Y_{t}(X)= & {} \frac{H}{2} + A \sin \left[ \frac{2\pi (X-X_{s})}{\gamma }\right] , \end{aligned}$$
(2.1)
$$\begin{aligned} Y_{b}(X)= & {} -\frac{H}{2} - A \sin \left[ \frac{2\pi (X-X_{s})}{\gamma }\right] . \end{aligned}$$
(2.2)

For the active-serpentine micromixer, however, the bottom wall is defined as follows:

$$\begin{aligned} Y_{b}(X)=-\frac{H}{2} - A \sin \left[ \frac{2\pi (X-X_{s})}{\gamma }+\pi \right] , \end{aligned}$$
(2.3)

where A is the wave amplitude and \(2\pi /\gamma\) is the period of the sinusoidal wavy profile.

3 Mathematical Formulation of the Mixing Process

The governing equations for the simulation of mixing process in a 2D microchannel are conservation of mass, momentum, and mass transfer equations. The Lagrangian format of these equations in a continuous framework reads

$$\begin{aligned}&\frac{1}{\rho}D_{t} \;\rho +\text {div}\;\mathbf{u} =0, \end{aligned}$$
(3.1)
$$\begin{aligned}&D_{t} \; \mathbf{u} =-\frac{1}{\rho }\mathbf{grad } \; P+ \nu \text {div}\;(\mathbf{grad }\; \mathbf{u} ) + \mathbf{g} , \end{aligned}$$
(3.2)
$$\begin{aligned}&D_{t}\;C=\alpha _{c}\text {div}\;(\mathbf{grad }\; C), \end{aligned}$$
(3.3)

where \(D_{t}\), \(\rho\), \(\mathbf{u}\), P, \(\nu\), \(\mathbf{g}\), C, and \(\alpha _{c}\) are the material derivative, density of the fluid, velocity vector, pressure, kinematic viscosity, body acceleration, concentration, and mass diffusivity, respectively.

The system of equations, which is composed of relations 3.1, 3.2, and 3.3, is closed through a relationship between density and pressure. Since the fluids are considered to have the same temperature, the following equation of state is used:

$$\begin{aligned} P=c_{0}^2(\rho -\rho _{0}), \end{aligned}$$
(3.4)

where \(c_{0}\) is the speed of sound in the fluid and \(\rho _{0}\) is the initial density. To decrease the fluctuation of density less than \(1\%\), \(c_{0}\) is usually taken higher than ten times the maximum velocity of the fluid.

The Knudsen number of the present study is less than \(10^{-3}\). Therefore, the assumption of continuum for the fluids is valid (Erickson and Li 2002); hence, the no-slip boundary condition for velocity and Neumann boundary condition for pressure and concentration at walls, Dirichlet boundary condition for inlet velocity and Neumann boundary condition for outlet pressure are applicable.

The governing dimensionless numbers in the present study include the Reynolds number (\(Re=H U_{in}/\nu\)), the ratio of advective mass transport to momentum transport, the Schmidt number (\(Sc=\nu /\alpha _{c}\)), the ratio of momentum transport to diffusive mass transport, and forced Strouhal number (\(St=fH/U_{in}\)), the ratio of two kinds of inertial forces caused by, respectively, local acceleration and convective acceleration. It is worth mentioning that H, \(U_{in}\), and f are, respectively, characteristic length, inlet velocity, and stirrer frequency.

Given that the mixing efficiency of micromixers is of crucial importance, there have already been different statistical methods to investigate it (Boss 1986; Fan et al. 2017). To study the process of mixing and mass transfer rate in the present work, a mixing index at each cross section of the microchannel is used as follows (Nguyen 2008):

$$\begin{aligned} M_{I}=\frac{1}{T}\int _{T}\left[ \frac{1}{N}\sum _{i} \left( \frac{C_{i}-{\bar{C}}}{{\bar{C}}}\right) ^2\right] ^{1/2}dt, \end{aligned}$$
(3.5)

where T, N, \(C_{i}\), and \({\bar{C}}\) are, respectively, the time period of sampling, the number of particles at considered cross section, normalized concentration of particle i, and expected normalized concentration (here \({\bar{C}}=0.5\)). It is worth mentioning that this mixing index mostly implements to quantify the degree of mixing in the study of micromixers. The mixing index ranges from 0 (fully mixed) to 1 (fully unmixed).

As touched upon in the previous sections, one of the main purposes of this simulation is to investigate and subsequently compare the effects of sinusoidal wavy and straight boundaries on the efficiency of mixing process. To this end, the mixing improvement, \(\eta _{mix}\), is defined as follows:

$$\begin{aligned} \eta _{mix}=\frac{M_{I,SC}-M_{I,SWC}}{M_{I,SC}}, \end{aligned}$$
(3.6)

where \(M_{I,SC}\) and \(M_{I,SWC}\) are the mixing indexes for the straight and sinusoidal wavy channels, respectively.

4 Numerical Solution Methodology

SPH is a meshless method based on the Lagrangian approach. It was initially devised to model the astrodynamics problems (Lucy 1977; Gingold and Monaghan 1977). Given the capability of SPH to model complex physical problems, it has been used in a variety of applications such as fluid–structure interactions (Rafiee and Thiagarajan 2009; Hashemi et al. 2011; Liu et al. 2013), free-surface problems (Jiang et al. 2011; Kiara et al. 2013, 2013; Monaghan 1994, 2005; Capone et al. 2010; Fourtakas and Rogers 2016), and multiphase flows (Cleary 1998; Monaghan and Kocharyan 1995; Hu and Adams 2006; Aristodemo et al. 2010; Monaghan and Rafiee 2013; Ulrich et al. 2013; Pourabdian et al. 2017). In this method, the macroscopic continuum is replaced with a collection of particles without connectionism. Accordingly, partial differential equations are converted to algebraic equations by approximating neighboring particles inside a support domain of a suitable weighting function (refer to (Monaghan and Kajtar 2009; Violeau 2012) for more details).

The interpolation function of a continuous scalar field A or vector field \(\mathbf{A}\) for particle a at position \(\mathbf{r} _{a}\) in SPH can be written as follows (Bonet and Lok 1999):

$$\begin{aligned} J\{A_{a}\}= & {} \sum _{b}V_{b}A_{b}w_{ab}\approx \{A_{a}\}, \end{aligned}$$
(4.1)
$$\begin{aligned} \mathbf{J} \{\mathbf{A }_{a}\}= & {} \sum _{b}V_{b}\mathbf{A }_{b}w_{ab}\approx \{\mathbf{A }_{a}\}, \end{aligned}$$
(4.2)

where J and \(\mathbf{J }\) are the discretized interpolation operators of scalar and vector fields, respectively, \(V_{b}\) is the volume of \(b\hbox {th}\) particle, \(w_{ab}=w_{h}(\mathbf{r} _{a}-\mathbf{r} _{b})\) is the interpolation function, and h is the smoothing length. The fifth-order Wendland kernel function is used here and is defined as follows (Monaghan 2005):

$$\begin{aligned} w_{h}(q)=\frac{\alpha _{w}}{h^{2}}\left\{ \begin{array}{lr} \left( 1-\frac{q}{2}\right) ^{4}(2q+1) &{} 0\le q\le 2\\ 0 &{} 2\le q,\\ \end{array} \right. \end{aligned}$$
(4.3)

where \(\alpha _{w}\) is a normalizer constant that is equal to \(7/4\pi\) in 2D and \(q= \frac{|\mathbf{r} _{a}-\mathbf{r} _{b}|}{h}\), \(\mathbf{r} _{a}\) and \(\mathbf{r} _{b}\) are the position vectors of particles a and b, respectively.

To discretize the gradient (\(\mathbf{grad }\)), divergence (div), and Laplacian (div(\(\mathbf{grad }\))) of a spatial scalar function A or a tensor function \(\mathbf{A}\), the following equations are used (Bonet and Lok 1999; Brookshaw 1985):

$$\begin{aligned} \mathbf{G } \{A_{a}\}= & {} \sum _{b}V_{b}A_{ba} \varvec{B}_{\varvec{a}}.{\acute{w_{ab}}}\approx \{(\mathbf{grad }A)_{a}\}, \end{aligned}$$
(4.4)
$$\begin{aligned} D \{\mathbf{A }_{a}\}= & {} \sum _{b}V_{b}{} \mathbf{A} _{ba} (\varvec{B}_{\varvec{a}}.{\acute{w_{ab}}})\approx \{(\text {div}{} \mathbf{A} )_{a}\}, \end{aligned}$$
(4.5)
$$\begin{aligned} D \{\mathbf{G }\{{A}_{a}\}\}= & {} \sum _{b}2V_{b}\frac{A_{ba}}{r_{ab}}\varvec{e}_{\varvec{ab}}. (\varvec{B}_{\varvec{a}}. \acute{w_{ab}})\approx \text {div} \{\mathbf{grad }\{{A}_{a}\}\}, \end{aligned}$$
(4.6)

where D and \(\mathbf{G}\) are the discretized interpolation operators of continuous operators div and \(\mathbf{grad }\), respectively, \(\varvec{e}_{\varvec{ab}}\) is the unit vector between particles a and b, and \(\varvec{B}_{\varvec{a}}\) is the renormalize factor that is computed as (Bonet and Lok 1999):

$$\begin{aligned} \varvec{B}_{\varvec{a}}=-\left[ \sum _{b}V_{b}(\mathbf{r} _{ab})\acute{w_{ab}}\right] ^{-1}. \end{aligned}$$
(4.7)

One of the main challenges in adopting the SPH method is applying boundary conditions. After all, boundary treatment plays a fundamental role in improving the accuracy of SPH. Accordingly, different methods to treat the boundary have been proposed in recent years (Monaghan and Kos 1999; Monaghan 2005; Lee et al. 2008). Using dummy particle boundary treatment which arranges two to four rows of dummy particles, depending on the radius of influence of kernel, beyond the boundaries particles, is implemented as one of the effective approaches to improve the accuracy of the SPH near edges. In this study, three rows of dummy particles are arranged close to the wall particles. The velocity of the dummy particles is the same as their corresponding wall particles. The pressure and concentration of dummy particles are as amount as the wall particles in the normal direction which satisfies the Neumann boundary condition. In the present study, however, the dummy particle method and in-/out-flow boundary conditions are used for wall boundaries and open-channel flow conditions, respectively (the interested reader is referred to (Lee et al. 2008; Federico et al. 2014) for more details). It is worth mentioning that the stir bar has been considered as a moving boundary condition, oscillating with a constant rotational velocity. Additionally, the effect of this oscillating boundary on each fluid particle has been weighted using a kernel function. It is worth noting that in the present work, four layers of particles have been arranged to apply dummy particles and in/out-flow boundary conditions. Moreover, 6000 particles have been used as a source of particles for injection in the channel inlet.

Non-uniformity of distribution of particles during the simulation is an undesirable phenomenon in the SPH method. There are different shifting/displacement algorithms to resolve this problem (Shadloo et al. 2011; Ozbulut et al. 2014; Rui et al. 2009; Tayebi and Dehkordi 2014). In the present study, use has been made of a particle displacement algorithm, adapted from (Abdolahzadeh et al. 2019). Furthermore, a time integration explicit scheme, namely predictor–corrector algorithm, is employed to update the physical variables over time (Gomez-Gesteira et al. 2012). Moreover, a variable time step is used as follows (Morris 1996):

$$\begin{aligned} \Delta t=\varepsilon _{t}\min \left( \frac{{h}}{c+V_{\max }}, \frac{{h^2}}{\nu },\sqrt{\frac{{{h}}}{g}}, \frac{{h^2}}{{\alpha _{c}}}\right) , \end{aligned}$$
(4.8)

where \(\varepsilon _{t}\) is a constant coefficient (\(0<\varepsilon _{t}<1\)) and \(V_{\max }\) is the maximum velocity of particles. The first term comes up from the Courant–Friedrichs–Lewy (CFL) condition, which implies that the condition of \(U_{max}\Delta t/h<1\) should be satisfied. Viscous stability is regarded in the second term. The stabilities of the body-force acceleration and concentration are taken to note in the last two terms, respectively.

5 Results and Discussion

5.1 Validation

To ensure the accuracy of the computational code, the results obtained by three types of particles resolutions, including 16700, 24000, and 32000 particles, are compared with the work of Kim et al. (2007), who investigated mixing process of Newtonian fluid in a microchannel, using the LBM method. Schematic of the geometry is the same as the first row of Fig. 1. Furthermore, the Reynolds number, based on the width of the channel, is \(Re=H U_{in}/\nu =240\) , Schmidt number \(Sc=\nu /\alpha _{c}=10\), Strouhal number \(St=fH/U_{in}=0.048\) (where f is the stirrer frequency), length of stir bar \(\hbox {D}=\hbox {UL}\) and width of the microchannel \(\hbox {H}=\hbox {3UL}\). Variations of time-averaged mixing index, (Eq. 3.5), versus the non-dimensional length of the channel are calculated and compared with those of Kim et al. (2007) (Fig. 2). As this figure suggests, the results are in acceptable agreement and particle independency is achieved with 24000 particles.

Fig. 2
figure 2

Comparison of variation of time-averaged mixing index versus the dimensionless length of the channel for different numbers of particles with the work of Kim et al. (2007)

Full size image

5.2 Mixing in Straight and Sinusoidal Wavy-Walled Channels

The main purpose of the present simulation is to compare the mixing process of Newtonian fluids through the microchannels with sinusoidal wavy and straight walls in 2D. Fields of flow and concentration are calculated, using a numerical solution of the conservation laws of mass, momentum, and mass transfer, adopting the SPH method. Furthermore, the effect of dimensionless wave amplitude (\(\alpha =A/L\)), dimensionless wavelength (\(\lambda =\gamma /2L\)), and Reynolds number on the mixing improvement is investigated. Wave amplitude physically represents the deviation of the walls of channel relative to the straight walls. Moreover, the wavelength is related to the number of the waves along the channel. In addition, the Reynolds number can be a good approximation of the effect of advective and diffusive transports on the flow field. The simulation parameters used in this study are presented in Table 1. It is worth noting that micromixers, as mentioned in Sect. 1, operate in a range of low Reynolds numbers. Therefore, in the present study, the Reynolds numbers of \(15\le Re\le 100\) are chosen in an almost regular interval of 30.

Table 1 Dimensionless parameters for the microchannels
Full size table

The initial distribution of two-phase fluids is illustrated in Fig. 3. As the figure obviously shows, the mixing fluids in top-half and down-half of all the microchannels have, respectively, concentrations of \(C=1\) and 0. Moreover, it is worth mentioning that the stir bar position is initiated in a vertical direction compared to the fluid flow.

Fig. 3
figure 3

Concentration distribution of two-phase mixing fluids in microchannels at initial time

Full size image

To ensure a better understanding of the fluid kinematic in each micromixer, contours of velocity distribution in flow direction and vorticity for three types of microchannels are plotted in Fig. 6. The contours are plotted for \(Re=100\), \(\alpha =0.5\) and various values of \(\lambda\) in Fig. 4a and for various Reynolds numbers, \(\alpha =0.5\) and \(\lambda =2.0\) in Fig. 4b.

Fig. 4
figure 4

Contours of velocity in flow direction and streamline. a Contours of velocity in flow direction and streamline for \(Re=100\), \(\alpha =0.5\) and different values of \(\lambda\). b Contour of velocity in flow direction and streamline for various Reynolds numbers with \(\alpha =0.5\) and \(\lambda =2\)

Full size image
Fig. 5
figure 5

Distribution of fluids particles in mixing process of straight and sinusoidal wavy walled channels for various Reynolds numbers with α = 0.5 and λ = 2.0

Full size image
Fig. 6
figure 6

Concentration contours of the straight and sinusoidal wavy walled channels at various Reynolds numbers and with α = 0.5 and \(\lambda =2.0\)

Full size image

In all the micromixers, the fluids enter the channel with a uniform velocity; however, due to the oscillation of stir bar, the rate of change of velocity around the blade is higher than the other parts of the channels (Fig. 6). Since the cross-sectional areas of the active-straight micromixer are constant, the velocity does not change very much along the channel. In the wavy parts of the active-raccoon micromixer, the cross-sectional area is diverging and then converging in each half of the wavelength; thus, the velocity magnitude decreases and increases, respectively. In the active-serpentine micromixer, however, the walls are parallel and thus the velocity variations are not very much along the channel.

An important feature of the flow that directly affects the efficiency of the mixers is the generation of recirculation zones. Generally speaking, potential of occurring the vortex shedding phenomenon by inserting moving and static objects in a flow with high Reynolds numbers is significantly higher than that of the flow with low Reynolds numbers. Nevertheless, in cases of low Reynolds number flows, where creeping regimes are governed, considering moving bluff bodies, such as oscillating stirrers, can create vortex shedding flow patterns. In other words, the stirrer with its regular oscillation exchanges the positions of mixing fluids between two adjacent areas, creates vortices, and blends the fluids effectively. It is also worth mentioning that creating vortices in the flow enhances interface between the two mixing fluids and improves the diffusion process and the mixing efficiency. In all such cases, the rotational oscillation of the stir bar leads to the generation of vortices along the channel remarkably. Therefore, diffusion of the fluids into one another increases. The deviations of the sinusoidal walls of the channels prevent the mixing fluids from following the wavy walls and thus separation occurs; consequently, recirculation zones which grow along the channel with increasing the wavelength (Fig. 4a) and Reynolds number (Fig. 4b) are created. Growing the advection strength with increasing the Reynolds number is one of the factors contributing to this phenomenon. It is worth mentioning that reversible fluid flow in the cavities of wavy channels leads to the recirculation zones. For both micromixers, raccoon and serpentine types, flow separation does not occur at low Reynolds numbers as much as high Reynolds numbers. This statement can be observed from contours of velocity and vorticity in Fig. 4. Therefore, using a stir bar with regular oscillation, especially at lower values of Reynolds numbers, enhances the vortex shedding patterns and ultimately improves the mixing efficiency.

As the SPH method is a Lagrangian description of fluid flow, motion of fluid particles and its effect on mixing process can be traced easily; accordingly, the distribution of fluid particles in mixing process of straight and sinusoidal wavy-walled channels for various Reynolds numbers with \(\alpha =0.5\) and \(\lambda =2.0\) is presented in Fig. 5. As shown in this figure, diffusion of fluid particles into each other for straight and raccoon micromixers is more intense, compared with the serpentine micromixer. Furthermore, the higher the Reynolds number, the more the non-uniformity of distribution of the fluid particles. Another common result that comes up from Fig. 5 is that the quality of mixed particles at outlets of all types of microchannels enhances with increase in the Reynolds number.

In the interest of better perception of mass transfer during the mixing process and the effect of rotationally oscillating blade on mixing fluids, the contours of concentration distribution for straight and sinusoidal wavy-walled channels with \(\alpha =0.5\) and \(\lambda =2.0\) in different Reynolds numbers are given in Fig. 6. As this figure shows, especially at high Reynolds numbers, vortex shedding phenomenon causes a mushroom-shaped mass transfer during the mixing process; consequently, the interface between the two fluids increases and thus the mixing efficiency improves. At low Reynolds numbers, however, a full homogeneity of mixing is achieved almost at the outlet of the channel. As mentioned in Sect. 1, at lower Reynolds number, diffusion is the dominant mechanism. Therefore, with increases in the contact time, which is due to the low Reynolds number, and also increases in the interface of fluids, which is the result of the vortex shedding, the mixing process improves.

Fig. 7
figure 7

Variations of the mixing improvement versus parameters α and β at the outlet of active-raccoon micromixers relative to active-straight micromixer

Full size image
Fig. 8
figure 8

Variations of the mixing improvement versus parameters α and λ at the outlet of active-serpentine micromixers relative to active-straight micromixer

Full size image

It is interesting to investigate the effects of geometrical parameters, including the dimensionless wave amplitude, \(\alpha\), and wavelength, \(\lambda\), on the efficiency of microchannel at different Reynolds numbers. In other words, the results of this parametric study allow engineers to design an optimal geometry for channels. To this end, the mixing improvement at the outlet of active-raccoon and active-serpentine micromixers with respect to the dimensionless wave amplitude, \(\alpha\), and wavelength, \(\lambda\), for each Reynolds number is given in Figs. 7 and 8. It is worth pointing out that these 3D surfaces use a color gradient, a yellow–blue range, to colorize mixing efficiency values, aimed at easier recognizing \(\eta _{mix}\) changes, from the minimum value (yellow) to the maximum value (blue). Via these surface plots, the effects of geometric parameters on mixing efficiency could be analyzed simultaneously for different Reynolds numbers. At a first glance, we can observe that the active-raccoon micromixer exhibits better efficiencies in wide ranges of \(\alpha\) and \(\lambda\), compared with the active-serpentine micromixer. The main reason for this result could be related to the contact time of fluids; in fact, in regions of the active-raccoon micromixer where cross-sectional area is diverging, the average velocity is lower than that of the active-serpentine micromixer. Accordingly, the local Reynolds number decreases and then the contact time of fluids increases during the mixing process.

As Fig. 7 shows, behaviors of the mixing improvement with respect to parameters \(\alpha\) and \(\lambda\) for all such Reynolds numbers, except \(Re=15\), are almost the same. In other words, at \(Re=45, 75\), and 100, the mixing improvement, \(\eta _{mix}\), smoothly increases with increases in \(\lambda\); whereas, at \(\hbox {Re} = 15\), for each value of \(\alpha\) there is a critical value of \(\lambda\), in which the mixing improvement is at its minimum level. Furthermore, for all the Reynolds numbers, the mixing improvement, \(\eta _{mix}\), continuously increases with increasing the wave amplitude \(\alpha\). In fact, when the wave amplitude increases, at \(\hbox {Re}=15\), in the domain of \(1<\lambda <2.5\), especially where \(\lambda\) tends to 1, the mixing efficiency is strongly and positively influenced, whereas, for the rest of the Reynolds numbers, the mixing efficiency is falling down in the mentioned domain of \(\lambda\).

As a general result, it is observed that for all the sinusoidal wavy-walled channels, the variation of \(\eta _{mix}\) strongly depends on the wavelength \(\lambda\) rather than the wave amplitude \(\alpha\). As Fig. 7a shows, the effect of the sinusoidal wave boundary on the mixing improvement in lower Reynolds numbers is weaker than that of the higher Reynolds numbers (Fig. 7b–d). Moreover, as Fig. 7b clearly indicates, the only case in which the operation of the active-raccoon micromixer is better than the active-straight micromixer for all the ranges of \(\alpha\) and \(\lambda\), is \(Re=45\) (\(\eta _{mix}\) is always positive). As mentioned earlier, the mixing process at low Reynolds numbers is diffusion dominant that in this case, both fluids can be in contact for more time and then a better mixing efficiency is resulted. In contrast, for high Reynolds numbers, inertial effects are so strong that provide handling the mixing process with the secondary flows. It seems that at Reynolds numbers around 45, both inertial effects, wherein the secondary/vortices flow grows in sinusoidal waves, and molecular diffusion, which effects directly on the mixing efficiency, take over mixing process optimally.

As Fig. 8 indicates, the performance of the active-serpentine micromixers is weaker than that of the active-straight micromixer in a wide range of \(\alpha\) and \(\lambda\). Furthermore, unlike the raccoon mixers, the mixing improvement decreases continuously with increases in \(\alpha\). The only case, which the active-serpentine micromixers have positive values of the mixing efficiency is the case of \(\hbox {Re}=45\). At this Reynolds number, concentrated on the domain of \(1<\lambda <2\), the mixing efficiency of the active-serpentine micromixers improves, especially where \(\alpha\) tends to low numbers.

Fig. 9
figure 9

Variations of the mixing improvement versus parameter λ at the outlet of active-raccoon micromixers relative to active-straight micromixer

Full size image

To gain useful insight into the improved mixing efficiency of the active-raccoon micromixers, the variations of the mixing improvement versus \(\lambda\) for different values of \(\alpha\) are presented in Fig. 9; generally speaking, it can be observed that the trend of mixing improvement for different \(\alpha\) is quite similar in any case.

It can also be deduced that the mixing improvement for \(\hbox {Re} = 75\) and 100 improves continuously with an increase in \(\lambda\), whereas for the other Reynolds numbers, it does not follow a regular trend with increasing \(\lambda\); for example, for \(\hbox {Re} =15\), it can be observed that for each \(\alpha\), there is a point in which the trend of the mixing improvement reverses with increasing \(\lambda\) . It should be pointed out that due to the poor efficiency of active-serpentine micromixers, the corresponding results are not reported here.

As a general conclusion for all the cases examined in this study, raccoon mixers can be considered as high-performance mixers, especially at \(Re =45\). It is worth pointing out that this kind of geometry provides excellent performance for \(\hbox {Re}=75\) and 100 in high values of \(\lambda\); however, its performance for \(\hbox {Re}=15\) is not as effective as that of the other Reynolds numbers.

6 Conclusions

In the present study, the mixing process of two fluids in sinusoidal wavy-walled and straight-walled channels with oscillating stir bar was investigated numerically. The simulation was focused significantly on how the mixing efficiency is affected through influential geometrical parameters, wave amplitude, and wavelength, and recognize their optimum values, considering a range of Reynolds numbers. Computational code has been set up based on an improved meshless SPH method compared to the standard SPH and validated with results obtained by other researchers. The main results of the present study can be summarized as follows:

  • Regarding flow dynamics, the vortex shedding phenomenon in all microchannels becomes more significant by increasing the Reynolds number. Furthermore, induced angular momentum by oscillating mode stir bar causes particles of two fluids to be well mixed and thus improves the mixing efficiency.

  • Even if the mixing improvement \(\eta _{mix}\) continuously increases with increases in the wave amplitude of the channels for the active-raccoon micromixer, nevertheless, it decreases for the active-serpentine micromixer.

  • At \(\hbox {Re}=45\): the performance of the raccoon micromixer is better than that of the active-straight micromixer in all wave amplitudes and wavelengths of the channel.

  • At \(\hbox {Re}=15\): the performance of the active-raccoon micromixers is not as effective as that of the other Reynolds numbers.

  • Active-serpentine micromixer is inefficient in a wide range of wave amplitudes and wavelengths of the channel. There is just a poor improvement of mixing efficiency at \(\hbox {Re}=45\). In the domain of \(1<\lambda <2\) especially where \(\alpha\) falls down to low numbers, the mixing efficiency fairly improves.