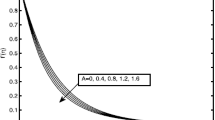1 Introduction

The industrial applications of producing plastic sheets of synthetic material are growing every day, and there is a need for describing the inherent phenomena involved in this process. Although numerical methods in this way have paved the path to solve almost all multidisciplinary phenomena and thermo-physical systems, however, based on the fact that solution of numerical method essentially suffers from both truncation and round-off errors, the analytical solution for any system and under any condition still has kept its privilege respect to numerical tools. As a routine validation procedure, numerical results have been benchmarked with experimental measurements or by the exact analytical solution of governing equations. This excelled position often attracts the researchers to conduct investigations on the interdisciplinary problems such as MHD flow passing over a stretching plate. At first Crane (Crane 1970) has studied the nature of the boundary layer produced by the stretching plate in the presence of viscous flow in the presence of ambient fluid medium. The Hiemenz boundary layer flow (Schlichting 2017) shows some certain similarities to the Crane problem. Motivated by Crane’s problem, many researchers conduct a research on stretching sheet problems. Siddappa and Khapate (1976) extended the Crane’s work to identify the impact of the non-Newtonian Rivlin–Ericksen fluid characteristics on the boundary layer flow. In that work, Siddappa and Khapate studied the Rivlin–Ericksen fluid in the presence of wall suction. Recently, the problem is extended to the study of viscoelastic boundary layer fluid flow, considering heat and mass transfer over a stretching sheet by many researchers. Siddappa and Abel (Siddappa and Abel 1986, 1985) worked on the boundary layer flow due to a stretching plate in the presence of suction and heat transfer. The stretching sheet problem in the presence of magnetic field exhibits a major role in controlling momentum and mass transfer for viscous and non-viscous fluid flows and also has useful industrial applications such as in polymer technology and metallurgy (see Benos et al. 2021).

Similarly, the flow of a fluid through a porous medium has been well discussed in Sheikhnejad et al. (2019); Sheikhnejad et al. 2017; Sheikhnejad et al. 2015; Ramzan et al. 2017) and has several applications in many industries dealing with polymer extrusion process, glass blowing, metallurgical processes, and allied areas (Fisher 1976). Siddheshwar et al. (Siddheshwar et al. 2015) worked on the MHD analysis of non-Newtonian Walters’ liquid B under different physical parameters and boundary conditions. Mahabaleshwar et al. (Mahabaleshwar et al. 2020a; Mahabaleshwar 2007) and Siddheshwar and Mahabaleshwar (Siddheshwar and Mahabaleshwar 2015) performed MHD study on the non-Newtonian fluid flows on the basis of Dufour and Soret mechanisms over a porous sheet, and also with micropolar fluids. Andersson (Andersson 1992) conducted an investigation on Walter’s B liquid with MHD due to a stretching sheet in the absence of suction/blowing. In the presence of porous medium, Mahabaleshwar et al. (Mahabaleshwar and Suvash 2013; Mahabaleshwar et al. 2018, 2019) examined the exact solution for the flow of a fluid with variable heat source and variable gravity under variety of boundary conditions. Merkin et al. (Merkin et al. 2014) studied on the flow and heat transfer due to permeable stretching/shrinking surface in a porous medium with the Brinkman model. Very recently Mahabaleshwar et al. (Mahabaleshwar et al. 2021a) worked on MHD and porous medium model with mass transpiration and thermal radiation in the presence of Navier slip. See other recent works on MHD and porous medium problems in the Ref. (Anusha et al. 2021; Sneha et al. 2021).

Andersson et al. (Andersson et al. 1994) have investigated chemical reaction impact of an isothermal laminar Newtonian flow due to stretching sheet and same problem inclusion of MHD and Jeffery fluid flow over flat plate in the presence of heat generation and absorption examined by Mohanty et al. (Mohanty et al. 2015).

By keeping these articles view in mind, the current work is on the flow of a MHD Rivlin–Ericksen fluid in the presence of mass transpiration and thermal radiation. The flow is caused due to the porous stretching/shrinking sheet in the inverse Darcy model. Several researchers already worked on Rivlin–Ericksen fluid (see. Siddappa and Khapate 1976; Malleswari 2018); however, none of them covered the extensive analysis on all the momentum, energy, and mass transfer equations with first order slip, also so-called Navier’s slip, and solved analytically and expressed in the form of Kummer’s function for two different thermal conditions, namely prescribed surface temperature (PST), prescribed power law surface concentration (PSC), prescribed heat flux (PHF) and prescribed power-law mass flux (PMF). The results of skin friction and Nusselt number are analyzed. In addition, the impact of different physical parameters is investigated with the help of graphical representation.

2 Problem Statement and Solution

A steady-state two-dimensional MHD flow of an electrically conducting incompressible Rivlin–Ericksen fluid over a porous stretching/shrinking sheet with inverse Darcy model is considered in this study. This is the generalization of the work of Siddappa and Hiremath (Siddappa and Prakash 1980), and Khan et al. (Khan et al. 2003). By considering the Cartesian coordinates \(\left( {x,y} \right)\) as depicted in Fig. 1, two equal and opposite forces from magnetic field along the x-axis are applied to the fluid flow.

Fig. 1
figure 1

Physical representation of Rivlin–Ericksen flow

Full size image

Maxwell’s equation (for no applied electric field)

$$ \begin{gathered} \vec{J} = \mu_{m} \sigma \left( {\vec{q} \times \vec{B}} \right), \hfill \\ \nabla \cdot \vec{B} = 0, \hfill \\ \nabla \times \vec{B} = \sigma \vec{E}_{{{\text{ind}}}} , \hfill \\ \nabla \times \vec{E}_{{{\text{ind}}}} = - \mu_{m} \frac{{\partial \vec{B}}}{\partial t}, \hfill \\ \end{gathered} $$
(a)

where \(\vec{E}_{{{\text{ind}}}} = \mu_{m} \vec{q} \times \vec{B}\) is the induced electric field, and the other quantities are as defined in the nomenclature. It is customary in magneto convection to combine the Maxwell equations into one equation called magnetic induction equation.

However, for a weak electrically conducting liquid the magnetic Rayleigh number \(Rm = \mu_{m} \sigma {\kern 1pt} \,Vd < < 1\)(V: characteristic velocity) and in this case the Lorentz force \(\mu_{m} \vec{J} \times \vec{B}\), on using the constitutive Eq. (a), can be written as

$$ \mu \left( {\vec{J} \times \vec{B}} \right) = - \mu_{{}}^{2} \sigma B_{0}^{2} u $$
(b)

In addition, temperature-dependent heat source/sink, suction/injection, viscous dissipation and inverse Darcy model are taken into account. A strength \(B_{0}\) of uniform magnetic field and porous medium is inserted in the flow of a fluid. Moreover, chemically reactive species is taken in the flow of a fluid. By keeping this view in mind, the resulting boundary layer equations can be expressed as following form (see Chen et al. (2021))

$$ \frac{\partial u}{{\partial x}} + \frac{\partial u}{{\partial y}} = 0 $$
(1)
$$ u\frac{\partial u}{{\partial x}} + v\frac{\partial u}{{\partial y}} = \nu \frac{{\partial^{2} u}}{{\partial y^{2} }} + k^{\prime}\left[ {\left( {u\frac{\partial u}{{\partial x}} + v\frac{\partial u}{{\partial y}}} \right)_{yy} + 2\left( {\frac{\partial u}{{\partial x}}\frac{\partial u}{{\partial y}}} \right)_{y} } \right] + \gamma \left( {\left( {\frac{\partial u}{{\partial y}}} \right)^{2} } \right)_{x} - \left( {\frac{{\sigma B_{0}^{2} }}{\rho } + \frac{\mu }{\rho K}} \right)u $$
(2)
$$ \begin{gathered} u\frac{\partial T}{{\partial x}} + v\frac{\partial T}{{\partial y}} = \frac{k}{{\rho C_{P} }}\frac{{\partial^{2} T}}{{\partial y^{2} }} + \frac{\mu }{{\rho C_{P} }}\left( {\frac{\partial u}{{\partial y}}} \right)^{2} + \left( {\frac{{\sigma B_{0}^{2} }}{{\rho C_{P} }} + \frac{\mu }{{\rho C_{P} K}}} \right)u^{2} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - \frac{1}{{\rho C_{P} }}\frac{{\partial q_{r} }}{\partial y} + \frac{{Q_{0} }}{{\rho C_{P} }}\left( {T - T_{\infty } } \right) - \frac{k^{\prime}}{{C_{P} }}\left\{ {\frac{\partial u}{{\partial y}}\frac{\partial }{\partial y}\left( {u\frac{\partial u}{{\partial x}} + v\frac{\partial u}{{\partial y}}} \right)} \right\} \hfill \\ \end{gathered} $$
(3)
$$ u\frac{\partial C}{{\partial x}} + v\frac{\partial C}{{\partial y}} = D\frac{{\partial^{2} C}}{{\partial y^{2} }} - k_{c} C^{n} $$
(4)

where the quantities have their meaning as mentioned in nomenclature. The governing equations are subject to the following boundary conditions (see Ramzan et al. (2017)) that for momentum equation:

$$ \left. \begin{gathered} u = dbx + L\frac{\partial u}{{\partial y}},\,\,\,v = - V_{w} \,\,\,\,{\text{at}}\,\,\,y = 0 \hfill \\ u = 0,\,\,\,\frac{\partial u}{{\partial y}} = 0,\,\,\,\,as\,\,\,\,y \to \infty \hfill \\ \end{gathered} \right\} $$
(5)

While for energy equation, in PST and PHF cases, the boundary conditions on temperature and concentration are, respectively, given by (See Refs. Siddheshwar and Mahabaleshwar (2005), Mastroberardino and Mahabaleshwar (2013)):

$$ \left. \begin{gathered} T = T_{w} = T_{\infty } + A_{0} \left( \frac{x}{l} \right)^{2} ,\,\,\,\,C = C_{w} = C_{\infty } + A_{1} \left( \frac{x}{l} \right)^{2} \,\,\,{\text{at}}\,\,\,y = 0 \hfill \\ T \to T_{\infty } ,\,\,\,\,C \to C_{\infty } \,\,\,\,\,{\text{as}}\,\,\,y \to \infty \hfill \\ \end{gathered} \right\} $$
(6)
$$ \left. \begin{gathered} - k\left( {\frac{\partial T}{{\partial y}}} \right)_{w} = q_{w} = E_{0} \left( \frac{x}{l} \right)^{2} ,\,\,\,\,\, - D\left( {\frac{\partial C}{{\partial y}}} \right)_{w} = m_{w} = E_{1} \left( \frac{x}{l} \right)^{2} \,\,\,\,\,{\text{at}}\,\,\,\,y = 0 \hfill \\ \,\,\,T \to T_{\infty } ,\,\,\,\,\,C \to C_{\infty } \,\,\,\,\,\,\,\,\,as\,\,\,\,\,\,\,\,\,\,y \to \infty \hfill \\ \end{gathered} \right\} $$
(7)

To demonstrate the analysis, we use the following subsequent similarity transformations in terms of stream function is given by (see Khan et al. (2003) and Ramzan (2015))

$$ \psi \left( {x,y} \right) = \sqrt {b\nu } \,x\,f\left( \eta \right),\quad \eta = y\sqrt {\frac{b}{\nu }} $$
(8a)

By using stream function, the velocities of the flow are given by \(u=bx{f}_{\eta }\left(\eta \right),\) and \(v = - \left( {b\nu } \right)^{1/2} f\left( \eta \right)\).

The transformations of the temperature case are given by

$$ \theta \left( \eta \right) = \frac{{T - T_{\infty } }}{{T_{w} - T_{\infty } }},\,\,\,\,\,\,\,\,\,\,\,\,\phi \left( \eta \right) = \frac{{C - C_{\infty } }}{{C_{w} - C_{\infty } }} $$
(8b)
$$ g\left( \eta \right) = \frac{{T - T_{\infty } }}{{\frac{{E_{0} }}{k}\left( \frac{x}{l} \right)^{2} \sqrt {\frac{\nu }{b}} }},\,\,\,\,h\left( \eta \right) = \frac{{C - C_{\infty } }}{{\frac{{E_{1} }}{D}\left( \frac{x}{l} \right)^{2} \sqrt {\frac{\nu }{b}} }} $$
(8c)

The symbols used in Eqs. (1) to (8) are defined in the nomenclature.

Thermal radiation can also be calculated by the Rosseland approach in which linear approximation is employed for radiative heat flux, \(q_{r}\) (see refs. (Mahabaleshwar et al. 2020b, c; Xenos et al. 2020))

$$ q_{r} = - \frac{{4\sigma^{*} }}{{3k^{*} }}\frac{{\partial T^{4} }}{\partial y}\,, $$
(8d)

Here, the Stefan–Boltzmann constant is given by \(\sigma^{*} = 5.6697 \cdot 10^{ - 8} \frac{{\text{W}}}{{{\text{m}}^{2} {\text{K}}^{4} }}\), and mean spectral absorption coefficient is denoted by k*. The Taylor series expansion for the fourth power of temperature, T4, about ambient temperature can be presented as:

$$ T^{4} = T_{\infty }^{4} + 4T_{\infty }^{3} \left( {T - T_{\infty } } \right) + 6T_{\infty }^{2} \left( {T - T_{\infty } } \right)^{2} + .... $$
(8e)

In Eq. (2), considering order of magnitude of each term, the quadratic terms onwards can be neglected.

$$ T^{4} \cong - 3T_{\infty }^{4} + 4T_{\infty }^{3} T $$
(8f)

Upon using equation above equations one can obtain:

$$ \frac{{\partial q_{r} }}{\partial y} = - \frac{{16\sigma^{*} T_{\infty }^{3} }}{{3k^{*} }}\frac{{\partial^{2} T}}{{\partial y^{2} }}. $$
(8g)

3 Analytical Solution of Momentum Equation

By using transformations defined in Eq. (8a) in Eq. (2) to obtain the following fourth-order non-linear ordinary differential equations. (see Mahabaleshwar et al. (Mahabaleshwar et al. 2021b))

$$ f_{\eta }^{2} - ff_{\eta \eta } = f_{\eta \eta \eta } + \beta \left\{ {2f_{\eta } f_{\eta \eta \eta } - ff_{\eta \eta \eta \eta } + 3f_{\eta \eta }^{2} } \right\} + 2\gamma f_{\eta \eta }^{2} - \left( {M + Da^{ - 1} } \right)f_{\eta } = 0 $$
(9)

where \(\beta = \frac{k^{\prime}b}{\gamma }\) is the dimensionless viscoelastic parameter, \(\gamma = \frac{b}{\nu }\) represents the cross-viscosity parameter, \(M = \frac{{\sigma B_{0}^{2} }}{\rho b}\) indicates the dimensionless magnetic parameter, and \(Da^{ - 1} = \frac{\mu }{\rho bK}\) is the inverse Darcy number.

Then, the corresponding momentum boundary conditions reduce to

$$ \left. \begin{gathered} f_{\eta } \left( 0 \right) = d + \lambda f_{\eta \eta } \left( 0 \right),\,\,f\left( 0 \right) = S\,\,\,\,\,\,{\text{at}}\,\,\,\,\,\,y = 0 \hfill \\ f_{\eta } \left( \infty \right) \to 0,\,\,\,f_{\eta \eta } \left( \infty \right) \to 0\,\,\,\,\,\,\,{\text{as}}\,\,\,\,\,\,\,\,y \to \infty \hfill \\ \end{gathered} \right\} $$
(10)

With the help of the boundary conditions defined in Eq. (10) to assume the solution of Eq. (9) in the following form

$$ f\left( \eta \right) = S + \frac{{d\left( {1 - e^{ - \alpha \eta } } \right)}}{{\alpha \left( {1 + \lambda \alpha } \right)}} $$
(11)

By utilizing this solution in Eq. (9), the following fourth-order algebraic equation for unknown parameter α will be obtained.

$$ \begin{gathered} \beta S\lambda \alpha^{4} + \left( {\beta S + \lambda } \right)\alpha^{3} + \left[ {\left( {1 - \lambda S} \right) + \beta d + \left( {4\beta + 2\gamma } \right)de^{ - \alpha \eta } } \right]\alpha^{2} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - \left( {S + \left( {M + Da^{ - 1} } \right)\lambda } \right)\alpha - \left( {d + \left( {M + Da^{ - 1} } \right)} \right) = 0 \hfill \\ \end{gathered} $$
(12)

In the following, two extreme cases, namely very small and very large value of similarity parameter η, will be discussed. The small and large value of η is corresponding to the regions close to wall and far-field, respectively.

3.1 Case 1. \({\varvec{\eta}}\) is very small

In the region close to the solid wall, where \(\eta \) is approaches to zero and becomes very small, Eq. (12) reduces to

$$ \begin{gathered} \beta S\lambda \alpha^{4} + \left( {\beta S + \lambda } \right)\alpha^{3} + \left[ {\left( {1 - \lambda S} \right) + \left( {5\beta + 2\gamma } \right)d} \right]\alpha^{2} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - \left( {S + \left( {M + Da^{ - 1} } \right)\lambda } \right)\alpha - \left( {d + \left( {M + Da^{ - 1} } \right)} \right) = 0 \hfill \\ \end{gathered} $$
(13)

There are four roots where two of them are imaginary and two of them are real. The real roots are:

$$ \alpha = \left\{ \begin{gathered} \frac{1}{4}\left( {\frac{S\beta + \lambda }{{S\beta \lambda }} \pm 2\sqrt {c_{1} + \frac{{c_{2} }}{{c_{3} }} + \frac{1}{{\sqrt[3]{2}c_{3} }}} - 2\sqrt {c_{5} } } \right), \hfill \\ \frac{1}{4}\left( {\frac{S\beta + \lambda }{{S\beta \lambda }} \pm 2\sqrt {c_{1} + \frac{{c_{2} }}{{c_{3} }} + \frac{1}{{\sqrt[3]{2}c_{3} }}} + 2\sqrt {c_{5} } } \right) \hfill \\ \end{gathered} \right. $$

3.2 Case 2. \(\eta\) is very large \(\left( {\eta \to \infty } \right)\)

For the far-field region, where \(\eta\) is very large Eq. (12) reduces to

$$ \begin{gathered} \beta S\lambda \alpha^{4} + \left( {\beta S + \lambda } \right)\alpha^{3} + \left[ {\left( {1 - \lambda S} \right) + \beta d} \right]\alpha^{2} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - \left( {S + \left( {M + Da^{ - 1} } \right)\lambda } \right)\alpha - \left( {d + \left( {M + Da^{ - 1} } \right)} \right) = 0 \hfill \\ \end{gathered} $$
(14)

Likewise, the corresponding four roots of Eqs. (13) and (14) are given by

$$ \alpha = \left\{ \begin{gathered} \frac{1}{4}\left( {\frac{S\beta + \lambda }{{S\beta \lambda }} \pm 2\sqrt {c_{1} + \frac{{c_{2} }}{{c_{3} }} + \frac{1}{{\sqrt[3]{2}c_{3} }}} - 2\sqrt {c_{5} } } \right), \hfill \\ \frac{1}{4}\left( {\frac{S\beta + \lambda }{{S\beta \lambda }} \pm 2\sqrt {c_{1} + \frac{{c_{2} }}{{c_{3} }} + \frac{1}{{\sqrt[3]{2}c_{3} }}} + 2\sqrt {c_{5} } } \right) \hfill \\ \end{gathered} \right. $$
(15)

The particular case of Eq. (11) is when \(S=\lambda =0, \text{and d=1}\) that will yield to the results of Andersson (Andersson 1992).

Moreover, skin friction coefficient \(C_{f}\) can be expressed as (See ref. (Nandeppanavar et al. 2010; Hakeem et al. 2014))

$$ C_{f} = \frac{{\tau_{w} }}{{\frac{1}{2}\rho \left( {u_{w} } \right)^{2} }} $$
(16a)

where the wall shear stress \(\tau_{w}\) is given by

$$ \tau_{w} = \left[ {\nu \frac{\partial u}{{\partial y}} - k^{\prime}\left( {u\frac{{\partial^{2} u}}{\partial x\partial y} - 2\frac{\partial u}{{\partial x}}\frac{\partial u}{{\partial y}}} \right)} \right]_{y = 0} $$
(16b)

on substituting Eq. (16a) into Eq. (16b) to get the following results

$$ C_{f} = 2{\text{Re}}_{x}^{ - 1/2} \left( {1 - 3\beta } \right)f_{\eta \eta } \left( 0 \right) $$
(16c)

where \({\text{Re}}_{x} = \frac{{\rho bx^{2} }}{\mu }\) is the local Reynold’s number. It should be emphasized here that the viscoelastic parameter (β) is within the formulation of α in Eq. (16), as expressed in Eq. (15)

4 Solutions of Heat and Mass Transfer Equations

Solution of governing equations under two main boundary conditions, namely Dirichlet and Neumann, where unknown variable and gradient of unknown variable will be prescribed, respectively. In this study, both temperature/concentration and their gradients, also known as heat/concentration flux, are prescribed by the power law equation. In the following, the mentioned boundary conditions will be applied one by one.

4.1 Prescribed Temperature and Concentration

In the following, governing equation under the prescribed power law surface temperature (PST) and prescribed power law surface concentration (PSC) will be presented. Derivation of solution started by the insertion of Eq. (8a) and (8b) into Eq. (3) and (4) to obtain analytical solution by setting \(n = 1,\,\,and\,\,C_{\infty } = 0\) for first-order chemical reaction. This leads to the non-dimensional form of temperature and concentration equation as follows:

$$ \left( {1 + R} \right)\theta_{\eta \eta } + \Pr f\theta_{\eta } - \Pr \left( {2f_{\eta } - Q} \right)\theta = - \Pr Ec\left\{ {f_{\eta \eta }^{2} - \beta f_{\eta \eta } \left( {f_{\eta } f_{\eta \eta } - ff_{\eta \eta \eta } } \right) + \left( {M + Da^{ - 1} } \right)f_{\eta }^{2} } \right\} $$
(17)
$$ \phi_{\eta \eta } + Scf\phi_{\eta } - Sc\left( {2f_{\eta } + \gamma_{1} } \right)\phi = 0 $$
(18)

where \(Q = \frac{{Q_{0} }}{{\rho C_{P} b}},\,\,\,\,\Pr = \frac{{\mu C_{P} }}{k},\,\,\,\,Ec = \frac{{b^{2} l^{2} }}{{A_{0} C_{P} }},\,\,\,\,M = \frac{{\sigma B_{0}^{2} }}{\rho b}\,\,{\text{and}}\,\,R = \frac{{16\sigma^{*} T_{\infty }^{3} }}{{3k^{*} k}}\) which are called as heat source/sink parameter, Prandtl number, Eckert number, magnetic parameter, and radiation parameter, respectively. Also, \(\gamma_{1} = \frac{{k_{c} }}{b}\,\,and\,\,Sc = \frac{\nu }{D}\) are called first-order chemical reaction and Schmidt number, respectively. Thermal radiation R can be calculated by using radiative heat flux of Rosseland’s approximation (see (Mahabaleshwar et al. 2020b, c; Xenos et al. 2020)).

The corresponding boundary conditions of PST and PSC cases are reducing to Eq. (19):

$$ \left. \begin{gathered} \theta \left( 0 \right) = 1,\,\,\,\,\,\,\,\,\,\phi \left( 0 \right) = 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{at}}\,\,\,\,\,y = 0 \hfill \\ \theta \left( \infty \right) \to 0,\,\,\,\phi \left( \infty \right) \to 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{as}}\,\,\,\,\,\,y \to \infty \hfill \\ \end{gathered} \right\} $$
(19)

Now, new variables for temperature and concentration are introduced as in Eq. (20):

$$ \xi = - \frac{\Pr }{{\alpha^{2} }}e^{ - \alpha \eta } ,\,\,\,\,\,\,\,\,\,\,\,\,\,\varepsilon = - \frac{Sc}{{\alpha^{2} }}e^{ - \alpha \eta } $$
(20)

By insertion of Eq. (11) and (20) in Eq. (17) and (18) to obtain the following results for non-dimensional energy equation:

$$ \begin{gathered} \left( {1 + R} \right)\xi \theta_{\xi \xi } + \left( {\left( {1 + R} \right) - a - \frac{d}{{\left( {1 + \lambda \alpha } \right)}}\xi } \right)\theta_{\xi } + \left( {\frac{2d}{{\left( {1 + \lambda \alpha } \right)}} + \frac{\Pr Q}{{\alpha^{2} \xi }}} \right)\theta = \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - \alpha^{2} Ec\left( {\frac{{\alpha^{2} d^{2} }}{{\left( {1 + \lambda \alpha } \right)^{2} }} + \frac{{\left( {M + Da^{ - 1} } \right)}}{{\left( {1 + \lambda \alpha } \right)^{2} }} - \frac{\beta d}{{\left( {1 + \lambda \alpha } \right)^{2} }}a\frac{{\alpha^{4} }}{\Pr }} \right)\xi \hfill \\ \end{gathered} $$
(21)
$$ \varepsilon \phi_{\varepsilon \varepsilon } + \left( {1 - c - \frac{\varepsilon d}{{\left( {1 + \lambda \alpha } \right)}}} \right)\phi_{\varepsilon } + \left( {\frac{2d}{{\left( {1 + \lambda \alpha } \right)}} - \frac{{\gamma_{1} Sc}}{{\left( {1 + \lambda \alpha } \right)}}} \right)\phi = 0 $$
(22)

where

$$ a = \frac{\Pr }{{\alpha^{2} }}\frac{d}{{\left( {1 + \lambda \alpha } \right)}} + \frac{\Pr S}{\alpha }\quad {\text{and}}\quad c = \frac{Sc}{{\alpha^{2} }}\left( {\frac{d}{{\left( {1 + \lambda \alpha } \right)}}} \right) + S\frac{Sc}{\alpha } $$
(23)

In addition, boundary conditions also will be transformed to:

$$ \left. \begin{gathered} \theta \left( { - \frac{\Pr }{{\alpha^{2} }}} \right) = 1,\,\,\,\,\,\,\,\,\,\,\theta \left( 0 \right) = 0 \hfill \\ \phi \left( { - \frac{Sc}{{\alpha^{2} }}} \right) = 1,\,\,\,\,\,\,\,\,\,\,\phi \left( 0 \right) = 0 \hfill \\ \end{gathered} \right\} $$
(24)

The solution of Eqs. (21) and (22) corresponding to the abovementioned boundary conditions, Eq. (24), is examined in the following form of confluent hypergeometric function in terms of similarity variable \(\eta\).

$$ \begin{gathered} \theta \left( \eta \right) = \left( {1 + C_{1} } \right)Exp\left[ { - \left( {\frac{{a_{0} + b_{0} }}{2}} \right)\alpha \eta } \right]\frac{{F\left( {\left( {\frac{{a_{0} + b_{0} }}{2}} \right)d - 2d,\,1 + b_{0} \,\frac{1}{1 + \lambda \alpha }\left( {\frac{ - \Pr }{{\alpha^{2} }}Exp[ - \alpha \eta ]} \right)} \right)}}{{F\left( {\left( {\frac{{a_{0} + b_{0} }}{2}} \right)d - 2d,\,1 + b_{0} \,\frac{1}{1 + \lambda \alpha }\left( {\frac{ - \Pr }{{\alpha^{2} }}} \right)} \right)}} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + C_{1} Exp[ - 2\alpha \eta ]\left( {\frac{ - \Pr }{{\alpha^{2} }}} \right)^{2} \hfill \\ \end{gathered} $$
(25)
$$ \phi \left( \eta \right) = Exp\left[ { - \frac{{\left( {c_{0} + d_{0} } \right)}}{2}\alpha \eta } \right]\frac{{F\left( {\frac{{\left( {c_{0} + d_{0} } \right)}}{2}d - 2d,\,1 + d_{0} \,\, - \frac{Sc}{{\alpha^{2} \left( {1 + \lambda \alpha } \right)}}Exp\left[ { - \alpha \eta } \right]} \right)}}{{F\left( {\frac{{\left( {c_{0} + d_{0} } \right)}}{2}d - 2d,\,1 + d_{0} \,\, - \frac{Sc}{{\alpha^{2} \left( {1 + \lambda \alpha } \right)}}} \right)}} $$
(26)

where

$$ C_{1} = - \frac{{\alpha^{2} Ec\left( {\frac{{\alpha^{2} d^{2} }}{{\left( {1 + \lambda \alpha } \right)^{2} }} + \frac{{\left( {M + Da^{ - 1} } \right)}}{{\left( {1 + \lambda \alpha } \right)^{2} }} - \frac{\beta d}{{\left( {1 + \lambda \alpha } \right)^{2} }}a\frac{{\alpha^{4} }}{\Pr }} \right)}}{{\Pr \left( {4\left( {1 + R} \right) - 2a + \frac{\Pr Q}{{\alpha^{2} }}} \right)}}\quad and $$
(27)
$$ a_{0} = a - R,\,\,\,\,\,\,\,\,\,b_{0} = \sqrt {a_{0}^{2} - \frac{4\Pr Q}{{\alpha^{2} }}} \quad c_{0} = c,\,\,\,\,\,\,\,d_{0} = \sqrt {c_{0}^{2} + \frac{{4Sc\gamma_{1} }}{{\alpha^{2} }}} $$
(28)

Wall temperature gradient \(\theta_{\eta } \left( 0 \right)\) and concentration gradient \(\phi_{\eta } \left( 0 \right)\) in the dimensionless form are given by

$$ \begin{gathered} \theta_{\eta } \left( 0 \right) = A\left\{ {\frac{{\left( {a_{0} + b_{0} } \right)d - 4d}}{{1 + b_{0} }}\left( {\frac{\Pr }{{2\alpha \left( {1 + \lambda \alpha } \right)}}} \right)F\left( {\frac{{\left( {a_{0} + b_{0} } \right)d - 4d + 2}}{2},\,\,2 + b_{0} ,\,\, - \frac{\Pr }{{\alpha^{2} \left( {1 + \lambda \alpha } \right)}}} \right)} \right. \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left. {\,\,\,\, - \alpha \left( {\frac{{a_{0} + b_{0} }}{2}} \right)F\left( {\frac{{\left( {a_{0} + b_{0} } \right)d - 4d}}{2},\,\,1 + b_{0} ,\,\, - \frac{\Pr }{{\alpha^{2} \left( {1 + \lambda \alpha } \right)}}} \right)} \right\} - 2C_{1} \alpha \left( { - \frac{\Pr }{{\alpha^{2} }}} \right)^{2} \hfill \\ \end{gathered} $$
(29)
$$ \begin{gathered} \phi_{\eta } \left( 0 \right) = B\left\{ { - \alpha \left( {\frac{{c_{0} + d_{0} }}{2}} \right)} \right.F\left( {\left( {\frac{{c_{0} + d_{0} }}{2}} \right)d - 2d,\,\,1 + d_{0} ,\,\, - \frac{Sc}{{\alpha^{2} \left( {1 + \lambda \alpha } \right)}}} \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left. { + \frac{Sc}{{\alpha \left( {1 + \lambda \alpha } \right)}}\frac{{\left( {c_{0} + d_{0} } \right)d - 4d}}{{2\left( {1 + d_{0} } \right)}}F\left( {\left( {\frac{{c_{0} + d_{0} }}{2}} \right)d - 2d + 1,\,\,2 + d_{0} ,\,\, - \frac{Sc}{{\alpha^{2} \left( {1 + \lambda \alpha } \right)}}} \right)} \right\} \hfill \\ \end{gathered} $$
(30)

where A and B are also given in Eq. (30a and 30b)

$$ A = \frac{{\left( {1 + C_{1} } \right)}}{{F\left( {\frac{{\left( {a_{0} + b_{0} } \right)d - 4d}}{2},\,\,1 + b_{0} ,\,\, - \frac{\Pr }{{\alpha^{2} \left( {1 + \lambda \alpha } \right)}}} \right)}} $$
(30a)
$$ B = \frac{1}{{F\left( {\left( {\frac{{c_{0} + d_{0} }}{2}} \right)d - 2d,\,\,1 + d_{0} ,\,\, - \frac{Sc}{{\alpha^{2} \left( {1 + \lambda \alpha } \right)}}} \right)}} $$
(30b)

Dimensionless local heat flux \(q_{w}\) and mass flux \(m_{w}\) are represented as

$$ \left. \begin{gathered} q_{w} = - k\left( {\frac{\partial T}{{\partial y}}} \right)_{w} + \left( {q_{r} } \right)_{w} = - k\sqrt {\frac{b}{\nu }} \left( {T_{w} - T_{\infty } } \right)\left( {1 + R} \right)\theta_{\eta } \left( 0 \right) \hfill \\ m_{w} = - D\left( {\frac{\partial C}{{\partial y}}} \right)_{w} = - D\sqrt {\frac{b}{\nu }} \left( {C_{w} - C_{\infty } } \right)\phi_{\eta } \left( 0 \right) \hfill \\ \end{gathered} \right\} $$
(31a)

Bu using Eq. (31), Nusselt number and Sherwood number can be derived as

$$ \left. \begin{gathered} \frac{Nu}{{\left( {{\text{Re}}_{x} } \right)^{1/2} }} = - \left( {1 + R} \right)\theta_{\eta } \left( 0 \right) \hfill \\ \frac{Sh}{{\left( {{\text{Re}}_{x} } \right)^{1/2} }} = - \phi_{\eta } \left( 0 \right) \hfill \\ \end{gathered} \right\} $$
(31b)

4.2 Prescribed Heat and Mass Flux

By applying the boundary conditions defined in Eq. (8a) and (8c) in Eq. (3) and (4) to obtain the following ODE for concentration:

$$ \left( {1 + R} \right)g_{\eta \eta } + \Pr fg_{\eta } - \Pr \left( {2f_{\eta } - Q} \right)g = - \Pr Ec\left\{ {f_{\eta \eta }^{2} - \beta f_{\eta \eta } \left( {f_{\eta } f_{\eta \eta } - ff_{\eta \eta \eta } } \right) + \left( {M + Da^{ - 1} } \right)f_{\eta }^{2} } \right\} $$
(32)
$$ h_{\eta \eta } + Scfh_{\eta } - Sc\left( {2f_{\eta } + \gamma_{1} } \right)h = 0 $$
(33)

The appropriate boundary conditions in the PHF case

$$ \left. \begin{gathered} g_{\eta } \left( 0 \right) = - 1,\,\,\,\,\,\,\,g\left( \infty \right) = 0 \hfill \\ h_{\eta } \left( 0 \right) = - 1,\,\,\,\,\,\,\,\,h\left( \infty \right) = 0 \hfill \\ \end{gathered} \right\} $$
(34)

The same procedure will also be applied to the non-dimensional concentration equation in which by using the same variables defined in Eq. (20), (32) and (33) to obtain the equations as given below:

$$ \begin{gathered} \left( {1 + R} \right)\xi g_{\xi \xi } + \left( {\left( {1 + R} \right) - a - \frac{d}{{\left( {1 + \lambda \alpha } \right)}}\xi } \right)g_{\xi } + \left( {\frac{2d}{{\left( {1 + \lambda \alpha } \right)}} + \frac{\Pr Q}{{\alpha^{2} \xi }}} \right)g = \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - \alpha^{2} Ec\left( {\frac{{\alpha^{2} d^{2} }}{{\left( {1 + \lambda \alpha } \right)^{2} }} + \frac{{\left( {M + Da^{ - 1} } \right)}}{{\left( {1 + \lambda \alpha } \right)^{2} }} - \frac{\beta d}{{\left( {1 + \lambda \alpha } \right)^{2} }}a\frac{{\alpha^{4} }}{\Pr }} \right)\xi \hfill \\ \end{gathered} $$
(35)
$$ \varepsilon h_{\varepsilon \varepsilon } + \left( {1 - c - \frac{\varepsilon d}{{\left( {1 + \lambda \alpha } \right)}}} \right)h_{\varepsilon } + \left( {\frac{2d}{{\left( {1 + \lambda \alpha } \right)}} - \frac{{\gamma_{1} Sc}}{{\left( {1 + \lambda \alpha } \right)}}} \right)h = 0 $$
(36)

Boundary conditions defined in Eq. (34) are also transformed into Eq. (37)

$$ \left. \begin{gathered} g_{\xi } \left( { - \frac{\Pr }{{\alpha^{2} }}} \right) = - \frac{\alpha }{\Pr },\,\,\,\,\,\,\,g\left( 0 \right) = 0 \hfill \\ h_{\xi } \left( { - \frac{Sc}{{\alpha^{2} }}} \right) = - \frac{\alpha }{Sc},\,\,\,\,\,\,\,\,h\left( 0 \right) = 0 \hfill \\ \end{gathered} \right\} $$
(37)

With the help of the same manipulation used in PST condition, Eq. (35) and (36) with respect to the boundary conditions defined in Eq. (34) are solved analytically and expressed in the form of confluent hypergeometric equation:

$$ \begin{gathered} g\left( \eta \right) = \left( {2C_{1} \alpha \left( { - \frac{\Pr }{{\alpha^{2} }}} \right)^{2} - 1} \right)\left\{ { - \alpha \left( {\frac{{a_{0} + b_{0} }}{2}} \right)F\left( {\frac{{\left( {a_{0} + b_{0} } \right)d}}{2} - 2d,\,\,1 + b_{0} ,\,\, - \frac{\Pr }{{\alpha^{2} \left( {1 + \lambda \alpha } \right)}}} \right)} \right. \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\left. { + \frac{{\left( {a_{0} + b_{0} } \right)d - 4d}}{{2\left( {1 + b_{0} } \right)}}\frac{\Pr }{{\alpha \left( {1 + \lambda \alpha } \right)}}F\left( {\frac{{\left( {a_{0} + b_{0} } \right)d}}{2} - 2d + 1,\,\,2 + b_{0} ,\,\, - \frac{\Pr }{{\alpha^{2} \left( {1 + \lambda \alpha } \right)}}} \right)} \right\}^{ - 1} \hfill \\ \,\,\,\,\,\,\,\,\,\,\, \times Exp\left[ { - \left( {\frac{{a_{0} + b_{0} }}{2}} \right)\alpha \eta } \right]F\left( {\frac{{\left( {a_{0} + b_{0} } \right)d}}{2} - 2d,\,\,1 + b_{0} ,\,\, - \frac{\Pr }{{\alpha^{2} \left( {1 + \lambda \alpha } \right)}}Exp\left[ { - \alpha \eta } \right]} \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\, + C_{1} Exp\left[ { - 2\alpha \eta } \right]\left( { - \frac{\Pr }{{\alpha^{2} }}} \right)^{2} \hfill \\ \end{gathered} $$
(38)
$$ \begin{gathered} h\left( \eta \right) = \left\{ {\alpha \left( {\frac{{c_{0} + d_{0} }}{2}} \right)F\left( {\frac{{\left( {c_{0} + d_{0} } \right)d}}{2} - 2d,\,\,1 + d_{0} ,\,\, - \frac{Sc}{{\alpha^{2} \left( {1 + \lambda \alpha } \right)}}} \right)} \right. \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\left. { - \frac{{\left( {c_{0} + d_{0} } \right)d - 4d}}{{2\left( {1 + d_{0} } \right)}}\frac{Sc}{{\alpha \left( {1 + \lambda \alpha } \right)}}F\left( {\frac{{\left( {c_{0} + d_{0} } \right)d}}{2} - 2d + 1,\,\,2 + d_{0} ,\,\, - \frac{Sc}{{\alpha^{2} \left( {1 + \lambda \alpha } \right)}}} \right)} \right\}^{ - 1} \hfill \\ \,\,\,\,\,\,\,\,\,\,\, \times Exp\left[ { - \left( {\frac{{c_{0} + d_{0} }}{2}} \right)\alpha \eta } \right]F\left( {\frac{{\left( {c_{0} + d_{0} } \right)d}}{2} - 2d,\,\,1 + d_{0} ,\,\, - \frac{Sc}{{\alpha^{2} \left( {1 + \lambda \alpha } \right)}}Exp\left[ { - \alpha \eta } \right]} \right) \hfill \\ \end{gathered} $$
(39)

Dimensionless wall temperature \(g\left( 0 \right)\) and wall concentration \(h\left( 0 \right)\) are given by

$$ \begin{gathered} g\left( 0 \right) = \left( {2C_{1} \alpha \left( { - \frac{\Pr }{{\alpha^{2} }}} \right)^{2} - 1} \right)\left\{ { - \alpha \left( {\frac{{a_{0} + b_{0} }}{2}} \right)F\left( {\frac{{\left( {a_{0} + b_{0} } \right)d}}{2} - 2d,\,\,1 + b_{0} ,\,\, - \frac{\Pr }{{\alpha^{2} \left( {1 + \lambda \alpha } \right)}}} \right)} \right. \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\left. { + \frac{{\left( {a_{0} + b_{0} } \right)d - 4d}}{{2\left( {1 + b_{0} } \right)}}\frac{\Pr }{{\alpha \left( {1 + \lambda \alpha } \right)}}F\left( {\frac{{\left( {a_{0} + b_{0} } \right)d}}{2} - 2d + 1,\,\,2 + b_{0} ,\,\, - \frac{\Pr }{{\alpha^{2} \left( {1 + \lambda \alpha } \right)}}} \right)} \right\}^{ - 1} \hfill \\ \,\,\,\,\,\,\,\,\,\,\, \times F\left( {\frac{{\left( {a_{0} + b_{0} } \right)d}}{2} - 2d,\,\,1 + b_{0} ,\,\, - \frac{\Pr }{{\alpha^{2} \left( {1 + \lambda \alpha } \right)}}} \right) + C_{1} \left( { - \frac{\Pr }{{\alpha^{2} }}} \right)^{2} \hfill \\ \end{gathered} $$
(40)
$$ \begin{gathered} h\left( 0 \right) = \left\{ {\alpha \left( {\frac{{c_{0} + d_{0} }}{2}} \right)F\left( {\frac{{\left( {c_{0} + d_{0} } \right)d}}{2} - 2d,\,\,1 + d_{0} ,\,\, - \frac{Sc}{{\alpha^{2} \left( {1 + \lambda \alpha } \right)}}} \right)} \right. \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\left. { - \frac{{\left( {c_{0} + d_{0} } \right)d - 4d}}{{2\left( {1 + d_{0} } \right)}}\frac{Sc}{{\alpha \left( {1 + \lambda \alpha } \right)}}F\left( {\frac{{\left( {c_{0} + d_{0} } \right)d}}{2} - 2d + 1,\,\,2 + d_{0} ,\,\, - \frac{Sc}{{\alpha^{2} \left( {1 + \lambda \alpha } \right)}}} \right)} \right\}^{ - 1} \hfill \\ \,\,\,\,\,\,\,\,\,\,\, \times F\left( {\frac{{\left( {c_{0} + d_{0} } \right)d}}{2} - 2d,\,\,1 + d_{0} ,\,\, - \frac{Sc}{{\alpha^{2} \left( {1 + \lambda \alpha } \right)}}} \right) \hfill \\ \end{gathered} $$
(41)

where

$$ \begin{gathered} c_{1} = \frac{{\left( {S\beta + \lambda } \right)^{2} }}{{4S^{2} \beta^{2} \lambda^{2} }} - \frac{2t}{{3S\beta \lambda }} \hfill \\ c_{2} = \sqrt[3]{2}\left( {12\left( { - d - M - Da^{ - 1} } \right)S\beta \lambda - 3\left( {S\beta + \lambda } \right)\left( { - S - M\lambda - Da^{ - 1} \lambda } \right) + t^{2} } \right) \hfill \\ c_{3} = 3S\beta \lambda \left( {27\left( { - d - M - Da^{ - 1} } \right)\left( {S\beta + \lambda } \right)^{2} + 27S\beta \lambda \left( { - S - M\lambda - Da^{ - 1} \lambda } \right) - 72\left( { - d - M - Da^{ - 1} } \right)S\beta } \right.\lambda \hfill \\ \,\,\,\,\,\,\,\,\,t - 9\left( {S\beta + \lambda } \right)\left( { - S - M\lambda - Da^{ - 1} \lambda } \right)t + 2t^{3} \left( { - 4} \right.\left( {12} \right.\left( { - d - M - Da^{ - 1} } \right)S\beta \lambda \hfill \\ \,\,\,\,\,\,\,\,\, - 3\left( {S\beta + \lambda } \right)\left( { - S - M\lambda - Da^{ - 1} \lambda } \right) + \left. {t^{2} } \right)^{3} + \left( {27\left( { - d - M - Da^{ - 1} } \right)\left( {S\beta + \lambda } \right)^{2} } \right. + \hfill \\ \,\,\,\,\,\,\,\,\,27S\beta \lambda \left( { - S - M\lambda - Da^{ - 1} \lambda } \right) - 72\left( { - d - M - Da^{ - 1} } \right)S\beta \lambda t - 9\left( {S\beta + \lambda } \right)\left( { - S - M\lambda - Da^{ - 1} \lambda } \right)t + \left. {\left. {\left. {2t^{3} } \right)^{2} } \right)^{1/2} } \right)^{1/3} \hfill \\ c_{4} = \left( {\frac{{ - \left( {S\beta + \lambda } \right)^{3} }}{{S^{3} \beta^{3} \lambda^{3} }} - 8\frac{{\left( { - S - M\lambda - Da^{ - 1} } \right)}}{S\beta \lambda } + 4\frac{{\left( {S\beta + \lambda } \right)t}}{{S^{2} \beta^{2} \lambda^{2} }}} \right), \hfill \\ c_{5} = \frac{1}{2}c_{1} - \frac{{c_{2} }}{{c_{3} }} - \frac{1}{{\sqrt[3]{2}c_{3} }} - \frac{{c_{4} }}{{\left( {4c_{1} + \frac{{c_{2} }}{{c_{3} }} + \frac{1}{{\sqrt[3]{2}c_{3} }}} \right)}}, \hfill \\ t = \left( {1 + 5d\beta + 2d\gamma - S\lambda } \right)\,\quad \left( {{\text{For}}\,\,\eta \,\,{\text{is}}\,\,{\text{small}}} \right) \hfill \\ t = \left( {1 + d\beta - S\lambda } \right)\,\,\,\quad \quad \,\,\quad \,\left( {{\text{For}}\,\,\eta \,\,{\text{is}}\,\,{\text{large}}} \right) \hfill \\ \end{gathered} $$

In the next chapter, graphical representation of these solutions will be presented.

5 Results and Discussion

A viscoelastic Rivlin–Ericksen fluid flow due to a stretching/shrinking porous sheet in the presence of transverse magnetic field with inverse Darcy model is examined. A suitable similarity transformation converted highly nonlinear partial differential equations into set of nonlinear ordinary differential equations, and their analytical solutions are expressed in terms of confluent hypergeometric function. These analytical functions are calculated for different boundary conditions, namely PST, PMC, PHF and PMF. Skin friction coefficient, local Nusselt number, temperature-dependent heat source/sink, and chemical reaction of the species are all also taken into account. In the process of calculation fourth root of Eq. (12) for \(\alpha\) is calculated for two different limiting cases, one is for \(\eta = 0\), and another one is for \(\eta \to \infty\). The following values are considered for the parameters \(\Pr = Sc = 6.2\) and R = 2, throughout all the computations.

Figures 2 and 3 represent the effect of suction/injection parameter S on the root of the equation \(\alpha\) for shrinking and stretching cases, respectively, at (a) and (b). Figures 1a and 2a represent the shrinking case, where it is observed that the effect of viscoelastic parameter \(\beta\) increases with increase in suction/injection parameter S under the function of root of the equation \(\alpha\). The same effect observed in Fig. 2b for stretching case means that \(\beta\) increases with increase in suction/injection parameter S under the function of root of the equation \(\alpha\). The \(\alpha\) used in Fig. 2 is calculated from Eq. (13) when \(\eta \to \infty\), and also, \(\alpha\) used in Fig. 2 is calculated from Eq. (14) when \(\eta = 0\).

Fig. 2
figure 2

Impact of suction/injection parameter \(S\) on the root of the equation \(\alpha\) for different values of visco-elastic parameter \(\beta\) for a the shrinking sheet \(d = - 1\) and b stretching sheet \(d = 1\), where \(M = 1,\,\,\lambda = 0.01,\,\,Da^{ - 1} { = 1,}\,\,{\text{and}}\,\,\gamma = 0.1.\)(for the limiting case \(\eta \to \infty\))

Full size image
Fig. 3
figure 3

Impact of suction/injection parameter \(S\) on the root of the equation \(\alpha\) for different values of visco-elastic parameter \(\beta\) for a: the shrinking sheet \(d = - 1\), and b: the stretching sheet \(d = 1\), where \(M=1,D{a}^{-1}= \text{1 and } \lambda =0.01\) (for the limiting case \(\eta = 0\))

Full size image

The behavior of transverse velocity \(f\left( \eta \right)\) with respect to variable \(\eta\) for different values of magnetic parameter M in shrinking and stretching cases is depicted in Fig. 4a and b, respectively. In Fig. 4a, it is clearly observed that the transverse velocity \(f\left( \eta \right)\) decreases with increase in magnetic parameter M. The similar effect is observed at Fig. 4b. Figure 5a and b represents the effect of tangential velocity \(f_{\eta } \left( \eta \right)\) on similarity variable \(\eta\) for different values of magnetic parameter M for the cases of shrinking and stretching cases, respectively. It is clearly observed that in both the cases, the tangential velocity \(f_{\eta } \left( \eta \right)\) decreases with increase in magnetic parameter M. The velocity boundary layer presented in Fig. 5 can be used to determine skin friction, discussed later in Fig. 10, and provides an accurate tools for special turbomachinery calculations such as Tesla turbine in which their principles are solely based on shear stress and fluid friction (Sheikhnejad et al. 2020a, b).

Fig. 4
figure 4

Profile of transverse velocity \(f\left( \eta \right)\) respect to similarity variable \(\eta\) for various values of magnetic parameter M, a: the shrinking sheet \(d = - 1\), and b: the stretching sheet \(d = 1\), where \(\gamma = 0.1,\,\,\beta = - 1,\,\,S = 1,\,\,Da^{ - 1} = 0.1\,\,{\text{and}}\,\,\lambda = 1,.\)

Full size image
Fig. 5
figure 5

Profile of tangential velocity \(f_{\eta } \left( \eta \right)\) respect to similarity variable \(\eta\) for various values of magnetic parameter M, a: the shrinking sheet \(d = - 1\), and b: the stretching sheet \(d = 1\), where \(\gamma = 0.1,\,\,\beta = - 1,\,\,S = 1,\,\,Da^{ - 1} = 0.1\,\,{\text{and}}\,\,\lambda = 1,.\)

Full size image

Figure 6a, b shows the variation of temperature profiles \(\theta \left( \eta \right)\) and \(g\left( \eta \right)\) respect to similarity variable \(\eta\), for different values of cross-viscosity parameter \(\gamma\) for PST and PHF cases, respectively. Effect of cross-viscosity parameter, which can be interpreted as reciprocal of fluid viscosity, on temperature profiles is more significant close to the solid wall as the higher shear rate is detected in this region. Moreover, in PST case, temperature profiles \(\theta \left( \eta \right)\) increases with increasing in the \(\gamma\) value, but this effect is reversed in PHF case, i.e., \(g\left( \eta \right)\) decreases with increasing the values of \(\gamma\). Increase in temperature as viscosity decreases is the peculiar effect of Rivlin–Ericksen fluid which is originated from nonlinearity of second terms on right had side of energy equation, Eq. (17). This is due to the fact that \(\theta \left( \eta \right)\) and \(g\left( \eta \right)\) are defined differently in such a way that \(g\left( \eta \right)\) has \(\gamma^{ - 0.5}\) in its denominator, while \(\theta \left( \eta \right)\) definition is not influenced by \(\gamma\). The temperature profile in boundary layer may have a very important application on renewable solar heater (Sheikhnejad and Gandjalikhan Nassab 2021), where natural convection starts on the wall of absorber.

Fig. 6
figure 6

Non-dimensional temperature profile for a: PST case, \(\theta \left( \eta \right)\), and b: PHF case, \(g\left( \eta \right)\), for different values of cross-viscosity parameter \(\gamma\), where \(S=0.5,M=1,d=-1,\beta =-3,Ec=0.01,D{a}^{-1}=1, \text{and }Q=-0.1\)

Full size image

The variation of temperature profiles \(\theta \left( \eta \right)\) and \(g\left( \eta \right)\) respect to similarity variable \(\eta\), for different values of viscoelastic parameter \(\beta\) for PST and PHF cases, respectively, observed in Fig. 7a, b. In PST case, the \(\beta\) value increases with increasing the temperature profiles \(\theta \left( \eta \right)\), but this effect is reversed in PHF case, i.e., \(g\left( \eta \right)\) decreases with increasing the values of \(\beta\). In addition, to provide better visual understanding, a blue level line with slop of − 1.0 is depicted together with tangent lines of all four curves at η = 0. The blue level line represents a plummet for tangent lines, to check out the parallel feature. Based on the abovementioned boundary condition for g-function, slope of g-function at η = 0 must be − 1.0.

Fig. 7
figure 7

Non-dimensional temperature profile for a: PST case, \(\theta \left( \eta \right)\), and b: PHF case, \(g\left( \eta \right)\), for different values of viscoelastic parameter \(\beta\), where \(S=0.5,M=1,d=-1,\gamma =-1,Ec=0.01,D{a}^{-1}=1, \text{and }Q=-0.1\)

Full size image

Figure 8a, b portrays the effect of concentration profiles \(\phi \left( \eta \right)\) and \(h\left( \eta \right)\) similarity variable \(\eta\) for different values of viscoelastic parameter \(\beta\), for the cases of PST and PHF, respectively. As seen, the \(\phi\)-function well follows the imposed boundary conditions where at the solid wall must be 1.0 to satisfy \(C = C_{w}\), and at infinity must approach to zero to satisfy \(C = C_{\infty }\). In Fig. 8b, h-function also can well follow the imposed boundary condition where gradient of all curves at wall (η = 0) is − 1.0 and simultaneously all curves approach zero to satisfy \(C = C_{\infty }\). Also, in both the case, the value of \(\beta\) decreases with increase in concentration profiles \(\phi \left( \eta \right)\) and \(h\left( \eta \right)\).

Fig. 8
figure 8

Concentration profile for a: PST case, \(\phi \left( \eta \right)\), and b: PHF case, \(h\left( \eta \right)\), for different values of visco-elastic parameter \(\beta\), where \(S=0.5,M=1,d=-1,\gamma =-1,{\gamma }_{1}=-0.25, \text{and }D{a}^{-1}=1.\)

Full size image

Similarly, Fig. 9a, b indicates the variation of concentration profiles \(\phi \left( \eta \right)\) and \(h\left( \eta \right)\) respect to similarity variable \(\eta\) for different values of first-order chemical reaction rate \(\gamma_{1}\). As seen, thickness of both concentration profiles \(\phi \left( \eta \right)\) and \(h\left( \eta \right)\) decreases with increase of \(\gamma_{1}\) value and the role of chemical conversion is to reduce the thickness of the concentration boundary layer. Although close to the solid wall effect of chemical reaction rate is significant, however, gradually disappear as η increases.

Fig. 9
figure 9

Concentration profile for a: PST case, \(\phi \left( \eta \right)\), and b: PHF case, \(h\left( \eta \right)\), for different values of first-order chemical reaction rate \(\gamma_{1}\), where \(S=0.5,M=1,d=-1,\gamma =-1,\beta =-0.1, \text{and }D{a}^{-1}=1.\)

Full size image

Figure 10a, b indicates the impact of skin friction coefficient on magnetic parameter M as a function of \(\gamma\) and S, respectively. Here, it is good to notice that \(\gamma\) is the reciprocal of viscosity, and decreasing viscosity and increasing \(\gamma\) are the same process. While skin friction is linearly proportional to the viscosity, it is expected to have an inverse proportionality with \(\gamma\), as depicted in Fig. 10a. In addition, upward pulling magnetic force will draw fluid toward positive y-direction and reduce the skin friction. By increasing suction parameter, that shows the strength of wall suction, thickness of boundary layer will decrease, and consequently, the gradient of velocity on the wall will increase as well. This effect will enhance skin friction that is shown in Fig. 10b. Moreover, as the magnetic force acts as a pulling force on the Rivlin–Ericksen liquid, higher magnitude of magnetic force directed toward positive y coordinate will tend to detach flow from the wall, and hence, skin friction will be reduced. Actually, suction parameter S and magnetic parameter M act against each other.

Fig. 10
figure 10

Variation of \(C_{f} {\text{Re}}_{x}^{1/2}\) respect to a: \(\gamma\) and b: \(S\) for different values of magnetic parameter \(M\), keeping the parameters as \(\lambda =1,d=-1,\beta =0.5,{\gamma }_{1}=D{a}^{-1}=0.1.\)

Full size image

Figure 11a, b indicates the impact of Nusselt number and Sherwood number on \(\gamma \,{\text{and}}\,\gamma_{1}\) as a function of Prandtl number and Schmidt number, respectively. In Fig. 11a, it is seen that the Nusselt number decreases with increase of \(\gamma\) value. Similarly, in Fig. 11b, it is observed that Sherwood number increases with increase of \(\gamma_{1}\) value.

Fig. 11
figure 11

a Variation of Nusselt number \(Nu/\sqrt {{\text{Re}}_{x} }\) respect to Pr number for different values of \(\gamma\), and b: variation of Sherwood number \(Sh/\sqrt {{\text{Re}}_{x} }\) respect to number \(Sc\) for different values of \(\gamma_{1}\). Keeping the parameters as \(S=0.5,M=1, d=\gamma =-1,\beta =-0.1,D{a}^{-1}=1.\)

Full size image

Moreover, in order to show how \(g\left( \eta \right)\) behave as η approaches to infinity for different \(\gamma\) values, Fig. 12 is depicted which indicates that \(g\left( \eta \right)\) monotonically increases by η such that its value asymptotically approaches to zero, because the fluid temperature must be approached to the free stream temperature, as it is expected. Also, Fig. 12 shows that increase of \(\gamma\) value would lead to a lower value of g-function which can be interpreted as lower temperature at the same height. The viscous dissipation in energy equation is responsible for this effect as it is always a positive source of heat generation that will cause fluid temperature to increase. Keeping in mind that \(\gamma = \frac{b}{\nu }\) (reciprocal of viscosity) which means that by decreasing viscosity, \(\gamma\) will increase and vice versa. Increasing viscosity to twofold will make the effect of heat dissipation double in energy equation and consequently lead to a higher temperature.

Fig. 12
figure 12

Profile of non-dimensional temperature \(g\left( \eta \right)\) for with range of \(\eta\) and for various values of \(\gamma\) where \(S = 0.5,\,\,M = 1,\,\,d = - 1,\,\,\gamma = - 1,\,\,Ec = 0.01,\,\,Da^{ - 1} = 1,\,\,{\text{and}}\,\,Q = - 0.1\)

Full size image

It should be noted here that the dual solutions for velocity distribution exist for certain values of velocity ratio parameter. The dual solutions and a unique solution for specific values of the ratio of shrinking and straining rates and further showed that for a faster-shrinking rate, the similarity solution does not exist. Thus, the physical nature of the first solution for the dual solutions and the unique solution is the same. Consequently, for dual similarity solutions, the first solution is the stable solution, and the second one is unstable.

6 Concluding Remarks

This study is conducted to answer a few research questions that has not been addressed yet in the literature. The most important one is providing analytical solution for the multiphysics boundary layer problem of non-Newtonian fluid flow within porous media under magnetic field including reactions and suction/injection. Mathematical formulation of the present work helps to study the MHD Rivlin–Ericksen fluid flow over a porous stretching/shrinking sheet with inverse Darcy model. The set of governing equations consisting of highly non-linear PDE’s is converted into a set of ODE’s through similarity transformation. Several inherent parameters such as suction/injection, temperature-dependent heat source/sink, stress work, fluid chemical reaction, skin friction and Nusselt number are taken for investigation. The resulting analytical solutions for temperature and concentration are expressed in terms of Kummer’s function for different boundary conditions, namely prescribed temperature and heat flux as well as prescribed concentration and mass flux. The following important conclusions can be drawn as listed below.

  • The uniform magnetic field directed toward positive y-direction decreases both the transverse and tangential velocities of the Rivlin–Ericksen fluid.

  • The impact of cross-viscosity decreases the temperature in both PST and PHF case.

  • The effect of viscoelastic parameter increases the temperature in PST case and decreases the temperature in PHF case.

  • Concentration of the fluid decreases in both PST and PHF cases, when the value of visco-elastic parameter increases.

  • Increasing the values of first-order chemical conversion rate will decrease the concentration of species in both PST and PHF cases.

  • For particular case where \(\lambda = R = Da^{ - 1} = 0\,\,\,{\text{and}}\,\,\,\beta = - \beta\), the present problem reduces into the work of Khan et al. (Khan et al. 2003)

  • There are several works that can be considered as the special case of the present study: \(\mathop {lim}\limits_{{\lambda = R = Da^{ - 1} = 0}} \left\{ {\text{Our results}} \right\} \to \left\{ {{\text{Results of Siddappa and Prakasha (See Ref}}{. [27])}} \right\}\)

  • The classical Crane (Crane 1970) flow is recovered from Eq. (9) for \(M = Da^{ - 1} = \beta = 0,\).

  • Mahabaleshwar et al. (Mahabaleshwar et al. 2018) can be recovered from Eq. (9) for \(Da^{ - 1} = 0.\)

  • Nandeppanavar et al. (Nandeppanavar et al. 2010) can be recovered from Eq. (9) for \(M = Da^{ - 1} = 0,\)