Study on Productivity Prediction of Multi-Stage Fractured Horizontal Well in Low-Permeability Reservoir Based on Finite Element Method

Abstract

Low-permeability reservoir is a porous medium of complex pore structure, which has the characteristic of narrow pore throat, poor connectivity and ultra-low permeability. At present, a lot of experimental studies confirmed that there are stress sensitive and threshold pressure gradient in low-permeability reservoir. It is incorrect to simulate the oil well production dynamic characteristics by numerical simulation method of traditional seepage theory. In order to evaluate the productivity of multi-stages fractured horizontal well in low-permeability reservoir, in this paper, a seepage mathematical model of multi-stage fracturing horizontal well considering the stress sensitivity and threshold pressure gradient is established based on the discrete fracture network model and solved by the finite element method. The results of numerical simulation show that the stress sensitive of reservoir matrix controls the evolution of reservoir physical properties, the threshold pressure gradient determines production time of oil wells and the fracture compression coefficient controls production. The sensitivity analysis shows that the increasing curves of the production reduction range due to the stress sensitive and fracture compression coefficient are logarithmic, and the curve of threshold pressure gradient and shut-in time is linear descent relation. When the stress sensitivity, threshold pressure gradient and fracture compression coefficient are considered separately, the production is reduced by 17.3, 54.7 and 35.5%, respectively. It has a great inhibiting effect on productivity due to stress sensitivity, threshold pressure gradient and fracture compression coefficient, and the productivity of the well will be overestimated if the above factors are not considered. The results can provide some theoretical guidance for fracturing optimization design and efficient development of low-permeability reservoir.

1 Introduction

There is a contradiction between the continuous decline of production of conventional oil and gas and the continuous increase in demand for global oil and gas, and the global oil exploration focus has gradually shifted to unconventional reservoir. The successful exploitation of shale gas in the USA changed the market of energy demand and affected the pattern of the world. Subsequently, the exploitation technologies and experiences of shale gas are used to the low-permeability reservoirs, namely tight oil (Sa et al. 2021; Debing 2021; Liu 2021). In North America, typical tight reservoirs mainly include Bakken oilfield in Williston Basin, Eagle Ford in Texas and Cardium in Alberta. In China, tight reservoirs are mainly distributed in Ordos Basin of Changqing Oilfield. Scholars have some differences in the definition of tight reservoir. On the whole, tight reservoir has the following characteristics: a. the source and storage are integrated or close to each other. b. the physical properties are poor, and most of the oil exists in micro and nano-pores. c. vertical wells have low or no production (Nengwu 2021). Conventional vertical and horizontal wells cannot be developed economically and effectively due to the extremely low porosity and permeability, so the combination of horizontal drilling and volumetric fracturing technology is needed. At present, the new challenge focuses on how to accurately predict the production of fractured horizontal wells. The classical production prediction methods, such as Arps (1945), Fetkovich (1980), Blasingame (1991), FMB (1998) and normalized pressure integral (Liu et al. 2010), fail to accurately predict and analyze the production of tight reservoir, because they do not consider the stress sensitivity and starting pressure gradient.

Low-permeability reservoirs have very low permeability because they have many small and complex throats (Lu et al. 2021; Rao et al. 2021). The rock skeleton is subjected to compression deformation due to the increase in effective stress in the reservoir during the development process, resulting in further reduction or closure of the rock pore throat, and the lack of pore connectivity (Li et al. 2017; Smart et al. 2001). Therefore, the permeability of the low-permeability reservoir is no longer a constant, but a variable dependent on reservoir pressure. The phenomenon that permeability decreases with the increase in effective stress is called permeability stress sensitivity (Zhong et al. 2020; Wang et al. 2010a, b; Wang et al. 2019). In 1940, Kusakov discovered that fluid flow in tight reservoirs need to overcome the resistance of hydration film (Ning et al. 2019). A large number of scholars combined theoretical research and experiments to prove that the fluid flow in low-permeability reservoir no longer follows the traditional Darcy's law due to the existence of very small throat and solid–liquid boundary, but must overcome the threshold pressure gradient (TPG) (Prada and Civan 1999).

In the past research, Pedrosa (1986) established the radial flow equation considering stress sensitivity based on the Raghavan's research, and solved the instantaneous pressure response under fixed production conditions. Tian et al. (2018) established a productivity model considering threshold pressure gradient, and verified the effectiveness of the model with experiments, and analysis showed that the production loss caused by threshold pressure gradient was gradually reduced with the decrease in bottom hole pressure (BHP). Wang et al. (2010a, b) proposed an interpretation mathematical model for dual media well testing considering stress sensitivity. Li et al. (2017) established the transient production decline analysis model of horizontal well in tight gas reservoir considering pressure gradient and stress sensitivity based on the seepage mechanism. Jie et al. established an eight-line flow mode to study the pressure response and performance of horizontal wells in low permeability fractured reservoirs, but the influence of stress sensitivity was not taken into account (Yin et al. 2014). Some scholars established a new non-Darcy model considering stress sensitivity based on formation damage experiments. They found that stress sensitivity was the main reason for the rapid decline of early production through sensitivity analysis (Liu et al. 2020; Li et al. 2019a, b; Zafar et al. 2020).

In general, there is no natural productivity in low-permeability reservoir without stimulation to improve the reservoir properties, because the throat diameter of low-permeability reservoir is less than 1um and the permeability is less than 0.1mD (Luo et al. 2019). Therefore, fracturing technology is one of the widely used stimulation measures at present, especially multi-stage fracturing horizontal well technology (Li et al. 2021). The flow of fluid in fractured porous media affects the physical properties and productivity of reservoir (Hosseini and Khoei 2021). Fractures provide high permeability pathways that can significantly impact the movement of fluids compared to homogeneous porous media. Due to the complex and uncertain geology factors of fractured reservoirs, it is very difficult to characterize, develop and manage them (Welch et al. 2021). Breakthroughs on theory and model are needed considering the nature of the multi-scale and multidisciplinary challenges in fractured porous media (Li et al. 2019a, b; Dongxu et al. 2021b). Flow and transport in fractured porous media are a complex phenomenon, ranging fluid mass transfer, stress sensitive, nonlinear and coupled processes. The complexity of the physical process is further exacerbated when considerations increase. It is important to understand the fluid flow properties of fractures and improve the predictive capability of current reservoir models (Dongxu et al. 2021a).

Complex fracture network structure will be formed after fracturing, and the seepage characteristics of these complex fracture networks are mainly described by analytical method, semi-and analytical method and numerical simulation method (Cong and Leng 2020; Lei et al. 2017). The analytical method generally refers to establishing the problem model according to the actual fracture grid problem, then solving it through strict formula derivation, and finally obtaining the corresponding pressure and productivity expressions. These formulas need some idealized assumptions in the derivation process, which simplifies some complex seepage processes, and often cannot be used to describe the seepage characteristics of complex fracture network after volume fracturing (Wenwu 2018). The analytical/semi-analytical models basing a physical model describe the flow seepage in the reservoir using pressure or production and determine a specific functional relation by solving the mathematical model. They offer a theoretical basis for the observed responses (Shunde 2008). In 1991, Roberts et al. (1991) studied the productivity of multistage fracturing horizontal wells in Tight Gas Reservoirs Considering fracture non Darcy flow by using semi analytical model and numerical method. In 2014, Zhou et al. obtained the semi-analytical production of multi-stage fractured horizontal wells with complex fracture network by coupling analytical solution and discrete numerical fracture solution (Ren et al. 2019). In 2017, Zhengming et al. (2017) established a productivity formula of staged fracturing horizontal wells under unsteady state considering the variation of fracture conductivity with time and using the Green function and Newman product principle. The numerical method does not need complex mathematical transformation and formula derivation. It only needs to solve the most basic mathematical equations to obtain the bottom hole pressure and productivity formula, which can deal with more types of complex reservoirs flexibly (Zhang et al. 2021). For fractured reservoirs simulation, the finite element methods (FEM), finite difference methods (FDM) and finite volume methods (FVM) are the three most common techniques (Zhao and Du 2019). Karcher et al. (1986) studied the productivity of multistage fractured horizontal wells using numerical simulator, and the results show that fractures can greatly improve the productivity of horizontal wells. Belyadi et al. (2010) studied the productivity and flow law of fractured horizontal wells in low-permeability reservoirs using commercial reservoir simulator, and analyzed its influencing factors. Cipolla and Gongtao (2013) used the numerical simulation method of encrypted structured grid to clearly describe the parameters such as length, conductivity, shape and density of fracture network. However, this method has obvious limitations, which is only applicable to orthogonal fracture network and cannot describe other types of fracture networks. Then, he used the numerical simulation method of unstructured network to describe and characterize the fracture network, and accurately described the parameters such as conductivity, direction and shape of fracture, but this method is more complex and the calculation speed is relatively slow. The FEM can flexibility deal boundaries and complex fracture network, which is becoming more and more popular in fractured reservoir simulation (Profit et al. 2016).

Based on the above analysis, the model has strong nonlinear characteristics under considering the factors such as threshold pressure gradient, stress sensitivity and specific well type. It is a difficult problem to solve the production prediction model of tight reservoir. In this paper, the multistage fracturing horizontal well in low-permeability reservoirs productivity calculation 2D model is established considering the factors of threshold pressure gradient and stress sensitivity and hydraulic fracture conductivity based on the discrete fracture network model, and is solved by the finite element method, and simulated calculation using MATLAB. For 3D problems, the reservoir is discretized by unstructured 3D tetrahedral meshes, the 2-D embedded surface is decomposed in triangular elements that are faces of the tetrahedral surrounding the reservoir-fracture interface. We analyze the effects of threshold pressure gradient, stress sensitivity, fracture properties and other factors on reservoir pressure and oil well productivity, which provides some theoretical guidance for optimal fracturing design and efficient development of low-permeability reservoirs.

2 Mathematical Modeling

2.1 Model Assumptions

For the conventional reservoirs, the formation temperature and the fluid viscosity are not high, and the injected fluid will not undergo phase change (Cai et al. 2021; Terzaghi 1943; Steeb and Renner 2019; Biot 1941). The basic assumptions for modeling multistage fractured horizontal wells in tight reservoirs are as follows: (a) The reservoir matrix is homogeneous and of equal thickness, (b) Oil flows isothermally, (c) Gravity and the change in oil viscosity with pressure are ignored, (d) The stress sensitivity of matrix permeability and threshold pressure gradient of matrix are considered, (e) The reservoir has closed boundaries, (f) Fractures are vertical.

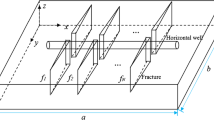
The physical model of multistage fractured horizontal well in low-permeability reservoir is shown in Fig. 1. The mathematical model of fluid flow in multistage fractured horizontal well in low-permeability reservoir is established based on the above assumptions.

Fig. 1

Schematic diagram of multistage fractured horizontal well

2.2 Fluid Flow in the Matrix System

The continuity equation for the fluid in the matrix of low permeable oil reservoir is as follows:

$$\nabla \cdot \left( {\rho \overrightarrow {{v_{m} }} } \right) + \frac{{\partial \left( {\rho \phi_{m} } \right)}}{\partial t} + q_{m} = 0$$

(1)

where the $\rho$ is the density of oil, $\overrightarrow {{v_{m} }}$ is the fluid velocity in matrix, $\phi_{m}$ is the matrix porosity, $t$ is the time and $q_{m}$ is the source-sink term of matrix.

Threshold pressure gradient (TPG) exists in the fluid flow in the unstimulated reservoir area in the low-permeable oil reservoir. The modified Darcy’s law for the fluid flow in the porous medium with TPG is as follows (Prada and Civan 1999):

$$\overrightarrow {{v_{m} }} = - \frac{{k_{m} }}{u}(\nabla p_{m} - G)$$

(2)

where $k_{m}$ is the matrix permeability, $u$ is the viscosity of fluid, $p_{m}$ is the pressure of matrix and $G$ is the threshold pressure gradient.

In this study, the TPG is expressed as a vector G in x and y directions, which can be expressed as follows (Prada and Civan 1999; Liu et al. 2016):

$$G = \left[ {\begin{array}{*{20}c} {\lambda_{x} } \\ {\lambda_{y} } \\ \end{array} } \right]$$

(3)

where the $\lambda_{x}$ and $\lambda_{y}$ is the threshold pressure gradients in the x and y directions, respectively.

The permeability modulus proposed by Nura and yilmazo can be used to characterize the stress sensitivity of reservoir, and its expression is as follows:

$$\gamma = \frac{1}{{k_{m} }}\frac{{\partial k_{m} }}{{\partial p_{m} }}$$

(4)

where $\gamma$ is the coefficient of stress sensitivity.

The fluid density is as follows:

$$\rho = \rho_{0} \exp \left( { - C_{\rho } \left( {p_{i} - p_{m} } \right)} \right)$$

(5)

where $\rho_{0}$ is the initial density of oil, $C_{\rho }$ is the compressibility coefficient of oil and $p_{i}$ is the initial pressure of matrix.

The porosity of the porous medium is as follows:

$$\phi = \phi_{0} \exp \left( { - C_{\phi } \left( {p_{i} - p_{m} } \right)} \right)$$

(6)

where $\phi_{0}$ is the initial porosity of matrix and $C_{\phi }$ is the pore compressibility.

Substituting Eqs. (2), (4), (5), (6) into Eq. (1), we can get the complete expression of the continuity equation:

$$\phi_{0} \rho_{0} C_{t} \frac{{\partial p_{m} }}{\partial t} = \frac{{\rho k_{0} }}{u}\nabla^{2} p_{m} - \frac{G}{u}(k_{m} \rho_{0} C_{\rho } + \rho k_{0} \gamma )\nabla p_{m} - q_{m}$$

(7)

where $C_{t}$ is the Comprehensive compressibility in matrix and $k_{0}$ is the initial permeability of matrix.

2.3 Fluid Flow in the Hydraulic Fractures

The continuity equation for the fluid in the hydraulic fracture is as follows:

$$\nabla_{T} \cdot \left( {\rho \overrightarrow {{v_{F} }} } \right) + \frac{{\partial \left( {\rho \phi_{F} } \right)}}{\partial t} + q_{F} = 0$$

(8)

where $\overrightarrow {{v_{F} }}$ is the fluid velocity in hydraulic fracture, $\phi_{F}$ is the porosity of hydraulic fracture and $q_{F}$ is the source-sink term of hydraulic fracture.

We think that fluid flow in fractures conforms to Darcy's law, and its motion equation is expressed as follows:

$$\overrightarrow {{v_{F} }} = - \frac{{k_{F} }}{u}\nabla p_{F}$$

(9)

where $k_{F}$ is the permeability of hydraulic fracture and $p_{F}$ is the pressure in hydraulic fracture.

The state equation of opening in hydraulic fracture is as follows:

$$w_{F} = w_{F0} \cdot exp\left[ { - \frac{1}{3}c_{F} \left( {p_{i} - p_{F} } \right)} \right]$$

(10)

where $w_{F}$ is the width of hydraulic fracture, $w_{F0}$ is the initial width of hydraulic fracture, $c_{F}$ is the compressibility coefficient of hydraulic fracture and $p_{i}$ is the initial pressure.

The expression between aperture and permeability is used to describe how permeability varies with pressure.

$$k_{F} = \frac{{w_{F}^{2} }}{12}$$

(11)

The continuity equation of fluid flow in hydraulic fractures is as follows:

$$\rho_{0} \phi_{F0} C_{Ft} \frac{{\partial p_{F} }}{\partial t} = \frac{{\rho k_{F} }}{u}\nabla_{T}^{2} p_{F} + q_{F}$$

(12)

where $\phi_{F0}$ is the initial porosity of fracture and $C_{Ft}$ is the Comprehensive compressibility of fracture.

2.4 Discretization of Governing Equations

In the matrix system, a strong nonlinear finite differential equation (FDE) system is formed by the governing equations considering the effect of threshold pressure gradient and stress sensitivity. The integral form of the whole region can be obtained by combining the matrix system with the hydraulic fracture system, which is as follows:

$$\int_{{\Omega_{e} }} {{\varvec{FDE}}} d\Omega_{e} = \int_{{\Omega_{m} }} {{\varvec{FDE}}} d\Omega_{m} + \sum\limits_{i} {w_{F,i} \cdot \int_{{\Omega_{F,i} }} {{\varvec{FDE}}} d\Omega_{F,i} }$$

(13)

where $m$ and $F$ represents the matrix system and hydraulic fracture system, respectively.

In this paper, the FEM is used to solve the flow equations in continuous medium. In the FEM, the continuous variables ${\mathbf{P}}\left( {x,y,t} \right)$ in the original governing equation are approximated with the nodal variables $p_{im}$ using the shape functions. This procedure is also generally known as discretization. To achieve this, we begin by defining a triangular element that contains three nodes, each node is at the triangular vertex.

In the matrix system, using the shape function, the approximation of the continuous variable can be written as:

$${\text{p}}_{m} \user2{ = }\sum\nolimits_{i = 1}^{3} {N_{i} p_{im} } = {\varvec{NP}}_{m}$$

(14)

where, $p_{im}$ is the unknown nodal pressure, $N_{i}$ is the shape function. The linear shape functions are defined as:

$$N_{1} = \frac{{xy_{2} - xy_{3} + x_{2} y_{3} - x_{2} y - x_{3} y_{2} + x_{3} y}}{d}$$

(15a)

$$N_{2} = \frac{{xy_{1} - xy_{3} + x_{1} y_{3} - x_{1} y - x_{3} y_{1} + x_{3} y}}{d}$$

(15b)

$$N_{3} = \frac{{xy_{1} - xy_{2} + x_{1} y_{2} - x_{1} y - x_{2} y_{1} + x_{2} y}}{d}$$

(15c)

where,

$$d = x_{1} y_{2} - x_{1} y_{3} - x_{2} y_{1} + x_{2} y_{3} + x_{3} y_{1} - x_{3} y_{2}$$

(16)

Here $x_{1}$, $y_{1}$ are the global coordinates of node 1, and so on.

In the fracture system, we use the reduction dimensional method to adopt the fracture model, that is, the fracture is n-1dimension model when the matrix system is n dimension model. For the one-dimensional fracture model, the interpolation function of node pressure of fracture can be written as:

$${\varvec{p}}_{F} \user2{ = }\sum\nolimits_{k = 1}^{2} {N_{k} } p_{kF} \user2{ = N}_{F} {\varvec{P}}_{F}$$

(17)

where $N_{k}$ is the shape function in fracture. The shape functions are typically chosen to be low order, piecewise polynomials. For the two-node element chosen here, the shape functions are two-parameter polynomials (i.e., linear functions),

$$N_{1F} = 1 - \frac{x}{L}$$

(18a)

$$N_{2F} = \frac{x}{L}$$

(18b)

where $L$ is the length of the element and $x$ is the spatial variable that varies from 0 at node 1 to L at node 2.

The discrete form of the continuity equation in the matrix system and the hydraulic fracture system is as follows:

Matrix:

$$[{\mathbf{MM}}]_{m} \frac{{\partial \left\{ {{\mathbf{P}}_{m} } \right\}}}{\partial t} - [{\mathbf{KM}}]_{m} \left\{ {{\mathbf{P}}_{m} } \right\} + [{\mathbf{GM}}]_{m} \left\{ {{\mathbf{P}}_{m} } \right\} = \left\{ {{\varvec{F}}_{m} } \right\}$$

(19)

Hydraulic Fracture:

$$[{\mathbf{MM}}]_{F} \frac{{\partial \left\{ {{\mathbf{P}}_{F} } \right\}}}{\partial t} - [{\mathbf{KM}}]_{F} \left\{ {{\mathbf{P}}_{F} } \right\} = \left\{ {{\varvec{F}}_{F} } \right\}$$

(20)

The details of the matrices in Eqs. (19 and 20) are expressed as follows.

In the matrix system: ${\mathbf{MM}} = \int\limits_{\Omega } {\phi_{0} \rho_{0} C_{t} N^{T} Nd\Omega }$, ${\mathbf{KM}} = \int\limits_{\Omega } {\frac{{\rho k_{0} }}{u}\left( {\nabla N} \right)^{T} \nabla Nd\Omega }$, ${\mathbf{GM}} = \int\limits_{\Omega } {\frac{k}{u}\nabla NGd\Omega }$ and ${\mathbf{F}}_{m} = \int\limits_{\Omega } {q_{m} } N^{T} d\Omega$.

In the hydraulic fracture system: ${\mathbf{MM}} = \int\limits_{\Omega } {\rho_{0} \phi_{F0} C_{Ft} N_{F}^{T} N_{F} d\Omega }$, ${\mathbf{KM}} = \int\limits_{\Omega } {\frac{{\rho k_{F} }}{u}\left( {\nabla N_{F} } \right)^{T} \nabla N_{F} d\Omega }$ and ${\mathbf{F}}_{F} = \int\limits_{\Omega } {q_{F} } N_{F}^{T} d\Omega$.

Forward difference is used for time term and the matrix of hydraulic fracture unit is superimposed into matrix to form the overall solution matrix of the whole region as follows (Zhang et al. 2013). The matrix assembly is shown in Fig. 2.

$$({\varvec{Q}} - {\varvec{H}} + {\varvec{S}})\left\{ {\mathbf{P}} \right\}_{k}^{n + 1} = {\varvec{Q}}\left\{ {\mathbf{P}} \right\}^{n} + \left\{ {\varvec{F}} \right\}$$

(21)

Fig. 2

Schematic of fracture and matrix elements

The details of the matrices are expressed as follows:

$${\varvec{Q}} = \frac{{[{\mathbf{MM}}]_{m} }}{\Delta t} + \sum\limits_{{l \in \left\{ F \right\}}} {\omega_{l} \frac{{[{\mathbf{MM}}]_{l} }}{\Delta t}}$$

(21a)

$${\varvec{H}} = [{\mathbf{KM}}]_{m} + \sum\limits_{{l \in \left\{ F \right\}}} {\omega_{l} [{\varvec{K}}{\mathbf{M}}]_{l} }$$

(21b)

$${\varvec{S}} = [{\mathbf{GM}}]_{m}$$

(21c)

$${\varvec{F}} = \left\{ {{\varvec{F}}_{m} } \right\} + \sum\limits_{{l \in \left\{ F \right\}}} {\omega_{l} {\varvec{F}}_{l} }$$

(21d)

We use the above expression to update the permeability and fluid density, and their iterative format is as follows:

$$k_{n + 1,k} = k_{n} + \gamma k_{n} \left( {p_{n + 1,k} - p_{n} } \right)$$

(22)

$$\rho_{n + 1,k} = \rho_{n} + \rho_{n} c_{f} \left( {p_{n + 1,k} - p_{n} } \right)$$

(23)

2.5 Boundary Conditions

To solve the seepage field equation, it is necessary to provide sufficient definite conditions, among which h the commonly used definite conditions are initial conditions and boundary conditions.

• (1) Initial condition. The initial condition mainly involves the initial pressure of the reservoir.

  $$p\left( {x,y} \right)\left| {_{t = 0} } \right. = p_{i}$$

  (24)

• (2) Boundary conditions of constant pressure. The outer boundary pressure of reservoir is as follows:

  $$p\left| {_{{r_{w} }} } \right. = p_{wf} \left( {x,y,t} \right)$$

  (25)

3 Model Verifications

In this paper, the mathematical model of multi-stage fractured horizontal well in low-permeability reservoir is established, is solved by finite element method, and is compiled and solved on the MATLAB. In order to verify the correctness of the program, the simulation results without considering stress sensitivity, threshold pressure gradient and fracture conductivity change are compared with the results of COMSOL software. A 1080 m long horizontal well with ten fracturing fractures is discretized in a 1600 × 600m² rectangular reservoir. The region is discretized using triangular elements for the matrix and line elements for the fractures, as shown in Fig. 3. The calculation parameters for the verification of the numerical model are as shown in Table 1. And Fig. 4 shows that the calculation result of the numerical model has a good agreement with the COMSOL software.

Fig. 3

Mesh schematics of discrete-fractured model

Table 1 Model simulation parameters (Zongxiao et al. 2016; Li et al. 2021; Ren et al. 2019; Sun et al. 2020)

Fig. 4

Comparison of the MATLAB model and COMSOL results

4 Results and Discussion

4.1 Variation of Reservoir Parameters

In order to analyze the influence of stress sensitivity, starting pressure and fracture shrinkage on the basic physical properties of reservoir, we simulated a 50 m half-length hydraulic fracture in the center of the 120 × 230 m² rectangular reservoir. The simulation parameters are shown in Table 1.

4.1.1 Reservoir Pressure

The reservoir pressure of 23 MPa is circled with a black dotted line in the pressure contours with different threshold pressure gradients. It can be clearly seen from Fig. 5 that with the gradual increase in threshold pressure gradient, the propagation velocity of pressure slows down. In low-permeability reservoirs, fluid conforms to non-darcy 's flow, which is due to the existence of threshold pressure gradient, but also can better maintain the reservoir pressure. At the same time, the displacement area under the same pressure difference is gradually reduced with the increase in threshold pressure gradient, resulting in a large amount of oil in the reservoir cannot being produced.

Fig. 5

Pressure contours at 200 days for different threshold pressure gradient

4.1.2 Reservoir Permeability

There are four observation points in the reservoir to analyze the changes of permeability in different positions of matrix system with stress sensitivity effect (Fig. 6). A Point is located 30 m away from the fracture end in the direction of the fracture, B point, C point and D point are all located 30 m away from the fracture in the vertical direction of fracture. The pressure drop presents elliptic distribution during the production process of tight reservoir (Fig. 7). The amplitude of pressure drop in different positions in the reservoir is different, so the permeability changes in different positions of the matrix also is different under the influence of stress sensitivity. Under the influence of stress sensitivity effect, the matrix permeability decreases with the decrease in reservoir pressure, and the amplitude of permeability loss decreases from near the fracture to far away matrix area. Among them, point D, which is closest to the wellhead, has the fastest pressure drop, is most affected by the stress sensitivity effect, and the permeability loss reaches 26% after 500 days of production.

Fig. 6

Pressure contours at 500 days

Fig. 7

Permeability change chart with different points

It can be concluded that the permeability loss rate is gradually increasing with the increase in stress sensitivity coefficient by comparing the average permeability loss rate of matrix under different stress sensitivity coefficient (Fig. 8). However, the loss of permeability does not increase in the same proportion exponentially with the increase in stress sensitivity coefficient, but decreases gradually with the increase in stress sensitivity coefficient. In the low-permeability reservoir, the narrow throat is compressed and deformed under the effect of stress sensitivity, but the compressible space of pore is limited, and the deformable space of throat is also very small, so the permeability will not decline indefinitely with the increase in stress sensitivity coefficient.

Fig. 8

Relationship between permeability loss rate and stress sensitivity coefficient

4.1.3 Fracture Conductivity

Conductivity of hydraulic fracture is a key factor affecting the productivity of horizontal wells in low-permeability reservoirs. It can be seen from Fig. 9 that the conductivity of fracture is decreasing rapidly and the fracture opening decreases sharply with the increase in the fracture compression coefficient, which is due to the large production pressure difference at the initial stage of production. After a period of production, the fracture conductivity tends to be stable because of the production pressure difference tending to be stable. The loss rate of fracture conductivity will reach 50% when the compression coefficient increases to 0.2. Therefore, in the early stage of development, the reservoir pressure level should be maintained as far as possible to avoid excessive productivity loss caused by rapid fracture closure. At the same time, it is also necessary to improve the fracturing technology and the working efficiency of proppant, in order to reduce the compression coefficient of hydraulic fracture as much as possible.

Fig. 9

Variation of fracture conductivity under different compression coefficient

The observation points are set at the start and end of the fracture in order to compare the conductivity of fracture at different positions. It can be seen from Fig. 10 that under the same fracture compression coefficient, the loss rate of conductivity at different positions is different. The loss of conductivity is the largest near the bottom of the well. Along the fracture direction from the bottom of the well, the pressure drop and seepage resistance gradually decrease, and the fracture opening is gradually increased.

Fig. 10

Loss rate of fracture conductivity at different positions

4.2 Sensitivity Analysis

In order to analyze the effects of stress sensitivity, threshold pressure gradient and compression coefficient on the production of multistage fractured horizontal wells, in this paper, a 1200 m long horizontal well with 11 fracturing fractures was simulated in a rectangular reservoir. The simulation parameters are the same as Table 1.

4.2.1 Effect of Stress Sensitivity

It can be known that the effect of stress sensitivity on production is mainly in the early stage of production according to the curves of daily production and cumulative production of horizontal wells with stress sensitivity changing (Fig. 11). The daily production and cumulative production decrease gradually with the increase in stress sensitivity coefficient. When the stress sensitivity coefficient was 0.06, 0.12 and 0.2 MPa⁻¹, the cumulative production of 1500 days decreased by 6.1, 11.8 and 17.3%, respectively. As mentioned in the previous section, stress sensitivity of matrix leads to poor reservoir physical properties, which reduces the supply capacity of matrix system to horizontal wells and affects the final production.

Fig. 11

Comparison of daily production and cumulative production under different stress sensitivity coefficients

It can be seen from Fig. 12 that the stress sensitivity coefficient has a logarithmic relationship with the loss rate of production at the initial stage of production. With the increase in stress sensitivity coefficient, the loss rate of production is increasing, but the increasing trend is decreasing, which is because the stress sensitivity of the matrix has a certain limit due to the mutual support of the rock particles.

Fig. 12

Relationship between loss rate of production at the initial stage of production and stress sensitivity coefficient

4.2.2 Effect of Threshold Pressure Gradient

Figure 13 shows the pressure cloud map of horizontal wells with threshold pressure gradients of 0.025, 0.05, 0.075 and 0.1 MPa/m after 1500 days of production. It can be seen from figure that the propagation velocity of pressure gradually decreases and the pressure gradually increases with the increase in the threshold pressure gradient.

Fig. 13

Pressure cloud map of 1500 days production under different threshold pressure gradients

It can be concluded that the daily production of horizontal wells decreases rapidly in the whole mining process until it cannot be mined by comparing the curves of daily production and cumulative production with the threshold pressure gradient changing (Fig. 14), which is due to the existence of the threshold pressure gradient. And the shutdown time is gradually ahead of time with the increase in threshold pressure gradient. In the development process, the reservoir pressure gradually decreases, and the production pressure difference is difficult to overcome the threshold pressure gradient to displace the oil, resulting in the production continuing to decrease until the production is stopped. The cumulative production at 1500 days decreased by 17.8%, 36% and 54.7%, respectively, when the threshold pressure gradient is 0.025, 0.05 and 0.075 MPa/m, which can be seen as the effect of the threshold pressure gradient on the production is very significant.

Fig. 14

Daily and cumulative production under different threshold pressure gradients

It can be concluded that the threshold pressure gradient is basically in a linear relationship with the off production time according to Fig. 15. The off production time is ahead of time with the increase in the threshold pressure gradient, and the trend will not slow down. Therefore, in the development process of low-permeability reservoir, a series of stimulation measures must be taken to maintain the formation pressure, so as to extend the production time of horizontal wells and reduce the remaining oil in the reservoir.

Fig. 15

Relational graph of threshold pressure gradient and off production time

4.2.3 Effect of Compression Coefficient of Hydraulic Fracture

The effect of fracture compressibility on production is mainly in the early stage of production according to Fig. 16, and the daily production and cumulative production decrease gradually with the increase in compression coefficient. In the early stage of development, the production decreases rapidly with the sudden change of reservoir pressure. As development progresses, the reservoir pressure is gradually stable, and the daily production is also gradually stable. The cumulative production of 1500 days decrease by 9.7, 24.1 and 35.5%, respectively, when the fracture compressibility is 0.3, 0.6 and 0.9, which can be seen that the shrinkage of hydraulic fractures is a key factor affecting the production.

Fig. 16

Daily and cumulative production under different compression coefficients

There is a logarithmic relationship between compression coefficient and loss rate of conductivity (Fig. 17). The loss rate of conductivity increases with the increase in compression coefficient, but the increasing range gradually slows down due to closing limit of fracture opening. In the development process, not only the formation pressure should be controlled, but also the proppant should be injected to maintain the fracture opening, so as to ensure the fracture conductivity.

Fig. 17

Relational graph of compression coefficient and loss rate of conductivity

5 Conclusions

This paper focuses on the effect of:

• 1. In this paper, the physical model of multistage fractured horizontal well considering multi-parameters in low-permeability reservoir is established, and is solved using the finite element method by MATLAB software. The production process in low-permeability reservoir is simulated numerically, and the key physical parameters in the model on reservoir physical properties and productivity of fractured horizontal wells are analyzed.

• 2. The stress sensitivity effect will lead to the deterioration of reservoir physical properties, mainly in the early stage of production, and gradually weakened with the development. It can be concluded from the simulation results that the cumulative production of 1500 days decreased by 6.1, 11.8 and 17.3%, respectively, when the stress sensitivity coefficient was 0.06, 0.12 and 0.2 MPa⁻¹.

• 3. The threshold pressure gradient is the key factor affecting the production time of oil well. With the increase in the threshold pressure gradient, the downtime of well is ahead of time, which has a great impact on the final production. The cumulative production at 1500 days decreased by 17.8, 36 and 54.7%, respectively, when the threshold pressure gradient is 0.025, 0.05 and 0.075 MPa/m. In the production process of tight reservoir, a series of stimulation measures must be taken to maintain the formation pressure level and extend the production time.

• 4. The multi-stage fracturing horizontal well is the key technology to improve the recovery of tight reservoir, and the conductivity of fracturing is the main factor affecting the production. The cumulative production of 1500 days decrease by 9.7, 24.1 and 35.5%, respectively, when the fracture compressibility is 0.3, 0.6 and 0.9. There is a closure limit of the fracture opening because of the proppant, and the conductivity will not decrease infinitely. In the process of fracturing, appropriate proppant should be injected to maintain the fracture opening and reduce the compression coefficient of hydraulic fracture.