1 Introduction

Two-dimensional, light-weight structures with high strength-to-mass ratio are important elements in multiple practical applications, e.g., high-speed vehicles, such as trains, automobiles, and planes. Many researchers investigated these structures by means of different numerical or analytical methods (Civalek and Avcar 2020; Safaei et al. 2017; Sobhani et al. 2021; Younesian et al. 2019). The increase of strength and reduction of mass have been achieved by employing composite, sandwich, and smart structures. Reinforcement of these elements in different directions, especially in the transverse direction, has been actively considered in the field of two-dimensional structures. In this regard, passive methods (Moradi-Dastjerdi et al. 2020a) and active methods (Moradi-Dastjerdi et al. 2020b) were suggested as vibration control approaches, and their dynamic behavior under complex loadings was studied (Safaei 2020; Sahmani and Safaei 2021; Hadji and Avcar 2021a, b). As a result of these efforts, there emerged a separate class of materials called as cellular mechanical metamaterials. These are man-made materials with carefully tailored architecture that delivers extraordinary properties. A special type of them constitutes auxetic (meta) materials exhibiting an effective Negative Poisson’s Ratio (NPR) (Farhangdoust et al. 2021; Ren et al. 2018; Wojciechowski et al. 2019). The NPR originates from the arrangement of constituent geometries rather than material constituents. It has been shown that the employment of the NRP materials can improve the mechanical behavior of a structure to satisfy the demands for a high strength-to-mass ratio as well as to control vibro-acoustic properties (Donescu et al. 2009; Boldrin et al. 2016; Smith et al. 2002). Auxetic materials were discovered by Lakes (1987), who showed that the effective negative Poisson’s ratio can improve mechanical and thermal material response. Subsequently, researchers proposed to use NPR materials in various fields, including biomedical, protection, sensors and actuators, and the vibro-acoustics (Eghbali et al. 2020; Ebrahimian et al. 2021; Liu and Hu 2010). Since this study is focused on the vibro-acoustic analysis, we further review only vibro-acoustic applications.

Structural noise and vibration is a serious problem for high-speed vehicles. It can be address by means of sandwich panels. However, the noise and vibration suppression by these structures made of commonly used materials often appears to be insufficient or requires large structure dimensions (Surjadi et al. 2019; Prawoto 2012; Vigé 2010). This issue can be addressed by using cellular mechanical metamaterials (Panahi et al. 2021; Qin and Yang 2019; Chekkal et al. 2012) that have already been employed to overcome the structural vibration/noise problem in high-speed vehicles (Mazloomi and Ranjbar 2021; Hosseinkhani et al. 2020).

Auxetics exhibit different acoustic and dynamic behavior as compared to conventional materials (Chekkal et al. 2010). In particular, Poisson’s ratio has significant effects on natural frequencies of flexible structures, as was derived by comparing vibration characteristics of thick auxetic and non-auxetic plates (Lim 2014). Besides, traditional assumptions on the mechanical properties of conventional materials are no longer applicable to auxetic materials. This refers, for instance, to a constant shear correction factor and negligible rotary inertia of layered plates. Chen and Feng investigated the variation of natural frequencies of a 5-layered sandwich plate composed of three PPR (Positive Poisson’s Ratio) layers and two NPR layers and concluded that the concept of NPR can be used to design materials with desired natural frequencies (Chen and Zhihua 2017). Furthermore, Poisson’s ratio can significantly influence structural damping as well as the effective shear and normal moduli (Maruszewski et al. 2013; Choi and Lakes 1995). For example, Scarpa and Tomlinson found that the NPR allows one to achieve a high out-of-plane shear modulus and to improve the bending stiffness of auxetic plates (Scarpa and Tomlinson 2000). The damping feature and dynamic performance of bio-based auxetic structures were investigated in Essassi et al. (2019). The effect of heterogeneity and disorder in the mechanical response of auxetic structures was evaluated by Horrigan et al. (2009). Mizzi et al. (2018) analyzed irregular hexachiral auxetics with a wide range of negative Poisson's ratios that opens promising functions and applications in various engineering fields. Alomarah et al. (2018) investigated the effects of topological parameters on the tensile properties of an auxetic built of re-entrant and chiral honeycombs. Topology optimization was first introduced by Sigmund in 1994 to identify center symmetric configurations that possess in-plane negative Poisson’s ratio (Sigmund 1994). Vogiatzis et al. (2017) introduced the topology optimization for these structures and developed a multi-material with negative Poisson’s ratio. Noise and vibration damping performance of auxetic sandwich panels was examined in Li et al. (2019), and they were attenuated by the use of gradient pattern used in the construction of the panel. Auxetic honeycombs have been also used to provide host platforms for nonlinear dampers made of granular systems to increase the vibration transmissibility (Ma et al. 2013).

More sophisticated design approaches were also used to develop auxetic materials for other applications (Lira et al. 2009). By optimizing the design of the unit cell arrangement in auxetic materials, one can achieve at least a 12% reduction of the vibration level as compared to the non-auxetic materials (Qin and Yang 2019). To further advance this approach, the concept of the gradient has been introduced recently as a technique to fine-tune the local and global dynamics of a cellular structure. This concept was applied to achieve predefined mechanical properties at specific locations in a structure in order to improve its general mechanical behavior. For example, Hou et al. (2013) applied it to the core of an auxetic sandwich beam and demonstrated that the gradient arrangement significantly influences the flexural behavior. Lira et al. (2011) used this concept to optimize the dynamics of an auxetic aerospace fan blade by considering the first three structural modes. They found that the optimized models reveal a reduced level of vibrations with a simultaneous reduction in mass. Later on, Kaminakis and Stavroulakis used a homogenized model in the topology optimization of auxetic structures (Kaminakis and Stavroulakis 2012). Hosseinkhani et al. optimized the topological distribution of local resonators embedded into chiral auxetic sandwich panels and provided low-frequency enhanced vibroacoustic performance in auxetic sandwich panels (Hosseinkhani et al. 2021). The homogenized model approach was further applied by Ranjbar et al. (2016) to optimize the vibro-acoustic performance of auxetic sandwich panels to analyze its dynamics by considering gradients along a single dimension. Mazloomi et al. (2018) extended this approach to two dimensions by considering an auxetic sandwich structure under harmonic excitation and limiting the analysis to a partial gradient topology.

Yet, the vibro-acoustic properties of auxetic materials are not fully understood. The available studies analyze the advantages of auxetic behavior on the reduction of noise radiation from structural vibrations as compared to materials with a positive Poisson’s ratio. In this study, we apply a non-restricted two-dimensional full–gradient optimization method for optimizing the geometry of an auxetic core with the aim to enhance the vibrational response of a sandwich panel subjected to a variety of random loads. This method gives more degrees of freedom for a topological arrangement of the design parameters, and thus more freedom to achieve directional and locally tunable mechanical properties. In this way, we can reduce the sound power level by about 20% at the cost of a small increase of the structural mass. Importantly, such a reduction can be counted as a big gain in vibro-acoustic optimization (Marburg 2002).

The remaining manuscript is structured as follows. First, the mechanical properties of the re-entrant hexagonal honeycomb structure are summarized, and these relations are used for homogenized finite-element (FE) modeling. Next, the modal and spectral analyses are performed. The latter is done considering several colored noise excitations with various frequency content applied at two different locations. Then, the optimization of the vibro-acoustic behavior is performed for the specified load conditions. The paper is finalized with conclusions and outlook of the obtained results.

1.1 Theoretical Formulation

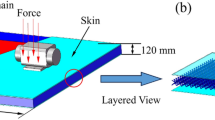
We consider a sandwich panel composed of two skin layers and an auxetic core (Fig. 1b). Our auxetic material is represented by a re-entrant hexagonal honeycomb with a unit cell shown in Fig. 1a. The material of the skins behaves isotropically, while the core is orthotropic. The mechanical properties of the core can be derived analytically under assumption that the ligaments forming the cell are modeled as Euler–Bernoulli beams (Liu and Hu 2010). The relevant geometric parameters are cell angle \(\theta\), relative ligament thickness \(\beta =\frac{t}{l}\), and sides aspect ratio \(\alpha =\frac{h}{l}\). The principal Young’s moduli and the in-plane Poisson’s ratio can then be calculated as follows:

$$E_{x} = E_{c} \beta^{3} \left( {\frac{\alpha + \sin \theta }{{\cos^{3} \theta }}} \right),$$
(1)
$$E_{y} = E_{c} \beta^{3} \left( {\frac{\cos \theta }{{\sin^{2} \theta \left( {\alpha + \sin \theta } \right)}}} \right),$$
(2)
$$E_{z} = E_{c} \beta \left( {\frac{\alpha + 2}{{2\left( {\alpha + \sin \theta } \right)\cos \theta }}} \right),$$
(3)
Fig. 1
figure 1

a Geometry and parameters of an auxetic hexagonal honeycomb unit cell. b Schematics of the sandwich panel with an auxetic core

Full size image
$$\upsilon_{xy} = \frac{{\sin \theta \left( {\alpha + \sin \theta } \right)}}{{\cos^{2} \theta }},\upsilon_{xz} = \upsilon_{yz} \simeq 0,\upsilon_{zx} = \upsilon_{zy} = \upsilon_{c} ,$$
(4)

where \({E}_{c}\) and \({\upsilon }_{c}\) are the Young’s modulus and the Poisson’s ratio of the base material. The in-plane shear moduli can be estimated as

$$G_{xy} = G_{c} \beta^{3} \left( {\frac{\alpha + \sin \theta }{{\left( {1 + 2\alpha } \right)\alpha^{2} \cos \theta }}} \right),$$
(5)

with \({G}_{c}\) being the shear modulus of the base material.

The expression for out-of-plane shear modulus \({G}_{yz}\) can be derived analytically:

$$G_{yz} = G_{c} \beta \left( {\frac{\cos \theta }{{\alpha + \sin \theta }}} \right),$$
(6)

while the other shear modulus, \({G}_{xz}\), can only be approximated through its upper and lower bounds:

$$\begin{gathered} G_{xz}^{{}} = G_{xz}^{{{\text{lower}}}} + \frac{K}{\gamma }\left( {G_{xz}^{{{\text{upper}}}} - G_{xz}^{{{\text{lower}}}} } \right), \, K = \left\{ {\begin{array}{*{20}c} {0.787 \, \theta \ge 0 \, } \\ {1.342 \, \theta < 0} \\ \end{array} } \right., \hfill \\ G_{xz}^{{{\text{upper}}}} = G_{c} \beta \left( {\frac{{\alpha + 2\sin^{2} \theta }}{{2\left( {\alpha + \sin \theta } \right)\cos \theta }}} \right), \, \hfill \\ G_{xz}^{{{\text{lower}}}} = G_{c} \beta \left( {\frac{\alpha + \sin \theta }{{\left( {1 + 2\alpha } \right)\cos \theta }}} \right). \hfill \\ \end{gathered}$$
(7)

when \(1<\gamma <10\) (Scarpa and Tomlin 2000).

Equations (1)–(7) provide all required mechanical properties to describe the response of our orthotropic auxetic material. (Note that this formulation refers to the most general case, and can be modified to a different number of cells (Mazloomi et al. 2018).) Then, by using Hook’s law for an orthotropic material in the form of:

$$\left\{ \varepsilon \right\} = \left[ S \right]\left\{ \sigma \right\},$$
(8)

with \(\left[S\right]\) designating a compliance matrix,

$$\left[ S \right] = \left[ {\begin{array}{*{20}c} {\frac{1}{{E_{x} }}} & { - \frac{{\upsilon_{xy} }}{{E_{y} }}} & { - \frac{{\upsilon_{xz} }}{{E_{z} }}} & 0 & 0 & 0 \\ { - \frac{{\upsilon_{yx} }}{{E_{x} }}} & {\frac{1}{{E_{y} }}} & { - \frac{{\upsilon_{yz} }}{{E_{z} }}} & 0 & 0 & 0 \\ { - \frac{{\upsilon_{zx} }}{{E_{x} }}} & { - \frac{{\upsilon_{zy} }}{{E_{y} }}} & {\frac{1}{{E_{z} }}} & 0 & 0 & 0 \\ 0 & 0 & 0 & {\frac{1}{{G_{xz} }}} & 0 & 0 \\ 0 & 0 & 0 & 0 & {\frac{1}{{G_{yz} }}} & 0 \\ 0 & 0 & 0 & 0 & 0 & {\frac{1}{{G_{xy} }}} \\ \end{array} } \right],$$
(9)

and supplementing it by the classic equations of motion, we can fully describe the dynamics of the core and, thus, of the whole sandwich panel.

In principle, the formulation (1)–(9) can be directly used to estimate the vibrational behavior. However, in multiple calculations implied by an optimization procedure, straightforward simulations are extremely inefficient, even by using modern computers (Chekkal et al. 2010). Therefore, we proceed by applying a homogenized finite-element modeling approach allowing to deal with large geometries in a computationally reasonable time.

2 Homogenized Finite Element Modeling

The homogenized finite-element modeling implies the replacement of a real material model by that of a homogeneous medium with effective properties (Chekkal et al. 2010; Sorohan et al. 2018). In other words, the inhomogeneous anisotropic lattice medium is substituted by a homogenous one with identical properties. We extract the mechanical properties from the force–deflection and stress–strain relations (Gibson and Ashby 1999) and derive for them closed-form expressions. Since the cellular core is orthotropic, the equivalent homogenized model should also describe an orthotropic material with Young’s modulus, shear modulus, and Poisson’s ratio different in prescribed spatial directions.

The considered core has 18 by 30 cells, each of which has the mechanical properties given by Eqs. (1–9). To derive the mechanical properties of the homogenized medium we use the methodology of Ref. (Lira et al. 2011) and introduce non-dimensional parameters of \(\alpha\) and \(\beta\) defining the mechanical properties of hexagonal honeycombs. The calculation of the properties is performed by means of macro-coding developed in ANSYS software. The equivalent parameters are substituted in the compliance matrix, Eq. (9), and are assigned to the corresponding cells. The mechanical properties of the faces are the same as those of a base material. The homogenized modeling enables to boost the speed of simulations that is crucial for optimization.

Specifically, we consider a square panel of size 960 mm and thickness 24 mm, including the thickness of the two skin layers of 2 mm. The geometric parameters of auxetic core are \(h=\) 36.95 mm, \(l=18.48\) mm, \(t=\) 1 mm, \(\theta =-30^\circ\). The panel geometry is the same as in Mazloomi et al. (2018). The boundary condition implies a simple support of the four faces of the panel.

The homogenized panel is meshed by two types of shell finite elements (Fig. 2). The interfaces between the core and skins are modeled by means of a node-merge option connecting the nodes on the common surface of the core with the skins. For this, the coordinates of the nodes on the common surfaces must be identical. The elements representing the skin layers and the core are made of the same material with linear elastic isotropic and orthotropic properties, respectively. The base material is Acrylonitrile Butadiene Styrene (ABS) with Young’s modulus \({E}_{c}=\) 1756 MPa, shear modulus \({G}_{c}=\) 618 MPa, and mass density \({\rho }_{c}=\) 1040 kg/m3.

Fig. 2
figure 2

Homogenized finite-element model of the sandwich panel with an auxetic core

Full size image

The finite element simulations are performed in the APDL environment of the ANSYS software. To verify the accuracy of the homogenized model, we compared its Power Spectral Density response (PSD) to that of the original (full-scale) model estimated in Mazloomi et al. (2018). The comparison shown in Fig. 3 reveals a good agreement in the 0–180 Hz range that includes the first five natural frequencies of the panel given in Table 1. Slight deviation is observed for the sixth natural frequency, 182.8 Hz, that is considered to be acceptable, as the current analysis is focused on optimizing the structural dynamics at low frequencies.

Fig. 3
figure 3

Harmonic response (Mazloomi et al. 2018) and PSD response (the current analysis) for the hexagonal honeycomb auxetic sandwich panel

Full size image
Table 1 First six frequencies (in Hz) of the sandwich panel with the reference parameters
Full size table

2.1 Vibro-Acoustic Response Under Different Random Loads

To optimize the vibro-acoustic performance of the panel under various excitation conditions, we analyze its dynamics for three load cases suggested in Refs. (Ranjbar 2011; Ranjbar et al. 2012). Namely, the top surface of the panel is loaded at locations indicated in Fig. 4. Two of the load cases (load case a and b) have asymmetrical patterns and the excitations are applied on three locations. The third load case is symmetrical and the excitation is applied on the whole top surface of the panel. The vibro-acoustic response is calculated as the velocity of particles at the bottom surface.

Fig. 4
figure 4

Locations of applied load in different load cases (Ranjbar 2011)

Full size image

To ensure different frequency content in the excitation, we apply standard white and colored noises. The white noise is defined as a pressure of uniform amplitude 2500 Pa in the considered frequency range, 0–200 Hz. In other words, this means that the white noise load has the power of \({\left(2500\text{ Pa}\right)}^{2}\) in this frequency range. By representing the noise power versus frequency, the other colored noises can be defined as follows. The pink noise has a negative slope of −3 dB per octave band; the Brownian (red) noise has a negative slope of −6 dB per octave band; the blue noise has a positive slope of + 3 dB per octave band, and the violet noise has a positive slope of + 6 dB per octave band (Dimian et al. 2012). To ensure identical power for all the noises, the integral under power curves of the colored noises must be identical to that of the white noise. The PSD of noises can be calculated as:

$${\text{PSD}} \left( f \right) = 10\log \left( {P^{2} \left( f \right)} \right)$$
(10)

where \(\mathrm{PSD} (f)\) is the power of applied pressure at frequency f. According to the described condition, the frequency content of the considered noises can be reach as shown in Fig. 5.

Fig. 5
figure 5

Pressure amplitude for different colored noises

Full size image

To evaluate vibro-acoustic performance of the panel, we apply the method of Equivalent Radiated Power (ERP). This method provides a good approximation for an upper bound of the radiated sound, since the same radiation efficiency is assumed at all frequencies (Fritze et al. 2009).

The power of the radiated sound is calculated through squared velocity integrated over the radiating surface (Fritze et al. 2009). Hence, for our surface, this power is as follows:

$$P\left( f \right) = \frac{1}{2}\rho_{0} c_{0} S\overline{{v_{{ \bot {\text{rms}}}}^{2} }} \left( f \right)\sigma \left( f \right),$$
(11)

where \({\rho }_{0}\) is the density of air, \({c}_{0}\) is speed of sound in air, \(S\) is the radiating surface area, \(\overline{{v}_{\perp \mathrm{rms}}^{2}}\) is Root Mean Square of velocity in normal direction, and \(\sigma \left(f\right)\) is radiation efficiency (as mentioned, in the ERP method \(\sigma \left(f\right)=1\)).

The Level of Radiated Sound Power (RSPL) in dB is:

$${\text{RSPL}}\left( f \right) = 10\log \left( {\frac{P\left( f \right)}{{P_{0} }}} \right)$$
(12)

where \(P\left(f\right)\) is the power of radiated sound at each frequency, \({P}_{0}\) is a hearing threshold equal to 1e–12 W.

To estimate the vibro-acoustic response on a frequency range, we use the Root Mean Square of the sound power Level (RMSL):

$${\text{RMSL}} = \sqrt {\frac{{\int_{{f_{\min } }}^{{f_{\max } }} {{\text{RSPL}}^{2} \left( f \right)df} }}{{f_{\max } - f_{\min } }}}$$
(13)

In the subsequent optimization, the RMSL is considered as an objective function to be minimized.

Figure 6 shows the RSPL versus frequency for the first two load cases. Note that at 100 Hz, all the loads excite the structure equally, because the considered noises have the same amplitude of power at the frequency. Also, both local load cases excite all six eigen frequencies of the panel that can be seen by the presence of local peaks at these frequency. The sound power is, however, differently distributed among the resonant modes in the two load cases. For example, the third and sixth modes have a lower contribution to acoustic response in load case a, while in load case b, the lowest contribution has the fifth mode. To some degree, these responses can be expected from observing Fig. 5. The more detailed contribution of the mode shapes to the response in each load case and the differences between the vibroacoustic response of the system to the random noises is better appreciated by inspecting Fig. 6.

Fig. 6
figure 6

RSPL vs. frequency for different colored noises

Full size image

An alternative representation of the same results can be obtained by plotting the averaged radiated sounds over the considered frequencies for each colored noise separately (Fig. 7). These values are calculated from Eq. (13) for the frequency range of 0–200 Hz. As can be seen, high-frequency loads such as the Blue and Violet noises cause higher RMSL than low-frequency loads, and this effect is preserved for both load cases. It shows that the system is more sensitive to high-frequency loads than to low-frequency ones. This perfectly fits our design purposes, as the reduction of structural-borne noise for a structure under a high-frequency excitation is more critical.

Fig. 7
figure 7

RMSL of the base model of the sandwich panel for different random loads

Full size image

Finally, the influence of the internal angle of the unit cells on the level of RMSL when the structure is excited by the Pink and Violet noises is analyzed. Figure 8 shows that for all considered angles, the averaged radiated sound is higher when the structure is subjected to the Violet noise (the load with a higher frequency content). Note that according to Eq. (4) and Fig. 1, the negative angle corresponds to a negative effective Poisson’s ratio, i.e., an auxetic behavior. Therefore, Fig. 8 is divided to two regions (auxetic and non-auxetic), according to the sign of cell angle. Besides, Poisson’s ratio affects the effective mechanical parameters such as density and shear moduli according to Eqs. (1–7). Previously, it was observed that the overall values of the elastic modulus within the auxetic region and along that particular direction of the unit cell configuration are higher as compared to the non-auxetic region. An auxetic material is denser than an equivalent non-auxetic case (Mazloomi et al. 2018). This feature also makes an auxetic material stronger. Indeed, one can see that the auxetic region in Fig. 8 has a lower acoustic response as compared to the non-auxetic region. Hence, the auxetic core is preferred in applications when it is necessary to reduce vibrations and radiated sound power. Based on this argumentation, we consider an auxetic material with the angle equals \(-3{0}^{\circ }\) as an initial guess for the subsequent optimizations. We call this sandwich panel as a base model, and its total weight is \(5.635\) kg.

Fig. 8
figure 8

RMSL of the base model of the sandwich panel for different random loads, Load case b

Full size image

2.2 Full-Gradient Geometry Optimization

The radiated sound induced by the structural vibrations can be minimized by optimizing the design parameters, i.e., the topology of the sandwich core from the vibro-acoustic perspective. For this purpose, we apply a gradient-based method of Moving Asymptotes (MMA) (Svanberg 1987). This method implies the separation of the optimization procedure into several steps. At each step, a strictly convex sub-problem is generated that can be solved separately, so that the solution obtained at a current step serves as an input for a next step.

In our case, the design variables are cell angles \(\theta\) of the core unit cells (Fig. 9). For the core with 18 cells along the horizontal direction and 30 cells along the vertical direction, we have 270 design variables.

Fig. 9
figure 9

Unit cell and its possible modification due to the change of the angle

Full size image

During the optimization, the six points shown in Fig. 9 are assumed to be fixed. Hence, length \(L\) remains constant, while the variations of \(\theta\) result in varied values of \(h\) and \(l\).To ensure a full-gradient distribution of the variables (a full-gradient model), all angles are allowed to be varied.

The optimization algorithm is implemented in the MATLAB software linked to the macro code for the FE modeling. If the objective function is represented by the RMSL over the analyzed frequency range, the optimization problem can be formulated as follows:

$$\begin{gathered} {\text{Objective function:}} \hfill \\ {\text{RMSL}}\left( {{\uptheta }_{1} ,{\uptheta }_{2} , \ldots ,{\uptheta }_{270} } \right) \hfill \\ {\text{Parameters range:}} \hfill \\ - 50^{ \circ } { } < {\uptheta }_{1} ,{\uptheta }_{2} , \ldots ,{\uptheta }_{270} < + 50^{ \circ } \hfill \\ {\text{Initial guess:}} \hfill \\ {\uptheta }_{1} ,{\uptheta }_{2} , \ldots ,{\uptheta }_{270} = - 30^{ \circ } \hfill \\ \end{gathered}$$
(14)

This problem converges fast to an optimized solution due to the gradient-based nature of the MMA algorithm. To illustrate this, Fig. 10 shows the values of the objective function versus the optimization steps for the Violet noise excitation. As can be seen, the convergence is achieved after about 6 iterations that allows stopping the optimization after 20 iterations.

Fig. 10
figure 10

Values of the optimization function vs. the iteration number for the Violet noise excitation of the load case a

Full size image

The effects of the load distribution and of the frequency content are shown in Fig. 11 in terms of the ratios of RMSL for an optimized model in respect to the base model vs. the load conditions. Specifically, in case of the Violet noise excitation, the noise is reduced by 1.04 dB (load case a) and by 0.99 dB (load case b) as compared to the base model. Thus, one can see that the optimization results in an overall noise reduction by around 0.9–1 dB for the whole frequency range. Besides, the RMSL reduction is higher for the high-frequency loads, as the maximum reduction is achieved for the Violet noise in both load cases. However, the optimization increases the mass of the panel. For example, the mass of the optimized structure is increased by 4.6% for the Violet noise case.

Fig. 11
figure 11

Noise reduction on RMSL for the optimized configurations

Full size image

It is interesting to investigate the noise reduction in terms of sound power. For this, the reduction of the optimized level of the sound power is plotted in percentage in Fig. 12 showing that the full-gradient geometry optimization enables to achieve up to 21% sound power reduction. The strongest reduction is achieved for the high-frequency Violet noise, and the lowest reduction is observed for the Brownian noise that has a low-frequency content. In this latter case, the amount of sound power reduction is below 20%.

Fig. 12
figure 12

Percentage of sound power reduction for the optimized structure

Full size image

To gain a deeper insight into the origin of the sound power reduction, the distribution of the unit cells with the optimized configurations are analyzed. The configuration in Fig. 13a corresponds to the structure optimized under the Violet noise excitation for load case a. We can see that the majority of the cells have large negative angles corresponding to the auxetic behavior, and these cells are located in the areas of the applied load. These unit cells have a higher stiffness as compared to the cells with positive angles. For this optimization case, the total amount of mass is increased about 4.6%, RMSL is reduced 1.04 dB constituting around 21% reduction of sound power (in W).

Fig. 13
figure 13

a Structure of the optimum core for the Violet noise excitation, load case a. b The RSPL of the optimized configuration in comparison with the base model

Full size image

Yet, the complete structure is not fully auxetic, since around 25% of the unit cells have a positive angle. Thus, we conclude that an initial auxetic configuration does not guarantee the lowest sound radiation, and the structural vibrations responsible for the sound radiation are rather complex even in the low-frequency range. This complicates the design of sandwich panels if one is aimed at obtaining panels with reduced sound radiation.

The derived conclusions are general, as they are valid for other optimized configurations. For example, Fig. 14 shows the structure of the optimized core under the Pink noise excitation for load case b and the corresponding PSRL. The optimization delivers in this case about 0.94 dB reduction of RMSL equivalent to the 20% of the sound power reduction at the cost of 4.29% increase of total mass. It is interesting to note that in contrast to the previous situation (Fig. 13), (close to) the excited areas contain auxetic unit cells with the less negative angles than the initial base model.

Fig. 14
figure 14

a Structure of the optimum core for the Pink noise excitation, load case b. b The RSPL of the optimized configuration in comparison with the base model

Full size image

Another remarkable feature of the optimized configurations is shifting of the natural frequencies to lower values (Figs. 13b and 14b) that is desirable in practical situations when the frequency content of applied loads is in the high-frequency range (e.g., in the aerospace industry). This also explains why the observed noise reduction is larger for the high-frequency loads (e.g., the Violet noise) as compared to the low-frequency loads (e.g., the Pink noise).

To summarize, two asymmetrical loading cases a and b, where the excitation was locally applied to the structure have been considered. We see that the optimization algorithm tried to make the structure stronger around the location of the applied loads, and as a result, the optimized panel has asymmetrical distributions of (non-)auxetic cells.

Finally, the topology optimization is also applied to the panel subjected to load case c that has a symmetric loading pattern distributed over the whole surface of the panel (Fig. 4c). The obtained optimization results are illustrated in Fig. 15. Subfigure Fig. 15a illustrates the distribution of the cell’s angles that appears to be symmetric. More auxetic cells are found in the middle part of the panel, away from boundaries with larger displacements and, thus, larger velocities. The locations close to the boundaries have nearly zero cell angles. This result is consistent with the data from Fig. 9 showing the highest amount of radiated structural sound for the zero internal angle.

Fig. 15
figure 15

a Structure of the optimum core for the Violet noise excitation, load case c. b The RSPL of the optimized configuration in comparison with the base model

Full size image

3 Conclusion and outlook

In this study, we studied the vibro-acoustic performance of the sandwich panels with a re-entrant hexagonal honeycomb core was analyzed and optimized. We applied a homogenized finite-element model and considered three load cases with the aim to investigate the effects of the loading location and various random loads on the sound radiation level. These cases provided some important information about the effects of the location and frequency content of the applied load on the vibroacoustic responses and optimization results. For the first time, we applied a non-restricted two-dimensional full–gradient optimization method that provides a complete freedom for the geometric distribution of the design variables. This freedom together with the topological optimization allowed to obtain an enhanced vibroacoustic response at the cost of a slight increase of the structural mass.

The structure of the core has a complex architecture formed by a carefully tailored arrangement of auxetic and non-auxetic unit cells. We found out that the auxetic structure (with negative cell angles) is preferable to reduce structural vibrations and noise. The optimization algorithm concentrates auxetic unit cells around the load application areas. In particular, the algorithm tries to make the structure stronger and stiffer around the locations with a stronger dynamic loading and to minimize the structural weight in the unloaded parts. Therefore, the optimized designs are not fully auxetic and can contain up to 25% of non-auxetic unit cells. This indicates a more complex noise radiation process that can be intuitively expected in a low-frequency range. Furthermore, we showed that the optimized designs allow shifting natural frequencies of initially auxetic structures to lower values due to slightly increased structural mass. This ensures better working performance for high-frequency loads that is beneficial for aerospace engineering.