On Optimal Designs Using Topology Optimization for Flow Through Porous Media Applications

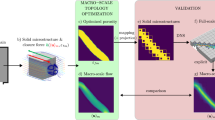
Abstract

Topology optimization (TopOpt) is a mathematical-driven design procedure to realize optimal material architectures. This procedure is often used to automate the design of devices involving flow through porous media, such as micro-fluidic devices. TopOpt offers material layouts that control the flow of fluids through porous materials, providing desired functionalities. Many prior studies in this application area have used Darcy equations for primal analysis and the minimum power theorem (MPT) to drive the optimization problem. But both these choices (Darcy equations and MPT) are restrictive and not valid for general working conditions of modern devices. Being simple and linear, Darcy equations are often used to model flow of fluids through porous media. However, two inherent assumptions of the Darcy model are: the viscosity of a fluid is a constant, and inertial effects are negligible. There is irrefutable experimental evidence that viscosity of a fluid, especially organic liquids, depends on the pressure. Given the typical small pore-sizes, inertial effects are dominant in micro-fluidic devices. Next, MPT is not a general principle and is not valid for (nonlinear) models that relax the assumptions of the Darcy model. This paper aims to overcome the mentioned deficiencies by presenting a general strategy for using TopOpt. First, we will consider nonlinear models that take into account the pressure-dependent viscosity and inertial effects, and study the effect of these nonlinearities on the optimal material layouts under TopOpt. Second, we will explore the rate of mechanical dissipation, valid even for nonlinear models, as an alternative for the objective function. Third, we will present analytical solutions of optimal designs for canonical problems; these solutions not only possess research and pedagogical values, but also facilitate verification of computer implementations.

Graphical Abstract

We have considered a pressure-driven problem with axisymmetry and got optimal material layouts using topology optimization by maximizing the total rate of dissipation. The left figure shows unphysical finger-like design patterns when the primal analysis does not enforce explicitly the underlying radial symmetry. The right figure shows that one can avoid such numerical pathologies if the primal analysis invokes axisymmetry conditions.

1 Introduction and Motivation

Topology optimization—referred to as TopOpt hereon—is a contemporary leading design procedure for obtaining optimal material layouts. TopOpt being mathematical-driven, the whole design procedure is automatic with minimal or no human intervention (Bendsoe and Sigmund 2013). Another attractive feature is TopOpt’s ability to introduce new boundaries into the design space (Bendsoe 1995; Rozvany and Lewiński 2014; Nakshatrala et al. 2013). Said differently, TopOpt could provide designs with holes even if the user-provided initial configuration had none; for example. Although present for over four decades, this design procedure has had a renewed interest. The reason for this resurgence is that new manufacturing techniques (e.g., additive manufacturing) allow us to fabricate, previously unrealized, intricate material layouts often provided by TopOpt (Zegard and Paulino 2016).

Initially introduced for structural design, researchers have extended TopOpt to other fields such as electronics (e.g., MEMS) (Maute and Frangopol 2003; Dede et al. 2015; Jang et al. 2012), automotive (Yang and Chahande 1995), biomedical (Fujii 2002; Vilardell et al. 2019), and aeronautical (James et al. 2014; Maute and Allen 2004) industries to get optimal designs for components as well as systems. These fields went beyond solid mechanics. TopOpt has also been applied to fluid mechanics (Gersborg-Hansen et al. 2005; Alexandersen and Andreasen 2020), nanophotonics (Jensen and Sigmund 2011), acoustics (Dühring et al. 2008), and flow and transport in porous media (Borrvall and Petersson 2003). The last topic is of central interest to this paper.

The emergence of ink-jet printers, which use tiny tubes carrying ink for printing, and additive manufacturing (3D printing) have triggered an interest in fluid flows through micropore networks. This interest has created fresh opportunities in the emerging research field of microfluidics (Whitesides 2006). As the name suggests, microfluidics concerns with the study of flows of tiny quantities (a few milliliters or smaller) of fluids in miniature-sized devices. In recent times, such devices have gained popularity in medical diagnostics, filters, and sensors. The success of these instruments across the application areas depends on the reliability of results and optimal performance (Fujii 2002). Hence, the primary challenge is to get optimal designs for producing reliable results.

Borrvall and Petersson (2003) were among the first to apply TopOpt for fluid problems. They used Stokes equations, which neglect nonlinear inertial effects, to get optimal fluid paths. Extending the mentioned work, Gersborg-Hansen et al. (2005) have included inertial effects but restricted their study to free flows. Wiker et al. (2007) have applied TopOpt for coupled flows—combining flow through porous media and free fluid flow. For the former class of flows, they used the Darcy model while the Stokes model for the latter; both these models neglect inertial effects. To drive the design, they used minimization of the total potential power as the objective function. Another relevant work is by Guest and Prévost (2006), who proposed a mixed formulation combining the Stokes and Darcy equations with the objective, again, to minimize the total potential power. These prior works manifest two main drawbacks: (i) model the flow through porous media using Darcy equations, and (ii) use the minimum power theorem (MPT) to drive the design problem. We elaborate these two points below.

Darcy equations are valid under a myriad of assumptions; see (Rajagopal 2007; Nakshatrala and Rajagopal 2011). Some of these assumptions are not valid to the working of typical microfluidic devices. Specifically, two fundamental assumptions of the Darcy model are: the viscosity of the fluid is constant, and the inertial effects are negligible. However, irrefutable experimental evidence shows that the viscosity of a fluid depends on the pressure, especially for organic liquids. Barus (1893) has shown that this dependence is exponential. Studies have shown that inertial forces can play an important role in determining the flow characteristics even with very low Reynolds numbers (Stone et al. 2004). A combination of various internal forces (like inertial and capillary forces) and external forces (e.g., pressure gradient) affects the microfluidic flow. As the size shrinks, surface forces become more significant than the gravity forces (Convery and Gadegaard 2019). Importantly, these nonlinearities give rise to velocity and pressure profiles that are qualitatively and quantitatively different from that of Darcy equations (Nakshatrala and Rajagopal 2011; Chang et al. 2017). Therefore, by using Darcy equations, the design process ignores these nonlinear effects, leading to non-optimal and unreliable products.

Returning to the second point, MPT is not a physical law but a mere restatement of Darcy equations, in the spirit of calculus of variations. A solution of Darcy equations satisfies MPT, and vice versa. Importantly, nonlinear models for flow through porous media, like the ones considered in this paper, do not meet MPT. Thus, there is a search for an alternative candidate with a universal appeal for the objective function; we articulate in this paper that the rate of mechanical dissipation is an ideal candidate.

Besides the above drawbacks, there are other aspects contributing to the knowledge gap. Even without nonlinearities, there is no general way to formulate a well-posed design problem. Should we maximize or minimize the rate of dissipation? Should we place a volume bound constraint on the material with high or low permeability? Do the boundary conditions—pressure-driven versus velocity-driven—affect the nature of the optimization problem? Last but not least, the lack of analytical solutions is impeding the verification of numerical solutions and the essential understanding of optimal designs required for translation to other scenarios.

The central aim of this paper is to fill these aspects of the knowledge gap. We will account for two nonlinearities—pressure-dependent viscosity and nonlinear inertial effects—into the primal analysis. We will answer the following key question, pertaining to the formulation of well-posed design problems under TopOpt for flow through porous media applications:

• (Q1) What are the proper objective function and volume constraint to drive the topology optimization for problems involving flow through porous media?

  • (i) Specifically, we will discuss the limited scope of MPT.

  • (ii) We show that extremization of the rate of dissipation, a physical quantity, can serve as a proper objective function. Whether it is maximization or minimization depends on the boundary conditions and the nature of the problem.

  • (iii) A volume constraint on the material with a higher permeability is compatible with a wide variety of problems.

To facilitate verification of numerical simulators, we will present analytical solutions for 1D and axisymmetric problems. We will also present numerical solutions for various representative problems. Using these analytical and numerical solutions, we will gain an understanding of the optimal designs and answer these fundamental questions:

• (Q2) What are the ramifications of the two nonlinearities (pervasive in microfluidic applications)—pressure-dependent viscosity and inertial effects—individually on the optimal designs?

• (Q3) How do the volumetric constraint, and (pressure-driven versus velocity-driven) boundary conditions affect the optimal material layout?

A few words on the scope of this paper are warranted. First, this paper does not concern with solution procedures, such as new filters or solvers, which dominate the current literature. Instead, constructing well-posed design problems and understanding the resulting optimal designs are the main themes of this paper. The innovation is that our approach is very general, applicable even to nonlinear models. This general approach along with the body of knowledge presented in this paper will be valuable to researchers and practitioners alike. The design problem under the proposed TopOpt framework is programmed using COMSOL Multiphysics (2018), and all the numerical results reported in this paper are generated using this computer implementation.

Second, this paper addresses the flow of single-phase fluids in rigid porous media. However, numerous applications exist that involve the flow of multi-phase fluid systems (Zhao et al. 2019). Also, some emerging applications derive their functionalities from the porous solid’s deformation; a few notable works include (Kim et al. 2013; Dalbe and Juanes 2018). These two phenomena—the flow of multi-phase fluids and deformable porous media—are beyond the scope of this paper. Applying topology optimization to such phenomena has not been explored adequately and can be an excellent topic for future works.

The outline for the rest of the paper is as follows. Section 2 presents the equations governing fluid flow in porous media (i.e., Darcy equations, pressure-dependent viscosity, and inertial effects). In Sect. 3, we will outline the minimum power theorem and discuss the appropriateness and limitations of using this theorem as an objective function to drive TopOpt. Using one-dimensional problems, we will then gain insights into how to construct well-posed design problems based on the rate of mechanical dissipation (Sect. 4), and construct analytical solutions for these design problems (Sect. 5). Sections 6 and 7 will consider axisymmetry problems in 2D and 3D and address two aspects: (i) how to get accurate designs respecting the underlying symmetry, and (ii) what is the nature of these designs. Section 8 discusses the ramifications of pressure-dependent viscosity and inertial effects on the optimal designs. The article will end with concluding remarks on using TopOpt for designing devices involving the flow of fluids through porous media (Sect. 9).

2 Governing Equations: Mathematical Models and Design Problem

2.1 Mathematical Models for Flow Through Porous Media

We will first document Darcy equations and then present the nonlinear generalizations considered in this paper. We denote the domain by $\Omega$ and its boundary $\partial \Omega$. A spatial point is denoted by ${\mathbf {x}} \in {\overline{\Omega }}$, where an overline denotes the set closure (i.e., ${\overline{\Omega }} := \Omega \cup \partial \Omega$), the unit outward normal to the boundary by $\widehat{{\mathbf {n}}}({\mathbf {x}})$, and the spatial gradient and divergence operators by ${\mathrm {grad}}[\cdot ]$ and ${\mathrm {div}}[\cdot ]$, respectively. ${\mathbf {v}}({\mathbf {x}})$ and $p({\mathbf {x}})$ denote the discharge (or Darcy) velocity and pressure¹, respectively. The boundary is divided into two complementary parts: $\Gamma ^{v}$ and $\Gamma ^{p}$. $\Gamma ^{v}$ is that part of the boundary on which the normal component of the velocity is prescribed, and $\Gamma ^{p}$ is the part of the boundary on which the pressure is prescribed.

The equations that govern the flow of fluids in porous media take the following form:

$$\begin{aligned}&\alpha {\mathbf {v}}({\mathbf {x}}) + {\mathrm {grad}}[p] = \rho {\mathbf {b}}({\mathbf {x}})&\quad {\mathrm {in}} \; \Omega \end{aligned}$$

(2.1a)

$$\begin{aligned}&{\mathrm {div}}[{\mathbf {v}}] = 0&\quad {\mathrm {in}} \; \Omega \end{aligned}$$

(2.1b)

$$\begin{aligned}&{\mathbf {v}}({\mathbf {x}}) \cdot \widehat{{\mathbf {n}}}({\mathbf {x}}) = v_{n}({\mathbf {x}})&\quad {\mathrm {in}} \; \Gamma ^{v} \end{aligned}$$

(2.1c)

$$\begin{aligned}&p({\mathbf {x}}) = p_0({\mathbf {x}})&\quad {\mathrm {on}} \; \Gamma ^{p} \end{aligned}$$

(2.1d)

where $\alpha$ is the drag coefficient, $\rho$ the density of the fluid, $p_0({\mathbf {x}})$ the prescribed pressure, $v_n({\mathbf {x}})$ the prescribed normal component of the velocity, and ${\mathbf {b}}({\mathbf {x}})$ the given specific body force. The drag coefficient is defined as:

$$\begin{aligned} \alpha = \frac{\mu }{k({\mathbf {x}})} \end{aligned}$$

(2.2)

where $\mu$ is the coefficient of viscosity of the fluid, and k is the permeability of the porous medium. The Darcy model assumes constant coefficient of viscosity and the permeability to be independent of the field variables (i.e., velocity and pressure), while the latter can vary spatially.

2.1.1 Pressure-Dependence Viscosity

Based on extensive experiments, Barus (1893) has shown that the coefficient of viscosity for many organic liquids depends exponentially on the pressure. Mathematically,

$$\begin{aligned} \mu (p) = \mu _0 \exp [\beta _{\mathrm {B}} p] \end{aligned}$$

(2.3)

where $\beta _\mathrm {B} \ge 0$ is a characteristic of the fluid, which can be determined experimentally, and $\mu _0$, a constant, is the viscosity of the fluid at a reference pressure. Often, the reference pressure is taken to be the atmospheric pressure. A non-zero value for the reference pressure implies that p should be interpreted as the relative pressure (i.e., difference between the absolute pressure and the reference pressure). Given Eq. (2.3), the drag coefficient takes the following mathematical form:

$$\begin{aligned} \alpha = \alpha _{\mathrm {B}}(p({\mathbf {x}}),{\mathbf {x}}) = \frac{\mu (p)}{k({\mathbf {x}})} = \frac{\mu _0}{k({\mathbf {x}})} \exp [ \beta _\mathrm {B} p] \end{aligned}$$

(2.4)

A linearized approximation, referred to as the linearized Barus model in this paper, takes the following form:

$$\begin{aligned} \alpha = \alpha _{\mathrm {LB}}(p({\mathbf {x}}),{\mathbf {x}}) = \frac{\mu _0}{k({\mathbf {x}})} [1 + \beta _\mathrm {B} p] \end{aligned}$$

(2.5)

2.1.2 Inertial Effects

Philipp Forchheimer, an Austrian scientist, proposed a model—often referred to as Darcy-Forchheimer model—to account for the inertial effects (Boer 2012). We follow Chang et al. (2017) and express this model in the following mathematical form:

$$\begin{aligned} \alpha = \alpha _{\mathrm {DF}} ({\mathbf {v}}({\mathbf {x}}),{\mathbf {x}}) = \frac{\mu }{k({\mathbf {x}})} \left( 1 + \beta _\mathrm {F} \Vert {\mathbf {v}}\Vert \right) \end{aligned}$$

(2.6)

where $\beta _\mathrm {F}$ is the Forchheimer coefficient, and $\Vert \cdot \Vert$ denotes the Euclidean 2-norm.

The rate of dissipation—a physical quantity with a strong mechanics and thermodynamics underpinning—will play a vital role in this paper. On this account, the total rate of dissipation is defined as:

$$\begin{aligned} \Phi = \int _{\Omega } \varphi ({\mathbf {x}}) \mathrm {d} \Omega \end{aligned}$$

(2.7)

where $\varphi ({\mathbf {x}})$ is the rate of dissipation density. The mathematical form for $\varphi ({\mathbf {x}})$ (valid for all the models mentioned above—Darcy, Barus, linearized Barus and Darcy-Forchheimer) reads:

$$\begin{aligned} \varphi ({\mathbf {x}}) := \alpha \, {\mathbf {v}}({\mathbf {x}}) \cdot {\mathbf {v}}({\mathbf {x}}) \end{aligned}$$

(2.8)

2.2 Design Problem Under TopOpt

Consider two porous materials with different permeabilities. The design question then is how to place these two porous materials within the domain to achieve the desired goal. We often place a volume constraint bound on one of the materials due to cost considerations or scarcity of resources; for example, the total volume of the expensive porous material should not be more than, say, 30% of the entire volume of the domain. We denote the design variable as $\xi ({\mathbf {x}})$ with the following representation:

$$\begin{aligned} \xi ({\mathbf {x}}) = \left\{ \begin{array}{ll} 1 &{} \text {if} \; {\mathbf {x}} \; \text {is occupied by the material with volume constraint }\\ 0 &{} \text {if} \; {\mathbf {x}} \; \text {is occupied by the material without volume constraint} \end{array} \right. \end{aligned}$$

In this paper, we formulate the design problem using the rate of dissipation for the objective function. The design problem can be either minimization or maximization of the dissipation functional. Under minimization, the proposed design problem using TopOpt takes the following form²:

$$\begin{aligned}&{\widehat{\xi }}({\mathbf {x}}) \leftarrow \mathop {\mathrm {argmin}}_{\xi ({\mathbf {x}})} \; \Phi [\xi ({\mathbf {x}}), {\mathbf {v}}({\mathbf {x}}),p({\mathbf {x}})]&\quad \text{(objective } \text{ functional) } \nonumber \\&\text{ subject } \text{ to: } \end{aligned}$$

(2.9a)

$$\begin{aligned}&\left. \begin{array}{ll} \alpha {\mathbf {v}}({\mathbf {x}}) + {\mathrm {grad}}[p] = \rho {\mathbf {b}}({\mathbf {x}}) &{}\; {\mathrm {in}} \; \Omega \\ {\mathrm {div}}[{\mathbf {v}}] = 0 &{}\; {\mathrm {in}} \; \Omega \\ {\mathbf {v}}({\mathbf {x}}) \cdot \widehat{{\mathbf {n}}}({\mathbf {x}}) = v_n({\mathbf {x}}) &{}\; {\mathrm {on}} \; \Gamma ^v \\ p({\mathbf {x}}) = p_0({\mathbf {x}}) &{} \; {\mathrm {on}} \; \Gamma ^p \end{array} \right\}&\quad \text{(state } \text{ equations) } \end{aligned}$$

(2.9b)

$$\begin{aligned}&\int _{\Omega } \xi ({\mathbf {x}}) \, \mathrm {d} \Omega \le \gamma \int _{\Omega } \mathrm {d} \Omega = \gamma \, \text{ meas }(\Omega )&\quad \text{(volume } \text{ constraint) } \end{aligned}$$

(2.9c)

$$\begin{aligned}&\xi ({\mathbf {x}})\in \left\{ 0,1\right\} \quad \forall {\mathbf {x}} \in \Omega&\quad \text{(design } \text{ set/space) } \end{aligned}$$

(2.9d)

where $0 \le \gamma \le 1$ is the bound for the volume constraint, and $\text{ meas }(\Omega )$ denotes the area/volume of the domain.

In its primitive form, the above optimization problem is an integer programming; $\xi$ takes either 0 or 1. Such integer programming optimization problems are notoriously difficult to solve. Hence, a regularization procedure, such as SIMP (Bendsoe and Sigmund 2013; Bendsoe and Kikuchi 1988; Rozvany 2001) and MMA (Svanberg 1987), is often used to convert the above problem (2.9) into a nonlinear programming problem. The design space will then be the entire interval between 0 and 1 (i.e., $\xi \in [0,1]$). However, an effective regularization technique will force the design variables toward 0 or 1. The corresponding nonlinear programming problem, after regularization, takes the following form:

$$\begin{aligned} \mathop {\mathrm {max}}_{\xi \; \in \; \left[ 0,1 \right] } \quad {\widetilde{\Phi }}_\xi [\xi ({\mathbf {x}}), {\mathbf {v}}({\mathbf {x}}),p({\mathbf {x}})] \end{aligned}$$

(2.10)

where ${\widetilde{\Phi }}_{\xi }$ is a regularized functional.

The design problem has two main ingredients: the primal analysis and the optimization procedure. In the literature, primal analysis also goes by several other names: forward problem/model (Tarantola 2005), direct problem in imaging (Bertero and Boccacci 2020), solution to equilibrium equations (especially in solid mechanics (Bendsoe and Sigmund 2013), or sometimes just plain analysis. The central piece of primal analysis is a solution procedure that solves the state Eq. (2.9b) for a fixed value of the design (field) variable $\xi ({\mathbf {x}})$. This solution procedure can be either analytical or numerical. The optimization procedure extremizes the objective function by satisfying the constraints as well as the state equations. The constraints can be bounds on the usage of each material, minimum length scale on the microstructure, manufacturing constraints to facilitate fabrication, to name a couple. In numerical simulations of complicated problems, both the ingredients—primal analysis and optimization procedure—are solved numerically. The selection and accuracy of numerical schemes for each of these ingredients will affect the final design outcome.

We have used the SIMP regularization and MMA algorithm in all our numerical results reported in this paper. The MMA algorithm used with SIMP (Solid Isotropic Material with Penalization) regularization method ensures that the solution steers toward a 0–1 solution where 1 indicates the presence of the controlled material, while 0 indicates the presence of uncontrolled material. The stopping criteria—for terminating the design procedure—are to satisfy any one of the following conditions: (i) Closeness to a 0–1 solution with no apparent change in the material distribution over several consequent iterations, and the maximum number of iterations reaches 100. (ii) The relative tolerance of objective function in successive iterations less than or equal to 0.001.

3 On the Use of Minimum Power Theorem

In the literature, the minimum power theorem (MPT) also goes by the name: the principle of minimum power. A few remarks about MPT are in order:

• (1) It is not a physical law, although its name might suggest some relation to the first law of thermodynamics. To the contrary, it is a mathematical result from the calculus of variations; a solution to the Darcy Eqs. (2.1a)–(2.1d) satisfies MPT, and vice versa.

• (2) It is not a general principle governing the flow of fluids through porous media. Notably, MPT is not valid for Barus and Darcy-Forchheimer models, considered in this paper.

The plan for the rest of this section is: we will first precisely state MPT. This will be followed by a discussion on how to pose a design problem, under TopOpt, based on MPT (but restricted to Darcy equations). Finally, we prove that MPT is not valid for nonlinear models.

We start by defining the space of kinematically admissible vector fields:

$$\begin{aligned} {\mathcal {K}} := \{\widetilde{{\mathbf {v}}}({\mathbf {x}}) \; | \; {\mathrm {div}} [\widetilde{{\mathbf {v}}}] = 0 \; {\mathrm {in}} \; \Omega , \; \widetilde{{\mathbf {v}}}({\mathbf {x}}) \cdot \widehat{{\mathbf {n}}}({\mathbf {x}}) = v_n({\mathbf {x}}) \; {\mathrm {on}} \; \Gamma ^v \} \end{aligned}$$

(3.1)

That is, a kinematically admissible vector field $\widetilde{{\mathbf {v}}}({\mathbf {x}}) \in {\mathcal {K}}$ needs to satisfy the continuity condition (2.1b) and the velocity boundary conditions (2.1c), but it is not necessary for a kinematically admissible vector field to satisfy either the balance of linear momentum (2.1a) or the pressure boundary condition (2.1d).³ We call a vector field ${\mathbf {v}} : {\overline{\Omega }} \rightarrow {\mathbb {R}}^{nd}$ the Darcy velocity, a special type of kinematically admissible field, if it satisfies Eqs. (2.1a)–(2.1d). That is, ${\mathbf {v}}({\mathbf {x}}) \in {\mathcal {K}}$ and satisfies Eqs. (2.1a) and (2.1d).

The central piece of MPT is the mechanical power functional, defined as follows:

$$\begin{aligned} \Psi [{\mathbf {w}}({\mathbf {x}})] := \int _{\Omega } \frac{1}{2} \; \alpha \; {\mathbf {w}}({\mathbf {x}}) \cdot {\mathbf {w}}({\mathbf {x}}) \; \mathrm {d}\Omega -\int _{\Omega } {\mathbf {w}}({\mathbf {x}}) \cdot \rho {\mathbf {b}}({\mathbf {x}}) \; \mathrm {d}\Omega +\int _{\Gamma ^p} {\mathbf {w}}({\mathbf {x}}) \cdot \widehat{{\mathbf {n}}}({\mathbf {x}}) \; p_0({\mathbf {x}}) \; \mathrm {d}\Gamma \end{aligned}$$

(3.2)

where $\mathbf {w(x)} \in {\mathcal {K}}.$

MPT can then be compactly written as:

$$\begin{aligned} \Psi [{\mathbf {v}}({\mathbf {x}})] \; \le \; \Psi [\widetilde{{\mathbf {v}}}({\mathbf {x}})] \quad \forall \widetilde{{\mathbf {v}}}({\mathbf {x}}) \in {\mathcal {K}} \end{aligned}$$

(3.3)

In plain words, MPT states that the Darcy velocity renders the minimum mechanical power among all the kinematically admissible vector fields. Using the language of optimization theory, an alternate form of MPT is:

$$\begin{aligned} {\mathbf {v}}({\mathbf {x}}) \leftarrow \mathop {\mathrm {argmin}}_{\widetilde{{\mathbf {v}}}({\mathbf {x}}) \in {\mathcal {K}} } \; \Psi [\widetilde{{\mathbf {v}}}({\mathbf {x}})] \end{aligned}$$

(3.4)

A design problem, under TopOpt, based on MPT can be posed as follows:

$$\begin{aligned} \mathop {\mathrm {min}}_{\xi \; \in \; \left\{ 0,1 \right\} } \quad \mathop {\mathrm {min}}_{\widetilde{{\mathbf {v}}}({\mathbf {x}}) \; \in \; {\mathcal {K}}} \quad \Psi [\widetilde{{\mathbf {v}}}({\mathbf {x}})] \end{aligned}$$

(3.5)

where $\xi$ is the design variable. The outer optimization problem is an integer programming (i.e., $\xi$ takes either 0 or 1). The corresponding nonlinear programming problem after regularization can be written as follows:

$$\begin{aligned} \mathop {\mathrm {min}}_{\xi \; \in \; \left[ 0,1 \right] } \quad \mathop {\mathrm {min}}_{\widetilde{{\mathbf {v}}}({\mathbf {x}}) \; \in \; {\mathcal {K}}} \quad {\widetilde{\Psi }}_\xi [\widetilde{{\mathbf {v}}}({\mathbf {x}})] \end{aligned}$$

(3.6)

where ${\widetilde{\Psi }}_{\xi }$ is a regularized functional.

Shabouei and Nakshatrala (2016) have provided a proof of MPT for Darcy equations. We now show that MPT will not hold for nonlinear models such as Darcy-Forchheimer and Barus. Thus, in our derivation, we allow the drag coefficient $\alpha$ to depend on the solution fields—${\mathbf {v}}({\mathbf {x}})$ and $p({\mathbf {x}})$. To handle the incompressibility constraint, it is convenient to use the Lagrange multiplier method. On this account, we define the following:

$$\begin{aligned} {\mathcal {V}}&:= \left\{ {\mathbf {v}}({\mathbf {x}}) \, | \, {\mathbf {v}}({\mathbf {x}}) \cdot \widehat{{\mathbf {n}}}({\mathbf {x}}) = v_{n}({\mathbf {x}}) \; {\mathrm {on}} \; \Gamma ^{v}\right\} \end{aligned}$$

(3.7)

$$\begin{aligned} {\mathcal {V}}_{0}&:= \left\{ {\mathbf {v}}({\mathbf {x}}) \, | \, {\mathbf {v}}({\mathbf {x}}) \cdot \widehat{{\mathbf {n}}}({\mathbf {x}}) = 0 \; {\mathrm {on}} \; \Gamma ^{v}\right\} \end{aligned}$$

(3.8)

Appealing to the Lagrange multiplier method, we consider the following equivalent optimization problem:

$$\begin{aligned} \mathop {\mathrm {extremize}}_{{\mathbf {v}}({\mathbf {x}}) \in {\mathcal {V}},\, p({\mathbf {x}})} \quad {\widehat{\Psi }}[{\mathbf {v}}({\mathbf {x}}),p({\mathbf {x}})] \end{aligned}$$

(3.9)

where $p({\mathbf {x}})$, in addition to being the (mechanical) pressure, serves as the Lagrange multiplier enforcing the incompressibility constraint, and

$$\begin{aligned} {\widehat{\Psi }}[{\mathbf {v}}({\mathbf {x}}),p({\mathbf {x}})]&:= \Psi [{\mathbf {v}}({\mathbf {x}})] - \int _{\Omega } p({\mathbf {x}}) {\mathrm {div}}[{\mathbf {v}}] \, \mathrm {d} \Omega \end{aligned}$$

(3.10)

For the solution fields to satisfy MPT, the necessary condition is:

$$\begin{aligned}&\delta {\widehat{\Psi }}[{\mathbf {v}}({\mathbf {x}}),p({\mathbf {x}})] \cdot \left( \delta {\mathbf {v}}({\mathbf {x}}), \delta p({\mathbf {x}})\right) := \left[ \frac{d}{d \epsilon } {\widehat{\Psi }}[{\mathbf {v}}({\mathbf {x}}) + \epsilon \, \delta {\mathbf {v}}({\mathbf {x}}),p({\mathbf {x}})+\epsilon \, \delta p({\mathbf {x}})]\right] _{\epsilon =0} = 0 \nonumber \\&\quad \quad \forall \delta {\mathbf {v}}({\mathbf {x}}) \in {\mathcal {V}}_0, \forall \delta p({\mathbf {x}}) \end{aligned}$$

(3.11)

Thus, it suffices to show that this necessary condition is not met if $\alpha$ depends on the solution fields. We proceed as follows:

$$\begin{aligned} \delta {\widehat{\Psi }}[{\mathbf {v}}({\mathbf {x}}),p({\mathbf {x}})] \cdot \left( \delta {\mathbf {v}}({\mathbf {x}}),\delta p({\mathbf {x}})\right)&= \int _{\Omega } \alpha \, {\mathbf {v}}({\mathbf {x}}) \cdot \delta {\mathbf {v}}({\mathbf {x}}) \, \mathrm {d} \Omega - \int _{\Omega } \rho {\mathbf {b}}({\mathbf {x}}) \cdot \delta {\mathbf {v}}({\mathbf {x}}) \, \mathrm {d} \Omega + \int _{\Gamma ^{p}} p_0({\mathbf {x}}) \, \delta {\mathbf {v}}({\mathbf {x}}) \cdot \widehat{{\mathbf {n}}}({\mathbf {x}}) \, \mathrm {d} \Gamma \nonumber \\&- \int _{\Omega } p({\mathbf {x}}) \, {\mathrm {div}}[\delta {\mathbf {v}}({\mathbf {x}})] \, \mathrm {d} \Omega - \int _{\Omega } \delta p({\mathbf {x}}) \, {\mathrm {div}}[{\mathbf {v}}({\mathbf {x}})] \, \mathrm {d} \Omega \nonumber \\&+ \int _{\Omega } \frac{1}{2} \left( \frac{\partial \alpha }{\partial {\mathbf {v}}} \cdot \delta {\mathbf {v}} + \frac{\partial \alpha }{\partial p} \cdot \delta p \right) {\mathbf {v}}({\mathbf {x}}) \cdot {\mathbf {v}}({\mathbf {x}}) \mathrm {d} \Omega \end{aligned}$$

(3.12)

Using the Green’s identity, noting that the solution fields satisfy Eqs. (2.1a)–(2.1d), and invoking $\delta {\mathbf {v}}({\mathbf {x}}) \in {\mathcal {V}}_0$, we end up with:

$$\begin{aligned} \delta {\widehat{\Psi }}[{\mathbf {v}}({\mathbf {x}}),p({\mathbf {x}})] \cdot (\delta {\mathbf {v}}({\mathbf {x}}),\delta p({\mathbf {x}}))&= \int _{\Omega } \frac{1}{2} \left( \frac{\partial \alpha }{\partial {\mathbf {v}}} \cdot \delta {\mathbf {v}} + \frac{\partial \alpha }{\partial p} \cdot \delta p \right) {\mathbf {v}}({\mathbf {x}}) \cdot {\mathbf {v}}({\mathbf {x}}) \mathrm {d} \Omega \end{aligned}$$

(3.13)

For the above integral to vanish for all $\delta {\mathbf {v}}({\mathbf {x}}) \in {\mathcal {V}}_0$ and for all $p({\mathbf {x}})$, we must have:

$$\begin{aligned} \frac{\partial \alpha }{\partial {\mathbf {v}}} = {\mathbf {0}} \quad {\mathrm {and}} \quad \frac{\partial \alpha }{\partial p} = 0 \end{aligned}$$

(3.14)

meaning that the drag function is independent of the solution fields.

Since MPT is limited in scope, we need a general way to pose design problems under TopOpt for flow through porous media applications. All the studies from hereon uses the rate of dissipation functional.

4 Insights from One-Dimensional Problems

We will use the Darcy model and one-dimensional problems to gain insights into three aspects:

• (1) Nature of the solution: How does the rate of dissipation density depends on permeability k?

• (2) Extremization of the objective function: Is it physical to minimize or maximize $\Phi$?

• (3) Volumetric bound constraint: On which material—high or low permeability—should we place a bound on its volume fraction?

We start by noting the rate of dissipation density under the Darcy model is:

$$\begin{aligned} \varphi ({\mathbf {x}}) = \frac{\mu }{k} {\mathbf {v}}({\mathbf {x}}) \cdot {\mathbf {v}}({\mathbf {x}}) \end{aligned}$$

(4.1)

A cavalier look at Eq. (4.1) might suggest answer to the first question is trivial;$\varphi$ is inversely proportional to k. This conclusion seems even more plausible by noting that the continuity equation (i.e., balance of mass considering the incompressibility of the fluid) in 1D is:

$$\begin{aligned} {\mathrm {div}}[{\mathbf {v}}] = \frac{{\rm d}v}{{\rm d}x} = 0 \end{aligned}$$

(4.2)

which implies that the velocity $v(x) = {\mathrm {constant}}$. But this reasoning does not consider the possibility that the velocity, although a constant for 1D problems, could depend on k. That is, the rate of dissipation density depends on k explicitly, while it could also depend on k implicitly via the velocity field. To prove this point and to establish the exact dependence of $\varphi$ on k, we will consider two types of boundary value problems: pressure-driven and velocity-driven. In a pressure-driven problem, pressure boundary conditions are prescribed on the entire boundary. While for a velocity-driven problem, velocity boundary conditions are prescribed at least on a part of the boundary.

4.1 Pressure-Driven Problem

Consider a one-dimensional problem with length L as detailed in Fig. 1. The pressure conditions are applied on the either ends of the domain with $p_L > p_R$.

Fig. 1

A pictorial description of the one-dimensional pressure-driven problem

The equations governing the flow of the fluid in the domain are:

$$\begin{aligned}&\frac{\mu }{k} v(x) + \frac{{\rm d} p}{{\rm d} x} = 0&\quad {\mathrm {in}} \; (0, L) \end{aligned}$$

(4.3a)

$$\begin{aligned}&\frac{{\rm d} v}{{\rm d} x} = 0&\quad {\mathrm {in}} \; (0, L) \end{aligned}$$

(4.3b)

$$\begin{aligned}&p(x = 0) = p_L \end{aligned}$$

(4.3c)

$$\begin{aligned}&p(x = L) = p_R \end{aligned}$$

(4.3d)

The corresponding analytical solution is:

$$\begin{aligned} p(x) = \left( 1-\frac{x}{L}\right) p_L + \frac{x}{L} p_R \quad {\mathrm {and}} \quad v(x)&= \frac{k}{\mu } \frac{(p_L - p_R)}{L} \end{aligned}$$

(4.4)

Although the velocity is a constant, as mentioned earlier, it depends on the permeability. Accordingly, the rate of dissipation density will be:

$$\begin{aligned} \varphi (x)&= \frac{\mu }{k} \mathbf {v(x) \cdot v(x)} = \frac{\mu }{k} v^{2}(x) = \frac{k}{\mu } \frac{\left( p_L - p_R \right) ^2}{L^2} \end{aligned}$$

(4.5)

Thus, for the chosen pressure-driven problem, $\varphi (x)$ is proportional to k (and not to $k^{-1}$).

4.1.1 A Design Problem for Pressure-Driven Problems

In the applications of pressure-driven problems, the goal often is to dissipate the (kinetic) energy as much as possible as the fluid passes through the porous domain. Thus, maximizing the total rate of dissipation is a physically meaningful choice for the objective function under TopOpt.

To decide on the volumetric bound, we need to assess the combined effect of this objective function alongside how the rate of dissipation density depends on the permeability for pressure-driven problems. Since $\varphi \propto k$, one needs to place a bound on the use of high-permeability material in the domain. Otherwise, we will end up with a trivial solution—placing the high-permeability material throughout the domain. Other reasons such as practical and economic could also compel to place a restriction on the use of high-permeability. On the practical front, a high-permeability material often has low strength, and too much use of such a material could comprise the structural integrity of the device. On the economic front, a high-permeability material is often an engineered material, making it expensive. All these factors justify placing a bound on the use of the high-permeability material.

Summarizing, a well-posed design problem for pressure-driven problems can be: maximization of the total rate of dissipation subject to a volume constraint bound on the high-permeability material.

4.2 Velocity-driven problem

We now consider a one-dimensional problem similar to the one used in Sect. 4.1, but the left end of the domain is prescribed with a velocity boundary condition (see Fig. 2).

Fig. 2

A pictorial description of the one-dimensional velocity-driven problem

The governing equations remain the same as the previous case expect Eq. (4.3c) is now replaced with:

$$\begin{aligned}&v(x=0) = v_L \end{aligned}$$

(4.6)

The corresponding analytical solution for the fields is:

$$\begin{aligned} v(x) = v_L \quad {\mathrm {and}} \quad p(x) = p_R + \frac{\mu }{k} v_L (L-x) \end{aligned}$$

(4.7)

For this case, the velocity is a constant independent of k. The corresponding rate of dissipation density is:

$$\begin{aligned} \varphi (x) = \frac{\mu }{k} v^2(x) = \frac{\mu }{k} v_L^2 \end{aligned}$$

(4.8)

Since $\mu$, L and $v_L$ are independent of k, $\varphi (x)$ is constant and is inversely proportional to k.

4.2.1 A Design Problem for Velocity-Driven Problems

In the applications involving velocity-driven problems, a continuous supply of power/energy will be needed for maintaining adequate flow—required to meet the velocity boundary condition. Therefore, it is desirable to minimize the rate of dissipation for these kinds of problems. Noting that $\varphi \propto k^{-1}$ for velocity-driven problems, the minimization of the total rate of dissipation will require a volume constraint bound on the high-permeability material. Otherwise, similar to pressure-driven problems, the solution to the design problem becomes trivial. Summarizing, a well-posed design problem for velocity-driven problems can be: minimization of the total rate of dissipation with a volumetric bound constraint on the high-permeability material.

Although our above arguments are based on prototypical 1D problems, the conclusions are applicable even to other problems and to the nonlinear models mentioned in Sect. 2. The two design problems given above can guide posing other design problems.

5 Optimal Layouts for One-Dimensional Problems

We will analyze one-dimensional problems similar to the ones considered in Sect. 4. But we will use nonlinear modifications of the Darcy model. The design problem is to place two porous materials with different permeabilities, $k_1$ and $k_2$, in the domain. The objective function and the volumetric bound constraint are the same as discussed earlier.

Using the analytical solutions to these 1D problems, the effect of nonlinearities on the optimal material layouts will be quantified. To derive analytical solution, we assume the presence of a single material interface; its location is at $x = \xi$. That is, the spatial distribution of the permeability is:

$$\begin{aligned} k(x) = \left\{ \begin{array}{ll} k_1 &{} 0< x< \xi \\ k_2 &{} \xi< x < L \end{array} \right. \end{aligned}$$

(5.1)

For convenience and for a later use, we will use $\xi ^{\pm }$ to denote the one-sided limits at the interface. That is, a superscript minus sign on $\xi$ indicates a limit from the left-side; a similar interpretation holds for the superscript plus sign on $\xi$.

5.1 Pressure-Driven Problem

For non-dimensionalization, we take the following (pressure, length and viscosity) as reference quantities:

$$\begin{aligned} p_{\mathrm {ref}} = p_L - p_R \; [\mathrm {M}^{1} \mathrm {L}^{-1} \mathrm {T}^{-2}], \quad L_{\mathrm {ref}} = L \; [\mathrm {M}^{0}\mathrm {L}^{1}\mathrm {T}^{0}] \quad {\mathrm {and}} \quad \mu _{\mathrm {ref}} = \mu _0 \exp [\beta _{\mathrm {B}} p_{\mathrm {R}}]\; [\mathrm {M}^{1} \mathrm {L}^{-1} \mathrm {T}^{-1}] \end{aligned}$$

(5.2)

Note that $\beta _{\mathrm {B}} = 0$ for the Darcy and Darcy-Forchheimer models. These references quantities give rise to the following non-dimensional quantities:

$$\begin{aligned}&{\bar{x}} = \frac{x}{L_{{\mathrm {ref}}}}, \; {\bar{k}} = \frac{k}{L^2_{{\mathrm {ref}}}}, \; {\bar{p}} = \frac{p - p_{\mathrm {R}}}{p_{{\mathrm {ref}}}}, \; {\bar{\mu }} = \frac{\mu }{\mu _{{\mathrm {ref}}}}, \; {\bar{v}} = \frac{v \mu _{{\mathrm {ref}}}}{L_{{\mathrm {ref}}} p_{{\mathrm {ref}}}}, \; \overline{\rho b} = \frac{\rho b L_{{\mathrm {ref}}}}{p_{{\mathrm {ref}}}}, \nonumber \\&{\bar{\beta }}_{\mathrm {F}} = \frac{\beta _{\mathrm {F}} L_{{\mathrm {ref}}} p_{{\mathrm {ref}}}}{\mu _{{\mathrm {ref}}}} \quad {\mathrm {and}} \quad {\bar{\beta }}_{\mathrm {B}} = \beta _{\mathrm {B}} p_{{\mathrm {ref}}} \end{aligned}$$

(5.3)

Then, the governing equations for the primal analysis can be written as follows:

$$\begin{aligned}&\frac{{\bar{\mu }}}{{\bar{k}}({\bar{x}})} {\bar{v}} + \frac{d {\bar{p}}}{d {\bar{x}}} = \overline{\rho b} = 0&\quad \forall {\bar{x}} \in (0, 1) \end{aligned}$$

(5.4a)

$$\begin{aligned}&\frac{d {\bar{v}}}{d {\bar{x}}} = 0&\quad \forall {\bar{x}} \in (0, 1) \end{aligned}$$

(5.4b)

$$\begin{aligned}&{\bar{p}}({\bar{x}} = 0) = 1 \end{aligned}$$

(5.4c)

$$\begin{aligned}&{\bar{p}}({\bar{x}} = 1) = 0 \end{aligned}$$

(5.4d)

In addition, the jump conditions at the material interface read:

$$\begin{aligned}&{\bar{v}}({\bar{x}} = {\bar{\xi }}^{-}) = {\bar{v}}({\bar{x}} = {\bar{\xi }}^{+}) \end{aligned}$$

(5.5a)

$$\begin{aligned}&{\bar{p}}({\bar{x}} = {\bar{\xi }}^{-}) = {\bar{p}}({\bar{x}} = {\bar{\xi }}^{+}) \end{aligned}$$

(5.5b)

where ${\bar{\xi }}^{\pm } = \xi ^{\pm } / L_{{\mathrm {ref}}}$. From hereon, we will drop the superposed overlines for convenience; all the quantities in the rest of this subsection should be considered as non-dimensional.

For convenience, we define:

$$\begin{aligned} \Upsilon _{\mathrm {1D}}(\xi ) := \frac{\xi }{k_1} + \frac{1 - \xi }{k_2} \end{aligned}$$

(5.6)

where $k_1$ and $k_2$ non-dimensional permeabilities of the two given materials (cf. Eqs. (5.1) and (5.3)$_2$). We will soon see that this quantity captures the variation of the total rate of dissipation with the design variable—the location of the material interface, and allows to express the analytical expressions in a compact form.

5.1.1 Primal Analysis Under the Barus Model

The balance of linear momentum (5.4a) for this case reads:

$$\begin{aligned}&\frac{1}{k} \exp [\beta _{\mathrm {B}} p] v + \frac{{\rm d}p}{{\rm d}x} = 0 \quad \forall x \in (0,1) \end{aligned}$$

(5.7)

The analytical solution for the velocity field is:

$$\begin{aligned} v(x)&= C = \frac{1}{\beta _{\mathrm {B}}} \left( 1 - \exp [-\beta _{\mathrm {B}}] \right) \Upsilon _{\mathrm {1D}}^{-1}(\xi ) \end{aligned}$$

(5.8)

The corresponding solution for the pressure field is:

$$\begin{aligned} p(x)&= \left\{ \begin{array}{ll} -\frac{1}{\beta _{\mathrm {B}}} \ln \left[ \frac{\beta _{\mathrm {B}} C x}{k_1} + \exp [-\beta _{\mathrm {B}}]\right] &{} \quad 0 \le x< \xi \\ \\ -\frac{1}{\beta _{\mathrm {B}}} \ln \left[ 1 - \frac{\beta _{\mathrm {B}} C (1 - x)}{k_2} \right] &{} \quad \xi < x \le 1 \end{array} \right. \end{aligned}$$

(5.9)

The corresponding total rate of dissipation is:

$$\begin{aligned} \Phi = \int _{0}^{1} \frac{\exp [\beta _{\mathrm {B}}p]}{k(x)} v^{2}(x) \mathrm {d} x = C = \frac{1}{\beta _{\mathrm {B}}} \left( 1 - \exp [-\beta _{\mathrm {B}}] \right) \Upsilon ^{-1}_{\mathrm {1D}}(\xi ) \end{aligned}$$

(5.10)

5.1.2 Primal Analysis Under the Darcy-Forchheimer Model

The governing equation for the balance of linear momentum for this case reads:

$$\begin{aligned} \frac{1}{k(x)}(1 + \beta _{\mathrm {F}}|v|) v + \frac{{\rm d}p}{{\rm d}x} = 0 \quad \forall x \in (0,1) \end{aligned}$$

(5.11)

There are two (mathematical) solutions for the velocity field of which one of them is unphysical. The physical solution for the velocity field is:

$$\begin{aligned} v(x) = C = \frac{\sqrt{1 + 4 \beta _{\mathrm {F}} \Upsilon _{\mathrm {1D}}^{-1}(\xi )} - 1}{2 \beta _{\mathrm {F}}} \end{aligned}$$

(5.12)

The corresponding pressure field is:

$$\begin{aligned} p(x) = \left\{ \begin{array}{ll} - \frac{1}{k_1} (1 + \beta _{\mathrm {F}} \, C) C x + 1 &{} \quad 0 \le x< \xi \\ \\ - \frac{1}{k_2} (1 + \beta _{\mathrm {F}} \, C) C (x - 1) &{} \quad \xi < x \le 1 \end{array} \right. \end{aligned}$$

(5.13)

Thus, the total rate of dissipation is:

$$\begin{aligned} \Phi (\xi ) = \int _{0}^{1} \left( \frac{1 + \beta _{\mathrm {F}} |v|}{k(x)}\right) v^{2}(x) \, \mathrm {d} x = C = \frac{\sqrt{1 + 4 \beta _{\mathrm {F}} \Upsilon _{\mathrm {1D}}^{-1}(\xi )} - 1}{2 \beta _{\mathrm {F}}} \end{aligned}$$

(5.14)

5.2 Velocity-Driven Problem

We take the following (velocity, length and viscosity) as the reference quantities for the non-dimensionalization:

$$\begin{aligned} v_{\mathrm {ref}} = v_{\mathrm {L}} \; [\mathrm {M}^{0} \mathrm {L}^{1} \mathrm {T}^{-1}], \quad L_{\mathrm {ref}} = L \; [\mathrm {M}^{0}\mathrm {L}^{1}\mathrm {T}^{0}] \quad {\mathrm {and}} \quad \mu _{\mathrm {ref}} = \mu _0 (1 + \beta _{\mathrm {B}} p_{\mathrm {R}}) \; [\mathrm {M}^{1} \mathrm {L}^{-1} \mathrm {T}^{-1}] \end{aligned}$$

(5.15)

where $v_{\mathrm {L}}$ is the prescribed velocity at the left end of the domain. Recall that $\beta _{\mathrm {B}} = 0$ for the Darcy and Darcy-Forchheimer models, and $\beta _{\mathrm {F}} = 0$ for the Darcy and Barus models. These reference quantities introduce the following reference pressure:

$$\begin{aligned} p_{{\mathrm {ref}}} = \frac{\mu _{{\mathrm {ref}}} v_{{\mathrm {ref}}}}{L_{{\mathrm {ref}}}} = \frac{\mu _0 (1 + \beta _{\mathrm {B}} p_{\mathrm {R}}) v_{\mathrm {L}}}{L} \end{aligned}$$

(5.16)

The corresponding non-dimensional quantities will be:

$$\begin{aligned} {\bar{v}} = \frac{v}{v_{{\mathrm {ref}}}}, \; {\bar{\beta }}_{\mathrm {F}} = \beta _{\mathrm {F}} v_{{\mathrm {ref}}} \quad {\mathrm {and}} \quad {\bar{\beta }}_{\mathrm {B}} = \frac{\beta _{\mathrm {B}} p_{{\mathrm {ref}}}}{1 + \beta _{\mathrm {B}} p_{\mathrm {R}}} = \frac{\beta _{\mathrm {B}} \mu _0 v_{\mathrm {L}}}{L} \end{aligned}$$

(5.17)

while the definitions for the rest of the quantities will be the same as before (i.e., Eq. (5.2)) but based on the new reference quantities defined above. The governing equations in non-dimensional form (without overlines) are:

$$\begin{aligned}&\frac{\mu }{k(x)} v + \frac{{\rm d} p}{{\rm d} x} = 0&\quad \forall x \in (0, 1) \end{aligned}$$

(5.18a)

$$\begin{aligned}&\frac{{\rm d} v}{{\rm d} x} = 0&\quad \forall x \in (0, 1) \end{aligned}$$

(5.18b)

$$\begin{aligned}&v(x = 0) = 1 \end{aligned}$$

(5.18c)

$$\begin{aligned}&p(x = 1) = 0 \end{aligned}$$

(5.18d)

5.2.1 Primal Analysis Under the Linearized Barus Model

We have considered the linearized Barus model as for velocity-driven problems primal solutions might not even exist under the (nonlinear) Barus model. This is the case with the above boundary value problem for some values of prescribed velocity at the inlet and prescribed pressure at the outlet. A thorough discussion of this issue is beyond the scope of this paper and will be dealt elsewhere.

The non-dimensional form of the balance of linear momentum reads:

$$\begin{aligned} \left( \frac{1 + \beta _{\mathrm {B}} p}{k(x)}\right) v + \frac{{\rm d}p}{{\rm d}x} = 0 \quad \forall x \in (0,1) \end{aligned}$$

(5.19)

The solution fields are:

$$\begin{aligned} v(x)&= 1 \end{aligned}$$

(5.20)

$$\begin{aligned} p(x)&= \left\{ \begin{array}{ll} \frac{1}{\beta _{\mathrm {B}}} \left( \exp [\beta _{\mathrm {B}} \Upsilon _{\mathrm {1D}}] \exp \left[ -\frac{x\beta _{\mathrm {B}}}{k_1}\right] - 1\right) &{} \quad 0 \le x< \xi \\ \\ \frac{1}{\beta _{\mathrm {B}}} \left( \exp \left[ \frac{\beta _{\mathrm {B}}}{k_2}(1 - x)\right] - 1\right) &{} \quad \xi < x \le 1 \end{array} \right. \end{aligned}$$

(5.21)

The total rate of dissipation is:

$$\begin{aligned} \Phi (\xi ) = \frac{1}{\beta _{\mathrm {B}}} \left( \exp [\beta _{\mathrm {B}} \Upsilon _{\mathrm {1D}}(\xi )] - 1\right) \end{aligned}$$

(5.22)

5.2.2 Primal Analysis Under the Darcy-Forchheimer Model

The governing equation for the balance of linear momentum will be the same as given in Eq. (5.11). The solution fields are:

$$\begin{aligned} v(x)&= 1 \end{aligned}$$

(5.23)

$$\begin{aligned} p(x)&= \left\{ \begin{array}{ll} (1 + \beta _{\mathrm {F}}) \Upsilon _{\mathrm {1D}} -\left( \frac{1 + \beta _{\mathrm {F}}}{k_1}\right) x &{} \quad 0 \le x< \xi \\ \\ \left( \frac{1 + \beta _{\mathrm {F}}}{k_2}\right) (1 - x) &{} \quad \xi < x \le 1 \end{array} \right. \end{aligned}$$

(5.24)

The total rate of dissipation is:

$$\begin{aligned} \Phi (\xi ) = (1 + \beta _{\mathrm {F}}) \Upsilon _{\mathrm {1D}}(\xi ) \end{aligned}$$

(5.25)

5.3 Optimal Material Layout

In the above solutions, $\Phi \propto \Upsilon _{\mathrm {1D}}^{-1}(\xi )$ for pressure-driven problems and $\Phi \propto \Upsilon _{\mathrm {1D}}(\xi )$ for velocity-driven problems. Noting the total rate of dissipation is maximized for pressure-driven problem, while it is minimized for velocity-driven; both these cases lead to the minimization of $\Upsilon _{\mathrm {1D}}(\xi )$ with respect to $\xi$ satisfying the volumetric bound constraint on the high-permeability material.

Under the single interface assumption, given two materials with permeabilities $k_{H} > k_L$, the design problem reduces to checking which of the two cases—placing the high-permeability material at the inflow or at the outflow—renders minimum $\Upsilon _{\mathrm {1D}}$. It so happens that in 1D, given the mathematical structure of $\Upsilon _{\mathrm {1D}}(\xi )$, high-permeability material can be placed either at the inflow or outflow as long as the volumetric constraint bound is met. In fact, it can be shown by considering multiple material interfaces that the high-permeability can be placed anywhere within the domain (need not be contiguous), as long as it takes up the whole volume constraint; however, this is not true in higher dimensions. Moreover, the optimal material layout is the same in all the models considered (i.e., Darcy model and its nonlinear generalizations).

6 Optimal Layouts for a 2D Axisymmetric Problem

Consider a two-dimensional domain comprising two concentric circles with an inner radius $r_i$ and an outer radius $r_o > r_i$. A pressure $p_i$ is applied on the inner boundary, and the outer boundary is subject to a pressure $p_o < p_i$; see Fig. 3. We will obtain the optimal material distribution in the domain under the Darcy model with two materials of different permeabilities: $k_1$ and $k_2$. A volume constraint, denoted by $\gamma$, is placed on the high-permeability material. We will take the maximization of rate of dissipation as the objective function.

Fig. 3

A pictorial description of the boundary value problem. The inner boundary is subject to a pressure $p = p_i$, and the outer boundary is subject to pressure $p = p_o$

6.1 Analytical Solution for the Optimal Design

In deriving the analytical solution, we assume that each material is present in a contiguous and symmetric manner, and a single boundary exists between the two materials over the entire domain (cf. material interface shown in Fig. 3). However, such material layout might not furnish us with the optimal solution. But we will show later that numerical simulations confirm the validity of our assumption.

We will use cylindrical polar coordinates to take the advantage of axisymmetry. Then, the assumption of a single material interface allows us to write the spatial dependence of the permeability as follows:

$$\begin{aligned} k(r) = \left\{ \begin{array}{ll} k_1 &{} r_i< r< \xi \\ k_2 &{} \xi< r < r_o \end{array} \right. \end{aligned}$$

(6.1)

The governing equations corresponding to the primal analysis take the following form:

$$\begin{aligned}&\frac{\mu }{k(r)} v_r + \frac{{\rm d} p}{{\rm d} r} = 0&\quad {\mathrm {in}} \; (r_i, r_o) \end{aligned}$$

(6.2a)

$$\begin{aligned}&\frac{1}{r} \frac{{\rm d} (r v_r)}{{\rm d} r} = 0&\quad {\mathrm {in}} \; (r_i,r_o) \end{aligned}$$

(6.2b)

$$\begin{aligned}&p(r = r_i) = p_i \end{aligned}$$

(6.2c)

$$\begin{aligned}&p(r = r_o) = p_o \end{aligned}$$

(6.2d)

where $v_r(r)$ denotes the radial component of the velocity. In addition, the jump conditions at the material interface take the following form:

$$\begin{aligned}&p(r = \xi ^{-}) = p(r = \xi ^{+}) \end{aligned}$$

(6.3a)

$$\begin{aligned}&v_{r}(r = \xi ^{-}) = v_r(r = \xi ^{+}) \end{aligned}$$

(6.3b)

where $\xi ^{\pm }$ denotes the one-sided limits.

Equations (6.2b) and (6.3b) imply:

$$\begin{aligned} v_r(r) = \frac{C}{r} \end{aligned}$$

(6.4)

where C is a constant that needs to be determined. However, it is imperative to note that C depends on the permeabilities. Using Eq. (6.2a), the solution for the pressure field takes the following form:

$$\begin{aligned} p(r) = \left\{ \begin{array}{ll} \frac{C \mu }{k_1} \ln (r) + C_1 &{} \quad r_i \le r< \xi \\ \\ \frac{C \mu }{k_2} \ln (r) + C_2 &{} \quad \xi < r \le r_o \end{array}\right. \end{aligned}$$

(6.5)

where $C_1$ and $C_2$ are constants. The boundary conditions (6.2c)–(6.2d) will furnish these constants, resulting in the following expression for the pressure field:

$$\begin{aligned} p(r) = \left\{ \begin{array}{ll} p_i + \frac{C \mu }{k_1} \ln (r/r_i) &{} \quad r_i \le r< \xi \\ \\ p_o + \frac{C \mu }{k_2} \ln (r/r_o) &{} \quad \xi < r \le r_o \end{array}\right. \end{aligned}$$

(6.6)

The jump condition for the pressure (6.3a) implies:

$$\begin{aligned} C = \frac{1}{\mu } (p_o - p_i) \Upsilon _{\mathrm {2D}}^{-1}(\xi ) \end{aligned}$$

(6.7)

where $\Upsilon _{\mathrm {2D}}(\xi )$, introduced for convenience, is defined as follows:

$$\begin{aligned} \Upsilon _{\mathrm {2D}}(\xi ) := \frac{1}{k_1} \ln \left( \frac{\xi }{r_i} \right) + \frac{1}{k_2} \ln \left( \frac{r_o}{\xi }\right) \end{aligned}$$

(6.8)

Based on the above solution, the total rate of dissipation takes the following form:

$$\begin{aligned} \Phi (\xi ) = \int _{r_i}^{r_o} \frac{\mu }{k} \left( v_r\right) ^2 (2 \pi r) dr&= 2 \pi \mu C^2 \left( \frac{1}{k_1} \int _{r_i}^{\xi ^{-}} \frac{1}{r} dr + \frac{1}{k_2} \int _{\xi ^{+}}^{r_o} \frac{1}{r} dr \right) = \frac{2 \pi (p_o - p_i)^2}{\mu } \Upsilon _{\mathrm {2D}}^{-1}(\xi ) \end{aligned}$$

(6.9)

Noting that $p_i$, $p_o$ and $\mu > 0$ are given constants and are independent of the design variable $\xi$. Thus, maximizing $\Phi (\xi )$ is equivalent to minimizing $\Upsilon _{\mathrm {2D}}(\xi )$. That is,

$$\begin{aligned} {\widehat{\xi }}_{\mathrm {2D}} \leftarrow \mathop {\mathrm {argmax}}_{\xi } \; \Phi (\xi ) \equiv \mathop {\mathrm {argmin}}_{\xi } \; \Upsilon _{\mathrm {2D}}(\xi ) \end{aligned}$$

(6.10)

where ${\widehat{\xi }}_{\mathrm {2D}}$ is the optimum location of the material interface. For further analysis, we will denote $k_L$ and $k_H$ to denote, respectively, the low and high permeabilities, and consider the following two cases.

6.1.1 High-Permeability Material Near the Inner Circle

Under this case, $k_1 = k_H$ and $k_2 = k_L$. By substituting these values into Eq. (6.8), we define the corresponding $\Upsilon _{\mathrm {2D}}(\xi )$ as:

$$\begin{aligned} \Upsilon ^{(1)}_{\mathrm {2D}}(\xi ) := \frac{1}{k_H} \ln \left( \frac{\xi }{r_i} \right) + \frac{1}{k_L} \ln \left( \frac{r_o}{\xi }\right) = \frac{1}{k_L} \ln (r_o) - \frac{1}{k_H} \ln (r_i) + \left( \frac{1}{k_H} - \frac{1}{k_L} \right) \ln (\xi ) \end{aligned}$$

(6.11)

Since $k_H \ge k_L$, we note that $\Upsilon _{\mathrm {2D}}(\xi )$ decreases with an increase in $\xi$. The volumetric constraint takes the following form:

$$\begin{aligned} \frac{2 \pi (\xi ^2 - r_i^2)}{2 \pi (r_o^2 - r_i^2)} \le \gamma \end{aligned}$$

(6.12)

which implies that

$$\begin{aligned} \xi ^2 \le (1 - \gamma ) r_i^2 + \gamma r_o^2 \end{aligned}$$

(6.13)

The above inequality implies that the minimum of $\Upsilon ^{(1)}_{\mathrm {2D}}(\xi )$ occurs at

$$\begin{aligned}&{\widehat{\xi }}^{(1)}_{\mathrm {2D}} := \sqrt{(1 - \gamma ) r_{i}^2 + \gamma r_o^2} \end{aligned}$$

(6.14)

We will denote this minimum as follows:

$$\begin{aligned} \Upsilon _{\mathrm {2D,min}}^{(1)} := \Upsilon ^{(1)}_{\mathrm {2D}}\left( {\widehat{\xi }}^{(1)}_{\mathrm {2D}}\right) = \frac{1}{k_L} \ln (r_o) - \frac{1}{k_H} \ln (r_i) + \left( \frac{1}{k_H} - \frac{1}{k_L}\right) \ln \left( {\widehat{\xi }}^{(1)}_{\mathrm {2D}}\right) \end{aligned}$$

(6.15)

The corresponding maximum rate of dissipation will be:

$$\begin{aligned} \Phi ^{(1)}_{\mathrm {max}} = \frac{2 \pi (p_o - p_i)^2}{\mu } \left( \Upsilon ^{(1)}_{\mathrm {2D,min}}\right) ^{-1} \end{aligned}$$

(6.16)

6.1.2 High-Permeability Material Near the Outer Circle

Under this case, $k_1 = k_L$ and $k_2 = k_H$. For this case, we define

$$\begin{aligned} \Upsilon ^{(2)}_{\mathrm {2D}}(\xi ) := \frac{1}{k_L} \ln \left( \frac{\xi }{r_i} \right) + \frac{1}{k_H} \ln \left( \frac{r_o}{\xi }\right) = \frac{1}{k_H} \ln (r_o) - \frac{1}{k_L} \ln (r_i) + \left( \frac{1}{k_L} - \frac{1}{k_H} \right) \ln (\xi ) \end{aligned}$$

(6.17)

and note that $\Upsilon ^{(2)}_{\mathrm {2D}}(\xi )$ decreases with a decrease in $\xi$. The volumetric constraint for the second case takes the following form:

$$\begin{aligned} \gamma r_i^2 + (1 - \gamma ) r_o^2 \le \xi ^2 \end{aligned}$$

(6.18)

The above inequality implies that the maximum of $\Upsilon ^{(2)}_{\mathrm {2D}}(\xi )$ occurs at

$$\begin{aligned}&{\widehat{\xi }}^{(2)}_{\mathrm {2D}} := \sqrt{\gamma r_{i}^2 + (1 - \gamma ) r_o^2} \end{aligned}$$

(6.19)

We will denote this minimum by

$$\begin{aligned} \Upsilon _{\mathrm {2D,min}}^{(2)} := \Upsilon ^{(2)}_{\mathrm {2D}}\left( {\widehat{\xi }}_{\mathrm {2D}}^{(2)}\right) = \frac{1}{k_H} \ln (r_o) - \frac{1}{k_L} \ln (r_i) + \left( \frac{1}{k_L} - \frac{1}{k_H}\right) \ln \left( {\widehat{\xi }}^{(2)}_{\mathrm {2D}}\right) \end{aligned}$$

(6.20)

The corresponding maximum rate of dissipation will be:

$$\begin{aligned} \Phi ^{(2)}_{\mathrm {max}} = \frac{2 \pi (p_o - p_i)^2}{\mu } \left( \Upsilon ^{(2)}_{\mathrm {2D,min}}\right) ^{-1} \end{aligned}$$

(6.21)

Proposition 6.1

For any volumetric constraint $0 \le \gamma \le 1$, $\Upsilon _{\mathrm {2D,min}}^{(1)} \le \Upsilon _{\mathrm {2D,min}}^{(2)}$.

Proof

We start by considering the following difference:

$$\begin{aligned} \Upsilon _{\mathrm {2D,min}}^{(2)} - \Upsilon _{\mathrm {2D,min}}^{(1)}&= \left( \frac{1}{k_L} - \frac{1}{k_H} \right) \ln \left( {\widehat{\xi }}^{(1)}_{\mathrm {2D}} \, {\widehat{\xi }}^{(2)}_{\mathrm {2D}}\right) + \left( \frac{1}{k_H} - \frac{1}{k_L}\right) \ln (r_i r_o) \nonumber \\&= \left( \frac{1}{k_L} - \frac{1}{k_H} \right) \ln \left( \frac{{\widehat{\xi }}^{(1)}_{\mathrm {2D}} \, {\widehat{\xi }}^{(2)}_{\mathrm {2D}}}{r_i r_o}\right) \end{aligned}$$

(6.22)

Since $k_H \ge k_L$, we have $\left( \frac{1}{k_L} - \frac{1}{k_H} \right) \ge 0$. Ergo, the task at hand is to show ${\widehat{\xi }}^{(1)}_{\mathrm {2D}} \, {\widehat{\xi }}^{(2)}_{\mathrm {2D}} \ge r_i r_o$ so that $\ln \left( {\widehat{\xi }}^{(1)}_{\mathrm {2D}} \, {\widehat{\xi }}^{(2)}_{\mathrm {2D}} / (r_i r_o)\right) \ge 0$.

Noting Eqs. (6.14) and (6.19), we now proceed as follows:

$$\begin{aligned} \frac{{\widehat{\xi }}^{(1)}_{\mathrm {2D}} \, {\widehat{\xi }}^{(2)}_{\mathrm {2D}}}{r_i r_o}&= \frac{1}{r_i r_o} \sqrt{ \left( (1- \gamma ) r_i^2 + \gamma r_o^2\right) \left( (1- \gamma ) r_o^2 + \gamma r_i^2 \right) } \nonumber \\&= \sqrt{ \gamma (1- \gamma ) \left( \left( \frac{r_i}{r_o}\right) ^2 + \left( \frac{r_o}{r_i}\right) ^2 \right) + (1 - \gamma )^2 + \gamma ^2 } \end{aligned}$$

(6.23)

The arithmetic-geometric mean inequality implies:

$$\begin{aligned} \left( \frac{r_i}{r_o}\right) ^2 + \left( \frac{r_o}{r_i}\right) ^2 \ge 2 \end{aligned}$$

(6.24)

Furthermore, noting that $0 \le \gamma \le 1$ (which implies $\gamma (1 - \gamma ) \ge 0$), Eq. (6.23) will give rise to the following inequality:

$$\begin{aligned} \frac{{\widehat{\xi }}^{(1)}_{\mathrm {2D}} \, {\widehat{\xi }}^{(2)}_{\mathrm {2D}}}{r_i r_o} \ge \sqrt{ 2 \gamma (1- \gamma ) + (1 - \gamma )^2 + \gamma ^2 } \equiv 1 \end{aligned}$$

(6.25)

which completes the proof. $\square$

On the account of Eq. (6.10), the above proposition implies that $\Phi _{\max }^{(1)} \ge \Phi _{\max }^{(2)}$. Hence, we have shown that the optimal layout of the material for pressure-driven problem with cylindrical symmetry is to place the high permeability material near the inner boundary. The optimal location of the material interface is

$$\begin{aligned} {\widehat{\xi }}_{\mathrm {2D}} = {\widehat{\xi }}^{(1)}_{\mathrm {2D}} = \sqrt{(1 - \gamma ) r_{i}^2 + \gamma r_o^2} \end{aligned}$$

(6.26)

6.2 Velocity-Driven

We now analyze the same two-dimensional domain comprising two concentric circles but with the following velocity boundary condition on the inner boundary:

$$\begin{aligned}&v_r(r = r_i) = v_o \end{aligned}$$

(6.27)

The governing equations will remain as that of the pressure-driven problem expect for Eq. (6.2c) is replaced with the above boundary condition. The jump conditions at the material interface (i.e., Eqs. (6.3a) and (6.3b)) remain the same. Equation (6.4) along with the boundary condition (6.27) and the velocity jump condition (6.3a) implies:

$$\begin{aligned} v_r(r) = v_o \, \frac{r_i}{r} \end{aligned}$$

(6.28)

The total rate of dissipation is:

$$\begin{aligned} \Phi (\xi ) = \int _{r_i}^{r_o} \frac{\mu }{k} \left( v_r\right) ^2 (2 \pi r) dr&= 2 \pi \mu v_o^2 r_i^2 \left( \frac{1}{k_1} \int _{r_i}^{\xi ^{-}} \frac{1}{r} dr + \frac{1}{k_2} \int _{\xi ^{+}}^{r_o} \frac{1}{r} dr\right) = 2 \pi \mu v_o^2 r_i^2 \Upsilon _{\mathrm {2D}}(\xi ) \end{aligned}$$

(6.29)

For velocity-driven problems, the design problem is posed as the minimization of the rate of dissipation with a volume constraint bound on the high-permeability material. Since $\Phi (\xi ) \propto \Upsilon _{\mathrm {2D}}(\xi )$, the minimization of $\Phi (\xi )$ is equivalent to the minimization of $\Upsilon _{\mathrm {2D}}(\xi )$. Recall that we have minimized $\Upsilon _{\mathrm {2D}}(\xi )$ even for the pressure-driven problem. (However, in the case of the pressure-driven problem, $\Phi (\xi ) \propto \Upsilon ^{-1}_{\mathrm {2D}}(\xi )$ and we maximized $\Phi (\xi )$.) Thus, the optimal material distribution for the velocity-driven problem will be the same as that of the pressure-driven problem—the high-permeability material should be placed near the inner boundary. The location of the material interface will be the same as for the pressure-driven problem (see Eq. (6.26)).

6.3 Numerical Results

Fig. 4

This figure shows the material distribution under the Darcy model, obtained by solving both the ingredients of the design problem—the primal problem and the optimization procedure—numerically. The numerical scheme for the primal analysis did not enforce radial symmetry explicitly. That is, the primal analysis is a two-dimensional finite element analysis using triangular elements rather than axisymmetric finite elements

Fig. 5

This figure shows the material distribution under the Barus model, obtained by solving both the ingredients of the design problem—the primal problem and the optimization procedure—numerically. The numerical scheme for the primal analysis did not enforce radial symmetry explicitly. That is, the primal analysis is a two-dimensional finite element analysis using triangular elements rather than axisymmetric finite elements

Numerical solutions are obtained for the above design problem; both the primal analysis and the optimization procedure are solved numerically. Table 1 provides the parameters used in the numerical simulation. Since the selection and accuracy of numerical schemes for primal analysis can affect the final design outcome, we compare the designs under two different approaches for the primal analysis. The first approach is a two-dimensional finite element analysis using triangular elements; the underlying radial symmetry is not built into the analysis. The second approach uses axisymmetric finite elements; hence, the radial symmetry is invoked in the primal analysis.

Table 1 Parameters used in the numerical simulation of the 2D axisymmetric problem—concentric cylinders

As shown in Figs. 4 and 5, TopOpt without invoking symmetry yields a material distribution in the form of dendrites or fingers. Despite using regularization (e.g., SIMP) and high-order discretizations, these finger-type design patterns are observed. However, using axisymmetric analysis, we could obtain a discrete 0–1 material distribution with high-permeability material being placed perfectly concentric and near to the inner circle; see Fig. 6.

Fig. 6

This figure shows the optimal material distributions for $\gamma$ = 0.3 under the Darcy and Barus models. The primal analysis invoked axisymmetry; that is, axisymmetric finite elements are employed

Fig. 7

Pressure distribution for $\gamma$ = 0.3 under different models corresponding to the material layout given in Fig. 6

Fig. 8

Graph of pressure versus the radius for $\gamma$ = 0.3 under different models corresponding to the material layout given in Fig. 6

Several reasons suggest that the dendrite-type solution is a numerical artifact, and hence, unphysical:

• (a) Since the boundary conditions and the geometry are all symmetric, the optimal material layout from the numerical simulation should respect the underlying symmetry. But the dendrite-type solution does not respect the radial symmetry.

• (b) This numerical solution did not match with the analytical solution, which is derived with reasonable assumptions.

• (c) The optimization procedure took over 350 iterations for the dendrite-type solution, while it took less than 25 iterations for the symmetric solution reported in Fig. 6.

• (d) Lastly, such designs with sharp irregular features, even if provided by TopOpt, are often treated as impractical designs and are rejected based on manufacturability; these designs are challenging to fabricate—even with additive manufacturing techniques.

The possibility of finger-type solutions or checkered board patterns under topology optimization is adequately discussed in the literature; for example, see (Bruns 2007; Bendsoe and Sigmund 2013). Herein, we have shown that such pathological numerical designs for an axisymmetric problem could arise if one does not explicitly enforce the underlying symmetry—by not using axisymmetric finite elements. The other main findings of this section are:

• (i) The numerical solution using axisymmetric finite elements matches the analytical solution, thereby justifying the single material interface assumption used in the analytical solution.

• (ii) Under an optimal solution for a 2D axisymmetric problem, the high-permeability material should be placed near the inner boundary. This material distribution in this problem is different from that of the 1D problem, where high-permeability material can be placed anywhere.

• (iii) The nonlinearity under the Darcy-Barus model does not seem to affect the optimal material distribution for the chosen problem; however, the pressure distribution within the domain under the Darcy and Darcy-Barus models vastly differs, as shown in Figs. 7 and 8. Although the inlet and outlet pressures remain the same, the internal pressure within the domain evaluated using the Darcy-Barus model is lower than the corresponding pressure under the Darcy model.

7 Optimal Layouts for a 3D Axisymmetric Problem

Consider a three-dimensional domain comprising two concentric spheres with an inner radius $r_i$ and an outer radius $r_o > r_i$. A pressure $p_i$ is applied on the inner boundary, and the outer boundary is subject to a pressure $p_o < p_i$. The design question is: Given two materials with permeabilities $k_1$ and $k_2$, what is the optimal material distribution of these two materials in the domain. The optimality is judged based on the maximization of the rate of dissipation with a volume constraint bound on the high-permeability material. We will first present the governing equations for the primal analysis. Next, we will obtain an analytical solution for the design problem. Finally, we will obtain numerical optimal solutions using TopOpt and compare them with the analytical solution.

7.1 Primal Analysis

For mathematical convenience, we will use the spherical polar coordinates:

$$\begin{aligned} r_i \le r \le r_o, \quad 0 \le \theta \le \pi , \quad 0 \le \phi \le 2\pi \end{aligned}$$

(7.1)

where r is the radial distance from the center, and $\theta$ and $\phi$ are the azimuth and polar angles, respectively. We assume that the body force is zero: ${\mathbf {b}}({\mathbf {x}}) = {\mathbf {0}}$. The permeability is assumed to vary only in the radial direction. That is,

$$\begin{aligned} k({\mathbf {x}}) = k(r) \end{aligned}$$

(7.2)

Noting the inherent symmetry in the problem, the velocity and pressure fields can be written as follows:

$$\begin{aligned} {\mathbf {v}}({\mathbf {x}}) = v_{r}(r) \, \hat{{\mathbf {e}}}_{r} \quad {\mathrm {and}} \quad p({\mathbf {x}}) = p(r) \end{aligned}$$

(7.3)

where $v_{r}$ is radial component of the velocity, and $\hat{{\mathbf {e}}}_r$ is the unit vector along the radial direction. The Darcy model is used to describe the flow.

7.1.1 Non-Dimensionalization

We take the following (pressure, length and viscosity) as reference quantities:

$$\begin{aligned} p_{\mathrm {ref}} = p_i - p_o \; [\mathrm {M}^{1} \mathrm {L}^{-1} \mathrm {T}^{-2}], \quad L_{\mathrm {ref}} = r_o \; [\mathrm {M}^{0}\mathrm {L}^{1}\mathrm {T}^{0}] \quad {\mathrm {and}} \quad \mu _{\mathrm {ref}} = \mu \; [\mathrm {M}^{1} \mathrm {L}^{-1} \mathrm {T}^{-1}] \end{aligned}$$

(7.4)

These references quantities give rise to the following non-dimensional quantities:

$$\begin{aligned} {\bar{r}} = \frac{r}{r_o}, {\bar{r}}_i = \frac{r_i}{r_o}, {\bar{r}}_o = 1, \; {\bar{k}} = \frac{k}{r^2_o}, \; {\bar{p}} = \frac{p - p_o}{p_i - p_o}, \; {\bar{p}}_i = 1, \; {\bar{p}}_o = 0, \; {\bar{\mu }} = 1, \; {\bar{v}}_{r} = \frac{v_{r} \mu }{r_o (p_i - p_o)} \end{aligned}$$

(7.5)

The governing equations, in non-dimensional form, for the primal analysis can be written as follows:

$$\begin{aligned}&\frac{1}{{\bar{k}}({\bar{r}})} {\bar{v}}_r + \frac{{\rm d} {\bar{p}}}{{\rm d} {\bar{r}}} = 0&\quad \forall {\bar{r}} \in ({\bar{r}}_i, 1) \end{aligned}$$

(7.6a)

$$\begin{aligned}&\frac{1}{{\bar{r}}^2} \frac{{\rm d} ({\bar{r}}^2 {\bar{v}}_r)}{{\rm d} {\bar{r}}} = 0&\quad \forall {\bar{r}} \in ({\bar{r}}_i, 1) \end{aligned}$$

(7.6b)

$$\begin{aligned}&{\bar{p}}({\bar{r}} = {\bar{r}}_i) = 1 \end{aligned}$$

(7.6c)

$$\begin{aligned}&{\bar{p}}({\bar{r}} = 1) = 0 \end{aligned}$$

(7.6d)

From hereon, we will drop the superposed overlines for convenience; all the quantities in the rest of this section should be considered as non-dimensional.

7.2 Analytical Solution for the Design Problem

We make the same assumption as we made for the 2D axisymmetric problem (Sect. 6): each material is present in a contiguous and symmetric manner, and a single boundary exists between the two materials over the entire domain. This assumption allows us to write the spatial dependence of the permeability as follows:

$$\begin{aligned} k(r) = \left\{ \begin{array}{ll} k_1 &{} r_i< r< \xi \\ k_2 &{} \xi< r < 1 \end{array} \right. \end{aligned}$$

(7.7)

where $r = \xi$ is the location of the material interface. The jump conditions along the interface take the following form:

$$\begin{aligned}&v_r(r = \xi ^{-}) = v_r(r = \xi ^{+}) \end{aligned}$$

(7.8a)

$$\begin{aligned}&p(r = \xi ^{-}) = p(r = \xi ^{+}) \end{aligned}$$

(7.8b)

Using Eqs. (7.6b) and (7.8a) and noting that r $\ne 0$, the velocity field can be written as follows:

$$\begin{aligned} v(r) = \frac{A}{r^2} \end{aligned}$$

(7.9)

where A is a constant to be determined. Using Eqs. (7.9) and (7.6a), the solution for the pressure field is:

$$\begin{aligned} p(r) = \left\{ \begin{array}{cc} \frac{1}{k_1 r} A + B_1 &{} \\ \\ \frac{1}{k_2 r} A + B_2 &{} \end{array} \right. \end{aligned}$$

(7.10)

where $B_1$ and $B_2$ are constants. The pressure boundary conditions (7.6c) and (7.6d) and the jump condition (7.8b) will establish:

$$\begin{aligned} A = \left[ \frac{1}{k_1 r_i} - \frac{1}{k_2} + \frac{1}{\xi } \left( \frac{1}{k_2} - \frac{1}{k_1} \right) \right] ^{-1}, \quad B_1 = 1 - \frac{A}{k_1 r_i} \quad {\mathrm {and}} \quad B_2 = -\frac{A}{k_2} \end{aligned}$$

(7.11)

Thus, the final expression for the velocity field is:

$$\begin{aligned} v_r(r) = \Upsilon _{\mathrm {3D}}(\xi ) \frac{1}{r^2} = \left[ \frac{1}{k_1 r_i} - \frac{1}{k_2} + \frac{1}{\xi } \left( \frac{1}{k_2} - \frac{1}{k_1} \right) \right] ^{-1} \frac{1}{r^2} \end{aligned}$$

(7.12)

Consequently, the total rate of dissipation takes the following form:

$$\begin{aligned} \Phi (\xi ) = \int _{r_i}^{1} \frac{4\pi r^2}{k(r)} \; v_r^2 \; dr&= 4 \pi A^2 \left( \int _{r_i}^{\xi } \frac{1}{k_1} \, \frac{1}{r^2} \; dr + \int _{\xi }^{1} \frac{1}{k_2} \, \frac{1}{r^2} \; dr \right) = 4 \pi \Upsilon _{\mathrm {3D}}(\xi ) \end{aligned}$$

(7.13)

Under the single material interface, the design problem—maximizing the rate of dissipation with a volume constraint bound on the high-permeability material—reduces to answering the following question:

Which of the two cases—placing the high-permeability material near the inner boundary or near the outer boundary—gives the higher rate of dissipation?

To answer this question, we will now explore these two cases separately. For further analysis, we will denote the high and low permeabilities by $k_H$ and $k_L$, respectively, with $k_L \le k_H$. We denote the optimal location of the material interface by ${\widehat{\xi }}$.

Case 1 High-permeability material near the inner boundary. Under this case, $k_1 = k_H$ and $k_2 = k_L$. The corresponding rate of dissipation is:

$$\begin{aligned} \Phi ^{(1)} = 4 \pi \left[ \frac{1}{k_H r_i} - \frac{1}{k_L} + \frac{1}{\xi } \left( \frac{1}{k_L} - \frac{1}{k_H} \right) \right] ^{-1} \end{aligned}$$

(7.14)

The volumetric constraint takes the following form:

$$\begin{aligned} \frac{4 \pi }{3} (\xi ^3 - r_i^3) \; \le \; \gamma \frac{4 \pi }{3} (1 - r_i^3) \end{aligned}$$

(7.15)

which implies that

$$\begin{aligned} \xi ^3 \le \gamma + (1 - \gamma ) r_i^3 \end{aligned}$$

(7.16)

(Recall that $\gamma$ is the bound in the volume constraint for the high-permeability material.) Since $k_{L} \le k_{H}$, $\Phi ^{(1)}$ increases monotonically with $\xi$. Thus, for this case, the maximum rate of dissipation occurs for

$$\begin{aligned} {\widehat{\xi }} = {\widehat{\xi }}_{\mathrm {3D}}^{(1)} := \root 3 \of { \gamma + (1 - \gamma ) r_i^3} \end{aligned}$$

(7.17)

with the corresponding value:

$$\begin{aligned} \Phi ^{(1)}_{\mathrm {max}} = 4 \pi \left[ \frac{1}{k_H r_i} - \frac{1}{k_L} + \frac{1}{{\widehat{\xi }}^{(1)}_{\mathrm {3D}}} \left( \frac{1}{k_L} - \frac{1}{k_H} \right) \right] ^{-1} \end{aligned}$$

(7.18)

Case 2: High-permeability material near the outer boundary. Under this case, $k_1 = k_L$ and $k_2 = k_H$. The corresponding rate of dissipation is:

$$\begin{aligned} \Phi ^{(2)} = 4 \pi \left[ \frac{1}{k_L r_i} - \frac{1}{k_H} + \frac{1}{\xi } \left( \frac{1}{k_H} - \frac{1}{k_L} \right) \right] ^{-1} \end{aligned}$$

(7.19)

The volumetric constraint takes the following form:

$$\begin{aligned} \frac{4 \pi }{3} (r_o^3 - \xi ^3) \; \le \; \gamma \frac{4 \pi }{3} (1 - r_i^3) \end{aligned}$$

(7.20)

which implies that

$$\begin{aligned} (1 - \gamma ) + \gamma r_i^3 \le \xi ^3 \end{aligned}$$

(7.21)

Using that $k_L \le k_H$, we conclude that $\Phi ^{(2)}$ decreases monotonically with $\xi$. Thus, the maximum rate of dissipation occurs for

$$\begin{aligned} {\widehat{\xi }} = {\widehat{\xi }}_{\mathrm {3D}}^{(2)} := \root 3 \of {(1 - \gamma ) + \gamma r_i^3} \end{aligned}$$

(7.22)

with the corresponding value:

$$\begin{aligned} \Phi ^{(2)}_{\mathrm {max}} = 4 \pi \left[ \frac{1}{k_L r_i} - \frac{1}{k_H} + \frac{1}{{\widehat{\xi }}^{(2)}_{\mathrm {3D}}} \left( \frac{1}{k_H} - \frac{1}{k_L} \right) \right] ^{-1} \end{aligned}$$

(7.23)

To answer the question of which of these two cases furnishes the optimal solution, we will use Eqs. (7.18) and (7.23) and consider the following difference:

$$\begin{aligned} \frac{1}{\Phi ^{(1)}_{\mathrm {max}}} - \frac{1}{\Phi ^{(2)}_{\mathrm {max}}}&= - \frac{1}{4 \pi } \left( \frac{1}{k_L} - \frac{1}{k_H}\right) \left( 1 + \frac{1}{r_i} - \left( \frac{1}{{\widehat{\xi }}_{\mathrm {3D}}^{(1)}} + \frac{1}{{\widehat{\xi }}_{\mathrm {3D}}^{(2)}} \right) \right) \end{aligned}$$

(7.24)

Since $k_H \ge k_L$, Lemma A.1 implies that

$$\begin{aligned} \frac{1}{\Phi ^{(1)}_{\mathrm {max}}} - \frac{1}{\Phi ^{(2)}_{\mathrm {max}}} \le 0 \end{aligned}$$

(7.25)

This father implies that

$$\begin{aligned} \Phi ^{(1)}_{\mathrm {max}} \ge \Phi ^{(2)}_{\mathrm {max}} \quad \forall \gamma \in [0,1] \end{aligned}$$

(7.26)

Thus, the optimal solution is the placement of high permeability material near the inner boundary satisfying the volume constraint, while the rest of the domain is occupied by the low permeability material. For a given volume constraint bound $\gamma$, the optimal location of the material interface is

$$\begin{aligned} {\widehat{\xi }}_{\mathrm {3D}} = {\widehat{\xi }}_{\mathrm {3D}}^{(1)} = \root 3 \of {\gamma + (1 - \gamma )r_i^3} \end{aligned}$$

(7.27)

7.3 Numerical Designs Using TopOpt

To validate the single material interface assumption, we obtained a numerical solution for the design problem. Again, the primal analysis as well as the optimization procedure is solved numerically. We enforced the underlying radial symmetry into the primal analysis by using two-dimensional triangular axisymmetric finite elements. Figure 9 shows the numerical optimal material layouts from TopOpt using the input parameters given in Table 2. Similar to the 2D axisymmetric analysis (Sect. 6) and in agreement with the analytical solution, the high-permeability material (represented by ‘red’) is placed near the inner boundary, while the low-permeability material (represented by ‘blue’) is placed near the outer boundary. This numerical solution also justifies the use of the single interface assumption in obtaining the analytical solution.

Table 2 Parameters used in the numerical simulation of the 3D axisymmetric problem—concentric spheres

Fig. 9

The top figure shows the material layout obtained using TopOpt for the 3D axisymmetric problem under the Darcy model. The bottom figure shows the corresponding pressure distribution in the domain

8 Effect of Pressure-Dependent Viscosity on Optimal Layouts

The aim of this section is to compare optimal solutions under the Darcy and linearized Barus models. Specifically, we study how $\beta _B$ and aspect ratio of the domain affect the optimal material layouts and the resulting velocity and pressure profiles. To see significant differences, we will allow for non-zero volumetric source. Then, the continuity Eq. (2.1b) should be altered as follows:

$$\begin{aligned} {\mathrm {div}}[{\mathbf {v}}] = Q \quad {\mathrm {in}} \; \Omega \end{aligned}$$

(8.1)

where $Q \; [\mathrm {M}^{0}\mathrm {L}^{0}\mathrm {T}^{-1}]$ is the strength of the volumetric source; a positive value for Q means source, while a negative value means sink.

We will consider two porous materials with different permeabilities—material 1 with high permeability ($k_H$) and material 2 with low permeability ($k_L$). We will find the optimal layout of these two materials within the domain by maximizing the total mechanical dissipation rate with a bound on the volume fraction of the high-permeability material. Table 3 provides the values of the parameters used in the numerical simulations.

Table 3 Parameters used in the numerical simulation for the pressure-driven and pipe-bend problems

The numerical simulation’s main inputs are the geometry, the boundary conditions, properties of the two constituent materials, and fluid properties (e.g., Barus coefficient). By placing an inequality constraint on the usage of the control material using the volume bound constraint, $\gamma$, we seek the optimal layout of the material distribution for the specified inputs. Topology optimization for a specific objective function (maximization of the rate of dissipation in this case) is carried out using the homogenization method with control variable, $\xi$, where $0 \le \xi \le 1$.

8.1 Pressure-Driven Problem

Consider a 2D computational domain of dimensions $2 \times 1.5$. (The problem is presented in a non-dimensional form.) A segment of the left boundary, $\Gamma ^p$, is subject to a pressure boundary condition, $p_i=100$, while a segment of the right face is subject to a lower pressure boundary condition, $p_o=1$. The rest of the boundary, $\Gamma ^v$, is subject to homogeneous velocity boundary condition (i.e., ${\mathbf {v}}({\mathbf {x}}) \cdot \widehat{{\mathbf {n}}}({\mathbf {x}}) = 0$ on $\Gamma ^{v}$). The computational domain along with the boundary conditions is shown in Fig. 10.

Figures 11 and 12 show the results (i.e., material distribution, and the corresponding solution fields) for zero volumetric source ($Q = 0$) and non-zero volumetric source ($Q = 1$), respectively, for various values of the Barus coefficient $\beta _B$, including $\beta _B = 0$, which corresponds to the Darcy model. The main observations for the zero volumetric source case are:

• (1) The optimal material distribution is unaffected by the value of the Barus coefficient. Specifically, the high-permeability material is placed along the flow path of the fluid from inlet to the outlet, irrespective of the value of the Barus coefficient.

• (2) However, the corresponding magnitude of the velocity and the spatial distribution of the pressure differ significantly.

For the case of non-zero volumetric source case, the main observations are:

• (1) The optimal material distribution varies with the Barus coefficient.

• (2) The Barus model yields a much different material layout than the Darcy model. In contrast to the Darcy model, the material distribution under the Barus model does not necessarily follow the flow path.

• (3) Notably, the qualitative nature of the material distribution under the Barus model could change from problem to problem and for different values of the Barus coefficients; this change is because of the nonlinearity in the Barus model. Figures 13 and 14 support this claim.

  • (a) Since viscosity and permeability are independent of the solution fields under the Darcy model, the magnitude of the velocity is proportional to the magnitude of the pressure. So, the high-permeability material under the Darcy model is placed in the regions with more significant pressure gradients. See Fig. 13.

  • (b) For the same problem under the Barus model, the high-permeability material is placed in the regions with high-pressure gradients for smaller values of $\beta _B$. But for a higher value of $\beta _B$, the high-permeability material is placed in the regions with smaller pressure gradients (cf. Fig. 14). It is, therefore, not possible to predict the optimal material layout with actually solving the design problem, as the layout depends on pressure (via pressure-dependent viscosity) as well as the pressure gradient. In general, the relative strengths—of pressure and pressure gradient—will not be known a priori.

Fig. 10

Pressure-driven problem: The flow of a fluid in a 2D rectangular porous domain (2.0 × 1.5) is driven by pressure boundary conditions. An inlet pressure $p_i = 100$ is applied on a part of the left face, and an outlet pressure $p_o = 1$ is applied on a part of the right face. On the rest of the boundary, the normal component of the velocity is prescribed to be zero. A uniform volumetric source Q is applied over the entire domain

Fig. 11

Pressure-driven problem with zero volumetric source: This figure shows the optimized material distribution (left panel) and the corresponding pressure (middle) and velocity (right) profiles for various values of the Barus coefficient $\beta _B$. A volumetric bound constraint is placed on the high permeability material with $\gamma = 0.1$. In the material distribution plots, the high permeability material regions are represented in ‘red’ color, while ‘blue’ color regions represent the low permeability. (See the online version for the color figure.) Three notable observations are: (i) The optimal material distribution remains almost the same for different Barus coefficient values. (ii) The magnitude of the velocity decreases with an increase in the Barus coefficient. (iii) The pressure spreads out lesser with an increase in the Barus coefficient

Fig. 12

Pressure-driven problem with non-zero volumetric source: This figure shows the optimal material distribution (left panel) and the corresponding velocity profile (right) for various values of the Barus coefficient $\beta _B$. The regions with high permeability material are shown in ‘red’, while ‘blue’ represents the low permeability material regions. (See the online version for the color figure.) The total area occupied by the high permeability material is limited to $\gamma = 0.1$. The value for the uniform volumetric source is $Q = 1$. Two notable differences compared to the case of zero volumetric source are (cf. Fig. 11): (i) The optimal material layout varies with the Barus coefficient. (ii) The material distribution under the linearized Barus model is not necessarily along the flow path. In comparison, under the Darcy model, the high permeability material is placed along the flow path of the fluid from inlet to the outlet

Fig. 13

Pressure-driven problem with non-zero volumetric source (Darcy model): This figure shows the optimal material distribution and the corresponding pressure profile, pressure gradients and velocity profile in the domain. The simulation parameters are: $\beta _B = 0$, $\gamma = 0.1$ and $Q = 1$. For the Darcy model, high permeability material (in ’red’ color) is placed along high velocity and pressure gradients. (See the online version for color.)

Fig. 14

Pressure-driven problem with non-zero volumetric source (Darcy-Barus model): This figure shows the optimal material distribution and the corresponding pressure profile, pressure gradients and velocity profile in the domain. The simulation parameters are: $\beta _B = 0.125$, $\gamma = 0.3$ and $Q = 1$. Under the optimal material layout, the regions with low pressure gradients have high-permeability material, indicated in ‘red’ on the left panel. (See the online version for color)

8.2 Pipe-bend problem

In order to ensure the abovementioned trend is not specific to the previous problem, we will consider another canonical problem. Figure 15 provides a pictorial description of this new problem. The difference between the previous and this problem lies in the location of the outlet (cf. Figs. 10 and 15).

Figure 16 shows the material distributions and associated velocity profiles for various values of the Barus coefficient. We also use this new problem to study the effect of aspect ratio on the optimal material layouts by solving the problem on two configurations—a square domain ($a = b = 1.0$) and a rectangular domain ($a = 2.0$ and $b = 1.5$); see Fig. 17. The following are the main observations:

• (1) Just like the pressure-driven problem, the optimal material distribution under the pipe-bend problem differs as the value of the Barus coefficient changes.

• (2) Under the Darcy model, the high-permeability material is placed in such a way as to provide maximum connectivity between the inlet and outlet. Specifically, the high-permeability is placed along the flow path, resulting in the form of a bent conduit from the inlet to the outlet. However, this trend is not observed under the linearized Barus model. Thus, due to the model’s inherent nonlinearity, one cannot guess the material placement under the (linearized) Barus model.

• (3) Similar to the trend observed under the pressure-driven problem, the magnitude of the velocity decreases with an increase in the Barus coefficient.

• (4) Under the Darcy model, keeping all the simulation parameters the same, TopOpt places material along the flow path for both square and rectangular domains. But the same is not true for the linearized Barus model. Because of the nonlinearity, the material layout for a square domain cannot be extrapolated to a rectangular domain for the Barus model. Said differently, a naïve scaling will not work for material designs involving nonlinear models.

Fig. 15

A square domain ($a = b = 1.0$) and a rectangular domain ($a = 2.0 \; {\mathrm {and}} \; b = 1.5$) are subjected to pressure boundary conditions with one inlet on left face and one outlet on bottom face. An inlet pressure $p_i = 100$ is applied on the left face of $\Gamma ^{p}$ and an outlet pressure $p_o = 1$ is applied on the bottom face of $\Gamma ^p$. At all other points on the boundary, the normal component of the velocity is prescribed to be zero. A uniform volumetric source $Q=1$ has been applied over the entire domain

Fig. 16

Pipe-bend problem (square domain): This figure shows the optimal material distributions and the corresponding velocity profiles for various values of the Barus coefficient $\beta _B$. The computational domain is a square ($a = b = 1.0$). A uniform volumetric source $Q = 1$ is applied. The volumetric bound constraint of $\gamma = 0.1$ is placed on the high-permeability material. The regions occupied by the high-permeability material is represented by ‘red’, while ‘blue’ represents the low-permeability material. The main observations are: (i) just like the pressure-driven problem, the optimal material distribution varies with the Barus coefficient. (ii) The placement of the high-permeability material does not follow the flow path under the linearized Barus model (i.e., for non-zero $\beta _B$ values). (iii) The magnitude of the velocity decreases with an increase in the Barus coefficient

Fig. 17

Pipe-bend problem (square vs. rectangular domains): This figure compares the optimal material layouts for a square domain (left panel) with that of a rectangular domain (right). All the other simulation parameters are the same. High permeability material is represented by ‘red’, while ‘blue’ represents the low permeability material. Under the Darcy model, the optimal material distributions are similar for both square and rectangular domains; the placement of the high-permeability material follows the flow path. But the same is not true for the linearized Barus model. Because of the nonlinearity, the material layout for a square domain cannot be extrapolated to a rectangular domain for the Barus model

9 Closure

In this paper, we have addressed obtaining optimal material layouts using topology optimization for flow through porous media applications. Some principal contributions of this article are:

• (C1) We have considered nonlinear models for flow through porous media that capture the pressure-dependent viscosity and inertial effects, thereby expanding the application space.

• (C2) We proposed a well-posed design problem under TopOpt using the mechanical dissipation rate—a physical quantity with strong mechanics and thermodynamic underpinning.

• (C3) Although often used in the literature under TopOpt, the minimum power theorem has limited scope. Notably, we have shown that this theorem does not hold for nonlinear models describing the flow of fluids in porous media.

• (C4) We have derived analytical solutions for 1D problems, and 2D and 3D problems with axisymmetric for different boundary conditions. These analytical solutions can be used to verify numerical simulators.

• (C5) Using analytical and numerical solutions, we have studied the ramifications of the nonlinearities—pressure-dependent viscosity and inertial effects—on the optimal designs.

• (C6) We have addressed how the boundary conditions—pressure-driven versus velocity-driven—affect the formulation of the design problem. When should we pose the problem as minimization or maximization? Should we place the volume constraint on the material with higher permeability or lower?

Our main findings are:

• (1) The analytical and numerical solutions using the dissipation rate have provided realistic material layouts, thereby establishing the appropriateness of the rate of dissipation to pose design problems under TopOpt.

• (2) In obtaining material designs of axisymmetric problems numerically, one should be wary of finger-like material layouts despite using the standard filters and SIMP regularization, especially when the primal analysis does not utilize the underlying symmetry. On the other hand, as shown in this paper, a primal analysis that invokes axisymmetry in its numerical scheme can provide a symmetric material design devoid of fingers. Next, for TopOpt involving flow through a porous annulus (either concentric cylinders or spheres), the high-permeability material is placed near the inner circle. This result will help the design of purifying water filters.

• (3) In the presence of a volumetric source, optimal designs under the Barus model are noticeably different from that of the Darcy model.

• (4) We provide the following guiding points to devise well-posed design problems:

  • (i) For pressure-driven problems, use the maximization of the rate of dissipation with a volume bound on the high-permeability material.

  • (ii) For velocity-driven problems, use the minimization of the rate of dissipation with a volume bound on the high-permeability material.

The proposed framework and the insights gained from the analytical and numerical solutions offer a way to achieve optimal material designs for devices with complicated domains, new functionalities, and greater accuracy. A plausible future work can be toward using topology optimization for flow of multi-phase fluid systems and devices in which the porous solid is deformable.

Appendix A. Mathematical Results

A function f(x) is said to be convex if

$$\begin{aligned} f(\lambda x_1 + (1 - \lambda ) x_2) \le \lambda f(x_1) + (1- \lambda ) f(x_2) \quad \forall \lambda \in [0,1] \end{aligned}$$

(A.1)

For twice-differentiable functions, a sufficient condition for convexity is (Boyd et al. 2004):

$$\begin{aligned} f^{''}(x)\ge 0 \end{aligned}$$

(A.2)

where a superscript prime denotes a derivative. Using this sufficient condition, it is easy to check the functions $x^3$ and 1/x are convex on the positive real line (i.e., $0< x < \infty$).

Lemma A.1

Given that $0 \le \gamma \le 1$ and $0 < r_i$, the quantities ${\widehat{\xi }}_{\mathrm {3D}}^{(1)}$ and ${\widehat{\xi }}_{\mathrm {3D}}^{(2)}$ defined in Eqs. (7.17) and (7.22), respectively, satisfy

$$\begin{aligned} 1 + \frac{1}{r_i} - \left( \frac{1}{{\widehat{\xi }}_{\mathrm {3D}}^{(1)}} + \frac{1}{{\widehat{\xi }}_{\mathrm {3D}}^{(2)}} \right) \ge 0 \end{aligned}$$

(A.3)

Proof

Noting that $f(x) = x^3$ is a convex function on the positive real axis and $\gamma \in [0,1]$, the definition of a convex function (A.1) implies the following:

$$\begin{aligned} ( \gamma (1) + (1 - \gamma ) r_i )^3 \; \le \; \gamma (1)^3 + (1 - \gamma ) r_i^3 \end{aligned}$$

(A.4)

This implies that

$$\begin{aligned} \frac{1}{{\widehat{\xi }}_{\mathrm {3D}}^{(1)}} = \frac{1}{\root 3 \of {\gamma + (1 - \gamma )r_i^3}} \le \frac{1}{\gamma + (1 - \gamma )r_i} \end{aligned}$$

(A.5)

Using the fact that $f(x) = 1/x$ is a convex function on the positive real line, we establish the following inequality:

$$\begin{aligned} \frac{1}{{\widehat{\xi }}_{\mathrm {3D}}^{(1)}} \le \frac{1}{\gamma + (1 - \gamma )r_i} \le \gamma + (1 - \gamma ) \frac{1}{r_i} \end{aligned}$$

(A.6)

By executing similar steps as above, we obtain the following inequality:

$$\begin{aligned} \frac{1}{{\widehat{\xi }}_{\mathrm {3D}}^{(2)}} = \frac{1}{\root 3 \of {(1 - \gamma ) + \gamma r_i^3}} \le \frac{1}{(1 - \gamma ) + \gamma r_i} \le (1 - \gamma ) + \gamma \frac{1}{r_i} \end{aligned}$$

(A.7)

Adding the above two inequalities, we get the desired inequality:

$$\begin{aligned} \frac{1}{{\widehat{\xi }}_{\mathrm {3D}}^{(1)}} + \frac{1}{{\widehat{\xi }}_{\mathrm {3D}}^{(2)}} \le 1 + \frac{1}{r_i} \end{aligned}$$

(A.8)

$\square$