Multiscale Characterization of Wettability in Porous Media

Abstract

Wettability is one of the key controlling parameters for multiphase flow in porous media, and paramount for various geoscience applications. While a general awareness of the importance of wettability was established decades ago, our fundamental understanding of how wettability influences transport and of how to characterize wettability has improved tremendously in recent years through breakthroughs in imaging technology and modeling techniques. Numerical modeling studies clearly show not only that macroscopic two-phase flow is influenced by the average wettability, but also that the spatial distribution of wetting significantly impacts the macroscopic parameters. Herein, we explore the thermodynamics for porous multiphase systems, and recent breakthroughs in wettability characterization. Our view is that bridging the multiscale characterization of wetting must consider two fundamental perspectives: geometry and energy. Advancing the overall description requires an improved understanding of the operative mechanisms that dominate at various scales, and the development of quantitative approaches to capture these effects. We take a multistage approach, looking at these fundamental perspectives from the sub-pore-to-pore length scales, followed by the pore-to-core length scales using various analytical techniques and numerical simulations. Within this context, there remain many open-ended questions, and we therefore highlight these issues to provide guidance on future research directions. Our overall aim is to provide comprehensive guidance on the multiscale characterization of wettability in porous media, in order to facilitate novel research.

1 Introduction

A fundamental understanding of wettability in porous media is paramount for various subsurface engineering applications such as geological storage of CO₂, oil and gas recovery, groundwater remediation, and energy storage. The oil and gas industry spends significant efforts on core analysis to determine rock properties such as porosity, permeability, relative permeability, and wettability, as a part of subsurface workflows (McPhee et al. 2015). Fundamental to these analyses is relative permeability, which measures the ease at which one phase flows in the presence of another, immiscible phase (Bear 2018, Bear 1970). However, a primary deficiency exists in our understanding and quantification of relative permeability for different wetting states. There are no simple rules that quantify the wide range of observed relative permeability behaviors despite great efforts to find them (Blunt 2017). Experimental and simulation data often provide conflicting results, such as trends of residual oil saturation and endpoint relative permeability versus wettability (Fan et al. 2020, Christensen and Tanino 2019, Jadhunandan and Morrow 1995). While relative permeability behavior is broadly understood as being dependent on surface wetting properties, pore structure, and residual fluid morphology, tools for quantifying these properties to an adequate level of detail have only recently become available. As displayed in Fig. 1, there is now a spate of tools for observing the influence of wettability over the entire range of relevant length scales. In addition, theoretical links exist between thermodynamic descriptions and geometrical properties when interfaces are well resolved, while fundamental links at the core scale remain an open question. With recent advancements in pore-scale imaging and modeling, however, the means to quantify flow mechanisms and wettability at their origin, and to link them to their core-scale properties, is a reality.

Fig. 1

Multiscale characterization of wettability from molecular-scale interactions to core-scale properties. The energetic and geometric perspectives are clearly linked at the sub-pore to pore length scales through thermodynamic principles; at the core scale, the relationship between thermodynamics and geometric structure remains elusive

Over the last two decades, there have been significant changes to how we study porous-media flows. These were initiated by our ability to model pore-scale fluid displacements with direct numerical methods and to validate with pore-scale imaging (Blunt et al. 2013). We can directly track the sequence of pore displacement events using dynamic synchrotron-based X-ray computed micro-tomography (micro-CT) (Berg et al. 2013, Bultreys et al. 2018, Bultreys et al. 2016) and measure resulting geometrical and topological parameters (Armstrong et al. 2019). We can also measure in situ contact angles under quasi-equilibrium or dynamic conditions, along with surface areas, curvatures, and topology (Andrew et al. 2014, Armstrong et al. 2012, Scanziani et al. 2017, AlRatrout et al. 2018, Herring et al. 2016, Klise et al. 2016). This provides a wealth of information on flow regimes, dominant mechanisms, and surface wetting characteristics that supply important physics for predictive pore-scale modeling (Armstrong et al. 2016, Akai et al. 2018, Zhao et al. 2019, McClure et al. 2021).

Early pore network models assigned pore-scale wettability using a probability density function without any particular spatial correlation, and very few studies assigned mixed wet conditions with small pores being water-wet, and larger pores oil-wet (Skauge et al. 2004, Djurhuus et al. 2006). Recent works, however, demonstrate that the pore-scale spatial distribution of wetting is perhaps one of the most important parameters (Foroughi et al. 2020, Murison et al. 2014, Jung et al. 2016, Zhao et al. 2016). What matters most for transport is the conductivity, which is represented by the fluid geometry at the pore scale. Furthermore, the fluid geometry is a consequence of pore filling sequences, which are controlled not only by pore structure but also by local wetting properties (Singh et al. 2019, Singh et al. 2017, Bear et al. 2011). Hence, the spatial distribution of wetting may be more important than the overall average wetting. Ignoring spatially correlated distributions of wettability, or assuming a spatially random distribution, may explain some of the discrepancies between our many-year experience of conceptual trends, e.g., how residual oil saturation, $S_{or}$, depends on wettability.

Fig. 2

QEMSCAN data (a) and 3D surface renderings (b, c) of sandstone rock. QEMSCAN data provide the complex arrangement of minerals Pirrie et al. (2004). Surface renderings of the pore space generated from micro-CT data provide an indication of surface roughness ($R_a$) that could impact wetting (b, c). Both roughness and chemical heterogeneity are known to influence surface wetting properties, see Sect. 4 and 5

The spatial variability of wettability originates from minerals being aged in hydrocarbons. Before the first charge with hydrocarbons, the reservoir rock is initially water-wet, as most minerals are hydrophilic, and completely saturated with brine. As hydrocarbons migrate into the reservoir rock, the brine is displaced, leaving a thin film of water over the rock surface and an accumulation of connate water in the crevices of the rock (Buckley and Liu 1998, Buckley et al. 1998). This system is then aged over geological time at elevated temperatures and pressures. The extent to which thin brine films cover the rock surface once the reservoir is discovered for production is a key factor that influences the final wetting state (Schmatz et al. 2015, Akai et al. 2018). In Fig. 2, quantitative evaluation of minerals by scanning electron microscopy (QEMSCAN, Thermo Fisher) and micro-CT data demonstrates that sandstone is mineralogically heterogeneous with surface roughness on the micrometer scale. The roughness of the associated minerals and surface chemistry is likely to influence the stability of thin brine films, and thus the degree to which a surface is rendered oil-wet during aging (Rücker et al. 2020, Shabaninejad et al. 2017). In addition, hydrocarbon comprises a variety of chemical species that can rupture thin films and interact with solid surfaces, rendering them oil-wet (Buckley and Liu 1998, Buckley et al. 1998). This can occur through a variety of known mechanisms, including interactions of crude oil components with polar functionality (Tweheyo et al. 1999), surface precipitation of asphaltenes (Hu et al. 2019), acid/base interactions between functional groups at oil/brine/solid interfaces (Kelleher et al. 2008), and ion binding between oil/solid interfaces through thin brine films (Liu et al. 2007, Hu et al. 2019). Most literature suggests that these interactions occur over time scales of weeks to months (Anderson 1986, Abdallah et al. 1986, McPhee et al. 2015), meaning that, over geological time, many of the intrinsically water-wet surfaces are rendered oil-wet.

It is difficult to imagine that such a complex oil/brine/rock system would be limited to uniform wetting, or even to a simple fractional distribution of wetting conditions (Fatt and Klikoff 1959, Anderson 1987). Accounting for wetting by using an average or from a limited number of measurements is likely outdated, given our current understandings of surface-altering mechanisms, establishment of wetting films and their influence on invasion processes, mineralogical heterogeneity of rocks and associated surface energies, and a plethora of other recent pore-scale insights (Singh et al. 2017, Singh et al. 2019, Jung et al. 2016, Murison et al. 2014, Zhao et al. 2016, Liu et al. 2018, Zou et al. 2018, Lin et al. 2019). Various experimental and simulation studies have also shown the influence of spatially correlated wettability (Akai et al. 2018, Kovscek et al. 1993, Zhao et al. 2016, Foroughi et al. 2020) with simulation results, providing a platform for a detailed assessment of spatial variability and its impact on flow properties.

Fig. 3

Conceptual fluid configuration in a water-wet (left, a) and an oil-wet pore (right, a). Compared with the water-wet case, for the oil-wet situation the respective relative permeability–saturation functions show a smaller residual oil saturation but higher water relative permeability and a crossover saturation shifted to lower water saturation. Contradictory residual oil saturation trends reported in the literature (b). The dashed and dotted lines display commonly reported trends

Various modeling and experimental studies have demonstrated the influence that spatially correlated wettability has on multiphase flow. Kovscek et al. (1993) showed that the complex wetting state that develops through aging can significantly impact relative permeability. Recent micromodel experiments have also shown that displacement flow regimes are directly influenced by the spatial distribution of surface wettability (Zhao et al. 2016). Various other works have also shown the importance of the wetting state when conducting core flooding experiments (Akai et al. 2018, Zou et al. 2018, Liu et al. 2018) or numerical simulations (Fan et al. 2020, Murison et al. 2014, Singh et al. 2019, Foroughi et al. 2020).

The commonly accepted core-scale trends provided as reference materials are shown in Fig. 3. These trends, however, do not hold true throughout the literature. For example, reported trends between residual oil saturation and wettability indices are conflicting. As displayed in Fig. 3, Jadhunandan et al. (1995) report the dashed curve, while Christensen and Tanino (2019) report the solid curve. The controversy dates back to the mid 1980s (e.g. Anderson 1987) and remains not fully resolved. Possible mechanistic explanations for the discrepancy are discussed by Masalmeh et al. (2014). Another possible reason is that these studies used traditional core-scale measures that treat wetting as a 1D spectrum ranging from oil-wet to water-wet, failing to capture the wetting state in sufficient detail. Overall, traditional core-scale measures of wetting do not capture the spatial variability of surface wettability, nor the complexity of surface interactions developed during aging, to an adequate level. It is our opinion, based on these previous works, that additional pore-scale information is required.

Refinement of experimental studies with pore-scale modeling and imaging is a necessary step toward resolving conflicting results. Current digital rock models, however, mostly deal with uniform wetting states or statistical distributions of wettability that do not necessarily represent realistic conditions. Network modeling is more advanced in this respect due to the natural adaptation of its framework to mixed-wet pores and throats (Valvatne and Blunt 2004), whereas direct flow simulations on rock images commonly consider only uniform surface wetting (Blunt et al. 2013, Armstrong et al. 2016, Bakhshian et al. 2021). Various groups have incorporated the concept of mixed wettability into pore network models by assigning fractional wettability to standard pore geometries (Landry et al. 2014, Valvatne and Blunt 2004, Wyckoff and Botset 1936). These network modeling studies have resulted in a wide range of behaviors caused by different spatial distributions of wettability, pore structure, and emergent displacement patterns alluding to the importance of accurate pore-scale characterization for model parameterization, and thus to predictive simulations.

Assigning wettability at the pore scale for reservoir rock has yet to be fully resolved. Pore-scale micro-CT images of sedimentary rocks provide complex 3D images on the spatial distributions of minerals (Wildenschild and Sheppard 2013) yet lack the resolution needed to define thin brine films. In addition, the accurate quantification of micro-CT data beyond distinguishing solid from void remains a challenge (Da Wang et al. 2020). Sedimentary rocks are commonly composed of many different solid materials, such as quartz, K-feldspar, muscovite, clay minerals, and other precipitated salts, as displayed in Fig. 2a. This rich mineralogical mixture is then aged in crude oil and brine over geological time, which can result in a different wetting state for each mineral because different electrostatic interactions, caused by mineral-specific surface charges, control crude oil adhesion (Drummond and Israelachvili 2004, Buckley 2001, Rücker et al. 2020, Rücker et al. 2020). For some minerals, such as clay, orientation can impact the resulting wetting state (Yesufu-Rufai et al. 2020). This is one possible reason why pore-scale images display such a wide distribution of contact angles (Andrew et al. 2014, Sun et al. 2020, Sun et al. 2020, Mascini et al. 2020, Klise et al. 2016). Results also suggest that wetting patterns may exist over the length scale of a single pore (AlRatrout et al. 2018). Considering these findings, the distribution of contact angles observed in reservoir rock is expected to vary over a range of values, with spatial correlations that could be linked to surface mineralogy and/or roughness (Morrow 1975). However, various important aspects remain unknown: (1) the numerical error and uncertainty associated with pore-scale contact angle measurements; (2) the range of possible contact angles for a given wetting condition; (3) the appropriate contact angles for different minerals in aged cores; and (4) the contact angle (or distribution of angles) appropriate for pore-scale simulations. In addition, spatial correlations of wetting behavior originating from geological factors should be considered and included within the pore-scale modeling framework.

So, what does it mean to measure pore-scale contact angles in situ? Contact angle measurements from micro-CT flow experiments are likely influenced by many physical processes. For the following, we assume that these measurements are numerically accurate regardless of recent works demonstrating shortcomings in one or another measurement method (Ibekwe et al. 2020, Khanamiri et al. 2020, Sun et al. 2020). Starting from Young’s equation, the concept of an intrinsic contact angle presumes an ideally smooth and homogeneous surface, as displayed in Fig. 4. Reservoir rocks, however, are neither smooth nor homogeneous, see Fig. 2. Therefore, the concept of an effective angle can be introduced. Different wetting models can be proposed by considering variational surface energies and how wetting films develop on rough surfaces, e.g., the Wenzel model, Cassie–Baxter model, or wicking state model (Bico et al. 2002). In addition, there are dynamic effects that cause contact angle hysteresis. Simple models for a fluid droplet under flow on a rough or chemically heterogeneous surface are shown in Fig. 4(c, d). During multiphase flow in porous media, fluid menisci can either advance or recede in spatially complex ways, producing a range of possible angles along with interfacial pinning at sharp corners (Morrow 1975) while only the intrinsic contact angle (which is not measured) would reflect the actual surface energy. The velocity field is also heterogeneous with local highly dissipative flows that would influence the contact angle. Models that include viscous dissipation produce contact angle as a function of capillary number, Ca (Malgarinos et al. 2014, Snoeijer and Andreotti 2013). When multiphase systems are imaged and their contact angles measured, the degree to which the system is at equilibrium, the hysteretic dependencies and the wetting state of the surfaces are largely unknown. Another concern is that measurements are available only along the three-phase contact line, and thus any attempt at quantifying surface wetting properties is biased toward where the three-phase contact line prefers to pin during flow. Considering all of these factors provides a broadened perspective into how these measurements could be used to parameterize pore-scale models.

Fig. 4

Fluid clusters (red) exist in a geometrically complex space (a) while wetting models are commonly used for an ideally flat and smooth surface (b) with the concepts of roughness (c) or chemical heterogeneity (d) resulting in advancing and receding effective contacts angles. Image (a) is reprinted by permission from Sun et al. (2020)

Another question concerns our fundamental approach to modeling. Given the wealth of information available from pore-scale imaging and modeling, it could be argued that we are moving away from parsimonious models and toward unnecessarily over-parameterized models. The previously expressed ideas, however, are not emerging from a theoretical vacuum, nor are they based solely on ‘black box’ experiments. We believe that pore-scale wettability and the (spatial) distribution of wetting properties should be included within the minimum set of parameters required to explain core-scale multiphase flow behaviors. The challenge lies in the details of how to actually do this. In particular, the physics relating to wetting behavior at each length scale, as depicted in Fig. 1, and methodologies for linking these scales, need to be well defined. Our view is that bridging the multiscale characterization of wetting must consider two fundamental perspectives: geometry and energy. Advancement of the overall description relies on an improved understanding of the operative mechanisms that dominate at various scales, and on the development of quantitative approaches to capture these effects. Key advances in experimental techniques can be identified, with opportunities to further the understanding achieved through each perspective. Improved resolution and fidelity in micro-tomography and SEM will provide critical insights into the geometric effects. Techniques such as atomic force microscopy provide ways to understand the energetic interactions between fluid and solid materials. Simulations also provide a critical tool within this context, informing both geometric and thermodynamic aspects, and providing core-scale relationships, such as relative permeability.

Overall, the aim of this paper is to focus on the physics of wetting from the sub-pore scale to the core scale, with an emphasis on how the various length scales can be linked. The following sections will provide guidance on the thermodynamics of wetting, effective contact angle models, geometrical and topological characterization of the wetting state, and relative permeability simulations for distinctly different wetting states. The aim is to provide comprehensive guidance on these issues to facilitate novel research.

2 Thermodynamics of Wetting in Porous Media

The following section will focus on the thermodynamics for upscaling wetting. The essential parameters controlling wetting from the molecular scales to core length scales are displayed in Fig. 1. Understanding how these parameters influence the wetting state, and how they can be simplified to provide predictive flow models has been a longstanding challenge. As displayed in Fig. 1, there are two perspectives on the wetting state: (1) the energy perspective and (2) the geometric perspective. The geometric perspective is restricted to the spatial arrangement of objects in the system with units of length only. The contact angle is an example of a geometric quantity, since it can be determined based on the spatial arrangement of materials. The energy perspective, in contrast, considers the surface energies. The associated contributions to the potential energy are needed to determine what forces act in the system. An obvious link between the two perspectives is found at the sub-pore to pore length scales where Young’s equation relates surface energies to geometric contact angles. The utility of this relationship is evident given that a geometric angle is fairly straightforward to measure, while measurement is not always straightforward for surface energies. So, is there a comparable relationship that exists at the core scale?

Pore-to-core-scale definitions of wetting start by considering the internal energy of a porous system with immiscible fluids (wetting fluid w, non-wetting fluid n) (Morrow 1970). Standard thermodynamic approaches define the internal energy of the fluids $i \in \{w,n\}$ based on the Euler equation

$$\begin{aligned} U_{i} = T_i S_i - p_i V_i + \sum _{j} \mu _j N_j, \end{aligned}$$

(1)

where $T_i$ is temperature, $S_i$ is entropy, $p_i$ is the pressure, $V_i$ is the volume, and $\mu _j$ and $N_j$ are the chemical potential and the molar fraction of species j, respectively. The internal energy associated with the interfaces is defined as

$$\begin{aligned} U_{ij} = T_{ij}S_{ij} + \gamma _{ij} A_{ij}, \end{aligned}$$

(2)

where $\gamma _{ij}$ is the interfacial energy associated with the interface ij, and $A_{ij}$ is the associated surface area. In reservoir rock with complex spatial distributions of crude oil interactions, a different surface energy could be associated with each of the possible surface interactions.

It can be assumed that the total internal energy of the system is the sum of the contributions from each entity

$$\begin{aligned} U= & {} U_w + U_n + U_{wn} + \sum _{ij} U_{ij} \end{aligned}$$

(3)

$$\begin{aligned}= & {} TS - (p_n V_n + p_w V_w) + \sum _i \mu _i N_i + \sum _{ij} \gamma _{ij} A_{ij}. \end{aligned}$$

(4)

Standard thermodynamics clearly expresses that the product of pressure and volume yields a contribution to the internal energy. The external pressure–volume work, W, is based on the change in the fluid volume

$$\begin{aligned} \frac{\partial W}{\partial t} = (p_w - p_n) \frac{\partial V_w}{\partial t} \;, \end{aligned}$$

(5)

where $V_w + V_n$ has been assumed constant.

The external work performed on the system is transferred to internal energy, such as generation of surface energy, or dissipated as heat. A common method for computing the external work is to integrate the capillary pressure as a function of saturation (Amott 1959, Ma et al. 1999). However, this introduces a shortcoming due to how experiments are conducted. When experimental measurements are conducted from the boundary of a system, measurements of the fluid volume will account for the disconnected parts of a phase, whereas measurements of the fluid pressure account only for the pressure of those parts of the phase that are connected to the boundary where the measurement is performed (Armstrong et al. 2012). Meaningful measurements of the thermodynamic pressure cannot, however, be obtained from the boundary at critical phase saturation where the fluid connectivity breaks down. To be consistent with Eq. (4), the pressure of all disconnected phases must be included since these contribute to the system’s internal energy. Currently, there are no practical ways to overcome this issue without using advanced micro-CT imaging to quantify the interfacial area and curvature of the disconnected phases.

Assuming that the total external work can be measured, a logical next step would be to quantify how this energy is distributed. Firstly, it is understood that changes to the surface energy account for a significant part of the external work. Consider a water-wet rock where all solid regions remain in contact with water regardless of saturation. This can be visualized by considering a thin film of water that covers the entire rock surface. Therefore, a change in surface free energy is proportional to the change in surface area $A_{wn}$ based on the interfacial tension $\gamma _{wn}$. Morrow (1970) therefore defined a displacement efficiency term, $E_d$, as the fraction of pressure–volume work converted to surface energy (Morrow 1970, Seth et al. 2006)

$$\begin{aligned} E_d = \frac{\gamma _{wn} \varDelta A_{n}}{\int (p_n - p_w) \; dV_w }\;, \end{aligned}$$

(6)

where $A_n$ is the boundary surface for the non-wetting fluid. Seth et al. (2006) showed that the efficiency for primary drainage varies from 10–95%, depending on the material type.

An ‘effective’ contact angle can be defined by assuming that the external work contributes to changes only in surface energy (Blunt et al. 2019, Akai et al. 2020). Micro-CT images allow for decomposing the non-wetting phase interfacial area into wetting/non-wetting and non-wetting/solid areas. Therefore, changes in surface energy $\varDelta F$ can be measured as a function of interfacial area created by the invading of a non-wetting phase

$$\begin{aligned} \varDelta F = \gamma _{wn}(\varDelta A_{wn} + \varDelta A_{ns} \cos \theta _{E_d}), \end{aligned}$$

(7)

where the interfacial area is $A_{ij}$ and $\theta _{e}$ is an effective contact angle. By assuming reversible displacement without energy-dissipating displacement events, i.e., $E_d = 1$ , we arrive at

$$\begin{aligned} \cos \theta _{e} = \Big [\int (p_w - p_n) \; dV_w - \gamma _{wn}\varDelta A_{wn} \Big ] / \gamma _{wn}\varDelta A_{ns}. \end{aligned}$$

(8)

Therefore, $\theta _e$ can be understood as an ‘effective’ contact angle associated with displacement within a control volume. This has been used as either a core-scale measure of wetting (Blunt et al. 2019) or on a pore-by-pore basis by tracking pressure and displacement events using micro-CT (Foroughi et al. 2020).

Surface area coverage can also be considered by assuming that all of the pressure–volume work is converted to surface energy (Garfi et al. 2020). Considering a porous solid with two fluid phases, the surface energy is

$$\begin{aligned} \varDelta F = \gamma _{nw} \; dA_{nw} + \gamma _{ns} \; dA_{ns} + \gamma _{ws} \; dA_{ws}. \end{aligned}$$

(9)

The pressure–volume work can be rewritten in terms of fluid/fluid interfacial curvature $\kappa$, using the Young–Laplace equation, $P_c = p_n - p_w = 2 \kappa \gamma _{nw}$. Therefore,

$$\begin{aligned} dA_{ns} = \frac{\gamma _{nw}}{\gamma _{ns}-\gamma _{ws}} \big [2 \kappa - \frac{dA_{nw}}{dS_n} \big ] \; dS_n, \end{aligned}$$

(10)

where $S_n$ is the saturation of phase n. A model for the surface area coverage of phase n can be provided by assuming functional forms for $\kappa (S_n)$ and $A_{nw}(S_n)$, and integrating with respect to saturation (Garfi et al. 2020). The pre-factor for Eq. (10) is the cosine of the intrinsic contact angle, as defined by Young’s equation, and the exact value of this term is not straightforward to measure as measurements may yield advancing or receding contact angles. While regression analysis can be used to fit the corresponding model to experimental data by adjusting the contact angle term, a single contact angle value might not be representative of the system due to the reasons previously discussed.

Both surface area coverage and ‘effective’ contact angle models provide a means to link the geometric and energy perspectives. Referring back to Fig. 1, these models use thermodynamic principles at the pore scale to provide measures of wetting. An outstanding issue, however, is that these methods are only applicable for flow regimes with negligible dissipation (Seth et al. 2006, Akai et al. 2020). To fully consider dissipation and sources of entropy production during multiphase flow, the framework of non-equilibrium thermodynamics should be considered (De Groot and Mazur 2013). This approach would start by providing a geometrical framework for multiphase systems at the pore scale, then the upscaling of these measures, followed by the development of evolution equations. Various modeling studies have taken this approach (e.g., Gray and Miller 2014, McClure et al. 2020, 2020, Kalaydjian 1987). To explicitly consider wetting in such a model, a multiscale geometrical term that is directly linked to the wetting state of the media would need to be defined. Integral geometry, as discussed in Sect. 6, provides a means to define such a term.

3 Core-Scale Wetting Indices

Fig. 5

Conventional wetting indices, such as the Amott index, rely on capillary pressure curves to infer the wetting properties for a particular material Amott (1959), Abdallah et al. (2007). The hysteresis loop defined by a drainage–imbibition cycle can be used to define an empirical understanding of complex wetting properties

Due to the difficulty associated with measuring interfacial area in conventional experiments, empirical wetting indices were developed based on the first three cycles of capillary pressure–saturation curves $p_c(S_w)$, where wettability is based on the first imbibition and second drainage (Amott 1959, Abdallah et al. 2007). Since the pressure originates from thermodynamics, traditional core-scale wetting indices should be considered as thermodynamic measures that can be inferred without any knowledge of the system’s geometric state. Looking at these measures in detail also provides an intuitive outcome caused by the irreversibility of fluid/fluid displacements that is readily captured in capillary pressure–saturation measurements.

The basic concepts are illustrated in Fig. 5. At zero capillary pressure, spontaneous imbibition will occur such that fluid remaining within the sample (at the pore-scale) will have either a neutral wetting condition or be trapped by capillary forces. Assuming that Young’s equation holds, the position of the contact line will not reach equilibrium until it reaches locations within the sample where the contact angle is zero. If such a configuration is possible, this will define a mechanical equilibrium and no further spontaneous imbibition will occur. Due to capillary pressure hysteresis, however, these balancing points are not uniquely defined. The situation shown in Fig. 5 is typical, with different balancing points being encountered during drainage and imbibition, labeled B and D. The capillary pressure curves are then subdivided into four sections: (i) spontaneous imbibition of oil from A$\rightarrow$B; (ii) forced water drainage from B$\rightarrow$C; (iii) spontaneous imbibition of water from C$\rightarrow$D; and (iv) forced oil drainage from D$\rightarrow$A. In most cases, $S_w^B\ne S_w^D$ due to the displacement being irreversible, implying that $E_d<1$. Nevertheless, it is the surface energy that does work against the pressure forces during spontaneous imbibition. This means that the associated pressure–volume work correlates with the change in surface energy, even if the two do not fully agree due to dissipation.

During forced drainage, from B$\rightarrow$C and D$\rightarrow$A, some portion of the pressure–volume work will generate surface energy. If the displacement were perfectly efficient and reversible, the path from C$\rightarrow$D would be the reverse of the path from B$\rightarrow$C (i.e. $S_w^D=S_w^B$), and the change in surface energy would exactly balance the pressure–volume work. The more typical situation is shown in Fig. 5. The blue portion of the curve is

$$\begin{aligned} \mathsf{W}_\text {water} = \epsilon V \Big [ \int _{S_w^B}^{S_w^C} p_c dS_w - \int _{S_w^D}^{S_w^C} p_c dS_w \Big ], \end{aligned}$$

(11)

which corresponds to the part of the capillary pressure curve that is associated with water-wet conditions. The red portion of the curve is associated with more oil-wet conditions

$$\begin{aligned} \mathsf{W}_\text {oil} = \epsilon V \Big [ \int _{S_w^D}^{S_w^A} p_c dS_w - \int _{S_w^B}^{S_w^A} p_c dS_w \Big ]. \end{aligned}$$

(12)

Wetting indices defined by the ratio of the two areas are only a proxy measure for the wetting state, since the true surface energy is typically unknown. However, there should be no net change in surface area when going around a full cycle. This means that the change in surface energy does not explain the net contribution from pressure–volume work when integrating around the complete cycle. The implication is that for an isothermal process with temperature T (due to the large heat capacity of rock and fluids, the temperature change caused by dissipative pore-scale events is in the millikelvin range (Berg et al. 2013)), the entropy generated by the dissipated energy over the cycle is

$$\begin{aligned} \varDelta S = \frac{\mathsf{W}_\text {water} + \mathsf{W}_\text {oil}}{T}. \end{aligned}$$

(13)

This does not identify which portions of the displacement dissipate energy. In contemporary experiments, it is possible to measure surface area and thereby provide more information about each portion of the displacement. An important area for future research will be to develop more precise accounting for the role of wetting on energy dynamics for displacement in porous media.

4 Wetting State of Rough Surfaces

One of the fundamental challenges in determining the wetting state of mineral surfaces by in situ contact angle measurements is to separate the surface energy-related intrinsic contact angle from the effects of roughness and chemical heterogeneity.

Effective wetting models provide a way to deal with surface roughness and chemical heterogeneity (Cassie and Baxter 1944, Onda et al. 1996, Bico et al. 2002). These models consider sub-pore-scale heterogeneity along the solid surface, as displayed in Fig. 4. From an energy perspective, the impact of sub-pore-scale heterogeneity on wetting can be studied by considering a small, hypothetical displacement, dx, of the contact line. Consider a sessile fluid droplet on a liquid/solid composite surface. The surface can be thought of as porous where the roughness is regarded as porosity, and the liquid resides within the surface pores due to capillary action. The porosity here is regarded as a representative value of the sub-pore-scale surface roughness; analogous to the Representative Elementary Volume used to upscale from the pore-to-core scales (Bear 2013). Liquid residing in the pores is often said to be in the ‘wicking state’ when the droplet fluid wicks along the surface pores. The solid fraction of the surface that remains dry is $\phi _d$, also a representative value of the surface. The associated change in surface energy per unit length is

$$\begin{aligned} dF = (\gamma _{ns}-\gamma _{ws})\phi _d \; dx - \gamma _{wn}(1-\phi _d)+\gamma _{wn}\cos \theta _a \; dx, \end{aligned}$$

(14)

where $\theta _{a}$ is the apparent contact angle. For the wicking state (WS), Young’s equation with the equilibrium condition $dF=0$ yields an apparent contact angle ($\theta _{WS}$),

$$\begin{aligned} \cos \theta _{WS} = \phi _d \cos \theta _Y - (1-\phi _d), \end{aligned}$$

(15)

where $\theta _Y$ is the intrinsic contact angle from Young’s equation. For reservoir rock, $(1-\phi _d)$ would be the fraction of the rock surface covered with connate water due to capillary action. The exposed solid surface of the rock could be in a clean state or rendered oil-wet by contact with crude oil during aging. The state of the exposed surface will influence $\theta _i$.

In addition to the wicking state model, other models can be derived for composite porous surfaces following the previous steps. The Wenzel state (W) corresponds to when the fluid droplet penetrates the surface roughness and is defined as

$$\begin{aligned} \cos \theta _W = r \cos \theta _{Y}, \end{aligned}$$

(16)

where $\theta _W$ is the Wenzel angle and r is the surface roughness factor that is defined as the ratio of the actual area to the projected area of the surface. It can be deduced from Eq. (16) that surface roughness amplifies the wettability of the original surface. A third type of wetting state is defined by the Cassie–Baxter (CB) model where the fluid droplet lies on the surface without penetrating. The Cassie–Baxter contact angle can be written as

$$\begin{aligned} \cos \theta _{CB} = \phi _s \cos \theta _Y + (1-\phi _s), \end{aligned}$$

(17)

where $\phi _s$ is the area fraction of the liquid/solid interface under the droplet. The surface area fraction under the droplet is important since, the larger the solid’s area fraction, the larger the apparent contact angle.

Fig. 6

Different wetting states observed in the experimental work of Morrow (1975). The arithmetic average of the reported advancing and receding contact angles is considered as an apparent contact angle. The apparent contact angle $\theta _A$ from the composite surface depends on both the wetting state and the intrinsic contact angle $\theta _Y$ for the surface material

The resulting apparent contact angle is known to depend on the surface’s wetting state. The Cassie–Baxter state will be thermodynamically stable if the energy variation expressed by the model is less than that leading to the Wenzel model. The stability condition is given by

$$\begin{aligned} \cos \theta _Y \ge \Big ( \frac{1-\phi _s}{r-\phi _s} \Big ). \end{aligned}$$

(18)

Likewise, the wicking state model will be thermodynamically stable when

$$\begin{aligned} \cos \theta _Y \le \Big ( \frac{\phi _s - 1}{r-\phi _s} \Big ). \end{aligned}$$

(19)

The experimental work of Morrow (1975) can be used to demonstrate how surface roughness and the wetting state influence the apparent contact angle. Note that, Morrow (1975) provide advancing and receding contact angles, whereas the previously discussed contact angle models for patterned surfaces are expressed as an apparent contact angle, i.e., neither advancing nor receding. By considering the arithmetic average of the reported advancing and receding contact angles, we approximate an apparent contact angle $\theta _A = (\theta _\text {advancing}+\theta _\text {receding})/2$ and focus on how surface wettability and roughness influence the apparent contact angle. The experimental results are provided in Fig. 6 and compared with the wicking model, Wenzel model and Cassie–Baxter model. While r and $\phi _s$ were not reported by Morrow (1975), reasonable values can be applied to match the experimental data. As observed in Fig. 6, three different wetting regimes are observed. The asymmetry between the hydrophobic ($\cos \theta _Y \ge 0$) and hydrophilic ($\cos \theta _Y \le 0$) sides is captured by the three models and their associated stability criteria. For the comparison, $r=2$ and $\phi _s=0.5$ are used. These results demonstrate how the apparent wetting of a surface is dependent on roughness and how the fluids interact with this roughness. An important area of research would be in relating these models to the actual roughness observed in reservoir rocks and dual-porosity systems that are inherently composite surfaces. In our opinion, incorporating these models into pore-scale numerical simulations would provide a means to bridge the sub-pore to pore length scales.

5 Restoring the Reservoir Wetting State

Rock samples are typically obtained from drilling operations where gas expansion and the invasion of drilling fluids with surface active components can alter the saturation, and hence alter the wetting state. While there are many considerations around wettability restoration, beginning with the selection of drilling fluids, cleaning procedures and aging conditions, we focus here on a central element in the de-saturation procedure where the native configuration of pore-scale fluids, i.e., brine and crude oil, is re-established.

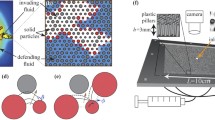
The common procedure of restoring a core to its native state is considered within the context of surface roughness. A 50 $\times$ 50 micrometer Ketton limestone surface measured by atomic force microscopy (AFM) with a resolution of 0.097 micrometer will be the standard used for the presented simulations. As visualized in Fig. 7a, the Ketton surface with a maximum height of 10 micrometer provides a complex topography of peaks and valleys at the micrometer to sub-micrometer length scale. The surface can be considered porous where water films reside within the valleys due to capillary action. When the core is aged with crude oil, the fraction of the rock surface that is covered with connate water is $(1-\phi _d)$. This coverage is controlled by capillary action and directly dictates the surface regions that contact the oil. After aging, surface peaks are rendered oil-wet while the valleys remain water-wet (Rücker et al. 2020).

Fig. 7

An AFM image of the Ketton carbonate surface (a), reprinted by permission from Rücker et al (2020). Simulation of a water droplet deposition on the rough surface in the presence of the immiscible oil phase (b)

Numerical simulations are performed by modeling a water droplet on the aged rock surface using the volume-of-fluid method (Shams et al. (2018). The fluid interface tracking method is based on a finite volume discretization of the Navier–Stokes equation. Interfacial forces are directly calculated on the reconstructed interface elements and added to the Navier–Stokes equations to preserve the total curvature and to remove spurious currents. The oil-wet and water-wet regions at the solid boundary are set in accordance with their prescribed intrinsic contact angles (Treiber and Owens 1972). The approach is to mimic the wetting state of the surface after aging. Firstly, a capillary-dominated invasion process is simulated on the rough surface to a given capillary pressure. Rock surface voxels exposed to oil are rendered oil-wet, while the rock surface voxels exposed to water remain water-wet. The contact angle is set to 130$^\circ$ for oil-wet surfaces, and to 30$^\circ$ for water-wet surfaces. These contact angle choices are based on the experimental work of Treiber and Owens (1972). Once the wetting condition of the rock surface is defined, deposition of a water droplet on the surface in the presence of oil is simulated, and the resulting contact angles are analyzed, as displayed in Fig. 7b.

Fig. 8

Simulation results demonstrate that the apparent wetting of a surface (a) and the water coverage fraction on the surface (b) depend on the capillary pressure at which a core is aged

The capillary pressure at which the surface is aged plays an important role in the apparent contact angle due to surface roughness. Figure 8 shows how contact angles and water coverage fraction vary with capillary pressure. The water coverage fraction is the fraction of the surface below the water droplet that is in direct contact with the solid. The contact angles are measured as an apparent angle within the water phase once the simulation reaches equilibrium. Both the mean apparent contact angle along the three-phase contact line and the macroscopic contact angle defined by deficit curvature (Sun et al. 2020) are comparable. Further details on the macroscopic contact angle are provided in Sect. 6. Intuitively, when the surface is ‘aged’ at higher capillary pressure, more of the surface is rendered oil-wet, resulting in less surface area coverage and a larger apparent contact angle (Lin et al. 2019). Intermediate-wet conditions are achieved at high capillary pressures when more of the surface is exposed to oil during aging. The transition from water-wet to intermediate-wet conditions occurs over a narrow range of capillary pressures from approximately 0–20 kPa. These simulation results align with experimental data where the wetting state of Ketton limestone is significantly influenced by the aging method (Rücker et al. 2020, Rücker et al. 2020).

Fig. 9

The distribution of apparent contact angles measured for the Ketton limestone surface aged at a theoretical capillary pressure of 70 kPa

The distribution of contact angles along the contact line is provided in Fig. 9 for the simulated condition of 70 kPa. A broad distribution of apparent angles is observed between 90$^\circ$ and 125$^\circ$ when the intrinsic angles used for the simulation are 30$^\circ$ and 130$^\circ$. Similar broad contact angle distributions, representing intermediate-wet conditions in aged Ketton limestone, have also been reported from experimental work (Andrew et al. 2014, Scanziani et al. 2017). Overall, these results indicate the influence that roughness has on pore-scale measured contact angles.

6 Geometrical and Topological Characterization of Wetting

Young’s equation provides a link between surface energies of the involved interfaces and the contact angle, which is a geometric concept. Geometric descriptions are only valid, however, at certain scales. At the molecular scale, the contact line is not well defined, so the contact angle and other derived quantities do not really exist. It is only at slightly larger length scales that the contact angle can be defined. At this scale, the spatial morphology of the fluids is also geometrical. However, only some of the geometrical measures, such as surface area coverage and interfacial curvature, may be used to infer the wetting state, while other measures, such as volume fraction, may not. For example, Eq. (10) provides an approach to relate fluid surface area coverage to wettability using reversible thermodynamics (Garfi et al. 2020). Another example, purely geometrical in origin, is the concept of deficit curvature derived from the Gauss–Bonnet theorem (Sun et al. 2020a, 2020b). By applying variational analysis using reversible thermodynamics, the concept of deficit curvature can be used to derive Young’s equation (Sun et al. 2020b). The characterization of wetting state by both deficit curvature and surface area coverage, however, is purely geometrical in perspective. The fundamental links between these geometrical measures and the energy perspective (Fig. 1) are currently limited to reversible thermodynamics. An important area of research would be to link these geometrical measures to the energy perspective using irreversible thermodynamics.

In the following, we will look at surface area coverage and deficit curvature via data from two-phase Lattice Boltzmann simulations on a North Sea sandstone. The data size is 1000$\times$1000$\times$750 voxels with a resolution of 1.8 micrometers. Further details on the micro-CT data are provided by Da Wang et al. (2020). For the simulations, a mixed-wet system was generated by using a morphological approach to achieve irreducible water saturation (McClure et al. 2021). Parts of the rock surface that touch oil get their own wetting conditions, while corners remain water-wet. The assigned surface wetting property represents an apparent wetting angle at the pore scale resulting from sub-pore-scale processes, as discussed in Sects. 4 and 5. Wettability of the system can then be defined by summing the cosines of the contact angles for each mineral/fluid/fluid combination, determined as

$$\begin{aligned} W = \sum (\gamma _{io}-\gamma _{iw})/\gamma _{wo} \phi _{i} \end{aligned},$$

(20)

where $\phi _{i}$ is the solid voxel fraction of mineral i, $\gamma _{io}$ is the interfacial tension between mineral i and the oil phase, and $\gamma _{iw}$ is the interfacial tension between mineral i and the water phase. This metric provides a scale from strongly water-wet ($W = 1.0$) to strongly oil-wet ($W = -1.0$). While there are certainly other ways to define the ‘wettability index,’ this approach is both practical and quantifiable for numerical simulation. For the following data, we simulated a homogeneous-wet system with $W = 1.0$ and a corner-wet system with $W = 0.1$, which we will look at in detail. We also simulate a large range of different wetting states characterized by W to establish overall trends.

Fig. 10

A sessile droplet on a smooth surface displaying one contact line loop ($N_c=1)$ and the conceptualized deficit curvature extending below the surface (a). A fluid cluster taken from a micro-CT flow experiment with Berea sandstone. The cluster has three contact line loops ($N_c = 3$) and Gaussian curvature for the fluid/solid and fluid/fluid interfaces. While the conceptualized deficit curvature cannot be visualized in 3D, this curvature is located within the curvature of the contact line loops

Deficit curvature explains the Gaussian curvature of an object that is due to the contact line and local contact angle. Recent works have shown how deficit curvature can be used to define a macro-scale (core-scale) contact angle $\theta ^\text {macro}$ that accounts for micro-scale variations along the contact line and the number of fluid rock contact points (Sun et al. 2020a, 2020b, 2020c). The macroscopic contact angle, $\theta ^\text {macro}$, is defined by normalizing the pore-scale deficit curvature $k_d$ with the number of contact line loops ($N_c$),

$$\begin{aligned} \theta ^\text {macro} =\frac{k_d}{4N_c} \end{aligned}$$

(21)

where $-\pi \le \theta ^\text {macro} \le \pi$, so that contact angle is on the interval $\left| \theta ^\text {macro}\right| \in [0,\pi ]$. An intuitive representation of $N_c$ and $k_d$ is provided in Fig. 10.

Fig. 11

Geometrical and topological measures that capture the wetting state. The relationship of deficit curvature and the number of contact line loops for 79 fluid droplets in the $W=0.1$ corner-wet condition (a) and 238 fluid droplets in $W=1.0$ homogeneous-wet condition (b). The relationship between surface area coverage and oil saturation for a range of wetting conditions W (c)

As shown in Fig. 11a, b, $k_d$ increases with $N_c$. The slope of the best-fit line by linear regression through the origin provides $4\theta ^\text {macro}$. The mean values of the local microscopic contact angle measurements ($\theta _\text {mean}$) for each contact point, and the macroscopic contact angle ($\theta ^\text {macro}$) by Eq. (21) for each fluid cluster, are measured for both data sets. For the homogeneous-wet system, $\theta ^\text {macro}$ is 74.5$^\circ$ and $\theta _\text {mean}$ is 86.2$^\circ$. For the corner-wet system, $\theta ^\text {macro}$ is 55.4$^\circ$ and $\theta _\text {mean}$ is 67.2$^\circ$. As expected, $\theta ^\text {macro}$ is not equal to the microscopic contact angle. Rather, it defines a core-scale geometric state (Sun et al. 2020a) analogous to how apparent contact angle defines the geometric pore-scale state; see Fig. 1. Since $k_d$ measures the contribution of the contact angle along the contact line to the object’s total Gaussian curvature, it naturally captures contributions from both advancing and receding contact angles. These contributions have been observed to ‘average’ in a way that corresponds to an intrinsic contact angle, $\theta _Y$. Therefore, the geometric approach could provide access to an intrinsic angle, while other methods do not. However, the correspondence has yet to be tested for a range of wetting conditions and topologically complex systems in which the target phase forms multiple loop-like structures.

Surface area coverage is shown in Fig. 11c, exhibiting trends similar to the experimental data reported by Garfi et al. (2020). With the numerical simulation, we are able to test a wide range of wetting conditions ($0.1<W<1.0$). Intuitively, as the system becomes less water-wet, the surface area coverage of oil increases. This effect is most evident for intermediate saturation. An important area of research would be the parameterization of surface coverage for different rock types and wetting states along with studies to elucidate the impact of dissipation. In addition, considering that the determination of deficit curvature also requires the measurement of surface area coverage along with the curvature of these interfaces, it is important to note that both measurements are intricately connected. This connection is observed in Fig. 11 where as $\theta ^\text {macro}$ increases, the surface coverage also increases. These geometrical measures are fundamentally linked through Hadwiger’s completeness theorem (Mecke 2000).

7 Influence of Spatial Wettability Distribution on Relative Permeability

Bentheimer sandstone was imaged with micro-CT and segmented for multiphase flow simulations using the lattice Boltzmann method presented by McClure et al. (2014). The image comprises 900$\times$900$\times$1600 voxels at 1.66 micrometer resolution (Dalton 2019). A mixed-wet system was generated by using the same morphological approach as explained in the previous Sect. 6. For the simulations, a wide range of wetting states defined by W were used.

Fig. 12

Effective permeability results based on lattice Boltzmann simulations using different wettabilities defined by W

Effective permeability results are presented in Fig. 12 for $8\times 10^{-6}<$ Ca $< 2 \times 10^{-5}$ and $-0.6< W < 0.9$. Steady-state simulations were performed using the LBPM software package, following open-source simulation protocols as described by McClure et al. (2021). Firstly, we observe a general increase in oil-phase effective permeability for any given saturation as the media becomes more water-wet. This is generally understood as the oil phase residing in larger pore regions under water-wet conditions, resulting in less resistance for flow. However, contrary to previous experimental work, we also observe a general increase in the water-phase effective permeability as the media becomes more water-wet. Under observation of the simulation results, we observe trapped water that is not mobilized at Ca $=1\times 10^{ -5}$, but even a slight increase in the Ca leads to the mobilization (and ultimately connection) of this trapped water. This may be partly due to the ‘corner wet’ situation, because the initial water configuration will have most of the water trapped in the corners, and with an energetically favorable local wetting condition (McClure et al. 2021). Apparently, a slightly higher Ca is needed to get these features to reconnect (as seen in Fig. 13b with Ca $=5\times 10^{-5}$). It is possible that experiments may not start by trapping quite as much water in the corners as the initial condition used in simulation. It is also possible that experiments may include transiently higher Ca that mobilize this water prior to establishing steady-state conditions. For example, local build-up of water could reconnect the connate water in the corners and then burst through the sample once the percolation threshold is exceeded.

The LBPM software package used also provides a framework to investigate disconnected phase flux (McClure et al. 2021). For the relative permeability data presented in Fig. 12, the connected and disconnected phase effective permeabilities are compared in Fig. 13. The disconnected oil-phase flux is nearly zero for all simulation cases. A contribution of disconnected phase flux is only observed for the water phase, which is likely an outcome of the ‘corner wet’ initial condition. An example of disconnected water-phase flux is observed when Ca increases to $5\times 10^{-5}$ for $W=-0.6$. A shift in $k_{rw}$ is observed; this is due to ganglion mobilization of disconnected water. This occurs over an intermediate range of saturation and likely in conjunction with transient connectivity effects, as presented by Gao et al. (2020) and Reynolds et al. (2017). This is currently an active area of research that is particularly important for enhanced oil recovery under flow with higher Ca (Lake 1989). Such effects can also be incorporated in advanced multiphase flow models, such as Picchi and Battiato (2019), Bedrikovetsky (2003), Khayrat and Jenny (2016) and/or used to encode relative permeability by using a phenomenological ‘equation of state’ (Khorsandi et al. 2017).

Fig. 13

Effective permeability results of the connected and disconnected phases. Ganglion mobilization is observed for the water phase under oil-wet conditions

Residual oil saturation is simply the saturation at which the oil-phase relative permeability is zero (Bear 2018). The actual determination of residual oil saturation, however, is nebulous, being highly dependent on the protocol used, in addition to the actual wetting state. Protocols range from unsteady-state floods at high Ca, steady-state flooding with a so-called bump flood, to centrifuging an oil saturated core (McPhee et al. 2015). For simulation purposes, the unsteady-state method at high Ca is convenient. The simulation curves display a minimum of residual oil saturation for intermediate-wet conditions ($W\approx 0$), in alignment with the results of Jadhunandan et al. (1995). It can also be observed that the smiley-face curve becomes more pronounced at higher Ca. Pore-scale modeling is sure to provide important insights into how these trends depend on method, spatially correlated wetting, and pore morphology (Foroughi et al. 2020, Akai et al. 2018). Another difficulty is that sufficiently large model domains need to be simulated to capture the correct viscous pressure drop (Hilfer et al. 2015) over the oil phase, and sufficiently long simulations must be conducted to reach residual saturation. This is particularly important for wetting conditions where the oil phase remains bi-continuous (Lin et al. 2019) at low saturation, which results in a low-conductivity percolating structure that requires significant simulation time to drain. The currently presented simulations required approximately $280 \times 10^6$ time steps to simulate all cases (Fig. 14).

Fig. 14

Residual oil saturation versus wettability (W) for relatively high-capillary number flows. Reprinted by permission from McClure et al. (2021)

8 Summary and Conclusions

In this work, we have consolidated the latest developments in wettability research, and we bring experimental measurements, theoretical understandings, and numerical modeling into the broader context of the multiscale nature of wettability in multiphase flow through porous media. Recent progress in pore-scale imaging and modeling clearly suggests that the spatial distribution of wettability exerts an important influence on pore-scale fluid occupancy and connectivity. The multiscale nature of wettability, however, complicates any direct interpretation of wettability at a given length scale. Therefore, a multistaged approach is suggested. Starting at the sub-pore scale, concepts of surface roughness, intrinsic contact angle, and the wetting state can be used to develop an effective contact angle model at the pore scale. As a consequence of effective contact angle distributions, the sequence of displacement events impacting the direction of contact-line movement and subsequent pinning, in situ-measured contact angles display a wide distribution bounded by advancing and receding contact angles. A geometrically consistent framework is then required to upscale the resulting wetting state to a core-scale measure. The concept of $\theta ^\text {macro}$ provides a measure of the deficit curvature per contact line loop, which is the amount of curvature along the contact line due to the wetting state. By understanding wettability through deficit curvature, within a general framework of integral geometry, we can provide a geometrical interpretation of the core-scale wetting state. This multistaged approach bridges the sub-pore length scale to the pore length, followed by bridging the pore length scale to the core length, through numerical simulations and integral geometry.

Linking the pore-scale and core-scale geometrical interpretations to a thermodynamically consistent model that accounts for energy dissipation remains an open challenge. The integral geometry concepts presented above, in combination with equilibrium thermodynamics and classical models for patterned surfaces (Cassie–Baxter and Wenzel), however, do largely explain experimentally observed relationships between dynamic and intrinsic contact angles. These concepts are also consistent with microscopic models for effective geometrical contact angles on rough surfaces where the microscopic fluid contacts are modeled explicitly. Thermodynamics-based models that bridge the pore to core length scales are largely based on reversible thermodynamics, but non-equilibrium thermodynamics would be required to account for entropy production during multiphase flow. Whether this is needed would depend on the flow regime and wetting state; conditions with low displacement efficiency ($E_d$) would warrant such an approach. By considering capillary pressure versus saturation measurements, the entropy dissipated over an entire cycle can be determined by Eq. (13). This would be a good starting point to assess the need for including dissipation, however, this approach does not identify the source(s) of entropy production. An important area for future research will be the development of more precise ways to account for dissipation and linking these to the wetting state.

Another goal is to estimate the 3D wettability maps required as input for numerical modeling to compute relative permeability functions on the basis of pore geometry and the surface energies of the constituents. Several experimental and modeling tools are required: a combination of micro-CT and SEM/EDX (e.g., QEMSCAN) to identify mineral phases, adsorption studies of surface-active crude oil components to estimate surface alteration, and AFM to measure surface roughness. The combination of surface energy and roughness in relation to the capillary pressure of interest then determines the stability of wetting layers and resulting microscopic fluid/solid contacts; these can then be used to estimate the effective contact angle on a mineral level using quasi-static modeling concepts. In this respect, the concept of surface area coverage would be useful for characterizing wetting on a per-mineral basis. While minerals are inherently water-wet; the establishing of thin films would likely differ between minerals due to differences in roughness and surface chemistry. Wettability maps are then a consequence of surface chemistry and roughness, which, in natural rock, can be estimated on the basis of 3D mineral distributions obtained from a sequence of analytical methods. Ultimately, the resulting wetting states can be used as input for numerical simulations to provide a 3D wettability map of the pore surface, in order to obtain relative permeability relationships. An important area of research would be establishing relationships (or lack thereof) between mineralogy and wettability at the pore scale for aged cores.

Overall, we extend the basic concepts of wetting to rock systems, introduce new characterization methodology, provide a review of reversible thermodynamics for multiphase systems, discuss the implications of irreversible processes, and suggest a multistage approach for numerical simulations. While wettability characterization and modeling from the sub-pore scale to the core-scale have been presented, there remain many open-ended questions. Therefore, the presented work is aimed at providing comprehensive guidance on the multiscale characterization of wettability in porous media that facilitates novel research.