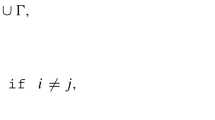1 Introduction

Multiphase flow through porous media is central to subsurface fluid transport processes, e.g., applicable to recovery of oil and gas, subsurface hydrology and \(\text{ CO }_2\) sequestration. Many biological systems and engineered systems such as fuel cells also rely on flow through porous media. Within such materials, the particular arrangement of fluids influences how flow and transport processes occur. The essential importance of geometric effects can be qualitatively understood based on the flow regime, which can involve both capillary and viscous fingering (Lenormand and Zarcone 1989; Saffman and Taylor 1958). The complex and varied structures that result lead to differences in macroscopic flow behavior, which are captured in continuum-scale models based on constitutive relations used to predict relative permeability and capillary pressure (Dullien 1991; Bear and Bachmat 1991; Morrow 1970). These standard constitutive models are usually assumed to depend on the fluid saturation, which leads to relationships that are both process-dependent and material-specific (Leverett 1941; Van Genuchten 1980). The effort to identify a more complete characterization for the geometric structure is motivated from the desire to construct constitutive models that hold for more general situations.

The fluid saturation corresponds to the only geometric quantity that can be directly measured in traditional experiments. As imaging techniques have become increasingly common, it is now possible to directly measure surface areas, interfacial curvatures, fluid connectivity and other geometric information (Armstrong et al. 2012; Porter et al. 2010; Wildenschild and Sheppard 2013). These measurements provide a basis to extend traditional models in a way that characterizes the system energy and behavior in a more complete way. In particular, the role of surface energy and fluid topology is known to be important for flows in porous media. A clear example is capillary trapping, which arises due the snap-off of regions of fluid that then become trapped within the pore space due to capillary forces (Roof 1970). The endpoints for traditional experiments correspond to cases where fluid connectivity breaks down such that only trapped fluid remains (Land 1968; Joekar-Niasar et al. 2013; Berg et al. 2013; Blunt et al. 2013; Rücker et al. 2015). At the endpoints, a connected pathway no longer exists within a particular fluid region, corresponding with the residual fluid saturation in reservoirs (Iglauer et al. 2011; Juanes et al. 2006). Since trapping pertains to the connectivity of the fluids, it relates to topological structure. Many important behaviors can be understood in terms of percolation theory (Larson et al. 1977; Berkowitz and Ewing 1998; Kueper and McWhorter 1992; Hunt 1998, 2004; Larson et al. 1981). Additional geometric effects are due the surface area and the interfacial curvature (Joekar-Niasar and Hassanizadeh 2012; Joekar-Niasar et al. 2012; Held and Celia 2001; Hassanizadeh and Gray 1990, 1993). A general geometric framework can be developed using the results of integral geometry (Mecke 1998; Vogel et al. 2010; Hilfer 2002; Arns et al. 2004; Schlüter and Vogel 2011; Lehmann et al. 2006, 2008; Arns et al. 2010; Schroeder-Turk et al. 2013; Armstrong et al. 2019). Within this context, the fluid topology is measured based on the Euler characteristic (Schlüter et al. 2016; Herring et al. 2013; Armstrong et al. 2016; Purswani et al. 2018). Existing evidence suggests that a unique relationship exists between the fluid volume, interfacial area, curvature and Euler characteristic (Herring et al. 2013; Schlüter et al. 2016; McClure et al. 2016; Miller et al. 2019; McClure et al. 2018). Efforts to use integral geometry to characterize the flow behavior are also underway (Purswani et al. 2018, 2020; Arne Slotte et al. 2020).

To be able to use the complete set of geometric invariants in extended models, adequate mechanisms are needed to evolve their behavior at the reservoir scale. New macroscopic equations must be formulated to predict the additional unknowns identified from integral geometry. A particular focus of this manuscript is to address the basic challenge of predicting discrete changes in fluid topology. Unlike other aspects of geometric evolution, topological changes are discontinuous in nature and therefore cannot be predicted based on differential geometry. Our approach addresses this fundamental challenge. The specific objectives of this manuscript are: (1) to develop an approach to model geometric relationships that is independent of both the material type and flow regime; (2) to link geometric measures with appropriate theory to understand and model the time evolution of fluid structures; and (3) to advance an approach to model the evolution of the Euler characteristic. To meet these objectives, we derive a non-dimensional relationship starting from the Minkowski–Steiner formula. The uniqueness of this relationship is evaluated by using a large number of fluid configurations obtained from systems with different porosity and considering structures that result from both capillary and viscous flow regimes. We demonstrate that our approach is able to predict the observed geometric relationships with near-perfect accuracy based on two degrees of freedom. The derived geometric state function is then used as a macroscopic equation to predict the evolution of the Euler characteristic during drainage and imbibition. The result is an important step toward the development of extended reservoir models for multiphase flow.

2 Geometric State of Fluids

Fig. 1
figure 1

An averaged description of the geometric state can be determined from the microscopic arrangement of fluids. Essential effects are due to material structure and flow regime: a synthetic Fontainebleau rock geometry with arrangement of quartz, feldspar and pore space; b fluid configuration obtained based on lattice Boltzmann simulation within Fontainebleau rock under viscous-dominated flow conditions with viscosity ratio \(M=100\); and c fluid configuration obtained for capillary-dominated conditions

Full size image

Integral geometry provides a theoretical basis to account for the structure of complex materials based on microscopic information. For fluids, the pore-scale configuration is influenced by material structure and flow regime as depicted in Fig. 1. An averaged description must account for the complexity of the resulting fluid distributions. Hadwiger’s characterization theorem establishes that only four invariant measures are needed to describe the structure of a three-dimensional object (Hadwiger 1957). These are the volume \(V_i\), the surface area \(A_i\), the integral mean curvature \(H_i\) and the Euler characteristic \(\chi _i\). A local relationship between these measures is stated in the Minkowski–Steiner formula, which is a kinematic evolution equation that predicts changes in volume based on the invariant properties of the boundary (Federer 1959). Here we consider structures that correspond with the shape of the non-wetting fluid, which is represented by the set \(\varOmega _i\). If we consider rolling a sufficiently small ball with radius \(\delta\) around the boundary of \(\varOmega _i\), the change in volume is predicted as a linear function of the scalar invariants

$$\begin{aligned} \varDelta V_i = \alpha _1 A_i \delta + \alpha _2 H_i \delta ^2 + \alpha _3 \chi _i \delta ^3 , \end{aligned}$$
(1)

where the change in volume is defined based on the set operation

$$\begin{aligned} \varDelta V_i \equiv V(\varOmega _i \oplus \delta ) - V(\varOmega _i) . \end{aligned}$$
(2)

The integral mean curvature is defined as

$$\begin{aligned} H_i = \int _{\varGamma _i} \frac{\kappa _1 + \kappa _2}{2} \mathrm{d}S \end{aligned}$$
(3)

where \(\kappa _1\) and \(\kappa _2\) are the principal curvatures along the surface. The Gauss-Bonnet theorem shows that Euler characteristic is directly proportional to the total curvature, which includes contributions from the Gaussian curvature of the object boundary \(\varGamma _i\) as well as the geodesic curvature \(\kappa _g\) associated with any non-smooth portions of the boundary \(\partial \varGamma _i\),

$$\begin{aligned} 4\pi \chi _i = \int _{\varGamma _i} \kappa _1 \kappa _2 \mathrm{d}S + \int _{\partial \varGamma _i} \kappa _g \mathrm{d}C. \end{aligned}$$
(4)

Note that the factor of \(4\pi\) is needed to account for the structure of a three-dimensional object rather than a two-dimensional surface (Serra 1983). Euler characteristic is related to the topology of the object and can be expressed as the alternating sum of the Betti numbers (Nagel et al. 2000),

$$\begin{aligned} \chi _i = B_0 - B_1 + B_2, \end{aligned}$$
(5)

where \(B_0\) is the number of connected components, \(B_1\) is the number of loops and \(B_2\) is the number of cavities enclosed within the object.

The Minkowski–Steiner formula is only valid for sufficiently small values of \(\delta\). The coefficients \(\alpha _1, \alpha _2\) and \(\alpha _3\) are particular functions of \(\varOmega _i\) and different coefficients may be obtained for different structures. However, recent work suggests that structures with identical geometric measures will be associated with identical coefficients when considered across the state space of many possible structures (McClure et al. 2019). For additional mathematical background pertaining to the scalar invariants, the reader is referred to the works of Federer (1959) and Klain (1995). Detailed reviews pertaining to the application to structural characterization are also available (Ohser et al. 2011; Armstrong et al. 2019; Mecke 1998; Hilfer 2002).

3 Non-dimensional Geometric Representation

Since length is the only unit that appears in Eq. 1, the Buckingham Pi theorem can be applied to reduce the number of independent variables from three to two (Buckingham 1914). Noting that the ratio \(r_i = A_i/H_i\) is the average radius of curvature for the boundary surface, we define a non-dimensional displacement

$$\begin{aligned} \delta ^\prime = \frac{H_i}{A_i}\delta . \end{aligned}$$
(6)

Based on a change of variables, a non-dimensional form is obtained to predict the change in volume fraction,

$$\begin{aligned} \varDelta \phi _i = \frac{A_i^2}{H_i V_\mathrm{total}} \Big (\alpha _1 \delta ^\prime + \alpha _2 \delta ^{\prime 2}\Big ) + \frac{\chi _i A_i^3}{H_i^3 V_\mathrm{total}} \alpha _3 \delta ^{\prime 3}. \; \end{aligned}$$
(7)

where \(\phi _i\) is the object volume fraction obtained by dividing the Minkowski–Steiner formula by a reference volume \(V_\mathrm{total}\). The result is a non-dimensional representation that is convenient for flow in porous media. In addition to the volume fraction, we identify two new non-dimensional parameters,

$$\begin{aligned} W_{i} = \frac{A_i^2}{H_i V_\mathrm{total}}, \quad X_{i} = \frac{\chi _i A_i}{ H_i^2}. \end{aligned}$$
(8)

The measure \(W_i\) is the product of the surface area density with the average radius of curvature for the surface of the object. The measure \(X_i\) is a surface-normalized Euler characteristic. The normalization factor \(H_i^2/A_i\) is equal to square of the average radius of curvature divided by the total surface area. Since the Euler characteristic measures the number of loops and connected components, the normalization factor can be interpreted as the average number of discrete features that the surface supports relative to surface area and curvature. The implication from the non-dimensional representation is that

$$\begin{aligned} F(\phi _i,W_i,X_i) = 0. \end{aligned}$$
(9)

This provides the basis to construct a non-dimensional hyper-surface that maps the relationships between different geometric states. We explore Eq. 9 within this more general context, as opposed to Eq. 7, which is an intrinsically local statement that pertains to a particular geometric configuration. The practical value of Eq. 9 depends on how it is manipulated to make predictions. Our effort will focus on developing a form to predict Euler characteristic. Since Euler characteristic measures the topology of an object, it undergoes a discontinuity each time the topology of the object changes. It is consequently not possible to derive an equation to predict the evolution of Euler characteristic based on results of differential geometry. An attractive alternative is to predict the Euler characteristic from the other geometric invariants. To do so we consider an alternate form for Eq. 9

$$\begin{aligned} X_i = f(\phi _i,W_i). \end{aligned}$$
(10)

While \(\chi _i\) can attain only integer values, \(X_i\) can vary continuously due to the dependence on \(H_i\) and \(A_i\). In the event that \(\phi _i\), \(A_i\) and \(H_i\) are known and an adequate approximate functional representation can be constructed, Eq. 10 can be used to predict Euler characteristic. The motivation for constructing such a function is understood by considering geometric evolution processes within a hierarchical perspective. Toward this end we seek to further understand how structures and their associated invariant measures change with time.

4 Geometric Evolution: A Hierarchical Perspective

One can gain insight into the nature of geometric discontinuities by considering the time evolution based on a hierarchical view of Eq. 1. The Minkowski–Steiner formula is derived for parallel sets, which restricts the generality of the result. The simplification to consider parallel sets addresses the underlying difficulty of deriving geometric results analytically. Given an arbitrary three-dimensional object, we consider continuous changes in volume such that the first derivative can be defined with respect to time. From Eq. 1 we can easily see that if \(\delta\) is sufficiently small

$$\begin{aligned} \varDelta V_i(t) = \alpha _1 A_i (t) \delta + \mathcal {O}(\delta ^2) . \end{aligned}$$
(11)

That is, the infinitesimal change in volume depends only on the movement of the boundary, and the surface area is the only boundary invariant on which the volume change depends. The same insight can be obtained by applying the Reynolds transport theorem to the region \(\varOmega _i\) to predict the time rate of change for the volume

$$\begin{aligned} \frac{d V_i}{d t} = \int _{\varGamma _i} (\varvec{w}_i \cdot \varvec{n}_i) \mathrm{d}S , \end{aligned}$$
(12)

where \(\varvec{n}_i\) is the outward normal to the boundary and \(\varvec{w}_i\) is the boundary velocity. The time derivative for the surface area and integral mean curvature can also be identified from boundary integrals. Since the change in surface area due to the deformation of a local surface element is determined by the curvature of the surface element (Gray and Leijnse 1993),

$$\begin{aligned} \frac{d A_i}{d t} = \int _{\varGamma _i} \frac{\kappa _1 + \kappa _2}{2} (\varvec{w}_i \cdot \varvec{n}_i) \mathrm{d}S , \end{aligned}$$
(13)

and similarly for the mean curvature,

$$\begin{aligned} \frac{d H_i}{d t} = 2 \int _{\varGamma _i} {\kappa _1 \kappa _2} (\varvec{w}_i \cdot \varvec{n}_i) \mathrm{d}S \; . \end{aligned}$$
(14)

Equations 12–14 describe how the geometric invariants evolve during the continuous portions of the geometric evolution of an object. These integrals capture both the growth and the deformation of the object boundary. They do not describe changes in the topological structure of the object, which are discrete. Since the Betti numbers in Eq. 5 are countable, a time derivative cannot be defined for \(\chi _i\) when a topological change occurs, since the limit defining the time derivative does not exist.

Since Eqs. 12–14 are integral equations, approximations are needed to define practical approaches to their solution. There is a clear link between these general expressions and the Minkowski–Steiner formula, which provides an intuitive basis for how topological source terms arise within geometric evolution. To see this link we make the following definitions

$$\begin{aligned} \xi _{1}\equiv & {} \frac{1}{A_i} \int _{\varGamma _i} \varvec{w_i} \cdot \varvec{n_i} \mathrm{d}S , \end{aligned}$$
(15)
$$\begin{aligned} \xi _{2}\equiv & {} \frac{1}{H_i} \int _{\varGamma _i} \frac{\kappa _1 + \kappa _2}{2}(\varvec{w_i} \cdot \varvec{n_i}) \mathrm{d}S , \end{aligned}$$
(16)
$$\begin{aligned} \xi _{3}\equiv & {} \frac{1}{\chi _i} \int _{\varGamma _i} \kappa _1 \kappa _2(\varvec{w_i} \cdot \varvec{n_i}) \mathrm{d}S . \end{aligned}$$
(17)

These quantities represent rates for the geometric displacement that functionally alter the scalar invariants based on infinitesimal change, a result that is not restricted to parallel sets. Each term can vary independently to allow the surface to stretch and deform in a general way. These changes are determined based on the boundary shape and the boundary speed in the normal direction, defined for convenience as

$$\begin{aligned} \xi \equiv \varvec{w}_i \cdot \varvec{n}_i \end{aligned}$$
(18)

It is easy to see that a parallel set will result for the special case where \(\xi\) is constant everywhere on \(\varGamma _i\). In this case the system of integral equations is simplified and we can make a direct link with Eq. 11. For a volume change over some time dt, it is evident that \(\delta = \xi _1 \mathrm{d}t = \xi _2 \mathrm{d}t= \xi _3 \mathrm{d}t = \xi \mathrm{d}t\) and \(\alpha _1=1\), meaning that Eqs. 12–14 may be expressed as

$$\begin{aligned} \frac{\mathrm{d} V_i}{\mathrm{d} t} = & {} A_i(t) \xi , \end{aligned}$$
(19)
$$\begin{aligned} \frac{\mathrm{d} A_i}{\mathrm{d} t} = & {} \alpha _2 H_i(t) \xi , \end{aligned}$$
(20)
$$\begin{aligned} \frac{\mathrm{d} H_i}{\mathrm{d} t} = & {} \frac{\alpha _3}{\alpha _2} \chi _i(t) \xi . \end{aligned}$$
(21)

That is, to predict the time evolution we need to know the coefficients \(\alpha _2\) and \(\alpha _3\) as well as the Euler characteristic \(\chi _i\). Based on these arguments, it is intuitive to express the Minkowski–Steiner formula in a hierarchical manner,

$$\begin{aligned} \varDelta V_i = \left[ A_i + \alpha _2 \left( H_i + \frac{\alpha _3}{\alpha _2 } \chi _i \delta \right) \delta \right] \delta . \end{aligned}$$
(22)

Within this hierarchical context, the Euler characteristic represents a source term that constrains how the overall shape of the object can evolve based on the effect of the microscopic Gaussian curvature.

While Eqs. 12– 14 represent a system of integral equations that can be approximated and solved to predict the evolution of \(V_i\), \(A_i\) and \(H_i\), it is evident from these expressions that \(\chi _i\) is required to close the system of equations. An additional equation is needed to predict Euler characteristic. To obtain this we rearrange Eq. 10,

$$\begin{aligned} \chi _i = V_\mathrm{total} \frac{H_i^3}{A_i^3} f(\phi _i,W_i) , \end{aligned}$$
(23)

where the right-hand side is entirely determined based on knowledge of \(\phi _i\), \(A_i\) and \(H_i\). In principle, once the form of \(f(\phi _i,W_i)\) is obtained it can be used to predict the Euler characteristic of any structure.

5 Geometric Evolution: A Simple Example

Consider first the change in volume that results when growing a sphere with radius r to the larger sphere with radius \(r+\delta r\)

$$\begin{aligned} V(\varOmega _i \oplus \delta r ) -V(\varOmega _i) = & {} \frac{4 \pi }{3} (r+\delta r )^3 - \frac{4 \pi }{3} r ^3\nonumber \\ = & {} A_i \delta r + H_i (\delta r)^2 + \frac{4\pi }{3}\chi _i (\delta r)^3 , \end{aligned}$$
(24)

where expressions for the geometric invariants associated with a sphere have been inserted: \(A_i=4\pi r^2\), \(H_i=4\pi r\) and \(\chi _i=1\). Comparing with Eq. 1 we quickly see that the coefficients are \(\alpha _1 = 1\), \(\alpha _2 = 1\) and \(\alpha _3 = 4\pi /3\). Next we consider a torus with major radius R and minor radius r

$$\begin{aligned} V(\varOmega _i \oplus \delta r \zeta ) -V(\varOmega _i) = & {} 2 \pi ^2 (r+\delta r )^2 R - 2 \pi ^2 r^2 R \nonumber \\ = & {} A_i \delta r + H_i (\delta r)^2 \end{aligned}$$
(25)

using the fact that for the torus \(A_i=4\pi ^2 rR\), \(H_i=2 \pi ^2 R\) and \(\chi _i=0\). Again referring to Eq. 1, we see that \(\alpha _1 = 1\) and \(\alpha _2 = 1\). Even though \(\chi _i=0\) for a torus, identical coefficients are obtained for the two structures.

Fig. 2
figure 2

The evolution of a torus into a sphere. The center hole of the torus closes at \(t=1\) causing a jump condition in the Euler characteristic. Plots showing the c surface area and d integral mean curvature as a function of time based on the evolution of a torus into a sphere. The hole in the center of the torus closes at time \(t=1\), resulting in time dependence that is non-smooth. Changes in connectivity are linked to a breakdown in local smoothness, presenting a fundamental challenge to modeling the geometric evolution and associated physics

Full size image

An important challenge associated with modeling geometric evolution is that changes in the connectivity of an object occur as discrete events: \(\chi _i(t)\) is not a continuous function. This means that while the volume, surface area and integral mean curvature will necessarily be continuous functions, the Euler characteristic will evolve based on a series of discrete jumps. To illustrate this behavior, we consider the geometric evolution of a torus into a sphere as shown in Fig. 2. This relatively simple problem is significant because it defines a change in connectivity. The initial torus has \(\chi =0\); for the final sphere \(\chi =1\). Based on Eq. 5 we can see that for the torus \(B_0 = 1\), \(B_1 = 1\) and \(B_2=0\); for the sphere \(B_0 = 1\), \(B_1 = 0\) and \(B_2=0\). The single handle disappears at the instant the hole in the center of the torus closes, representing a discontinuity in the geometric evolution process. We now examine the ramifications for this change. Specifically, we will show that the discontinuity in the time evolution for the Euler characteristic leads to non-smooth behavior for the other geometric invariants.

The torus is defined based on a surface of revolution for a circle with minor radius r that is displaced from the origin based on the major radius R. We choose initial minor radius \(r_0= 1/4\) with r an increasing function of time,

$$\begin{aligned} r(t) = r_0 + \frac{t}{4} . \end{aligned}$$
(26)

We enforce \(r+R =1\) such that the object has constant unit width. For time \(t<1\), the circle has radius \(r < R\) and the surface of revolution is a torus. At time \(t=1\) the circle has radius \(r=R=1/2\), closing the hole in the center. The surface becomes a spindle torus for \(1<r<3\). At \(t=3\) the object is the unit sphere. The associated three-dimensional structures are shown in Fig. 2.

To compute the geometric invariants, we rely on expressions derived for surfaces of revolution. The circle is parameterized by

$$\begin{aligned} x(s) = & {} R + r \cos (s) \end{aligned}$$
(27)
$$\begin{aligned} y(s) = & {} r \sin (s). \end{aligned}$$
(28)

Since the surface of revolution is self-intersecting for \(r>R\), the limits of integration are defined based on the angle

$$\begin{aligned} \alpha = \left\{ \begin{array}{cl} \arccos (R / r) &{} \text{ if } r>R \\ 0 &{} \text{ otherwise. } \end{array} \right. \end{aligned}$$
(29)

The principle curvatures are

$$\begin{aligned} \kappa _1= & {} \frac{1}{({x}^{\prime 2} + {y}^{\prime 2})^{3/2} } \big ( -{x}^{\prime \prime } {y}^{\prime } + {x}^{\prime } {y}^{\prime \prime } \big ), \end{aligned}$$
(30)
$$\begin{aligned} \kappa _2= & {} \frac{1}{({x}^{\prime 2} + {y}^{\prime 2})^{1/2} } \frac{{y}^{\prime }}{x} . \end{aligned}$$
(31)

The surface area is

$$\begin{aligned} A(t) = & {} 2 \pi \int _{-\pi + \alpha }^{\pi - \alpha } x(s) \sqrt{{x}^{\prime 2} + {y}^{\prime 2}} \mathrm{d}s \nonumber \\ = & {} 2 \pi [Rr (2 \pi - 2\alpha ) +2r^2 \sin (\alpha )] \end{aligned}$$
(32)

For time \(t<1\), \(\alpha =0\) and the expression reduces to \(A=4\pi Rr\). For time \(t=3\), the expression for a sphere is obtained, \(A=4\pi r^2\), since \(R=0\). Based on a similar calculation, we can calculate the integral mean curvature

$$\begin{aligned} H(t) = & {} \pi \int _{-\pi + \alpha }^{\pi - \alpha } (\kappa _1 + \kappa _2) x \sqrt{{x}^{\prime 2} + {y}^{\prime 2}} \mathrm{d}s\nonumber \\ = & {} 2 \pi R (\pi - \alpha ) + 4 \pi r \sin (\alpha ). \end{aligned}$$
(33)

Eqs. 32 and 33 are plotted in Fig. 2, clearly showing that while A(t) and H(t) are both continuous functions, the time derivatives are discontinuous at the instant that the hole in the middle of the torus closes (\(t=1\)). This is also associated with a jump condition in the Euler characteristic from \(\chi =0\) to \(\chi =1\). Predicting when such topological changes occur requires non-local information regarding the geometric structure of the object.

The jump condition due to the topological change produces a cascade effect that propagates to other variables. Equations 19– 21 offer further insight into how the jump condition for the Euler characteristic propagates to the other geometric invariants. From Eq. 21 we can deduce that \(H_i(t)\) is not differentiable whenever the topology of the system changes, which is implied by the dependence on \(\chi _i\). \(A_i(t)\) inherits a discontinuity in the second-order time derivative from \(H_i\). Both results are confirmed based on inspection of Fig. 2c, d. It can also be seen that since the spindle torus does not satisfy the requirement of positive reach, \(\alpha _2\) and \(\alpha _3\) are time-dependent. However, this apparently does not alter the associated differentiability class for \(H_i\) or \(A_i\). Of course, more favorable smoothness properties should be expected for time regions where no topological changes occur.

In general, geometric evolution may be described by a sequence of continuous geometric transformations \(G_k^t: \varOmega \rightarrow \varOmega\) that describe deformation at constant topology from time \(t_{k-1}< t < t_k\). These are separated by a sequence of discrete geometric transformations \(G_k^*: \varOmega \rightarrow \varOmega\) occurring at times \(t_k\) and defining topological changes. For any topological change, a one-to-one mapping cannot be defined for the geometric evolution. This is evident from considering the evolution shown in Fig. 2 at \(t=1\). Prior to the topological change we can identify the ring of points at the interior boundary of the torus \(x,y: x^2+y^2-(R-r)^2 = 0; z=0\). At time \(t=1\) the ring closes such that the entire ring of points are mapped to the origin, which means that the associated mapping is not one-to-one. The geometric evolution can be modeled based on continuous deformation of the structure for \(t<1\) and then again for \(t>1\), but not for \(t=1\).

6 Classification of Topological Changes

Only a limited number of topologically distinct structures are possible within a particular dimensional space (Thurston 1997). In a three-dimensional system, all possible topological states can be reduced to the analysis of three fundamental shapes: the sphere, the torus, and the spherical shell. These shapes are linked to the Betti numbers: the sphere is a single connected component and links to \(B_0\); the torus has a single loop and links to \(B_1\); the spherical shell contains a single cavity and links to \(B_2\). To form more complex structures, these shapes can be placed in a system, first gluing objects together as needed, then stretching and deforming the resulting object until a desired structure is obtained. Based on this, it is possible to characterize the possible topological changes that may occur during geometric evolution, i.e., the discontinuous maps \(G^*_k\). These eight possibilities are depicted in Fig. 3.

Fig. 3
figure 3

Discontinuous geometric maps in three dimensions fall into eight categories based on homeomorphism. The associated topological changes increase or decrease Euler characteristic by exactly one

Full size image

Objects on left side of Fig. 3 can be produced by continuously stretching and deforming a sphere (i.e., homeomorphisms). The depicted topological transformations increase or decrease the Euler characteristic by exactly one. Moving left to right for case A, the snap-off mechanism generates two regions homeomorphic to a sphere from a single such region. The consequence is to increase Euler characteristic by one due to the corresponding increase in \(B_0\). The coalescence mechanism corresponds to the opposite situation, where two regions merge together to destroy one connected component. The pair of transformations labeled as B rely on the same underlying mechanism, in this case either forming or destroying a loop. Moving left to right, the Euler characteristic decreases by one due to a corresponding increase to \(B_1\). Snap-off has the opposite effect.

For the four transformations labeled as A and B, the singularities are isolated to particular points, which represent the sub-regions of the set for which the mapping is not bijective. For the four transformations labeled as C and D, the singularity involves a ring structure. For the pair of transformations labeled as C, the puncture mechanism forms a ring of points at the location of the singularity. This transformation increases \(B_1\) and decreases \(\chi\). The closure mechanism involves the collapse of a ring of points to the singularity, destroying the loop. This is the evolution considered in Fig. 2. The pair of transformations shown in Fig. 3 D demonstrate that the closure mechanism can also form a cavity starting from a bowl-shaped region. This increases both \(B_2\) and \(\chi\) by one. The puncture mechanism can re-open the hole to destroy the cavity. For each of the eight cases, the associated mappings are not bijective. Noting that a single object can undergo multiple such transformations, we can always identify a neighborhood of points that surround the singular point, effectively isolating each discontinuity in space and time.

7 Approximation for the Mean Curvature

Of the four Minkowski functionals, only the volume fraction is included explicitly in traditional reservoir-scale models (Trangenstein and Bell 1989). Geometric theory suggests that three additional variables are needed to capture the geometric state from a macroscopic perspective. Our work shows that only two of these are independent, with the length scale simply scaling the non-dimensional relationship. Additional equations are therefore needed to predict the additional unknowns. The logical path to obtain a closed system of equations is by approximating the integral equations given by Eqs. 12–14. It is evident from Eq. 21 that the time derivative for the integral mean curvature will be discontinuous during a topological change due to the contribution of the Gaussian curvature. The associated fluid singularities are already well-established based on simple experiments involving droplet coalescence (Orme 1997; Wu 2004; Ristenpart et al. 2006; Dirk et al. 2005; Case and Nagel 2008; Paulsen et al. 2011, 2012, 2014). Here we present an approximation to replace the mean curvature dependence with the fluid pressure difference based on the capillary pressure. The integral mean curvature for the non-wetting fluid boundary can be obtained by decomposing the integral into two parts using the additive property of a definite integral. The first contribution is associated with fluid-fluid interfaces; the second contribution is associated with the interface between the non-wetting fluid and solid,

$$\begin{aligned} H_i = J_\mathrm{wn} A_\mathrm{wn} + J_\mathrm{ns} A_\mathrm{ns} , \end{aligned}$$
(34)

where \(J_\mathrm{wn}\) is the average meniscus curvature for the interface between fluids, \(A_\mathrm{wn}\) is the associated interfacial area, \(J_\mathrm{ns}\) is the curvature for the interface between the non-wetting fluid and the solid grain, and \(A_\mathrm{ns}\) is the associated interfacial area (McClure et al. 2018). To eliminate the mean curvature of the meniscus, we introduce an approximation to replace the contribution from the mean curvature with the fluid pressure difference, which is defined relative to the non-wetting fluid. Based on the Young–Laplace equation for a water-wet system, we introduce the approximation

$$\begin{aligned} J_\mathrm{wn} \approx \frac{p^\mathrm{n}-p^\mathrm{w}}{\gamma } , \end{aligned}$$
(35)

where \(p^\mathrm{n}\) and \(p^\mathrm{w}\) are the average fluid pressure within the non-wetting fluid n and water w with \(\gamma\) the interfacial tension between fluids. This form is not exact since the Young–Laplace equation holds only at equilibrium and is constrained by the connectivity of the fluids. We nevertheless expect the approximation to be reasonable. We assume that the curvature of the solid is inversely related to the Sauter mean grain diameter \(D_\mathrm{s}\),

$$\begin{aligned} J_\mathrm{ns} \approx \frac{2}{D_\mathrm{s}} . \end{aligned}$$
(36)

Using these approximations we introduce an approximation for the integral mean curvature

$$\begin{aligned} H_{i} \approx \frac{p^\mathrm{n} - p^\mathrm{w}}{\gamma } A_\mathrm{wn} + 2 \frac{A_\mathrm{ns}}{D_\mathrm{s}} . \end{aligned}$$
(37)

This approximation is convenient because the fluid pressures \(p^\mathrm{w}\) and \(p^\mathrm{n}\) are already included in macroscopic reservoir models. The interfacial tension \(\gamma\) is usually a known parameter, and the grain diameter \(D_\mathrm{s}\) is tabulated for many geologic materials and linked to the permeability. We substitute this approximation for \(H_i\) in the results presented in this work. In combination with Eq. 10, two additional unknowns remain, which are the interfacial areas \(A_\mathrm{wn}\) and \(A_\mathrm{ns}\). Geometric evolution equations for interfacial area have been previously published for flows in porous media (Gray et al. 2015).

8 Materials and Methods

The focus of our effort is to construct an approximation for Eq. 10 and evaluate the extent to which this form is able to model geometric states in general porous media. To accomplish this it is essential that many fluid configurations be considered and that data capture the effects of fluid history within a wide range of geological materials. In previous work, six different materials were used to evaluate material-specific relationships in various types of porous media (McClure et al. 2018). Additional digital rock models used in this study are based on Fountainebleau sandstones. Fountainebleau sandstone is a type of outcrop that produces samples with a well-sorted and regular grain size distribution and are considered as a simple natural porous media. They have a good reproducibility of flow patterns in various types of flooding experiments, and hence Fontainebleau outcrops are widely used for investigation of pore-scale physics and flow properties. The geology and physical properties of Fontainebleau are well documented in the literature, e.g., in Fredrich et al. (1993). Fountainebleau sandstones consist almost entirely of quartz minerals with very little presence of clay. The grain size distribution is regular and well-sorted with grain size distributions in the range of 150 to 300 \(\mu\)m and pore body diameters generally ranging from 16 to 30 \(\mu\)m. However, the porosity can vary widely, in the range from 0.02 to 0.35, due to natural quartz cementation in the pore space. This natural variation in porosity makes the outcrop well suited for studies of properties that correlates with porosity and flow permeability. Such studies include porosity and permeability correlations (Gomez et al. 2010) and pore space geometric and tortuosity relationships. Sensitivity of trapped and residual fluid distributions from initial states are also well studied in Fontainebleau geometries (Tanino and Blunt 2012; Ruspini et al. 2017). Images of Fontainebleau sandstones were also one of the first realistic geometries used for lattice Boltzmann flow simulations (Martys and Chen 1996).

Four different synthetic digital pore-scale models were generated based on grain size distributions from 2D thin sections of Fontainebleau sandstone. The 3D models were made using a process-based approach that simulates grain sedimentation and diagenesis (Øren and Bakke 2002). We used Thermo-Fisher Scientific’s commercial software e-Core for this purpose. The same grain distributions were used, but porosity was adjusted using a quartz cementation algorithm in the diagenesis. This mimics the natural rock forming process found in Fontainebleau sandstones that generates the variation in porosities. The rock porosities for the four digitized samples were 0.104, 0.150, 0.200 and 0.252. An illustration of the resulting models is shown in Fig. 1a. Simulations generated for these systems were aggregated with previously generated data for granular packings, sandstones, and a carbonate system. A wide range of fluid states were thereby generated based on porous materials with porosity varying from 0.10 to 0.38. Our approach considers the prediction of all possible fluid states from a single relationship.

Pore-scale simulation provides a convenient means to generate realistic fluid configurations. A two-fluid color lattice Boltzmann method was used to perform flow simulations using the generated digital rock geometries (McClure et al. 2014). For each media, initial fluid configurations were established based on the morphological drainage operation with water saturation ranging from 0.15–0.90. Morphological drainage provides a reasonable approximation for observed fluid configurations along primary drainage in water-wet porous media (Hilpert and Miller 2001; Adalsteinsson and Hilpert 2006). This provides a convenient initial condition to simulate various displacements such that a wide range of possible fluid configurations can be explored. Imbibition, secondary drainage, and secondary imbibition processes were simulated by setting constant flux boundary condition to inject fluids into the system to alter the fluid geometry (McClure et al. 2018). Capillary and viscous effects also play a role in determining the fluid structure, which can lead to topological changes even when the volume fractions are constant (Armstrong et al. 2016). To account for these effects, simulations were performed over a range of capillary numbers and for viscosity ratio \(M=1\) and \(M=100\) as a means to generate states linked with both viscous and capillary-dominated regimes. The overall objective of the simulation design was to produce a wide range of fluid configurations based on different initial conditions and flow histories as a means to cover the space of possible geometric states. Example fluid configurations obtained within Fontainebleau rock are shown in Fig. 1b, c. These figures show that topological structure for fluids will vary depending on the flow regime. The different shapes associated with viscous and capillary fingering lead to different loop formation and snap-off patterns, which alter the fluid topology. Viscous fingers are comparatively narrower, less stable, and more prone to break apart during displacement.

9 Results

Fig. 4
figure 4

Data points obtained from simulation in ten different porous media with porosity varying between 0.10 and 0.38. The shape of a representative hysteresis loop is plotted for each measure, including drainage (solid line) and imbibition (dashed line). The measures include: a normalized capillary pressure; b surface area per unit volume; c integral mean curvature per unit volume; and d Euler characteristic per unit volume. All data points can be collapsed onto a single two-dimensional hyper-surface based on the non-dimensional representation given in Eq. 10

Full size image

Several hundred simulations were performed across the ten different porous media, yielding 239, 203 distinct fluid configurations. Within each material sixteen different initial conditions were used, and one set of simulations with viscosity ratio (oil-to-water) \(M=1\) and a second set with \(M=100\). The flow rate was controlled based on a flux boundary condition, and multiple flow reversals were performed within each simulation. The duration of individual simulations varied between \(1.4\times 10^6\) and \(2.516 \times 10^6\) timesteps. The minimum capillary number for the displacements was \(7.15\times 10^{-8}\) and the maximum capillary number was \(1.2\times 10^{-4}\), which was determined based on the flux of water

$$\begin{aligned} \mathrm{Ca} = \frac{\mu _\mathrm{w} |\varvec{v}_\mathrm{w}|}{\gamma } , \end{aligned}$$
(38)

where \(\mu ^\mathrm{w}\) is the water viscosity, \(\varvec{v}_\mathrm{w}\) is the water velocity, and \(\gamma\) is the interfacial tension between fluids. Geometric measurements obtained from the fluid flow simulations are shown in Fig. 4. Scatter plots show how relevant measures are distributed in terms of the fluid volume fraction \(\phi _i\). The scatter plots show that the data is dense with respect to the range of observed values, and that measurements obtained from different materials overlap. To aid in the interpretation of the data, the shape of a typical hysteresis loop is inscribed on each sub-figure, with the solid line depicted a drainage process and the dashed line depicting imbibition. Scanning curves enhance the density of the measurements such that a wider range of states are included for each material. Based on Eq. 10 there are two degrees of freedom associated with \(\phi _i\) and \(W_i\). The latter quantity is directly computed from data in Fig. 4. The domain for the function \(f(\phi _i,W_i)\) corresponds to the points shown in Fig. 5.

Fig. 5
figure 5

Non-dimensional form for geometric state relationship obtained based on simulation data from ten different porous media based on a wide range of flow conditions. The volume fraction \(\phi _i\) and normalized surface area density \(W_i\) are the independent variables for the non-dimensional relationship

Full size image

The non-dimensional relationship stated in Eq. 10 was assessed by fitting a generalized additive model (GAM) to obtain an approximate form. GAMs are statistically optimized smooth splines that are constructed to minimize errors for the fitting surface. The GAM approximates the dependence of \(X_i\) along the two-dimensional hyper-surface defined based on \(\phi _i\) and \(W_i\). For each point in Fig. 5 there is a corresponding measured value of \(X_i\) determined from the lattice Boltzmann simulations. The function \(f(\phi _i,W_i)\) is optimized using this data to predict \(X_i\). If two simulations produce data with identical \((\phi _i,W_i)\) but different \(X_i\), the function cannot simultaneously represent both values. These situations are the sources of error for the GAM. If these situations are common, the error measures for the model will be high and the constructed approximation to \(f(\phi _i,W_i)\) will fail to reliably predict \(X_i\). We consider two error measures to assess the quality of the fit: the coefficient of variation (\(R^2\)) and the generalized cross-validation (GCV). For a perfect fit \(R^2=1\) and GCV \(=0\). For the data shown in Fig. 5 the GAM was able to explain 97.5% of the variance in the underlying data (\(R^2 = 0.975\)) and the generalized cross-validation (GCV) was \(6.91 \times 10^{-6}\). The uniqueness of \(V_i(A_i, H_i, \chi _i )\) was also assessed by comparing the geometric invariants using a GAM fit. Including all generated data, the 3D GAM was able to explain 99.7% of the variance in the underlying data (\(R^2 = 0.997\)). The associated GCV was \(1.13 \times 10^{-5}\). The quality of fit for both cases is comparable to the quality of fit for material-specific relationships developed to predict capillary pressure (McClure et al. 2018). It is notable that the quality of fit for the non-dimensional form remains excellent even though there is one fewer degree of freedom. The essential meaning of the geometric state function is to characterize the possible shapes that can exist based on the associated geometric invariants. An important implication of this result is that geometric relationships can be developed that are independent of the type of material considered, with the state function providing a map of the shapes that can exist. Potential applications for this result are quite broad.

10 Predicting Euler Characteristic from the Geometric State

Since Euler characteristic is linked to the topology of an object, changes to \(\chi _i\) are inherently discrete. As the fluid geometry evolves, new loops can be formed or regions of fluid may snap off to increase the number of connected components. These changes are countable in nature and cannot be predicted from differential equations. The form of Eq. 10 is constructed to address this dilemma. The non-dimensional measure \(X_i\) includes the effects of topology based on the dependence on \(\chi _i\) and also depends on the curvature and surface area due to \(H_i\) and \(A_i\). Even though \(\chi _i\) is integer valued, \(X_i\) can vary in a smooth way. This is important, since smoothness is an underlying assumption used to construct local splines within the GAM. With the geometric state function given by Eq. 10 known, Euler characteristic can be predicted from Eq. 23. The previously constructed GAM provides a numerical representation for this function that has been optimized based on simulation data from all ten porous media. We now evaluate this function to show that Eq. 23 can be used to predict history-dependent \(\chi _i\) for a drainage-imbibition sequence within a sand pack.

Simulated data for the drainage-imbibition sequence provides \(\phi _i\) and \(W_i\) based on measured values for \(V_i\), \(A_i\) and \(H_i\). The trajectory along the non-dimensional hyper-surface is shown in Fig. 6a. Increasingly negative values for \(X_i\) are encountered as \(\phi _i\) and \(W_i\) increase, which is due to the decrease in \(\chi _i\) that results from the formation of loops as the capillary pressure increases. Many of the loops formed during primary drainage are preserved during imbibition. This effect is mirrored by the history-dependence of \(W_i\). With both \(\phi _i\) and \(W_i\) known, \(\chi _i\) can be predicted with reasonable accuracy; Fig. 6b shows a comparison between the measured and predicted values of \(\chi _i\) for the displacement. The essential characteristics for the behavior of \(\chi _i\) are captured, showing that the evolution of Euler characteristic can be identified from the geometric state function as given by Eq. 10.

Fig. 6
figure 6

Evaluation of the non-dimensional form to predict Euler characteristic: a hysteresis loop for simulated drainage-imbibition sequence within a sand pack based on the non-dimensional representation obtained from Eq. 8. The star represents the residual non-wetting fluid that remains trapped within the pore structure following first imbibition; b prediction of Euler characteristic for a simulated drainage-imbibition sequence within a sand pack based on application of Eq. 23 with the GAM approximation for \(f(\phi _i,W_i)\)

Full size image

In practice, the most significant errors in the GAM approximation are encountered for structures with very low volume fraction. This is due to the fact that scale-dependent measures will be poorly represented when \(V_\mathrm{total}>> V_i\) (McClure et al. 2016). The consequences of this are most evident when attempting to predict Euler characteristic early in a primary drainage process, when the non-wetting fluid volume fraction is small and below the percolation threshold. Noting that \(\chi _i=0\) corresponds to the percolation threshold, a simple solution is to anchor the prediction \(X_i(\phi _i = 0, W_i = 0) = 0\). Note that this solution is always physical along primary drainage. Results of percolation theory further suggest that along primary drainage \(\chi _i\) will not change until the entry pressure for the porous medium is exceeded (Hilfer 1992; Hunt 2004; Kueper and McWhorter 1992; Larson et al. 1977; Berkowitz and Balberg 1993). Indeed, simulation results demonstrate that loop formation is most significant after breakthrough, particularly near the irreducible water saturation when capillary pressure attains larger values as the interfacial curvature increases. The strategy of anchoring the boundary point is used to establish the limiting behavior for primary drainage for the results shown in Fig. 6b.

The fluid volume fraction is typically evolved in existing macroscale simulators, as are the fluid pressures. We use this information to predict \(H_i\) according to the approximation given in Eq. 37. The Euler characteristic can thereby be obtained by adding only two new unknowns, which are the surface areas \(A_\mathrm{wn}\) and \(A_\mathrm{ns}\). Both surface areas are needed by Eq. 37, with their sum providing the total surface area of the non-wetting fluid. Evolution equations for interfacial area have been previously published within the context of multiphase flow in porous media (Gray and Miller 2014). The described approach thereby provides a realistic path to formulate closed models for the geometric aspects of macroscopic theory.

11 Summary

Fig. 7
figure 7

Modeling geometric evolution for fluids in porous media. a–b Predicting how the average fluid geometry changes with time must account for topological effects such as loop formation, which are measured based on the Euler characteristic; c Invariant measures identified from integral geometry are the basis for the averaged description; d Three of the four scalar invariants are linked with continuous evolution equations established from differential geometry; e Fluid topology can be predicted from a non-dimensional geometric state function that characterizes the possible fluid structures

Full size image

We propose a non-dimensional geometric state function to predict Euler characteristic from the fluid volume fraction, surface area and integral mean curvature. Context for this approach is summarized in Fig. 7. Invariant measures that account for the fluid configuration have been previously established based on integral geometry. Continuous evolution equations have also been established for three of the four invariants, which can in turn be linked with the Minkowski–Steiner formula. The remaining quantity is Euler characteristic, which accounts for the fluid topology and appears as a source term within the hierarchy of geometric evolution equations. An approach to predict Euler characteristic is thereby necessary to predict how the average fluid geometry changes with time. The state function addresses a basic challenge associated with predicting topological changes, which are inherently discontinuous. We show that the evolution for the Euler characteristic can be predicted based on the geometric state, providing a viable mechanism to model fluid connectivity from the macroscale.

A key advantage of the formulation is that it allows for geometric measurements to be aggregated from different materials, removing the need to rely on different constitutive relationships. This means that constitutive laws that are typically expressed as material-specific relations can be generally described, for any material, based on an appropriate choice of geometric variables. The non-dimensional form is shown to hold for a wide range of states that include both viscous and capillary dominated systems. The geometric description is capable of capturing the effect for different flow regimes, system history and material type. An approximation is also introduced to replace mean curvature with the fluid pressure difference, which eliminates one of the unknown variables not already present in existing reservoir models. To apply the approach at the reservoir scale, additional evolution equations are needed to predict the fluid-fluid interfacial area as well as the interfacial area between one of the fluids and the solid.

Due to the complexity of fluid arrangements within the pore structure, it has been previously argued that characterizing the effects of geometry in porous media presents an intractable problem. However, integral geometry and non-dimensional theory suggests that there are only two independent scalar measures of geometric structure. Data from pore-scale simulation confirms that two non-dimensional quantities are sufficient to represent a very wide range of fluid structures with minimal error. This result offers the possibility to understand how geometric effects contribute to overall uncertainty in a quantitative way. A reasonable hypothesis is that uncertainties pertaining to geometric structure can be effectively captured using two of the three dimensionless numbers: \(\phi _i\), \(W_i\) and \(X_i\). A corollary to this hypothesis is that uncertainties that do not correlate with these measures are attributable to other physical causes that are not a fundamental consequence of geometry. It is clear that any quantity expressed in units other than length cannot be intrinsically geometric in nature. Time-dependent effects such as the rate of energy dissipation for physical processes fall into this category. While the energy dissipation rate for a process can depend on geometric structure, such effects cannot be described in a complete way based on geometry alone: energy requires units of mass and time in addition to length. A complete characterization for any dissipative process must therefore account for both geometric and physical effects.

In the context of reservoir modeling, more complete characterization of geometry can reduce uncertainties associated with process-dependent effects that are attributed to the arrangement of fluids, as in traditional constitutive relationships to predict capillary pressure and relative permeability. Geometric characterization may also be applied to understand length scale heterogeneity associated with complex material structures, or other situations where the underlying sources of uncertainty are essentially geometric in nature. Effects such as viscous mobilization, capillary number effects, and transient phenomena have additional physical dependencies that are independent from geometric structure. Understanding the degree to which improved geometric characterization can address long-standing challenges associated with these effects presents intriguing possibilities for future research.