1 Introduction

A fractured shale reservoir has multiscale nature in geometry and multiple transport mechanisms in gas flow. Generally, a fractured shale reservoir has hydraulic fractures, natural and induced fracture network, and matrix. The transport mechanism of shale gas in a fractured shale gas reservoir varies with geometrical scales. In fractures, gas transport follows Darcy or non-Darcy law (Wang et al. 2018). In matrix, the matrix contains plenty of inorganic and organic matters and pores; thus, multiple transport mechanisms are coexisted, such as molecular diffusion, Knudsen diffusion, surface diffusion, and viscous flow (Cai et al. 2018; Wang et al. 2018). Meanwhile, massive gas is adsorbed on the surface of matrix pores. The adsorbed gas reduces the effective volume of matrix pores, causes surface diffusion, and desorbs into free gas (Pang et al. 2017). The monolayer Langmuir adsorption has been widely used to describe the gas desorption in shale gas reservoirs (Sun et al. 2015; Sheng et al. 2018; Wang et al. 2018). But Yu et al. (2016) experimentally found that multilayer adsorption is more suitable. Therefore, both multilayer adsorption and multiple transport mechanisms of gas in different scales are important to the gas transport in a fractured shale gas reservoir. However, they have not been well included in the gas transport model in previous studies. This study will describe the multiscale fractal transport of gas and the multilayer adsorption of gas on pore surfaces based on fractal theory and multilayer adsorption.

Multiple transport mechanisms in shale matrix have been studied. For example, Javadpour (2009) developed an apparent permeability model based on slip flow and Knudsen diffusion in a single straight cylindrical nanotube. Both porosity/tortuosity (\( {\phi \mathord{\left/{\vphantom{\phi \tau}}\right.\kern-2pt}\tau}\)) and fractal dimension (\( D_{f} \)) were later introduced to the Knudsen diffusion by Darabi et al. (2012). The surface diffusion in the adsorbed gas layer was included by Wu et al. (2015). The viscous flow, the Knudsen diffusion, and the influence of the adsorbed layer were further considered (Sun et al. 2015), and the compactions of effective stress were also introduced (Sheng et al. 2018). However, these gas transport models have not considered the impact of pore microstructure on gas transport properties. The pore microstructure can be described by the parameters of pore shape, pore size distribution, and surface roughness. Experiments have observed the fractal characteristics of pores on many physical and geometrical properties of sandstone, coal, and shale matrix (Lee et al. 2014; Liu and Ostadhassan 2017; Xia et al. 2018). These parameters of pore microstructure significantly affect the gas transport property and the storage capacity of shale matrix (Liu and Ostadhassan 2017; Zhang et al. 2017; Hu et al. 2019). Therefore, the characteristics of pores should be carefully included in a gas transport model.

Many fractal permeability models have been established. For example, a permeability model was proposed by Yu and Cheng (2002) based on the fractal characteristics of bi-dispersed porous media. Their model showed that the fractal dimension of pore sizes (called pore fractal dimension later), tortuosity fractal dimension, and structural parameters were key parameters (Yu and Cheng 2002; Wu and Yu 2008). Further, both permeability and porosity models were proposed for the bi-fractal porous medium (Hunt et al. 2013; Tan et al. 2017). By assuming the fractal size distribution of the bundle of tortuous capillary tubes, an effective fractal permeability model was derived by using the Bautista–Manero–Puig (BMP) model in a porous medium (Turcio et al. 2013). The above-mentioned models considered only the viscous flow mechanism of fluid flow or gas transport. Recently, Zheng et al. (2018) derived a relative gas diffusion coefficient which was validated with experimental data. Cai et al. (2018) developed a gas transport model in 3D fractal shale matrix. This model considered the viscous flow, Knudsen diffusion, and surface diffusion. As a summary, these above-mentioned fractal models all focused on the effects of fractal characteristics of porous media on fluid flow or gas transport in porous media. They assumed that the flow occurs in a bundle of fractal tortuous capillary tubes; thus, they did not consider the effect of pore connectivity. The surface roughness of flow path and the impact of multiscale gas flow mechanisms are not included, too. Therefore, it is necessary to develop a permeability model with consideration of slip flow, Knudsen diffusion, and fractal properties. Fractal theory is an effective tool to describe the properties of pore microstructures and may bridge the parameters of pore microstructure with gas flow mechanisms.

On the other hand, gas adsorption is important to the transport mechanisms in shale matrix. Free gas and adsorbed gas are the two main forms of gas in shale reservoirs (Miller 2015; Pang et al. 2017). The adsorbed gas desorbs into free gas when gas pressure decreases. The free gas flows into fractures and finally to the horizontal well (Wang et al. 2018). Patzek et al. (2014) found that gas adsorption can be neglected in Barnett shale but becomes more important to shallower and cooler shale reservoirs such as Woodford shale and Fayetteville shale. After analyzing four wells in Barnett shale reservoirs, Mengal and Wattenbarger (2011) found that the adsorbed gas can account for about 30% of original gas in place (OGIP). Miller (2015) measured the methane adsorption isotherm for 34 samples from the Marcellus shale of various thermal maturity and mineralogy, and suggested that the gas desorption is an important factor of OGIP. In the simulations for shale gas reservoirs, the Langmuir adsorption is widely applied to estimate the storage of shale gas when shale gas production is concerned (Cao et al. 2016; Wang et al. 2017, 2018). However, the Langmuir adsorption is based on a monolayer adsorption assumption. It is found that monolayer adsorption is not a good approximation to actual situations of shale gas reservoirs (Yu et al. 2016). Therefore, multilayer adsorption should be carefully applied.

Two multilayer adsorption models of Brunauer–Emmett–Teller (BET) (Brunauer et al. 1938) and Frenkel–Halsey–Hill (FHH) (Pfeifer et al. 1989a) were proposed based on smooth solid surface. The assumption of smooth surface cannot accurately describe the nature of irregular pore surfaces in shale matrix. The complexity of pore surfaces can be described by the surface fractal dimension in fractal theory. Pfeifer et al. (1989b) developed the fractal BET and FHH adsorption models, in which the fractal FHH adsorption model is the most widely used due to its convenient calculation compared to the fractal BET adsorption model. The surface fractal dimension can be measured by low pressure N2 adsorption tests for shale rocks. It is found that the range of surface fractal dimension is 2.16–2.42 for Shanxi shale in the southeastern Ordos Basin, China (Yang et al. 2017), and 2.523–2.696 for Longtan formation shale of Sichuan basin, Southwestern China (Zhang et al. 2017). This study will introduce a multilayer fractal FHH adsorption into the effective porosity model, permeability model, and the governing equation of gas flow. These proposed permeability models and numerical model for gas production are then verified by experimental data or field data. It is found that the multilayer fractal FHH adsorption is better than Langmuir adsorption in the simulations of fractured shale gas reservoir. Our model can well describe the coupling of fractal microstructure of pores and multiscale flow mechanisms.

2 Fractal Porosity and Permeability Models for Gas Flow

2.1 A Porosity Model for Fractal Multilayer Adsorption in Matrix

The gas adsorption in pores has a great impact on the gas flow in shale gas reservoirs. In this study, this impact is described by both multilayer adsorption and effective porosity. The following Frenkel–Halsey–Hill model is used to calculate the adsorption volume of pores with smooth surfaces:

$$ \frac{V}{{V_{m} }} = \ln \left( {\frac{{p_{0} }}{{p_{m} }}} \right), $$
(1)

where \( V \) is the adsorption volume per unit mass of shale, m3/kg; \( V_{m} \) is the maximum adsorption gas volume when the entire pore surface is covered by a complete monolayer, m3/kg; \( p_{0} \) is the saturation pressure, MPa; and \( p_{m} \) is the matrix gas pressure, MPa.

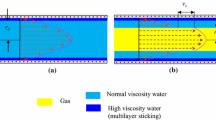
This FHH model assumes the smooth pore surface. Figure 1 shows the adsorption difference between smooth pore surface and rough pore surface. Experimental observations found that the surface roughness is of fractal characteristics (Pfeifer et al. 1989b; Ahmad and Mustafa 2006; Vajda and Felinger 2014). The roughness of pore surfaces can be expressed by a surface fractal dimension. That is, larger surface fractal dimension means rougher pore surface. The concept of surface fractal dimension has been successfully applied to a variety of complex surface geometries for the understanding of geometric effects on the physical properties (Pfeifer et al. 1989a, b). Millán et al. (2013) proposed a truncated fractal FHH model for water vapor adsorption in soil and found better fitting of adsorption data than conventional fractal FHH model (Yang et al. 2017; Zhang et al. 2017). This study still uses the conventional fractal FHH adsorption model but introduces the surface roughness effect on gas adsorption into shale matrix as

$$ \frac{V}{{V_{m} }} = \left[ {\ln \left( {\frac{{p_{0} }}{{p_{m} }}} \right)} \right]^{{D_{s} - 3}} , $$
(2)

where \( D_{s} \) is the surface fractal dimension.

Fig. 1
figure 1

Adsorption schematic of smooth and rough pore surfaces

Full size image

On the other hand, the adsorbed gas on the solid surface occupies some volume of pores for free gas flow (also see Fig. 1). The shaded (red dots) region is the volume of the adsorbed methane, and the blank region is the effective volume for free gas flow. The ratio of this pore volume occupied by adsorbed gas to the total volume of shale matrix is called adsorbed gas porosity. Yu et al. (2016) experimentally found that the adsorbed gas porosity of Marcellus shale can be as high as 3.8%. Thus, the effect of adsorbed gas porosity cannot be ignored when the gas production in a shale gas reservoir is estimated. We propose an effective porosity here to consider this effect:

$$ \phi_{\text{eff}} = \phi - \phi_{\text{ads}} , $$
(3)

where \( \phi_{\text{eff}} \) is the effective porosity of porous medium; \( \phi \) is the porosity of porous medium without consideration of adsorption effect; and \( \phi_{\text{ads}} \) is the adsorbed gas porosity.

Based on the fractal theory, Yu and Li (2001) obtained the expression of porosity \( \phi \) as

$$ \phi = \left( {\frac{{\lambda_{\hbox{min} } }}{{\lambda_{\hbox{max} } }}} \right)^{{d_{E} - D_{\lambda } }} , $$
(4)

where \( \lambda_{\hbox{min} } \) and \( \lambda_{\hbox{max} } \) are the minimum and maximum pore diameters in shale matrix, respectively. \( d_{E} \) is the Euclidean dimension whose value is 3 for three-dimensional space and 2 for two-dimensional space. Equation (4) is based on a bundle of capillary tubes and thus assumes that the gas flow tubes do not cross each other.\( D_{\lambda } \) is the fractal dimension of pore diameter and can be calculated based on the scanning electron microscope (SEM) images, micro-CT images, and gas adsorption data (Xia et al. 2018; Hu et al. 2019). The micro-CT images of sandstone samples show that \( D_{\lambda } \) ranges from 1.926 to 2.746 (Xia et al. 2018).

Further, the adsorbed gas porosity \( \phi_{\text{ads}} \) is expressed as (“Appendix A” gives the detail of this calculation):

$$ \phi_{\text{ads}} = \frac{{\rho_{s} \rho_{\text{ga}} }}{{\rho_{\text{ads}} }}V{ = }V_{m} \frac{{\rho_{s} \rho_{\text{ga}} }}{{\rho_{\text{ads}} }}\left[ {\ln \left( {\frac{{p_{0} }}{{p_{m} }}} \right)} \right]^{{D_{s} - 3}} , $$
(5)

where \( \rho_{s} \) is the density of shale rock, kg/m3; \( \rho_{\text{ga}} \) is the density of methane at standard conditions (273.15 K, 101 kPa), kg/m3; and \( \rho_{\text{ads}} \) is the density of the adsorbed phase methane, which is assumed as the van der Waals density (0.373 g/cm3) or the liquid-phase methane density (0.423 g/cm3) (Zhou et al. 2018).

Recently, Pang et al. (2017) calculated the total porosity and effective porosity for five shale core samples. They used the McKee correlations with experimentally measured pore compressibility, non-adsorptive gas (helium), and adsorptive gas (methane). The effective porosity in shale gas reservoirs was analyzed with considering gas adsorption and stress effects. We also calculated the adsorbed gas porosity of these five shale core samples by subtracting effective porosity from total porosity. Our calculation results are listed in Table 1, and the curve fitting of adsorbed gas porosity with Eq. (5) is presented in Fig. 2. In the fitting, \( \rho_{s} \), \( \rho_{\text{ga}} \), and \( \rho_{\text{ads}} \) are taken as 2580 kg/m3, 0.717 kg/m3, and 373 kg/m3, respectively. The saturation pressure is fixed as 80 MPa. The reservoir temperature is assumed as 360 K (Yu et al. 2016). The fitting parameters of \( V_{m} \) and \( D_{s} \) and \( R^{2} \) are presented in Table 2.

Table 1 Values of adsorbed gas porosity for five shale core samples
Full size table
Fig. 2
figure 2

Fitting curve of Eq. (5) and our calculated data for five shale core samples

Full size image
Table 2 Fitting parameters and \( R^{2} \) value of Eq. (5)
Full size table

Substituting Eqs. (4) and (5) into Eq. (3) gives the effective porosity as

$$ \phi_{\text{eff}} = \left( {\frac{{\lambda_{\hbox{min} } }}{{\lambda_{\hbox{max} } }}} \right)^{{d_{E} - D_{\lambda } }} - V_{m} \frac{{\rho_{s} \rho_{\text{ga}} }}{{\rho_{\text{ads}} }}\left[ {\ln \left( {\frac{{p_{0} }}{{p_{m} }}} \right)} \right]^{{D_{s} - 3}} . $$
(6)

This is our new effective porosity model after coupling the fractal theory and the multilayer adsorption. Figure 3 presents the verification of this model with the calculated data of effective porosity for their sample A-4 and A-5 (Pang et al. 2017). Our porosity model can well fit these experimental data, especially when pressure is larger than 6 MPa.

Fig. 3
figure 3

Verification of our model with Pang et al. (2017) calculated data of effective porosity, \( \lambda_{\hbox{min} } = 1\;{\text{nm}} \), \( \lambda_{\hbox{max} } = 100\;{\text{nm}} \), \( D_{\lambda } = 2.48 \), \( D_{s} = 2.9 \), \( p_{0} = 80\;{\text{MPa}} \), \( V_{m} = 3.23\;{\text{cm}}^{ 3} / {\text{g}} \)

Full size image

2.2 A Fractal Permeability Model for Shale Matrix

2.2.1 Fractal Properties of Pores in Shale Matrix

First, the fractal properties of pore size distribution are described. The accumulated number of pores (\( N_{\lambda } \)) with pore diameter larger than \( \lambda \) follows the fractal scaling law as (Yu and Li 2001)

$$ N_{\lambda } = \left( {\frac{{\lambda_{\hbox{max} } }}{\lambda }} \right)^{{D_{\lambda } }} . $$
(7)

Differentiating Eq. (7) with respect to \( \lambda \) gets the increment of pore number in the interval of \( \left[ {\lambda ,\;\lambda + d\lambda } \right] \)

$$ - dN_{\lambda } = D_{\lambda } \lambda_{\hbox{max} }^{{D_{\lambda } }} \lambda^{{ - (D_{\lambda } + 1)}} d\lambda . $$
(8)

Second, the tortuosity of flow path is analyzed. The flow paths in shale matrix are composed of tortuous capillary bundles with different diameters. The tortuous length \( L\left( \lambda \right) \) of pores relative to pore diameter \( \lambda \) is assumed as (Yu and Cheng 2002)

$$ L\left( \lambda \right) = L_{0}^{{D_{\tau } }} \lambda^{{1 - D_{\tau } }} , $$
(9)

where \( L_{0} \) is the straight length for the gas flow path in the representative elementary volume of matrix, m. \( D_{\tau } \) is the tortuosity fractal dimension which is \( 1 < D_{\tau } < 3 \). The tortuosity \( \tau \) is defined as (Cai and Yu 2011)

$$ \tau { = }\frac{L\left( \lambda \right)}{{L_{0} }} = \left( {\frac{{L_{0} }}{\lambda }} \right)^{{D_{\tau } - 1}} . $$
(10)

2.2.2 Slip Flow of Free Gas

The Knudsen number \( {\text{Kn}} \) is the ratio of the mean free path \( l \) to the pore diameter \( \lambda \) as

$$ {\text{Kn}} = \frac{l}{\lambda }\quad {\text{and}}\quad l = \frac{\mu }{{p_{m} }}\sqrt {\frac{\pi RT}{2M}} , $$
(11)

where \( R \) is the universal gas constant, J/(mol K); \( T \) is the temperature, K; \( \mu \) is the dynamic viscosity of methane, Pa s; and \( M \) is the gas molar mass of methane, kg/mol.

When the Knudsen number is less than 0.1 (\( {\text{Kn}} < 0.1 \)), the gas transmission is mainly affected by the collisions between gas molecules. When both slip and rarified effects are considered, the gas volumetric slip flow rate \( q_{s} \) along a single tortuous capillary tube of pore diameter \( \lambda \) is (Karniadakis et al. 2005)

$$ q_{s} \left( \lambda \right) = \frac{{\phi_{\text{eff}} }}{\tau }\frac{{\pi \lambda^{4} }}{128\mu }\left( {1 + a{\text{Kn}}} \right)\left( {1 + \frac{{4{\text{Kn}}}}{{1 - b{\text{Kn}}}}} \right)\frac{{{\text{d}}p}}{{{\text{d}}x}}, $$
(12)

where \( {\text{d}}p/{\text{d}}x \) is the gas pressure gradient, MPa/m; \( x \) is the distance along the gas flow direction, m; \( a \) is the rarefaction coefficient; and \( b \) is the slip coefficient. According to Beskok and Karniadakis (1999), \( a = 0 \) and \( b = - 1 \) for the slip flow.

Beskok and Karniadakis (1999) pointed out that when the gas flow rate is evaluated under an average state, \( {\text{d}}p/{\text{d}}x = \Delta p/L_{0} \) is true if the Knudsen number \( {\text{Kn}} \) is evaluated at the average gas pressure. \( \Delta p \) is the pressure difference between the inlet and the outlet. The average gas pressure in the representative volume element of the matrix should be the matrix gas pressure \( p_{m} \) in Eq. (11) based on our previous work (Wang et al. 2018). Thus, Eq. (12) can be written as

$$ q_{s} \left( \lambda \right) = \frac{{\phi_{\text{eff}} }}{\tau }\frac{{\pi \lambda^{4} }}{128\mu }\left( {1 + \frac{4l}{\lambda }} \right)\frac{\Delta p}{{L_{0} }}. $$
(13)

The total volumetric slip flow rate \( Q_{s} \) (m3/s) is obtained by integrating the slip flow rate \( q_{s} \left( \lambda \right) \) (m3/s) from \( \lambda_{\hbox{min} } \) to \( \lambda_{\hbox{max} } \).

$$ Q_{s} = \int_{{\lambda_{\hbox{min} } }}^{{\lambda_{\hbox{max} } }} {q_{s} } \left( \lambda \right)\left( { - dN_{\lambda } } \right). $$
(14)

Equation (14) is based on the assumption of the bundle of capillary tubes without the effect of pore connectivity. The pore connectivity can be expressed by the average pore coordination number and used in the calculation of gas permeability (Ghanbarian and Javadpour 2017). Without considering the pore connectivity, substituting Eqs. (8), (9), and (13) into Eq. (14) gives

$$ \begin{aligned} Q_{s} & = \frac{{\pi \phi_{\text{eff}} D_{\lambda } \lambda_{\hbox{max} }^{{3 + D_{\tau } }} \Delta p}}{{128\mu L_{0}^{{D_{\tau } }} \left( {3 + D_{\tau } - D_{\lambda } } \right)}}\left[ {1 - \left( {\frac{{\lambda_{\hbox{min} } }}{{\lambda_{\hbox{max} } }}} \right)^{{3 + D_{\tau } - D_{\lambda } }} } \right] \\ & \quad { + }\frac{{4l\pi \phi_{\text{eff}} D_{\lambda } \lambda_{\hbox{max} }^{{2 + D_{\tau } }} \Delta p}}{{128\mu L_{0}^{{D_{\tau } }} \left( {2 + D_{\tau } - D_{\lambda } } \right)}}\left[ {1 - \left( {\frac{{\lambda_{\hbox{min} } }}{{\lambda_{\hbox{max} } }}} \right)^{{2 + D_{\tau } - D_{\lambda } }} } \right]. \\ \end{aligned} $$
(15)

If \( 1 < D_{\tau } < 3 \), \( 2 < D_{\lambda } < 3 \), and \( \eta = {{\lambda_{\hbox{min} } } \mathord{\left/ {\vphantom {{\lambda_{\hbox{min} } } {\lambda_{\hbox{max} } }}} \right. \kern-0pt} {\lambda_{\hbox{max} } }} < 10^{ - 3} \), we can obtain \( 1 - \left( {{{\lambda_{\hbox{min} } } \mathord{\left/ {\vphantom {{\lambda_{\hbox{min} } } {\lambda_{\hbox{max} } }}} \right. \kern-0pt} {\lambda_{\hbox{max} } }}} \right)^{{3 + D_{\tau } - D_{\lambda } }} \approx 1 \). Equation (15) is simplified as

$$ Q_{s} = \frac{{\pi \phi_{\text{eff}} D_{\lambda } \lambda_{\hbox{max} }^{{3 + D_{\tau } }} }}{{128\mu L_{0}^{{D_{\tau } }} \left( {3 + D_{\tau } - D_{\lambda } } \right)}}\Delta p{ + }\frac{{4l\pi \phi_{\text{eff}} D_{\lambda } \lambda_{\hbox{max} }^{{2 + D_{\tau } }} \left( {1 - \eta^{{2 + D_{\tau } - D_{\lambda } }} } \right)}}{{128\mu L_{0}^{{D_{\tau } }} \left( {2 + D_{\tau } - D_{\lambda } } \right)}}\Delta p. $$
(16)

Substituting the mean free path \( l \) into Eq. (16) gives the apparent permeability in the slip regime as

$$ K_{s} = \frac{{\mu L_{0} Q_{s} }}{\Delta pA} = K_{\infty } \left[ {1 + \frac{\beta }{{p_{m} }}} \right] $$
(17a)
$$ K_{\infty } { = }\frac{{\pi \phi_{\text{eff}} D_{\lambda } \lambda_{\hbox{max} }^{{3 + D_{\tau } }} }}{{128L_{0}^{{D_{\tau } { + }1}} \left( {3 + D_{\tau } - D_{\lambda } } \right)}} $$
(17b)
$$ \beta { = }\frac{{4\mu (3 + D_{\tau } - D_{\lambda } )\left( {1 - \eta^{{2 + D_{\tau } - D_{\lambda } }} } \right)}}{{\lambda_{\hbox{max} } \left( {2 + D_{\tau } - D_{\lambda } } \right)}}\sqrt {\frac{\pi RT}{2M}} , $$
(17c)

where \( A = L_{0}^{2} \) is the total cross-sectional area of the representative elementary volume (Xu and Yu 2008), \( K_{\infty } \) is the Klinkenberg-corrected permeability, and \( \beta \) is the slippage effect factor. Table 3 lists typical expressions of slippage factor for comparison. The relationship between the ratio of the permeability to the Klinkenberg-corrected permeability (\( {{K_{s} } \mathord{\left/ {\vphantom {{K_{s} } {K_{\infty } }}} \right. \kern-0pt} {K_{\infty } }} \)) and the pressure is presented in Fig. 4. The ones by Javadpour (2009) and Michel et al. (2011) are also plotted for comparison. It is observed that this ratio \( {{K_{s} } \mathord{\left/ {\vphantom {{K_{s} } {K_{\infty } }}} \right. \kern-0pt} {K_{\infty } }} \) decreases with the increase in pore pressure. The curve of our model is between theirs.

Table 3 Different expressions of slippage factor \( \beta \)
Full size table
Fig. 4
figure 4

Relationship between \( {{K_{s} } \mathord{\left/ {\vphantom {{K_{s} } {K_{\infty } }}} \right. \kern-0pt} {K_{\infty } }} \) and gas pressure from Javadpour (2009), Michel et al. (2011) and our model. The value of parameters can be obtained by Cai et al. (2018) and Hu et al. (2019), \( \lambda_{\hbox{min} } = 1\;{\text{nm}} \); \( \lambda_{\hbox{max} } = 200\;{\text{nm}} \); \( D_{\tau } = 1.4 \)\( D_{\lambda } = 2.35 \)

Full size image

2.2.3 Knudsen Diffusion of Free Gas

When the Knudsen number is larger than 1 (\( {\text{Kn}} > 1 \)), the gas volumetric flow rate of the Knudsen diffusion \( q_{k} \) (m3/s) can be expressed as (Wu et al. 2015)

$$ q_{k} = \frac{{\phi_{\text{eff}} }}{\tau }\frac{{\pi \lambda^{3} }}{12}\left( {\frac{8RT}{\pi M}} \right)^{0.5} \sigma^{{D_{\lambda } - 2}} \frac{\Delta p}{{L_{0} }} $$
(18)
$$ \sigma { = }\frac{{d_{m} }}{\lambda }, $$
(19)

where \( d_{m} \) is the diameter of methane molecule, nm; \( \sigma \) is the ratio of the methane molecule diameter to the pore diameter. It is noted that Eq. (18) considered the tortuosity of capillary tubes.

Substituting Eqs. (9) and (19) into Eq. (18) gets the total gas volumetric flow rate \( Q_{k} \) (m3/s) by integrating the Knudsen diffusion \( q_{k} \) from \( \lambda_{\hbox{min} } \) to \( \lambda_{\hbox{max} } \):

$$ Q_{k} = \frac{{\pi \phi_{\text{eff}} D_{\lambda } d_{m}^{{D_{\lambda } - 2}} \lambda_{\hbox{max} }^{{4{ + }D_{\tau } - D_{\lambda } }} \left( {1 - \eta^{{4 + D_{\tau } - 2D_{\lambda } }} } \right)}}{{12L_{0}^{{D_{\tau } }} \left( {4 + D_{\tau } - 2D_{\lambda } } \right)}}\left( {\frac{8RT}{\pi M}} \right)^{0.5} \frac{\Delta p}{{L_{0} }}. $$
(20)

Comparing Eq. (20) with the Darcy’s law gives the apparent permeability (\( K_{k} \)) in the Knudsen flow regime as

$$ k_{k} = \frac{{\mu L_{0} Q_{k} }}{\Delta pA} = \frac{{\mu \pi \phi_{\text{eff}} D_{\lambda } \lambda_{\hbox{max} }^{{4 + D_{\tau } - D_{\lambda } }} d_{m}^{{D_{\lambda } - 2}} \left( {1 - \eta^{{4 + D_{\tau } - 2D_{\lambda } }} } \right)}}{{12L_{0}^{{D_{\tau } + 1}} \left( {4 + D_{\tau } - 2D_{\lambda } } \right)}}\left( {\frac{8RT}{\pi M}} \right)^{0.5} . $$
(21)

The total permeability \( k_{m} \) of matrix is contributed from the slip flow permeability \( k_{s} \) and the Knudsen flow permeability \( k_{k} \) with different weight factors (Wu et al. 2015). Combining Eqs. (17a) and (21), our new total permeability \( k_{m} \) for the matrix in shale reservoirs can be expressed as

$$ \begin{aligned} k_{m} & = \omega_{s} k_{s} + \omega_{k} k_{k} \\ \, & = \frac{{\omega_{s} \pi \phi_{\text{eff}} D_{\lambda } \lambda_{\hbox{max} }^{{3 + D_{\tau } }} }}{{128L_{0}^{{D_{\tau } + 1}} \left( {3 + D_{\tau } - D_{\lambda } } \right)}}\left[ {1 + \frac{{4\mu (3 + D_{\tau } - D_{\lambda } )\left( {1 - \eta^{{2 + D_{\tau } - D_{\lambda } }} } \right)}}{{\lambda_{\hbox{max} } \left( {2 + D_{\tau } - D_{\lambda } } \right)p_{m} }}\sqrt {\frac{\pi RT}{2M}} } \right] \\ & \quad + \frac{{\omega_{k} \mu \pi \phi_{\text{eff}} D_{\lambda } \lambda_{\hbox{max} }^{{4 + D_{\tau } - D_{\lambda } }} d_{m}^{{D_{\lambda } - 2}} \left( {1 - \eta^{{4 + D_{\tau } - 2D_{\lambda } }} } \right)}}{{12L_{0}^{{D_{\tau } + 1}} \left( {4 + D_{\tau } - 2D_{\lambda } } \right)}}\left( {\frac{8RT}{\pi M}} \right)^{0.5} , \\ \end{aligned} $$
(22)

where \( \omega_{s} = {1 \mathord{\left/ {\vphantom {1 {\left( {1 + {\text{Kn}}} \right)}}} \right. \kern-0pt} {\left( {1 + {\text{Kn}}} \right)}} \) and \( \omega_{k} = {{\text{Kn}} \mathord{\left/ {\vphantom {{\text{Kn}} {\left( {1 + {\text{Kn}}} \right)}}} \right. \kern-0pt} {\left( {1 + {\text{Kn}}} \right)}} \) are the weight factors for slip flow and Knudsen diffusion, respectively, according to Wu et al. (2015).

The accuracy of this total matrix permeability is checked here. This check was done by the experimental data of shale plug samples measured by Zamirian et al. (2014). The permeability model proposed by Sun et al. (2015) (see “Appendix B”) and the permeability model proposed by Darabi et al. (2012) (see “Appendix B”) were used for comparison. Table 4 lists all parameters used by this total matrix permeability model. The mathematical equation and parameters can be seen in “Appendix B.” As shown in Fig. 5, Darabi’s model can match the experimental data when pore pressure is high and Sun’s model matches the experimental data when pore pressure is low. The permeability in this study is in a better agreement with the experimental data in the whole range. In addition, our permeability model, Sun’s model, Darabi’s model, and experimental data all decrease with the increase in pore pressure. This is because that the increase in pore pressure will decrease the mean free path length of gas molecule, which increases the collision frequency between gas molecules and decreases the collision frequency of gas molecules with pore wall. The gas slip effect will decrease with the increase in pore pressure.

Table 4 Parameters used in the proposed matrix permeability model
Full size table
Fig. 5
figure 5

Validation of the matrix permeability model in this study with experimental results from Zamirian et al. (2014) and other two models (Darabi et al. 2012; Sun et al. 2015)

Full size image

2.3 A Fractal Permeability Model for Fracture Network

The permeability of fracture network plays a vital role in the gas production from a fractured shale gas reservoir. This permeability depends on the aperture distribution, the fracture length distribution, and the roughness of fractures. The relationship between the maximum aperture \( e_{\hbox{max} } \) (m) and the length \( l \) (m) of fractures is assumed to follow a power law (Olson 2003; Klimczak et al. 2010):

$$ e_{\hbox{max} } = \delta l^{n} , $$
(23)

where \( \delta \) is the proportionality coefficient and its value ranges from \( 10^{ - 1} \) to \( 10^{ - 3} \); \( n \) is an exponent. For the sliding (or tearing) mode fracture, \( n = 1 \)(a linear relationship); for an opening mode fracture, \( n = 0.5 \)(a nonlinear relationship) (Liu et al. 2016). Ghanbarian et al. (2019) theoretically showed that fracture aperture should be linearly proportional to the length of the fractal fractures. Klimczak et al. (2010) validated this nonlinear relationship by 10 field data of dikes, veins, and joints as shown in Fig. 6. In this study, we assume that the fractures are the opening model fractures, and the average aperture \( e_{\text{avg}} \) of the opening mode fracture is expressed by (Olson 2003)

$$ e_{\text{avg}} = \frac{\pi }{4}e_{\hbox{max} } = \gamma l^{0.5} , $$
(24)

where \( \gamma = {{\pi \vartheta } \mathord{\left/ {\vphantom {{\pi \vartheta } 4}} \right. \kern-0pt} 4} \)

$$ \vartheta { = }\frac{{K_{1C} \left( {1 - \nu } \right)^{2} }}{E}\sqrt {\frac{8}{\pi }} , $$
(25)

where \( K_{1C} \) is the fracture toughness; \( \nu \) is the Poisson’s ratio; and \( E \) is the Young’s modulus of shale, MPa.

Fig. 6
figure 6

Nonlinear relationship between fracture length and fracture aperture of 10 opening mode fractures (exponent n is in 0.2191–0.6975 and its average is 0.5 (Klimczak et al. 2010))

Full size image

The distribution of fracture length follows a fractal scaling law (Miao et al. 2015):

$$ N_{f} \left( l \right) = \left( {\frac{{l_{\hbox{max} } }}{l}} \right)^{{D_{l} }} , $$
(26)

where \( N_{f} \left( l \right) \) is the total number of fractures whose length is larger than \( l \); \( D_{l} = d_{E} - {{\ln \phi_{f} } \mathord{\left/ {\vphantom {{\ln \phi_{f} } {\ln \left( \zeta \right)}}} \right. \kern-0pt} {\ln \left( \zeta \right)}} \) is the fractal dimension of fracture length; \( \phi_{f} \) is the porosity of fracture network, and \( \zeta { = }{{l_{\hbox{min} } } \mathord{\left/ {\vphantom {{l_{\hbox{min} } } {l_{\hbox{max} } }}} \right. \kern-0pt} {l_{\hbox{max} } }}{ = }\phi_{f}^{{ - \left( {d_{E} - D_{l} } \right)}} \), where \( l_{\hbox{min} } \) and \( l_{\hbox{max} } \) are the minimum and maximum fracture lengths, respectively.

By differentiating Eq. (26) with respect to \( l \), the fracture number increment is

$$ - dN_{f} = D_{l} l_{\hbox{max} }^{{D_{l} }} l^{{ - (D_{l} + 1)}} dl. $$
(27)

The volumetric flow rate of gas in a single fracture is (Neuzil and Tracy 1981)

$$ q_{\text{f}} = \frac{{e_{\text{avg}}^{3} l}}{12\mu }\frac{\Delta p}{{L_{0} }} = \frac{{\gamma^{3} l^{2.5} }}{12\mu }\frac{\Delta p}{{L_{0} }}, $$
(28)

where \( q_{\text{f}} \) is the volumetric flow rate of gas in the single fracture, m3/s;

We assume that the fractures are parallel to each other, and the gas flow in fractures is along only one direction. The total flow rate from all fractures \( Q_{f} \) (m3/s) can be obtained by integrating Eq. (28) from the \( l_{\hbox{min} } \) to the \( l_{\hbox{max} } \):

$$ Q_{f} = \int_{{l_{\hbox{min} } }}^{{l_{\hbox{max} } }} {q_{f} \left( { - dN_{f} } \right)} = \frac{{\gamma^{3} D_{l} l_{\hbox{max} }^{2.5} }}{{12\mu \left( {2.5 - D_{l} } \right)}}\left[ {1 - \zeta^{{2.5 - D_{l} }} } \right]\frac{\Delta p}{{L_{0} }}. $$
(29)

The permeability of the fracture network \( k_{f} \) can be back-calculated by the Darcy’s law:

$$ k_{f} = \frac{{Q_{f} \mu L_{0} }}{{A_{\text{f}} \Delta p}}, $$
(30)

where \( A_{\text{f}} \) is the cross-sectional area of fracture network. The total cross-sectional area \( A_{fp} \) of all fractures is

$$ A_{fp} = \int_{{l_{\hbox{min} } }}^{{l_{\hbox{max} } }} {e_{avg} l\left( { - dN_{f} } \right)} = \frac{{\gamma D_{l} l_{\hbox{max} }^{1.5} }}{{\left( {1.5 - D_{l} } \right)}}\left( {1 - \zeta^{{1.5 - D_{l} }} } \right). $$
(31)

The porosity of fracture network \( \phi_{f} \) is defined as (Miao et al. 2015)

$$ \phi_{f} = \frac{{A_{fp} }}{{A_{\text{f}} }}. $$
(32)

Introducing Eqs. (29), (31), and (32) into (30) gives the permeability of fracture network \( k_{f} \) as

$$ k_{f} = \frac{{\gamma^{2} l_{\hbox{max} } \left( {1.5 - D_{l} } \right)\phi_{f} }}{{12\left( {2.5 - D_{l} } \right)}}\frac{{1 - \phi_{f}^{{\frac{{2.5 - D_{l} }}{{d_{E} - D_{l} }}}} }}{{1 - \phi_{f}^{{\frac{{1.5 - D_{l} }}{{d_{E} - D_{l} }}}} }}. $$
(33)

This is our new permeability for fracture network. It is based on the porosity of fractures and varies with the following parameters (\( \gamma \), \( l_{\hbox{max} } \), \( D_{l} \), and \( \phi_{f} \)). It is noted that our permeability model of Eq. (33) does not consider the tortuosity of fracture. The tortuosity of fracture may be an important factor to affect the gas flow and will be carefully considered in the future. Fan and Ettehadtavakkol (2017) estimated the permeability and porosity in different regions based on the microseismic information of hydraulic fracturing. In Fig. 7, the permeability data are the actual data and the porosity data are the estimated data for two regions. The solid line represents the cubic law. The dash dot line and dash line represent the fracture permeability models when the fracture length fractal dimension is taken as 2.57 and 2.63, respectively. Our fracture permeability model is in better agreement than cubic law with the actual permeability data in different regions.

Fig. 7
figure 7

Validation of fracture permeability model with cubic law and actual data from Fan and Ettehadtavakkol (2017), \( \gamma = 0.001 \), \( l_{\hbox{max} } = 0.5\;{\text{m}} \)

Full size image

3 Governing Equations of Gas Flow in Fractured Gas Reservoirs

3.1 Gas Flow Equation in Matrix

The mass conservation law of gas in the matrix of shale gas reservoir is (Wang et al. 2018)

$$ \frac{{\partial m_{m} }}{\partial t} + \nabla \left( { - \rho_{g} \frac{{k_{m} }}{\mu }\nabla p_{m} } \right) = - Q_{m,f} , $$
(34)

where \( m_{m} \) is the gas mass content in matrix, kg/m3; \( t \) is the production time, s; \( \rho_{g} { = }{{M_{g} p_{m} } \mathord{\left/{\vphantom{{M_{g}p_{m}}{RT}}}\right.\kern-2pt} {RT}} \) is the gas density in matrix, kg/m3; and \( Q_{m,f} \) is the gas source exchange between matrix and fractures, kg/(m3 s). The gas mass content \( m_{m} \) includes free gas and adsorbed gas and is expressed as

$$ m_{m} = \rho_{g} \phi_{\text{eff}} + \rho_{\text{ga}} \rho_{s} V_{m} \left[ {\ln \left( {\frac{{p_{0} }}{{p_{m} }}} \right)} \right]^{{D_{s} - 3}} . $$
(35)

The exchange gas source \( Q_{m,f} \) is defined as (Lim and Aziz 1995)

$$ Q_{m,f} = \frac{{\pi^{2} \rho_{g} k_{m} }}{\mu }\left( {\frac{1}{{l_{x}^{2} }} + \frac{1}{{l_{y}^{2} }}} \right)\left( {p_{m} - p_{f} } \right), $$
(36)

where \( l_{x} \) and \( l_{y} \) represent the fracture space in \( x \) and \( y \) directions, respectively. \( p_{f} \) is the fracture gas pressure, MPa; and \( p_{m} - p_{f} \) represents the driving force of gas flow from shale matrix to fractures.

Substituting Eqs. (35) and (36) into Eq. (34) gives the gas flow equation in the matrix as

$$ \begin{aligned} & \left[ {\phi_{\text{eff}} + \rho_{s} V_{m} \left( {D_{s} - 3} \right)\left( {\ln \left( {\frac{{p_{0} }}{{p_{m} }}} \right)} \right)^{{D_{s} - 4}} \left( {\frac{{\rho_{\text{ga}} }}{{\rho_{\text{ads}} }} - \frac{{p_{a} }}{{p_{m} }}} \right)} \right]\frac{{\partial p_{m} }}{\partial t} - \nabla \left( {\frac{{k_{m} }}{\mu }p_{m} \nabla p_{m} } \right) \\ & = \frac{{\pi^{2} p_{m} k_{m} }}{\mu }\left( {\frac{1}{{l_{x}^{2} }} + \frac{1}{{l_{y}^{2} }}} \right)\left( {p_{f} - p_{m} } \right). \\ \end{aligned} $$
(37)

3.2 Gas Flow Equation in Fracture Network

Fracture network has only free gas. The mass conservation law in fracture network is

$$ \frac{{\partial m_{f} }}{\partial t} + \nabla \left( { - \frac{{k_{f} }}{\mu }\rho_{g} \nabla p_{f} } \right) = \frac{{\pi^{2} \rho_{g} k_{m} }}{\mu }\left( {\frac{1}{{l_{x}^{2} }} + \frac{1}{{l_{y}^{2} }}} \right)\left( {p_{m} - p_{f} } \right), $$
(38)

where \( m_{\text{f}} \) is the gas mass content in fractures. It is expressed by only free gas as

$$ m_{\text{f}} = \rho_{g} \phi_{f} . $$
(39)

Further, the evolution of fracture porosity with stress is (Cui and Bustin 2005)

$$ \phi_{f} = \phi_{f0} \exp \left\{ {c_{f} \left[ {\left( {\bar{\sigma } - \bar{\sigma }_{0} } \right) - \left( {p_{f} - p_{f0} } \right)} \right]} \right\}, $$
(40)

where the subscript 0 represents the initial state; \( c_{f} \) is the compressibility of fractures, 1/MPa; and \( \bar{\sigma } = - {{\sigma_{kk} } \mathord{\left/ {\vphantom {{\sigma_{kk} } 3}} \right. \kern-0pt} 3} \) is the mean compression stress and \( \sigma_{kk} { = }\sigma_{11} { + }\sigma_{22} { + }\sigma_{33} \), MPa.

Substituting Eqs. (39) and (40) into Eq. (38) yields

$$ \phi_{f} \frac{{\partial p_{f} }}{\partial t} + p_{f} \frac{{\partial \phi_{f} }}{\partial t} - \nabla \left( {p_{f} \frac{{{\text{k}}_{\text{f}} }}{\mu }\nabla {\text{p}}_{f} } \right) = \frac{{\pi^{2} p_{f} k_{m} }}{\mu }\left( {\frac{1}{{l_{x}^{2} }} + \frac{1}{{l_{y}^{2} }}} \right)\left( {p_{\text{m}} - p_{f} } \right). $$
(41)

This is the equation of gas flow in the fracture network of fractured shale gas reservoirs.

3.3 Gas Flow Equation in Hydraulic Fractures

The gas flow equation in a hydraulic fracture is (Wang et al. 2018)

$$ b_{\text{hf}} \frac{{\partial \left( {\rho_{g} \phi_{\text{hf}} } \right)}}{\partial t} + \nabla \left( { - \frac{{k_{\text{hf}} }}{\mu }\rho_{g} b_{\text{hf}} \nabla p_{\text{hf}} } \right) = 0. $$
(42)

In a hydraulic fracture, \( b_{\text{hf}} \) is the aperture, m; \( \phi_{\text{hf}} \) is the porosity; \( k_{\text{hf}} \) is the permeability, m2; and \( p_{\text{hf}} \) is the gas pressure, MPa.

3.4 Deformation of Shale Gas Reservoir

The Navier equation of shale gas reservoir is expressed as (Wang et al. 2018)

$$ Gu_{i,jj} + \frac{G}{1 - 2\nu }u_{j,ji} - \alpha p_{{{\text{m}},i}} - K\varepsilon_{s,i} + f_{i} = 0, $$
(43)

where \( u_{i} \) is the displacement component; \( G = {E \mathord{\left/ {\vphantom {E {\left( {1 + 2\nu } \right)}}} \right. \kern-2pt} {\left( {1 + 2\nu } \right)}} \) is the shear modulus of the shale, GPa; \( K = {E \mathord{\left/ {\vphantom {E {3(1 - 2\nu )}}} \right. \kern-2pt} {3(1 - 2\nu )}} \) is the bulk modulus of shale, MPa; \( \alpha = 1 - {K \mathord{\left/ {\vphantom {K {K_{s} }}} \right. \kern-2pt} {K_{s} }} \) is the Biot coefficient, \( K_{s} {{ = E_{s} } \mathord{\left/ {\vphantom {{ = E_{s} } {3(1 - 2\nu )}}} \right. \kern-2pt} {3(1 - 2\nu )}} \) is the bulk modulus of shale gains, MPa; \( E_{s} \) is the Young’s modulus of shale gains, MPa; \( E \) is the Young’s modulus of shale, MPa; \( \nu \) is the Poisson’s ratio of shale; \( \varepsilon_{s} = \varepsilon_{g} V \) is the adsorption-induced strain (Cui and Bustin 2005); \( \varepsilon_{g} \) is the coefficient of sorption-induced volumetric strain, kg/m3; and \( f_{i} \) is the component of body force.

4 Model Verifications Through Field Data of Gas Production Rate

The porosity and permeability models for shale matrix and fractures are incorporated into these partial differential equations for the deformation and gas flow in fractured shale gas reservoirs. These equations are numerically solved by finite element method within the platform of COMSOL Multiphysics. The deformation equation (Eq. (43)) for shale reservoir is solved by solid mechanics module, the gas flow governing equation in matrix (Eq. (37)) and fracture network (Eq. (41)) are solved by the PDE module, and the gas flow equation in hydraulic fracture (Eq. (42)) is implemented by the weak form in COMSOL Multiphysics software.

Figure 8 is the geometry of this computational model. The true geometry is very complex due to the fracture network created by hydraulic fracturing. Warpinksi and Teufel (1987) indicated that the hydraulic fractures cannot be regarded as ideal planar ones in many reservoirs. Recently, some scholars (Patzek et al. 2013; Yu and Sepehrnoori 2014; Yu et al. 2015; Eftekhari et al. 2018; Wang et al. 2018; Hu et al. 2019) have demonstrated that the ideal planar hydraulic fractures can be successfully applied to the estimation of shale gas production. As shown in Fig. 8, the normal stress on the top and right boundaries is set to 40 MPa, and the four boundaries around the domain are no-flow boundaries. The wells in this study are in the Marcellus shale reservoir and the Barnett shale reservoir, respectively. All computational parameters used in simulations of these two wells are listed in Table 5. These parameters are determined based on the papers for the Marcellus shale well (Yeager and Meyer 2010; Yu et al. 2015) and the papers for the Barnett shale well (Yu and Sepehrnoori 2014), respectively. The fractal parameters of matrix and fractures are determined based on the papers (Yang et al. 2017; Xia et al. 2018) and further checked by matching the history gas production data.

Fig. 8
figure 8

Geometry of computational model

Full size image
Table 5 Reservoir parameters of the Marcellus shale and Barnett shale
Full size table

In this study, the multilayer fractal FHH adsorption is introduced into the effective porosity model and the gas flow equation within matrix. The simulation results with the fractal FHH model in this study and the Langmuir adsorption model are compared with the results from the published papers (Yu and Sepehrnoori 2014; Wang et al. 2018) and field data in Fig. 9 for the Marcellus shale and Fig. 10 for the Barnett shale. From Fig. 9, the prediction curve of Wang et al. (2018) has similar tendency with the field data, but not accurate enough. Yu and Sepehrnoori (2014) can accurately estimate the gas production rate before 100 days, and they overestimated the production rate after 150 days. It is observed that the gas production rate with the fractal FHH adsorption is larger than that with the Langmuir adsorption. The simulation results with fractal FHH adsorption model in this study are the most accurate one. From Fig. 10 for Barnett shale, the gas production rate with the fractal FHH adsorption is the largest before 300 days. This illustrates that the multilayer adsorption contributes more significantly at early time of gas production than the Langmuir adsorption model. This finding is consistent with that of Yu et al. (2016). Figures 9 and 10 comprehensively show that the fractal FHH adsorption in our model is more reasonable matching with field data during the gas production.

Fig. 9
figure 9

Comparison of gas production rate among this simulation (Yu and Sepehrnoori 2014; Wang et al. 2018) and field data from Marcellus shale

Full size image
Fig. 10
figure 10

Comparison of gas production rate among this simulation (Yu and Sepehrnoori 2014; Wang et al. 2018) and field data from Barnett shale

Full size image

5 Sensitivity Analysis for Key Parameters

The impacts of reservoir parameters on gas production are investigated here. The geometry of the Marcellus shale well is used as the simulation model. All parameters used in this simulation model are listed in Table 6. The effects of monolayer gas adsorption volume (\( V_{m} \)), surface fractal dimension \( D_{s} \), tortuosity fractal dimension \( D_{\tau } \), and pore diameter fractal dimension \( D_{\lambda } \) on the gas production will be investigated.

Table 6 All parameters used in computations for sensitivity analysis
Full size table

5.1 Effect of Gas Adsorption

The impact of the FHH adsorption on gas production is firstly studied. The monolayer adsorption volume \( V_{m} \) is taken as 0 cm3/g (without adsorption), 1.18 cm3/g, and 2 cm3/g (high adsorption), respectively. Figure 11 presents the increase in cumulative gas production with the monolayer adsorption volume \( V_{m} \). Bigger monolayer adsorption volume \( V_{m} \) represents higher adsorption ability, having more adsorbed gas in the shale matrix. The adsorbed gas is released to free gas, and the free gas flows into the fracture network during gas production. After 8000 days, the cumulative gas production is increased by 26% when the monolayer adsorption volume \( V_{m} \) increases from 0 to 2 cm3/g. The result is very close to the theoretical value calculated by Mengal and Wattenbarger (2011). Therefore, gas adsorption plays a vital role in gas production, and the monolayer adsorption volume \( V_{m} \) is an important parameter.

Fig. 11
figure 11

Impact of monolayer adsorption volume \( V_{m} \) on cumulative gas production

Full size image

5.2 Effect of Surface Fractal Dimension \( D_{s} \)

The surface fractal dimension \( D_{s} \) is used to quantitatively describe the surface roughness of pore cross section. Larger surface fractal dimension means rougher surface. The surface fractal dimension \( D_{s} \) is taken as 2.1, 2.5, and 2.9. Figure 12 clearly shows that the cumulative gas production is sensitive to the surface fractal dimension. The cumulative gas production increases with the decrease in surface fractal dimension \( D_{s} \). The cumulative gas production after 6000 days decreases from 6.5 × 107 to 3.0 × 107 m3 when the surface fractal dimension increases from 2.1 to 2.9. Therefore, smaller surface fractal dimension of the cross section has higher gas production. Surface fractal dimension has a significant impact on gas production.

Fig. 12
figure 12

Impact of surface fractal dimension \( D_{s} \) on cumulative gas production

Full size image

5.3 Effect of Tortuosity Fractal Dimension \( D_{\tau } \)

The tortuosity fractal dimension \( D_{\tau } \) describes the surface roughness along pore length. When the tortuosity fractal dimension \( D_{\tau } \) is 2, the surface is extremely rough. When \( D_{\tau } \) is equal to 1, the surface is smooth. In order to investigate the influence of the surface roughness along pore length on the cumulative gas production, the tortuosity fractal dimension \( D_{\tau } \) is assumed as 1.0, 1.1, and 1.3. The cumulative gas production with these \( D_{\tau } \) is plotted in Fig. 13. When the tortuosity fractal dimension increases from 1.0 to 1.3, the cumulative gas production at the 8000th day is 7.0 × 107 m3, 6.5 × 107 m3, and 6.2 × 107 m3, respectively. Gas can flow more easily in the pore with smooth surface than with rough surface. Therefore, the cumulative gas production increases with the decrease in tortuosity fractal dimension. The surface roughness along pore length has some impacts on the cumulative gas production.

Fig. 13
figure 13

Impact of tortuosity fractal dimension \( D_{\tau } \) on cumulative gas production

Full size image

5.4 Effect of Pore Diameter Fractal Dimension \( D_{\lambda } \)

The pore diameter fractal dimension \( D_{\lambda } \) represents the distribution of pore sizes in shale matrix. The \( D_{\lambda } \) is between 2 and 3, so three values were taken as 2.5, 2.7, and 2.9 to investigate the impact of \( D_{\lambda } \) on the cumulative gas production and the permeability evolution in shale gas reservoirs. As illustrated in Fig. 14, the cumulative gas production is increasing with the increases in pore diameter fractal dimension \( D_{\lambda } \). When pore diameter fractal dimension \( D_{\lambda } \) changes from 2.5 to 2.9, the cumulative gas production after 6000 days increases from 7.57 × 107 m3 to 3.57 × 108 m3. Further, the impact of pore diameter fractal dimension \( D_{\lambda } \) on the permeability evolution at the center point (450 m, 150 m) was studied. Figure 15 shows that the permeability is increasing during gas extraction and reaches the largest when \( D_{\lambda } = 2.9 \). Larger \( D_{\lambda } \) represents larger number of pores in shale matrix, and thus the permeability increases. This permeability enhancement increases the cumulative gas production. Therefore, the pore diameter fractal dimension \( D_{\lambda } \) has vital impacts on permeability evolution and gas production.

Fig. 14
figure 14

Impact of pore diameter fractal dimension \( D_{\lambda } \) on cumulative gas production

Full size image
Fig. 15
figure 15

Impact of pore diameter fractal dimension \( D_{\lambda } \) on permeability evolution of point (450 m, 150 m)

Full size image

6 Conclusions

A multiscale gas transport model with multilayer sorption and effective porosity effects was developed based on the fractal theory for a fractured shale reservoir. Numerical simulations observed that this model better matches the history gas production data from Marcellus shale and Barnett shale than other models. This model was used to investigate the impacts of gas adsorption, surface roughness, pore diameter distribution on cumulative gas production and permeability. Based on these results, the following conclusions can be drawn:

Firstly, the effective porosity model with multilayer adsorption is developed for gas flow based on the fractal FHH adsorption. This multilayer fractal FHH adsorption model can well describe the pore surface roughness and has higher accuracy than monolayer Langmuir adsorption in the numerical simulation of shale gas production.

Secondly, the multiscale permeability model can well describe the experimental data. This model can bridge pore microstructures and multiscale gas flow mechanisms through pore fractal properties. The permeability model includes two important microstructure parameters of pore diameter fractal dimension \( D_{\lambda } \) and tortuosity fractal dimension \( D_{\tau } \).

Thirdly, a nonlinear fractal relationship is proposed between fracture aperture and length and incorporated to formulate a new permeability model of fracture network. Such an inclusion can better describe the shale fracture permeability.

Fourth, the shale gas production is heavily affected by three key microstructure parameters of surface fractal dimension \( D_{s} \), tortuosity fractal dimension \( D_{\tau } \), and pore diameter fractal dimension \( D_{\lambda } \). The surface fractal dimension \( D_{s} \) is for adsorption capacity. Higher \( D_{s} \) has lower gas production due to lower adsorption capacity. Bigger tortuosity fractal dimension \( D_{\tau } \) means higher flow resistance along pore length and lower gas production. Bigger \( D_{\lambda } \) represents larger number of pores and higher permeability and cumulative gas production.