Numerical Simulation of Gas/Solid Heat Transfer in Metallic Foams: A General Correlation for Different Porosities and Pore Sizes

Abstract

In the present research work, numerical simulations were performed to investigate the effects of structural parameters on fluid flow and heat transfer under unsteady state conditions in aluminium foams, with various physical specifications such as different porosities (76–96%), pores diameter (100–500 μm) and tortuosity (1.024–1.14), by meshing computed micro-tomography images. In all the simulated cases, the fluid was considered as air with a temperature of 500 K and different superficial velocities (1–6 m/s) entered the foam with a temperature of 300 K. Calculation of the pressure gradient based on a generic formula ΔP/L = αv + βv² shows that by increasing porosity and pore diameter, coefficients α and β decrease. Moreover, heat transfer analysis shows that the average convection heat transfer coefficient (h_ave) depends on the geometrical parameters of the foam and also on the superficial velocity of the fluid. In fact, the minor changes in the pore diameter can greatly affect h_ave (e.g. the variation of h_ave for samples with 86% porosity at inlet velocity of 5 m/s and different pore diameters from 500 to 100 μm: 250 to 600 J/m² s K). However, the porosity variations do not have significant effects on h_ave. On the other hand, by using the nonlinear least square fitting technique and also including the structural factor (F_s, function of the foam geometrical parameters) to the Nu correlation, the equation Nu = 0.0305 Re^0.77 F_s [where F_s = ((1 − ε)/τ)^−0.27 (d_p/d_t)^−5.108] for determining the Nu in the different foams has been proposed. The equation and simulated results are agreed with each other very well and additionally are similar to the previous studies. Therefore, it’s expected that this equation can be used in design and performance evaluation of porous heat exchangers and porous catalysts.

1 Introduction

Metallic foams are extensively used in various industries and engineering applications during the recent years. In fact, these porous materials have unique properties such as high porosity, low relative density, low pressure drop, high thermal conductivity, high surface area-to-volume ratio, capability to absorb sonic and impact energies and high strength (Zafari et al. 2014; Ambrosio et al. 2016; Panerai et al. 2017). Thermal converters, catalysts, batteries and fuel cells, thermal insulators, etc., are some examples of the extensive applications of the metallic foams (Bidault et al. 2009; Huang et al. 2008; Zafari et al. 2016). Therefore, clear understanding of the foams characteristics is of great importance, considering the wide variety of their applications, for instance, for a precise design of engineering systems with high efficiency like catalysts, filters and heat exchangers (Pop et al. 2017; Mahjoob and Vafai 2008; Du et al. 2017). Additionally, some parameters like porosity, shape, size, porosity distribution, as well as the existence of open or closed pores, could influence the efficiency of fluid flow, heat transfer and mass transfer) and the design of foams (Lafdi et al. 2007; Bodla et al. 2010; Odabaee and Hooman 2012).

In recent years, several experimental and numerical studies have been performed to investigate fluid flow and heat transfer inside the foams. Bhattacharya et al. (2002) experimentally examined heat transfer of different aluminium foams (40–50 ppi and 89–97% porosity) and determined the average heat transfer coefficient, Nusselt number and Reynolds number. Their results verified the increase in Nusselt number with the Reynolds number. Hsieh et al. (2004) conducted an experimental study to determine heat transfer characteristics of aluminium foam. They found that the Nusselt number rises when the porosity is increased. Giani et al. (2005) performed several experiments to identify the heat transfer coefficients for copper and FeCr alloys foams at unsteady state conditions. Their results yield a correlation for the calculation of heat transfer coefficient in foams. Hwang et al. (2002) measured the convection heat transfer coefficients for the air flow in aluminium foams by a transient single-blow technique. They found that the heat transfer coefficient rises as the mass velocity of air increases or the porosity decreases. Noh et al. (2006) showed that heat transfer coefficient depends on the Reynolds number. Dukhan et al. (2005) found that heat transfer intensifies as the Reynolds number rises up to a certain value.

Since the actual geometry of foams is rather complicated, experimental evaluation of fluid flow and heat transfer in porous scale geometry is a challenging task (Banhart et al. 1999; Zhao 2012). The structure of foams is very complicated and irregular, and it is not feasible to introduce a general geometry for them, so experimental studies cannot reveal the details of heat transfer in metallic foams (Wang and Pan 2008). Therefore, numerical simulation methods are employed to study foams with ideal geometries. As mentioned before, a wide range of applications available in porous media have led to numerous investigations in this area. From the viewpoint of the energy equation, there are two different models, local thermal equilibrium model (LTE) and the local thermal non-equilibrium (LTNE). The first model assumes that the solid temperature is equal to the fluid temperature; thus, local thermal equilibrium between the fluid and the solid phases is achieved at any location in the porous media. This model simplifies theoretical and numerical models, but the assumption of local thermal equilibrium between the fluid and the solid is inadequate for a number of problems (Zafari et al. 2016). The LTNE model assumes that there is a finite temperature difference between the fluid and the solid phase in the porous medium. In this model, two energy equations are solved to describe the heat transfer within the bulk porous media. Many numerical studies (Badruddin et al. 2007; Jiang and Ren 2001; Khashan et al. 2006) have used the LTNE model. Specifically, Coussirat et al. (2007) and Guardo et al. (2006) investigated the particle-to-fluid heat transfer in metallic foams by numerical simulation. Boomsma et al. (2003) developed a thermal model based on an ideal three-dimensional unit cell by considering the effect of thermal conductivity of the metallic foam matrix. Their results confirmed that the thermal conductivity of the solid phase is an effective thermal conductivity factor even at high porosity. Wu et al. (2011) simulated heat transfer between fluid flow and ceramic foams. They investigated the effect of significant parameters such as porosity and the average size of Kelvin cell on heat transfer coefficient. Their results revealed that heat transfer coefficient sharply decreases with the increase in the pore diameter. Kumar and Murthy (2004) confirmed that in addition to the porosity distribution, size, orientation and specific surface area of the pores affect the amount of heat transfer.

Since the ideal geometries like Kelvin or Weaire–Phelan are always accompanied by limiting assumptions that may adversely affect the accuracy of the simulation calculations, it would be more beneficial to use the actual geometry of the foams. Petrasch et al. (2008) obtained the actual geometry of porous environment by computer tomography and examined the characteristics of heat transfer between porous environment and fluid, using numerical methods. The results of their study were much closer to the experimental data as compared to the ideal geometries, but their approach requires long-term calculations and encounters descriptive complexities. Bodla et al. (2010) studied the significant parameters of heat transfer at various porosities for aluminium foams in air and water, based on the micro-tomographic images. One important outcome of their study is that as the pore diameter decreases, no significant changes occur in effective thermal conductivity. Ranut et al. (2014) showed that micro-tomography is a precise method for investigating the effect of foam geometry on the heat transfer rate. Zafari et al. (2015) followed this subject by using the actual foam geometry, assuming thermal non-equilibrium condition. They showed that convection heat transfer coefficient and Nusselt number decreases when porosity increases.

According to the geometrical parameters of the foams such as mean cell size, specific surface area and mean pore size that influence on the heat transfer, numerous equations in the general form of Nu = C₁Reⁿ¹Prⁿ² have been proposed for calculating the heat transfer coefficient (Zafari et al. 2015; Dittus and Boelter 1930; Demirel et al. 2000; Younis and Viskanta 1993). Regarding the structural complexities of the foams and lack of a general geometry in them, the effects of all structural parameters of the foam have not been considered in most of the proposed equations; thus, it is not possible to define a general and inclusive equation that can provide an acceptable application even in a limited range of the foams porosities and structural properties.

The aim of this study is to investigate the heat transfer characteristics between the flowing fluid and the strut surface of metal foams. Then, the role of significant parameters such as tortuosity, strut diameter, pores diameter and porosity in heat transfer characteristics of aluminium foams is evaluated by using the actual geometry. Based on the numerical results, a correlation of Nusselt number in the LTNE condition as a function of pore diameter, porosity and strut diameter is proposed.

2 Simulation Methodology

2.1 Foam Geometry

The geometrical structure of foams depends basically on the manufacturing process. Considering the fact that the microscopic structure of foams is very complex and irregular, a general geometry cannot represent them (Kopanidis et al. 2010). Despite this fact, the elementary volume method is generally utilized in lieu of the geometric model. In this method, the geometrical structure of the foam is described as a mesh structure by a regular 12- or 14-face structure whose sides are assumed to be pentagonal or hexagonal faces. Of these models, Kelvin model and Weaire–Phelan model are among the most used representatives of typical geometrical structures for foams (Xu et al. 2008). In most cases, due to the limiting assumptions considered for the aforementioned geometrical models, the numerical simulation results deviate from the experimental measurements. Such deviations become more rigorous in heat transfer computations where the thermal conductivity of fluid and solid is highly different, and the prediction of flow field significantly depends on the geometrical structure of the foam (Ranut et al. 2014; Boomsma and Poulikakos 2001). Using solid modelling based on the real structure of the porous medium is a remedy to such discrepancies.

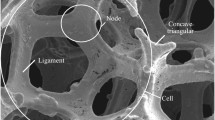
In order to determine the structure and composition of the materials, X-ray CT, a powerful and non-destructive method, can be utilized for a wide range of porous materials. The required geometry for the simulation was designed and constructed using the images of a micro-tomography software (GeoDict, trial version). In order to perform simulations, a system with eight-core (3.2 GHz, Xeon) and 64 GB RAM was utilized. Figure 1 exhibits a view of the generated geometry (voxel length of 20 µm) and the definition for the foam diameter, respectively. Table 1 presents the characteristics of the constructed foam geometry enlisting a detailed description of the used samples. The tortuosity was calculated by tracking the paths of particles in foams. For this reason a large number of particles were injected in different directions and different positions of foams. Dividing the path length of each particle (L′) to the straight length (L) of foam results in the tortuosity for that particle (τ = L′/L). Then τ was averaged for all the injected particles.

Fig. 1

a 3D image of a foam with 500 µm pore diameter and 86% porosity, b computational network employed in this study and c desired position for measurement of pore and strut diameter

Table 1 Characteristics of the foams examined in this study

2.2 The Governing Equations

The governing equations of unsteady flow and energy transfer for an incompressible flow are given by (de Lemos and Rocamora 2002):

$$ \frac{\partial \rho }{\partial t} + \frac{\partial }{{\partial z_{i} }}\left( {\rho v_{i} } \right) = 0\quad {\text{Continuity}} $$

(1)

$$ \frac{{\partial (\rho v_{i} )}}{\partial t} + \frac{\partial }{{\partial z_{i} }}\left( {\rho v_{i} v_{j} } \right) = - \frac{\partial P}{{\partial z_{i} }} + \frac{\partial }{{\partial z_{j} }}\left( {\mu \frac{{\partial v_{j} }}{{\partial z_{i} }}} \right)\quad {\text{Momentum}} $$

(2)

$$ \frac{\partial }{\partial t}\left( {\rho c_{\text{p}} T} \right)_{\text{f}} + \frac{\partial }{{\partial z_{i} }}\left( {\rho c_{\text{p}} v_{i} T} \right)_{\text{f}} = \frac{\partial }{{\partial z_{i} }}\left( {k\frac{\partial T}{{\partial z_{i} }}} \right)_{\text{f}} \quad {\text{Energy}} - {\text{Fluid}}\;{\text{Phase}} $$

(3)

$$ \frac{\partial }{\partial t}\left( {\rho c_{\text{p}} T} \right)_{\text{s}} = \frac{\partial }{{\partial z_{i} }}\left( {k\frac{\partial T}{{\partial z_{i} }}} \right)_{\text{s}} \quad {\text{Energy}} - {\text{Solid}}\;{\text{Phase }}\left( {{\text{Porous}}\;{\text{Matrix}}} \right) $$

(4)

where subscripts f and s refer to fluid and solid phases, respectively. Here, T is the temperature, k_f is the fluid thermal conductivity, and k_s is the solid thermal conductivity. C_p, p and v are specific heat, pressure and velocity, respectively. Furthermore, it is assumed that the problem is unsteady state and three-dimensional, and the fluid utilized for passing through the porous medium simulation is air. The variation of air properties with temperature is accounted for in the present simulations. In order to simulate the flow inside the domain, a finite volume method (Zafari et al. 2014; Pahlevaninezhad et al. 2014) has been used to solve the governing equations in a sequential solution algorithm. All the terms in the governing equations are discretized via finite volume discretization by second-order accurate schemes (central difference for the diffusion terms and second-order upwind for the convection terms). The SIMPLE algorithm was used to solve the velocity–pressure coupling, and the convergence criterion for solving equations was considered 10⁻⁶. The gravity effect in the momentum equations is neglected for the present simulation as suggested by Wu et al. (2010).

An important feature of flow in a porous medium is the Reynolds number. Several definitions of Reynolds number in porous media have been proposed in the literature. The studied methods result in Reynolds number values that are very close to each other. In this study, the pore diameter was used as the characteristic length. The Reynolds number, which is based on the pore diameter and the superficial velocity (Re = ρvd_p/µ), ranges from 10 to 200 in the present study. According to Kaviany (2012), in this range of Reynolds numbers with the defined characteristic length, the flow regime is laminar.

2.3 Boundary Condition

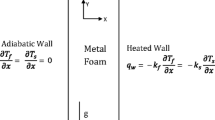
Figure 2 depicts the boundary conditions that are used for the present simulations. The Dirichlet boundary condition is assumed for the velocities at the inlet with a uniform value. The pressure outlet boundary condition with zero gauge pressure is defined at the outlet boundary, and the no-slip condition is imposed for all of the strut surfaces (all solid surfaces). For all peripheral boundaries, the symmetry condition is applied. Temperature of the inlet fluid ($T_{\text{f}}^{0}$) at all the times and the initial temperature of the solid matrix, foam, ($T_{\text{s}}^{0}$) are set at 500 and 300 K, respectively, so that the fluid warms up the foam as moves through it. An assessment of grid independency and time independency of the solution has been carried out to ensure that the numerical solution is independent of the number of computational grids and time step. Based on this computational assessment, a structured computational mesh (hexahedral) of eight million computational cells (Fig. 3a) and time step of 0.001 s (Fig. 3b) were found to be appropriate.

Fig. 2

Boundary conditions applied

Fig. 3

Assessment of a grid and b time independency

3 Results and Discussion

3.1 The Main Characteristics of Flow Field

In order to investigate the effect of geometrical parameters, simulation of air flow with a uniform inlet velocity of 2 m/s passing through a foam has been performed. The simulation was done for different pores diameter and porosities. Figure 4a compares the effects of different porosities (76–96%) on the averaged fluid velocity along the longitudinal direction of foam with 500 µm pore diameter. In Fig. 4b, the effects of different pores diameter on the local velocity are depicted. The results clearly show that the effect of porosity on the velocity of the main stream is significantly higher than pore diameter. It confirms the traditional assumption of macro-modelling in porous media, where the local velocity is directly related to the superficial velocity and the porosity.

Fig. 4

Variation of the fluid flow velocity versus non-dimensional length (z/z₀) for the foams with a pore diameter of 500 µm and different porosities and b porosity of 86% and different pores diameter

In addition, the obtained results reveal that the velocity fluctuations decrease as the porosity of the foam increases. In other words, the main reason for these fluctuations can be the heterogeneous porosity distribution along the foam length. To verify this issue, the variation of porosity along the foam length of the sample with a pore diameter of 500 µm and mean porosity of 86% is plotted in Fig. 5. As shown in the plot, the porosity locally varies at different planes of the foams, which indicates the anisotropic behaviour of the mentioned foams. Moreover, by comparing the graphs shown in Fig. 4a, b, it can be inferred that the porosity is the most prominent parameter affecting the velocity field.

Fig. 5

Variation of porosity along the foam length with pore diameter of 300 µm and mean porosity of 86%

In order to examine the influence of different parameters on the fluid flow, the Forchheimer equation with the coefficients mentioned in Eq. 5 was used (Wu et al. 2010). Based on this equation, the fluid flow is governed by diffusivity and inertia, whose coefficients are defined by Eqs. 6 and 7:

$$ \frac{\Delta P}{L} = \alpha v + \beta v^{2} $$

(5)

$$ \alpha = \frac{\mu }{K} $$

(6)

$$ \beta = \frac{{\rho C_{\text{f}} }}{\sqrt K } $$

(7)

In these equations, ΔP/L is the pressure gradient along the foam length, v is the inlet velocity (superficial velocity), α is the Darcy coefficient, β is the non-Darcy coefficient, K is the specific permeability, and C_f is the inertia coefficient. This equation shows that pressure drop along the foam is basically calculated by two terms; both of them are affected by velocity. In fact, this equation reveals that at low velocities, the main factor controlling the amount of pressure gradient is the viscous force, whereas at high velocities, inertia forces mainly control the pressure gradient. Therefore, the pressure gradient has a linear relationship at low velocities, while the relationship turns to nonlinear at higher velocities. Figure 6 depicts the pressure gradient of the samples at a range of inlet (superficial) velocities between 0.1 and 8 m/s in the foams having different pores diameter and porosities. According to Fig. 6a, at a constant pore diameter of 500 µm, the foam with 76% porosity shows maximum pressure gradient, and the foam with 96% porosity has the lowest pressure gradient. Decrement in pressure gradient by increasing the porosity at a constant pore diameter is attributed to a reduction in the inertia effects. On the other hand, at a constant porosity (Fig. 6b), it is observed that with increasing the pore diameter (300–500 µm), the value of pressure drop is approximately similar at these pores diameter. In fact, by increasing the pores diameter, the specific surface area reduces and as a result, the friction decreases. By fitting the results of the pressure gradient with Eq. 5, the value of K and C_f can be determined. These coefficients are presented in Fig. 7. According to Fig. 7a, b, it is observed that the value of K increases by increasing the porosity and pore diameter. In addition, based on the obtained results presented in Fig. 7c, d, the C_f value decreased when the porosity and pore diameter were increased. As a result, the sample with 100 µm pore diameter and 76% porosity exhibits the lowest K value and the highest C_f value, representing the highest resistance against the flow. On the other side, as the pore diameter and porosity of the foam increase, the resistance against passing the fluid flow decreases. For instance, the foam with 500 µm pore diameter and 96% porosity possesses the highest K value and the lowest C_f value. Based on these graphs, it can be concluded that the variation of specific permeability can be substantial when the pore diameter is high. However, the inertia coefficient does not change significantly as a function of pore diameter.

Fig. 6

Variation of pressure gradient versus velocity in the foams with a pore diameter of 500 µm and different porosities and b porosity of 86% and different pores diameter

Fig. 7

a, b Variation K versus pore diameter at different porosity and versus porosity at constant pores diameter, c, d variation C_f versus pore diameter at different porosity and versus porosity at constant pores diameter

3.1.1 Friction Factor

Friction factor is calculated according to Eq. 8 (Xu et al. 2008):

$$ f = - \,\frac{{\frac{{{\text{d}}P}}{{{\text{d}}x}}\sqrt K }}{{\rho v^{2} }} $$

(8)

Friction factor (f) is written as a function of Reynolds number:

$$ Re_{K} = \frac{\rho v\sqrt K }{\mu } $$

(9)

$$ f = \frac{1}{{Re_{K} }} + C_{\text{f}} $$

(10)

The friction factor coefficient for the foam with 96% porosity along with the correlations of Vafai and Tien (1982) and Bodla et al. (2010)is shown versus the Reynolds number in Fig. 8. As indicated in Fig. 8, at low Reynolds numbers, a linear relationship exists between friction factor and Reynolds number since the viscosity forces are more influential. However, with increasing the Reynolds number, the nonlinear term begins to dominate because of the inertial effects (Re_K ~ > 1). The present study has been done in lower Reynolds numbers (Re_K < 4), and such behaviour could not be detected in this range. As shown in Fig. 8, the present result show good agreement with others data and show the dependence observed by Vafai and Tien (1982) and Paek et al. (2000).

Fig. 8

Friction factor as a function of Reynolds number for foams of different porosities: present calculations and comparisons with results from the literature

3.2 Distribution of Fluid Temperature

In order to investigate the effect of time on the profiles of temperature in samples with different pore diameter and porosity under unsteady conditions, a dimensionless temperature parameter was defined as:

$$ \theta = \frac{{T_{\text{sl}} - T_{\text{s}}^{0} }}{{T_{\text{f}}^{0} - T_{\text{s}}^{0} }} $$

(11)

where T_sl is the solid local temperature, averaged over the cross-sectional area. Regarding this equation, it should be noted that the equilibrium conditions (i.e. equilibrium temperature, T_eq) corresponds to θ = 1. The results of θ variations versus the length of foam at different times, for a sample with a pore diameter of 500 μm and 86% porosity, at a superficial inlet velocity of 3 m/s are shown in Fig. 9. As shown in this figure, at a specified time, first the initial part of the foam is influenced by the thermal energy of fluid, and then this influence is convicted towards the exit plane. Moreover, at a specified length of foam, as time increases, so is the temperature of solid matrix until the equilibrium temperature is reached (i.e. θ = 1).

Fig. 9

Variation of θ versus length in the foams with pore diameter of 500 µm and porosity of 86%

In order to explain the effect of the geometrical parameters of the foam when θ = 1 (i.e. at equilibrium time, t_eq), the variation of θ at different times along the length of foam is shown in Fig. 10 for samples with different pore diameters and porosity at a velocity inlet of 3 m/s. As shown in Fig. 10a, b, the temperature of sample with a pore diameter of 100 μm and porosity of 86% reaches the temperature of the fluid in shorter time (i.e. t_eq at θ = 1) in comparison with one with the pore diameter of 500 μm. On the other hand, at constant pore diameter of 500 μm, as shown in Fig. 10c, d, a decrease in porosity from 96 to 76% reduced the time elapsed to reach the equilibrium condition. However, based on these results, it may be noted that the pore diameter has a more significant effect on reducing the equilibrium time than porosity. The reason for such behaviour can be attributed to the specific surface area of the foam. In Fig. 11, the average specific area versus porosity is plotted for different pore diameters. Despite being a function of both pore diameter and porosity, the specific area is more influenced by the pore diameter than porosity, as is observed in this figure. The traditional correlations regarding specific area also support such conclusion, as in most of the correlations the specific area is proportional to (1 − ɛ)^1/2, but is inversely proportional to pore diameter (Inayat et al. 2011) In addition, in a constant porosity, the foam with a pore diameter of 100 μm has the highest specific surface area compared to the other two. Therefore, the elapsed equilibrium time for the 100 μm pore medium is much less than the corresponding time of the others.

Fig. 10

Variation of θ versus time in the foams with different porosity and pore

Fig. 11

Variation of specific surface area versus porosity and pores diameter of 100–500 µm

One of the other effective parameters that may be used to investigate the t_eq is the inlet velocity of fluid. The effect of changes in the inlet velocity of fluid on the equilibrium time is shown in Fig. 12. As shown in this figure, at a constant velocity, by increasing the pore diameter or the porosity, the equilibrium time is increased. The reason is again related to change to the specific area of the foam (as seen in Fig. 11). In fact, by increasing the pore diameter or the porosity, the specific area is reduced, causing less heat transfer and more time to reach the equilibrium condition. It is also evident from Fig. 12 that by increasing the inlet velocity, the equilibrium time (t_eq) is increased. As the inlet velocity is increased, the flow Reynolds number, and thus the heat transfer coefficient, is also increased, but the residence time of the fluid is reduced. The overall result is an increase in the elapsed time to reach the thermal equilibrium condition.

Fig. 12

Variation of equilibrium temperature velocity a pore diameter of 500 µm and different porosities and b porosity of 86% and different pores diameter

3.3 Convection Heat Transfer Parameters in the Porous Medium

3.3.1 Local Heat Transfer Coefficient

Equation 12 is used to calculate the local heat transfer coefficient at different cross sections of the foam:

$$ h_{\text{l}} = \frac{q}{{A \left( {T_{\text{fl}} - T_{\text{sl}} } \right)}} $$

(12)

where A is the averaged surface area of the porous at each cross plane, q is the averaged heat rate between the fluid and the solid at the cross section, and T_fl is the fluid local temperature (averaged over the cross section area). In Fig. 13, the variation of the local heat transfer coefficient over the length of foam at different times ($0 < t < t_{\text{eq}}$) for an inlet velocity of 3 m/s is shown. As shown in this figure, the local heat transfer coefficient has increased slightly with time in the initial regions (z/z₀ < ≈ 0.3). However, in other parts of the foam (z/z₀ > ≈ 0.3), there is no significant changes in the local heat transfer coefficient over time, so that the graphs in these regions coincide with an acceptable approximation. The mismatch may be expected to occur in the entrance region due to the effect of the local inhomogeneity of flow in this part. Also, this claim can be confirmed by Figs. 21 and 22 (Appendix) in the region of flow entrance. Finally, in order to calculate the local Nusselt number, an average plot of local heat transfer coefficient ($\bar{h}_{\text{l}}$) over the time is presented in Fig. 13.

Fig. 13

Variation of local heat transfer coefficient versus z/z₀ at different times samples with different porosity and pore diameter

Figure 14 illustrates the distribution of a time-averaged local heat transfer coefficient for samples with 100–500 µm pore diameters and 76–96% porosity as a function of z/z₀ at inlet velocities of 3 and 5 m/s.

Fig. 14

Variation of average local heat transfer coefficient versus z/z₀ for samples at inlet velocities of 3 and 5 m/s a, b 86% porosity and different pores diameter, c, d pore diameter of 500 µm and different porosities

By using the obtained coefficients of local convection heat transfer, the local variation of the Nusselt number versus foam length is plotted in Fig. 15. Equation 13 was used for calculating the local Nusselt number, where k_f is thermal conductivity of the fluid and d_p is pore diameter:

Fig. 15

Variations of local Nusselt number in the fluid flow direction for fluid inlet velocity of 3 m/s in the foam with a different pores diameter and 86% porosity and b 500 µm pore diameter and different porosities

$$ Nu_{\text{l}} = \frac{{\bar{h}_{\text{l}} d_{\text{p}} }}{{k_{\text{f}} }} $$

(13)

The obtained results are shown only for two cases: an inlet velocity of 3 m/s for a porosity of 86% and different pore sizes, and an inlet velocity of 5 m/s for a pore size of 500 μm and different porosities. Similar profile shapes are obtained for other conditions used in the simulations. The local variations of Nusselt number (Fig. 15) are similar to the variation of the local convection heat transfer coefficient in Fig. 14. As indicated in these figures, the coefficient of local heat transfer and the local Nusselt number initially increases to a maximum value and then decreases to reach a constant value. In fact, the Nusselt number is generally a function of Reynolds and Prandtl numbers (Nu = f (Re, Pr)) so that, in this research in porous environments, the parameters corresponding to structural factor (F_s) can be considered as one of the effective variables in calculating the Nusselt number:

$$ Nu \, = \, F\left( {Re, \, Pr, \, F_{\text{s}} } \right) $$

(14)

$$ F_{\text{s}} = \, F\left( {\varepsilon , \, d_{\text{p}} , \, \tau , \, d_{\text{t}} } \right) $$

(15)

Therefore, the variation of local heat transfer could be categorized into three regions: I, II and III as shown in Figs. 14 and 15. Since viscosity, density and velocity of fluid varied due to the temperature changes along the foam length, these three regions are recognized as distinctive sections in the mentioned plots. In the first region (I), since the temperature of fluid decreases, density of flow increases while the viscosity of fluid decreases. Therefore, the Reynolds number (Re = ρ_fvd_p/µ_f) increases in this region and the coefficient of local convection heat transfer is also increased in this part, meaning that the Nusselt number is proportional to a positive power of the Reynolds number. In the second region (II), although the Reynolds number increases, the amount of heat transfer and thermal flow decrease when the local profiles of temperature of the solid matrix and fluid become similar to each other. Hence, the coefficient of local convention heat transfer becomes primarily constant and then decreases until the third region (III) where equilibrium temperature between the solid matrix and fluid (i.e. T_fl ≈ T_sl) is approximately equal. In this region, the local Nusselt and the coefficient of local convection heat transfer reach a constant value. Based on Figs. 14 and 10, the effect of structural parameters of the foams on the coefficient of local convection heat transfer is significant, so that its value is highly dependent on the pore diameter while its dependency on the porosity is weak. Besides, it is evident from Fig. 14 that the local temperature of fluid and solid reaches the equilibrium sooner for the sample with the lowest pore diameter, and the equilibrium length has been increased as the pore diameter and porosity increase.

3.3.2 Average Heat Transfer Coefficient

The average heat transfer coefficient of the foam is calculated by using the coefficient of local convection heat transfer, based on Eq. 16:

$$ h_{\text{ave}} = \frac{{\mathop \smallint \nolimits_{0}^{L} \bar{h}_{\text{z}} *{\text{d}}z}}{L} $$

(16)

Correlation between the average convection heat transfer coefficient, pore diameter, superficial velocity and porosity is illustrated in Fig. 16a–c.

Fig. 16

Variation of the average convection heat transfer coefficient of the foam function of a pore diameter, b porosity and c inlet fluid flow velocity

The obtained results indicate that the convection heat transfer coefficient highly relies on the pore diameter and inlet velocity, while it has a low dependency on the porosity within the pore diameter and porosity ranges examined in this study. (These results are similar to Wu et al. 2011.)

Moreover, the average convention heat transfer coefficient is noticeably reduced as the pore diameter increases, because the specific surface area decreases (Fig. 16a). The variation of specific surface area of the foam versus porosity is demonstrated in Fig. 11 for several pore diameters. As indicated, with increasing the pore diameter, the specific surface area of the samples is remarkably reduced. Furthermore, it is observed that at a constant pore diameter (100 µm), the average convention heat transfer coefficient does not show significant changes when the porosity ranges are within 86–96% (Fig. 16b). This is caused by the fact that the specific surface area of these samples does not substantially change as the porosity increases (Fig. 11) in this range, and the average convection heat transfer coefficient can be increased through the velocity increment. However, for the sample with 76% porosity and pore diameter 100 µm, owing to the higher specific surface area compared to 86% and 96% porosity, a greater average convection heat transfer coefficient has been achieved.

For more elucidation, the velocity vectors of the flow at the midway section along the foams with 100–500 µm diameter and 86% porosity are depicted in Fig. 17. As seen in this figure, at small pores diameter (100 µm), the vertical flow is significant in the vicinity of the pores. By increasing the pore diameter of the foams more than 100 µm, the intensity of vertical flow decreases and the foam walls have a lower effect on the flow.

Fig. 17

Velocity vectors for the foams with 86% porosity and a 100, b 300 and c 500 µm at the inlet velocity of 1 m/s

3.4 Generalized Correlation

Numerous correlations have been presented in the literature to calculate the average Nusselt number in porous environments (Zafari et al. 2015; Wu et al. 2011), most of which are a functions of Reynolds and Prandtl numbers and their general form is as follows:

$$ Nu \, = \, A\;Re^{n1} \;Pr^{n2} $$

(17)

Since air is applied as the inlet fluid and its Prandtl number has little variation with respect to temperature and pressure, the effect of Prandtl number is cast into coefficient A in some of these equations. In this study, based on the use of air as the inlet fluid in simulation, the Prandtl number has not been considered explicitly.

Although the convection heat transfer depends on the fluid conditions and the geometry of porous environment, the effect of structural parameters of the foam geometry has not been considered in the most of the mentioned equations; hence, these equations do not accurately calculate the value of Nusselt number. In order to take the geometrical characteristics of the foam into account for calculating the Nusselt number, a parameter F_s (ε, d_p, τ, d_t) is included:

$$ Nu \, = \, A\;Re^{n1} F_{\text{s}} \left( {\varepsilon ,\;d_{\text{p}} ,\;\tau ,\;d_{\text{t}} } \right) $$

(18)

Considering the geometrical parameters of the foam, the following equation can be presented for calculating the Nusselt number:

$$ Nu = A\;Re^{n1} \left( {\left( {1 - \, \varepsilon } \right)/\tau } \right)^{n2} \left( {d_{\text{p}} /d_{\text{t}} } \right)^{n3} $$

(19)

$$ Fs = \left( {\frac{1 - \varepsilon }{\tau }} \right)^{n1} \left( {\frac{{d_{\text{p}} }}{{d_{\text{t}} }}} \right)^{n2} $$

(20)

$$ Nu = \frac{{h_{\text{ave}} d_{\text{p}} }}{{k_{\text{f}} }} $$

(21)

In the aforementioned equation, the average Nusselt number has been calculated by using the average convection heat transfer coefficient and pore diameter, porosity, the strut diameter and tortuosity as the length characteristics of the porous environment. Figure 18 shows the variation of the Nusselt number versus Reynolds number for different pores diameter and porosities. As illustrated, with increasing the Reynolds number, the Nusselt number rises. Moreover, at a constant Reynolds number, increasing the pore diameter and decreasing the porosity rise the average Nusselt number.

Fig. 18

Variation of Nusselt number versus Reynolds number a pore diameter of 500 µm and different porosity and b porosity of 86% and different pores diameter

According to the results obtained from Fig. 18 and geometrical characteristics of the foams, the coefficients of Eq. 18 were derived through the variable changes and linear regression method for the samples with 100–500 µm pores diameter and 76–96% porosity. Therefore, Eq. 22 was obtained as a function of structural parameters of the foam:

$$ Nu = 0.0305\left( {Re} \right)^{0.77} \left( {\frac{1 - \varepsilon }{\tau }} \right)^{ - \,0.27} \left( {\frac{{d_{\text{p}} }}{{d_{\text{t}} }}} \right)^{ - \,5.108} $$

(22)

It should be noted, however, that the above equation is strictly valid for the range of porosities, pores diameter and Reynolds numbers appeared in Fig. 19 and is not recommended to be used outside this range. In this figure it is shown that Eq. 22 has acceptable accuracy with result of simulation. In order to validate the results, the obtained equation (Eq. 22) is compared with other studies (Fig. 20). As shown in Fig. 20, the proposed equation yields satisfactory agreement with other studies. So also by using the results obtained by including the structural factor to the Nusselt number correlation, it’s expected that the prediction of convection heat transfer coefficient in the foams with an acceptable accuracy could be applied.

Fig. 19

Comparison of the results of simulation and Eq. 22

Fig. 20

Comparison of the obtained equation with other studies

4 Conclusions

In this research, computational fluid dynamic method was applied to investigate fluid flow and heat transfer inside foams with 76–96% porosity and 100–500 µm pores diameter based on their actual geometry. In the presented model, air with a temperature of 500 K entered an aluminium foam with an initial temperature of 300 K and increased the foam temperature. Considering the structural parameters, it was possible to present a structural model in terms of a structural factor (F_s) for calculating the heat transfer coefficient. Adding this structural parameter to the Nusselt equation affects accuracy and inclusiveness for the applicability through the ranges of pore diameter and porosity of the examined foams. Consequently, it’s expected that this equation could estimate the convection heat transfer coefficients of the foams with an acceptable accuracy.

The obtained results revealed that the pressure gradient decreases with increasing the porosity and pore diameter. The difference in the pressure gradient became more pronounced with rising inlet flow velocity. Besides, as the porosity and pore diameter increased, the specific surface area decreased, so the required length to achieve temperature equilibrium (z_eq/z₀) between the solid matrix and fluid increased. The coefficient of local convection heat transfer versus the foam length showed distinctive changes based on variation of viscosity and fluid density with temperature. On the other hands, the average coefficient convection heat transfer substantially varied with pore diameter, while it was not highly dependent on the foam porosity.

Appendix

The variation of (q/A) and T_fl − T_sl versus z/z₀ is shown in Figs. 21 and 22.

Fig. 21

Variation of (q/A) versus z/z₀ with 86% porosity and pore diameter of 100 µm at the inlet velocity of 3 m/s

Fig. 22

Variation of T_fl − T_sl versus z/z₀ with 86% porosity and pore diameter of 100 µm at the inlet velocity of 3 m/s