1 Introduction

Shale gas reservoir is playing an important role in the world energy market, due to its significant advantages of less pollution in combustion compared with conventional fuel resources like oil and coal. Starting from the beginning of the twenty-first century (Le 2018; Wang et al. 2014; Hefley and Wang 2016; Zhang et al. 2015b), shale gas exploitation has become an essential component to bridge the growing gap between domestic production and consumption and thus secure the energy supply in North America (Hefley and Wang 2016). The USA successfully became the largest natural gas producer in 2009, thanks to the high progress in shale gas production (Bros 2012; Wang and Hefley 2016. In another large energy exporter, shale gas resources in Canada are estimated with an amount larger than 1000 tcf (tera cubic feet). A paradigm shift has been made toward the exploration of shale gas in one of the main reservoir blocks, the Western Canada sedimentary basin (WCSB) (Cipolla et al. 2010; Rubin 2010). With the development and popularity of shale gas exploration all over the world, there have also been other countries and areas reported with great potential of exploitation. For example, shale gas resources in China are estimated about \(31\times 10^{12}\,\mathrm{m}^{3}\) (Wang and Wang 2011)

Properties of shale gas reservoir are essentially needed for successful estimation and extraction. As a result, accurate characterization and detailed description of reservoirs should be considered as the prior purpose of relevant researches. Due to the complex hydraulic and thermal reservoir environment in production, it is hard to reproduce the same process in laboratory. Thus, numerical simulation has been a popular trend in the study of unconventional shale gas reservoirs. After a quick investigation on Web of Science Core Collection , it is found that published papers related with shale gas numerical simulation have been greatly increased, as shown in Fig. 1. A significant increase could be found from 2012 and continues increasing until now.

Fig. 1
figure 1

Paper numbers related with shale gas numerical simulation on Web of Science in recent years

Full size image

This paper is designed to conclude and comment on the flow mechanism and simulation approaches. First, the adsorption and deadsorption process is introduced, as well as the flow regime description. Besides, numerical simulation on micro- and mesoscales, e.g., molecular dynamics and lattice Boltzmann method, are reviewed. Meanwhile, apparent permeability correction, which is the macroscopic focus, is concluded. Afterward, we focus on the gas flow simulations at reservoir scales, including numerical models and the effect of geomechanics. Finally, the common macroscopic numerical simulation approaches, including finite element method, finite difference method and other schemes, will be presented.

2 Flow Mechanism of Shale Gas

Permeability is always relatively low in shale gas reservoirs, generally less than 1 md, and stratigraphic composition can be divided into different types of intervals (e.g., Devonian, Jurassic and Cretaceous strata) (Reis et al. 2001; Barree and Conway 2004). The stress-sensitive parameters, including organic richness, porosity, thickness and lateral extent, can vary significantly with in situ stress changes. Consequently, the fluid flow and geomechanics’ impacts are always effected by the change (Babadagli et al. 2015). Such extremely tight rock formations in shale gas reservoirs with different parameters result in the gas transportation which occurs through them by different mechanisms. With more efforts been devoted to the researches of such flow mechanisms, the inherent limitations of the conventional macroscopic methods used in petroleum industry have been overcome and new microscopic and mesoscopic approaches including molecular dynamics (MD) and lattice Boltzmann method (LBM) are introduced.

2.1 Adsorption/Desorption Mechanism

There are three states of gas reserved in shale reservoir: free gas, adsorbed gas and dissolved gas (Pollastro 2007). In previous study, it is found that adsorbed gas is the main state among the above three states, with statistical results, indicating that \(20-80\%\) of the total gas is adsorbed in reservoirs (Lu et al. 1995; Huan-zhi and Yan-qing 2010; Ross and Marc Bustin 2007; Curtis 2002). Adsorption properties can provide critical information to help characterize shale structures and optimize hydraulic fracturing. With the decrease in environment pressure, adsorbed gas will become free gas in the early period of exploitation (Grieser et al. 2009). As a result, gas adsorption/desorption description is of great importance to investigate the well production.

A plenty of work has been conducted to study the methane adsorption mechanisms (Zhang et al. 2012; Wei et al. 2012; Zhang and Yang 2012; Tan et al. 2014; Bjørner et al. 2013; Rexer et al. 2013). In some studies, molecular accumulation is viewed as the main origin of adsorption on shale surface. It is the consequence of the minimization theory of surface energy (Zhang and Yang 2012). Meanwhile, potential theory is sometimes used to identify the adsorption process, with Van der Waals forces leading to physisorption (Bjørner et al. 2013; Rexer et al. 2013). Besides, properties including pressure, temperature and geological characteristics have also caused much attention recently on how to affect the adsorption capacity (Zhang and Yang 2012; Tan et al. 2014). TOC content, which is short for total organic carbon, is found of high relevance with adsorption capacity. Generally speaking, samples with high TOC content will present high values of contents including total cumulative pore volume, surface area and total porosity, which directly lead to a higher adsorption capacity than the sample with less TOC. Compared with other rocks, shale contains high organic matter, which results in a high gas adsorption amount.

Table 1 Comparison of different isotherm adsorption models
Full size table

Shale permeability will be changed, due to the desorption of gas in the production process (Guo et al. 2017a). For example, gas desorption process is found in organic grids, known as kerogen, where pressure drop occurs (Guo et al. 2014). Meanwhile, pressure difference will be generated between the bulk matrix and the pores, with the pore pressure decreasing in the free gas production process; thus, the desorption on the surface of bulk matrix is reinforced.

A large number of gas adsorption isotherm models have been proposed in previous studies, such as Langmuir’s type model, Freundlich-type model, Langmuir–Freundlich-type model, D-R-type model, BET-type model and Toth-type models (Herzog 2010; Langmuir 1918; Brunauer et al. 1938; Dubinin 1960, 1965; Yang et al. 2014; Su et al. 2008; Bae and Bhatia 2006; Dada et al. 2012). Most available adsorption models, including their basic equation and the basins where they are applied, are listed in Table 1. In this table, V denotes the adsorbate volume, P denotes the pressure, K denotes an associated equilibrium constant, k denotes the Henry’s constant, b denotes the adsorption affinity, D denotes the empirical binary interaction parameter, x and m denote a constant for a given absorbate and absorbent at a particular temperature, and c is a constant related to the adsorption net heat. The subscript L in \(P_\mathrm{L}\) and \(V_\mathrm{L}\) denotes the Langmuir pressure and Langmuir volume.

Among the above models, the Langmuir’s type model is always considered as the simplest and most effective (Tang et al. 2016). With its long history and wide application, model parameters have been reasonably explained and different evaluated models have been proposed based on the original equation. This large set of enhanced models have been used for describing methane and other gas adsorption behaviors with satisfactory performance (Mertens 2009; Tang and Ripepi 2017; Stadie et al. 2015). For example, a widely used evaluated form of Langmuir isotherm is given by:

$$\begin{aligned} q=\frac{\rho _\mathrm{s}M_\mathrm{g}}{V_\mathrm{std}}q_\mathrm{a}=\frac{\rho _\mathrm{s}M_\mathrm{g}}{V_\mathrm{std}}\frac{q_\mathrm{L}P}{P_\mathrm{L}+P}, \end{aligned}$$
(1)

where \(\rho _\mathrm{s}(\mathrm{kg/m}^{3})\) denotes the material density of the porous sample, \(q(\mathrm{kg/m}^{3})\) is the mass of gas adsorbed per solid volume, \(q_\mathrm{a}(\mathrm{m}^{3}/\mathrm{kg})\) is the standard volume of gas adsorbed per solid mass, \(q_\mathrm{L}(\mathrm{m}^{3}/\mathrm{kg})\) is the Langmuir gas volume, \(V_\mathrm{std}(\mathrm{m}^{3}/\mathrm{kmol})\) is the molar volume of gas at standard temperature (273.15 K) and pressure (101,325 Pa), p (Pa) is the gas pressure, \(p_\mathrm{L}\) (Pa) is the Langmuir gas pressure, and \(M_\mathrm{g}\) (kg/mol)is the molecular weight of gas.

In reservoir scale, the effect of gas adsorption capacity is highly extrapolated in regions. As a result, gas-in-place evaluation and production prediction are quite easy to be overestimated or underestimated and then severely impact the energy industry and social economy (Saulsberry et al. 1996; Ge et al. 2018). However, the existing models are still in developing and continuous optimization. For example, the original BET model is seldom used at present due to the weak theoretical foundations. It has been found that some assumptions in these models, like multilayer formation, small pore capillary condensation, adsorbed liquid phase and saturation pressure, are no longer suitable for special flow mechanisms of shale gas fluid (Zhou and Zhou 2009; Dubinin 1960). Another shortcoming of the classical model is that extrapolated data beyond the test range cannot be fully relied due to different empirical correlations in different temperature regimes. The original physical meanings inside these models, coming from the well-designed experiments, are weakened due to the introduction of some empirical constants. These constants are manually corrected to improve the fitting performance but make the models less reliable (Tang et al. 2016). There remains a lot to do to meet the realistic industry conditions better and to help the industry with more accuracy on the production forecast and control.

It has been pointed out that gas-in-place volumes in reservoirs are often incorrectly determined for cases with multi-component sorbed gas phase (Ambrose et al. 2011; Hartman et al. 2011; Fathi and Akkutlu 2014). Especially for shale gas fluid flow with high composition of varieties of hydrocarbons (C2+) and subsequently high total organic content (TOC), the adjustment of taking multi-component effect into account has been more necessary in the gas-in-place predictions. Compared to conventional approach, the new multi-component model will show a 20 percent decrease in total gas storage capacity calculations (Ambrose et al. 2011). Besides, multi-component sorption phenomena, in particular in the primary (micro-) pore structure of the shale matrix, e.g., co- and counter diffusion and competitive adsorption process, are the fundamental interests in the study of CO\(_2\) sequestration and enhanced shale gas recovery (Fathi and Akkutlu 2014). However, the current multi-component adsorption model is still limited on just modifications based on classical single-component Langmuir sorption model (Jiang et al. 2014; Hartman et al. 2011). A more uniform and widely applicable model is still in urgent requirement to meet the complex physical and chemical environment of shale gas reservoirs. With the rapid development of fully coupled multi-component multi-continuum compositional simulator which incorporates several transport/storage mechanisms of shale gas reservoirs, a more comprehensive adsorption/desorption model is needed to capture and predict the transport process in shale gas reservoirs.

2.2 Flow Mechanisms of Gas Transport in Shale Gas Reservoir

It is important to study the flow mechanism of gas transport in shale gas reservoir. A particular interest has been focused on the multiscale flow simulation on the subsurface porous media with pore size ranging from macroscale (\(>1\) mm) to nanoscale (\(<100\) nm) (Gerke et al. 2015; Di and Jensen 2015). Different pore-scale characteristics are presented with different flow regimes identified by Knudsen number (McCain 1990; Kärger 1996; Zhao et al. 2014; He et al. 2013). Slippage and diffusion processes are often viewed as the main flow mechanisms (Berkowitz and Ewing 1998). New approaches, including molecular dynamics (MD) and lattice Boltzmann method (LBM), are rapidly developed in these years to study the flow mechanisms.

2.2.1 Flow Regime

Knudsen number (Kn) is a parameter introduced in gas flow description to identify flow regimes with different rarefaction degrees of gas encountered. Generally, four regimes are characterized based on Kn: continuous flow (\(Kn<10^{-3}\)), slip flow (\(10^{-3}<Kn<10^{0.1}\)), transition flow (\(0.1<Kn<10\)) and Knudsen flow (\(Kn>10\)) (Beskok et al. 1996). Different interfacial effects are found effective in different flow regimes in small porous structure. For large tube diameter, the gas flow is mainly viewed as continuous flow with only slip regime near the wall (Ozkan et al. 2010). Strong interfacial effects are found in shale nanotubes, which are believed to be caused by two important flow regimes including Knudsen flow and transitional flow. It should be noted that the flow pattern of single-phase gas flow and gas–water two-phase flow is of big difference (Zhao et al. 2012). In this paper, we focus on the single-phase flow (Fig. 2).

Fig. 2
figure 2

Schematic diagram of shale gas transport mechanism with different flow regimes (Song et al. 2016)

Full size image

A main usage of flow regime characterization is that different governing models, resulting in different simulation approaches, are corresponding to the Knudsen number and flow regimes. Table 2 shows the gas flow regimes and corresponding governing equations along with boundary conditions. When Kn varies from 0.001 to 0.1, gas transportation is in the regime of slip flow and slip boundary condition should be incorporated into Navier–Stokes equation or lattice Boltzmann method (LBM) to take into account the slippage on the gas solid interface. When Kn is in a higher range of 0.1 and 10, gas flow enters the transitional regime, where neither Navier–Stokes equation nor lattice Boltzmann model is applicable any more. Then, Burnett equation based on higher-order moments of Boltzmann equation should be solved or numerical method of direct simulation Monte Carlo (DSMC) should be used to represent the fluid flow behavior. As Kn goes beyond 10, gas stream is considered as free molecules, and molecular dynamics (MD) must be adopted to capture the physics controlling the gas flow.

Table 2 Knudsen number and flow regimes with applicable mathematical models
Full size table

For gas flow in nanotubes, it has been demonstrated that slippage effects will change the flow regime identification (Tian et al. 2012). The concept of slip has a long history, starting from the famous scientist Navier (Neto et al. 2005; Matthews and Hill 2008) , and has been used in a large range of practices. For fluid flow passing rough surface, slip boundary condition is often applied with the slip length relevant to roughness height. When \(Kn<10^{-2}\), flow is in continuous regime and Darcy’s law is enough to describe the flow. As Kn increases from 0.01, diffusive flux is no longer ignorable and additional term should be considered in the flow equations, which makes it nonlinear.

To correct the permeability with consideration of gas slippage effect, Klinkenberg approach is often applied in previous studies (Li et al. 2015; Whitaker 1986). For example, to handle flow in all the four flow regimes, a new equation is proposed in Ziarani and Aguilera (2012), Shan and Wang (2013), Li et al. (2015), with the gas slip factor modified based on the dusty gas model:

$$\begin{aligned} v=-\left( \frac{D}{p}+\frac{k}{\mu }\right) \nabla p. \end{aligned}$$
(2)

A comprehensive model capable of handling gas flow through multiscale porous media varying from nanoscale to macroscale is generated based on the above equation, with the prospective of molecular kinetics (Song et al. 2016). Knudsen diffusion process is often considered as driven by collisions of wall with molecule, and collective diffusion process is driven by collision of molecule with molecule. In the new formulation, the collision coefficient is determined based on the consideration of both Knudsen and collective diffusion. It is figured out that for single-phase fluid flow in nanotubes, the interfacial effects existed in the wall surface will lead to form a thin liquid film and the flow characteristics will be changed then (Myers 2011). The stress singularity is removed in thin film theory, and fluid front is thought to move over dry surface. It has been shown in previous simulations that separations of about ten molecular diameters down will be resulted in the fluid viscosity with the bulk value (Neto et al. 2005). There has also been assumptions (de Gennes 2002; Eijkel and Berg 2005) that the formed gas film has a thickness between the molecular size and the gas mean free path. Molecular dynamics simulation has proved that Myer’s model is correct (Ambrose et al. 2010).

Geometrical properties of fractured porous media are vital to predict and evaluate the hydraulic transport properties of fracture networks (Wei and Xia 2017; Tan et al. 2017). Although a variety of subjects have been studied related to geometrical, fractal and hydraulic properties of fractured porous media such as rock masses and reservoirs, a gap still exists between theoretical knowledge and field practice (Yinghao et al. 2018). It is of great importance to seek new theoretical and numerical studies and advances in various subjects addressing flow and transport mechanism as well as hydrocarbon recovery improvement, such as innovative stimulation techniques, reservoir characterization and other approaches. Specifically, not all the length distribution of fractures and fracture networks follows the fractal law. They may be multi-fractal and even non-fractal. Thus, more elaborate explorations are needed for adequately characterizing the complex fractured networks. As we discussed in the above section, fractal dimension is one of the most important parameters to quantitatively characterize the complexity of fractures. However, fractal dimension is sensitive to prediction methods; even some irrational values may be obtained (Cai et al. 2017). Future works also should be focused on the influence of fracture surface roughness, hydraulic gradient, and coupled thermo-hydro-mechanical-chemical processes.

2.2.2 Molecular Dynamics for Shale Gas Transportation

Molecular dynamics (MD) simulation approaches recognize the fluid flow as a swarm of discrete particles and is suitable for flow simulation with high Kn number. It is often seen as an accurate approach due to the deterministic (Hadjiconstantinou 2006) or probabilistic (Heer 2012) calculation of the particle properties at every time step (Bird 1994; Koplik and Banavar 1995; Hadjiconstantinou 2006). These properties include particle inertia, position and state. Boltzmann distribution is often used to describe individual particle dynamics at different temperatures. Newton’s equation of motion is integrated numerically to determine the two-body potential energy and transient evaluation of two particles and then to find the particle positions.

A general purpose of using MD simulation is to investigate the adsorption and desorption (displacement) process of shale gas flow (Sharma et al. 2015; Jin and Firoozabadi 2015; Wu et al. 2015). Some researchers have performed numerous studies using molecular dynamic simulations to model gas flow through a single nanotube, in which the interface microstructure phenomenon is of special interest (Thomas and McGaughey 2009). The results have shown that the interaction between fluid and solid wall is a great cause of flow promotion. Meanwhile, MD studies have been performed to understand the shale gas diffusion process in special pores (Yang and Zhang 2005) and study thermodynamical properties of gas transport in montmorillonite (MMT) (Botan et al. 2010; Cygan et al. 2012). MD studies are also carried out to help describe the pore structures in shale formations (Firouzi et al. 2014), and it can also be used in the general gas recovery process (Yuan et al. 2015) In Table 3, we listed five recent papers with high citing rates relevant to molecular dynamics simulation of shale gas reservoirs. The citations of each paper are searched from Web of Science Core Database.

Table 3 Five high-citing papers of MD simulation of shale gas reservoirs
Full size table

It should be noted that modern computation capability, represented by supercomputers, is still not enough to handle a reasonable, practical and very detailed flow simulation through nanotubes network in time and space scale of the real production process in shale gas reservoir. Although MD models are designed to capture microscopic interactions, which are the foundation of macroscopic phenomena, time steps are generally strictly limited to femtoseconds (\(10^{-15}\) s), which results in the limitation of simulation timescale generally ranging from picoseconds (\(10^{-12}\) s) to nanoseconds (\(10^{-9}\) s) (Hadjiconstantinou 2006)

2.2.3 Lattice Boltzmann Method

The lattice Boltzmann method (LBM) has been proved to be a useful and efficient approach to study the shale gas reservoirs (Zhang et al. 2014; Chen et al. 2015). Knudsen diffusion has already been incorporated in the general LBM flow models to describe transport properties of shale gas fluid flows (Zhang et al. 2014) For multiphase flow, the famous Shan–Chen model of single-component multiphase flow is commonly used (Chen et al. 2015)

The first attempt to take Knudsen diffusion into account of the fluid flow using LBM simulation approach is said to be in Chen et al. (2015). In their study, compared to commonly used shale tortuosity, which is an important component of Bruggeman equation, the improved model will lead to a much higher tortuosity result and consequently the intrinsic permeability is said to be extremely lower (Chen et al. 2015). For relative permeability, it is found that the countercurrent relative permeabilities, as a function of wetting saturation, usually seem smaller than the concurrent ones with a Lattice Boltzmann scheme derived for two-phase steady-state flow (Huang and Lu 2009).

Characteristics of gas flow in organic nanopores in shale gas reservoirs can be evaluated effectively using developed LBM simulation. Under assumptions of small Knudsen number, flow properties simulated with LBM models agree well with the classical macroscopic Poiseuille’s law. Flow capacity, or flow rate, is found to be proportional to the square of pore size (Zhang et al. 2014). However, the relaxation time used in LBM models should be corrected to cover simulations at high Kn value. Permeability is increased as the result of velocity enhancement caused by slippage effect on pore walls. Adsorptive and cohesive forces among particles in gas fluid flow are used to simulate molecular-level interactions accounting with LBM scheme in Fathi and Akkutlu (2012). With slip boundary condition of Langmuir type at organic pore walls, mass transport along the tube walls is partitioned into two components: hopping of adsorbed gas molecules and slippage of free gas molecules. Hopping is the process of surface transport. In Table 4, we listed five recent papers with high citing rates relevant to lattice Boltzmann simulation of shale gas reservoirs. The citations of each paper are searched from Web of Science Core Database.

Table 4 Five high-citing papers of LBM simulation of shale gas reservoirs
Full size table

Previous researches have shown that approaches belonging to Lattice Boltzmann scheme are still limited in the application of rapidly recovering the imaging of pore structure and furthermore in the simulation and visualization of fluid flow in porous media, especially less effective in three dimensions. Pore network models, which is also a mesoscopic approach, are capable of simplifying detailed large-scale pore structures into a readable network constituting of pore bodies connected by pore throats (Ma et al. 2014; Cao et al. 2015; Huang et al. 2016; Wua et al. 2015). Each pore body is associated with different numbers of attributes, which are called coordinate numbers, and the spatial location is then specified explicitly. In this way, the highly irregular porous space is reduced to a network with topology and geometry easily captured (Zhang et al. 2015b).

2.3 Apparent Permeability Correction

A standard approach to study gas transportation in porous media is the famous Darcy’s law (Darcy 2007). In this theory, the average macroscopic gas velocity v is assumed to be determined by global permeability k and the pressure gradient \(\nabla p\) across the media

$$\begin{aligned} v=-\frac{k}{\mu }\nabla p, \end{aligned}$$
(3)

where \(\mu \) is the gas viscosity. The permeability k is a macroscopic parameter defined to describe the relation between gas flow and pore structure. Same as many other classical macroscopic theories, Darcy’s law was first concluded from experiments conducted by Darcy (2007). It is proved that Darcy’s law can also be derived from Navier–Stokes equation as a simplification and extension in porous media (Li et al. 2015).

However, the long history research of shale gas reservoir has brought insights of special percolation characteristics and flow mechanisms in the tight rock structures. The original Darcy’s equation is no longer capable of explaining these phenomena. A strict limitation of flow velocity is found in the application of classical Darcy’s law. For highly fractured reservoir structures, gas flow is at relatively high velocity and the original Darcy’s law will lead to misleading results, sometimes with an overprediction of productivity as much as \(100\%\) (Nguyen 1986). To facilitate the inclusion of this phenomenon into reservoir simulators, many multipliers are generated to correlate the apparent permeability to the absolute permeability in different flow regimes.

Experimental studies on permeability enhancement effects in tight formations date back to the early twentieth century. In 1941, based on gas flooding experiments, Klinkenberg (1941) proposed a correlation equation of the apparent gas permeability ka to the absolute permeability \(k_{\infty }\) via

$$\begin{aligned} k_\mathrm{a}=\left( 1+\frac{b}{p}\right) k_{\infty }, \end{aligned}$$
(4)

where b is the Klinkenberg factor and p represents average pressure across the core. The Klinkenberg factor is usually obtained by matching experimental data. Klinkenberg’s correction can be applied in the low Knudsen number range (\(<0.1\)); therefore, it is widely adopted for simulating low permeability gas reservoirs. The Klinkenberg factor is often calculated by a function of the absolute permeability and the rock porosity. Different expressions of Klinkenberg factor b can be found in Jones and Owens (1980), Sampath and Keighin (1982), Civan (2010).

So far, no satisfactory apparent permeability correction has been developed for the transitional flow regime due to its complexity. A widely accepted correlation equation is proposed in 1999 by Beskok and Karniadakis (1999), with the multiplier relevant to Kn, and many other correlations have been developed based on it:

$$\begin{aligned} K=K_{\infty }f(Kn). \end{aligned}$$
(5)
Table 5 Comparison of different apparent permeability correction models
Full size table

In the above equation, f(Kn) is a flow condition function given as a function of the Knudsen number Kn, the dimensionless rarefaction coefficient \(\alpha \) and the slip coefficient b, which is an empirical parameter by:

$$\begin{aligned} f(Kn)=(1+\alpha Kn)\left( 1+\frac{4Kn}{1-bKn.}\right) \end{aligned}$$
(6)

The most important parameter is the slip coefficient, which is described as “the vorticity flux into the surface divided by the vorticity of flow field on the surface, obtained by the no-slip approximation” (Beskok et al. 1996). To obtain the value, direct simulation Monte Carlo (DSMC) method and linearized Boltzmann equation are the two main approaches commonly used and sometimes laboratory experiments are designed for this. Slippage effects are enhanced at low pressure condition, and the adsorption layer thickness is reduced, which results in a larger coefficient measured at ambient condition experiments (Sakhaee-Pour and Bryant 2012). The linearity property of Darcy’s law is broken as the permeability increases. A new developed model of Beskok-type scheme to calculate multiplier is proposed recently as Sakhaee-Pour and Bryant (2012)

$$\begin{aligned} f\left( K_{n}\right) ={\left\{ \begin{array}{ll} 1+5K{n} &{} {\text{ Slip } \text{ Regime }}\\ 0.8453+5.4576K{n}+0.1633K{n}^{2} &{} {\text{ Transition } \text{ Regime }} \end{array}\right. } \end{aligned}$$
(7)

Within the free molecular or Knudsen flow regime, the apparent gas permeability can be calculated by considering the diffusivity for Knudsen diffusion from gas kinetics.

$$\begin{aligned} D=\frac{1}{3}du=\frac{1}{3}d\sqrt{\frac{8RT}{\pi M_\mathrm{A}}}, \end{aligned}$$
(8)

where u is gas molecules thermal velocity, R is the gas constant, and \(M_\mathrm{A}\) is the gas molecular weight. The derivation of Knudsen diffusion coefficient can be found in Pollard and Present (1948). By rearranging the above equation, we can get an apparent gas permeability formulation similar to the Klinkenberg’s correlation:

$$\begin{aligned} k_\mathrm{a}=\left( 1+\frac{b}{p}\right) k_{\infty }, \end{aligned}$$
(9)

where \(b_\mathrm{a}=pc_\mathrm{g}\mu _\mathrm{g}D/k_{\infty }\) (Sun et al. 2015).

Slip flow, transition diffusion and surface diffusion are incorporated in a flux model proposed in 2017 (He et al. 2017), and the apparent permeability is derived as:

$$\begin{aligned} k_\mathrm{app}=\frac{Fr^{2}}{8}+\frac{\mu D_\mathrm{T}}{p}+\frac{\mu D_\mathrm{s}\varsigma _\mathrm{ms}RTC_\mathrm{s}}{p^{2}}. \end{aligned}$$
(10)

In Table 5, we listed different types of apparent permeability correction models that have been proposed. It is noted that Sun’s model is a developed model based on classical Klinkenberg equation, which is proved with better accuracy (Sun et al. 2015).

2.4 Improved Darcy Model in Fractures

It is important to modify original Darcy’s equation to consider turbulent flow pattern of the gas transport in shale fractures where the inertial forces are relatively high (Ghanbarian and Javadpour 2017). Forchheimer equation is a commonly used formula to describe non-Darcy flow. It is observed that the linear relationship between the fluid velocity and pressure gradient in traditional Darcy’s law is no longer valid at high flow rates. The non-Darcy flow coefficient, \(\beta \), is then defined as a secondary proportional constant in addition to the permeability k to introduce the nonlinearity. The improved model with the two coefficients can be written as

$$\begin{aligned} - \frac{{{\text {d}}p}}{{{\text {d}}x}} = \frac{\mu v}{k} + \beta \rho v^{2}. \end{aligned}$$
(11)

Non-Darcy coefficient \(\beta \) is of growing interest as it can be easily used in reservoir simulation (Li and Engler 2001). Many theoretical correlations have been developed to calculate this parameter. A comprehensive model derived from experimental data is applied in numerical simulation, which is proved to be valid for single-phase gas flow in porous media belonging to all ranges of flow regimes (Belhaj et al. 2003). A parallel and serial two-type model is proposed to describe the porous structure (Takhanov 2011). In this classification, the porous medium is assumed to be made up of straight bundle and parallel capillaries with uniform diameter in parallel type. The serial type is assumed to the structure serially lined pore space. For both the models, non-Darcy coefficient \(\beta \) is given as

$$\begin{aligned} \beta = \frac{c}{{K^{0.5} \phi ^{1.5} }}\,\,{\text {Parallel type model}}. \end{aligned}$$
(12)

It is found that the above equation with additional quadratic term of velocity is limited within certain range of data set (Bejan 2013). To handle deviations, another cubic term of velocity is introduced to better meet all data sets:

$$\begin{aligned} - \frac{\partial p}{\partial x} = \frac{\mu v}{k} + \beta \rho v^{2} + \gamma \rho v^{3}. \end{aligned}$$
(13)

However, the above Forchheimer cubic equation with constant \(\beta \) and \(\gamma \) parameters still not meet all the data sets very well. Apparent permeability is observed to be larger than predictions using Forchheimer-type equations at high flow rate. Based on extensive laboratory and field experimental data sets, a new and more general model, which is known as Barree and Conway model (Barree and Conway 2004), is proposed in 2004 to overcome the problems caused by constant \(\beta \) and \(\gamma \) values. Darcy’s now is again valid in the Barree and Conway model, with apparent permeability:

$$\begin{aligned} - \frac{\partial p}{\partial L} = \frac{\mu v}{k_\mathrm{app}}. \end{aligned}$$
(14)

Barree and Conway model is proved to address the discrepancies, which may cause significant impact on the relationship between pressure and flow rate distribution in porous media (Lai et al. 2012). As shown in Fig. 3, the Barree and Conway model meets much better with the experimental data of pressure drop and flow rate, while Forchheimer quadratic equation will overestimate the pressure drop at high flow rate, but Forchheimer cubic equation underestimate the pressure drop.

Fig. 3
figure 3

Comparison between pressure gradient and mass flow rate under certain conditions with different models (Lai et al. 2012)

Full size image

The Barree and Conway model (BCM) has been widely applied in modern petroleum industry as a basic mathematical model of shale gas reservoir simulator. A 3D single-phase fluid flow scheme is derived according to Forchheimer and BCM equations to simulate pressure transient analysis in fractured reservoirs (Al-Otaibi and Wu 2011). On combining both the equations, an equivalent non-Darcy flow coefficient can be calculated to describe all non-Darcy flow phenomena coupling with near-wellbore effects. Besides, the BCM has already been extended to model the multiphase flow in porous media, which is widely used in practical shale gas reservoir simulator (Wu et al. 2011).

The recent development of shale gas reservoir simulation techniques has witnessed new evolutions based on Barree and Conway model. Barree and Conway (2007) improved this model with no more assumptions of a constant permeability or a constant \(\beta \). In the new model, correlations of pressure drop and flow velocity can be valid for the whole porous media (Lai et al. 2012):

$$\begin{aligned} \frac{\partial p}{\partial L} = \mu v/k_{\text {d}} \left[ {k_{\text {mr}} + \frac{{\left( {1 + k_{\text {mr}} } \right) }}{{\left( {1 + \frac{\rho v}{\mu T}} \right) }}} \right] . \end{aligned}$$
(15)

3 Gas Flow Simulation at Reservoir Scale

3.1 Flow Models

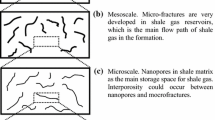
Shale is generally viewed as sediments with very fine grains and obvious fissility (Javadpour 2009). The porous media, constituting of pores with diameters ranging from nanometer to micrometer, are classified into inter-particle and intra-particle pores. The intra-particle pores are associated with organic matter pores within kerogen and mineral particles (Loucks et al. 2012).

Different physical properties have been illustrated in the organic matter pore compared with rock constituents commonly seen. The special properties play significantly impact on the gas storage and flow in shale. Numerous small pores are found in larger pores residing on their interior walls in kerogen (Curtis et al. 2010). Besides, cross section of pores in kerogen is observed to be round. Kerogen is also thought to be the place where gas adsorbs on the wall and dissolves within it (Javadpour (2009); Jarvie et al. (2004)). The pore structure in organic matter is generally considered as gas wetting because it is formed in hydrocarbon generation process (Sulucarnain et al. 2012; Wang and Reed 2009). As the organic matter is so unique with these features, a four-type classification of organic-rich shale structure is commonly accepted, where the porosity systems are divided into hydraulic fractures, natural fractures, kerogen (organic matrix) and inorganic matter, with the decrease in pore size (Wang and Reed 2009), as shown in Fig. 4. Another classification approach is to categorize the shale reservoir into four different pore systems as organic porosity, inorganic porosity, natural fractures and hydraulic fractures (Hudson et al. 2012)

Fig. 4
figure 4

Schematic of microscale model: a grid system for instance, with one organic matrix unit randomly distributed in shale matrix core surrounded by natural fracture grid (Yan et al. 2016)

Full size image

Different approaches have been developed to capture the shale properties in reservoir simulations. Multiple interacting continua (MINC) and explicit fracture modeling are proposed to generate an efficient scheme with single porosity for shale gas simulation (Wu et al. 2009). A coarse-grid model incorporating numerical dynamic skin factor is presented for shale reservoirs with hydraulic fractures (Ding et al. 2013). To handle practical well performance in a long term as well as common transient behavior, the coarse-grid model is improved to better describe the fractures and wells (Ding et al. 2014).

For different connections in organic matters with different pore sizes, free gas flow mechanism varies. Generally speaking, for connections between nanopores and micropores in organic matter, only Fickian diffusion is driven of desorbed gas flow. For connections between micropores in organic matters, both Darcy’s law and Fickian diffusion should be considered. For other connections, Darcy’s law is often assumed to be the only driven force. A general mass conservation equation is derived to accommodate all the three assumptions and describe a single-component and single-phase isothermal flow system (Yan et al. 2016):

$$\begin{aligned} \nabla \cdot \left[ \rho _\mathrm{g}\left( D_\mathrm{f}C_\mathrm{g}\nabla P+\frac{K}{\mu _\mathrm{g}}\left( \nabla p+\rho _\mathrm{g}g\nabla z\right) \right) \right] =-\left[ \frac{\partial \left( \rho _\mathrm{g}\varphi \right) }{\partial t}+\frac{\partial \left( q_\mathrm{a}\left( 1-\varphi \right) \right) }{\partial t}\right] , \end{aligned}$$
(16)

where \(D_\mathrm{f}\) is the Fickian diffusion coefficient, \(C_\mathrm{g}\) is the gas permeability, \(\mu _\mathrm{g}\) is the gas viscosity, K is the media permeability, \(q_\mathrm{a}\) is the mass of gas adsorbed on unit volume of media, and \(\varphi \) is the porosity of the porous media. The first term on the left-hand side of above equation represents the Fickian diffusion flux, and the second term represents the Darcy flow flux. On the right-hand side, the first term refers to the compressed gas in all the grids and the second term refers to the accumulation of desorbed gas in organic grid blocks.

Darcy’s law is quite limited in shale matrix as the permeability is extremely low there. As a result, many innovative methods have been proposed to investigate the flow mechanisms instead of dual-permeability and dual-porosity models commonly used in conventional oil and gas reservoirs. One approach is called the dual-mechanism model, which considers both the Fickian diffusion and Darcy flow, and dynamic gas slippage factor is introduced to describe the gas flow in tight formations (Clarkson and Ertekin 2010; Curtis et al. 2012). Another method is proposed in 2012 (Ziarani and Aguilera 2012), using a flow condition function of Knudsen number to correct apparent permeability with intrinsic permeability. However, further confirmation is still needed to validate the suitability to various flow regimes. An improved multiple-porosity model is recently developed (Yan et al. 2016), where several porosity systems are tied through arbitrary connectivities against each other, as shown in Fig. 5. It is illustrated that upscaling techniques can be used to extend this model to shale gas flow simulation at reservoir scale with complex mechanisms.

Fig. 5
figure 5

Dual-porosity model used for validation of variable permeability, left map: fracture; right map: matrix (Yan et al. 2016)

Full size image

3.2 Flow Model Coupled with Geomechanics

Geomechanics is of critical importance to be incorporated in the reservoir simulation to better describe the underground pressure and velocity distribution. An efficient and reliable prediction on hydrocarbon production is closely relevant to an accurate description of rock physics which might be changed by field operations.

Due to the complex rock characteristics in shale gas reservoirs, geological conditions are hard to depict and model with conventional methods (Guo et al. 2018b). After a quick review on previous studies, coupling geomechanics and flow models in shale gas reservoirs, two classifications are concluded with different focuses. Some researches are concentrated on the improvement in model accuracy, efficiency and reliability (Dean et al. 2006; Wheeler and Xiuli 2007; Alpak 2015; Cai and Yu 2011; Cai et al. 2010). Iterative methods are developed (Dean et al. 2006), space discretization is optimized (Wheeler and Xiuli 2007), and solution convergence is improved (Alpak 2015). Meanwhile, practical applications of coupled models on shale gas reservoir exploration processes are discussed (Guo et al. 2017b; Minkoff et al. 2003). Effects of plasticity on production performance are taken into account (Guo et al. 2017b), and the difference of introducing responses to field operations is demonstrated (Minkoff et al. 2003). A well-established flow model coupled with geomechanics is proposed recently to examine the effects of hydraulic fracture geometry and rock mechanics on hydrocarbon production and pressure distribution in unconventional reservoirs. The fully coupled numerical model is validated with an analytical solution and used to history match with field data. This model has been proved to be successful in the investigation of reservoir performance and in the characterization of the pressure distribution in cases with various rock elastic properties and hydraulic fracture designs (Guo et al. 2018a):

$$\begin{aligned} \rho _\mathrm{g}\left[ \frac{\alpha -\phi }{K_\mathrm{s}}+\phi \frac{M_\mathrm{g}}{RT\rho _\mathrm{g}}\left( \frac{1}{z_\mathrm{g}}-\frac{p}{z_\mathrm{g}^{2}}\frac{\partial z_\mathrm{g}}{\partial p_\mathrm{g}}\right) \right] \frac{\partial p_\mathrm{g}}{\partial t}+\rho _\mathrm{g}\alpha \frac{\partial e_{v}}{\partial t}+\nabla \cdot \left( \rho _\mathrm{g}v\right)= & {} \rho _\mathrm{g}q_\mathrm{g} \end{aligned}$$
(17)
$$\begin{aligned} \nabla \cdot \left[ \sigma _{0}+\lambda tr\left( \varepsilon \right) I+2\mu \varepsilon -\alpha \left( p-p_{0}\right) I\right]= & {} 0, \end{aligned}$$
(18)

where \(z_\mathrm{g}\) is the real gas factor, \(M_\mathrm{g}\) is the gas molar mass, R is the gas constant, T is the absolute temperature, \(\alpha \) is the Biot’s coefficient, \(\sigma _{0}\)is the initial total stress tensor, \(\lambda \) is the first Lame’s constant, \(\mu \) is the second Lame’s constant, and \(tr\left( \varepsilon \right) \) is the trace of strain tensor.

Necessary properties needed for production workflow, like pressure and deformation process, can be better provided from the coupling models (Gupta et al. 2012). It is found in previous research (Yu et al. 2014) that gas production will be overestimated if geomechanics is not incorporated in the flow models. The production rate in naturally fractured reservoirs is proved to be highly sensitive to fracture aperture changes (Moradi et al. 2017). With the introduction of stress sensitivity, well production will be reduced. The effect of total organic carbon (TOC) on gas production is studied with a model coupling geomechanics and flow, and the cumulative production is said to be increased if TOC is larger (An et al. 2017).

Generally, only linear elasticity is considered in geomechanics numerical model, which leads to the disability of recovering nonlinear elastic behaviors caused by hydrocarbon depletion and stress changes in shale gas reservoirs (An et al. 2017; Shovkun and Espinoza 2017). To handle this problem, an enhanced coupling model is proposed recently to consider nonlinear elasticity (Wei et al. 2018). It is found that as rocks are being compacted and consolidated during the production process, permeability values are quite different and meet experiment data better than linear elasticity models on samples obtained from the Longmaxi formation in China. It is indicated that permeability will be overestimated by 1.6 to 53 times if nonlinear elasticity is not considered.

4 Macroscopic Numerical Simulation Approaches

Analytical methods are not capable of solving the mathematical formulas constituting flow models of shale gas reservoirs. As a result, numerical methods are strongly needed to solve the model. In petroleum industry, numerical simulations can go back to the 1950s, and now they have been applied in a wide range of complex fluid flow processes. Except for microscopic and mesoscopic approaches discussed in Sect. 2, macroscopic approaches are also common methods to provide numerical solutions of fluid flow in shale gas reservoirs. Due to the long history of the application, some macroscopic approaches, like finite difference method (FDM) and finite element method (FEM), are more commonly used and well developed. Recently, efforts have also been paid on other methods including finite volume method (FVM) and fast matching method(FMM).

4.1 Finite Difference Method

In reservoir simulation, and even larger scale of flow simulation, FDM is always viewed as the most commonly used and best developed method. Discretization of ordinary and partial differential equations modeling flow in reservoirs is the first procedure in the technique. Afterward, a finite difference grid should be constructed on the simulated reservoir area and the method implementation is conducted on the grids. For boundary conditions, pressure information is commonly used at each boundary point at the block (Shabro et al. 2012). It is found that the accuracy of numerical results using finite difference methods is deeply relevant to the grid division and boundary conditions (Nacul et al. 1990). Truncations on Taylor series expansion are used to solve unknown velocity and pressure distribution with spatial derivatives (Ertekin et al. 2001).

The main advantage of FDM over FEM is the efficiency and simplicity. Rectangular and triangular grids, uniform and non-uniform meshes, Cartesian and curvilinear coordinates have all been proved to be easy to implement in reservoir simulations extended from 1D to 3D. Especially for 3D complex flow problems, FDM is said to be far superior, although problems like numerical dispersion and grid dependence may occur (Firoozabadi 1999).

4.2 Finite Element Method

Compared to FDM, FEM is said to be more accurate in reservoir simulations. Opposed to piecewise constant approximation, FDM results in a linear approximation solution (Jayakumar et al. 2011). Besides, the flexibility of accommodations to unstructured meshes is demonstrated in studies using FEM. As a result, FEM is more capable of describing flow properties in complex porous structures in reservoir geometry from fracture to matrix, and excellent efficiency could still be preserved (Logan et al. 1985; Jayakumar et al. 2011).

Complex rock structures in special geometry of shale gas formations, such as non-planar and non-orthogonal fractures, make Cartesian grids inadequate to be used in shale gas reservoir simulation using FEM. Thus, unstructured meshing is required to capture the fracture geometry (Moridis et al. 2010). Starting from 1979 (Aziz and Settari 1979), unstructured meshing skills have been widely used and extended to incorporations with local grid refinement (Heinemann et al. 1989; Nacul et al. 1990). A new compositional model based on unstructured PEBI (perpendicular bisector) is proposed in 2015 (Zhang et al. 2015a) to characterize the properties of non-Darcy flow in a wide range of slip, transitional and free molecular flow regimes and multi-component adsorption processes. Although much time and effort should be paid on the grids generation, the advantages of unstructured meshing skills are still worthwhile. Complex boundary conditions such as pinch out and faults can be represented much more easily, and local refinement is more flexible. To orient grids when needed, it is easier as well compared to structured grids. The improvement in accuracy by unstructured grids is proved in previous studies (Sun et al. 2016), as well as CPU performance. An example of two kinds of unstructured is illustrated in Fig. 6.

Fig. 6
figure 6

Comparison between a the tartan grid and b the PEBI grid for 2D synthetic model (Sun et al. 2016)

Full size image

Upscaling or homogenization techniques are widely used in traditional researches to develop effective parameters that represent subscale behavior in an averaged sense on a coarser scale as flow modeling needs to be concerned on a wide range of spatial and temporal scales in practical reservoir simulation (Yang et al. 2018; Chung et al. 2015; Alotaibi et al. 2015; Chen et al. 2017). In an attempt to overcome some of the limitations of upscaling methods, the so-called multiscale discretization methods have been proposed over the past two decades to solve second-order elliptic equations with strongly heterogeneous coefficients (Efendiev and Hou 2009). This includes methods such as the generalized finite element methods (Babuška et al. 1994), numerical subgrid upscaling (Arbogast 2002), multiscale mixed finite element methods (Chen and Hou 2003) and mortar mixed finite element methods (Arbogast et al. 2007). The key idea of all these methods is to construct a set of prolongation operators (or basis functions) that map between unknowns associated with cells of the fine geo-cellular grid and unknowns on a coarser grid used for dynamic simulation. Over the past decade, there have primarily been main developments in this direction focusing on the multiscale mixed finite element (MsMFE) method. The main process is to make this method as geometrically flexible as possible and developing coarsening strategies that semiautomatically adapt to barriers, channels, faults and wells in a way that ensures good accuracy for a chosen level of coarsening. In order to produce high-quality approximate solutions for complex industry standard grids with high aspect ratios and unstructured connections, a new multiscale formulation has been presented recently (Møyner and Lie 2016), which could guarantee the robustness, accuracy, flexibility as well as simplification on the implementation. Besides, many works have been done on the weighted Jacobi smoothing on interpolation operators with a large degree of success in the algebraic multigrid (AMG) community where fast coarsening is combined with simple operators constructed via one or two smoothing steps (Vanek et al. 1994; Vaněk et al. 1996; Brezina et al. 2005) as an inexpensive alternative to the interpolation operators used in standard AMG (Stüben 2001). Many high-performance multigrid solvers have been proposed to support smoothed aggregation as a strategy for large, complex problems (Gee et al. 2006) due to the inexpensive coarsening and interpolation strategies.

4.3 Other Methods

For reservoir simulations incorporating complex rock geometries, finite volume method (FVM) is said to be more easily implemented with unstructured grids. It is a fairly new developed technique and mainly focusing on discretization methodologies (Reis et al. 2001). It is proved that to get numerical approximations at the same level of accuracy, FVM is easier and faster compared to FEM. Compared to FDM, FVM is believed to have better versatility.

Another comprehensive approach in shale gas reservoir simulation is a class of front-tracking methods called fast marching method (FMM) (Datta-Gupta et al. 2011; Xie et al. 2012, 2015; Zhang et al. 2013). The well drainage volume can be computed efficiently using this method, where the propagation equation (Eikonal equation (Sethian 1999) is directly solved of a maximum impulse response (Datta-Gupta and King 2007). FMM is proved to be very efficient in solving the Eikonal equation, where CPU times are only in seconds level, but other comparable methods need hours. Besides the close corresponding with the analytic solution, the common front resolution problems are also solved (Datta-Gupta et al. 2011). Figure 7 shows two illustrative examples using FMM method with unstructured triangular grids.

Fig. 7
figure 7

Fast matching approach simulation examples using unstructured grids a 2D examples with isotropic permeability, b 3D example with anisotropic permeability (Zhang et al. 2013)

Full size image

5 Conclusion

This paper reviews the flow mechanism and numerical simulation approaches of shale gas reservoirs. Investigation of gas adsorption/desorption is important to predict well production, and gas adsorption isotherm can be concluded into different models. With the classification of flow regimes based on Knudsen number, different governing equations and numerical approaches are suitable for different gas transport mechanisms. Microscopic and mesoscopic approaches, represented by molecular dynamics (MD) and lattice Boltzmann method (LBM), have successfully been applied in the study of shale gas mechanisms, in particular interests of studying Klinkenberg effect, Knudsen diffusion, molecular velocity and many other details of special mechanisms of shale gas flow in reservoirs. Due to the special mechanisms and percolation characteristics of shale gas transport, classical Darcy’s law should be corrected and the concept of apparent permeability is introduced. For flow at high rate, e.g., in fractures, improved Darcy’s model with high-order terms of velocity is presented to better describe the gas flow.

In reservoir-scale flow models, shale is usually classified into four types: inorganic matter, organic matrix (kerogen), natural fractures and hydraulic fractures. Various models of gas transport in shale with detailed description on fracture characterizations have been developed, including single porosity, dual porosity and many others. Besides, it is critical to incorporate general reservoir flow model with geomechanics in order to better understand the pressure and reservoir performance in hydrocarbon development. Due to the long history and better visibility, the petroleum industry is more familiar with macroscopic numerical approaches, including the finite difference method (FDM) and finite element method (FEM). Recent progress has also been made on other methods, like finite volume method (FVM) and fast matching method(FMM).