1 Introduction

Heat transfer in porous media (Kaviany 1995) is relevant to a wide variety of problems of fundamental and practical interests, ranging from conduction in disordered porous solids (Torquato 2002; Sahimi 2003) to extraction of heat from geothermal reservoirs (Okandan 1988), enhanced recovery of oil by thermal methods (Mohammadzadeh and Chatzis 2010; Heidari et al. 2016), leakage detection in CO2 storage (Mao et al. 2017), and many other phenomena. Conduction of heat in porous media, and in particular in granular media, has also been studied extensively (for comprehensive reviews, see Torquato 2002; Sahimi 2003). For example, Mohanty (1997), Ghanbarian and Daigle (2016), and Sadeghi et al. (2018) investigated the effect of saturation on the effective thermal conductivity of porous media. Vargas and McCarthy (2001, 2002a, b) studied heat conduction in both single- and multiphase flows in granular materials when they are under an external stress. Tsory et al. (2013) utilized the well-known discrete-element method to compute the effective thermal conductivity of packings of particles that are under an external pressure. Wang et al. (2013) examined the effect of the grain size on the effective thermal conductivity of granular porous media. Choo et al. (2013) evaluated the induced anisotropy in conduction in dry granular media when they are subject to an external stress, while Askari et al. (2017a) assessed the effect of the particles’ shape on the conduction properties of anisotropic granular porous media.

Although it appears deceptively simple, characterization of thermal conduction in a granular porous medium is a difficult problem that has been studied for decades. One reason for the complexity of the problem is that, unlike the problems of fluid flow and electrical conduction that occur only in the pore space, heat is conducted through both the fluid and solid phases, with the added complexity that there is usually a large difference between the conductivity of the particles and that of the fluid. Hence, modeling of heat conduction in granular media requires consideration of the effect of thermal contact resistance on the overall transport process. At the same time, natural grains do not take on perfectly regular and symmetrical shapes, such as spheres or ellipsoids, as has been assumed in almost all modeling of conduction through granular media. Instead, their surface is rough, giving rise to significant contact resistance and a temperature gradient along the contact area. In particular, in granular porous media in which the ratio of the thermal conductivities of the solid and the fluid is high, the roughness effect is more pronounced (Askari et al. 2015). Due to the importance of the effect of thermal resistance of the contact area, numerous analytical, experimental, and numerical studies have been carried out to gain a better understanding of heat transfer in the contact area. Lambert and Fletcher (1997), for example, provided a comprehensive review of some of the analytical models for thermal contact resistance of metals.

Many experimental studies have shown that pores and grains of natural porous media, whether granular, like soil, or consolidated, have rough surfaces that are characterized by self-affine fractal structures (for a comprehensive review, see Sahimi 2011). This has, in turn, provided the impetus for studies of the effect of such surfaces on flow and flow and transport properties of porous media (see, for example, Zhang et al. 1996; Madadi et al. 2003; Madadi and Sahimi 2003). As far as conduction in systems with such rough surfaces is concerned, assuming that the roughness profiles of two contacting surfaces exhibit fractal properties over the length scale relevant to the two surfaces, Majumdar and Tien (1991) presented a contact model for the two rough surfaces in which the roughness profile was characterized by a fractal dimension. The model was capable of providing accurate estimates of the thermal contact resistance between two rough surfaces. We will return to this model shortly. Assuming that the roughness is periodic, Fyrillas and Pozrikidis (2001) developed an analytical model for small-amplitude fluctuations. Laraqi and Bairi (2002) developed an analytical model in which the contact area was composed of numerous circles with various radii, randomly distributed over the two contacting surfaces. Zhang et al. (2004) proposed an equiperipheral grid in cylindrical geometries in order to improve estimation of the effect of the contact points of the two contact surfaces. More recent developments in the area of analytical solutions for thermal contact resistance were reported by Lee et al. (2008), Wang and Zhao (2010), and Belghazi et al. (2010). Thermal contact resistance has also been a subject of experimental studies (Baïri and Laraqi 2005; Zhu et al. 2013; Babua et al. 2015; Ding and Wang 2015), and its effect has been investigated in dry porous media in which the ratio of thermal conductivities of the solid and the fluid is large (Yun and Santamarina 2008).

The effect of surface roughness on thermal contact resistance has also been studied extensively by numerical simulation (see, e.g., Irawan et al. 2013, for references). Orain et al. (2001) developed a computational methodology based on the genetic algorithm (GA) to estimate the thermal contact resistance of thin films. In addition to surface roughness, Kumar and Ramamurthi (2003) investigated the effect of waviness, as well as flatness, on thermal contact conductance. As for granular porous media, computer simulations have shown the roughness to be an important factor in the properties of such media. Wang et al. (2013), for example, demonstrated the effect of the grain size and roughness of its surface on the effective thermal conductivity. Tsory et al. (2013) demonstrated how including roughness improves the numerical accuracy of the computed effective thermal conductivity relative to experimental data. Askari et al. (2015) elaborated on the potential of incorporating surface roughness in computer simulations in order to predict effective thermal conductivity of Utah oil sand. Askari et al. (2017a) demonstrated the effect of surface roughness on thermal conduction anisotropy in granular porous media.

In the realm of the pore-scale modeling, most studies have focused on incorporating thermal resistance in contact area between grains by either using its experimental value or estimating it by some analytical models (Feng et al. 2008, 2009; Tsory et al. 2013), rather than directly simulating roughness on the grains’ surfaces and calculating possible deformation due to the loading pressure. Some studies (Wang et al. 2013; Askari et al. 2015, 2017a) have explored the possibility of including thermal contact resistance in numerical calculations by incorporating roughness on the grains’ surfaces. For example, Askari et al. (2015) used a small dented layer around each grain as a representation of the effect of surface roughness.

In a more recent study, Askari et al. (2017b) developed a comprehensive computer simulation approach for including the effect of roughness of grains’ surface, based on the aforementioned model of Majumdar and Tien (1991), in order to simulate the effect of thermal contact resistance on the macroscopic transport properties of granular porous media that are under an external pressure loading. As mentioned earlier, Majumdar and Tien (1991) showed that the deformation between two rough surfaces, where the roughness profile is assumed to have a self-affine fractal structure, can be calculated with respect to a reference flat rigid surface that lies between the two surfaces. Following Majumdar and Tien (1991), several studies (Ciavarella et al. 2004; Xua et al. 2006; Zou et al. 2008; Jiang and Zheng 2009; Chen et al. 2010; Ji et al. 2013) demonstrated the usefulness of their approach in the analysis of thermal conduction. Askari et al. (2017b) also demonstrated the robustness of the approach for the numerical simulation of the thermal conduction in the granular porous media under a variety of conditions. They showed that the degree of deformation is a function of roughness and the Young’s modulus of the grains, such that rougher grains with a higher Young’s modulus exhibit higher resistance to deformation for a given confining pressure and, hence, give rise to a higher thermal contact resistance to the transport process. In the present paper, we use the model developed by Askari et al. (2017b) for including the effect of roughness of grains’ surfaces in order to analyze the effects of various factors on the effective thermal conductivity of granular porous media.

The rest of this paper is organized as follows. First, we describe briefly the methodology for simulating surface roughness developed by Askari et al. (2017b). Thereafter, for a given surface roughness profile that is characterized by a fractal dimension, as well as the Young’s modulus of the material, we study, using extensive computer simulations, the effect of the porosity of a granular medium on its thermal conductivity and its variations with respect to a compressing pressure applied externally. We also explore the effect of the ratio of thermal conductivities of the solid and of the fluid, \( K_{\text{s}} /K_{\text{f}} \) and the porosity, on the macroscopic thermal conductivity. In addition, we investigate the effect of deformation of the rough contact area under an increasing external pressure, as well as the ratio \( K_{\text{s}} /K_{\text{f}} \), on the anisotropy due to grain shape and overlap by considering two models of anisotropic granular media. We do not consider anisotropy due to mineralization or crystal orientation in our study.

2 Model of Granular Porous Media and Roughness of the Grains’ Surface

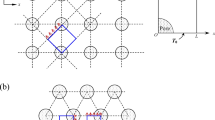
The first step of the study is generating a model of granular porous media. To do so, we use the so-called swelling grains algorithm (Roberts and Schwartz 1985; Fyrillas and Pozrikidis 2001; Askari et al. 2015) to simulate a two-dimensional (2D) granular medium. The algorithm constructs the porous medium gradually. A set of points are distributed within the simulation cell that represent the grains’ centers. A radius is attributed to each grain from a grain size distribution. Then, the grains expand (swell) gradually, with their growth rate being a function of their size, with larger grains growing faster, and vice versa. As the grains grow, some of them eventually overlap. Two cases are then considered. In one case, the grains are not allowed to overlap by, for example, slightly shrinking the overlapping grains. In the second model, which is somewhat similar to the so-called cherry-pit model (Torquato 2002), some overlaps are allowed. Figure 1a, b presents examples of the two models, while Fig. 1c shows an example of a granular medium consisting of equal elliptical particles that we also study. Note that the algorithm is capable of generating granular media with any particle shape.

Fig. 1
figure 1

a An example of a granular medium using the swelling grain algorithm. b The directional cherry-pit model of the porous media in (a) by moving the grains centers 15% along the x-axis. c A granular medium with elliptical grains

Full size image

The self-affine roughness profile can be generated by several methods, the advantages and disadvantages of which were discussed by Mehrabi et al. (1997). In the present work we generate the roughness profile using the Weierstrass–Mandelbrot method (Komvopoulos 1996), according to which the “height” z(x) of the rough surface at position x is given by

$$ z\left( x \right) = L\left( {\frac{G}{L}} \right)^{{\left( {D - 1} \right)}} \mathop \sum \limits_{n = 0}^{\infty } \frac{{\cos 2\pi \nu^{n} x/L}}{{\nu^{{\left( {2 - D} \right)n}} }}, $$
(1)

where \( L \) is the sample’s length whose roughness is characterized by the fractal dimension \( 1 < D < 2 \), \( G \) is a fractal roughness parameter that, for a given fractal dimension \( D \), controls the amplitude of the roughness, and \( \nu > 1 \) is a scaling parameter. Majumdar and Tien (1991) suggested the scaling parameter \( \nu \) to be 1.5, which we utilize in our study.

Figure 2 shows three roughness profiles for various fractal parameters, generated by the Weierstrass–Mandelbrot method. The fractal dimension D is related to the Hurst exponent H by \( H = 2 - D \). For \( H > 0.5\;(H < 0.5) \) the fluctuations are positively (negatively) correlated, corresponding to smoother (rougher) profiles. Thus, increasing \( D \) (and \( G \)) produces rougher surface topography. Given an actual self-affine roughness profile, we can numerically compute its power spectrum \( S(\omega ) \), the Fourier transform of its covariance. The parameter \( G \) and fractal dimension \( D \) of the profile are then estimated by fitting the numerical results to the analytical equation for the power spectrum:

$$ S\left( \omega \right) = \frac{{G^{{2\left( {D - 1} \right)}} }}{2\ln \nu }\frac{1}{{\omega^{{\left( {5 - 2D} \right)}} }}, $$
(2)

In addition to D and G, the variances of the heights, the slope and the curvature can be computed based on the power spectrum.

Fig. 2
figure 2

Three rough profiles that were generated by using the parameters (D, G, L): a (1.3, 1.5 × 10−4, 4 mm); b (1.7, 1.5 × 10−2, 4 mm), and c (1.7, 2 × 10−2, 2 mm)

Full size image

3 The Fractal Contact Model

As mentioned briefly, Majumdar and Bhushan (1991) developed a fractal contact model in order to quantify deformation of a rough surface with respect to a specified elastic load, assuming the roughness to be statistically isotropic and the interactions among adjacent asperities and the frictional forces to be negligible during contact. Using the Majumdar and Bhushan model, we determine the type of a deformation and the load required for it. Under a loading pressure of a flat rigid surface, the contact area \( a \) of a deforming rough surface is given by Majumdar and Bhushan (1991),

$$ a = \left( {{{3P_{\text{e}} } \mathord{\left/ {\vphantom {{3P_{\text{e}} } {4\sqrt \pi YG^{D - 1} }}} \right. \kern-0pt} {4\sqrt \pi YG^{D - 1} }}} \right)^{\zeta } , $$
(3)

where Y is the Young’s modulus (Johnson 1985), and \( \zeta \) is given by

$$ \zeta = \frac{2}{3 - D}. $$
(4)

Accordingly, the height of the deformation is given by Majumdar and Bhushan (1991),

$$ \delta = G^{D - 1} a^{(2 - D)/2} . $$
(5)

It is clear that according to Eq. (5), if \( \delta \) increases by incremental increase of a compressing pressure, a wider area a of the rough surface is deformed. As discussed by Majumdar and Bhushan (1991), small and large deformations are, respectively, plastic and elastic. Thus, since small deformations, corresponding to small contact areas between grains, do not make significant contribution to heat transfer in a granular medium, we consider only the elastic deformation. Indeed, in an experimental study by Williamson and Majumdar (1992), the dominant deformations were elastic after several loading and unloading of two rough surfaces. Thus, the assumption of elastic deformation is more realistic for granular porous media that are exposed to numerous loading and unloading circumstances.

4 Calculation of Deformation of the Grains with Rough Surface

Our goal is to study heat conduction in a granular porous medium that is under an external compressive pressure, and whose grains have rough self-affine surface. Under such conditions, one must take into account the elastic deformation of the rough surfaces of two grains that are in contact. Consider two rough surfaces coming together at a flat rigid plane R, as shown in Fig. 3. The overlap region between the two surfaces constitutes the contact region—line \( aa^{{\prime }} \) in Fig. 3. For a given contact pressure \( P_{\text{e}} \), the Young’s moduli of the two rough surfaces and the roughness parameters \( G \) and D, we calculate the total deformation of the two surfaces with respect to the rigid flat surface R. Clearly, maximum deformation occurs when the apexes of the two rough surfaces face each other. Therefore, instead of directly incorporating roughness on the grains’ surface, we calculate the deformed areas of the roughness profile with respect to the smooth flat surface. Figure 4a shows a rough surface whose deformed area with respect to a rigid surface (the gray line in Fig. 4a) is shown in Fig. 4b. In other words, what is computed for the grains’ surfaces is the deformed areas as shown in Fig. 4b, after converting it to the radial coordinate in the model. To illustrate the method more clearly, consider the contact areas of two rough surfaces, I and II, an example of which is shown in Fig. 4c. Figure 4d shows the corresponding computed heights under deformation.

Fig. 3
figure 3

The contact area \( aa^{{\prime }} \), shown by the dashed lines, for two rough surfaces, S1 and S2.\( aa^{{\prime }} \) is computed based on the deformation of the two surfaces with respect to the rigid flat line R between the two surfaces

Full size image
Fig. 4
figure 4

a A rough surface with respect to a rigid surface (the flat line), b the deformed area. c Two rough surfaces, I and II, and d their calculated deformations due to a uniform compressing pressure. We note that the deformed areas in (d) approximately predict the contact areas in (a). Therefore, instead of embedding the roughness function on each grain, we calculate the deformed roughness areas with respect to a rigid circular surface that encircles the grain and embed it on the grain surface

Full size image

Figure 5 presents two examples of a deformed granular medium with rough grain surface. For the sake of simplicity, a uniform compressing pressure was applied to the packing. A more complex boundary condition, such as a non-uniform compressing pressure, can be implemented using other techniques, such as the particle dynamics method (Vargas and McCarthy 2001). The maximum amplitude of the rough surfaces with the given values of the fractal parameters is 1 mm.

Fig. 5
figure 5

Deformation of the granular medium with grains whose surface is rough. The Young’s modulus is Y =20 GPa, the compressing pressure Pe = 1 MPa, and \( L = 1\;{\text{cm}} \)

Full size image

5 Numerical Simulation of Conduction

A computer simulator was developed that not only constructs the 2D granular media for a given grain size distribution, but also determines the solution of the steady-state heat conduction in the medium. Based on our ongoing experimental work, we set the medium’s dimension to be 10 cm × 10 cm in which the grains’ sizes were uniformly distributed with an average radius of 6 mm and a standard deviation of 0.2 mm. Our experiments have indicated that the size is larger than the representative elementary volume (REV) of the system. To include roughness on the grains, we assume that its maximum amplitude is 1 mm, which is superimposed on the outer surface of the grains. Various granular media were constructed to study the effect of the porosity. In all the simulations the roughness parameters \( (D,G) = (1.4,12 \times 10^{ - 7} ) \), fractal length L = 1 cm, and a Young’s modulus of \( Y = 10\;{\text{GPa}} \) were used. The compressing pressure was varied from 0.2 to 1.2 MPa with an increment of 0.1 MPa.

The steady-state equation for heat conduction was numerically solved for each deformed packing using the finite-volume method. The upper and lower boundaries of the system were assumed to be insulated, while heat flowed between the other two external surfaces. We further assumed that the pores between the grains were saturated by a single fluid. To discretize the medium, orthogonal gridding was used, since the grid’s size was small. Therefore, one pixel in each grid block represented either the solid or the fluid with a constant heat flux through the solid–fluid boundaries.

6 Results

We carried out extensive numerical simulation in order to study several important issues. In what follows, we present the results and discuss their implications.

6.1 Isotropic Packings

Figure 6 shows the computed effective thermal conductivity \( K_{\text{e}} \) of the granular medium with four porosities and four values of \( K_{\text{s}} /K_{\text{f}} \), the ratio of the conductivities of the solid and the fluid. Since \( K_{\text{s}} \gg K_{\text{f}} \), the porosity is a decisive factor in controlling the thermal conductivity of the granular medium: by increasing the porosity, the overall thermal conductivity decreases significantly, since some of the contacts between the grains are lost. In addition, the granular media with the two highest porosities, 38 and 45%, exhibit only slight variations of their thermal conductivity with respect to the compressing pressure, since their open pore space and low conductivity of the fluid render the applied pressure ineffective. As Fig. 6d indicates, the effect of the porosity is, however, more pronounced when \( K_{\text{s}} /K_{\text{f}} \), is high, due to the dominance of the solid phase in the condition process.

Fig. 6
figure 6

Variations of the thermal conductivity with the compressing pressure when the porosities are 25% (circles), 30% (squares), 38% (triangles), and 45% (diamonds). The curves are only guides to the eye

Full size image

6.2 Effect of Grain Overlap

Next, we investigated the effect of grain overlap by using a variation of the aforementioned cherry-pit model. Consider a circular or spherical particle of diameter 2R that is composed of a hard core of diameter 2mR, encompassed by a perfectly penetrable shell of thickness R(1 − m), with 0 < m < 1. The limits m = 0 and 1 correspond, respectively, to consolidated porous media composed of fully penetrable grains—sometimes called the Swiss cheese model—and completely unconsolidated granular media with fully impenetrable particles, studied so far. Thus, varying the parameter m generates a wide variety of porous media, from completely unconsolidated granular materials to porous media with various degrees of consolidation.

In the present study, we used a variation of this basic algorithm, which was motivated by some past experimental work (see Kato et al. 2001; Razeghi and Romiani 2015; Al-rkaby et al. 2016 for references). Some rocks are consolidated directionally, i.e., on average the grains are consolidated (fused) in one direction (or planes in 3D), but not so much in the other direction(s) as they are brittle in those direction(s). Thus, after generating the granular medium and identifying the particles that were very close, we moved them all in one direction, say the horizontal x direction in Fig. 1, so that they would overlap with their neighbors. We studied the cases with the overlap parameter being m = 0.95 and 0.9; that is 5 and 10% overlap. It is clear that since the grains are moved in only one direction, the resulting packing is anisotropic. Therefore, the method that we used may also be considered as a way of generating anisotropic packings. To carry out the simulations, the Young’s modulus was taken to be \( Y = 10 {\text{GPa}} \), \( K_{s} /K_{f} = 100 \), the roughness parameters were, \( \left( {D,G} \right) = (1.4, 12 \times 10^{ - 7} \)), the initial porosity was 30%, with the mean and standard deviation of the grains’ sizes being, respectively, 6 and 0.2 mm. To characterize conduction, we computed two the thermal conductivities, namely, \( K_{\parallel } \), parallel to the overlap direction x, and, \( K_{ \bot } \), perpendicular to that direction.

Figure 7 presents the dependence of the directional effective thermal conductivities on the applied pressure. For comparison, we also show the thermal conductivity of an isotropic packing with no particle overlap, but the same characteristics mentioned earlier. In general, overlap, i.e., consolidation, enhances heat conduction in the parallel direction relative to the direction perpendicular to it, because it increases the surface contacts among the grains in the overlap direction that enhance heat conduction. In addition, as usual, the thermal conductivity increases with increasing compressing pressure, due to the enhancement of the contact surfaces in the deformed rough areas.

Fig. 7
figure 7

Effect of the grain overlap on the thermal conductivity with the overlap parameter, m = 0.05 (triangles) and 0.1 (circles), and \( K_{\text{s}} /K_{\text{f}} = 100 \). The solid and empty triangles and circles represent, respectively, the conductivities parallel and perpendicular to the overlap direction, the horizontal direction x in Fig. 1. The squares indicate the thermal conductivities of the isotropic granular medium with the same porosity and other properties. The curves are only guides to the eye

Full size image

The directional consolidation, as measured by the amount of particle overlap, increases the gap between the direction-dependent thermal conductivities as the overlap increases. Figure 8 presents the dependence of the anisotropy ratio, \( \alpha = K_{\parallel } /K_{ \bot } \), on the pressure for two cases. Note, compressing pressure brings all particles into contact with each other and the anisotropy is eventually lost.

Fig. 8
figure 8

The anisotropy ratio for 5% (squares) and 10% (circles) overlaps. Note the decrement of the anisotropic ratio by increasing the compressing pressure. The \( K_{\text{s}} /K_{\text{f}} \) ratio is 100. The curves are only guides to the eye

Full size image

Next, we studied the effect of \( K_{\text{s}} /K_{\text{f}} \), the ratio of the solid and fluid conductivities, on the conduction anisotropy. The results are shown in Fig. 9. As \( K_{\text{s}} /K_{\text{f}} \) decreases, so also does the anisotropy because the distinction between the fluid and solid phases is lost, the effect of the grain overlap that induces the anisotropy declines and, therefore, the packing approaches a homogeneous material.

Fig. 9
figure 9

Dependence of the anisotropy ratio on the compressing pressure for a 5% and b 10% overlap, and \( K_{\text{s}} /K_{\text{f}} = 100 \) (squares), \( K_{\text{s}} /K_{\text{f}} = 50 \) (triangles), \( K_{\text{s}} /K_{\text{f}} = 25 \) (diamonds), and \( K_{\text{s}} /K_{\text{f}} = 10 \) (circles). The curves are only guides to the eye

Full size image

6.3 Granular Media with Elliptical Grains

To further analyze the effect of anisotropy and deformation on the thermal conductivity of a granular medium under a compressing pressure, we also studied conduction in granular media with elliptical grains, an example of which is shown in Fig. 1. We assumed that the major and minor axes of the elliptical grains are, respectively, 7.3 and 3.65 mm, and that the initial porosity is 30%. For the same ranges of the compressing pressures as before, the effective thermal conductivities \( K_{\parallel } \) and \( K_{ \bot } \) were computed for two values of the Young’s modulus, \( Y = 10 \) and \( 50\;{\text{GPa}} \) with the roughness parameters, \( (D,G) = (1.4,12 \times 10^{ - 7} ) \). As shown recently (Askari et al. 2017b), with the lower Young’s modulus the rough contact area is deformed more significantly than the case with the higher Y. Hence, the medium with the lower Young’s modulus should have higher directional thermal conductivities \( K_{\parallel } \) and \( K_{ \bot } \), with the latter always being smaller than the former. This is indeed confirmed by the results shown in Fig. 10.

Fig. 10
figure 10

Effective directional thermal conductivities of granular media with elliptical grains, with the Young’s modulus of \( Y = 10\;{\text{GPa}} \) (circles), and \( 50\;{\text{GPa}} \) (triangles). The curves are only guides to the eye

Full size image

Similar to the case of the granular media with directional overlap, we also calculated the anisotropy ratio, \( \alpha = K_{\parallel } /K_{ \bot } \), in order to investigate how the compressing pressure influences the anisotropy. The same two values of the Young’s modulus of Fig. 10 were also utilized. The results are shown in Fig. 11. Two points are worth pointing out. One is that the granular medium with the higher Young’s modulus, \( Y = 50\;{\text{GPa}} \), is more strongly anisotropic with higher values of \( \alpha \) than the medium with the lower Young’s modulus, \( Y = 10\;{\text{GPa}} \). The reason is that with the higher Y the particles deform less and, therefore, the anisotropy is affected more weakly by the deformation. The second point is that, similar to the granular media with directional overlap, the anisotropy decreases with increasing compressing pressure. Unlike the case of directional overlap, however, the anisotropy never vanishes, because the elliptical grains ensure that the medium remains anisotropic, regardless of the compressing pressure, unless, of course, they are broken. Note also that the anisotropy declines faster in the medium with the smaller Young’s modulus of \( Y = 10\;{\text{GPa}} \) because, relative to the grains with the larger Young’s modulus of 50 GPa, the rough surface is deformed more significantly.

Fig. 11
figure 11

Anisotropy ratio for the granular media with elliptical grains, with the Young’s modulus of \( Y = 10\;{\text{GPa}} \) (circles) and \( 50\;{\text{GPa}} \) (squares). Note that the model the higher Young modulus (\( E = 50\;{\text{GPa}} \)) exhibits higher anisotropic ratios at different pressures. The curves are only guides to the eye

Full size image

The anisotropy is affected by the deformation of the rough contact areas because of the difference between the number of contact points along the major and minor axes of the elliptical grains in the granular porous medium (Askari et al. 2017a). In the presence of the roughness, the contacts impose an additional anisotropy by the difference between the lengths of the major and minor axes of the grains. There are a larger number of contact points along the minor axes than that on the major axes of the particles. When the effect of the roughness is significant, e.g., at lower compressing pressures, higher Young’s modulus, and higher values of the fractal parameters \( D \) and \( G \), heat transfer is impeded more strongly along the minor axes than along the major axes. Such a difference in hindering of transport of thermal energy intensifies thermal anisotropy in a granular porous medium with elliptical grains (Askari et al. 2017a).

7 Summary and Conclusions

Utilizing the computer simulation approach developed by Askari et al. (2017b), we studied the effect of various parameters on thermal conduction in a deforming granular medium with grains whose surface is rough, with the roughness profile following the characteristics of self-affine fractals. The parameters included the porosity and grain overlap, as well as the grain shape. While, as one may expect, the porosity is an important factor influencing thermal conduction, particularly when the difference between the thermal conductivities of the fluid and the grains is large, other factors also play important roles in determining the macroscopic thermal conductivity of granular media. Increasing the compressing pressure enhances heat transfer and thermal conductivity because of the improved contacts among the grains. In addition, by increasing the compressing pressure when the fluid is compressible, the fluid volume in the pore space will decrease. The decrease in the fluid volume will further increase heat conduction.

In addition, overlap between the grains (i.e., consolidation) increases thermal conductivity by increasing contact area, but also by improving the connectivity of the grains. The particular type of grain overlap that we considered, which was motivated by some experimental observations, gives rise to anisotropy in the thermal conductivity. The induced anisotropy decreases, however, with increasing compressing pressure and essentially vanishes at very high compressing pressures. The anisotropy increases further if the grains, in addition to having rough surfaces, are elliptical. Unlike the case of directional overlap, however, the anisotropy persists even at very high compressing pressures, because the grains remain elliptical.