Steady Flow from an Array of Subsurface Emitters: Kornev’s Irrigation Technology and Kidder’s Free Boundary Problems Revisited

“Singularity is almost invariably a clue.”

Sherlock Holmes.

Abstract

Kornev’s (Subsurface irrigation, Selhozgiz, Moscow-Leningrad, 1935) subsurface irrigation with a periodic array of emitting porous pipes is analytically modeled as a steady potential Darcian flow from a line source generating a phreatic surface. The hodograph method is used. The complex potential strip is mapped onto the triangle of the inverted hodograph. An analogy with the Deemter (Theoretische en numerieke behandeling van ontwaterings-en infiltratie stromings problemen (in Dutch). Theoretical and numerical treatment of flow problems connected to drainage and irrigation. Ph.D. dissertation, Delft University of Technology, 1950) drainage problem and Kidder (J Appl Phys 27(8):867–869, 1956) free-surface flow toward an array of oil wells underlain by a “wavy” oil–water interface is drawn. For a half-period of Kornev’s flow, the “wavy” phreatic surface has an inflection point. The “waviness” of the phreatic surface is controlled by the spacing between emitters, the strength of line sources, and the pipe pressure and radius. Numerical modeling with HYDRUS involved two factors which constrained the saturated–unsaturated flow: the positive pressure head at the outlet of the modeled domain and lateral no-flow boundaries, with a qualitative corroboration of analytical solutions for potential (fully saturated) and purely unsaturated flows. HYDRUS is also applied to a generalized Philip’s regime of an unsaturated flow past a subterranean hole, which is impermeable at its top and leaks at the bottom.

1 Introduction

Kornev (1935) (hereafter abbreviated K-35) proposed and tested a new technology of subsurface irrigation (SI) that uses an array of porous pipes (PP) that are buried at the same depth $d_{p}$ (practically ranging from 0.2 to 1 m), with a period of 2L (0.5–2 m), and a constant discharge 2Q (up to several tens of l/h/m) per a unit length in the direction of the pipe axis. Fig. 1 (see also the original Fig. 38 in K-35) shows a vertical cross section of one period of this SI system. A homogenous soil has the saturated hydraulic conductivity $K_{1}$. The emitting PP of a radius $r_{C}$ (2–5 cm) is modeled as a line source at point A. In this paper, we study steady flows at a constant, positive, and relatively high pressure in PP (the pressure heads in standard SI range between a few tens of centimeters to a few meters).

Fig. 1

One period of subsurface irrigation from an array of porous pipes maintained at a positive pressure and Kidder’s (1956) free boundary oil flow. The mathematical source is placed at a depth, d, under the summit F of a “wavy” phreatic surface $F_{2}{} { FF}_{1}$; m/2 is an amplitude of the “wave” as compared with an average horizon $W_{2}W_{1}$; the flow rate from a constant total head emitter is 2Q; the emitter’s radius is $r_{C}$. The soil above $W_{2}W_{1}$ is of a thickness D, the top soil layer of thickness B contrasts with the main soil in texture, hydraulic conductivity, and capillarity

Several decades after the publication of K-35, numerous SI projects used PP in France, Iran, Israel, Japan, Oman, Russia, Spain, Saudi Arabia, the USA and other countries with arid/semi-arid agriculture (see, e.g., Al-Rawahy et al. 2004; Ashrafi et al. 2002; Communar and Friedman 2015; El-Nesr et al. 2014; Honari et al. 2017; Iwama et al. 1991; Kato and Tejima 1982; Lazarovitch et al. 2005; Moniruzzaman et al. 2011; Shani et al. 1996; Siyal and Skaggs 2009; Tanigawa et al. 1988; Warrick and Shani 1996; Yabe and Tanigawa 1992).

Kacimov and Obnosov (2016, 2017) and Obnosov and Kacimov (2017) revisited K-35 and modeled an isolated subsurface emitter in homogeneous and two-layered soils, at both positive and negative pipe pressures. If the pressure in PP is positive and permeability of walls is not too small, in particular, for mole emitters which have no walls (Bobchenko 1957), then seepage from an array of these emitters into the soil forms a “wavy” water table $F_{2}{} { FF}_{1}$ with a capillary fringe, which is a “subdued replica” of $F_{2}{} { FF}_{1}$ (see Kacimov 2006). Similarly, undulating phreatic surfaces emerge above periodic tile drains, although the troughs and crests appear above and between the drains (Deemter 1950; Ilyinsky and Kacimov 1992).

The soil surface $S_{2}S_{1 }$ and curve $F_{2}{} { FF}_{1 }$ in Fig. 1 sandwich a tension-saturated and unsaturated zone. The plant roots uptake moisture from this zone. Evaporation from the soil surface, although relatively small (as compared with surface irrigation), is undesirable because it reduces water use efficiency and causes secondary salinization, among other negative consequences (see K-35 for details). The effective thickness D of the unsaturated zone (20–25 cm in Kornev’s SI projects) in Fig. 1 is high enough to serve as an anti-evaporation sheath. This partially saturated layer also serves as a thermal insulator for the plant roots, provided they penetrate deeply from the superheated soil surface. This dual “smart” wetting and heat-stress mitigation of the unsaturated layer has been confirmed by numerous data on improved harvest/biomass/plant morphologies for a variety of crops cultivated by Kornev in the USSR and France (K-35).

In Sect. 2 of this paper, we consider a saturated 2-D steady flow from a source A capped by a free boundary $F_{1}{ FF}_{2}$. Correspondingly, we solve a free boundary value problem (BVP) for a potential flow that is laterally confined by the rays $F_{2}D_{2 }$ and $F_{1}D_{1}$ in Fig. 1. For this purpose, we use complex variables (the hodograph method), which gives the positions of points F and $F_{1}$ and therefore the value of D (the locus of horizon $W_{1}W_{2}$) for a given $d_{p}$ and emitter characteristics. This free BVP is mathematically equivalent to Deemter’s (1950) tile drainage problem with a phreatic surface and Kidder’s (1956) coning problem of oil flow to an array of producing wells (sinks) in an inclined formation with a subjacent stationary “wavy” oil–water contact (a free boundary as a sharp interface between a moving oil and static groundwater in the oil formation). Our Fig. 1 also sketches Kidder’s formation, for which the angle of a dip is a scaling constant. Kidder only studied a limiting case of a critical production rate, for which the sink strengths assume the largest value for which a stable front free boundary can exist without water being drawn into the well, other factors remain the same. Within one period, Kidder’s free surface has a cusp–crest at point F beneath the well and zero-slope troughs at points $F_{1}$ and $F_{2}$. Kornev’s flow from the sources in Fig. 1 is a mathematical inversion of Deemter’s and Kidder’s flow to sinks.

For a general (subcritical) flow to sinks and SI flow from Kornev’s sources, the free boundary within one flow period (Fig. 1) has two inflection points, $N_{1}$ and $N_{2}$, where the slope of the free boundary is maximal.

In Sect. 3, we use the HYDRUS-2D finite element (FE) code (Šimůnek et al. 2016) and simulate a saturated–unsaturated system shown in Fig. 1. We illustrate that numerical solutions of Richards’ equation are in agreement with the analytical results in Sect. 2. We also simulate unsaturated flows past subterranean holes with a small water level at the hole bottom, combining unsaturated and saturated regimes from Philip et al. (1989) and Warrick and Zhang (1987). These HYDRUS applications are motivated by the design and operation of mole drains-emitters and tunnels for which the boundaries of contact between the ambient soil (rock) and porous-fractured medium can be either impermeable to the descending infiltration due to the capillary barrier phenomenon or permeable (e.g., Wang and Bodvarsson 2003).

We assume that all flows are Darcian, one-phase (vapor/gas and solute motions, depositions/dissolutions on/of the soil matrix are neglected), and isothermal and that the bare (rootless) stratified soils are isotropic.

We answer the following questions:

• (a) How do values of $L, K_{1}$, the pressure in PP, and the flow rate, 2Q, in the saturated fragment of the free boundary flow affect the position of $F_{2}{} { FF}_{1}$ in Fig. 1? In particular, how large is the trough-crest difference, m, in the ordinates of points F and $F_{1}$?

• (b) What are the results of HYDRUS simulations for flow in a positive-pressure zone consisting of a “mound” created by seepage from a cascade of positive-pressure PP on the top of an already existing unconfined aquifer, which is hydraulically drainable to a thick highly permeable substratum?

• (c) Is there agreement between the numerical results for these “nonstandard” drainage conditions of the irrigated topsoil and the results obtained by simplified analytical models and solutions, which ignore capillarity and consider flow domains not confined from below?

2 Steady 2-D Saturated Flow from Array of Sources

Strack (1989) modeled an arbitrary number of interfering emitters and drains (line sources and sinks), which generate a positive pore pressure zone around the emitters (line sources), with the flow domain bounded by a phreatic surface. Kacimov and Obnosov (2016) revisited the Riesenkampf solution for a single emitter (see Polubarinova-Kochina 1962), used the Vedernikov (1939) model of a capillary fringe and tension-saturated flow, and modeled a single PP. This model just rescales the pressure head at $F_{2}{} { FF}_{1}$ in Fig. 1 by a summand $-p_{c}$, in comparison with the water table pressure $p=0$. Mathematical models in the Strack (1989) and Riesenkamf solutions are the same. Therefore, without any loss of mathematical generality, we ignore the fringe in Fig. 1.

To connect our analytical solution with Kidder’s (1956), we assume that $F_{2}{} { FF}_{1 }$ is a streamline, i.e., evapotranspiration losses from the water table are neglected. The “saturated bulbs” around the line sources of the whole array (laterals) of SI in Fig. 1 coalesce, and—sufficiently deep under the sources—a descending, 1-D, positive-pressure flow with a Darcian velocity $v_\mathrm{D}=Q/L$ occurs, where 2Q is the strength of the line source in Fig. 1. Similar flows are shown in Fig. 7.38 of Strack (1989).

Fig. 2

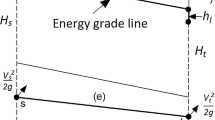
A vertical cross section for a half-period of the flow domain in Fig. 1. A “wavy” phreatic surface has an inflection point $N_{1}$ (a), the complex potential plane (b), and the hodograph plane (c), corresponding to the physical flow domain in a

2.1 Conformal Mappings

Due to symmetry, we follow Deemter (1950) and Kidder (1956) and consider only the right half of the period, a physical domain $G_{{z}}$, as shown in Fig. 2a. The origin of the Cartesian coordinates (x, y) coincides with the apex F of the free surface. At this point, the Darcian total hydraulic head $h(x,y)=0, h=p+y,$ where p is the pressure head. The total (hydraulic) head in the pipe is $H_{p}=\hbox {const} > 0$. The source is located at $z=-\,id$, where $d=\hbox {const} > 0$ is to be found. Obviously, a posteriori, we must check that $d < d_{p}$ (Fig. 1). Otherwise, the assumed flow scheme is not valid and, practically, the water table seeps out as a “wet spot” on $S_{1}S_{2}$ in Fig. 1 (the situation to be avoided in SI, see K-35).

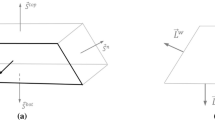
We introduce the complex potential $w=\phi +i\psi$, where $\phi =-\,{K}_{1 }h$ is the velocity potential and $\psi$ is the stream function. At point F, the potential $\phi =0$, and $\psi =0$ along ${ AD}_{1}$. Therefore, $\psi =Q$ along ${ AFN}_{1}F_{1}D_{1}$. We also introduce a complex Darcian velocity $V=u+{i}v$. The complex potential domain $G_{w}$, which corresponds to $G_{{z}}$, is then the strip of a width Q (Fig. 2b), and the hodograph domain $G_{{V} }$ is the right half-plane with a circular cut ${ FN}_{1}F_{1}$ (Fig. 2c). At the inflection point $N_{1 }$ (the tip of the cut in Fig. 2c), the magnitude of the Darcian velocity vector attains its maximum along ${ FN}_{1}F_{1}$. At this point, the angle $\pi \gamma$ of this vector with the x-axis is also maximal. The complex velocity at point D (infinity) is given and is $V_{D}={-\,i}v_{D}={-\,i}Q/L$. At a certain depth, $d_{h}$, flow becomes almost 1-D vertical, i.e., a horizontal line $D_{l}D_{\mathrm{r} }$ in Fig. 2a (a dashed line) is almost an equipotential line, which is imaged by the corresponding almost vertical segment in Fig. 2b (dashed line). Along $D_{l}D_{\mathrm{r}}$ in Fig. 2a, the pressure head is also almost constant. We note that in Kidder’s (1956) solution, the incident Darcian velocity (far upstream of his production wells) is also constant (actually, a scaled parameter a in Kidder’s parametrization). McCarthy (1994) studied flows to a solitary line sink with free boundaries, but with an alternative to Deemter (1950) and Kidder (1956) condition at infinity, viz. McCarthy’s flow domains are laterally unbounded, whereas Deemter–Kidder’s and ours are vertically unbounded. First, the circular quadrilateral $G_{V }$ is mirror-imaged with respect to the real axis. The corresponding domain $G_{{\omega }}$ (Fig. 3a) is inverted with respect to the coordinate origin to obtain the domain $G_{\omega _1 }$ (Fig. 3b), which has a straight cut ${ FN}_{1}F_{1}$. The function $\omega _{1}(z)=1/(u{-\,i}v)=\hbox {d}z/\hbox {d}w$ is holomorphic. Polubarinova-Kochina (1962) gives full details about the hodograph method, which irrigation engineers (e.g., Swamee and Chahar 2015) use for designing of irrigation channels. Hodographs similar to one in Fig. 2c and their inversions are used for analytical studies of flow from rectangular irrigation-MAR channels (e.g., Choudhary and Chahar 2007).

We map $G_{w}$ onto an auxiliary half-plane $G_{\zeta }$ (Fig. 3c) by the function

$$\begin{aligned} w(\varsigma )={i}Q-\frac{Q}{\pi }\log \frac{\varsigma +\mu }{1+\mu }. \end{aligned}$$

(1)

Similarly, as for Strack’s and Riesenkampf’s emitters-drains, flow determined by Eq. (1) is radial 1-D in the vicinity of point A in Fig. 2a. The affixes $-\mu ,\nu$ of points $D_1 ,\;N_1$ (Fig. 3c) will be found later. At point C, i.e., the apex (the contact of the exterior of the PP wall with the ambient soil), the hydraulic head $H_{C }$ is easily calculated from $H_{p}$, the given wall thickness (approximately 1 cm in K-35) and the permeability (see Kacimov and Obnosov 2016, 2017). In the simplest situation of a mole drain (an emitter with no seepage-impeding wall, Bobchenko 1957), $H_{C}=H_{p}$. Then, at point $C, w(c)=-K_1 H_C +{i}Q$, and affix c is

$$\begin{aligned} c=\left( {1+\mu } \right) \exp (\pi K_1 H_C /Q)-\mu . \end{aligned}$$

(2)

Fig. 3

Mirrored hodograph domain (a) and its inversion with respect to the origin (b); an auxiliary half-plane (c); Deemter–Kornev’s flow with evaporation from the phreatic surface (d); the hodograph plane for an evaporating free surface (e)

We map $G_{\omega _1 }$ onto $G_{\zeta }$ using the function

$$\begin{aligned} \omega _1 (\varsigma )=\frac{{i}}{2K_1 }\frac{2\varsigma +\hbox {cosec}\pi \gamma -1}{\sqrt{\varsigma (\varsigma -1)}}-\frac{{i}}{K_1 }. \end{aligned}$$

(3)

The angle $\pi \gamma$ (Fig. 3a) will be found later. The mapping function (3) is the inversion of the elementary function:

$$\begin{aligned} \varsigma _1 (\omega _1 )=\frac{\sqrt{(K_1 \omega _1 +{i})^{2}-\cot ^{2}\pi \gamma }}{K_1 \omega _1 +{i}},\quad \quad \varsigma (\omega _1 )=\frac{1-\hbox {sin}\pi \gamma }{2}\frac{1+\varsigma _1 (\omega _1 )}{1-\hbox {sin}\pi \gamma \varsigma _1 (\omega _1 )}. \end{aligned}$$

(4)

In Eq. (4), $\varsigma _1 (\omega _1 )$ maps $G_{\omega _1 }$ onto the upper half of the $\varsigma _1$-plane, with the correspondence of points $(F_1 ,F,A)\rightarrow (-\,1\hbox {,} 1\hbox {,} 1/\sin \pi \gamma )$, and $\varsigma (\varsigma _1 )$ is the automorphism of the upper half-plane, which gives the correspondence of points $(F_1 ,F,A)\rightarrow (0,1,\infty )$.

Note that $\omega _1 =(\hbox {cotan}\pi \gamma -{i})/K_1$ at point $N_{1 }$ in the $\omega _1$-plane. From Eq. (4), it then follows that the affix $\nu =(1-\sin \pi \gamma )/2$.

Using Eqs. (1) and (3), we get

$$\begin{aligned} z(\varsigma )=\int \limits _1^\varsigma {\omega _1 (u)\frac{\hbox {d}w}{\hbox {d}u}\hbox {d}u} =-\frac{{i }Q}{2K_1 \pi }\left( {\int \limits _1^\varsigma {\frac{2u+\hbox {cosec}\pi \gamma -1}{(u+\mu )\sqrt{u(u-1)}}\hbox {d}u} -2\log \frac{\varsigma +\mu }{1+\mu }} \right) . \end{aligned}$$

(5)

The last integral is evaluated in elementary functions:

$$\begin{aligned} \int \limits _1^\varsigma {\frac{\hbox {d}u}{\sqrt{u(u-1)}}} =2\log \left( {\sqrt{\varsigma }+\sqrt{\varsigma -1}} \right) =\log (\varsigma +\mu )+2\log \left( {\sqrt{\frac{\varsigma }{\varsigma +\mu }}+\sqrt{\frac{\varsigma -1}{\varsigma +\mu }}} \right) , \end{aligned}$$

and

$$\begin{aligned} \int \limits _1^\varsigma {\frac{\hbox {d}u}{(u+\mu )\sqrt{u(u-1)}}} =\frac{2}{\sqrt{\mu (\mu +1)}}\log \left( {\frac{\sqrt{(\mu +1)\varsigma }+\sqrt{\mu (\varsigma -1)}}{\sqrt{\varsigma +\mu }}} \right) . \end{aligned}$$

That transforms (5) into

$$\begin{aligned} z(\varsigma )= & {} \frac{-\,{i}Q}{K_1 \pi }\left( \frac{\left( {\hbox {cosec}\pi \gamma -1-2\mu } \right) }{\sqrt{\mu (\mu +1)}}\log \frac{\sqrt{\varsigma (\mu +1)}+\sqrt{\mu (\varsigma -1)}}{\sqrt{\mu +\varsigma }}\right. \nonumber \\&\left. +\,2\log \frac{\sqrt{(\mu +1)\varsigma }+\sqrt{(\mu +1)(\varsigma -1)}}{\sqrt{\varsigma +\mu }} \right) . \end{aligned}$$

(6)

To find $\gamma$ and $\mu$, we use the coordinates of points A and C:

$$\begin{aligned} z(\infty )=-\,{i}d,\quad \hbox {and}\quad z(c)=-\,{i}(d-r_C ). \end{aligned}$$

(7)

In accordance with Eqs. (6) and (7), we obtain

$$\begin{aligned} d=\frac{Q}{K_1 \pi }\left( {\frac{(\hbox {cosec}\pi \gamma -1-2\mu )}{\sqrt{\mu (1+\mu )}}\log \left( \sqrt{\mu }+\sqrt{1+\mu }\right) +\log [4(1+\mu )]} \right) . \end{aligned}$$

(8)

From the second condition (7) and (2), (6), we get

$$\begin{aligned} d= & {} r_C +\,\frac{Q}{K_1 \pi }\left( \frac{\left( {\hbox {cosec}\pi \gamma -1-2\mu } \right) }{\sqrt{\mu (\mu +1)}}\log \frac{\sqrt{c(\mu +1)}+\sqrt{\mu (c-1)}}{\sqrt{\mu +c}}\right. \nonumber \\&\left. +\,2\log \left( {\sqrt{c-1}+\sqrt{c}} \right) \right) -H_C , \end{aligned}$$

(9)

where $\mu =-\varsigma (-{i}/v_D )=-\varsigma (-{i}L/Q)$.

We introduce dimensionless quantities $\hbox {z}^{*}=z/L, d^{*}=d/L, m^{*}=m/L, H_{C}^{*}=H_{C}/L, r_{C}^{*}=r_{C}/L, \hbox {w}^{*}=w/(K_{1}L), v_{D}^{*}=v_{D}/K_{1 }$ and $Q^{*}=Q/(K_{1}L)$ and drop the “*” for the sake of brevity.

From (3), we derive

$$\begin{aligned} \mu =\frac{1-\sin \pi \gamma }{2}\frac{Q-1+\sqrt{(\hbox {Q}-1)^{2}+Q^{2}\cot ^{2}\pi \gamma }}{1-Q+\sin \pi \gamma \sqrt{(\hbox {Q}-1)^{2}+Q^{2}\cot ^{2}\pi \gamma }}\quad . \end{aligned}$$

(10)

Eliminating d from Eqs. (8) and (9) and taking into account (2) and (10), we obtain the following nonlinear equation to determine $\gamma$:

$$\begin{aligned}&H_C -r_C +\frac{Q}{\pi }\left( \frac{\left( {\hbox {cosec}\pi \gamma -1-2\mu } \right) }{\sqrt{\mu (\mu +1)}}\log \frac{\left( \sqrt{\mu +1}+\sqrt{\mu }\right) \exp (\pi H_C /2Q)}{\sqrt{c}+\sqrt{\mu (\exp (\pi H_C /Q)-1)}}\right. \nonumber \\&\quad \left. +\,2\log \left( {\frac{2\sqrt{\mu +1}}{\sqrt{c-1}+\sqrt{c}}} \right) \right) =0. \end{aligned}$$

(11)

We used the FindRoot Mathematica (Wolfram 1991) routine to solve this and subsequent nonlinear equations.

The separation of the real and imaginary parts in Eq. (6) gives a parametric equation of the free boundary:

$$\begin{aligned} x(\xi )= & {} \frac{Q}{\pi }\left( {2\arccos \sqrt{\xi }+\frac{\hbox {cosec}\pi \gamma -1-2\mu }{\sqrt{\mu (1+\mu )}}\arccos \sqrt{\frac{(1+\mu )\xi }{\mu +\xi }}} \right) ,\quad \nonumber \\ y(\xi )= & {} \frac{Q}{\pi }\log \frac{\xi +\mu }{1+\mu },\quad 0<\xi <1. \end{aligned}$$

(12)

The depth of point $F_{1}$ is $m=-\hbox {Im}z(0)=-y(0)$, and the second Eq. (12) gives

$$\begin{aligned} m=\frac{Q}{\pi }\log \frac{1+\mu }{\mu }\;. \end{aligned}$$

(13)

We note that along with the hodograph method, one can use the complex potential and Zhukovsky function and the Zhukovsky-Chaplygin method (see e.g. Anderson 2013; Strack 1989).

We used the ParametricPlot Mathematica routine to plot the free surfaces ${ FF}_{1}$. For the sake of further comparisons with HYDRUS, in Fig. 4a, we show dimensionless free surfaces and loci of sources for the following dimensional input parameters: $r_{C}=0.025~\hbox {m}, H_{C}=0.85~\hbox {m}$, $K_{1}=0.25~\hbox {m/day}$, fixed $L=1.0~\hbox {m}$ with varying $Q=0.265$, 0.275, 0.285, 0.295, 0.305 $0.315~\hbox {m}^{2}$/day (curves 1–6) with the corresponding position of the source indicated by a solid dot. In Fig. 4b we fixed $Q=0.3~\hbox {m}^{2}$/day and plotted three free surfaces for varying L: (1) $L=0.8~\hbox {m}$, (2) $L=1.2~\hbox {m}$, (3) $L=2.4~\hbox {m}$ (curves 1–3). The corresponding dimensionless d and m are: (1) $d=0.87, m=0.16$, (2) $d=0.50, m=0.58$, (3) $d=0.25, m=0.81$.

As is evident from Fig. 4a, an increase in Q makes the phreatic surface steeper. Also, the range of variation of Q is quite narrow (we recall that $H_{C}$ and L are fixed for the examples computed in Fig. 4a). Curve 1 in Fig. 4a illustrates the case of an “almost confined” flow, for which FF $_{1}$ is an almost horizontal straight line. A mathematically equivalent problem for a confined flow to horizontal sinks placed above a horizontal bedrock and fed from a ponded soil surface has been analyzed by Vedernikov (1939) (see also Polubarinova-Kochina 1962). Curve 6 in Fig. 4a corresponds to an “almost critical” flow regime. In case of $L>Q/K_{1}$, the neighboring emitters do not interfere with each other and one arrives at Riesenkampf’s critical regime for a solitary emitter (Polubarinova-Kochina 1962).

For comparisons, we used Kidder’s Eqs. (18) and (19) as the degree of waviness of his free boundary. We also computed a dimensionless area Ar between ${ FF}_{1}$ and a horizontal oil–water contact (a dashed line in Kidder’s flow, our Fig. 1). For $Q\rightarrow \infty$ in Kidder’s solution, when his free surface degenerates into a cycloid, the maximum waviness parameters are $m\rightarrow 2/\pi ,\;\mathrm{Ar}\rightarrow 0.15$ (obviously, $\mathop {\lim }\nolimits _{Q\rightarrow 0} (m, \mathrm{Ar})=(0\hbox {,}0)$, which corresponds to a horizontal oil–water interface). Therefore, even in the limit of the “most perturbed equilibrium”, the Kidder cycloid is only moderately wavy. Kidder’s “critical” flow regime gives the most undulating free boundary because this regime is a precursor to water breakthrough into the oil wells i.e. at subcritical oil flows the free boundary (with inflection points) differs even less from a straight oil–water interface.

Fig. 4

Phreatic surfaces and loci of sources in dimensionless coordinates for Kornev’s subsurface irrigation. Dimensional input parameters for a are $r_{C}=0.025\,\hbox {m}, H_{C}=0.85~\hbox {m}, K_{1}=0.25~\hbox {m}$/day, $L=1.0~\hbox {m}$, and $Q= 0.265$, 0.275, 0.285, 0.295, 0.305, and 0.315. For b $r_{C}=0.025\,\hbox {m}$, $H_{C}=0.85~\hbox {m}$, $K_{1}=0.3~\hbox {m}$/day, $Q=0.3~\hbox {m}^{2}$/day, and 1 $L=0.8~\hbox {m}$, 2 $L=1.2~\hbox {m}$, and 3 $L=2.4~\hbox {m}$

Fig. 5

A flow net for $r_{C}=0.025~\hbox {m}, H_{C}=0.85~\hbox {m}$, $K_{1}=0.25~\hbox {m}$/day, $L=1.0~\hbox {m}$, and $Q=0.295~\hbox {m}^{2}$/day. The streamlines are for $\psi =0.11j\,Q$ where $j=1,2,\ldots ,9$ (solid lines) and the equipotential lines (dashed lines) are for $\phi =0.1j$, $j=-\,2, -\,1, 0, 1, {\ldots }, 5$

In Fig. 5 we use the ParametricPlot, Re, and Im  routines of Mathematica applied to Eq. (6) and show the flow net for $r_{C}=0.025~\hbox {m}$, $H_{C }=0.85~\hbox {m}$, $K_{1}=0.25~\hbox {m}$/day, $L=1~\hbox {m}$, and $Q=0.295~\hbox {m}^{2}$/day, for which $m=0.32~\hbox {m}$, $\gamma =0.155, \mu = 0.74$. In Fig. 5, the streamlines are plotted by solid lines for $\psi =0.11j\, Q$, where $j=1$,2,...9; as the phreatic surface is shown by a dashed-dotted line; the equipotential lines are plotted for $\phi =0.05j, j={-}\,2, -1, 0, 1, {\ldots } 8$ by dashed lines. The lowermost equipotential almost coincides with a horizon $D_{l}D_{\mathrm{r}}$ depicted in Fig. 2a, b.

For the situation of a fixed L and varying Q in Fig. 4a, the mathematical problem is solvable in the range $Q_\mathrm{min}<Q<Q_\mathrm{max}$ (curves 1 and 6 illustrate the regimes close to the lower and upper bounds of Q). Physically, for a given circular PP operated at a given pipe pressure in a given soil, i.e., for a given triad $K_{1}, r_{C}$, and $H_{C}$, the value of Q is a part of the solution (Kacimov and Obnosov 2016, 2017). Modeling of a real PP by a mathematical source bypasses the involvement of the real geometry of the emitter contour into the analysis. Namely, the equipotential lines close to the source are believed to be “almost circular” and one of these small-radius ($r_{C})$ “circles” is considered as a PP-soil contact boundary (see PK-77, Fujii and Kacimov 1998). If the “deep drainage” conditions at infinity (point $D_{1}$–$D_{2}$) in Fig. 1 are known by specification of the pore pressure for saturated flows (as for example, in Kidder 1956; Kacimov and Obnosov 2016) or moisture content for unsaturated flows (as for example, in Kacimov and Obnosov 2017), then Q for a “circular” (or any other shape) emitter is determined by the above-mentioned triad. Vedernikov (1939) analyzed the shape of real equipotential lines around mathematical sinks-sources and found when they deviate from prescribed circles, although this affects flow in the very vicinity of the mathematical singularities.

In the conceptual model of Fig. 2a, the pore pressure at infinity (point $D_{1})$ is not known, which is often common in practical SI when farmers do not have details about the subsurface deeper than a couple of meters. Therefore, in our model with the “infinity” of z in Fig. 2a, Q is “conditioned” by the triad. This “conditioning” will be rectified in Section C, where we consider finite modeling domains with prescribed pressure boundary conditions along the inlet and outlet of a “stream tube” (flow domain) of the Richards’ equation.

With the emphasized mathematical commonality between our and Deemter–Kidder’s solutions, there are some physical differences. Namely, the solvability of Kidder’s (1956) problem is determined by his Eq. (16); for a given difference in the ordinates of the sink and points $F_{1}$ and $F_{2 }$ (Kidder’s parameter b), the oil production rate Q cannot exceed a critical value. The Darcian velocity in the oil far upstream of Kidder’s wells (Kidder’s parameter a) can be arbitrarily high at a given distance between neighboring wells. The infinite increase in Kidder’s a requires an infinite increase in his b.

In Kornev’s flow (Fig. 2a), Q can be mathematically arbitrarily high if $H_{C}$ is allowed to rise to infinity for a given emitter radius (of course, in this case, the source in Fig. 1 should be deep enough such that the free surface does not “bounce” the soil surface from below). Kornev’s Q and $v_{D}$ can be, however, bounded from below. As in Strack’s (1989) “free drainage” flows from a cluster of sinks and sources, the Darcian velocity in the saturated plume at infinity (our $v_{D})$ is $K_{1}$. If the pore pressure at infinity (point $D_{1}$ in Fig. 2a) is atmospheric (we recall that capillarity in this Section is neglected), then the criticality of Kornev’s flow commences at $Q=Q_{m }$ such that at $Q<Q_{m}$ the saturated plumes of neighboring emitters in Fig. 1 are disconnected (the dotted line in Fig. 1 shows one isolated plume for this case). In other words, at this pressure, for any $Q<Q_{m}$, Kornev’s flow degenerates into Riesenkapmf’s flow (Kacimov and Obnosov 2016).

3 HYDRUS-2D Simulations

In this Section, we use HYDRUS (2D/3D) (Šimůnek et al. 2016) and compare numerical (FE) and analytical solutions. In all transient flow simulations, time, t, is in days. We use several default HYDRUS options: iteration criteria, time step controls, an initial (at $t=0$) pressure head of ${-}\,$100 cm throughout the modeled 2D domains, the VGM capillary pressure and phase permeability functions, and the soil catalog.

3.1 Flow From Emitters

Ashrafi et al. (2002), El-Nesr et al. (2014), Siyal and Skaggs (2009), Wang et al. (2017), among many others (see also Šimůnek et al. 2016), used HYDRUS for modeling SI from a PP either as a solitary emitter, i.e., without overlapping of flows generated by laterally neighboring emitters, or as a system of parallel emitters. In their conceptual HYDRUS models, they assumed a “free drainage” or specified negative pressure head boundary condition at the bottom of the flow domain. Hanson et al. (2008) modeled in HYDRUS SI with a shallow water table, the case analytically investigated by Philip (1989). Both Hanson et al. (2008) and Philip (1989) assumed a zero-pressure (water table) boundary condition at the outlet of their flow domain that takes place if drainage water flows out of the domain without raising the water table, assuming that sufficient natural groundwater drainage occurs. Hanson et al. (2008) solved Richards’ equation for an infinite number of emitters 2L apart as in Fig. 1 with no-flow boundary conditions on both the left and right sides (at a distance of L) of the HYDRUS domains. Here, we also consider a half-period of an array of emitters, but our flow domain is bounded by a horizontal positive-pressure interface $I_{1}I_{2 }$ between a soil layer where the emitter is placed and a highly permeable “water-bearing” substratum, into which the emitted water drains. Vedernikov (1939) (see also PK-77, Bouwer 1978) distinguished pre-irrigation hydrogeological conditions with this “groundwater bearing” hydrostratigraphic unit, which is also called the “main”, confined aquifer. The aquifer creates a “backwater” condition above $I_{1}X_{H}$ (Fig. 6), such that in the soil layer with the emitter or another irrigation source (Ilyinsky and Kacimov 1991) the water table “bulges” even if the flow rate from the emitters is small. In other words, even for Kornev’s “negative pressure” emitters the originally flat water table “waves” due to the accretion from the superjacent soil.

We start with a homogeneous rectangle 100 cm $\times$ 200 cm, shown in Fig. 6a and use the “2D - Simple” (rectangular) type of geometry of HYDRUS. Finite element discretization is as follows: 40 $\times$ 40 nodes in both horizontal and vertical directions, with 160 1-D and 3200 2-D finite elements. The soil is loam with $K_{1}=24.96\hbox { cm}$/day. We model the right half of the subsurface emitter by a rectangle ${ ACC}_{1}C_{2}C_{3}A$ of a height and width of 5 and 2.5 cm, respectively, point A having $X_{H}=0, Z_{H}=L_{v}=112.5\hbox { cm}$ in the HYDRUS Cartesian coordinate system. The interior of this rectangle consists of sand of the hydraulic conductivity $K_{\mathrm{s}}=713~\hbox {cm}$/day. This large conductivity ensures that the total head in the emitter rectangle is not lost from line ${ CAC}_{3}$ to the sand–loam interface, i.e., the “sand” filling of the rectangle is almost equivalent to no-filling in an irrigation pipe with a zero Darcian resistance of the pipe walls (mole hole emitters, Bobchenko 1957). The boundary conditions are shown in Fig. 6a: the upper and left faces of the rectangle are no-flow boundaries; at point $C_{3}$ the pressure head $p =90~\hbox {cm}$; along ${ CAC}_{3}$ the pressure head is hydrostatic, i.e., decreases from 90 cm to $p_{{o}}=85\hbox { cm}$ at point C (i.e., the total head, h, is constant along $C_{3}C_{2})$.

Fig. 6

HYDRUS modeling results: a the finite element mesh and a rectangular “sand lens” as a model of a constant total head subsurface emitter. b Undisturbed hydrogeological conditions with a static horizontal water table in an unconfined aquifer and a subjacent highly permeable confined aquifer. c A “degenerate” case of the constant total head sand lens stretched into a strip. d Isobars close to the phreatic surface for the “free drainage” boundary condition along the bottom $I_{1}I_{2}$ of the modeled rectangle, the maximum pressure head at the “lens” apex is $p_{o}=85\hbox { cm}$ ($t=10\hbox { days}$). e A colored map of isobars in the whole flow domain ($p_{o}=85\hbox { cm}; t=30\hbox { days}$). f Isobars close to the phreatic surface for the “backwater” boundary condition $p_{i}=110\hbox { cm}$ along $I_{1}I_{2}$ and $p_{o}=85\hbox { cm}$ in the rectangular “lens” ($t=50\hbox { days}$). g Isobars close to the phreatic surface for the “backwater” boundary condition $p_{i}=45\hbox { cm}$ along $I_{1}I_{2}$ and $p_{o}=85\hbox { cm}$ in the rectangular “lens” ($t=50\hbox { days}$). h Isobars close to the phreatic surface for the “backwater” boundary condition $p_{i}=0\hbox { cm}$ along $I_{1}I_{2}$ and $p_{o}=85\hbox { cm}$ in the rectangular “lens” ($t=50\hbox { days}$). i Isobars close to the phreatic surface for the “backwater” boundary condition $p_{i}=45\hbox { cm}$ along $I_{1}I_{2}$ and $p_{o}=85\hbox { cm}$ along the semi-circular emitter ($t=50\hbox { days}$). j Isobars around a semi-circular emitter: $r_{C}=2.5\hbox { cm}$, $p_{o}=85\hbox { cm}$, $p_{i}=138\hbox { cm}$, $d_{p}=85\hbox { cm}$, an emitter axis is 188 cm above a horizon $D_{l}D_{\mathrm{r}}$. k Isobars for flow past an empty hole: $r_{C}=15\hbox { cm}$, $p_{i}=10\hbox { cm}$, $d_{p}=75\hbox { cm}$, a hole axis is 147.5 cm above a “backwater” horizon (the outlet side of the rectangle), the inlet of the rectangle receives infiltration at a rate of $q_{i} =3\hbox { cm}$/day. l Isobars for flow past a hole with a small quantity of water at its bottom: $r_{C} =15\hbox { cm}$, $p_{i} =10\hbox { cm}$, $d_{p} =75\hbox { cm}$, the hole axis is 147.5 cm above a “backwater” horizon, $q_{i}$ =6 cm/day

Along the bottom $I_{1}I_{2}$ of the flow domain (Fig. 6a), the choice of the boundary condition depends on the knowledge of the “deep subsurface” into which water is drained. In common applications of HYDRUS (see, e.g., El-Nesr et al. 2014; Siyal and Skaggs 2009), the “free drainage” boundary condition (in a steady-state flow this implies a unit gradient), i.e., free gravitational flow at the bottom, $I_{1}I_{2}$, of the modeled flow domain. In other words, the water table is postulated to be “somewhere deep”.

We assume that prior to irrigation from emitters, groundwater is static, the water table is horizontal and positioned at an elevation $p_{i }>0$ above $I_{1}I_{2}$ in the “minor” aquifer, as indicated in Fig. 6b. We repeat that the boundary condition $p=p_{i}$ along $I_{1}I_{2}$ holds also at any $t>0$ during recharge from the emitters. Vedernikov (1939) explained that this unaltered isobaricity of the line $I_{1}I_{2}$ is realized if the substratum is “mighty” enough. Then, the irrigation water seeping from a furrow, channel, emitter, or other sources is well drained either laterally (this is indicated by the horizontal arrow in the substratum, Fig. 6c) or vertically into an even deeper aquifer. A steady saturated–unsaturated flow (at $t>0$) in the soil layer (above $I_{1}I_{2})$ makes a 2-D groundwater mound (“unconfined aquifer”) as compared with an undisturbed situation of Fig. 6b. We repeat that this 2-D flow is occluded by $p_{i}$ and L, viz. a decrease of L or an increase of $p_{i}$ (provided all other parameters are fixed) reduces Q and increases the locus of the phreatic surface. This follows from both our HYDRUS simulations and from the variational principles (Gol’dsheteĭn and Entov 1994). Moreover, if one increases $p_{i}$ above a certain threshold value, the constant total head line ${ CAC}_{3}$ works as a drain (mathematical sink), i.e., groundwater seeps from the minor aquifer into this line (the situation modeled by Deemter 1950). This draining action of the subsurface pipes and mole drains after heavy rains was detected and described in K-35 and Bobchenko (1957).

What if a hypothetical emitter is not a small square (as in Fig. 6a) but a “stretched” thin strip of a length L shown in Fig. 6c? In this case, if we ignore capillarity—recalling the prescribed no head loss along the sand strip from $C_{3}C$ to $C_{2}C_{1}$—we arrive at another 1-D flow regime. Above ${ CC}_{1}$, groundwater stands still at an elevation $p_{i}$. From $C_{3}C_{2 }$ to $I_{1}I_{2}$, a fully saturated 1-D vertical flow takes place, with a Darcian velocity of $v_{ZH}=K_{1}(p_{o}+L_{v}-p_{i})/L_{v}$. Flow in Fig. 6c reflects a standard conceptualization and a hydraulic connection between two highly permeable units, the strip ${ CC}_{1}C_{2}C_{3}$ (an upper “aquifer”) and the “main aquifer”. The rectangle $C_{3}I_{1}I_{2}C_{2}$ (Fig. 6c) acts as a “thick aquitard“. We recall that in agreement with common assumptions of groundwater hydraulics (PK-77), in aquifers the water flow is prevalently horizontal while in aquitards it is mostly vertical.

We used HYDRUS to simulate the two 1-D regimes sketched in Fig. 6b, c as asymptotic limits. HYDRUS confirmed these hydrogeologically “degenerate” scenarios. Next, we simulated 2-D flows for realistic $r_{C}$ (Fig. 6a). A steady-state regime is established in about 10 days.

In the scenario shown in Fig. 6d, e, we assumed $p_{o}=85\hbox { cm}$ and a HYDRUS “free drainage” condition along $I_{1}I_{2}$. The colored images of the pressure heads in the vicinity of the phreatic surface $p=0$ and in the whole rectangle are shown in Fig. 5d, e, respectively. The computed values of d and m are 53.5 and 40 cm, respectively. The distribution of velocity along $I_{1}I_{2}$ showed a variation from 25.1 cm/day at point $I_{1}$ ($X_{H}=0, Z_{H}=0$) to 24.8 cm/day at point $I_{2}$ ($X_{H}=100~\hbox {cm}, Z_{H}=0$).

In scenarios shown in Fig. 6f–h, we assumed $p_{o}=85\hbox { cm}$ and $p_{i}=110$, 45, and 0 cm, respectively, along $I_{1}I_{2}$. The obtained pairs of (d, m) and the range of variations of the vertical component of the Darcian velocity vector along $I_{1}I_{2}$ are: (60, 10 cm), (13–14.6 cm/day); (50, 30 cm), (22.2–25.2 cm/day); and (43, 90 cm), (27.3–32.2 cm/day), respectively. If $p_{i}$ is decreased to negative values (as in Ashrafi et al. 2002), then the water table drops further, Q increases and the saturated zone around the emitter shrinks (and may even convolute into Philip’s “saturated bulb”).

Next, we used a “2D - General” type of geometry of HYDRUS and modeled a semi-circular arc $C_{3}C_{1}C$ of a diameter of 5 cm (Fig. 6i) as the emitter boundary. This constant total head contour was placed at the same $L_{v}$ as the rectangular “sand lens” (in Fig. 6d–h). The emitter boundary condition corresponds to $p_{{o}}=85\hbox { cm}$ at the semicircle’s apex C. The colored map of the moisture content (Fig. 6i) illustrates the water table position, in particular, $d=46\hbox { cm}$, $m=40\hbox { cm}$. Similarly to Ashrafi et al. (2002) Siyal and Skaggs (2009), and Wang et al. (2017), we can include a thin pipe wall made of a low permeable clay.

The results of HYDRUS simulations qualitatively agree with the analytical solutions in Fig. 4. To illustrate this, we compared the case shown in Fig. 5 with numerical results for a loamy soil, a circular emitter of a radius of 2.5 cm subject to a total head of 85 cm, and placed 188 cm above a horizon $D_{l}D_{\mathrm{r}}$ (Fig. 2a) where a positive pressure head (“backwater”) is 138 cm. The upper no-flow boundary of a rectangular flow domain is placed 85 cm ($d_{p}$ in Fig. 1) above the emitter axis (this “cap” segment can be selected at any sufficiently high elevation above the emitter). Fig. 6j shows the computed isobars in the range of −10 cm$<p<$10 cm. The middle isobar is a phreatic surface. Its point F (see Fig. 2a) is about 48 cm above the drain axis as compared to 64 cm in the analytical solution (Fig. 5). Point $F_{1 }$ is about 34 cm above the drain axis (32 cm in the analytical solution, Fig. 5). The presence of the inflexion point on all isobars in Fig. 6j (including the phreatic line) is also apparent, similarly to Khan and Rushton (1996a, Figs. 1a, 2, 4, 8a) and Rushton (2003, Figs. 4.23, 4.25a).

We note that even at $p_{i}=0$ (Fig. 6f), i.e., in the case of no “backwater” in the substratum (Fig. 6b), the pore pressure is positive along $I_{2}F_{1}$. If we keep $p_{\mathrm{i}}=0$ and increase L above 100 cm, then at a certain value $L=L_\mathrm{cr}$, a purely unsaturated flow will take place close to $X_{H}=L_\mathrm{cr}$. In the analytical solution, this corresponds to the regime discussed in Sect. 2: the free surfaces of the neighboring sources do not intersect (Kacimov and Obnosov 2016), the corresponding water tables are “ lighthouse-shaped” (dotted line in Fig. 1a). If, however, $p_{i}>0$ (“backwater” regime), then the phreatic surfaces in both analytical and numerical solutions always intersect and within one half-period (Fig. 2a) an inflection point exists.

3.2 Infiltration Over Subterranean Holes in the Philip Regime

HYDRUS has been successfully used in studies of 2D and 3D flows toward horizontal drains, including mole drains (e.g., Boivin et al. 2006; Brunetti et al. 2017; Filipović et al. 2014; Karandish et al. 2017). In these studies, drains were represented with a standard seepage face boundary condition along the drain contour (i.e., the drain was assumed to be empty). Therefore, the drains acted as water sinks, as in Khan and Rushton (1996a, b) and Rushton (2003) who used saturated flow models in their analysis. However, Philip et al. (1989) showed that an empty cavity (hole) may act as an obstruction to an unsaturated descending flow if its intensity is small enough (see also Stormont and Zhou 2005). In other words, the hole hydrodynamically behaves as neither a sink or a source but as a dipole (Kacimov 2007). Therefore, if one models an empty hole in this regime, then the HYDRUS seepage face boundary condition along the contour can be expected to be equivalent to the no-flow condition. This capillary barrier effect has been used in design and hydrological analysis of the Yucca Mountain tunnels as elements of subsurface nuclear waste repositories (e.g., Wang and Bodvarsson 2003). Birkholzer et al. (1999) investigated a descending unsaturated flow in the regime of Philip et al. (1989), without considering an opportunity of water dripping from the roof of the tunnel and accumulation at the bottom of the drift. In this subsection, we consider a flow regime past a hole with a shallow water level accumulated at the hole bottom that is a common situation in mole drains and emitters (Bobchenko 1957).

In Fig. 6k, we selected the same soil and the rectangular domain as in Fig. 6j, except the hole size ($r_{C} =15\hbox { cm}$) much larger than that of the emitter in Fig. 6j. We set $d_{p}=75\hbox { cm}$ and the bottom draining boundary $D_{l}D_{\mathrm{r}}$ at the depth of 147.5 cm under the axis. The boundary condition along the outlet is $p_{i}=10\hbox { cm}$ (“mild “backwater”). The infiltration rate $q_{i} =3\hbox { cm}$/day was assumed along the top of the rectangle. Fig. 6k shows for a steady-state flow the pressure head contours in the range of ${-}$ 20 cm$<p<10\hbox { cm}$. They, as well as the moisture and velocity fields computed by HYDRUS, are qualitatively similar to what is depicted in Fig. 1 of Philip et al. (1989). The pressure head profile shows a roof-drip lobe, a retarded zone on the upflow side of the hole, and a dry shadow on the downflow side. Along the vertical axis $x=0$ (Fig. 6k), the minimum of the pressure head (the driest point) of $p\approx -\,25$ cm is attained at the bottom of the hole, while the maximum of $p\approx -\,5.8$ cm is attained at the hole’s apex, i.e., the upper stagnation point (Philip et al. 1989), similarly to what Wang and Bodvarsson (2003) and Birkholzer et al. (1999) reported for large tunnels. Due to the encumbrance of our hole, groundwater mounds in the right bottom corner of the flow domain (Fig. 6k). An increase of the infiltration rate $q_{i}$ to approximately 5 cm/day would result in a breakthrough of moisture into the hole through its apex. For higher values of $q_{i}$, water would drip through the hole’s upper segment (see Kacimov 2000).

Fig. 7

Descending infiltration flow past a hole with an impermeable roof and constant-head bottom section seeping into the soil

Figure 7 shows the case of a hole partially filled with a static water and placed into an ambient unsaturated flow of a small $q_{i}$. The segment ${ Ch}_{2}{} { Ch}_{1}$ is a constant total head boundary, the segments ${ Ch}_{1}$ Sf and SfAp are impermeable. If the water level in the hole is small and the draining horizon $D_{l}D_{\mathrm{r}}$ (Fig. 2a) is deep enough with a small “backwater”, then a “perched” water table (as in Warrick and Zhang 1987), rather than a “dry shadow” of Philip et al. (1989) is formed just under the hole. The hole in Fig. 7 again does not drain the incident infiltration but replenishes the “regional” water table by seepage from ${ Ch}_{2}{} { Ch}_{1}$. Obviously, the regional water table (not shown in Fig. 7) mounds in response to this seepage just close to the hole axis, unlike mounding at the corner in Fig. 6k. Figure 6l shows HYDRUS simulations for a steady-stated flow and the same soil and geometry as in Fig. 6k, with the following difference in boundary conditions along the hole contour: the topsoil is subject to an infiltration flux $q_{i}=6\hbox { cm}$/day, the water level in the hole is 2.9 cm. A constant total head boundary condition was specified along ${ Ch}_{2}{} { Ch}_{1}$, and a seepage face boundary condition was imposed along ${ Ch}_{1}$ Ap. The computations in Fig. 6l are qualitatively in congruency with the flow topology and the soil wetness field from Philip et al. (1989) and Warrick and Zhang (1987).

4 Conclusions and Perspectives

We decoupled a saturated–unsaturated steady-state Darcian flow from an infinite line of equally spaced PPs that emit water under a positive pressure, each at the same rate. For the first flow fragment of a potential flow, we followed Holmes (see the epigraph) and used Deemter’s (1950) and Kidder’s (1956) “singularity clues” when applying the hodograph method for line sources. From an explicit analytical solution to a free BVP in a homogenous and isotropic soil stratum, the computed phreatic surface is wavy with inflection points. This surface bulges above the emitters and is depressed between two neighboring linear sources. In the limiting case, the circular cut in the hodograph domain (Deemter 1950) degenerates into a full half-circle (see Kidders’ Fig. 2) that corresponds to cusps of the phreatic surface.

In our Kidder-type phreatic flow, we ignored evaporation from $F_{1}F$ (Fig. 2a), i.e., we assumed that unsaturated flow does not affect potential flow. The Deemter (1950) and Polubarinova-Kochina (1962) evaporation model takes into account coupling between two flows by assuming that along the phreatic surface $\psi =ex +Q$, where $e=\hbox {const}> 0$ is a given intensity of evaporation. Flow from the source (Fig. 3d) then splits into ascending and descending parts, with a separatrix AE and a stagnation point E (see Fig. 3 of Deemter 1950). Along this curve, as well as along ${ EF}_{1 }$ and ${ ED}_{1}$, the stream function $\psi =Q_{E}$, where $Q_{E}<Q$ is the part of the source-emitted water that descends as deep percolation. The hodograph domain (Fig. 3e) remains the same as in Fig. 2a, modulo translated upward to a distance $\mu$.

Our HYDRUS simulations substantiate the analytical findings. For saturated–unsaturated flows, we followed Hanson et al. (2008), i.e., we considered a HYDRUS rectangular domain with an emitter modeled as a constant total head contour (a semicircle or rectangle). However, in order to compare the numerical and analytical solutions, we bounded the bottom of the rectangle from below by a positive-pressure horizon (“backwater”) similarly to Choudhary and Chahar (2007), which represents a common hydrogeological “outlet drainage” (see, also Vedernikov 1939, PK-77). This “backwater” is routinely encountered in regular surface irrigation projects with seepage from earth channels and furrows (Bouwer 1978; Ilyinsky and Kacimov 1991; Kacimov and Youngs 2005), but was not previously modeled in SI. We also modeled unsaturated–saturated zonation more general than in Philip et al. (1989) for a subterranean hole placed in a descending infiltration-induced ambient flow, with a mixed boundary condition along the hole contour, which is impermeable near hole’s roof and leaks through a constant total head segment at hole’s bottom. The future HYDRUS analysis might be warranted to show how flow fields from emitters and past holes are affected by soil layering and fluxes.