1 Introduction

Advances in the understanding of coal–gas interactions have changed the manner in which human treats coalbed methane (CBM): from mitigating its danger as a mining hazard to developing its potential as an unconventional gas resource.

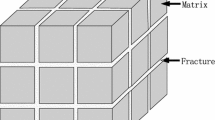
Coal reservoirs contain porous matrix blocks bounded by a well-developed cleat network and are usually idealized as a collection of matchsticks, as shown in Fig. 1 (Laubach et al. 1998). Micropores inside the matrix form the major share of the porous structure and are more responsible for gas storage. On the other hand, macropores refer to mutually orthogonal face and butt cleats and are more responsible for fluid mobility. Note that the matrix pore contribution to fluid mobility is assumed to be small; all permeability mentioned hereinafter refers to the cleat permeability. While fluid mobility is primarily controlled by the developed cleat network, methane desorption has a significant influence on cleat deformation.

Fig. 1
figure 1

Matchstick geometry (Laubach et al. 1998)

Full size image

Two competing effects will occur during the primary recovery of CBM, as shown in Fig. 2. The former effect is reservoir compaction. The effective stress will increase as the pore pressure decreases, resulting in the closure of cleats and the decrease in cleat permeability. Matrix shrinkage has an opposite effect on the cleat and permeability evolutions as pore pressure reduces and gas desorbs. Thus, an initial permeability decrease due to reservoir compaction is usually compensated by the subsequent increase owing to matrix shrinkage. Whether the permeability is higher than its initial value depends on the net effect of these two competing mechanisms. Therefore, understanding the transient characteristics of permeability in coals is critical to CBM recovery.

Fig. 2
figure 2

Reservoir compaction and matrix shrinkage effects on coal permeability

Full size image

According to the characteristics of coal reservoir and CBM recovery, a variety of analytical permeability models have been developed with three assumptions: (1) matchstick geometry, (2) uniaxial strain, and (3) constant overburden stress (Palmer 2009; Liu et al. 2011; Wang et al. 2011; Pan and Connell 2012). Gray (1987) first proposed the coal permeability model on the basis of stress change, accounting for both the geomechanical effects and sorption-induced swelling/shrinkage. Sawyer et al. (1990) first proposed the coal permeability model based on the porosity change instead. Seidle and Huitt (1995) also developed a model based on porosity change, but only the porosity change induced by coal swelling/shrinkage was considered. Levine (1996) developed a permeability model considering that the cleat width change is due to reservoir compaction and matrix shrinkage. Palmer and Mansoori (1996, 1998) used the three assumptions mentioned above to derive a simple, concise relationship for porosity changes. With the same three assumptions, Shi and Durucan (2004, 2005), Cui and Bustin (2005), and Cui et al. (2007) developed a permeability model from the constitutive equation of a linear poroelasticity media; however, effective horizontal stress is assumed in the former study, while effective mean stress is assumed for the later study. Liu and Rutqvist (2010) introduced an internal swelling stress concept to account for the impact of matrix swelling/shrinkage on cleat width change. Connell et al. (2010) used the general linear poroelastic constitutive law to extend the permeability model to triaxial conditions. Among these analytical models, Shi–Durucan (S&D) model, Cui–Bustin (C&B) model, Palmer–Mansoori (P&M) model, and its improved version are most commonly used. However, no final conclusion has yet been reached on which model gets the best performance.

The remainder of this paper is organized as follows: Sect. 2 revisits and compares the existing coal permeability models; Sect. 3 presents a new cleat volume compressibility–stress relation and re-derives the permeability model; and Sect. 4 analyses the influences of elastic properties on coefficient ratio, rebound pressure, and recovery pressure.

2 Permeability Models Revisited and Compared

In this section, three permeability models are revisited, evaluated against the same experimental data (Mitra 2010; Mitra et al. 2012), and compared to each other.

2.1 Shi–Durucan (S&D) Model

Shi and Durucan (2004, 2005, 2010, 2014) derived a permeability model accounting for both the geomechanical effect and desorption-induced coal shrinkage, believing that the cleat permeability ratio varies exponentially with effective horizontal stress normal to the cleats. The S&D model was derived from the constitutive equation of a linear thermoelastic porous medium, but replacing the thermal expansion term with an analogous matrix shrinkage term.

$$\begin{aligned} \frac{k}{k_i }=e^{-3C_f \Delta \sigma _h^e } \end{aligned}$$
(1)

where \(C_f \) is the cleat volume compressibility with respect to the changes in effective horizontal stress normal to the cleats.

$$\begin{aligned}&\displaystyle \Delta \sigma _h^e =\sigma _h^e -\sigma _{hi}^e =-\frac{v}{1-v}\left( {p_p -p_{pi} } \right) +\frac{E\varepsilon _{s\max } }{3\left( {1-v} \right) }\left( {\frac{p_p }{p_p +p_\varepsilon }-\frac{p_{pi} }{p_{pi} +p_\varepsilon }} \right) \end{aligned}$$
(2)
$$\begin{aligned}&\displaystyle C_f =-\frac{\partial \phi /\phi }{\partial \sigma _h^e } \end{aligned}$$
(3)

2.2 Cui–Bustin (C&B) Model

The derivation process of C&B model was similar to that of S&D model. However, Cui and Bustin (2005) and Cui et al. (2007) believed that the permeability evolution is mainly controlled by effective mean stress, rather than effective horizontal stress.

$$\begin{aligned} \frac{k}{k_i }=e^{-3\Delta \sigma _m^e /K_p } \end{aligned}$$
(4)

where \(K_p \) is the pore volume modulus and can be simply approximated as \(\phi K\).

$$\begin{aligned} \Delta \sigma _m^e =\sigma _m^e -\sigma _{mi}^e =-\frac{1+v}{3\left( {1-v} \right) }\left( {p_p -p_{pi} } \right) +\frac{2E\varepsilon _{s\max } }{9\left( {1-v} \right) }\left( {\frac{p_p }{p_p +p_\varepsilon }-\frac{p_{pi} }{p_{pi} +p_\varepsilon }} \right) \end{aligned}$$
(5)

2.3 Palmer–Mansoori (P&M) Model

Palmer and Mansoori (1996, 1998) started from the strain change of a linear thermoelastic porous medium instead of the stress change, ignored the grain compressibility, and employed the cube relationship between permeability ratio and porosity ratio to calculate the permeability change.

$$\begin{aligned} \frac{k}{k_i }=\left( {\frac{\phi }{\phi _i }} \right) ^{3}=\left( {\frac{\Delta \phi }{\phi _i }+1} \right) ^{3} \end{aligned}$$
(6)

where

$$\begin{aligned} \Delta \phi =\phi -\phi _i= & {} \frac{\left( {1+v} \right) \left( {1-2v} \right) }{E\left( {1-v} \right) }\left( {p_p -p_{pi} } \right) \nonumber \\&-\frac{2\left( {1-2v} \right) \varepsilon _{s\max } }{3\left( {1-v} \right) }\left( {\frac{p_p }{p_p +p_\varepsilon }-\frac{p_{pi} }{p_{pi} +p_\varepsilon }} \right) \end{aligned}$$
(7)

However, P&M model did not match well with the permeability evolution trend observed in the field and then, a suppression factor (\(g=0.3\)) was introduced into the compaction term to improve its performance (Palmer 2009).

$$\begin{aligned} \Delta \phi =\phi -\phi _i= & {} \frac{g\left( {1+v} \right) \left( {1-2v} \right) }{E\left( {1-v} \right) }\left( {p_p -p_{pi} } \right) \nonumber \\&-\frac{2\left( {1-2v} \right) \varepsilon _{s\max } }{3\left( {1-v} \right) }\left( {\frac{p_p }{p_p +p_\varepsilon }-\frac{p_{pi} }{p_{pi} +p_\varepsilon }} \right) \end{aligned}$$
(8)

2.4 Model Verification and Comparison

As noted above, these models are either porosity based or stress based. For porosity-based ones (P&M model and its improved version), the porosity change with respect to reservoir pressure should be first calculated and then introduced to the cube relationship between permeability ratio and porosity ratio. For stress-based ones (S&D and C&B models), the effective stress change with respect to reservoir pressure should be first calculated and then introduced to the exponential relationship between permeability and stress. Regardless of the differences in these formulas, each model is comprised of main variable and cleat parameter, wherein the main variable describes the competitive relation between reservoir compaction and matrix shrinkage, and the cleat parameter represents the cleat property. In particular, the main variable in S&D model is effective horizontal stress, while that in C&B model is effective mean stress. In addition, the cleat parameters (specifically, cleat volume compressibility in S&D model, pore volume modulus in C&B model, and initial porosity in P&M model) should be determined by fitting experimental data prior to permeability ratio calculation,

$$\begin{aligned} C_f= & {} -\frac{\ln \left( {k/k_i } \right) }{3\Delta \sigma _h^e } \end{aligned}$$
(9)
$$\begin{aligned} K_p= & {} -\frac{3\Delta \sigma _m^e }{\ln \left( {k/k_i } \right) } \end{aligned}$$
(10)
$$\begin{aligned} \phi _i= & {} \frac{\Delta \phi }{\root 3 \of {k/k_i }-1} \end{aligned}$$
(11)

Three series of experimental data under uniaxial strain (Mitra 2010; Mitra et al. 2012), which is consistent with the model assumptions, are used to determine the cleat parameters and to evaluate the model performances. The mechanical and adsorption properties of the coal samples are shown in Table 1, wherein the elastic parameters can be obtained from the stress–strain relation, while the adsorption parameters are estimated from the sorption-induced strain data. During the permeability measurement, the coal samples were first sealed in the triaxial cell and stressed vertically and horizontally to replicate the mechanical conditions in situ. Then methane was injected into the triaxial cell to apply pore pressure. After the coal samples had reached the state of adsorption equilibrium, flow test was conducted and coal permeability was measured. Next, pore pressure was reduced gradually to simulate the recovery of CBM. The horizontal stress should decrease along with pore pressure to ensure that there was no obvious horizontal strain change during the experiment, wherein the strain was monitored by circumferential extensometer. The stress loads applied and the corresponding circumferential strains of the coals are shown in Table 2. In addition, since porosity was not monitored during the measurement, the porosity change in Eq. 11 can be estimated from the effective mean stress change as follows,

$$\begin{aligned} \Delta \phi =-\frac{3\left( {1-2v} \right) }{E}\Delta \sigma _m^e \end{aligned}$$
(12)

The cleat parameters regressed are also shown in Table 1. The fitting results between the permeability models and experimental data for permeability–stress are shown in Figs. 3, 4, and 5. As can be observed, the permeability of these three coals increases gradually as the pore pressure decreases and eventually reaches almost 13 times, double, and quadruple of the initial permeability by the end of the experiment, respectively. For the San Juan coal, the average relative error between the experimental data and S&D model is 11.11%, while that is 54.83, 73.97, and 17.49% for C&B model, P&M model, and the improved P&M model, respectively. Similarly, the average relative errors between Survant coal’s experimental data and S&D, C&B, P&M, improved P&M models are 8.99, 9.75, 13.73, and 9.35%, respectively. The average relative errors between Seelyville coal’s experimental data and S&D, C&B, P&M, improved P&M models are 11.95, 63.42, 23.88, and 75.96%, respectively. Overall, S&D model has the best performance among these three models, which means that the experimental data measured under uniaxial strain can be better reflected by effective horizontal stress. Constant cleat volume compressibility over the stress range was used to assumed for S&D model (Shi and Durucan 2004, 2005); however, recent studies show that the cleat volume compressibility should be stress dependent Shi and Durucan (2010, 2014).

Table 1 Elastic, adsorption, and cleat properties of the coal samples (Mitra 2010; Mitra et al. 2012)
Full size table
Table 2 Stress loads applied and the corresponding circumferential strains (Mitra 2010; Mitra et al. 2012)
Full size table

3 A New \(\hbox {C}_{\mathrm{f}}\) Determination Method and the Corresponding Modification to Permeability Model

In this section, the relation between cleat volume compressibility and effective horizontal stress is first re-derived on the basis of dimensional analysis and then introduced to the derivation of permeability model. The modified permeability model is also evaluated against the experimental data (Mitra 2010; Mitra et al. 2012) and compared with other models.

3.1 \(\hbox {C}_{\mathrm{f}}\) Determination Based on Dimensional Analysis

According to the theory of dimensional homogeneity, the dimension of each term should be homogeneous in a physical equation which reflects the objective law correctly and completely. That is, if the equation includes m variables and n basic dimensions, then the variables can and will compose \((m-n)\) dimensionless variables and satisfy the physical equation. Wang et al. (2014) used this theory to determine the relation between permeability and its impact factors, however, cleat volume compressibility was not conisdered.

The variables, which affect the permeability greatly, contain the cleat volume compressibility, effective horizontal stress, gas viscosity, and coal density. Using mass (M), time (T), and length (L) as basic dimensions, the dimensions of the variables can be expressed as follows,

$$\begin{aligned}{}[k]=L^{2}, \left[ C_f \right] =M^{-1}T^{2}L, \left[ \sigma _h^e \right] =MT^{-2}L^{-1}, \left[ \mu _g \right] =MT^{-1}L^{-1}, \left[ \rho _c \right] =ML^{-3} \end{aligned}$$
(13)

Eliminating the mass dimension,

$$\begin{aligned}{}[k]=L^{2},\quad [C_f \rho _c ]=T^{2}L^{-2},\quad \left[ \frac{\sigma _h^e }{\rho _c }\right] =T^{-2}L^{2}, \quad \left[ \frac{\mu _g }{\rho _c }\right] =T^{-1}L^{2} \end{aligned}$$
(14)
Fig. 3
figure 3

Permeability ratio versus pore pressure for San Juan coal

Full size image
Fig. 4
figure 4

Permeability ratio versus pore pressure for Survant coal

Full size image

Eliminating the time dimension,

$$\begin{aligned}{}[k]=L^{2}, \quad \left[ \frac{C_f \mu _g^2 }{\rho _c }\right] =L^{2},\quad \left[ \frac{\sigma _h^e \rho _c }{\mu _g^2 }\right] =L^{-2} \end{aligned}$$
(15)

Eliminating the length dimension, two dimensionless variables are eventually obtained.

$$\begin{aligned} \left[ \frac{k\sigma _h^e \rho _c }{\mu _g^2 }\right] =D_1 , [C_f \sigma _h^e ]=D_2 \end{aligned}$$
(16)

As can be observed, \(D_1\) describes the relation between cleat permeability and effective horizontal stress, which potentially considers both the reservoir compaction and matrix shrinkage effects as a function of effective horizontal stress, and \(D_2\) shows that the cleat volume compressibility should change with effective horizontal stress, and inverse proportional function is assumed between them.

$$\begin{aligned} C_f =C_{fi} +\alpha \left( {\frac{1}{\sigma _h^e }-\frac{1}{\sigma _{hi}^e }} \right) \end{aligned}$$
(17)

where \(\alpha \) is the increasing rate of cleat volume compressibility with respect to effective horizontal stress changes. While cleat volume compressibility physically stands for the porosity change rate with respect to effective horizontal stress change, Eq. 17 implies that the porosity change is more remarkable at a lower effective horizontal stress.

Fig. 5
figure 5

Permeability ratio versus pore pressure for Seelyville coal

Full size image

3.2 Derivation of Permeability Model

As mentioned above, coal reservoirs are usually idealized as a collection of matchsticks, which implies that the flow in coal reservoirs is along the axis of matchsticks. Thus, permeability for this geometry is shown as (Reiss 1980),

$$\begin{aligned} k=\frac{1}{96}a^{2}\phi ^{3} \end{aligned}$$
(18)

where

$$\begin{aligned} \phi =\frac{2b}{a} \end{aligned}$$
(19)

Differentiating Eq. 18 with respect to the effective horizontal stress,

$$\begin{aligned} \frac{\partial k}{\partial \sigma _h^e }=\frac{2a\phi ^{3}}{96}\frac{\partial a}{\partial \sigma _h^e }+\frac{3a^{2}\phi ^{2}}{96}\frac{\partial \phi }{\partial \sigma _h^e } \end{aligned}$$
(20)

where

$$\begin{aligned} \frac{\partial a}{\partial \sigma _h^e }=a\frac{\partial \varepsilon }{\partial \sigma _h^e } \end{aligned}$$
(21)

Substituting Eqs. 3, 18, and 21 into Eq. 20 yields

$$\begin{aligned} \frac{\partial k}{\partial \sigma _h^e }=\frac{2a^{2}\phi ^{3}}{96}\frac{\partial \varepsilon }{\partial \sigma _h^e }+\frac{3a^{2}\phi ^{3}}{96}\frac{\partial \phi /\phi }{\partial \sigma _h^e }=k\left( {2\frac{\partial \varepsilon }{\partial \sigma _h^e }-3C_f } \right) \end{aligned}$$
(22)

The first term in the parentheses in Eq. 22 is the coal fabric contribution, while the second term represents the cleat volume contribution to the permeability–stress relation. Since the cleat volume term is two or three orders of magnitude larger than the coal fabric term, Eq. 22 can be approximated as,

$$\begin{aligned} \frac{\partial k}{\partial \sigma _h^e }=-3kC_f \left( {\sigma _h^e } \right) \end{aligned}$$
(23)

Substituting Eq. 17 into Eq. 23, and replacing the partial differentials with total differentials, permits solution by the separation of variables,

$$\begin{aligned} \frac{\partial k}{k}=-3\left[ {C_{fi} +\alpha \left( {\frac{1}{\sigma _h^e }-\frac{1}{\sigma _{hi}^e }} \right) } \right] \partial \sigma _h^e \end{aligned}$$
(24)

Integrating and initializing Eq. 24, the permeability ratio can be obtained as follows,

$$\begin{aligned} \frac{k}{k_i }=e^{-3\left( {C_{fi} -\frac{\alpha }{\sigma _{hi}^e }} \right) \left( {\sigma _h^e -\sigma _{hi}^e } \right) }\times \left( {1+\frac{\sigma _h^e -\sigma _{hi}^e }{\sigma _{hi}^e }} \right) ^{-3\alpha } \end{aligned}$$
(25)

For ease of comparison, the permeability model derived above is termed W&Z model.

3.3 Model Validation and Error Analysis

Two parameters should be determined prior to permeability ratio calculation with W&Z model, wherein the initial cleat volume compressibility is from S&D model and declining rate can be obtained by fitting Eq. 25 with experimental data.

The declining rates are 0.091, 0.315, and 0.169 for San Juan, Survant, and Seelyville coals, respectively. The fitting results between the permeability model and experimental data for permeability–stress are also shown in Figs. 3, 4, and 5. As can be observed, the average relative errors for the San Juan, Survant, and Seelyville coals are 7.22, 5.05, and 9.00%, respectively.

To sum up, the new model has a good prediction performance. This is primarily due to the following reasons. Firstly, the new model is essentially an effective horizontal stress model, which is consistent with the characteristics of coal reservoir and CBM recovery mode. Secondly, the relationship between cleat volume compressibility and effective horizontal stress can be better reflected by the inverse proportional function. Finally, the dimensionless cleat volume compressibility coefficient, which eliminates the effect of index dimension during the experimental data fitting, can better reflect the permeability change induced by stress change.

4 Sensitivity Analysis

Since coal reservoirs usually demonstrate strong anisotropy and heterogeneity, the influences of elastic and adsorption properties on the coefficient ratio, rebound pressure, and recovery pressure are further tested to reveal the overall trend of permeability.

4.1 Coefficient Ratio, Rebound and Recovery Pressures

As mentioned, these models essentially include the compaction term and shrinkage term. The terms have just the opposite effects on permeability. That is, coal permeability evolution during CBM recovery is dependent on the relative strength of these two terms. Shi and Durucan (2014) used the coefficient ratio (B / A) of these two terms to quantize their relative strength and believed that the larger the coefficient ratio is, the greater the matrix shrinkage term will be. The primary variable changes of all the models can be expressed as a general equation consisting of two competing terms.

$$\begin{aligned} \Delta Q{=}-A\left( {p_p -p_{pi} } \right) +B\left( {\varepsilon _s -\varepsilon _{si} } \right) \end{aligned}$$
(26)

However, the fact that the two terms have different units adds difficulty in quantifying their relative strength in this case. To describe the relative strength change corresponding to the pore pressure change more accurately, the general equation is rewritten as,

$$\begin{aligned} \Delta Q {=}-A^{\prime }\left( {\frac{p_p }{p_{pi} }-1} \right) +B^{\prime }\left( {\frac{\varepsilon _s }{\varepsilon _{si} }-1} \right) \end{aligned}$$
(27)

where

$$\begin{aligned} A^{\prime }{=}A\cdot p_{pi} \end{aligned}$$
(28)
$$\begin{aligned} B^{\prime }{=}B\cdot \varepsilon _{si} \end{aligned}$$
(29)

In addition, since methane adsorption in coals follows the Langmuir isotherm, which is flat at high pressure and steep at low pressure, the coal permeability may reduce during the early production stage with limited gas desorption, but may rebound at a lower pressure where significant gas desorption occurs. The pressure at which the permeability starts to increase is called the rebound pressure, while the pressure at which the permeability rebounds to its initial value is referred as the recovery pressure. That is, the derivative of permeability ratio relative to pore pressure should be zero at rebound pressure, while the permeability should equal its initial value at recovery pressure,

$$\begin{aligned} \left. {\frac{\partial \left( {k/k_i } \right) }{\partial p_p }} \right| _{p_p =p_{rb} }= & {} 0 \end{aligned}$$
(30)
$$\begin{aligned} \left. {\frac{k}{k_i }} \right| _{p_p =p_{rc} }= & {} 1 \end{aligned}$$
(31)

Substituting Eqs. 1, 4, 6, and 25 into Eqs. 30 and 31, both rebound and recovery pressures for S&D, C&B, P&M, and W&Z models can be obtained.

The coefficient ratios, rebound pressure, and recovery pressures of various models are shown in Table 3. As can be observed, the coefficient ratio, rebound pressure, and recovery pressure of W&Z model equal those of S&D model, which means that W&Z model is essentially an effective horizontal stress model. For the same reason, both C&B and P&M models are effective mean stress based.

Table 3 Coefficient ratios, rebound pressures, and recovery pressures of different models
Full size table

The rebound pressures of S&D and W&Z models, C&B and P&M models, and improved P&M model are \(\sqrt{\frac{E\varepsilon _{s\max } p_\varepsilon }{3v}}-p_\varepsilon \), \(\sqrt{\frac{2E\varepsilon _{s\max } p_\varepsilon }{3\left( {1+v} \right) }}-p_\varepsilon \), and \(\sqrt{\frac{2E\varepsilon _{s\max } p_\varepsilon }{3g\left( {1+v} \right) }}-p_\varepsilon \), respectively. The recovery pressures of S&D and W&Z models, C&B and P&M models, and improved P&M model are \(\frac{E\varepsilon _{s\max } p_\varepsilon }{3v\left( {p_{pi} +p_\varepsilon } \right) }-p_\varepsilon \), \(\frac{2E\varepsilon _{s\max } p_\varepsilon }{3\left( {1+v} \right) \left( {p_{pi} +p_\varepsilon } \right) }-p_\varepsilon \), and \(\frac{2E\varepsilon _{s\max } p_\varepsilon }{3g\left( {1+v} \right) \left( {p_{pi} +p_\varepsilon } \right) }-p_\varepsilon \), respectively. The coefficient ratios of S&D and W&Z models, C&B and P&M models, and improved P&M model are \(\frac{E\varepsilon _{s\max } }{3v\left( {p_{pi} +p_\varepsilon } \right) }\), \(\frac{2E\varepsilon _{s\max } }{3\left( {1+v} \right) \left( {p_{pi} +p_\varepsilon } \right) }\), and \(\frac{2E\varepsilon _{s\max } }{3g\left( {1+v} \right) \left( {p_{pi} +p_\varepsilon } \right) }\), respectively. The coefficient ratio of S&D and W&Z models is \(\frac{1+v}{2v}\) and \(\frac{g\left( {1+v} \right) }{2v}\) times as large as that in C&B and P&M models and improved P&M model, respectively. The coefficient ratio differences of these models only relate to Poisson’s ratio, while their magnitudes are also affected by Young’s modulus, maximum swelling strain, and pressure corresponding to half maximum swelling strain.

4.2 Sensitivity Analysis

For a typical coal, the Young’s modulus is usually between 1000 and 5000 MPa, Poisson’s ratio is located between 0.2 and 0.4 (Jones et al. 1984; Bell et al. 1985; Gray 1987; Levine 1996; Gu and Chalaturnyk 2005; Gentzis et al. 2007; Seidle 2011), maximum swelling strain is between 0.001 and 0.02, and pressure corresponding to half maximum swelling strain ranges from 1 to 5 MPa (Moffat and Weale 1955; Levine 1996; Robertson 2005; Bustin et al. 2008; Ottiger et al. 2008; Harpalani and Mitra 2010; Pan and Connell 2011). The parameter ranges studied are shown in Table 4.

Table 4 Elastic and adsorption properties sensitivity projects
Full size table

The coefficient ratio variations with Young’s modulus, Poisson’s ratio, maximum swelling strain, and half maximum swelling strain pressure are shown in Figs. 6, 7, 8, and 9. As can be observed, the coefficient ratio is larger than 1 for most of the coal properties studied, which means that matrix shrinkage is more obvious than reservoir compaction. Within the coal properties studied, the coefficient ratio of improved P&M model is the largest, followed by those of S&D and W&Z models, and those of C&B and P&M models. According to the model evaluation results, the S&D and W&Z models have the best performance in describing the competitive relation between reservoir compaction and matrix shrinkage. That is, the reservoir compaction in C&B and P&M models may be overestimated, while that in improved P&M model is underestimated. In addition, the coefficient ratios increase with Young’s modulus and maximum swelling strain, but decrease with Poisson’s ratio and pressure corresponding to half maximum swelling strain. Young’s modulus and maximum swelling strain have a larger impact on coefficient ratio.

Fig. 6
figure 6

Coefficient ratio versus Young’s modulus

Full size image
Fig. 7
figure 7

Coefficient ratio versus Poisson’s ratio

Full size image
Fig. 8
figure 8

Coefficient ratio versus maximum swelling strain

Full size image
Fig. 9
figure 9

Coefficient ratio versus pressure corresponding to half maximum swelling strain

Full size image

The rebound and recovery pressures with Young’s modulus, Poisson’s ratio, maximum swelling strain, and half maximum swelling strain pressure are shown in Figs. 10, 11, 12, and 13. As can be observed, the rebound and recovery pressures based on improved P&M model are the largest, followed by those based on S&D and W&Z models, and those based on C&B and P&M models. The larger the rebound and recovery pressures are, the more attention the matrix shrinkage effect is paid. In addition, both rebound and recovery pressures increase with Young’s modulus and maximum swelling strain, but decrease with Poisson’s ratio and pressure corresponding to half maximum swelling strain. For C&B and P&M models, however, both rebound and recovery pressure will first increase then decrease with pressure corresponding to half maximum swelling strain.

Fig. 10
figure 10

Rebound and recovery pressures versus Young’s modulus

Full size image
Fig. 11
figure 11

Rebound and recovery pressures versus Poisson’s ratio

Full size image
Fig. 12
figure 12

Rebound and recovery pressures versus maximum swelling strain

Full size image
Fig. 13
figure 13

Rebound and recovery pressures versus pressure corresponding to half maximum swelling strain

Full size image

Since the magnitude of rebound pressure relative to recovery pressure will reverse once their values reach the original pore pressure, there are three possible situations according to their relative values, \(P_{rc}< 0< P_{rb} < P_{pi}\), \(0< P_{rc}< P_{rb} < P_{pi}\), and \(0< P_{pi}< P_{rb} < P_{rc}\).

  1. (I)

    \(P_{rc}< 0< P_{rb} < P_{pi}\). In this case, the permeability will first decrease, followed by a rebound at \(P_{rb}\). However, the permeability rebound is too weak to recover its initial value. In fact, this situation will hardly happen in typical coal reservoirs. However, since reservoir compaction in improved P&M model is usually underestimated, this may happen with low Young’s modulus and small maximum swelling strain in this case.

  2. (II)

    \(0< P_{rc}< P_{rb} < P_{pi}\). In this case, the permeability will first decrease, followed by a rebound at \(P_{rb}\). The permeability will exceed its initial value once the pore pressure is lower than \(P_{rc}\). This is more likely to occur at coal reservoirs with lower Young’s modulus, higher Poisson’s ratio, smaller maximum swelling strain, and lower half maximum swelling strain pressure.

  3. (III)

    \(0< P_{pi}< P_{rb} < P_{rc}\). In this case, the permeability will increase monotonously as pore pressure reduces. This is more likely to occur at higher Young’s modulus, lower Poisson’s ratio, larger maximum swelling strain, and higher half maximum swelling strain pressure situations.

5 Conclusions

In this paper, the relation between cleat volume compressibility and effective horizontal stress is re-derived by dimension analysis and introduced to the derivation of permeability model. The modified model is verified with experimental data under uniaxial condition, compared with the existing permeability models, and further tested with varying elastic and adsorption properties. The results show that S&D model and its modification with the primary variable of effective horizontal stress have the best performances in matching the experimental data under uniaxial strain. The relationship between cleat volume compressibility and effective horizontal stress can be better reflected by the inverse proportional function. In addition, the strengths of matrix shrinkage effect relative to reservoir compaction effect in different models only vary with Poisson’s ratio, while their magnitudes are also affected by Young’s modulus. For a typical coal reservoir, the C&B and P&M models will observe a stronger permeability decline at the initial, while the improved P&M model will receive an earlier and more rapid rebound than the S&D and W&Z models.