Theoretical Approach to the Onset of Convection in a Porous Layer

Abstract

A new theory is proposed to determine the critical wave number and the critical Rayleigh number at the onset of convection. We consider a problem of the onset of instability in convection in a horizontal layer embedded in a fluid-saturated porous medium. The upper wall of the layer is maintained at uniform temperature and concentration. On the lower wall, an Arrhenius-type exothermic surface reaction and surface radiation are assumed to occur. The heat released from the surface reaction and surface radiation causes convection in the porous medium and thereby can lead instability in the system. Results showed that the new theory can reasonably predict the critical wave number and the critical Rayleigh number. Moreover the influences of the heat release parameter, the mass diffusion parameter, the activation energy parameter and the conduction–radiation parameter on the critical wave number and the critical Rayleigh number have been presented. In the presence of surface radiation there must have a maximum value of the heat release parameter and the activation energy parameter while there must a minimum value of the mass diffusion parameter for the onset of convection in a porous medium.

1 Introduction

Convective flow in a porous media has received considerable attention due to its occurrence in many environmental and industrial processes (Nield and Bejan 2013), for example, contaminant transport in groundwater systems (Postelnicu 2009), mineralizations of the Earth’s crust (Scott 2012a), the extraction of geothermal energy by underground heating (Cheng 1978), oil recovery, food processing, casting and welding of a manufacturing process, the dispersion of chemical contaminants in various processes in the chemical industry and in the environment (Minto et al. 1998), the flow of saline groundwater driven by evaporation from the surface (Wooding et al. 1997), packed-bed processing, in situ coal gasification (Homsy and Sherwood 1976) and the formation of freckles in alloy castings (Fowler 1985). In addition, the convective transport of the long-term storage of $\hbox {CO}_{2}$ by geological sequestration belongs to this type of problem (Orr 2009) which is considered to be the way of controlling the growing concentration of atmospheric $\hbox {CO}_{2}$ (Metz et al. 2005).

As the convective flow in porous media has been an active area of research for few decades, there are several excellent reviews of convection in porous media, such as, Ingham and Pop (2005), Nield and Bejan (2013), Pop and Ingham (2001), Straughan (2008), Vadasz (2008) and Vafai (2005, 2010). The convective instabilities of a thermally stratified, saturated porous media with through flow were examined by Homsy and Sherwood (1976). A comprehensive stability theory has been provided for the net fluid discharge through a medium which was heated uniformly from below. Hewitt et al. (2013) studied the stability of a density-driven heat exchanger flow in a porous medium. They explored the controlling mechanism for which the convective flow in a porous medium demonstrates quasi-steady columnar structure relating to a well-defined Rayleigh number dependent horizontal scale. Rees and Genç (2011) have performed a linear stability analysis for revealing the onset of convection in a horizontally partitioned porous layer heated from below. Moreover, Banu and Rees (2002) investigated the onset of convection in a porous layer heated from below. They have conducted both numerical and asymptotic analysis to determine the modified criterion for the onset of convection in the presence of the thermal non-equilibrium between the solid and fluid phases.

Merkin and his group published a series of papers (Chaudhary and Merkin 1994, 1996; Merkin and Chaudhary 1994; Chaudhary et al. 1995; Mahmood and Merkin 1998; Merkin and Mahmood 1998) on the free convection boundary layers driven by surface reaction (Chaudhary and Merkin 1994, 1996; Merkin and Chaudhary 1994; Chaudhary et al. 1995) as well as the convective boundary-layer flow on reactive surfaces in porous media (Mahmood and Merkin 1998; Merkin and Mahmood 1998). Chaudhary and Merkin (1994, 1996), Merkin and Chaudhary (1994) and Chaudhary et al. (1995) considered the free convection boundary-layer flow near a stagnation point. Due to catalytic surface reaction, the flow in the boundary layer is mainly driven by free convection. Chaudhary and Merkin (1994) presented analytic expressions for the bifurcation points while multiple solutions are recognized within the range of parameter values which lies below the critical points. Besides the subsequent study (Chaudhary and Merkin 1996) focuses on the heat release parameter and the time evolution for the solution after the heat release parameter exceeds its critical value. The convective boundary-layer flow in a fluid-saturated porous medium was investigated by Mahmood and Merkin (1998) and Merkin and Mahmood (1998) where the heat released from the catalytic surface reaction causes convective flow. Merkin and Mahmood (1998) observed multiple solution branches and critical points for stable and unstable solutions. Moreover, Minto et al. (1998) theoretically analyzed the steady free convection, driven by catalytic surface reaction, along a vertical flat surface placed in a fluid-saturated porous media.

A few years ago, Postelnicu (2009) examined the onset of convection in a horizontal fluid-saturated porous layer. In the problem the upper wall was maintained at uniform temperature and concentration while an exothermic surface reaction is assumed to occur on the lower wall. The influences of three reaction parameters and the Lewis number on the critical Rayleigh and wave numbers at the commencement of convection were presented numerically. Scott and Straughan (2011) revisited the problem of Postelnicu (2009). Having found several misprints in Postelnicu (2009), they have again developed the basic equations of the problem. Numerical results demonstrated oscillatory convection when the reaction parameter B defined by Postelnicu (2009) exceeds a critical value. Scott (2012a) also examined the same problem taking into account the effects of higher derivatives of the velocity for a high porosity porous medium. In order to investigate the convection in highly porous media Brinkman equation was used instead of Darcy equation. The effects of the boundary condition parameters and the Brinkman term on the stability curves are discussed. Scott (2012b) studied the influences of Soret coefficient on the convection in a saturated porous medium with the variation of boundary parameters and Lewis number. In contrast to the previous studies the nonlinear stability bounds for a horizontal layer of a Darcy porous medium have been determined using the energy method (Scott 2013a). Besides Scott and Straughan (2013) examined the continuous dependence of the solution on the coefficients of the reaction terms for the convection of Brinkman type porous medium. Later, Scott (2013b) investigated the similar problem considered by Scott and Straughan (2013) for a porous medium of Darcy type. However it was mathematically much harder than the problem of Scott and Straughan (2013) as the momentum equation is of lower order. Although Scott (2012a) claims that the catalytic surface reaction may create high temperature on the surface but the surface radiation was not included in the model. In addition, it worthy of mentioning that the previous studies (Postelnicu 2009; Scott 2012a; Scott and Straughan 2011; Scott 2012b, 2013a) performed numerical simulation in determining the critical wave number and the critical Rayleigh number which is generally difficult to carry out for anybody.

In this study, a new theory is proposed to identify the characteristics of the critical wave number and the critical Rayleigh number at the onset of convection. We consider the model developed by Postelnicu (2009) taking into account the effect of surface radiation. It is noted that the heat released from the exothermic surface reaction is transferred to the fresh reactant by conduction and radiation. Recently, Roy et al. (2014) showed that the radiative heat transfer is one of the controlling mechanisms of the propagation of reaction front and it could be extinguished due to higher radiative heat transfer from the porous medium. Accordingly, it seems that the surface radiation can significantly affect the onset of the convection in a porous medium and hence modify the stability criterion. Thus the objective of this study is to provide a comprehensive idea about the controlling mechanisms for the stability of the convection process in a porous medium. The effects of the heat release parameter, the mass diffusion parameter, the activation energy parameter and the conduction–radiation parameter on the critical wave number and the critical Rayleigh number are presented.

2 Formulation of the Problem

A horizontal layer of Darcy type porous material is considered for the present problem. It is filled with an incompressible, viscous and non-isothermal fluid. The schematic of the geometry of the problem is shown in Fig. 1. We assume that the upper wall is kept at uniform temperature and concentration; however, there occurs exothermic surface reaction on the lower wall. Due to high temperature, surface radiation is also included into it. With a view to simplifying the problem, it is assumed that the reactant P is directly converted to an inert product W following a single-step exothermic Arrhenius type surface reaction

$$\begin{aligned} P\rightarrow W+\hbox {heat},\quad \hbox {rate}=k_0 C\exp \left( {-\frac{E}{R^{*}T}} \right) . \end{aligned}$$

(1)

Here $k_{0}$ is the pre-exponential factor assumed to be constant, $R^{*}$ is the universal gas constant, E is the activation energy, T is the temperature and C is the concentration of the reactant P which is dissolved within the convective fluid. It is worthwhile to note that this single-step reaction model can describe the combustion process (Postelnicu 2009; Scott 2012a, b; Chaudhary and Merkin 1994, 1996; Merkin and Chaudhary 1994; Chaudhary et al. 1995; Mahmood and Merkin 1998; Merkin and Mahmood 1998; Scott and Straughan 2011). When the surface reaction takes place on the lower wall, heat is released to the system. Because of the temperature differences it causes a convective flow near the surface which creates a vacuum of fresh reactant there. Then the unburned reactant will immediately be present there penetrating through the porous material. Accordingly there occurs an interaction between the convective flow, heat transfer and mass transport of the reactant.

Fig. 1

Schematic of the geometry of the problem

We assume that the porous medium embedded in a fluid occupies the infinite layer $\left\{ {\left( {\bar{{x}},\bar{{z}}} \right) \in {\mathbb {R}}^{2}} \right\} \times \left\{ {\bar{{y}}\in \left( {0,h} \right) } \right\} ,$ where h is the depth of the layer, $\bar{{x}}$ and $\bar{{z}}$ are horizontal coordinates and $\bar{{y}}$ is the vertical coordinate. Under the Boussinesq approximation, the governing equations, as set out by Rees (2000) and Scott and Straughan (2011), are

$$\begin{aligned}&\displaystyle \frac{\partial \bar{{u}}}{\partial \bar{{x}}}+\frac{\partial \bar{{v}}}{\partial \bar{{y}}}+\frac{\partial \bar{{w}}}{\partial \bar{{z}}}=0 \end{aligned}$$

(2)

$$\begin{aligned}&\displaystyle \left( {\bar{{u}},\bar{{v}},\bar{{w}}} \right) =-\frac{K}{\mu }\nabla \bar{{p}}+\frac{\rho g\beta K\left( {T-T_{\mathrm{r}} } \right) }{\mu }\left( {0,1,0} \right) \end{aligned}$$

(3)

$$\begin{aligned}&\displaystyle \frac{1}{M}\frac{\partial T}{\partial \bar{{t}}}+\bar{{u}}\frac{\partial T}{\partial \bar{{x}}}+\bar{{v}}\frac{\partial T}{\partial \bar{{y}}}+\bar{{w}}\frac{\partial T}{\partial \bar{{z}}}=\kappa \left( {\frac{\partial ^{2}T}{\partial \bar{{x}}^{2}}+\frac{\partial ^{2}T}{\partial \bar{{y}}^{2}}+\frac{\partial ^{2}T}{\partial \bar{{z}}^{2}}} \right) \end{aligned}$$

(4)

$$\begin{aligned}&\displaystyle \phi \frac{\partial C}{\partial \bar{{t}}}+\bar{{u}}\frac{\partial C}{\partial \bar{{x}}}+\bar{{v}}\frac{\partial C}{\partial \bar{{y}}}+\bar{{w}}\frac{\partial C}{\partial \bar{{z}}}=\phi D\left( {\frac{\partial ^{2}C}{\partial \bar{{x}}^{2}}+\frac{\partial ^{2}C}{\partial \bar{{y}}^{2}}+\frac{\partial ^{2}C}{\partial \bar{{z}}^{2}}} \right) \end{aligned}$$

(5)

where $\bar{{u}}, \bar{{v}} \text { and } \bar{{w}}$ are the velocity components in the $\bar{{x}}, \bar{{y}} \text { and } \bar{{z}}$ directions, $\mu$ and K are the fluid’s dynamic viscosity and the permeability of the porous medium, $\rho$ and $\bar{{p}}$ are the reference density and pressure, g is the acceleration due to gravity, $\beta$ is the coefficient of thermal expansion, $T_{\mathrm{r}}$ is the reference temperature, $\kappa = k_{m}/(\rho \hbox {c})_{f}$ is the thermal diffusivity of the porous medium where $k_m =\kappa _T \left( {1-\phi } \right) +\kappa _f \phi ,\kappa _{T}$ and $\kappa _{f}$ are respectively the thermal conductivities of the surface and fluid, $\phi$ is the porosity of the medium, D is the diffusivity of the reactant and

$$\begin{aligned} M=\frac{\left( {\rho c} \right) _f }{\left( {1-\phi } \right) \left( {\rho c} \right) _s +\phi \left( {\rho c} \right) _f} \end{aligned}$$

(6)

is the heat capacity ratio of the fluid to that of the medium.

The system of Eqs. (2)–(5) are nondimensionalized using the following transformations

$$\begin{aligned} x= & {} \frac{\bar{{x}}}{h}, y=\frac{\bar{{y}}}{h}, z=\frac{\bar{{z}}}{h}, t=\frac{M\kappa }{h^{2}}\bar{{t}}, u=\frac{\kappa }{h}\bar{{u}}, v=\frac{\kappa }{h}\bar{{v}}, w=\frac{\kappa }{h}\bar{{w}}, \nonumber \\ \theta= & {} \frac{E}{R^{{*}}T_{\mathrm{r}}^2 }\left( {T-T_{\mathrm{r}} } \right) , \varphi =\frac{C}{C_\mathrm{r} }. \end{aligned}$$

(7)

where $C_\mathrm{r}$ is the reference concentration.

Thus we have

$$\begin{aligned}&\displaystyle \frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}=0 \end{aligned}$$

(8)

$$\begin{aligned}&\displaystyle \left( {u,v,w} \right) =-\nabla p+Ra\left( {0,\theta ,0} \right) \end{aligned}$$

(9)

$$\begin{aligned}&\displaystyle \frac{\partial \theta }{\partial t}+u\frac{\partial \theta }{\partial x}+v\frac{\partial \theta }{\partial y}+w\frac{\partial \theta }{\partial z}=\frac{\partial ^{2}\theta }{\partial x^{2}}+\frac{\partial ^{2}\theta }{\partial y^{2}}+\frac{\partial ^{2}\theta }{\partial z^{2}} \end{aligned}$$

(10)

$$\begin{aligned}&\displaystyle M\phi \frac{\partial \varphi }{\partial t}+u\frac{\partial \varphi }{\partial x}+v\frac{\partial \varphi }{\partial y}+w\frac{\partial \varphi }{\partial z}=\frac{1}{Le}\left( {\frac{\partial ^{2}\varphi }{\partial x^{2}}+\frac{\partial ^{2}\varphi }{\partial y^{2}}+\frac{\partial ^{2}\varphi }{\partial z^{2}}} \right) \end{aligned}$$

(11)

where $Le=\kappa /{\left( {\phi D} \right) }$ is the Lewis number and Ra is the Rayleigh number defined as

$$\begin{aligned} Ra=\frac{\rho g\beta Kh}{\mu \kappa }\frac{R^{{*}}T_{\mathrm{r}}^2 }{E}. \end{aligned}$$

Following Rees (2000), the onset of two-dimensional disturbances can be elucidated by defining the stream function $\psi$ as

$$\begin{aligned} u=-\frac{\partial \psi }{\partial y}, v=\frac{\partial \psi }{\partial x} \end{aligned}$$

(12)

and taking $w = 0$.

Using the relations (12), equations in (9) can be combined as

$$\begin{aligned} \frac{\partial ^{2}\psi }{\partial x^{2}}+\frac{\partial ^{2}\psi }{\partial y^{2}}=Ra\frac{\partial \theta }{\partial x} \end{aligned}$$

(13)

Thus, Eqs. (10) and (11) reduce to

$$\begin{aligned} \frac{\partial \theta }{\partial t}+\frac{\partial \psi }{\partial x}\frac{\partial \theta }{\partial y}-\frac{\partial \psi }{\partial y}\frac{\partial \theta }{\partial x}= & {} \frac{\partial ^{2}\theta }{\partial x^{2}}+\frac{\partial ^{2}\theta }{\partial y^{2}} \end{aligned}$$

(14)

$$\begin{aligned} M\phi \frac{\partial \varphi }{\partial t}+\frac{\partial \psi }{\partial x}\frac{\partial \varphi }{\partial y}-\frac{\partial \psi }{\partial y}\frac{\partial \varphi }{\partial x}= & {} \frac{1}{Le}\left( {\frac{\partial ^{2}\varphi }{\partial x^{2}}+\frac{\partial ^{2}\varphi }{\partial y^{2}}} \right) \end{aligned}$$

(15)

On the upper wall, the temperature and reactant concentration are assumed to be constant and no slip boundary condition is there. Thus the boundary conditions are

$$\begin{aligned} T=T_{\mathrm{r}} , C=C_\mathrm{r} , \bar{{v}}=0\; \text { on } \bar{{y}}=h \end{aligned}$$

(16)

However, on the lower wall the heat and mass are transferred from the surface into the surrounding fluid-porous medium by conduction and diffusion, respectively. It is also assumed that there takes place surface radiation owing to high temperature experienced by surface reaction. Therefore, the boundary conditions on the lower wall, according to Song et al. (1991), Postelnicu (2009), Scott (2012a) and Caram and Amundson (1977), are

$$\begin{aligned} \bar{{v}}=0, \;\;\kappa _T \frac{\partial T}{\partial \bar{{y}}}=-Qk_0 C\exp \left( {-\frac{E}{R^{*}T}} \right) -\chi \sigma \left( {T^{4}-T_{\mathrm{r}}^4 } \right) ,\;\; D\frac{\partial C}{\partial \bar{{y}}}=k_0 C\exp \left( {-\frac{E}{R^{*}T}} \right) \end{aligned}$$

(17)

where $\chi$ is the emissivity of the surface, Q is the heat of the reaction and $\sigma$ is the Stefan–Boltzman constant.

Now the boundary conditions (16) and (17) combined with the relations (7) and (12) take the form

$$\begin{aligned} \psi= & {} 0, \frac{\partial \theta }{\partial y}=-A\varphi \exp \left( {\frac{\theta }{1+\varepsilon \theta }} \right) +R_d \left\{ {\left( {1+\varepsilon \theta } \right) ^{4}-1} \right\} ,\nonumber \\ \frac{\partial \varphi }{\partial y}= & {} B\varphi \exp \left( {\frac{\theta }{1+\varepsilon \theta }} \right) \text { on }y = 0 \end{aligned}$$

(18)

$$\begin{aligned} \psi= & {} 0,\; \theta =0,\; \varphi =1\; \text { on }y = 1. \end{aligned}$$

(19)

where the dimensionless parameters are defined by

$$\begin{aligned} A=\frac{Qk_0 C_0 h}{\kappa _T }.\frac{E}{R^{{*}}T_{\mathrm{r}}^2 },\; B=\frac{k_0 h}{D},\; \varepsilon =\frac{R^{{*}}T_{\mathrm{r}}^2 }{E},\; R_d =\frac{\chi \sigma T_{\mathrm{r}}^3 h}{\kappa }. \end{aligned}$$

(20)

Here A is the heat release parameter, B is the mass diffusion parameter, $\varepsilon$ is the activation energy parameter and $R_{d}$ is the conduction–radiation parameter.

3 Linear Stability Theory

3.1 Basic State Solution

We assume that the basic state variables are indicated by subscript b. It is well known that the basic state is determined by $\partial /\partial {t} = 0$ and the velocity components are zero. Accordingly, we can immediately take the solutions for velocity components and stream function as $u_{b}=v_{b} = {\psi }_{b} = 0$. However the boundary conditions for temperature and concentrations suggest that the linear solutions for temperature and concentration could be of the form

$$\begin{aligned} \theta _b =\beta _1 y+\beta _2 ,\; \varphi _b =\beta _3 y+\beta _4 . \end{aligned}$$

(21)

The constants $\beta _{1}$, $\beta _{2}$, $\beta _{3}$ and $\beta _{4}$ are obtained by applying the boundary conditions (18) and (19).

Using the relations (21) into (18) and (19), we find

$$\begin{aligned} \beta _1= & {} -A\beta _4 \exp \left( {\frac{\beta _2 }{1+\varepsilon \beta _2 }} \right) +R_d \left\{ {\left( {1+\varepsilon \beta _2 } \right) ^{4}-1} \right\} , \nonumber \\ \beta _3= & {} B\beta _4 \exp \left( {\frac{\beta _2 }{1+\varepsilon \beta _2 }} \right) \end{aligned}$$

(22)

$$\begin{aligned} \beta _1 +\beta _2= & {} 0, \beta _3 +\beta _4 =1. \end{aligned}$$

(23)

Eliminating the constants $\beta _{2}$, $\beta _{3}$ and $\beta _{4}$ from Eqs. (22) and (23), we obtain the equation

$$\begin{aligned}&\beta _1 +\left( {A+\beta _1 B} \right) \exp \left( {-\frac{\beta _1 }{1-\varepsilon \beta _1 }} \right) \nonumber \\&\quad +\,R_d \left\{ {\left( {1-\varepsilon \beta _1 } \right) ^{4}-1} \right\} \left[ {1+B\exp \left( {-\frac{\beta _1 }{1-\varepsilon \beta _1 }} \right) } \right] =0. \end{aligned}$$

(24)

For fixed values of A, B, $\varepsilon$ and $R_{d}$, Eq. (24) gives the solution for $\beta _{1}$. It subsequently yields the solutions of $\beta _{2}, \beta _{3}$ and $\beta _{4}$.

3.2 Stability Analysis

In order to find the perturbed solutions, we superimpose small perturbations on the basic state (Nield and Bejan 2013; Banu and Rees 2002; Chandrasekhar 1961; Drazin and Reid 2004) so that the quantities $\psi$, $\theta$ and $\varphi$ are expressed as

$$\begin{aligned} \psi =\Psi , \theta =\theta _b +\Theta \text { and } \varphi =\varphi _b +\Phi \end{aligned}$$

(25)

where $\Psi$, $\Theta$ and $\Phi$ are taken to be $\left| \Psi \right|<<1, \left| \Theta \right|<<1 \text { and } \left| \Phi \right|<<1.$

Substituting (25) into (13)–(15) and using (21), we obtain the linearized stability problem as

$$\begin{aligned} \frac{\partial ^{2}\Psi }{\partial x^{2}}+\frac{\partial ^{2}\Psi }{\partial y^{2}}= & {} Ra\frac{\partial \Theta }{\partial x} \end{aligned}$$

(26)

$$\begin{aligned} \frac{\partial \Theta }{\partial t}+\beta _1 \frac{\partial \Psi }{\partial x}= & {} \frac{\partial ^{2}\Theta }{\partial x^{2}}+\frac{\partial ^{2}\Theta }{\partial y^{2}} \end{aligned}$$

(27)

$$\begin{aligned} \frac{\partial \Phi }{\partial t}+\beta _3 \frac{\partial \Psi }{\partial x}= & {} \frac{1}{Le}\left( {\frac{\partial ^{2}\Phi }{\partial x^{2}}+\frac{\partial ^{2}\Phi }{\partial y^{2}}} \right) . \end{aligned}$$

(28)

The corresponding boundary conditions are

$$\begin{aligned} \Psi= & {} 0, \frac{\partial \Theta }{\partial y}=-A\Phi \exp \left( {\frac{\Theta }{1+\varepsilon \Theta }} \right) +R_d \left\{ {\left( {1+\varepsilon \Theta } \right) ^{4}-1} \right\} , \nonumber \\ \frac{\partial \Phi }{\partial y}= & {} B\Phi \exp \left( {\frac{\Theta }{1+\varepsilon \Theta }} \right) \text { on }y = 0 \end{aligned}$$

(29)

$$\begin{aligned} \Psi= & {} 0, \Theta =0, \Phi =0 \text { on } y = 1. \end{aligned}$$

(30)

Since $\left| \Psi \right|<<1, \left| \Theta \right|<<1 \text { and } \left| \Phi \right|<<1,$ the boundary conditions (29) and (30) can be linearized as

$$\begin{aligned} \Psi= & {} 0, \frac{\partial \Theta }{\partial y}=-A\Phi , \frac{\partial \Phi }{\partial y}=B\Phi \text { on } y = 0 \end{aligned}$$

(31)

$$\begin{aligned} \Psi= & {} 0, \Theta =0, \Phi =0 \text { on }y = 1. \end{aligned}$$

(32)

We now seek the solutions for $\Psi$, $\Theta$ and $\Phi$ in the following form, as considered by Postelnicu (2009),

$$\begin{aligned} \Psi= & {} \mathrm{e}^{\lambda t}f\left( y \right) \cos kx \end{aligned}$$

(33)

$$\begin{aligned} \Theta= & {} \mathrm{e}^{\lambda t}g\left( y \right) \sin kx \end{aligned}$$

(34)

$$\begin{aligned} \Phi= & {} \mathrm{e}^{\lambda t}h\left( y \right) \sin kx \end{aligned}$$

(35)

where $\lambda$ is the exponential growth rate and k is the wave number of the disturbance.

Substituting (33)–(35) into (26)–(28), we obtain the system of ordinary differential equations

$$\begin{aligned}&\displaystyle {f}''-k^{2}f-kRag=0 \end{aligned}$$

(36)

$$\begin{aligned}&\displaystyle {g}''-\left( {k^{2}+\lambda } \right) g+\beta _1 kf=0 \end{aligned}$$

(37)

$$\begin{aligned}&\displaystyle {h}''-\left( {k^{2}+\lambda Le} \right) h+Le\beta _3 kf=0 \end{aligned}$$

(38)

subject to the boundary conditions

$$\begin{aligned} f\left( 0 \right)= & {} 0, {g}'\left( 0 \right) =-Ah\left( 0 \right) , {h}'\left( 0 \right) =Bh\left( 0 \right) \end{aligned}$$

(39)

$$\begin{aligned} f\left( 1 \right)= & {} 0, g\left( 1 \right) =0, h\left( 0 \right) =0. \end{aligned}$$

(40)

Equations (36)–(38) form an eigenvalue problem for $\lambda$ in terms of k and Ra. It should be mentioned that the previous studies (Postelnicu 2009; Scott 2012a, b; Scott and Straughan 2011) computed the critical Rayleigh number numerically using a traditional shooting method (Postelnicu 2009), the natural D Chebyshev–Tau method (Scott 2012a, b) and both D and $D^{2}$ Chebyshev–Tau methods (Scott and Straughan 2011). Of course, the methods are not only difficult to implement for anybody but also time consuming and troublesome task when it is required to find a lot of data with the variations of a few parameters. Accordingly, a new theory is proposed to determine the critical wave number and the critical Rayleigh number from the above-mentioned eigenvalue problem. Details of the theory are described below.

4 Theoretical Approach for Determining the Critical Wave Number and the Critical Rayleigh Number

As the system of Eqs. (36)–(38) cannot be solved analytically, we consider the solution for f(y) to be of the form

$$\begin{aligned} f\left( y \right) =C\sin \left( {\pi y} \right) \end{aligned}$$

(41)

which satisfies the boundary conditions $f (0) = 0$ and $f (1) = 0$. Here the constant C is the amplitude of f and may be taken an arbitrary value.

Solving Eqs. (37) and (38) combined with (41) and using the boundary conditions, we find

$$\begin{aligned}&g\left( y \right) =\frac{Ce^{-\gamma y}k\pi \Gamma \left( {\mathrm{e}^{2\gamma }-\mathrm{e}^{2\gamma y}} \right) +\beta _1 \left( {\mathrm{e}^{\gamma y}+\mathrm{e}^{\gamma \left( {2+y} \right) }} \right) \gamma \left( {B\chi _1 +\chi _2 \delta \sqrt{Le}} \right) \left( {Le\delta ^{2}+\pi ^{2}} \right) \sin \left( {\pi y} \right) }{\left( {1+\mathrm{e}^{2\gamma }} \right) \gamma \left( {B\chi _1 +\chi _2 \delta \sqrt{Le}} \right) \left( {\gamma ^{2}+\pi ^{2}} \right) \left( {Le\delta ^{2}+\pi ^{2}} \right) } \nonumber \\ \end{aligned}$$

(42)

$$\begin{aligned}&h\left( y \right) \nonumber \\&\quad =\frac{\beta _3 Ce^{-\delta \sqrt{Le}y}kLe\left\{ {\left( {\mathrm{e}^{2\delta \sqrt{Le}}-\mathrm{e}^{2\delta \sqrt{Le}y}} \right) \pi +\mathrm{e}^{\delta \sqrt{Le}y}\left( {B\chi _1 +\chi _2 \delta \sqrt{Le}} \right) \sin \left( {\pi y} \right) } \right\} }{\left( {B\chi _1 +\chi _2 \delta \sqrt{Le}} \right) \left( {Le\delta ^{2}+\pi ^{2}} \right) } \end{aligned}$$

(43)

where

$$\begin{aligned} \Gamma= & {} A\beta _3 \chi _1 Le\left( {\gamma ^{2}+\pi ^{2}} \right) +\beta _1 \left( {Le\delta ^{2}+\pi ^{2}} \right) \left( {B\chi _1 +\chi _2 \delta \sqrt{Le}} \right) , \\ \gamma= & {} \sqrt{k^{2}+\lambda }, \delta =\sqrt{k^{2}+\lambda Le}, \chi _1 =-1+\mathrm{e}^{2\delta \sqrt{Le}} \text { and } \chi _2 =1+\mathrm{e}^{2\delta \sqrt{Le}}. \end{aligned}$$

Substituting the relations (41) and (42) into (36), we obtain an expression for the Rayleigh number, Ra, as

$$\begin{aligned}&r\left( {k,y} \right) \nonumber \\&\quad =-\frac{\mathrm{e}^{\gamma y}\left( {1+\mathrm{e}^{2\gamma }} \right) \gamma \left( {B\chi _1 +\chi _2 \delta \sqrt{Le}} \right) \left( {k^{2}+\pi ^{2}} \right) \left( {\gamma ^{2}+\pi ^{2}} \right) \left( {Le\delta ^{2}+\pi ^{2}} \right) }{k^{2}\pi \Gamma \left( {\mathrm{e}^{2\gamma }-\mathrm{e}^{2\gamma y}} \right) +\beta _1 \gamma \left\{ {\mathrm{e}^{\gamma y}+\mathrm{e}^{\gamma \left( {2+y} \right) }} \right\} \left( {B\chi _1 +\chi _2 \delta \sqrt{Le}} \right) \left( {Le\delta ^{2}+\pi ^{2}} \right) \sin \left( {\pi y} \right) }\qquad \end{aligned}$$

(44)

which is to be minimized for the wave number k while the value of y is kept fixed.

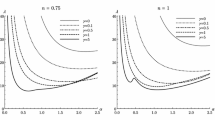
It is known that $\lambda = 0$ corresponds to marginal stability or neutral stability which implies that the disturbance neither grows nor decays. In this study, the marginal stability (i.e., when $\lambda = 0$) is our main concern. Before going into details of the method considered here, the variations of the Rayleigh number, $r\left( {k,y} \right)$, owing to change the wave number, k, for different values of y are shown in Fig. 2. It is seen that for a fixed value of y there is a minimum Rayleigh number corresponding to a wave number. Results indicate that both the minimum Rayleigh number and its wave number increase with increasing values of y and finally they tend to asymptotic values. It is due to the fact that the minimum Rayleigh number and the corresponding wave number for $y = 0.8$ and $y = 0.99$ are almost equal.

Fig. 2

Variations of r(k, y) against k for different values of $y=y_{i} (i = 1, 2,{\ldots },9)$ while $A = 1.0, B = 1.0$, $\varepsilon = 0.5$, Le = 0.1 and $R_{d} = 0.05$

Fig. 3

Variation of $(k_{c})_{i}$ and $({ Ra}_{c})_{i}$ for y while Le = 0.1 and $R_{d} = 0.05$

Based on the above discussion, it can be concluded that there is a minimum Rayleigh number for a wave number while keeping y fixed. So, for a fixed value of $y =y_{0}$, the wave number k = $(k_{c})_{0}$ at which the minimum value of r(k, $y_{0})$ occurs is found by solving the equation ${\mathrm{d}r}/{\mathrm{d}k}=0$ for k. The minimum value of r(k, $y_{0})$ is then easily determined by $r((k_{c})_{0}$, $y_{0})$. Similarly, we find the wave numbers $k = (k_{c})_{i}$ and $({ Ra}_{c})_{i}=r((k_{c})_{i}, y_{i})$ for $y_{i}=y_{i-1} + { dy} (i = 1, 2,{\ldots },n$) with ${ dy} = 0.01$. It is noteworthy that the value of $y_{i}$ is chosen in the interval $0< y_{i} <1\;\hbox {for}\; i = 0, 1, 2,{\ldots }, n$. Figure 3 illustrates the variations of $(k_{c})_{i}$ and $({ Ra}_{c})_{i}$ against y for different values of the parameters A, B and $\varepsilon$ while Le = 0.1 and $R_{d} = 0.05$ are fixed. It is found that both the minimum Rayleigh number and its corresponding wave number increase with y and reach their asymptotic values as $y\rightarrow 1$. When the heat release parameter, A, is increased (solid and dash–dot curves),the wave number $(k_{c})_{i}$ remains almost same;however, the minimum Rayleigh number $({ Ra}_{c})_{i}$ decreases. On the other hand, with an increase in the mass diffusion parameter, B, (dash–dot and dash–dot–dot curves) the wave number $(k_{c})_{i}$ is lower for $y <0.23$ and after that it becomes higher. But the minimum Rayleigh $({ Ra}_{c})_{i}$ number is higher for larger B. In addition, the minimum Rayleigh number $({ Ra}_{c})_{i}$ decreases and the wave number $(k_{c})_{i}$ remains more or less unchanged owing to the increase in the activation energy parameter, $\varepsilon$, (dashed and dash–dot–dot curves).

Table 1 A comparison of critical wave number and Rayleigh number for $\varepsilon = 0.5$ and different values of A, B and Le

Table 2 A comparison of critical Rayleigh number for different values of A, B, $\varepsilon$ and Le

Finally, the average wave number and the average Rayleigh number defined below are, respectively, considered to be the critical wave number and the critical Rayleigh number at the onset of convection

$$\begin{aligned} k_c =\frac{1}{n}\sum _{i=1}^n {\left( {k_c } \right) _i } \text { and }Ra_c =\frac{1}{n}\sum _{i=1}^n {r\left( {\left( {k_c } \right) _i ,y_i } \right) } \end{aligned}$$

(45)

Fig. 4

Variations of ${\vert }{\beta }_{1}{\vert }$ and $\beta _{3}$ with A for different $R_{d}$ while $B = 1.0$, $\varepsilon = 0.5$ and ${ Le} = 0.1$

In order to validate the definitions of the critical wave number, $k_{c}$, and the critical Rayleigh number, ${ Ra}_{c}$, a comparison is made in Tables 1 and 2 for different values of A, B and $\varepsilon$ taking Le = 0.1 and 1.0. It is evident from Tables 1 and 2 that when Le = 0.1 the results obtained by the present theory gives a good agreement with the results of Postelnicu (2009). But there is discrepancy between the present results for Le = 1.0 and those of Postelnicu (2009). It seems that the numerical methods (shooting and maple) used by Postelnicu (2009) could not predict the results accurately when the Lewis number is ${\ge }1$. This can be understood from the results of Postelnicu (2009) for $A = 0.5$, $B = 0.5$ and Le = 1.0 tabulated in Table 1 which shows that the critical wave numbers and Rayleigh numbers obtained by Postelnicu (2009) using two different methods (i.e., shooting method and maple) demonstrate a significant discrepancy compared to those for Le = 0.1. Moreover, it is well known that the shooting method highly depends on the guess value. In a future study, the model developed by Scott and Straughan (2011) will be considered and validated by the present method.

5 Results and Discussion

Now we are in a position to discuss the stability of convection with the help of the above expression (45) for Rayleigh number. It is also seen that some of the results obtained below using the present theory conform the tendency to available results.

The variations of ${\vert }{\beta }_{1}{\vert }$ and $\beta _{3}$ in terms of the heat release parameter, A, and for different conduction–radiation parameter, $R_{d}$, are shown in Fig. 4. When $R_{d}$ = 0.0, both of ${\vert }{\beta }_{1}{\vert }$ and $\beta _{3}$ are found to increase with larger values of A. It is clear from Eq.  (21) that the unknown parameters $\beta _{1}$ and $\beta _{3}$ represent the thermal and concentration gradients. Also the heat release parameter A is involved between the thermal gradient $\beta _{1}$ and the concentration gradient $\beta _{3}$ by the relations (22), that is, by $\beta _1 =-{A \beta _3 }/B$. It reveals that the value of the thermal gradient ${\vert }{\beta }_{1}{\vert }$ increases linearly with the heat release parameter A and ${\vert }{\beta }_{1}{\vert }$ tends to 0 as $A \rightarrow$0. On the other hand, since ${\vert }{\beta }_{1}{\vert }$ increases from 0 when A is increased from 0 hence the value of $\beta _{3} = -{ B} \beta _{1}/A$ gradually increases from 0 with proportional to $\beta _{1}/A$ and attains a value 0.535402 at $A = 5.0$. These results imitate the findings of Postelnicu (2009) and Scott (2012a). Now for $R_{d} \ne 0.0$ the lower branch curves (solid lines) are found to increase with higher values of A, while the upper branch curves (dashed lines) decrease with A. So there exist two types of solutions, namely stable and unstable. Recently, Roy et al. (2014) demonstrate the similar types of solutions for opposed flow combustion of solid fuel over an inert porous medium. From the past studies, it can be concluded that the lower branch corresponds to stable solutions while the upper branch corresponds to unstable solutions. Even one might have no idea of what are stable solutions; it is noteworthy that if A is increased from 0, one could easily find stable solutions for $\beta _{1}$ from the Eq. (24) by assuming any initial value. Since the stable solutions describe the physical phenomena, the main focus of interest is the behavior of lower branch. Now the values of ${\vert }{\beta }_{1}{\vert }$ and $\beta _{3}$ relating to $R_{d}\ne 0.0$ are always higher than those for $R_{d} = 0.0$. Their increasing rates are also changed with A and for a certain value of A the tangents to the curves of ${\vert }{\beta }_{1}{\vert }$ and $\beta _{3}$ are perpendicular to the axis of A. Accordingly there exists a turning point at which a tail is attached. The turning points for $R_{d} = 0.05$, 0.10, and 0.15 occur at $A = 1.73, 0.96$, and 0.60, respectively.

The effects of varying the mass diffusion parameter, B, on the parameters ${\vert }{\beta }_{1}{\vert }$ and $\beta _{3}$ are demonstrated in Fig. 5. Results show that when $R_{d} = 0.0$ and B is increased from 0, the value of ${\vert }{\beta }_{1}{\vert }$ decreases but $\beta _{3}$ is found to increase. In case of $R_{d} \ne 0$, both stable and unstable solutions are recognized and the upper branch curves (dashed lines) represent the stable solutions. For a fixed value of A, $\varepsilon$ and $R_{d}$, there must be a minimum B for obtaining stable solutions and this minimum B indicates the turning point. Due to the increase in $R_{d}$, the turning points occur for higher value of B. It is noted that the turning points for $R_{d} = 0.05, 0.10$, and 0.15 are $B = 0.43$, 1.06, and 2.03 respectively.

Fig. 5

Variations of ${\vert }{\beta }_{1}{\vert }$ and $\beta _{3}$ with B for different $R_{d}$ while A = 1.0, $\varepsilon = 0.5$ and ${ Le} = 0.1$

Fig. 6

Variations of ${\vert }{\beta }_{1}{\vert }$ and $\beta _{3}$ with $\varepsilon$ for different $R_{d}$ while $A = 2.0$, $B = 1.0$ and Le = 0.1

Fig. 7

Effects of A on a the critical wave number and b the critical Rayleigh number for different $R_{d}$ while $B = 1.0, \varepsilon = 0.5$ and ${ Le} = 0.1$

Figure 6 depicts the variations of ${\vert }{\beta }_{1}{\vert }$ and $\beta _{3}$ with the change of $\varepsilon$ and for different $R_{d}$. Both stable and unstable solutions are determined. The lower branch curves (solid lines) represent the stable solutions. When $R_{d} = 0.0$, the parameters ${\vert }{\beta }_{1}{\vert }$ and $\beta _{3}$ slowly decreases owing to an increase of $\varepsilon$. Results also indicate that the concentration gradient $\beta _{3}$ corresponding to $R_{d} \ne 0$ first decreases and then increases with increasing values of $\varepsilon$ so long as the tangent to the curve of $\beta _{3}$ is perpendicular to the axis of $\varepsilon$. The thermal gradient ${\vert }{\beta }_{1}{\vert }$ also demonstrates the similar tendency of $\beta _{3}$ for $R_{d} = 0.05$ and 0.10. But for $R_{d} = 0.15$ it always increases with an increase of $\varepsilon$. It is observed that the larger values of $R_{d}$ reduce the turning points. It is seen that the turning points for $R_{d} = 0.05, 0.10$ and 0.15 are $\varepsilon = 0.46, 0.32$, and 0.26 respectively.

Figure 7a, b depict the effects of the heat release parameter A on the critical wave number, $k_{c}$, and the critical Rayleigh number, $R_{c}$, for different conduction–radiation parameter, $R_{d}$. For $R_{d} = 0.0$, Postelnicu (2009) and Scott (2012a) observed that the critical Rayleigh number decreases owing to an increase of A. The present result also confirms this finding. In addition, it is found from Fig. 7a that the critical wave number increases with higher values of A and with further increase of A, it slowly decreases and finally tends to an asymptotic value 2.69215 at A = 10.0. On the contrary, when $R_{d} \ne 0$ Fig. 7b shows that the upper branch (solid line) lying above the turning point upholds the similar tendency as for $R_{d} = 0$. In the lower branch (dashed line), the critical Rayleigh number gradually increases with A so long as it meets the upper branch. After that the rate of change of the critical Rayleigh number with respect to an increase in A is different from the previous rate so that it makes a tail (dashed line). In case of the critical wave number, it is evident from Fig. 7a that when the value of A is increased the upper branch (solid line) first increases and then decreases after attaining a maximum value. It is worthwhile to note that these striking characteristics are not reported yet in the literature available in this field. Under consideration of the previous findings (Postelnicu 2009; Scott 2012a, b), the upper branches are of physical interest. So the main concern has been paid to stable solutions. Results indicate that the increasing heat release parameter A reduces the critical Rayleigh number. The reason for such a reduction can be understood from the boundary condition $g'(0) = -{ Ah}(0)$ at the lower boundary. This reveals that when A is increased, heat is released from the boundary reaction at a higher rate. Consequently, the stationary convection is accelerated and destabilizes the system. Fig. 4 also supports this conclusion. It is because increasing A causes a more negative thermal gradient $\beta _{1}$ and a more positive concentration gradient $\beta _{3}$. This implies that the destabilizing effect increases but the stabilizing effect decreases. As the convection is due to the thermal gradient caused by the surface reaction, the increasing negative thermal gradient $\beta _{1}$ is tremendously destabilizing the system. Accordingly, the critical Rayleigh number, $R_{c}$, stops to decrease for a certain value of A. Moreover the critical Rayleigh number and the critical wave number are found to decrease with increasing values of $R_{d}$. The turning points for $R_{d} = 0.05$, 0.10 and 0.15 are at $A = 1.73, 0.96$ and 0.60. The critical wave number and the critical Rayleigh number for $R_{d} = 0.05$, 0.10, and 0.15 are (2.68456, 12.331), (2.68294, 20.2939) and (2.6815, 29.3269), respectively.

The influences of the mass diffusion parameter B on the critical wave number, $k_{c}$, and the critical Rayleigh number, $R_{c}$, for different conduction–radiation parameter, $R_{d}$, are shown in Fig. 8a, b. Results suggest that whatever be the value of $R_{d}$ both the critical wave number and the critical Rayleigh number decrease with decreasing values of B. For $R_{d} = 0.0$ they gradually decrease until B becomes 0. In case of $R_{d} \ne 0.0$, there must be a minimum B for which stability curves cease to decrease. The reason for such a characteristic might be clear from the Fig. 5. It shows that increasing B reduces negative thermal gradient $\beta _{1}$ and increases positive concentration gradient $\beta _{3}$. Consequently, the thermal gradient lessens the destabilizing effect while the concentration gradient reduces the stabilizing effect. A competitive consequence of these two effects is observed on the critical wave number and the critical Rayleigh number. Since the convection is mainly driven by the thermal gradient which is proportional to the surface reaction, it appears that the thermal gradient effect controls over the concentration gradient effect. Thus, for increasing the mass diffusion parameter B the resulting effect is stabilizing the system and causes an increase in the critical wave number and the critical Rayleigh number. On the contrary, when B is assumed to lower the destabilizing effect becomes increasingly prominent and the critical wave number and the critical Rayleigh number cease to decrease for a certain value of B. For $R_{d} = 0.05, 0.10$ and 0.15, the turning points are observed at $B = 0.43, 1.06$ and 2.03, respectively, where the critical wave number, $k_{c}$, and the critical Rayleigh number, $R_{c}$, are found to be (2.67909, 12.8376), (2.68332, 20.2434), and (2.68547, 28.5423) respectively.

Fig. 8

Effects of B on a the critical wave number and b the critical Rayleigh number for different $R_{d}$ while $A = 1.0, \varepsilon = 0.5$ and ${ Le} = 0.1$

Fig. 9

Effects of $\varepsilon$ on a the critical wave number and b the critical Rayleigh number for different $R_{d}$ while $A = 2.0$, $B = 1.0$ and ${ Le} = 0.10$

Figure 9a, b illustrates the effects of the activation energy parameter, $\varepsilon$, on the critical wave number, $k_{c}$, and the critical Rayleigh number, $R_{c}$, for different conduction–radiation parameter, $R_{d}$. It is evident from figures that when $R_{d}$ = 0.0 both the critical wave number and the critical Rayleigh number increase with increasing values of $\varepsilon$. However, for $R_{d} \ne 0.0$ the stability curves show completely different characteristics from $R_{d} = 0.0$. They are found to decrease exponentially so long as the tangents to the curves are perpendicular to the axis of $\varepsilon$. It can easily be understood from the boundary condition (29) that when $R_{d} \ne 0.0$ the heat released from the surface radiation is exponentially increasing for higher values of $\varepsilon$. It should be mentioned that no study has reported these results till now. For $R_{d} = 0.05, 0.10$ and 0.15, the turning points occur at $\varepsilon = 0.452, 0.318$, and 0.258, respectively, while the critical wave number and the critical Rayleigh number at these points are (2.6847, 10.4681), (2.68393, 9.21499) and (2.68356, 8.63032) respectively.

Fig. 10

Effects of $R_{d}$ on a the critical wave number and b the critical Rayleigh number

Figure 10a, b demonstrates the variations of the critical wave number, $k_{c}$, and the critical Rayleigh number, $R_{c}$, with the change of the conduction–radiation parameter, $R_{d}$. As the value of $R_{d}$ increases, the critical wave number and the critical Rayleigh number decrease. It is because increasing $R_{d}$ means heat is released more and more due to surface radiation from the bottom boundary which is destabilizing and hence reduces the critical Rayleigh number. When A is increased [(i) and (iii)], the critical wave number and the critical Rayleigh number becomes lower. But the converse characteristics are observed for increasing values of B [(i) and (ii)]. On the other hand, the critical wave number and the critical Rayleigh number increase with a decrease of $\varepsilon$ [(i) and (iv)].

Fig. 11

Effects of Le on a the critical wave number and b the critical Rayleigh number for different $R_{d}$ while $A = 1.0, B = 1.0 \text { and }\varepsilon = 0.5$

The effects of the Lewis number, Le, on the critical wave number, $k_{c}$, and the critical Rayleigh number, $R_{c}$, for different conduction–radiation parameter, $R_{d}$, are illustrated in Fig. 11a, b. Results indicate that irrespective of the values of $R_{d}$ the critical wave number and the critical Rayleigh number increase owing to increasing values of ${ Le} > 0$. When Le is further increased, both $k_{c}$ and $R_{c}$ slowly decrease attaining maximum values at ${ Le} = 3.1$ and 2.35 respectively. The result for $R_{d} = 0.0$ is similar to that of Scott (2012a). From the definition of Lewis number, ${ Le} = { \kappa /D}$, it is clear that the Lewis number would be increasingly higher when the diffusivity of the reactant, D, is increasingly lower or the thermal conductivity $\kappa$ is getting higher. As Le increases from a very small value the competing effect of these physical quantities becomes stronger and it is stabilizing the system up to some extent. With further increase in Le the destabilizing effect dominates over the stabilizing effect and consequently the stability curves are found to decrease. Moreover the critical wave number and the critical Rayleigh number decrease with an increase of $R_{d}$.

6 Conclusions

In this study, a new theory is developed to compute the critical wave number and the critical Rayleigh number at the onset of convection. We consider the convection in a horizontal layer of porous material. An Arrhenius type exothermic surface reaction and surface radiation take place on the lower wall while the upper wall is kept at uniform temperature and concentration. Results demonstrated that the new theory can predict the critical wave number and the critical Rayleigh number up to a great degree. It is found that the critical wave number and the critical Rayleigh number decrease for higher values of the conduction–radiation parameter. For stability of the convection in a porous medium, there must have a maximum value of it. Moreover, in the presence of surface radiation, we can draw the following conclusions:

• (i) When the heat release parameter is increased the critical Rayleigh number decreases, however, the critical wave number first increases and then decreases after the point of inflection. Also there is a maximum value of the heat release parameter which indicates the critical value for the stable convection in a porous medium.

• (ii) For decreasing values of the mass diffusion parameter, both the critical wave number and the critical Rayleigh number decrease. A minimum value of the mass diffusion parameter is required for the commencement of convection.

• (iii) The critical wave number and the critical Rayleigh number are found to decrease owing to increase of the activation energy parameter. The stability curves cease to decrease after a certain value of this parameter.

• (iv) When the Lewis number is increased from a small value, the critical wave number and the critical Rayleigh number increase and with further increase in the Lewis number they gradually decrease.