Effective Permeability of Heterogeneous Fractured Porous Media

Abstract

We compute the effective permeability of a model fractured porous medium in which rectangular fractures with finite thickness are distributed in the matrix with random orientations. The local permeability of the porous matrix is spatially distributed according to a fractional Brownian motion, which induces long-range correlations in the permeabilities. Using numerical solution of the Stokes’ equation, the effective macroscopic permeability is calculated as a function of a variety of factors, including the Hurst exponent that characterizes the type of the correlations, and the number density and width of the fractures. The results indicate that the correlations give rise to non-trivial effects on the effective permeability and that the assumption of a uniform matrix in a fractured porous medium leads to overall permeabilities that differ significantly from those in which the matrix is heterogeneous.

1 Introduction

Large-scale porous media, such as oil and gas reservoirs and groundwater resources, are often fractured (Adler and Thovert 1999; Sahimi 2011). Fossil fuel is currently the most important source of energy, and groundwater aquifers play a vital role in human life. At the same time, contamination of the aquifers and the threat that it poses have also come to the forefront of political and social debates. As a result, predicting flow and transport properties of such large-scale porous media has attracted great attention for decades (Barenblatt and Zheltov 1960; Barenblatt et al. 1960). Since fluid flow in fractures is much faster than in the porous matrix, the main flow and transport processes controlled by the fracture network (Bogdanov et al. 2003a, b), if they form interconnected networks over significant length scales.

To investigate how fluids flow in fractured porous media, it is necessary to study the interaction between the fracture network and the porous matrix. Since the permeability of a pore space is the most important factor in fluid flow through the pores, any reasonable model of a fractured porous medium must represent accurately the spatial distribution of the permeability throughout the matrix. While it was assumed for many decades that the spatial distribution of the permeability at most contains short-range correlations, if not distributed randomly, the pioneering work of Hewett (1986; see also Arya et al. 1988; Hewett and Behrens 1990) indicated that most large-scale porous media contain long-range correlations in the spatial distribution of their porosity $\phi$ and permeability K. Such correlations give rise to fractal distribution of $\phi$ and K. Extensive analyses of vast amount of data have indicated that in many cases the distributions can be well represented by the fractional Brownian motion (FBM) (Neuman 1994; Babadagli et al. 2004; Hamzehpour and Sahimi 2006a, b; Hamzehpour et al. 2007; for comprehensive reviews see Molz et al. 2004; Sahimi 2011). Sahimi and Tajer (2005) reported evidence indicating that even the spatial distribution of the elastic moduli and wave speeds in large-scale porous media may follow the FBM. Thus, Mukhopadhyay and Sahimi (2000) calculated the effective permeability of isotropic and anisotropic field-scale porous media with long-range correlations, while Saadatfar and Sahimi (2002) studied diffusion processes in such porous media.

In recent years, properties of fracture networks with various fracture shapes have been studied by many research groups (e.g., Mourzenko et al. 1997; Hamzehpour et al. 2009; for reviews see Adler and Thovert 1999; Sahimi 2011). Pike and Seager (1974) were among the first who analyzed the two-dimensional (2D) systems in which fractures were represented as sticks. They computed percolation properties of such systems by Monte Carlo simulation and estimated their percolation or connectivity threshold. Huseby et al. (1997) investigated the geometric and topological properties of various fracture networks in which the fractures were represented by polygons with random locations and orientations. De Dreuzy et al. (2001) studied the influence of various geometrical parameters of fractures on the permeability of 2D fracture networks with power-law distribution of lengths.

Many numerical studies of flow in 2D models of fracture networks have been carried out with fractures with zero thickness. Natural fractures have, however, a finite thickness that strongly influences fluid flow in fractured porous media. Sangare and Adler (2009) investigated a network of circular cylinder as fractures and showed that the maximum value of the percolation threshold is obtained for cylinders whose length and diameter are equal. Yazdi et al. (2011) considered fluid flow in a model of 2D fracture network with rectangular fractures and computed the macroscopic permeability and average porosity of the system as functions of the fractures’ number density and width. In their model, the permeability of porous matrix was zero. Other studies of fluid flow in fractured porous media include those of Bogdanov et al. (2003a, b, 2007) and Sangare et al. (2010). In all such cases, the permeability of the porous matrix was a constant, which is tantamount to assuming that the matrix is homogeneous even over large length scales.

In this paper, we extend our previous study of fluid flow in fractured porous media (Yazdi et al. 2011) by carrying our numerical simulations in a model 2D fractured porous medium in which the permeability of the porous matrix is spatially distributed. Following the aforementioned evidence for the existence of long-range correlations in the spatial distribution of the permeability, we use a FBM to generate such a permeability distribution for the porous matrix. We show that the effect of heterogeneity of the porous matrix, and particularly the long-range correlations, is particularly strong and important and cannot be neglected.

The rest of this paper is as follows. In Sect. 2, the geometry of both the porous matrix and the fracture network is described. Section 3 provides the details of the flow equations and their numerical solution for computing the effective permeability. The results are presented and discussed in Sect. 4. Some remarks conclude the paper in Sect. 5.

2 The Geometry of Fractured Porous Medium

Let us first describe the details of the morphology of fractured porous media.

2.1 Model of the Porous Matrix and its Permeability Distribution

To generate a porous matrix with a permeability distribution that follows the FBM, we consider a square network of size $L\times L$ with $L = Na$, where a is the elementary square cell size and $N=1024$ is the number of cells in the two main directions, x and y. The permeabilities of the cells are selected from a FBM and are normalized to be between zero and 1. Briefly, the FBM is a non-stationary stochastic process $B_{H}(\mathbf{r})$ with the properties that

$$\begin{aligned} \langle B_{H} (\mathbf{r}) - B_{H} (\mathbf{r_0})\rangle = 0, \end{aligned}$$

(1)

and

$$\begin{aligned} \langle [B_{H}(\mathbf{r})-B_{H}(\mathbf{r_0}) ]^2 \rangle \sim {|\mathbf{r} - \mathbf{r_0}|}^{2H}, \end{aligned}$$

(2)

where $\mathbf{r}=(x,y,z)$ and $\mathbf{r_0}=(x_0,y_0,z_0)$ are two arbitrary points and H is the Hurst exponent (Sahimi 2003). As mentioned earlier, a main property of the FBM is that it generates correlations with an extent that is infinite (i.e., the extent of the correlations is as large as the linear size of the system in which the problem is studied). Moreover, the type of the correlations is tuned by varying H. For $H>1/2$ ($H<1/2$) one has persistent or positive (anti-persistent or negative) correlation, while for $H=1/2$ the trace of a FBM follows Brownian motion and, thus, its successive increments are uncorrelated. The two-point covariance function $C(\mathbf{r})$ of the FBM is given by

$$\begin{aligned} C(\mathbf{r})-C(0) \sim \mathbf{r}^{2H}. \end{aligned}$$

(3)

As long as $H>0$ (which is the only physically acceptable range for H) the covariance increases with increasing r. Several algorithms have been used for the generation of a FBM distribution (e.g., Ausloos and Berman 1985; Voss 1985; Hamzehpour and Sahimi 2006a, b). We use the fast Fourier transformation (FFT) method. The spectral density $S({\varvec{\omega }})$ of the FBM, i.e., the Fourier transform of its covariance in d dimensions, is given by

$$\begin{aligned} S({\varvec{\omega }})=\dfrac{a(d)}{\left( \sum _{i=1}^{d}w_i^2\right) ^{H+d/2}}, \end{aligned}$$

(4)

where ${\varvec{\omega }}=(\omega _1,\ldots ,\omega _d)$ is the Fourier variable and a(d) is a d-dependent constant (Sahimi 2011).

In this method, the random numbers are generated uniformly in range [0,1) and are assigned to the sites of a d-dimensional lattice. The Fourier transform (FT) of the resulting d-dimensional array is then computed numerically, and the results are multiplied by $\sqrt{S({\varvec{\omega }})}$. The inverse FT of the results represents an array of correlated numbers with a correlation function given by Eq. (3). The probability distribution functions (PDF) of some FBM distributions with various Hurst exponents are presented in Fig. 1.

Fig. 1

Probability distribution functions (PDF) as functions of local permeability values $K_m$ for some samples of FBM porous matrixes with a $H=0.2$, b $H=0.4$, c $H=0.6$, and d $H=0.8$

2.2 Geometry of the Fracture Network

We use a model of fracture networks that was recently introduced by Yazdi et al. (2011). The fractures are modeled by rectangles of length l and width b. The fractures’ centers and orientations are randomly and uniformly distributed. Each elementary square cell belongs to a fracture if its center is inside or on perimeter of the fracture’s rectangle. The permeability of the cells that belong to the fractures is set to 1. Considering of constant permeability value for all points of fractures is an approximation. In this paper, one of our goal is to study the effect of Hurst exponent of porous matrix on effective permeability $\overline{K}$ of the fractured porous media. By assigning of various permeability values to fractures, the parameters that $\overline{K}$ depends on them, increases and this make the problem more complicated.

To characterize the fracture network, we must specify the fractures’ number density $\rho$, the length l and the width b. We use the average excluded area $A_{{\mathrm{ex}}}$ to make the density dimensionless, denoted by $\rho '$, and defined it as the number of fractures per average excluded area $A_{{\mathrm{ex}}}$,

$$\begin{aligned} \rho '= A_{{\mathrm{ex}}}\rho . \end{aligned}$$

(5)

$A_{{\mathrm{ex}}}$ is the area around an object into which another similar object is not allowed, if overlapping of the two objects is to be avoided. The average excluded area $A_{{\mathrm{ex}}}$ is given by (Balberg et al. 1984; Hamzehpour et al. 2014; Li and Östling 2013)

$$\begin{aligned} A_{{\mathrm{ex}}}=2bl\left( 1 + \dfrac{4}{\pi ^2}\right) + \dfrac{2}{\pi }\left( l^2+b^2\right) . \end{aligned}$$

(6)

In this study, we use a fracture length $l=64a$ to make some geometrical quantities dimensionless, as

$$\begin{aligned} L'=\dfrac{L}{l}, \quad b'=\dfrac{b}{l}. \end{aligned}$$

(7)

In our simulations, $b'$ is between 0.031 and 0.125, or equally $b=2a-8a$, and $L'=16$. Periodic boundary conditions in both directions were assumed. Thus, the fractured porous medium that we study consists of a fracture network embedded in a porous matrix. The interactions between porous matrix and fracture network are controlled by the permeabilities of them. Certainly, the distributions of permeabilities of porous matrix and fracture network are very important in this interaction. Some of the generated fractured porous media for various $\rho '$, b and H are shown in Fig. 2.

Fig. 2

Fractured porous media for various H, $\rho '$ and b values with fractures’ length $l=64a$ and network size $L=1024a$. For the first row $H=0.2$ and $b=2a$, and for the second one $H=0.8$ and $b=8a$. The $\rho '$ values from left to right are 1.37 and 3.9. Colors correspond to the matrix local permeabilities, ranges between zero (blue) and 1 (red)

3 The Flow Equations

For low-Reynolds-number flow of an incompressible and Newtonian fluid, the Darcy’s equation

$$\begin{aligned} \mathbf{v}=-\frac{K}{\mu }{\varvec{\nabla }} P, \end{aligned}$$

(8)

is applicable, where $\mathbf{v}$ is the local seepage velocity, $\mu$ the fluid viscosity, ${\varvec{\nabla }}P$ the macroscopic pressure gradient and K the permeability that vary spatially. The continuity equation is given by

$$\begin{aligned} {\varvec{\nabla }}\cdot {\mathbf {v}}=0, \end{aligned}$$

(9)

and we have

$$\begin{aligned} {\varvec{\nabla }}\cdot (K{\varvec{\nabla }}P)=0. \end{aligned}$$

(10)

Discretization of Eq. (10) by the finite-volume method at a square network point (i, j) yields

$$\begin{aligned} K_{i,j-\frac{1}{2}}(P_{i,j-1}-P_{i,j})+K_{i-\frac{1}{2},j}(P_{i-1,j}-P_{i,j}) +K_{i,j+\frac{1}{2}}(P_{i,j+1}-P_{i,j})+K_{i+\frac{1}{2},j}(P_{i+1,j}-P_{i,j})=0, \end{aligned}$$

(11)

where, for example, $P_{i,j}$ is the pressure at grid point (i, j) and $K_{i+1/2,j}$ is the permeability between two neighbor blocks, centered at (i, j) and (i + 1, j), given by

$$\begin{aligned} K_{i+1/2,j}=\dfrac{2 K_{i,j} K_{i+1,j}}{K_{i,j} + K_{i+1,j}}. \end{aligned}$$

(12)

Thus, the governing equations for the pressures at all the grid points constitute a system of linear equations, which is solved by the biconjugate gradient method (Press et al. 1992). To obtain the effective permeability of the medium, the boundary condition for fluid flow must be specified. Here, we assume a constant pressure difference $\Delta P=P_l-P_r$ between the left and right sides of the system, or equally $P(i=1,j=1:N)=P_l$, and $P(i=N,j=1:N)=P_r$. Periodic boundary conditions were assumed in the transverse direction as $P(i=1:N,j=N+1)=P(i=1:N,j=1)$, and $P(i=1:N,j=0)=P(i=1:N,j=N-1)$. After computing the pressure distribution (see Fig. 3) and using Eq. (8), the volume flow rate Q is deduced as

$$\begin{aligned} Q=\int _S \mathbf{v} \cdot \mathrm{d}{} \mathbf{s}, \end{aligned}$$

(13)

where S is the length of the left-side boundary. Finally, the macroscopic permeability $\overline{K}$ of the fractured porous medium is computed through the Darcy’s law

$$\begin{aligned} Q=\frac{{\overline{K}} S}{\mu }\frac{\Delta P}{L}, \end{aligned}$$

(14)

where L is the width of the medium.

Fig. 3

The pressures distributions in a fracture network with non-permeable matrix part, b FBM porous matrix and c fractured porous media of Fig. 2d

Figure 3 presents the pressure distributions of fracture network with non-permeable matrix part, FBM porous matrix and fractured porous media of Fig. 2d. Figure 3a shows that in non-permeable regions the pressures are zero, while in all regions of porous and fractured porous medium the pressures are not zero. Since the porous matrix is high permeable, the effect of fractures in fluid flow is not so clear to see the fractures in pressure distribution. But we can see their effect in total value of flow rate and consequently the effective permeability $\overline{K}$ of the fractured porous medium.

Fig. 4

Percolation probability $\Pi$ versus $\rho '$ for $L'=16$ and fractures’ width $b'=0.0313$ (blacksquare), 0.0625 (red triangle), 0.09375 (blue inverted triangle) and 0.125 (green circle)

4 Results

Let us first investigate the percolation properties of fracture networks of fractured porous media that we study. Then, we study the behavior of the effective permeability as a function of $\rho '$, $b'$ and H, given that the mean and standard deviation of the matrix permeability are kept equal to 0.5 and 0.18, respectively. The fractures permeabilities are equal to 1, the maximum of the matrix permeability. Thus, we write,

$$\begin{aligned} \overline{K}=\overline{K}(\rho ',b',H). \end{aligned}$$

(15)

4.1 Percolation

Similar to unfractured porous media, the effective permeability of a fractured porous medium is strongly affected by the percolation threshold of the fracture network. Thus, we first study the percolation properties of the fracture networks, using a geometrical method (Yazdi et al. 2011) to identify the sample-spanning percolating clusters of fractures. The numerical data for the percolation probability are fitted by an error function as (Stauffer and Aharony 1992; Sangare and Adler 2009)

$$\begin{aligned} \Pi (\rho ',b',L')=\frac{1}{\sqrt{2\pi }}\int _{-\infty }^{\rho '}\frac{1}{\Delta _L}\exp \left[ -\frac{[\xi -\rho '_{c}(b',L')]^2}{2\Delta _L^2}\right] \mathrm{d}\xi , \end{aligned}$$

(16)

where $\Delta _L$ is the width of the transition region of $\Pi (\rho ',b',L')$ which follows a scaling relation in the limit of large $L'$,

$$\begin{aligned} \Delta _L \propto L'^{-1/\nu }. \end{aligned}$$

(17)

$\nu$ is the critical exponent. $\Delta _L$ tends to zero at large $L'$ values. The percolation threshold $\rho '_{c}(b',L')$ is that value of $\rho '$ at which $\Pi =0.5$. Monte Carlo calculations were carried out with $N_r=200$ realizations and $L'=16$. Figure 4 shows the percolation probability as a function of $\rho '$ for various values of $b'$. $\Pi$ decreases with increasing $b'$ for the same values of $\rho '$, implying that values of $\rho '_c$ increase with $b'$. This conclusion is confirmed in Fig. 5 that shows $\rho '_c$ as a function of $b'$. The value of $\rho '_c$ is around 3.5; its importance to the effective permeability of fractured porous media is demonstrated below. Our results are about 3 % less than Li and Östling (2013) data. This is due to the finite-size effects. Our system size is $L'=16$ which is small comparing with 256, in their simulation systems (Li and Zhang 2009). However, $L'=16$ is a good value with negligible finite-size effect, in numerical solution of flow equation (Yazdi et al. 2011).

4.2 Effective Permeability

We first study fracture networks (FNs) with impermeable matrix. Then, we present the results for $\overline{K}$ for porous media in which the local permeabilities are distributed according to the FBM with various Hurst exponents. Finally, $\overline{K}$ for fractured porous media with the FBM distribution of the local permeabilities of porous matrix (FN-FBM) are presented.

Fig. 5

$\rho '_{c}$ versus $b'$

Fig. 6

$\overline{K}$ as a function of $\rho '$ for fractures networks with zero permeabilities of matrix parts. The data are for fracture widths $b'=0.0313$ (red left triangle), 0.0625 (blue square), 0.09375 (green circle) and 0.125 (pink right triangle). The dimensionless network size is $L'= 16$

4.2.1 Fracture Networks

Figure 6 presents the effective permeabilities $\overline{K}$ of fracture networks, versus $\rho '$ for various $b'$. The local permeabilities of matrix parts are supposed equal to zero. Increasing the fracture density $\rho '$ and fracture width $b'$ also increases the effective permeability, in agreement with the previous study (Mourzenko et al. 2011; Yazdi et al. 2011). Similar results for the effective permeability of fracture networks were discussed extensively in our previous paper (Yazdi et al. 2011). Thus, in this paper we compare such results with the effective permeability of fractured porous media with a porous matrix.

4.2.2 Porous Media

Figure 7 presents the effective permeability $\overline{K}$ of model porous media as a function of the Hurst exponent H, while the mean and standard deviation of the local permeabilities are constant. The results represent the average over $N_r=100$ realizations and indicate that the effective permeability of the porous media decreases with increasing Hurst exponent, in agreement with the results of Babadagli (2006). The reason is that increasing H creates more positive correlations between the local permeabilities. So the medium is divided into several broad areas with low, even in some cases close to zero and high permeabilities. When the fluid reaches to the points with very low permeabilities, there is less chance to find a path to flow, in cases the neighbor points have low permeabilities. On the other hand, as $H\rightarrow 0$, the permeability distribution becomes a “rugged” landscape in which the local permeabilities are highly anti-correlated. This means that the local permeabilities strongly changes from a point to neighbor points. In other words, the permeabilities of first neighbors of a point with low permeability are not necessarily low. So in these cases, even though the fluid reaches to a point with low permeability still it has a chance to flow through the neighbor points.

Fig. 7

$\overline{K}$ versus Hurst exponent H for porous media without fracture network

Fig. 8

$\overline{K}$ as a function of $\rho '$ for $L'=16$ and Hurst exponents H equal to a 0.2, b 0.35, c 0.5, d 0.65 and e 0.8 of fractured porous media. The results are for the fractures’ width $b'=0.0313$ (red left triangle), 0.0625 (blue square), 0.09375 (green circle) and 0.125 (pink right triangle). The plot (f) compares the data of (a) and (e) with $H=0.2$ (black square) and 0.8 (bullet) of $b'=0.0313$

4.2.3 Fractured Porous Media

Figure 8 presents the overall permeability $\overline{K}$ as a function of the fracture density $\rho '$ for various $b'$ and H, representing the average permeability with the average taken over 40 realizations. The number of required realizations depends on the heterogeneity of the system. We do average on realizations to obtain the macroscopic properties of the system. If the exceeding of realizations number does not change the average value, it means that the number of realizations is large enough.

Fig. 9

$\overline{K}$ as a function of H for $L'=16$ and fractures’ widths a $b'=0.0313$, b 0.0625, c 0.09375 and d 0.125. The data are for $\rho ' = 0.5, 1.5,\ldots ,40$ from bottom to top, respectively, same as the data of Fig. 7. Some examples of statistical error bars are shown in (b), (c) and (d)

The results indicate that $\overline{K}$ increases by increasing $\rho '$ and $b'$. This is expected because as both fracture density and width increase, the porous medium is increasingly dominated by a network of large fracture. On the other hand, the overall permeability of the fractured porous medium decreases with increasing the Hurst exponent H, in agreement with the results presented above for unfractured porous media. Note that the general trends of $\overline{K}$ as a function of $\rho '$ and $b'$ are similar to those of fracture networks. Unlike the network, however, for $\rho '=0$, $\overline{K}$ is not zero, because the porous matrix, even in the absence of any fracture, is still permeable. Figures 8a–e look identical at first sight, so we compare the results of different Hurst exponents, $H=0.2$ and 0.8 of $b'=0.0313$ in Fig. 8f. These data show the decreasing $\overline{K}$ with H in agreement with the data of Fig. 7.

To understand $\overline{K}$ as a function of the geometrical properties of the medium, we plot in Fig. 9 the effective permeability versus the Hurst exponent H for various fracture densities $\rho '$. Some statistical error bars are estimated and plotted in Fig. 9, too. These data show that the error bars are so small. This means that the assumed number of realizations is enough. The results indicate that $\overline{K}$ is a linearly decreasing function of H for all fracture densities $\rho '$ and widths $b'$. Thus, we may write $\overline{K}$ as,

$$\begin{aligned} \overline{K}\propto -\beta (\rho ',b')H, \end{aligned}$$

(18)

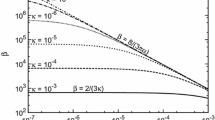
where the slope $\beta$ is expected to be a function of $\rho '$ and $b'$. Plotting $ln(\beta )$ versus $\rho '$ in Fig. 10 indicates that one has two distinct regions of linear dependence of $ln(\beta )$, one around and a second one far from percolation threshold $\rho '_c$ of the fracture network. Therefore, the two different regimes are given by

$$\begin{aligned} ln(\beta ) \propto -\gamma (b')\rho '\quad 0.5\lesssim \rho '\lesssim 11, \end{aligned}$$

(19)

and

$$\begin{aligned} ln(\beta ) \propto -\Gamma (b')\rho '\quad 12\lesssim \rho '\lesssim 42. \end{aligned}$$

(20)

We now plot $\gamma$ and $\Gamma$ versus fracture width $b'$, see Fig. 11. It is, then, clear that they both are linear functions of $b'$ and are approximately given by

$$\begin{aligned} \gamma (b')=0.47b'+0.02, \end{aligned}$$

(21)

and

$$\begin{aligned} \Gamma (b')=0.96b'+0.001. \end{aligned}$$

(22)

The error bars are estimated by the least square method of fitting error of Fig. 10. The values of error bars show that the linear fitting of data in Fig. 11 is reasonable. Thus, overall, the effective permeability may be written as

$$\begin{aligned} \overline{K} \propto -(e^{-(0.47b'+0.02)\rho '})H \quad 0.5\lesssim \rho '\lesssim 11 \end{aligned}$$

(23)

and

$$\begin{aligned} \overline{K} \propto -(e^{-(0.96b'+0.001)\rho '})H \quad 12\lesssim \rho '\lesssim 42. \end{aligned}$$

(24)

Note that the coefficient of $b'\rho '$ for the smaller range of the dimensionless fracture number densities of Eq. (23) is smaller than that for the high-density region of Eq. (24), implying that the effective permeability varies smoothly with the Hurst exponent in the high fracture number densities, while the changes are more noticeable at low $\rho '$. This, of course, is strictly a percolation effect. It is noteworthy that the obtained relations here are valid for fractured porous media with high permeable porous matrix or equally with small fractures permeabilities. We also assume constant length and permeability values for all fractures. The fractures orientation is isotropically distributed.

Fig. 10

$ln(\beta )$ versus $\rho '$ for $L'=16$ and fractures’ width $b'=0.0313$ (pink square), 0.0625 (blue circle), 0.09375 (green diamond), 0.125 (red triangle)

4.2.4 Comparison of Fractured Porous Media

In Fig. 12, we compare the dependence on the fracture density of the effective permeability $\overline{K}$ or various fracture widths $b'$ for systems that contain a fracture network (FN), namely FN-FBM, fractured porous media with white noise random distribution of local permeabilities of porous matrix (FN-WN) and fractured porous media with homogeneous local permeabilities of porous matrix (FN-homogeneous). Here, our mean by white noise is random numbers with uniform PDF, ranging between zero and 1, which are spatially uncorrelated. The local permeability in the FN-homogeneous system is equal to the average permeability of the heterogeneous porous media, FN-FBM and FN-WN, which are about 0.5. The results indicate that for all the fracture densities $\rho '$ and fracture widths $b'$ the $\overline{K}$ of the FN-homogeneous medium are larger than that of the heterogeneous ones. The reason is that attributing a constant permeability to the porous matrix eliminates completely the low-permeability regions that act as a barrier to fluid flow. Thus, use of a homogeneous matrix in conjunction with a fracture network does not provide accurate estimates of flow properties of a fractured porous medium. According to Fig. 12, the $\overline{K}$ decreases with increasing Hurst exponent, in agreement with Fig. 7. Thus, one may expect the $\overline{K}$ of the FN-WN media to be larger than that of the FN-FBM medium, whereas the simulation indicates the opposite. This is, therefore, a non-trivial, counterintuitive result.

Fig. 11

The values of a $\gamma$ and b $\Gamma$ versus $b'$. The error bars are obtained by fitting error of Fig. 9

Fig. 12

$\overline{K}$ as a function of $\rho '$ for some fractured porous media with fractures’ widths a $b'=0.0313$, b 0.0625, c 0.09375 and d 0.125. The data are for FN-FBM with H values equal to 0.8 (asterisk), 0.65 (green inverted triangle), 0.5 (red circle), 0.35 (blue square) and 0.2 (pink right triangle), FN-WN (dashed red left triangle) and FN-homogeneous (dashed black circle) media. The network size is $L'=16$

These results indicate that correlations between the local permeabilities in the porous matrix increase the effective permeability of a fractured porous medium. It may then act as a distinction criterion between correlated and uncorrelated fractured porous media.

5 Summary

The effective permeability and percolation properties of disordered fractured porous media were computed as a function of the Hurst exponent of the spatial distribution of the permeability of the porous matrix, and fractures’ number density and width. The most important results of the study are that (1) assuming a uniform matrix in a fractured porous medium results in estimates of the permeability that are significantly different from those in which the matrix itself is heterogeneous and (2) long-range correlations, as has been reported in the spatial distributions of the permeability of large-scale porous media, has a non-trivial, and in some respect unexpected, effect on the permeability and, hence, the flow properties of fractured porous media.

It would be important to extend the present study to three-dimensional fractured porous media. In that case, both the porous matrix and the fracture network can be sample-spanning and percolating, in which case a variety of interesting cases may arise.