Unsteady Flow of Shear-Thinning Fluids in Porous Media with Pressure-Dependent Properties

Abstract

In this paper, a model for injection of a power-law shear-thinning fluid in a medium with pressure-dependent properties is developed in a generalized geometry (plane, radial, and spherical). Permeability and porosity are taken to be power functions of the pressure increment with respect to the ambient value. The model mimics the injection of non-Newtonian fluids in fractured systems, in which fractures are already present and are enlarged and eventually extended and opened by the fluid pressure, as typical of fracing technology. Empiric equations are combined with the fundamental mass balance equation. A reduced model is adopted, where the medium permeability resides mainly in the fractures; the fluid and porous medium compressibility coefficients are neglected with respect to the effects induced by pressure variations. At early and intermediate time, the flow interests only the fractures. In these conditions, the problem admits a self-similar solution, derived in closed form for an instantaneous injection (or drop-off) of the fluid, and obtained numerically for a generic monomial law of injection. At late times, the leak-off of the fluid towards the porous matrix is taken into account via a sink term in the mass balance equation. In this case, the original set of governing equations needs to be solved numerically; an approximate self-similar solution valid for a special combination of parameters is developed by rescaling time. An example of application in a radial geometry is provided without and with leak-off. The system behaviour is analysed considering the speed of the pressure front and the variation of the pressure within the domain over time, as influenced by the domain and fluid parameters.

1 Introduction

The research on non-Newtonian fluid flow in porous and fractured media has encountered a renewed interest since the development of new, economically advantageous technologies for aquifer remediation and enhanced gas recovery. Extraction of crude oils, well drilling, and soil remediation also involve the injection of a non-Newtonian fluid in the subsurface environment. The rheology of the fluids utilized in these applications and technologies is described by complex models with numerous parameters, like the Cross or Carreau–Yasuda relations, able to interpret in detail the response of the fluid to a wide range of shear stress. However, in many flows the shear rate (and the applied shear stress) varies in a limited range, making it sufficient to adopt a simple two-parameter Ostwald–deWaele model. This simplification has the advantage of a simple macroscopic description of the relationship between pressure gradient and flux at the Darcy scale, represented by a nonlinear modification of the Darcy’s law (Cristopher and Middleman 1965; Kozicki et al. 1967; Teeuw and Hesselink 1980; Pascal and Pascal 1985; Pearson and Tardy 2002; Adler et al. 2013a).

The nonlinear Darcy’s law has been theoretically applied and experimentally verified in numerous geometries for unconfined (Pascal and Pascal 1993; Bataller 2008; Longo et al. 2013; Di Federico et al. 2014, 2012a, b; Longo et al. 2015a, b) and confined flow of non-Newtonian power-law fluids. In the latter case, the (medium and fluid) compressibility becomes a key element: the disturbance created by a pulse injection of mass in a porous medium of infinite extent and homogeneous properties was analysed by several authors (Pascal 1991a, b; Di Federico and Ciriello 2012) considering different geometries. A further extension for a time variable fluid injection and a monotonic spatial variation of permeability is due to Ciriello et al. (2013); joint variations of porosity can be easily incorporated into the scheme.

In other instances, changes of permeability and porosity are mainly due to pressure variations within the domain. Fractured media, having macroscopic properties drastically modified by the presence of fractures (Adler et al. 2013b), are a typical example. In these media, permeability is inherently coupled with the micromechanical behaviour of the porous rock and evolves with the applied pressure (Yao et al. (2015) and references therein). The stress-dependent nature of the permeability of mudrocks was demonstrated experimentally by Bhandari et al. (2015). In fracing technology (Fjaer et al. 2008), fractures typically show a permeability increasing with pressure as a consequence of an increment of their width; they also show a porosity increasing with pressure as a consequence of an increment of both width and length. This second phenomenon, i.e. the extension of existing fractures or the generation of new branches, is directly linked to the hysteretic response of the domain to cycles of increasing/decreasing pressure. With the stress increasing, the width of the fractures may respond linearly in the elastic regime and return to the original width after the pressure decrease; however, the generation of new fractures increases permanently the permeability. A second cause of hysteresis is the presence of small particles added to the fracing fluid (Mader 1989) which inhibit the closure of the fractures after pressure reduction. While the complexity of fracture generation and propagation cannot be easily implemented analytically, a simplified model of pressure diffusion in subsurface media incorporating a monotonic relationship between the variation of medium properties (permeability and porosity) and pressure increments may shed light on the fundamental properties of non-Newtonian flow in such media and help to estimate the sensitivity of the pressure diffusion to plausible ranges of variation of the parameters.

The objective of this study is to derive such a model for unsteady state flow of a non-Newtonian power-law fluid, analysing the influence of various geometries. Some empiric equations representing the fluid rheology and spatial variations of the porous medium properties are combined with the mass balance equation. The diffusion of pressure within the medium can be due to fluid injection (e.g. in hydraulic fracturing), to a perturbation of seismic origin, or to the breaking of a cap limiting a pressurized fluid reservoir. The reference model is the crack-and-block medium described in Phillips (2009), with a clear distinction between the permeability and the porosity due to the network of fractures and to the matrix. We assume that the fracture network, already present within the medium or generated by an external cause, is isotropic with a typical length scale much smaller than the scale of the porous formation, with a permeability much greater and a porosity decidedly smaller than the matrix. Hence, the storage of the fluid is essentially due to the matrix, whereas the flow paths, and the overall permeability, are due to fractures. This ‘double porosity’, or fractured-matrix model, has been developed and applied in several fields by Barenblatt (see Barenblatt et al. 1990; Bai et al. 1993; De Smedt 2011). It entails a pressure diffusion much faster than in a uniform medium, as two phenomena take place with different time and length scales. At short or intermediate timescales, the fluid flows in the fractures, and little or no storage is present. At long timescales, the fluid is transferred from the fractures to the matrix, having large storage (leak-off phase). In the present work, we adopt a simplified continuum approach, geared at understanding the response of this type of system to significant pressure variations. To this end, we analyse the pressure dynamics up to an intermediate timescale, neglecting the leak-off towards the matrix and considering the fracture network to dominate the dynamics of the flow; this allows deriving a closed-form solution in self-similar form, extending the results of Di Federico and Ciriello (2012) to pressure-dependent properties. Secondly, we refine the model by including the leak-off phenomenon, which becomes dominant at late times and is used in hydraulic fracturing technology to monitor the efficiency of the process. The leak-off is approximated via a sink term in the mass balance equation of the fracture network, neglecting the details of the fluid flow within the matrix. The resulting set of equations can be solved numerically; we show it is amenable to a similarity solution under a special combination of parameters.

It is worth mentioning that we also simplify the geometry of the system under analysis: real fractures have an elliptic shape (Rahim and Holditch 1995), open in the direction of the least principal stress, and propagate in the plane of the two other principal stresses (greatest and intermediate). Hence, different scenarios are observed depending on the depth of the formation interested by the fractures. Near the surface, the vertical (parallel to gravity) normal stress is limited and the confining stresses are dominant; hence, the fractures open in horizontal planes. In deep formations, the normal stress parallel to gravity is dominant, and fractures open and develop in vertical planes. This potential source of anisotropy adds further complexity to the problem.

The exposition is organized as follows. The mathematical problem is formulated in Sect. 2 for a generalized geometry and is solved in Sect. 3 in self-similar form. Section 4 discusses the limits existing on problem parameters by virtue of formulated assumptions. An application involving the injection of shear-thinning fluid in a cylindrical geometry is presented in Sect. 5. The effect of leak-off is treated in Sect. 6, while concluding remarks are formulated in Sect. 7.

2 Problem Formulation

We consider an infinite porous domain, initially at constant ambient pressure $p_0$, and having a plane ($d=1$), cylindrical ($d=2$), or spherical ($d=3$) geometry (Fig. 1). A mass of a non-Newtonian power-law fluid, increasing with time as $m_0t^{\alpha }$ (with $m_0$ (dimensions M T$^{-\alpha }$) and $\alpha$ being constants), is injected in the domain origin starting at time $t=0$; $\alpha =0,\;1$ corresponds to the instantaneous release of a given mass and to a constant mass flux, respectively. The fluid injection generates a pressure disturbance that propagates as an one-dimensional transient process within the domain as a function of its shape, properties, and rheology of the injected fluid.

For plane ($d=1$) or cylindrical ($d=2$) geometry, the domain has constant thickness h. For $d=1$, the injection zone is a plane of area $\delta h^2$, with $\delta$ being the width/height ratio of the domain; for $d=2,\;3$, the injection zone is a cylindrical or spherical well of radius $r_w$, and the area of the injection zone is $2\pi h r_w$ or $4\pi r_w^2$.

Fig. 1

Domain schematic for plane ($d=1$), cylindrical ($d=2$), and spherical geometry ($d=3$)

The permeability k and the porosity $\phi$ of the domain vary with the pressure p according to

$$\begin{aligned} k(p)=k_0\left( \frac{p-p_0}{p^*}\right) ^{\beta },\quad \phi (p)=\phi _0\left( \frac{p-p_0}{p^*}\right) ^{\gamma -1}, \end{aligned}$$

(1)

where $k_0$ and $\phi _0$ are the reference permeability and porosity for $p=p_0$, $p^*$ is a pressure scale to be defined later for convenience, and $\beta \ge 0$ and $\gamma \ge 1$ are real numbers governing the degree of variation of the permeability and porosity with pressure. Physically, $\beta$ is representative of the permeability compliance, and $\gamma$, of the volumetric compliance. For $\beta =0$ and $\gamma =1$, the domain properties are independent of the pressure, while for $\beta >0$ and $\gamma >1$ the permeability and the porosity increase with the pressure: the larger the values of $\beta$ and $\gamma$, the larger the increment of permeability and of porosity, respectively, for a unit pressure increment. As permeability and porosity are strictly related (and depend on the local stress tensor and on the mechanical properties of the medium), so are the two exponents $\beta$ and $\gamma$, depending on the nature of the medium and of the adopted model (Bai et al. 1993). In particular, the adoption of the ‘cubic law’ for transmissivity in single-fracture flow (Witherspoon et al. 1980) implies a square dependence of permeability and a linear dependence of porosity upon aperture, resulting in $\beta =2(\gamma -1)$. Higher exponents for transmissivity [e.g. the ‘quintic law’ in Klimczak et al. (2010), as a consequence of a correlated length–aperture relationship in fractures] imply a ratio $\beta /(\gamma -1)>2$.

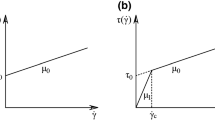
The rheological power-law model describing the injected fluid reads $\tau =-\widetilde{\mu }\dot{\gamma }\left| \dot{\gamma }\right| ^{n-1}$ for simple shear flow, with $\tau$, $\dot{\gamma }$, $\widetilde{\mu }$, and n being the shear stress, shear rate, fluid consistency index, and behaviour index, respectively; $n \lesseqgtr 1$ indicates shear-thinning/Newtonian/shear-thickening behaviour. In the following, only the case $n<1$ will be considered. Flow of such fluids in porous media is usually described macroscopically by a modified Darcy’s law accounting for nonlinearity (e.g. Shenoy 1995), corroborated by experimental evidence (Cristopher and Middleman 1965; Yilmaz et al. 2009). The one-dimensional version of the flow law along the generalized spatial coordinate r reads (neglecting gravity effects for the case $d=3$)

$$\begin{aligned} v=-\left( \frac{k}{\mu _{{\text {eff}}}}\right) ^{1/n}\frac{\partial p}{\partial r}\left| \frac{\partial p}{\partial r}\right| ^{1/n-1}, \end{aligned}$$

(2)

where v and p are the fluid Darcy velocity and pressure, k the medium permeability, and $\mu _{{\text {eff}}}$ the effective viscosity, given by

$$\begin{aligned} \frac{k}{\mu _{{\text {eff}}}}=\frac{1}{2\widetilde{\mu }C_t}\left( \frac{n\phi }{3n+1}\right) ^n\left( \frac{50k}{3\phi }\right) ^{(n+1)/2}, \end{aligned}$$

(3)

in which the tortuosity factor $C_t=C_t(n)$ can take different expressions; the formulation $C_t=(25/12)^{(n+1)/2}$ by Pascal and Pascal (1985) will be adopted in the following.

The local mass balance equation for a generalized geometry described by d is

$$\begin{aligned} \frac{1}{r^{d-1}}\frac{\partial }{\partial r}\left( \rho r^{d-1}v\right) =-\frac{\partial (\rho \phi )}{\partial t}, \end{aligned}$$

(4)

where t is the time, $\rho$ the fluid mass density, and $\phi$ the porosity. Substituting Eq. (3) in (2), then Eq. (2) in (4), and taking (1) into account, one obtains:

$$\begin{aligned}&\left( \dfrac{1}{2\widetilde{\mu }C_t}\right) ^{1/n}\dfrac{n\phi _0}{3n+1}\left( \dfrac{50k_0}{3\phi _0}\right) ^{(n+1)/(2n)}\dfrac{1}{p^{*F_1}}\nonumber \\&\quad \times \left[ \underbrace{\dfrac{1}{r^{d-1}}\dfrac{\partial }{\partial r}\left( r^{d-1}(p-p_0)^{F_1}\dfrac{\partial (p-p_0)}{\partial r}\left| \dfrac{\partial (p-p_0)}{\partial r}\right| ^{1/n-1}\right) }_\text {I}\right. \nonumber \\&\quad +\left. \underbrace{c_f(p-p_0)^{F_1}\dfrac{\partial (p-p_0)}{\partial r}\left| \dfrac{\partial (p-p_0)}{\partial r}\right| ^{1/n}}_\text {II}\right] \nonumber \\&\quad =\dfrac{(p-p_0)^{\gamma -2}}{p^{*\gamma -1}}\phi _0\left[ \underbrace{(\gamma -1)}_\text {III}+\underbrace{(p-p_0)c_0}_\text {IV}\right] \dfrac{\partial (p-p_0)}{\partial t}, \end{aligned}$$

(5)

where $c_0=c_f+c_p\equiv (1/\rho )\partial \rho /\partial p$ is the total compressibility coefficient, $c_f$ and $c_p$ are the compressibility coefficients of the fluid and of the porous medium, respectively, and $F_1=[\beta (n+1)+(\gamma -1)(n-1)]/(2n)$ is a factor incorporating the fluid rheology and the pressure–permeability and pressure–porosity relationships.

The initial condition is

$$\begin{aligned} p(r,t=0)=p_0, \end{aligned}$$

(6)

while the general expression for the conservation of mass

$$\begin{aligned} \int _{{\mathcal {V}}}\dfrac{{\text {d}}[\rho (p(t))\phi (p(t))]}{{\text {d}}t}{\mathrm {d}}{\mathcal {V}}=\dot{m}(t) \end{aligned}$$

(7)

where $\dot{m}(t)$ is the mass discharge entering the domain, and ${\mathcal {V}}$ is the volume of integration becomes via Eq. (1)

$$\begin{aligned}&\omega h^{3-d}\left[ \int _0^{r_N(t)}\rho \phi _0\left( \dfrac{p-p_0}{p^*}\right) ^{\gamma -1}r^{d-1}{\text {d}}r\right. \nonumber \\&\quad +\left. \int _0^{r_N(t)}\dfrac{\rho \phi _0c_0p^*}{\gamma }\left( \dfrac{p-p_0}{p^*}\right) ^{\gamma }r^{d-1}{\text {d}}r\right] =m(t)\equiv m_0t^{\alpha }, \end{aligned}$$

(8)

where the geometrical factor $\omega$ takes the values $\delta$ for plane, $2\pi$ for radial, and $4\pi$ for spherical geometry ($d=1,\,2,\,3$, respectively) and $r_N(t)$ denotes the position of the advancing pressure front.

The full model outlined above, given by Eqs.  (5) and (8) with (6), can be simplified using order of magnitude considerations. First, term II in Eq.  (5), representing the contribution of fluid compressibility, is of a smaller order than term I, associated with permeability and porosity variations with pressure (this assumption will be checked a posteriori, see Sect. 5). Further, terms III and IV represent the effect of storage due to the opening of fractures and to fluid–porous medium compressibility, respectively. It is assumed that their ratio $(\gamma -1)/[(p-p_0)c_0]\gg 1$; hence, only the contribution due to fracture opening (term III) is considered. Considering now the global mass balance given by Eq. (8), the ratio between the first and the second term on the l.h.s. is $\gamma /[(p-p_0)c_0]$. As $\gamma \ge 1$, it follows that $\gamma /[(p-p_0)c_0]>(\gamma -1)/[(p-p_0)c_0]\gg 1$, and consequently the second term within brackets can be neglected. The reduced model, in which the fluid and porous medium compressibility coefficients are negligible, then reads

$$\begin{aligned}&\left( \dfrac{1}{2\widetilde{\mu }C_t}\right) ^{1/n}\dfrac{n\phi _0}{3n+1}\left( \dfrac{50k_0}{3\phi _0}\right) ^{(n+1)/(2n)}\dfrac{1}{p^{*F_1}}\nonumber \\&\quad \times \dfrac{1}{r^{d-1}}\dfrac{\partial }{\partial r}\left( r^{d-1}(p-p_0)^{F_1}\dfrac{\partial (p-p_0)}{\partial r}\left| \dfrac{\partial (p-p_0)}{\partial r}\right| ^{1/n-1}\right) \nonumber \\&\quad =\dfrac{(p-p_0)^{\gamma -2}}{p^{*\gamma -1}}\phi _0(\gamma -1)\dfrac{\partial (p-p_0)}{\partial t}, \end{aligned}$$

(9)

$$\begin{aligned}&\omega h^{3-d}\int _0^{r_N(t)}\rho \phi _0\left( \dfrac{p-p_0}{p^*}\right) ^{\gamma -1}r^{d-1}{\text {d}}r= m_0t^{\alpha }. \end{aligned}$$

(10)

The mathematical statement of the problem is completed by the boundary conditions at the pressure front $r_N(t)$, i.e.

$$\begin{aligned} p\left( r_N(t),t\right)= & {} p_0, \end{aligned}$$

(11)

$$\begin{aligned} \left. \dfrac{\partial p}{\partial r}\right| _{r_N(t)}= & {} 0, \end{aligned}$$

(12)

$$\begin{aligned} r_N(0)= & {} 0, \end{aligned}$$

(13)

valid for a shear-thinning fluid with $n<1$ (Pascal and Pascal 1985, 1990; Di Federico and Ciriello 2012; Ciriello and Federico 2012). The velocity of the pressure front in this case is finite and given by $u(t)=\phi {\text {d}}r_N/{\text {d}}t$.

Dimensionless variables are defined as follows:

$$\begin{aligned} (R,H,R_N,T,P,P_0,V,U,M_0)=\left( \dfrac{r}{r^*},\dfrac{h}{r^*},\dfrac{r_N}{r^*},\dfrac{t}{t^*},\dfrac{p}{p^*},\dfrac{p_0}{p^*},\dfrac{v}{v^*},\dfrac{u}{v^*},\dfrac{m_0t^{*\alpha }}{\rho r^{*3}}\right) ,\qquad \end{aligned}$$

(14)

where $p^*=1/c_0$ is the pressure scale introduced in (1), $t^*$ is a timescale given by

$$\begin{aligned} t^*=\dfrac{\rho ^{(n+1)/2}c_0^{(n-1)/2}k_0^{(n+1)/2}}{\widetilde{\mu }}, \end{aligned}$$

(15)

$r^*$ is a length scale defined as

$$\begin{aligned} r^*=\dfrac{\rho ^{n/2}c_0^{(n-2)/2}k_0^{(n+1)/2}}{\widetilde{\mu }}, \end{aligned}$$

(16)

and $v^*$ is the velocity scale given by

$$\begin{aligned} v^*=\sqrt{\dfrac{1}{\rho c_0}}. \end{aligned}$$

(17)

Equations (2–9–10) become, in non-dimensional form,

$$\begin{aligned}&V=-\dfrac{(\gamma -1)\phi _0}{A}(P-P_0)^{F_1}\left| \dfrac{\partial (P-P_0)}{\partial R}\right| ^{1/n-1}\dfrac{\partial (P-P_0)}{\partial R}, \end{aligned}$$

(18)

$$\begin{aligned}&\dfrac{1}{R^{d-1}}\dfrac{\partial }{\partial R}\left( R^{d-1}(P-P_0)^{F_1}\left| \dfrac{\partial (P-P_0)}{\partial R}\right| ^{1/n-1}\dfrac{\partial (P-P_0)}{\partial R}\right) \nonumber \\&\quad =A(P-P_0)^{\gamma -2}\dfrac{\partial (P-P_0)}{\partial T}, \end{aligned}$$

(19)

$$\begin{aligned}&\int _0^{R_N(T)}(P-P_0)^{\gamma -1}R^{d-1}{\text {d}}R=\varLambda _0T^{\alpha }, \end{aligned}$$

(20)

where the two parameters

$$\begin{aligned} A=(\gamma -1)(2C_t)^{1/n}\dfrac{3n+1}{n}\left( \dfrac{3\phi _0}{50}\right) ^{(n+1)/(2n)},\quad \varLambda _0=\dfrac{M_0}{\omega H^{3-d}\phi _0} \end{aligned}$$

(21)

are proportional to the volumetric compliance coefficient and to the strength of the injection, respectively. Equations (6) and (11–13) expressing initial and boundary conditions are formally unchanged, except that dimensionless quantities (in capital letters) replace dimensional ones.

3 Solution to the Problem

The mathematical problem is amenable to a self-similar solution, with the similarity variable defined as

$$\begin{aligned} \eta =A^{F_4}R/T^{F_2}. \end{aligned}$$

(22)

The solution then takes the form

$$\begin{aligned} R_N(T)= & {} \eta _NA^{-F_4}T^{F_2}, \end{aligned}$$

(23)

$$\begin{aligned} P(R,T)= & {} P_0+A^{dF_4/(\gamma -1)}\eta _N^{F_5}T^{F_3}\varPsi (\zeta ), \end{aligned}$$

(24)

$$\begin{aligned} F_2= & {} \dfrac{\alpha [(n+1)(\beta -\gamma +1)+2]+2 n (\gamma -1)}{d[(n+1)(\beta -\gamma +1)+2]+2(n+1)(\gamma -1)}, \end{aligned}$$

(25)

$$\begin{aligned} F_3= & {} \dfrac{2\alpha (n+1)-2nd}{d[(n+1)(\beta -\gamma +1)+2]+2(n+1)(\gamma -1)}, \end{aligned}$$

(26)

$$\begin{aligned} F_4= & {} \dfrac{2n(\gamma -1)}{d[(n+1)(\beta -\gamma +1)+2]+2(n+1)(\gamma -1)}, \end{aligned}$$

(27)

$$\begin{aligned} F_5= & {} \dfrac{2(n+1)}{(n+1)(\beta -\gamma +1)+2}, \end{aligned}$$

(28)

where $\zeta =\eta /\eta _N$ and the coefficient $\eta _N(\alpha ,\beta ,\varLambda _0)$ indicates the value of $\eta$ at the pressure front. Hence, (19) and (20) transform, respectively, into

$$\begin{aligned}&\displaystyle \dfrac{{\text {d}}}{{\text {d}} \zeta }\left( \zeta ^{d-1}\varPsi ^{F_1}\dfrac{{\text {d}}\varPsi }{{\text {d}}\zeta }\left| \dfrac{{\text {d}}\varPsi }{{\text {d}}\zeta }\right| ^{1/n-1}\right) =F_3\zeta ^{d-1}\varPsi ^{\gamma -1}-F_2\zeta ^d\varPsi ^{\gamma -2}\dfrac{d\varPsi }{d\zeta }, \end{aligned}$$

(29)

$$\begin{aligned}&\displaystyle \eta _N=\left( \dfrac{1}{\varLambda _0}\int _0^1\zeta ^{d-1}\varPsi ^{\gamma -1}{\text {d}}\zeta \right) ^{-1/[d+F_5(\gamma -1)]}, \end{aligned}$$

(30)

with boundary conditions

$$\begin{aligned} \varPsi (1)=0,\quad \dfrac{{\text {d}}\varPsi }{{\text {d}}\zeta }(1)=0. \end{aligned}$$

(31)

When the injection is instantaneous ($\alpha =0$), a closed-form solution is derived in the form

$$\begin{aligned}&\displaystyle \varPsi (\zeta )=D(1-\zeta ^{n+1})^{F_5/(n+1)},\quad \eta _N=\left( \dfrac{\varLambda _0}{D^{\gamma -1}E}\right) ^{1/[d+F_5(\gamma -1)]}, \end{aligned}$$

(32)

$$\begin{aligned}&\displaystyle D=\left[ \dfrac{1}{F_5}\left( \dfrac{F_2}{\gamma -1}\right) ^n\right] ^{F_5/(n+1)}, \end{aligned}$$

(33)

$$\begin{aligned}&\displaystyle E=\dfrac{1}{n+1}{\mathrm {B}}\left( \dfrac{d}{n+1},1+\dfrac{F_5(\gamma -1)}{n+1}\right) , \end{aligned}$$

(34)

where ${\mathrm {B}}(\cdot ,\cdot )$ is the beta function.

For $\alpha \ne 0$, the integration is performed numerically; a second boundary condition on the first derivative near the front end is computed by expanding the shape function in series, obtaining

$$\begin{aligned}&\left. \dfrac{{\text {d}}\varPsi }{{\text {d}}\zeta }\right| _{\zeta \rightarrow 1}=a_0(1-\zeta )^{a_1}, \end{aligned}$$

(35)

$$\begin{aligned}&a_0=\left( \dfrac{F_2}{a_1^{1/n}F_1+(a_1-1)/n}\right) ^{na_1},\quad a_1=\dfrac{1}{nF_1+1+n(1-\gamma )}. \end{aligned}$$

(36)

Fig. 2

Shape factor $\varPsi$ as a function of dimensionless rescaled similarity variable $\zeta$ for cylindrical geometry, $d=2$; results are shown for $n=0.25,0.50,0.75$ (upper, intermediate, and lower row) and $\alpha =0,1$ (left and right column), with $\beta =0.25,0.50,0.75$ (dashed, solid, and dash-dotted line) and $\gamma =1.25$

Fig. 3

Prefactor $\eta _N$ as a function of $\alpha$ for cylindrical geometry, $d=2$, for $\varLambda _0=1.0,0.1,0.01$ (upper, intermediate, and lower panel), with $n=0.25,0.50,0.75$ (dashed, solid, and dash-dotted line), $\beta =0.25,0.50,0.75$ (thin, medium, and thick line) and $\gamma =1.25$

The shape factor $\psi (\zeta )$ obtained analytically or by numerical integration is depicted in Fig. 2 for cylindrical geometry ($d=2$), instantaneous and constant rate injection ($\alpha =0$ and 1), various values of n and $\beta$, and $\gamma =1.25$. The shape factor is seen to increase with rate of injection $\alpha$ and permeability compliance $\beta$, and to decrease with rheological index n. The shape factor also decrease with permeability compliance $\gamma$ and geometry parameter d (not shown). The dependence on $\beta$ is attenuated as $\alpha$ increases. The prefactor $\eta _N$ is likewise illustrated in Fig. 3 for $d=2$, various values of n and $\beta$, and $\gamma =1.25$, showing its dependency on $\alpha$ for different values of the parameter $\varLambda _0=1.0,0.1,0.01$. It is seen that $\eta _N$ consistently decreases with $\alpha$ and $\varLambda _0$ for all cases, while it increases or decreases with n and $\beta$ depending on the $\alpha$ value. The dependence on $\varLambda _0$ and n is more marked than that on $\alpha$ and $\beta$ except for values of $\alpha$ close to zero. The shape factor decreases for increasing $\gamma$ (not shown); it also decreases for increasing d but only for $\alpha =0$, and the opposite is true for $\alpha =1$ (not shown).

4 Limits of Validity

It is noted that for the solution to retain a physical meaning, the expression (23) of the distance of propagation of the pressure front $R_N(T)$ needs to increase with time, hence $F_2>0$. This leads to a set of limitations on the values of model parameters $\gamma ,\beta ,\alpha ,n$. Upon setting $(\gamma -1)/(\beta +2)<3$, or equivalently $\gamma < \gamma _0 \equiv 3 \beta +7$ (a bound needed only for the case of spherical geometry with $d=3$, a plausible assumption since for a single fracture $\beta =2(\gamma -1)$), these limitations simplify as follows: i) for $\gamma \le \gamma _1 \equiv (n+3)/(n+1)$, $F_2>0$ for any $\beta ,\alpha ,n$; ii) for $\gamma > \gamma _1$ and $\beta \ge \beta _1 \equiv \gamma -\gamma _1 = \gamma -(n+3)/(n+1)$, $F_2>0$ for any $\alpha ,n$; iii) for $\gamma > \gamma _1$ and $\beta < \beta _1$, $F_2>0$ for

$$\begin{aligned} \alpha < \alpha _0 \equiv \dfrac{2 n (\gamma -1)}{(n+1)(\beta -\gamma +1)+2}, \end{aligned}$$

(37)

i.e. the injection rate ($\alpha$) must not exceed a critical limit value $\alpha _0$ depending on domain properties ($\beta$ and $\gamma$) and fluid behaviour index (n) but not on geometry (d). In practice, a threshold value is set to the strength of the injection only when the permeability–pressure coefficient $\beta$ and porosity–pressure coefficient $\gamma -1$ are markedly different.

Under these assumptions, the pressure front accelerates, has constant speed, or decelerates depending on whether $F_2-1\gtreqless 0$. A detailed analysis, reported in “Appendix”, shows that the critical parameters $\gamma _1(n)$, $\gamma _2(n,d)$, $\beta _1(n,\gamma )$, $\beta _2(n,\gamma ,d)$, $\alpha _1(n,\gamma ,\beta ,d)$ govern this dependency. For plane geometry ($d=1$), only $\gamma _1(n)$, $\beta _1(n,\gamma )$, and $\alpha _1(n,\gamma ,\beta ,d)$ are relevant, while for cylindrical or spherical geometry ($d=2,3$) two additional critical parameters $\beta _2(n,\gamma ,d)$ and $\gamma _2(n,d)$ emerge. Some critical parameters are defined only beyond a threshold value of (an)other critical parameter(s). $\beta _1(n,\gamma )$ and $\gamma _1(n)$ coincide with the parameters reported above discussing the positivity of the exponent $F_2$.

Finally, the pressure field increases or decreases with time at a given location if $F_3\gtrless 0$, equivalent to $\alpha \gtrless \alpha _2(n,d)$, with $\alpha _2 = dn/(n+1)$.

Fig. 4

Constraints on the parameters $\alpha$ and $\beta$ for $n=0.5$ and $d=1,\,2,\,3$ ($\gamma _c=2.33$). i) The combination of parameters leading to an accelerated pressure front lies to the right of the curve for given $\gamma$ (also to the left for $d=3$). The cross-hatched areas represent valid combinations for $\gamma =4$; the corresponding critical value $\beta _1$ of $\beta$ is shown with the vertical dotted line $\beta =\beta _1$, which is an asymptote for $\alpha _1$; the asymptotes for different values of $\gamma$ are not shown for clarity. ii) The condition of decreasing pressure within the porous domain is given by $\alpha <\alpha _2$; the coloured area (yellow online), delimited by the dashed line $\alpha =\alpha _2$, represents these conditions

Figure 4 depicts the combinations of values leading to an accelerated current and to a time-decreasing pressure field for a fluid with $n=0.5$ and for different geometries ($d=1,\;2,\;3$), for different values of $\gamma$ and highlighting the case $\gamma =4$. We observe that increasing $\beta$ (i.e. increasing the efficiency of the overpressure in widening the fractures, with a consequent increment of the permeability) or reducing $\gamma$ (the compliance) requires lower $\alpha$ values to generate an accelerating pressure front. In conditions of large enough compliance ($\gamma > \gamma _1$, as shown in the figure), the critical value $\beta _1$ is an asymptote for $\alpha _1$, and for $\beta < \beta _1$ the pressure front is decelerated for any strength of the injection ($\alpha$). In conditions of lower compliance ($\gamma \le \gamma _1$), the permeability–pressure relationship ($\beta$) is not influential, and the type of pressure front (decelerated/accelerated) is linked only to $\alpha$.

An accelerating pressure front can appear for low $\beta$ and $\alpha$ and high $\gamma$, see the right lower corner of the lower panel for $d=3$. This is the case of a ‘stiff’ system with strong increment of storage capacity with overpressure (e.g. a system where a network of microfractures develops, with a limited increment of permeability but a strong increment of porosity), subject to inflow with moderate $\alpha$. The figure also shows that the pressure field increases in time if $\alpha >\alpha _2$; this limit increases with dimensionality as expected. For $d=1$, an accelerating pressure front can only be coupled with a time-increasing pressure. For $d=2,3$, an accelerating pressure front can be also coupled with time-decreasing pressure, provided that $\gamma >\gamma _2$ and $\beta <\beta _2$.

Focusing on the most common cases of injection, i.e. impulsive ($\alpha =0$), and constant influx ($\alpha =1$), we conclude that: (i) impulsive injection generates a pressure field always decreasing in time, with the pressure front never accelerating for $d=1$, and possibly accelerating for a combination of sufficiently high values of $\gamma$, and sufficiently low values of $\beta$, for $d=2,\,3$. (ii) Constant influx injection generates a pressure field always increasing in time, for $d=1$; generally increasing in time (and stationary in the limit case $n=1$), for $d=2$; decreasing/increasing in time for $n\gtrless 1/2$, for $d=3$. (iii) Constant influx injection generates a pressure front always decelerating for $d=1,\,2$ and accelerating for $\gamma >\gamma _3 \equiv [\beta (n+1)+n+2]/n$, for $d=3$.

5 An Example Application

We consider the injection of a power-law shear-thinning fluid following the procedures of fracing for stimulating oil or gas production in existing wells. The fluid rheology during the initial phase of the fracing procedure (no significant leak-off) is described by a power-law model with behaviour index $n=0.5$, consistency index $\widetilde{\mu }=1.5\,{\mathrm {Pa}}\,{\mathrm {s}}^n$, and mass density $\rho =1000\,{\mathrm {kg}}\,{\mathrm {m}}^{-3}$. We assume that a vertical well allows a constant flow rate injection ($\alpha =1$) equal to $3.0\,{\mathrm {kg}}\,{\mathrm {s}}^{-1}$in a horizontal gas or oil-bearing formation with thickness $h=10\,{\mathrm {m}}$ and a nominal permeability and porosity of the fractures equal to $k_0=1.1\times 10^{-12}\,{\mathrm {m}}^2$ and $\phi _0=0.01$, respectively. The permeability of the matrix is taken to be $k_M=1.1\times 10^{-15}\,{\mathrm {m}}^2$ (including the effect of the filter cake at the interface between fractures and matrix); its porosity is equal to $\phi _M=0.1$. The ratio between the permeabilities of fractures and matrix is 1000, that between corresponding porosities is 0.1, rendering the simplified model described in the previous section applicable for a radial geometry ($d=2$). The pressure front is decelerated ($\alpha =1 < \alpha _1 = 2.25$). Figure 5 shows the pressure distribution within the domain at a given time, and the position of the pressure front versus time, for different values of $\beta$ and $\gamma$. It is seen that increasing $\beta$ and $\gamma$ implies higher pressures. The sensitivity to variations of $\gamma$ is higher than to variations of $\beta$, implying that the compliance parameter $\gamma$ is a key factor in determining system behaviour. The diffusion of pressure is faster for decreasing $\beta$ and increasing $\gamma$. Increasing the fluid behaviour index of the fluid, or the consistency, reduces the mobility; hence, the speed of the pressure front is reduced and the pressure at the injection well is enhanced (not shown).

Fig. 5

a Left panel pressure distribution after 30  min with a constant rate injection ($\alpha =1$) in cylindrical geometry ($d=2$). b Right panel front-end position against time. $\beta =0.25$ (continuous line); $\beta =0.5$ (dashed line); $\beta =0.75$ (dashdot line). $\gamma =1.25$ (thick lines), $\gamma =1.5$ (thin lines). The mass flow rate is $m_0=3.0\,{\mathrm {kg}}\,{\mathrm {s}}^{-1}$. Shear-thinning fluid with $n=0.5$, $\widetilde{\mu }=1.5\,{\mathrm {Pa}}\,{\mathrm {s}}^n$, $\rho =1000\,{\mathrm {kg}}\,{\mathrm {m}}^{-3}$

Figure 6 shows the absolute value of the ratios I/II and III/IV between the terms in Eq. (5). The left panel shows that term II is smaller than term I except near the origin for $\zeta \lessapprox 0.1$, with a weak dependence on time. The right panel shows that term IV is smaller than term III for $\zeta \lessapprox 0.2$ for $T=T_{{\text {max}}}$. Hence, the assumptions in deriving the simplified model are satisfied in most of the domain.

Fig. 6

a Left panel absolute value of the ratio between terms I and II in Eq. (5). b Right panel absolute value of the ratio between terms III and IV in Eq. (5). Curves refer to $10^{-2}T_{{\text {max}}}$ (continuous line), $10^{-1}T_{{\text {max}}}$ (dashed line), and $T_{{\text {max}}}$ (dashdot line)

6 The Effect of Leak-Off

The much higher permeability of the fractures with respect to the matrix justifies a model where the flow into the matrix is neglected at least during the early stage of injection. In addition, fluid loss is also limited because the fracing fluids favour the building of a filter cake on the fracture face. At larger times, the fluid seeps into the matrix and leak-off can be very high. A further distinction can be made between matrix leak-off and fissure leak-off. The former is controlled by the characteristics of the matrix, e.g. permeability, compressibility, pore size, fluid rheology, and by the wall filter cake; the latter is controlled by the characteristics of the fissured rock. A first approximation of the leak-off phenomenon can be obtained by neglecting the details of the fluid flow within the matrix, considering only its effects on mass balance. By assuming that the internal pressure in the matrix is equal to the initial ambient value $p_0$, the internal pressure gradient controlling the flow from the fractures to the matrix is of order $(p-p_0)/l$, being l a characteristic size of the block. The velocity of the leaking-off fluid hence can be expressed as

$$\begin{aligned} u\approx \left( \dfrac{k_M}{\mu _{{\text {eff}}}}\right) ^{1/n}\dfrac{(p-p_0)^{1/n}}{l^{1/n}}, \end{aligned}$$

(38)

and Eq. (9) becomes

$$\begin{aligned}&\left( \dfrac{1}{2\widetilde{\mu }C_t}\right) ^{1/n}\dfrac{n\phi _0}{3n+1}\left( \dfrac{50k_0}{3\phi _0}\right) ^{(n+1)/(2n)}\dfrac{1}{p^{*F_1}}\nonumber \\&\qquad \times \dfrac{1}{r^{d-1}}\dfrac{\partial }{\partial r}\left( r^{d-1}(p-p_0)^{F_1}\dfrac{\partial (p-p_0)}{\partial r}\left| \dfrac{\partial (p-p_0)}{\partial r}\right| ^{1/n-1}\right) \nonumber \\&\qquad -\left( \dfrac{1}{2\widetilde{\mu }C_{tM}}\right) ^{1/n}\dfrac{n\phi _M}{3n+1}\left( \dfrac{50k_M}{3\phi _M}\right) ^{(n+1)/(2n)}\dfrac{(p-p_0)^{1/n}}{l^{1+1/n}}\nonumber \\&\quad =\dfrac{(p-p_0)^{\gamma -2}}{p^{*\gamma -1}}\phi _0(\gamma -1)\dfrac{\partial (p-p_0)}{\partial t}, \end{aligned}$$

(39)

where the subscript M indicates the variable or parameter is referred to the matrix.

In dimensionless form, the previous equation becomes

$$\begin{aligned}&\dfrac{1}{R^{d-1}}\dfrac{\partial }{\partial R}\left( R^{d-1}(P-P_0)^{F_1}\left| \dfrac{\partial (P-P_0)}{\partial R}\right| ^{1/n-1}\dfrac{\partial (P-P_0)}{\partial R}\right) \nonumber \\&\quad -\lambda \left( P-P_0\right) ^{1/n}= A(P-P_0)^{\gamma -2}\dfrac{\partial (P-P_0)}{\partial T}, \end{aligned}$$

(40)

where the leak-off term is proportional to the parameter

$$\begin{aligned} \lambda =\left( \dfrac{C_t}{C_{tM}}\right) ^{1/n}\left( \dfrac{k_M}{k_0}\right) ^{(n+1)/(2n)}\left( \dfrac{\phi _0}{\phi _M}\right) ^{(1-n)/(2n)}\left( \dfrac{r^*}{l}\right) ^{1+1/n}. \end{aligned}$$

(41)

The modified integral mass balance reads in dimensionless form as

$$\begin{aligned}&\int _0^{R_N(T)}(P-P_0)^{1/n}R^{d-1}{\text {d}}R\nonumber \\&\quad +\,F\int _0^T\int _0^{R_N(T)}(P-P_0)^{1/n}R^{d-1}{\text {d}}R\,{\text {d}}T=\varLambda _0T^{\alpha }, \end{aligned}$$

(42)

with

$$\begin{aligned} F= & {} \left( \dfrac{r^*}{l}\right) ^{(n+1)/n}\left( \dfrac{k_M}{k_0}\right) ^{(n+1)/(2n)}\nonumber \\&\times \dfrac{n}{3n+1}\dfrac{1}{\phi _0\phi _M^{(1-n)/(2n)}}\left( \dfrac{50}{3}\right) ^{(n+1)/(2n)}\left( \dfrac{1}{2C_{tM}}\right) ^{1/n}, \end{aligned}$$

(43)

and where the second term on the left-hand side in Eq.  (42) is the mass leak-off.

The initial and the boundary condition are still coincident with Eqs. (6) and (11–13) with dimensionless quantities replacing dimensional ones.

The differential problem outlined above, including mass leak-off, does not have a general self-similar solution and needs to be solved numerically. However, for the special case $\gamma -1=1/n$ (implying $2<\gamma <6$ for $0.2<n<1$), the following transform

$$\begin{aligned} \left\{ \begin{aligned}&f=\left( P-P_0\right) \exp (\lambda T)\\&\tau =\dfrac{1-\exp (-\lambda F_{1l} T)}{\lambda F_{1l}}, \end{aligned} \right. \end{aligned}$$

(44)

with $\,F_{1l}\equiv F_1(\gamma -1=1/n)$, reduces Eq. (40) to

$$\begin{aligned} \dfrac{1}{R^{d-1}}\dfrac{\partial }{\partial R}\left( R^{d-1}f^{F_{1l}}\left| \dfrac{\partial f}{\partial R}\right| ^{1/n-1}\dfrac{\partial f}{\partial R}\right) = Af^{1/n-1}\dfrac{\partial f}{\partial \tau }. \end{aligned}$$

(45)

The transform was suggested by Gurtin and MacCamy (1977) and later on used by King and Woods (2003) in a similar context.

By assuming the further constraint

$$\begin{aligned} \int _0^{R_N(T)}f^{1/n}R^{d-1}{\text {d}}R=\varLambda _0\tau ^{\alpha }, \end{aligned}$$

(46)

coincident with Eq. (20) for $T\rightarrow 0$, a self-similar solution formally identical to Eqs.(22–23–24) can be obtained upon defining

$$\begin{aligned} \eta _l=A_l^{F_{4l}}R/\tau ^{F_{2l}}. \end{aligned}$$

(47)

Fig. 7

Mass injection function for the original problem, $M(T)\propto T^{\alpha }$ with $\alpha =1$ (bold line), and for the problem with leak-off for $F_{1l}=0.5$ and $\lambda =0.001$ (dashed line) and 0.01 (dashdot line). The corrected exponents are $\alpha _{{\text {corr}}}=1.008,\,1.084$, respectively

The similarity solution then takes the form

$$\begin{aligned} R_{Nl}(\tau )= & {} \eta _{lN}A_l^{-F_{4l}}\tau ^{F_{2l}}, \end{aligned}$$

(48)

$$\begin{aligned} f(R,\tau )= & {} A_l^{ndF_{4l}}\eta _{lN}^{F_{5l}}\tau ^{F_{3l}}\varPsi (\zeta _l), \end{aligned}$$

(49)

where $\zeta _l=\eta _l/\eta _{lN}$ and the subscript l indicates the leak-off solution for the special case considered, i.e. $\gamma -1=1/n$. The new similarity solution is an approximation of the real solution under certain hypotheses. In terms of the original variables P and T, the constraint represented by Eq. (46) reads

$$\begin{aligned} \int _0^{R_N(T)}(P-P_0)^{1/n}R^{d-1}{\text {d}}R=\varLambda _0\left[ \dfrac{1-\exp (-\lambda F_{1l} T)}{\lambda F_{1l}}\right] ^{\alpha }\exp \left( -\dfrac{\lambda }{n} T\right) , \end{aligned}$$

(50)

and implies an injection of mass with a different law with respect to the monomial expression $\varLambda _0T^{\alpha }$ adopted in Eq. (42). Moreover, the leak-off mass is not included in the balance. However, at short times the contribution of the leak-off to the integral mass balance can be neglected since the value of F is usually very low, being $k_M/k_0\approx 10^{-1}-10^{-3}$ and being the other coefficients in Eq. (43) of O(1). In addition, a small correction of the exponent $\alpha$ renders

$$\begin{aligned} \left[ \dfrac{1-\exp (-\lambda F_{1l} T)}{\lambda F_{1l}}\right] ^{\alpha _{{\text {corr}}}}\exp \left( -\dfrac{\lambda }{n} T\right) \approx T^{\alpha }, \end{aligned}$$

(51)

where $\alpha _{{\text {corr}}}$ is the corrected value of $\alpha$, at least for a time interval $0<T<T_{{\text {max}}}$, with $\alpha _{{\text {corr}}}$ and $T_{{\text {max}}}$ depending on $\lambda ,\,F_{1l},\,n$. Figure 7 shows the mass injection function for the original problem and for the problem with leak-off for $n=0.5$, $F_{1l}=0.5$, and $\lambda =0.001,0.01$. The values $\alpha _{{\text {corr}}}=1.008,\,1.084$ are computed imposing the mass injected in the system to be identical at time $T=10$.

Figure 8 shows the pressure distribution within the domain and the position of the pressure front versus time, comparing results obtained with and without leak-off. We note that the inclusion of the leak-off phenomenon entails a reduced speed of the pressure front and reduced values of pressure at each section. A more intense leak-off (larger values of parameter F) increases the discrepancy with respect to the ‘sealed’ fracture model not including leak-off.

Fig. 8

Comparison between results without leak-off (continuous lines) and with leak-off (dashed lines) for a constant injection rate ($\alpha =1$) in cylindrical geometry ($d=2$). The mass flow rate is $m_0=1.0\,{\mathrm {kg}}\,{\mathrm {s}}^{-1}$. Fluid parameters are $n=0.75$, $\widetilde{\mu }=1.0\,{\mathrm {Pa}}\,{\mathrm {s}}^n$, $\rho =1000\,{\mathrm {kg}}\,{\mathrm {m}}^{-3}$. Domain parameters are $\beta =1.0$, $\gamma =1+1/n=2.33$, $\lambda =0.00021$. The mass leak-off factor is $F=0.048$, and the corrected value of the injection exponent for the approximated self-similar solution is $\alpha _{{\text {corr}}}=0.999$. a Left panel pressure distribution after 10–30 min. b Right panel front-end position against time

7 Conclusion

We have presented a novel model describing the one-dimensional diffusion of a pressure front in generalized geometry (plane, radial, and spherical) due to the injection of a shear-thinning fluid in a fractured medium, when the fractures widen proportionally to the pressure level with a monotonic law. Upon starting the injection, the fluid widens the fractures and flows at a progressively larger rate due to the increased permeability of the fractures and, at a second stage, also filtrates into the porous matrix surrounding the fractures (leak-off phenomenon).

The properties of the fractured medium controlling the process are the nominal storage capacity $\phi _0$ and permeability $k_0$, with the two exponents $\beta >0$ and $\gamma >1$ expressing the permeability and compliance variation with pressure, respectively.

When the leak-off towards the porous matrix is negligible, a self-similar solution is obtained when the injected mass increases with time according to $m\propto t^{\alpha }$. A closed-form expression is derived for an instantaneous injection ($\alpha =0$), while numerical integration is warranted for the general case $\alpha \ne 0$. When mass leak-off is included, the more realistic case including mass leak-off can be solved via numerical integration of the differential problem; an approximate self-similar solution can be obtained in the special case $\gamma =1+1/n$.

The self-similar solutions allow deriving the time behaviour of the pressure within the domain, and the rate of advancement of the pressure front, as a function of model parameters. An analysis of their effect on the solution suggests some combinations of parameters yield unphysical results; hence, the possible ranges of variation of the parameters are defined with the help of some critical values of the inflow rate $\alpha$. In most cases of practical interest, a constant injection rate ($\alpha =1$) entails a decelerated pressure front and a decay over time of the pressure within the domain. The pressure diffusion is faster for high volumetric compliance ($\gamma$) and low permeability compliance ($\beta$). Very shear-thinning ($n\ll 1$) fluids propagate faster than shear-thinning or quasi-Newtonian fluids. The effect of leak-off is the reduced speed of the pressure front and lower pressure within the domain. In general, the pressure at the origin decays quite fast and is highly sensitive to the fluid rheological characteristics and to the mass discharge. In a linear or cylindrical geometry ($d=1,\,2$), a constant influx ($\alpha =1$) always generates a time-increasing pressure and a decelerated pressure front. In radial geometry ($d=3$), the same behaviour is obtained provided $n<1/2$; otherwise, the pressure is time-decreasing.

Appendix

The purpose of this Appendix is to illustrate the combinations of model parameters $\gamma ,\beta ,\alpha$ associated with a decelerated ($F_2-1<0$), constant-speed ($F_2-1=0$), or accelerated pressure front ($F_2-1>0$), respectively; the fluid rheology (n) and the domain geometry (d) are not subject to constraints. First of all, the critical parameters listed in Table 1 are derived; the parameters $\gamma _1$ and $\beta _1$ are those reported in Sect. 4 discussing the positivity of the exponent $F_2$. The combinations of parameters leading to $F_2-1\gtreqless 0$ are reported in Table 2 for plane geometry and in Table 3 for cylindrical and spherical geometry. Tables 2 and 3 include the conditions derived in Sect. 4 for the positivity of $F_2$. Note that when the conditions $\gamma >\gamma _i, i=1,2$ appear, it is also implied that $\gamma <\gamma _0$ for $d=3$, as the latter condition is required for the validity of the solution in spherical geometry; there is no contradiction since for $d=3$, $\gamma _i<\gamma _0$ for all combinations of parameters.

Table 1 Critical parameters $\gamma _1(n)$, $\gamma _2(n,d)$, $\beta _1(n,\gamma )$, $\beta _2(n,\gamma ,d)$, $\alpha _1(n,\gamma ,\beta ,d)$ for plane geometry ($d=1$, first column) and cylindrical or spherical geometry ($d=2,3$, third column). Parameters in the second column hold for $d=1, 2, 3$

Table 2 Conditions for decelerated ($F_2<1$), constant-speed ($F_2=1$), and accelerated ($F_2>1$) pressure front for plane geometry ($d=1$)

Table 3 Conditions for decelerated ($F_2<1$), constant-speed ($F_2=1$), and accelerated ($F_2>1$) pressure front for cylindrical and spherical geometry ($d=2,3$)