1 Introduction

In recent times, everybody across the world acutely concerns about the safety of the environment of our planet and the mathematics related to the “system Earth” finds itself challenged by new problems nearly every day. Some of these problems are related to the earth’s response under excitation, and causes and damages due to earthquake can be better predicted by studying and analyzing the theory of wave propagation in layer media.

The theory of wave propagation deals with small periodic and aperiodic disturbance in a medium. When these elastic waves propagate in the earth as a result of an earthquake or other disturbance, these waves are usually called seismic waves. An important approach to the knowledge of the interior of the earth is the study in which way the elastic waves travel through it. The two main types of seismic waves are body waves and surface waves. When traveling through the interior of the earth, body waves arrive before the surface waves emitted by an earthquake. These waves are of higher frequency than surface waves. But surface waves usually have larger amplitudes and longer wavelengths than body waves. Although these surface waves arrive after body waves, then also they are almost entirely responsible for any type of damage and destruction associated with earthquakes. These waves provide most direct and rich information regarding the structure of earth’s interior to seismologists. Surface wave which appears to travel along the earth’s surface consists approximately of harmonic waves of varying amplitudes and of progressively diminishing periods. There are mainly two types of surface waves as Love waves and Rayleigh waves.

Rayleigh waves, also called ground roll, are surface waves that travel as ripples with motions. The particle motion in these waves is confined to the neighborhood of the free surface and involves both the body waves, P and S waves. The effect of these waves decreases rapidly with depth from the free surface, and they are slower than body waves, and velocity is roughly 90 % of the velocity of S waves for typical homogeneous elastic media. The existence of these waves was predicted by Lord Rayleigh, in 1885. Most of the shaking felt from an earthquake is due to the Rayleigh wave which can be much larger than the other waves.

Love waves are surface waves that cause circular shearing of the ground, the particle motion during the passage of these waves is purely horizontal and normal to the direction of wave propagation. In 1911, A. E. H. Love, a British mathematician presented a mathematical model of these waves in a layered structure. They usually travel slightly faster than Rayleigh waves, and velocity is about 90 % of the S wave velocity and have the largest amplitude creating most of the damage and destruction associated with earthquakes.

Love (1911) demonstrated that these waves propagate by multiple reflections between the top and the bottom surfaces of the low-speed layer. These waves are dispersive, the velocity increasing with wave length. However, the homogeneous and isotropic layered model of the earth considered by Love does not describe the real situation very well.

As a matter of fact, all the materials of the earth are not always elastic and isotropic. The layer of the soil in the earth is supposed to be more sandy than elastic. A dry sandy mantle may be defined as a layer consisting of sandy particles retaining no moistures or water vapors. Weiskopf (1945) has discussed the mechanics of dry sandy soil, and it reveals that due to the slippage of granular particles in a dry sandy soil, \(\frac{E}{\mu }>2(1+\sigma )\), where E is the Young’s modulus of elasticity, \(\mu \) is the rigidity and \(\sigma \) is the Poisson’s ratio. Weiskopf suggested that the relationship \(\frac{E}{\mu }=2\eta (1+\sigma )\) could be appropriate for the dry sandy soil, where \(\eta \) (\(>\)1) is termed as sandy parameter and \(\eta =1\) corresponds to an elastic solid.

The earth also contains fluid-saturated porous rocks in the form of sandstone, limestone and others permeated by groundwater or oil. The diffusion of fluid and readjustment of fluid pressure have been acting as a triggering mechanism for earthquakes. Due to the factors such as external pressure, slow process creep, difference in temperature, and manufacturing processes, the media stay under high stress, known as initial stress for which the layers of the earth exhibit anisotropy, i.e., deviates from the directionally regular elastic behavior of an isotropic material. The Earth is also a gravitating medium due to the presence of overburden layers. The presence of gravity field and internal friction of dry sandy material will have effect on the propagation of the surface waves. So it is more worthy to study the propagation of Love waves in an initially stressed dry sandy layer over a fluid-saturated anisotropic porous half-space under the influence of gravity.

A detailed information about the propagation of seismic waves in layered media is presented by Ewing et al. (1957). Porous materials are linked with soil and rocks. Naturally occurring media are generally porous and liquid filled with amazing characteristics such as anisotropy, heterogeneity, and sandiness. The pore size is assumed to be very small, so the average distribution is uniform. Poro-elastic models describe the interaction between fluid motion and deformation in porous media.

Biot (1955, 1956a, b, c) developed the dynamic theory of wave propagation in fluid-saturated porous media. He extended the theory of acoustic propagation in the wider context of the mechanics of porous media (Biot 1962a, b). By virtue of Biot’s theory, many researchers studied Love waves in numerous layered media.

Deresiewicz (1961) discussed analytically the frequency equation for the propagation of Love waves in a porous layer lying over an elastic solid half-space. He generalized this study by assuming isotropic elastic layer sandwiched between a porous elastic solid layer and an isotropic elastic half-space. Paul (1964) deduced the dispersion equation for the propagation of Love waves in a porous layer sandwiched between two impermeable elastic half-spaces. Deresiewicz (1964, 1965) then discussed the effects of boundaries on the propagation of Love waves in a liquid-filled double-surface layer as well as double-internal stratum. Rao et al. (1977) discussed the propagation of Love wave in poro-elastic medium and observed that SH wave propagation in a semi-infinite poro-elastic body is not possible except in a layer of another poro-elastic medium over it. Chattopadhyay et al. (1986) considered the propagation of Love waves in a homogeneous, isotropic porous layer overlying an inhomogeneous half-space generated by a point source situated at the interface of the layer and the half-space. The propagation of Love waves in a fluid-saturated porous layer has been discussed by Konczak (1989). Propagation of Love waves in an initially stressed medium consisting of a slow elastic layer over a liquid-saturated porous half-space with small porosity was reported by Sharma and Gongna (1991); it has been observed that the presence of pores and initial stress change the upper and lower bounds of Love wave velocity in comparison with the isotropic elastic medium. Wang and Zhang (1998) studied the propagation of Love waves in a transversely isotropic fluid-saturated porous layered half-space. Sahay et al. (2001) discussed the seismic wave propagation inhomogeneous and anisotropic porous medium. Sharma (2004) studied the propagation of surface waves in a general anisotropic poro-elastic solid half-space by iterative numerical method. Ke et al. derived the dispersion equation of Love wave in an inhomogeneous fluid-saturated porous layer over a half-space and found that the inhomogeneity of the saturated layer has the significant effects on the dispersion of the Love wave. It has been also noticed that the inhomogeneity influences the attenuation slightly in the low-frequency regime and significantly in the high-frequency regime (Ke et al. 2006). Gupta et al. (2010a) studied the effect of initial stress on propagation of Love waves in an anisotropic porous layer and observed that for small initial tensile stress in the porous medium, the velocity of the wave increases, but the large magnitude of tensile stress does not allow Love waves to propagate. Kundu et al. (2013) discussed the propagation of Love waves in porous rigid layer lying over an initially stressed half-space and revealed that the phase velocity of Love waves is considerably influenced by rigidity, porosity, and anisotropy of the porous layer and inhomogeneity of the half-space as well.

The acceleration due to gravity is an important factor for analyzing the dynamic and static problems in earth. Biot (1965) considered the effect of gravity on Rayleigh waves in an incompressible half-space. Dey and Chakraborty (1983) have analyzed the effect of gravity and initial stresses on the propagation of Love waves in a transversely isotropic medium. The propagation of Love waves in a fluid-saturated porous layer under a rigid boundary and lying over an elastic half-space under gravity have been studied by Ghorai et al. (2010). Chattaraj et al. presented the effects of transverse and longitudinal rigidity of reinforced material, as well as gravity and porosity over the propagation of Love waves in the fiber-reinforced layer over a gravitating porous half-space (Chattaraj and Samal 2013).

Dai et al. reported the Love wave propagation in double-porosity media (Dai and Kuang 2006) and concluded that Love wave speed is higher in single-porosity layer/half-space than in the double-porosity medium, while the attenuation of Love waves is lower in single-porosity layer/half-space than in double-porosity medium.

Nurhandoko et al. (2012) have done a case study and observed the seismic wave propagation in porous media (carbonate rock) for various frequencies.

However, the study about the propagation of Love waves in initially stressed dry sandy layer over a poro-elastic half-space under the influence of gravity appears to have remained less attempted. In the present paper, an attempt has been made to study the propagation of Love waves in sandy layer under initial stress above anisotropic porous half-space under gravity. The theoretical study of wave propagation consists of finding the solution of a partial differential equation or a system of partial differential equations, under initial and boundary conditions. The equation of motion has been formulated following Biot separately, for different media using suitable boundary condition at the interface of sandy layer and porous half-space under gravity. The presence of gravity, porosity, and sandy parameters in the frequency equation approves the effects of these parameters in the propagation of Love waves in a porous layer, bounded above by sandy layer and below by a gravitating half-space. This problem can be related to the real-world problem, which exists in oil prospecting and surveying technique especially in Gulf region. Augustin (2012) has considered the role of poro-elasticity for modeling of stress fields in geothermal reservoirs. Also the effect of porosity in the propagation of surface wave may be useful in the problem related to structural health monitoring. Kumar and Chakraborty (2014) have studied the displacement response of multistory structures with flexible foundation due to plane–shear wave excitation. So the mathematical expression obtained here may provide the bridge between modeling results and field application.

2 Formulation of the Problem

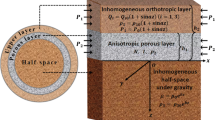
We have considered a model consisting of initially stressed dry sandy layer of finite thickness h overlying an anisotropic porous half-space under gravity.

To study the propagation of Love waves, the cylindrical coordinates have been considered where r and \(\theta \) are the radial and circumferential coordinates, respectively, and the z axis is taken positive vertically downward. The interface is at \(z=0\) between the two layers. The region \(-h <z <0\) is occupied by the dry sandy layer, and the wave is assumed to propagate along the radial direction as shown in Fig. 1.

Fig. 1
figure 1

Geometry of the problem

Full size image

3 Dynamics of Prestressed Dry Sandy Layer and its Solution

As the surface waves propagate along the radial direction r only, all material properties are independent of \(\theta \) and neglecting the body forces, and the dynamic equation of motion for the initially stressed dry sandy layer according to Biot (1965) can be written as

$$\begin{aligned} \frac{\partial \tau _{r\theta } }{\partial r}+\frac{\partial \tau _{z\theta } }{\partial z}+\frac{2}{r}\tau _{r\theta } -\frac{\partial }{\partial z}\left( {Pe_{ \theta z} } \right) =\rho \frac{\partial ^{2}v}{\partial ^{2}t} \end{aligned}$$
(1)

where P is the initial compressive stress along r and \(\rho \) is the density of the medium. \(\tau _{r\theta }\) and \(\tau _{z\theta }\) are the incremental stress components for dry sandy layer under initial stress.

The displacement components are independent of \(\theta \)

i.e., \(u_r =0,u_z =0,u_\theta =v(r, z, t)\)

The nonzero stress components related to strain components are given by

$$\begin{aligned} \tau _{r\theta } =2Ne_{r\theta } , \quad \tau _{z\theta } =2Ne_{z\theta } \end{aligned}$$
(1a)

and the strain–displacement relation is given by

$$\begin{aligned} e_{r\theta } =\frac{1}{2}\left( {\frac{\partial v}{\partial r}-\frac{v}{r}} \right) , \quad e_{\theta z} =\frac{1}{2}\frac{\partial v}{\partial z}\,\hbox {and}\,N=\eta \mu \end{aligned}$$
(1b)

where \(\eta \) is the sandy parameter and \( \mu \) the shear modulus.

Using (1a) and (1b), Eq. (1) can be written as

$$\begin{aligned} \eta \mu \left( {\frac{\partial ^{2}v}{\partial r^{2}}+\frac{1}{r}\frac{\partial v}{\partial r}-\frac{v}{r^{2}}} \right) +\left( {\eta \mu -\frac{P}{2}} \right) \frac{\partial ^{2}v}{\partial z^{2}}=\rho \frac{\partial ^{2}v}{\partial ^{2}t} \end{aligned}$$
(2)

To solve Eq. (2), let us assume

$$\begin{aligned} v=f_1 (r)f_2 (z)\text {e}^{i\omega t} \end{aligned}$$

where \(\omega \) is the angular frequency.

Then, Eq. (2) is reduced to

$$\begin{aligned}&\eta \mu \left( {\frac{\text {d}^{2}f_1 (r)}{\text {d} r^{2}}+\frac{1}{r}\frac{\text {d}f_1 (r)}{\text {d}r}-\frac{f_1 (r)}{r^{2}}} \right) f_2 (z)\nonumber \\&\quad +\left( {\eta \mu -\frac{P}{2}} \right) f_1 (r)\frac{\text {d}^{2}f_2 (z)}{\text {d}z^{2}}+\rho \omega ^{2}f_1 (r)f_2 (z)=0 \end{aligned}$$
(3)

Introducing the nondimensional parameter \(R=k r\), Eq. (3) becomes

$$\begin{aligned}&\eta \mu k^{2} \left( {\frac{\text {d}^{2}f_1 }{\text {d} R^{2}}+\frac{1}{R}\frac{\text {d}f_1 }{\text {d}R}+\left( {1-\frac{1}{R^{2}}} \right) f_1 } \right) f_2 \nonumber \\&\quad +\left( {\eta \mu -\frac{P}{2}} \right) \frac{\text {d}^{2}f_2 }{\text {d}z^{2}}f_1 +\left( {\rho \omega ^{2}-\eta \mu k^{2}} \right) f_1 f_2 =0 \end{aligned}$$
(4)

The equation

$$\begin{aligned} \frac{\text {d}^{2}f_1 }{\text {d} R^{2}}+\frac{1}{R}\frac{\text {d}f_1 }{\text {d}R}+\left( {1-\frac{1}{R^{2}}} \right) f_1 =0 \end{aligned}$$

is Bessel’s equation of the first kind with solution as \(f_1 =J_1 \left( R \right) =J_1 \left( {kr} \right) \).

Hence, Eq. (4) reduces to

$$\begin{aligned} \frac{\text {d}^{2}f_2 }{\text {d}z^{2}}+\alpha ^{2}f_2 =0 \end{aligned}$$
(5)

where

$$\begin{aligned} \alpha =\sqrt{\frac{1}{\left( {1-\xi _1 } \right) }\left( {\frac{c^{2}}{\eta c_1^2 }-1} \right) } k, \end{aligned}$$
(6)

\(c=\omega /k\), the velocity of Love waves,

\(c_1 =\sqrt{\mu /\rho }\), the shear wave velocity along the radial direction in initially stressed sandy layer,

\(k=\) the wave number and \({\xi _1 =P}/{2\mu \eta }\), the nondimensional initial stress parameter.

The solution of Eq. (5) is given by

$$\begin{aligned} f_2 =A\text {e}^{i\alpha z}+B\text {e}^{-i\alpha z} \end{aligned}$$

where A and B are arbitrary constants.

And hence the solution of Eq. (2) is

$$\begin{aligned} v=J_1 (kr) \left( {A\text {e}^{i\alpha z}+B\text {e}^{-i\alpha z}} \right) \text {e}^{i\omega t} \end{aligned}$$
(7)

4 Solution of Anisotropic Porous Half-Space Under Gravity

The wave is assumed to propagate along the radial direction r. Neglecting the viscosity, the equation of motion for fluid-saturated anisotropic porous half-space under gravity is given by Biot (1965),

$$\begin{aligned} \left. {\begin{array}{l} {\displaystyle \frac{\partial {\tau }'_{r\theta } }{\partial r}+\frac{\partial {\tau }'_{z\theta } }{\partial z}+\frac{2}{r}{\tau }'_{r\theta } -\frac{\partial }{\partial z}\left( {{d}'gz{e}'_{z\theta } } \right) -\frac{\partial }{\partial r}\left( {{d}'gz {\omega }'_z } \right) =\frac{\partial ^{2}}{\partial t^{2}}\left( {\rho _{rr} {u}'_\theta +\rho _{r\theta } {U}'_\theta } \right) } \\ {\displaystyle \frac{\partial {\tau }'}{\partial \theta }=\frac{\partial ^{2}}{\partial t^{2}}\left( {\rho _{r\theta } {u}'_\theta +\rho _{\theta \theta } {U}'_\theta } \right) } \\ \end{array}} \right] \end{aligned}$$
(8)

where \({\tau }'_{ij} \left( {i,j=r,\theta ,z} \right) \) are the incremental stress components of solid in the radial, circumferential, and axial directions, respectively, and \({\tau }'\) is the stress in liquid.

\({u}'_i\) and \({U}'_i \left( {i=r,\theta ,z} \right) \) are the components of the displacement vectors of the solid and the liquid in the radial, circumferential, and axial directions, respectively, and are independent of \(\theta \).

i.e., \({u}'_r ={u}'_z =0\); \({u}'_\theta ={u}'_\theta \left( {r,z,t} \right) \); \({U}'_r ={U}'_z =0\); \({U}'_\theta ={U}'_\theta \left( {r,z,t} \right) \)

so that \({\tau }'_{rr} ={\tau }'_{\theta \theta } ={\tau }'_{zz} ={\tau }'_{zr} =0\); \({e}'_{r\theta } =\frac{1}{2}\left( {\frac{\partial {u}'_\theta }{\partial r}-\frac{{u}'_\theta }{r}} \right) \); \({e}'_{\theta z} =\frac{1}{2}\frac{\partial {u}'_\theta }{\partial z}\)

and \({\omega }'_r =-\frac{1}{2}\frac{\partial {u}'_\theta }{\partial z}\); \({\omega }'_\theta =0\); \({\omega }'_z =\frac{1}{2r}\frac{\partial }{\partial r}\left( {r {u}'_\theta } \right) \)

And the nonzero stress–strain relations for fluid-saturated anisotropic porous layer are given by

$$\begin{aligned} {\tau }'_{r\theta } =2{N}' {e}'_{r\theta } ={N}' \left( {\frac{\partial {u}'_\theta }{\partial r}-\frac{{u}'_\theta }{r}} \right) ; \quad {\tau }'_{z\theta } =2{L}' {e}'_{z\theta } ={L}' \frac{\partial {u}'_\theta }{\partial z} \end{aligned}$$

where \({N}'\) and \({L}'\) are the shear modulus of anisotropic layer along r and z directions, respectively.

The stress vector \(\vec {\tau }'\) is related to the fluid pressure \(\vec {p}_\mathrm{f}\) by the relation

$$\begin{aligned} \vec {\tau }'=-f \vec {p}_\mathrm{f} \end{aligned}$$

where f is the porosity of the porous layer.

Using above relations, the equations in (8) are transformed to

$$\begin{aligned}&\left( {{N}'-\frac{{d}'gz}{2}} \right) \left( {\frac{\partial ^{2}{u}'_\theta }{\partial r^{2}}+\frac{1}{r}\frac{\partial {u}'_\theta }{\partial r}-\frac{{u}'_\theta }{r^{2}}} \right) +\left( {{L}'-\frac{{d}'gz}{2}} \right) \frac{\partial ^{2}{u}'_\theta }{\partial z^{2}}-\left( {\frac{{d}'g}{2}} \right) \frac{\partial {u}'_\theta }{\partial z} \nonumber \\&\quad =\frac{\partial ^{2}}{\partial t^{2}}\left( {\rho _{rr} {u}'_\theta +\rho _{r\theta } {U}'_\theta } \right) \end{aligned}$$
(9a)
$$\begin{aligned}&\frac{\partial ^{2}}{\partial t^{2}}\left( {\rho _{r\theta } {u}'_\theta +\rho _{\theta \theta } {U}'_\theta } \right) =0 \end{aligned}$$
(9b)

Now substituting \({u}'_\theta =v_1 \left( {r,z,t} \right) \) and using (9b), Eq. (9a) reduces to

$$\begin{aligned}&\left( {{N}'-\frac{{d}'gz}{2}} \right) \left( {\frac{\partial ^{2}v_1 }{\partial r^{2}}+\frac{1}{r}\frac{\partial v_1 }{\partial r}-\frac{v_1 }{r^{2}}} \right) +\left( {{L}'-\frac{{d}'gz}{2}} \right) \frac{\partial ^{2}v_1 }{\partial z^{2}}\nonumber \\&\quad -\left( {\frac{{d}'g}{2}} \right) \frac{\partial v_1 }{\partial z}={d}'\frac{\partial ^{2}v_1 }{\partial t^{2}} \end{aligned}$$
(9c)

where

$$\begin{aligned} {d}'={{\rho }_{rr}'} -\frac{{\rho }_{r\theta }'^{2}}{{\rho }_{\theta \theta }' } \end{aligned}$$
(9d)

Under the assumption that there is no relative motion between liquid and solid in the porous structure, the mass coefficients \({\rho }'_{rr} ,{\rho }'_{r\theta }\) and \({\rho }'_{\theta \theta }\) are related to the total mass density of solid–liquid aggregate \({\rho }'\) and mass densities \({\rho }'_\mathrm{s} ,{\rho }'_\mathrm{f} \) for solid and liquid, respectively, by Biot (1956a)

$$\begin{aligned} {\rho }'_{rr} +{\rho }'_{r\theta } =\left( {1-f} \right) {\rho }'_\mathrm{s} , {\rho }'_{r\theta } +{\rho }'_{\theta \theta } =f {\rho }'_\mathrm{f} \end{aligned}$$

and \({\rho }'={\rho }'_{rr} +2{\rho }'_{r\theta } +{\rho }'_{\theta \theta } ={\rho }'_\mathrm{s} +f\left( {\rho }'_\mathrm{f} -{\rho }'_\mathrm{s } \right) \)

Further the dynamic coefficients obey the following inequalities too (Biot 1956a, b, c):

$$\begin{aligned} {\rho }'_{ rr} >0, {\rho }'_{r\theta } \le 0, {\rho }'_{ \theta \theta } >0, {\rho }'_{ rr} {\rho }'_{\theta \theta } -{\rho }_{r\theta }^{'2} >0. \end{aligned}$$

The above relation shows that if the fluid of lighter density \({\rho }'_\mathrm{f}\) is filled up in the solid matrix of density \({\rho }'_\mathrm{s}\), the mass density of the aggregate \({\rho }'\) will be less than the density of the solid \({\rho }'_\mathrm{s}\) and in case of heavier fluid such as mercury and molten metal, the density of the aggregate \({\rho }'\) will be more than the density of the solid \({\rho }'_\mathrm{s}\) (Gupta et al. 2010b).

Moreover, this relation also shows that as the porosity factor f decreases from 1 to 0, i.e., as the volume of pores decreases, the density of the aggregate \({\rho }'\) tends to the density of the solid \({\rho }'_\mathrm{s}\).

The parameters for the materials of porous half-space may be nondimensionalized as

$$\begin{aligned} \gamma _{rr} =\frac{{\rho }'_{rr} }{{\rho }'}, \quad \gamma _{r\theta } =\frac{{\rho }'_{r\theta } }{{\rho }'}, \quad \gamma _{\theta \theta } =\frac{{\rho }'_{\theta \theta } }{{\rho }'}\quad \hbox {and}\quad d_1 =\frac{{d}'}{{\rho }'}=\gamma _{rr} -\frac{\gamma _{r\theta }^2 }{\gamma _{\theta \theta } }. \end{aligned}$$

If the layer is nonporous solid, then \(f\rightarrow 0\) and \(\rho _\mathrm{s} \rightarrow {\rho }'\), which leads to \(\gamma _{rr} +\gamma _{r\theta } \rightarrow 1\) and \(\gamma _{r\theta } +\gamma _{\theta \theta } \rightarrow 0\) and hence \(d_1 =\gamma _{rr} -\frac{\gamma _{r\theta }^2 }{\gamma _{\theta \theta } }\rightarrow 1\).

Again if \(f\rightarrow 1\), then \(\rho _\mathrm{f} \rightarrow {\rho }'\) and the medium becomes fluid giving \(d_1 \rightarrow 0\).

Thus, we have the following:

  1. i)

    \(d_1 \rightarrow 1\), when the layer is nonporous solid;

  2. ii)

    \(d_1\rightarrow 0\), when the layer is fluid;

  3. iii)

    \(0<d_1 <1\), when the layer is porous.

Following previous section, let us assume the solution of Eq. (9c)

$$\begin{aligned}&\left( {{N}'-\frac{{d}'gz}{2}} \right) \left( {\frac{\partial ^{2}v_1 }{\partial r^{2}}+\frac{1}{r}\frac{\partial v_1 }{\partial r}-\frac{v_1 }{r^{2}}} \right) +\left( {{L}'-\frac{{d}'gz}{2}} \right) \frac{\partial ^{2}v_1 }{\partial z^{2}}\nonumber \\&\quad -\left( {\frac{{d}'g}{2}} \right) \frac{\partial v_1 }{\partial z}={d}'\frac{\partial ^{2}v_1 }{\partial t^{2}} \end{aligned}$$
(10)

as \(v_1 =J_1 (kr)f_2 (z)\text {e}^{i\omega t}\)

where \(J_1\) is the Bessel function first kind of order 1,

which reduces Eq. (9c) as

$$\begin{aligned} \frac{\text {d}^{2}f_2 }{\text {d}z^{2}}-\frac{\frac{d_1 {\rho }'g}{2}}{{L}'-\frac{d_1 {\rho }'gz}{2}}\frac{\text {d}f_2 }{\text {d}z}+\left[ {\frac{\left\{ {\frac{d_1 {\rho }'gz}{2{N}'}-\left( {1-d_1 \frac{c^{2}}{c_2^2 }} \right) } \right\} {N}'k^{2}}{{L}'-\frac{d_1 {\rho }'gz}{2}}} \right] f_2 =0 \end{aligned}$$
(11)

Again, substitute \(f_2 (z)=\frac{v_2 (z)}{\sqrt{{L}'-\frac{d_1 {\rho }'gz}{2}}}\)

Equation (11) reduces to

$$\begin{aligned} \frac{\text {d}^{2}v_2 }{\text {d}z^{2}}+\left[ {\frac{1}{4}.\left( {\frac{d_1 {\rho }'g}{2}} \right) ^{2}.\frac{1}{\left( {{L}'-\frac{d_1 {\rho }'gz}{2}} \right) ^{2}}+\frac{\left\{ {\frac{d_1 {\rho }'gz}{2{N}'}-\left( {1-d_1 \frac{c^{2}}{c_2^{2}}} \right) } \right\} {N}'k^{2}}{\left( {{L}'-\frac{d_1 {\rho }'gz}{2}} \right) }} \right] v_2 =0\nonumber \\ \end{aligned}$$
(12)

Introduce a new variable, \(t=\left( {\frac{4}{Gd_1 }-2kz} \right) \)

Equation (12) becomes

$$\begin{aligned} \frac{\text {d}^{2}v_2 \left( t \right) }{\text {d}t^{2}}+\left[ {\frac{1}{4t^{2}}+\frac{R}{t}-\frac{1}{4}} \right] v_2 \left( t \right) =0 \end{aligned}$$
(13)

where \(R=\frac{\left[ {1-\frac{{N}'}{{L}'}\left( {1-d_1 \frac{c^{2}}{c_2^{2}}} \right) } \right] }{Gd_1 }\), \(G=\frac{{\rho }'g}{{L}'k}\), the Biot’s gravity parameter,

\(d_1\), the porosity parameter, \(\frac{{N}'}{{L}'}\), the nondimensional anisotropic parameter,

\(c_2 =\sqrt{\frac{{N}'}{{\rho }'}}\), the share wave velocity in the porous half-space.

Equation (13) is a well-known Whittaker differential equation whose solution can be written as

$$\begin{aligned} v_2 \left( t \right) =A_1 \text {W}_{R,0} \left( t \right) +B_1 \text {W}_{-R,0} \left( {-t} \right) \end{aligned}$$
(14)

where \(\text {W}_{R,0} \left( t \right) \) and \(\text {W}_{-R,0} \left( {-t} \right) \) are Whittaker functions and \(A_1 \hbox { and B}_{1}\) are arbitrary constants.

As the lower medium being a half-space, the solution should vanish at \(z=\infty \) (i.e., for \(t = - \infty \)).

So the solution of (14) can be taken as

$$\begin{aligned} v_2 \left( t \right) =B_1 \text {W}_{-R,0} \left( {-t} \right) \end{aligned}$$

The solution of Eq. (9c) becomes

$$\begin{aligned} v_1 =C J_1 \left( {kr} \right) \frac{\text {W}_{-R,0} \left( {-t} \right) }{\sqrt{{L}'-\frac{d_1 {\rho }'gz}{2}}}\text {e}^{i\omega t} \end{aligned}$$
(15)

where C is the arbitrary constant.

Expanding Whittaker’s function up to second degree, Eq. (15) reduces to

$$\begin{aligned} v_1 =C J_1 \left( {kr} \right) \left( {{L}'-\frac{d_1 {\rho }'gz}{2}} \right) ^{- \frac{1}{2}} \left[ {\text {e}^{\frac{t}{2}}\left( {-t} \right) ^{-R}\left\{ {1+\frac{(R+\frac{1}{2})^{2}}{t}} \right\} } \right] \text {e}^{i\omega t} \end{aligned}$$
(15a)

5 Boundary Conditions

We have assumed that the surface of the sandy layer is stress free and the displacements and stress components to be continuous at the interface of the medium, which leads to the following boundary conditions.

$$\begin{aligned} \left. \begin{array}{lll} \hbox {a}. &{} \eta \mu \frac{\partial v}{\partial z}=0 &{} \hbox {at } z=-h\hbox { (stress-free boundary)}\\ \hbox {b}. &{} v=v_1 &{} \hbox {at } z=0\hbox { (continuity conditions for displacement)}\\ \hbox {c}. &{} \eta \mu \frac{\partial v}{\partial z}={N}'\frac{\partial v_1 }{\partial z} &{} \hbox {at }z=0\hbox { (continuity conditions for stress)}\\ \end{array}\right) \end{aligned}$$
(16)

Using the boundary conditions (16), we have

$$\begin{aligned} \left. {\begin{array}{l} A\text {e}^{-i\alpha h}-B\text {e}^{i\alpha h}=0 \\ A + B =C\gamma \\ \eta \mu \alpha i(A-B)={N}'C\gamma _2 \\ \end{array}} \right\} \end{aligned}$$
(17)

Eliminating the arbitrary constants from (17), we have the dispersion equation as

$$\begin{aligned} \left| {{\begin{array}{c@{\quad }c@{\quad }c} {\text {e}^{-i\alpha h}}&{} {-\text {e}^{i\alpha h}}&{} 0 \\ 1&{} 1&{} {-\gamma } \\ {\eta \mu i\alpha }&{} {-\eta \mu i\alpha }&{} {-{N}'\gamma _2 } \\ \end{array} }} \right| =0 \end{aligned}$$

or,

$$\begin{aligned} \tan \left( {\alpha h} \right) =-\frac{{N}'\gamma _2 }{\eta \mu \alpha \gamma } \end{aligned}$$
(18)

where

$$\begin{aligned}&\alpha =k\sqrt{\left( {\frac{c^{2}}{\eta c_1^{2}}-1} \right) \left( {\frac{\eta \mu }{\eta \mu -\frac{P}{2}}} \right) }, \quad \gamma =\left[ {\frac{W_{-R,0} \left( {-t} \right) }{\sqrt{{L}'-\frac{d_1 {\rho }'gz}{2}}}} \right] _{z=0}\hbox { and }\\&\gamma _2 =\frac{\partial }{\partial z}\left[ {\frac{W_{-R,0} \left( {-t} \right) }{\sqrt{{L}'-\frac{d_1 {\rho }'gz}{2}}}} \right] _{z=0} \end{aligned}$$

After simplifying by taking asymptotic expansion of the Whittaker function for large argument up to the second term, Eq. (18) reduced to

$$\begin{aligned}&\tan \left[ {kh\sqrt{\frac{\eta }{\eta -\frac{P}{2\mu }}\left( {\frac{c^{2}}{\eta c_1^{2}}-1} \right) }} \right] \nonumber \\&\quad =\frac{{N}'}{\eta \mu \sqrt{\frac{\eta }{\eta -\frac{P}{2\mu }}\left( {\frac{c^{2}}{\eta c_1^{2}}-1} \right) }}\left[ 1-\frac{1}{2}\left\{ {\left( {d_1 \frac{c^{2}}{c_2^{2}}-1} \right) \frac{{N}'}{{L}'}+1} \right\} -\frac{3}{4}Gd_1 \right. \nonumber \\&\qquad \left. +\frac{8G^{2}d_1^{2}}{16Gd_1 +\left\{ {2\left( {d_1 \frac{c^{2}}{c_2^{2}}-1} \right) \frac{{N}'}{{L}'}+2+Gd_1 } \right\} ^{2}} \right] \end{aligned}$$
(19)

Equation (19) can also be approximately written as

$$\begin{aligned}&\tan \left[ {kh\sqrt{\frac{\eta }{\eta -\frac{P}{2\mu }}\left( {\frac{c^{2}}{\eta c_1^{2}}-1} \right) }} \right] \nonumber \\&\quad = \frac{{N}'}{\eta \mu \sqrt{\frac{\eta }{\eta -\frac{P}{2\mu }}\left( {\frac{c^{2}}{\eta c_1^{2}}-1} \right) }}\left[ \frac{1}{2}\left( {\frac{{N}'}{{L}'}-1} \right) +\sqrt{1-d_1 \frac{{N}'}{{L}'}\frac{c^{2}}{c_2^{2}}}-\frac{3}{4}Gd_1 \right. \nonumber \\&\qquad \left. +\frac{G^{2}d_1^{2}}{2Gd_1 +2\left\{ {\frac{1}{4}Gd_1 -\frac{1}{2}\left( {\frac{{N}'}{{L}'}+1} \right) +\sqrt{1-d_1 \frac{{N}'}{{L}'}\frac{c^{2}}{c_2^{2}}}} \right\} ^{2}} \right] \end{aligned}$$
(19a)

5.1 Particular Cases

  • If the upper layer is free from initial stress, i.e., \(P=0\), the dispersion Eq. (19) takes the form as

    $$\begin{aligned}&\tan \left[ {kh\sqrt{\left( {\frac{c^{2}}{\eta c_1^{2}}-1} \right) }} \right] =\frac{{N}'}{\eta \mu \sqrt{\left( {\frac{c^{2}}{\eta c_1^{2}}-1} \right) }}\left[ 1-\frac{1}{2}\left\{ {\left( {d_1 \frac{c^{2}}{c_2^{2}}-1} \right) \frac{{N}'}{{L}'}+1} \right\} \right. \nonumber \\&\quad \left. -\frac{3}{4}Gd_1 +\frac{8G^{2}d_1^{2}}{16Gd_1 +\left\{ {2\left( {d_1 \frac{c^{2}}{c_2^{2}}-1} \right) \frac{{N}'}{{L}'}+2+Gd_1 } \right\} ^{2}} \right] \end{aligned}$$
    (20)

    Equation (20) exhibits that the surface wave will also propagate in dry sandy layer lying above the fluid-saturated poro-elastic anisotropic half-space under the influence of gravity in the absence of initial stresses.

  • If the upper layer is initially stress elastic layer and the lower one is fluid-saturated poro-elastic anisotropic half-space free from the influence of gravity i.e., \(G=0,\eta =1\),

    $$\begin{aligned}&\tan \left[ {kh\sqrt{\frac{1}{1-\frac{P}{2\mu }}\left( {\frac{c^{2}}{c_1^{2}}-1} \right) }} \right] \nonumber \\&\quad =\frac{{N}'}{\mu \sqrt{\frac{1}{1-\frac{P}{2\mu }}\left( {\frac{c^{2}}{c_1^{2}}-1} \right) }}\left[ {1-\frac{1}{2}\left\{ {\left( {d_1 \frac{c^{2}}{c_2^{2}}-1} \right) \frac{{N}'}{{L}'}+1} \right\} } \right] \end{aligned}$$
    (21)

    Equation (21) exhibits that the Love waves will also propagate in initially stressed elastic layer lying above the fluid-saturated poro-elastic anisotropic half-space (Gupta et al. 2010a).

  • If the upper layer and the porous half-space are homogeneous and isotropic and lower half-space is free from the influence of gravity, i.e., homogeneous and isotropic layer lying over homogeneous isotropic half-space.

    Then \(G=0,\eta =1,P=0\) and \(\frac{{N}'}{{L}'}=1\), the above Eq. (19) gives approximately

    $$\begin{aligned} \tan \left[ {kh\sqrt{\left( {\frac{c^{2}}{c_1^{2}}-1} \right) }} \right] =\frac{{N}'}{\mu \sqrt{\left( {\frac{c^{2}}{c_1^{2}}-1} \right) }}\left[ {1-\frac{1}{2}\frac{c^{2}d_1 }{c_2^{2}}} \right] \end{aligned}$$
    (22)

    Equation (22) shows that the surface wave will also propagate in elastic homogeneous and isotropic layer lying above the fluid-saturated poro-elastic homogeneous and isotropic half-space in the absence of the influence of gravity and initial stresses.

  • If the upper layer is an initial stress-free isotropic, i.e., \(P=0, \eta =1\) and the lower half-space is elastic homogeneous isotropic in the absence of the influence of gravity, i.e., \({N}'={\mu }', G=0 , d_1 =1\), and \(\frac{{N}'}{{L}'}=1\), then the dispersion Eq. (19) takes the form

    $$\begin{aligned} \tan \left[ {kh\sqrt{\left( {\frac{c^{2}}{c_1^{2}}-1} \right) }} \right] =\frac{{\mu }'}{\mu }\left[ {\frac{\sqrt{1-\frac{c^{2}}{c_2^{2}}}}{\sqrt{\frac{c^{2}}{c_1^{2}}-1}}} \right] \end{aligned}$$
    (23)

    Equation (23) gives the dispersion equation for Love waves in homogeneous and isotropic layer lying over nonporous elastic homogeneous isotropic half-space (Achenbach 1999).

6 Range of Love Waves Speed

Determination of the lower and upper bounds of the Love wave speed has great importance in both theoretical and practical aspects and is also helpful in solving the complex dispersion equation of Love waves given by Eq. (19). From Eq. (19a), we can say that Love waves can propagate in initial stress dry sandy layer overlying an anisotropic porous half-space when

$$\begin{aligned} \sqrt{\eta }c_1 <c<\sqrt{\frac{{L}'}{{N}'d_1 }}c_2 \end{aligned}$$
(24)

The relation (24) indicates the role of porosity, sandiness, and anisotropy of the medium for the existence and nonexistence of Love waves.

It may be noted that the dispersion equation of Love waves given by (19) is a complex transcendental implicit equation between the frequency and the phase velocity. The dispersion equation contains a periodic function (function tangent), which implies that the frequency is a multivalued function of phase velocity and the number of branches of the corresponding dispersion curves is infinite. The individual waves are called modes of the surface wave. So for a given value of phase velocity, it can be shown that for all modes the range of \(k_n h\) is such that

$$\begin{aligned} \left( {n-\frac{1}{2}} \right) \pi <k_n h\sqrt{\frac{\eta }{\eta -\frac{P}{2\mu }}\left( {\frac{c^{2}}{\eta c_1^{2}}-1} \right) }<n\pi \end{aligned}$$
(25)

And for the higher modes,

$$\begin{aligned} k_n h\rightarrow \frac{n\pi }{\sqrt{\frac{\eta }{\eta -\frac{P}{2\mu }}\left( {\frac{c^{2}}{\eta c_1^2 }-1} \right) }} \end{aligned}$$
(26)

The branch for \(n=0\) is called the fundamental mode, the branch for \(n=1\) is the first higher mode, and the modes form a harmonic series.

7 Numerical Calculations and Discussions

Based on the dispersion Eq. (19), numerical results are provided to show the propagation characteristics of Love waves in dry sandy layer under initial stress above anisotropic porous half-space under gravity. The main attention is paid on the influence of sandy parameter \(\eta \), Biot’s gravity parameter G, and porosity \(d_1\) along with the effect of nondimensional parameters \(\frac{{N}'}{{L}'}\), \(\frac{P}{2\eta \mu }\), \(\frac{c_1 }{c_2}\). Following Biot (1962a; b) and Sharma and Gongna (1991), we have made the above parameters dimensionless so that the following data values can be used. The chosen values for these nondimensional parameters are as follows: \(\frac{{N}'}{{L}'}=1, 2\), \(\frac{{N}'}{\mu }=1\), \(\frac{P}{2\eta \mu }=0.8\), \(\frac{c_1 }{c_2 }=0.8\) (for Figs. 2a, b, 3a, b, 4a, b, 5a, b, 6, 7, 8a, b, 9, 10).

Fig. 2
figure 2

Variation of phase velocity with kh for different values of G when \(d_1 =0.9, \frac{{N}'}{{L}'}=1, \frac{{N}'}{\mu }=0.6\), \(\eta =1.5\), \(\frac{p}{2\eta \mu }=0.8\), \(\frac{c_1 }{c_2 }=0.8\)

Full size image
Fig. 3
figure 3

Variation of phase velocity with kh for different values of G when \(d_1 =0.9, \frac{{N}'}{{L}'}=2, \frac{{N}'}{\mu }=0.6\), \(\eta =1.5\), \(\frac{p}{2\eta \mu }=0.8\), \(\frac{c_1 }{c_2 }=0.8\)

Full size image
Fig. 4
figure 4

Variation of phase velocity with kh for different values of \(d_1\) when \(G=0.6, \frac{{N}'}{{L}'}=1, \frac{{N}'}{\mu }=0.6\), \(\eta =1.5\), \(\frac{p}{2\eta \mu }=0.8\), \(\frac{c_1 }{c_2 }=0.8\)

Full size image
Fig. 5
figure 5

Variation of phase velocity with kh for different values of \(d_1\) when \(G=0.6, \frac{{N}'}{{L}'}=2, \frac{{N}'}{\mu }=0.6\), \(\eta =1.5\), \(\frac{p}{2\eta \mu }=0.8\), \(\frac{c_1 }{c_2 }=0.8\)

Full size image
Fig. 6
figure 6

Variation of phase velocity with kh for different values of \(\eta \) when \(d_1 =0.9, G=0.6\), \(\frac{{N}'}{{L}'}=1\), \(\frac{{N}'}{\mu }=0.6\), \(\frac{p}{2\eta \mu }=0.8, \frac{c_1 }{c_2 }=0.8\)

Full size image
Fig. 7
figure 7

Variation of phase velocity with kh for different values of \(\eta \) when \(d_1 =0.9, G=0.6\), \(\frac{{N}'}{{L}'}=2\), \(\frac{{N}'}{\mu }=0.6\), \(\frac{p}{2\eta \mu }=0.8, \frac{c_1 }{c_2 }=0.8\)

Full size image

In all the figures, curves have been plotted as phase velocity \(\frac{c}{c_1}\) along vertical axis against dimensionless wave number kh along horizontal axis. Range of kh is taken between the values of 0 and 3.5. Upper range value of kh corresponds to the height of dry sandy layer of around \(\frac{\lambda }{2}\) where \(\lambda \) is the wave length. For all the plots of phase velocity (Figs. 2a, b, 3a, b, 4a, b, 5a, b, 6, 7, 8a, b), it has been observed that the maximum changes happen in phase velocity between \(kh=0\) (i.e., h is around 0) and \(kh=0.5\) (i.e., h is around \(0.08\,\lambda \)) and the plots accumulate beyond \(kh=2.0\) (i.e., h is around \(0.032\,\lambda \)). In order to get a better view of this range, more number of data points are taken. It has been found that with the increase in wave number, the phase velocity decreases rapidly in each of these figures under the considered values of various parameters. When \(h\rightarrow 0\), i.e., the thickness of the sandy layer reduces to zero, the observations may be considered as to show the effect of the parameters in the propagation of Love waves in anisotropic porous half-space under gravity.

Figures 2a to 3b display the effect of gravity parameter in the propagation of Love waves in an initially stressed sandy layer over isotropic and anisotropic porous half-space, respectively. The value of G has been taken as 0.2, 0.4, 0.6, and 0.8. Following observations and effects are obtained under the above-considered values when other parameters are fixed, as shown in figures:

  • As the gravity parameter increases, the phase velocity \(\frac{c}{c_1}\) decreases at a particular wave number in both isotropic and anisotropic layers.

  • The curves are accumulating at \(kh=2\) onward, showing that although the gravity parameter varies, velocity remains closure at the higher values of kh.

  • In Figs. 2b and 3b, we can see the better effect for the smaller values of kh.

Figures 4a to 5b have been plotted to understand the effect of the porosity \(d_1\) on the propagation of Love wave velocity. The value of \(d_1\) has been varied from 0.7 to 1, and other parameters are fixed. We observed that:

  • As the porosity increases in the above-mentioned range, the phase velocity of Love waves in the layer decreases in both isotropic and anisotropic layers.

  • From Figs. 4b and 5b, we have seen that phase velocity is decreasing in both isotropic and anisotropic cases when we increase the porosity and we observed that decreasing nature is slightly more in isotropic case rather in anisotropic case.

  • The curves shift closer to each other as the value of kh increases, which reveals that the effect of porosity parameter \(d_1\) is very less as it approaches \(kh = 2\), which means it has a negligible effect for the higher magnitude of kh, as shown in Figs. 2a and 3a.

  • The curves apart from each other between \(kh = 0.0\) and 1.0 show that \(d_1\) has a perfect influence over the phase velocity of Love waves.

  • Also the study reveals that the Phase velocity is less for nonporous \((d_1 \rightarrow 1)\) elastic half-space with comparison with porous elastic half-space

Figures 6 and 7 describe the effect of sandy parameter \(\eta \) on the velocity of Love waves for the various values of \(\eta \), i.e., 1.0, 1.5, and 2.0. Following results are noticed:

  • The curves reflect that in the presence of fixed value of gravity, porosity, and other nondimensional parameter, as the value of sandy parameter \(\eta \) increases, the phase velocity of Love waves also increases.

  • For \(\eta = 1\), the medium turns out to be perfectly elastic, thereby allowing Love waves to propagate with less velocity as compared to other values of \(\eta \) (i.e., 1.5, 2.0) for which the medium becomes sandy. Hence, it can be concluded that under the above-considered values of various parameters, the possibility of Love wave propagation in the layer is least when the upper layer is elastic as compared to the case when the upper layer is sandy.

Figure 8a, b displays that the phase velocity is decreased in isotropic layer \(\frac{{N}'}{{L}'}=1\) and anisotropic layer \(\frac{{N}'}{{L}'}=2\) when the other parameters are fixed.

  • Velocity of the Love waves decreases more rapidly in isotropic layer than in anisotropic layer for small values of kh (0 to 0.5).

  • Fig. 8b displays the clear view of the effect.

Figures 9 and 10 show the dispersive curves for the first- and second-mode Love waves in an initially stressed dry sandy layer, respectively. The observations are as follows:

  • As the sandy parameter increases, the phase velocity of Love waves increases for different modes.

  • The differences in phase velocity for different modes are noticeable in low frequency than in high frequency, that is the increasing nature of phase velocity is stronger in higher mode.

Fig. 8
figure 8

Variation of phase velocity with kh for different values of \(\frac{{N}'}{{L}'}\) when \(d_1 =0.9, G=0.6, \frac{{N}'}{\mu }=0.6\), \(\eta =1.5\), \(\frac{p}{2\eta \mu }=0.8\), \(\frac{c_1 }{c_2 }=0.8\)

Full size image
Fig. 9
figure 9

Variation of phase velocity curves for the first-mode Love waves against kh for different values of \(\eta \)

Full size image
Fig. 10
figure 10

Variation of phase velocity curves for the second-mode Love waves against kh for different values of \(\eta \)

Full size image

8 Conclusion

A mathematical modeling of propagation of Love waves in dry sandy layer with initial stress above anisotropic porous half-space under gravity is presented. The equation of motion has been formulated following Biot, separately, for different media using suitable boundary condition at the interface of sandy layer, porous half-space under gravity. The closed form expression for dispersion has been derived for the surface waves in terms of Whittaker function and its derivative, which are further expanded asymptotically, retaining the terms up to the second degree. The presence of gravity, porosity, and sandy parameter in the frequency equation approves the effects of these parameters in the propagation of Love waves in a porous layer, bounded above by sandy layer and below by a gravitating half-space. We have observed that the presence of gravity field allows Love waves to propagate and with the increase in gravity parameter, the phase velocity decreases. It has been noticed that porosity also has dominant role on the propagation of Love waves. When the porosity of the porous half-space increases, the phase velocity decreases, whereas the sandy parameter has the increasing effect in the propagation of Love waves. This problem can be related to the real-world problem, which exists in oil prospecting and surveying technique especially in Gulf region (Augustin 2012). Also the effect of porosity in the propagation of surface wave may be useful in the problem related to structural health monitoring (Kumar and Chakraborty 2014). So the present result may provide the bridge between modeling results and field application.