Three-Phase Permeabilities: Upscaling, Analytical Solutions and Uncertainty Analysis in Elementary Pore Structures

Abstract

Immiscible three-phase flow in a rigid porous medium is upscaled from the pore to the continuum (Darcy) scale through homogenization relying on multiple scale expansion. We solve the Stokes flow problem at the pore level upon imposing continuity of velocity and shear stress at the fluid–fluid interfaces. This enables one to explicitly account for the momentum transfer between the moving phases. A macroscopic model describing the system at the Darcy scale is then rigorously obtained. This allows defining a tensor of three-phase effective relative permeabilities, $\mathbf{K}_{\alpha \eta ,r}$, as a function of the distribution of the fluids in the system, phase saturations and fluid viscosity ratios. We present an analytical solution for $\mathbf{K}_{\alpha \eta ,r}$ corresponding to a scenario where three-phase fluid flow takes place within (a) a plane channel and (b) a capillary tube with circular cross-section. These geometrical settings are typical of microfluidics applications and are archetypal to the analysis of key processes occurring in topologically complex porous or fractured systems. Our results show the relevance of the viscous coupling effects between the three phases on the continuum-scale system behavior and demonstrate that the traditional extension of Darcy’s law to model multiphase relative permeabilities might be inadequate. We then exploit our analytical solutions to investigate the way the uncertainty associated with the characterization of the phase viscosities propagates to $\mathbf{K}_{\alpha \eta ,r}$ through a global sensitivity analysis approach. We quantify the relative contribution of the considered uncertain parameters to the total variability of $\mathbf{K}_{\alpha \eta ,r}$ by relying on the variance-based Sobol indices which are derived analytically for the investigated settings.

1 Introduction

Three-phase flow in porous media and fracture networks is ubiquitous in environmental and industrial applications. For example, proper understanding of the effect of key parameters driving migration of Non-Aqueous Phase Liquids through variably saturated regions across a multiplicity of scales is nowadays considered as a key issue in groundwater protection policies and procedures. Flow of oil, gas, and water is typically observed in oil bearing formations, both at the reservoir and basin scales. Commonly applied methods for Enhanced Oil Recovery (McGuire et al. 2005) require the injection of gaseous phases, such as natural gas, $\hbox {CO}_{2}$ or nitrogen, in two-phase (oil-water) environments. The use of three immiscible fluids is also considered in microfluidics experiments and industrial applications, to prevent coalescence of microfluidic plugs (Chen et al. 2007) and to screen a small volume of solution from the effect of a large number of reagents (Zheng and Ismagilov 2005).

At the pore scale and for small values of the Reynolds number, multiphase flow of immiscible fluids is described by the Stokes and continuity equations complemented by appropriate boundary conditions at solid-fluid and fluid-fluid interfaces. The rigorous derivation of upscaled or continuum (Darcy) scale equations starting from such pore scale formulations is still posing significant challenges. In this context, multiphase flow in porous media at the Darcy scale is traditionally described via the Darcy–Buckingham equation. The latter was heuristically derived as an extension of Darcy’s law to multiphase flow. In the Darcy–Buckingham model the upscaled velocity of a fluid phase is proportional through the phase relative permeability only to the pressure gradient which is applied to the same phase. Therefore, interfaces between phases are assumed to be rigid and no momentum transfer takes place between the flowing fluids. Since direct experimental data on three-phase relative permeabilities are seldom available (Oak et al. 1990; DiCarlo et al. 2000), estimates of three-phase relative permeabilities typically relies on empirical models starting from two-phase data (e.g, amongst others, Stone 1970, 1973; Aziz and Settari 1979; Baker 1988; Blunt 2000; DiCarlo et al. 2000; Ranaee et al. 2014).

Upscaling procedures based on homogenization via multiple scale expansion (Auriault 1987, 1989; Auriault et al. 2009) or volume averaging techniques (Withaker 1986a, b) have been proposed to analyze one- and two-phase flows (e.g., Auriault 1987, 1989; Withaker 1986b) as well as non reactive (e.g., Ariault and Adler, 1995; Wood and Valdès-Parada 2013) and reactive (e.g., Porta et al. 2013) transport settings. Some of these studies showed that a pressure gradient applied to a phase affects the flow of the other phase. This phenomenon is termed viscous coupling effect and its relevance has also been deduced through approaches based on thermodinamics principles of irreversible processes (Kalaydjian 1990), two-phase mixture models (Wang 1997) or within an overlapping continua framework (Hassanizadeh and Gray 1979, 1980). Gray and Miller (2005) introduced a thermodynamically constrained averaging theory for modeling flow and transport phenomena in porous systems consistent with microscale constraints. Within this framework, single (Gray and Miller 2006, 2009) and connected two-phase (Jackson et al. 2009) flow have been analyzed. The viscous coupling effect has also been studied through co- and counter-current steady-state two-phase flow experiments performed in sandpacks (e.g., Bensen and Manai 1993; Dullien and Dong 1996) and planar pore network models of the glass etched chamber-and-throat type (Avraam and Payatakes 1995). The occurrence of viscous coupling in two-phase flows has also been supported through pore network modeling (e.g., Bravo et al. 2007) and investigations performed in (a) porous media consisting of bundles of noncircular capillary tubes via a semi-analytical procedure (e.g., Ehrlich 1993), (b) microscopic models of porous media via solutions of pore scale multiphase flow by means of Lattice Boltzman techniques (e.g., Gunstensen and Rothman 1993; Li et al. 2005; Huang and Lu 2009), (c) angular capillaries via numerical (finite element) solution of the flow field (e.g.,Ranshoff and Radke 1988; Patzek and Kristensen 2001).

The phenomenon of viscous coupling in three-phase flow has been addressed by Kats and Egberts (1999) via Lattice Boltzman pore-scale modeling of steady-state flow though a two-dimensional porous medium. These authors found that a generalized form of Darcy’s law accounting for viscous coupling can adequately describe the simulated flow features. Key limitations associated with the above mentioned study are that (a) a viscosity value which is common to the three fluid phases and (b) only a single arrangement of phase saturations are considered. Al-Futaisi and Patzek (2003) studied the dependence of three-phase relative permeability of oil on wettability, geometry and interface boundary conditions through a numerical solution of a creeping flow setting in angular capillaries. These authors did not consider momentum transfer boundary conditions between the fluid phases. Their results clearly indicate that it might be relevant to include such an effect to obtain reliable simulation outcomes. Dehghanpour et al. (2011a) conducted three-phase drainage experiments in a sandpack column. The authors observed that oil flow is influenced much more significantly by the water than by oil saturation due to coupling phenomena. Dehghanpour et al. (2011a) derived an analytical solution for relative permeability coefficients associated with a capillary tube model under the assumption that shear stress at the oil-gas interface is negligible. The same hypothesis has been employed by Dehghanpour et al. (2011b) for the numerical solution of three-phase flow in the corner of angular capillaries. These authors showed that viscous coupling can be more marked in three- rather than two-phase systems because the ratio of oil–water interface to oil volume is larger in the former than in the latter setting.

As mentioned above, Dehghanpour et al. (2011a, b) assumed negligible shear stresses at the oil–gas interface, where a perfect slip boundary condition is applied. Under these circumstances, the upscaled three-phase flow equation has the same format as the two-phase formulation, i.e., coupling between gas and other fluids is not considered, relying on the assumption that gas viscosity is much smaller than that of oil and water. However, it can be noted that (a) oil viscosity may be markedly reduced during the application of WAG techniques (McGuire et al. 2005) and (b) increased pressure and temperature conditions, which are typical of reservoir settings, may cause oil and water viscosities to decrease and gas viscosity to increase. All these evidences should also be framed in the context of field applications where the actual values of fluid viscosities (and in particular oil viscosity) can be affected by significant uncertainty.

In this paper, we start by performing formal upscaling of three-phase flow in porous media from pore- to Darcy-scale by means of the Multiple Scale Expansion approach (Auriault et al. 2009; Bear and Cheng 2010). We consider a Stokes flow problem at the pore level upon imposing the continuity of velocity and shear stress at all fluid–fluid interfaces. These conditions enable us to account for momentum transfer, i.e., coupling effects, between all three moving phases, including gas. This leads to a macroscopic model describing the system at the Darcy scale and to the definition of a tensor of three-phase effective relative permeabilities, $\mathbf{K}_{\alpha \eta ,r}$, which depends on the distribution of the fluids in the system, phase saturations and fluid viscosity ratios. We then derive an analytical solution for the components of $\mathbf{K}_{\alpha \eta ,r}$ for settings corresponding to three-phase (oil–water–gas) flow taking place between two parallel plates and within a capillary tube with circular cross-section. These settings have been selected because they (i) allow highlighting the effect on $\mathbf{K}_{\alpha \eta ,r}$ of key dimensionless quantities through analytical solutions of the three-phase flow problem, (ii) are archetypal to the analysis of key processes occurring in porous media with increased topological complexity (Glanz and Hilpert 2014), and (iii) have been employed in the literature as benchmarks to validate the robustness of a series of numerical algorithms (e.g., Gunstensen and Rothman 1993; Huang and Lu 2009). Finally, we exploit our analytical solutions to explore the way uncertainty associated with fluid viscosities, which are typically hard to characterize under field conditions, propagates to $\mathbf{K}_{\alpha \eta ,r}$. We do so in the context of a global sensitivity analysis (GSA) methodology. GSA is performed upon relying on the Sobol indices (e.g., Sobol 1993; Sudret 2008). The latter are derived analytically for the configurations examined and provide variance-based metrics which allow quantifying the relative importance of the selected uncertain parameters on $\mathbf{K}_{\alpha \eta ,r}$.

2 Methodology

We consider isothermal three-phase flow taking place in a rigid porous medium of characteristic length, $L,$ formed by a collection of periodic unit cells of representative size, $l$. The unit cell, $\Omega$, is formed by a solid matrix, $\Omega _s$, and a pore space, $\Omega _f$. The latter is filled by three fluid phases, i.e., water, $\Omega _w$, oil, $\Omega _o$, and gas, $\Omega _g$. The vector $\mathbf{x}^{*}=\left( {x_1^*\mathbf{e}_1 +x_2^*\mathbf{e}_2 +x_3^*\mathbf{e}_3 } \right)$ represents a physical (dimensional) location, where $\left( {\mathbf{e}_1 ,\mathbf{e}_2 ,\mathbf{e}_3 } \right)$ are unit vectors of a three-dimensional Cartesian coordinate system. In this Section we provide theoretical details of the derivation of the homogenized three-phase flow equations. Our developments hold under the following assumptions: (i) the porous medium is rigid, (ii) the unit cell $\Omega$ is periodic, (iii) $\varepsilon =l/L <<1$, (iv) each individual volume $\Omega _w$, $\Omega _o$ and $\Omega _g$ is fully connected and no isolated portions of any given phase are present in the pore space, (v) the fluids are immiscible and Newtonian, (vi) there are no points $\mathbf{x}^{*}\in \Omega _f$ at which all three fluid phases are in contact, and (vii) the flow is steady-state and characterized by small values of the Reynolds numbers.

2.1 Local Flow Equations and Multiple Scale Expansion

According to the hypotheses summarized above, three-phase flow at the pore scale is accurately described by the Stokes and the continuity equations, subject to appropriate boundary conditions on the solid–fluid interface, $\Gamma _{\alpha s}$, and on the fluid–fluid interfaces, $\Gamma _{\alpha \eta }$. Here and in the following, subscript $s$ is employed to represent the solid phase while subscripts $\alpha$ and $\eta$ are associated with fluid phases, $\alpha$ and $\eta$ being equal to $w$, $o$ and $g$ for water, oil and gas, respectively.

The flow field is then described by

$$\begin{aligned}&\mu _\alpha ^*\left[ {\nabla ^{*2} \mathbf{v}_\alpha ^*+\frac{1}{3}\nabla ^{*}\left( {\nabla ^{*}\cdot \mathbf{v}_\alpha ^*} \right) } \right] =\nabla ^{*}p^{\prime *}_\alpha +\rho _\alpha ^*g^{*}\mathbf{e}_3 ,\nonumber \\&\nabla ^*\cdot \left( {\rho _\alpha ^*\mathbf{v}_\alpha ^*} \right) =0, \quad \hbox {in } \Omega _{\alpha } \;\hbox {with}\;\;\alpha \;=\;w,\;o,g \end{aligned}$$

(1)

where $\mathbf{v}_\alpha ^*,\rho _\alpha ^*,\mu _\alpha ^*, p^{\prime *}_\alpha$ respectively are velocity, density, dynamic viscosity and pressure of the $\alpha$-phase. We treat water, oil and gas as Newtonian barotropic fluids, i.e., $\rho _\alpha ^*$, is only a function of pressure, $p^{\prime *}_\alpha$, via the equation of state

$$\begin{aligned} f\left( {p^{\prime *}_\alpha ,\rho _\alpha ^*} \right) =0 \end{aligned}$$

(2)

Equation (2) reduces to $\rho _\alpha ^*$ = constant for incompressible fluids (as typically assumed for water and oil). Boundary conditions of (1) are: (a) no-slip condition at the solid boundary, (b) static fluid-fluid interfaces, and (c) continuity of tangential velocity and stresses at all fluid–fluid interfaces, i.e.,

$$\begin{aligned}&\mathbf{v}_\alpha ^*=0\;\;\hbox {on}\;\Gamma _{\alpha s} ; \nonumber \\&\mathbf{v}_\alpha ^*\cdot \mathbf{n}_{\alpha \eta } =0,\;\;\mathbf{v}_\alpha ^*=\mathbf{v}_\eta ^*\;,\;\;\left( {{\varvec{ \sigma }}}_\alpha ^*-{{\varvec{\sigma }}_\eta ^*} \right) \mathbf{n}_{\alpha \eta } =\left( {p^{\prime *}_{c,\alpha \eta } \mathbf{I} } \right) \mathbf{n}_{\alpha \eta } \;\;\hbox {on}\;\Gamma _{\alpha \eta } ;\\&\hbox {with}\;\alpha ,\eta =w,\;o,\;g \nonumber \end{aligned}$$

(3)

Here, $p^{\prime *}_{c,\alpha \eta }$ is the capillary pressure between two phases $\alpha$ and $\eta$, $\mathbf{n}_{\alpha \eta }$ is the unit vector normal to the interface $\Gamma _{\alpha \eta }$, pointing from phase $\alpha$ towards phase $\eta$, and ${\varvec{\sigma }}_\alpha ^*$ denotes the stress tensor of the $\alpha$-phase whose elements are given by

$$\begin{aligned} \sigma _{\alpha ,ij}^*=-p^{\prime *}_\alpha +\mu _\alpha ^*\left( {\frac{\partial v_{\alpha ,i}^*}{\partial x_j^*}+\frac{\partial v_{\alpha ,j}^*}{\partial x_i^*}} \right) ; \quad i, j=\hbox { 1},\hbox { 2},\hbox { 3} \end{aligned}$$

(4)

We introduce the following dimensionless quantities

$$\begin{aligned} \mu _\alpha&= \frac{\mu _\alpha ^*}{\mu _c } ,\;\;\mathbf{v}_\alpha =\frac{\mathbf{v}_\alpha ^*}{v_c }, \;\;p^{\prime }_\alpha =\frac{p^{\prime *}_\alpha }{P}, \;\;\rho _\alpha = \frac{\rho _\alpha ^*}{\rho _c },\nonumber \\ \mathbf{x}&= \frac{\mathbf{x}^{*}}{L}, \;\;\mathbf{y}=\frac{\mathbf{x}^{*}}{l}, \;\nabla =L\nabla ^*\quad \hbox {with}\;\alpha ,\eta \;=\;w,\;o,\;g \end{aligned}$$

(5)

where $\mu _c ,v_c ,\rho _c$ and $P$ are characteristic values of dynamic viscosity, velocity, density, and pressure, respectively. The two dimensionless spatial coordinates, x and y, are associated with the macro- and micro-scale description of the system, respectively. We present in Appendix A the details of the derivation of the dimensionless format of (1) for small Reynolds numbers, i.e., $Re_l =\rho _c v_c l/\mu _c =\mathcal{O}\left( \varepsilon \right)$, and for conditions corresponding to settings where flow is driven (a) by pressure gradient and gravity (Case I); (b) only by pressure gradient while neglecting the effect of gravity (Case II); and (c) only by gravity in the absence of externally imposed pressure gradient (Case III).

Following the Multiple Scale Expansion approach, all quantities in (48), (51) and (54) depend on both the macro-, x, and micro-scale, $\mathbf{y}=\varepsilon \mathbf{x}$, dimensionless spatial coordinates. Spatial derivatives should then be expressed as (e.g., Auriault and Adler 1995)

$$\begin{aligned} \nabla \left( {\bullet } \right) =\nabla _x \left( {\bullet } \right) +\varepsilon ^{-1}\nabla _y \left( {\bullet } \right) \end{aligned}$$

(6)

where the subscript indicates that the gradient operator refers to dimensionless coordinates x or y.

We further assume that each state variable can be expressed as

$$\begin{aligned} \mathfrak {I}_\alpha \left( \mathbf{x,y} \right) =\mathfrak {I}_\alpha ^{(0)} \left( \mathbf{x,y} \right) +\varepsilon \mathfrak {I}_\alpha ^{(1)} \left( \mathbf{x,y} \right) +\varepsilon ^{2}\mathfrak {I}_\alpha ^{(2)} \left( \mathbf{x,y} \right) +\cdots \end{aligned}$$

(7)

where $\mathfrak {I}_\alpha$ denotes a scalar (i.e., pressure or density for compressible fluids) or a vector (i.e., velocity) state variables for the $\alpha$-phase and $\mathfrak {I}_\alpha ^{(i)}$ represents the $i$-th order component of $\mathfrak {I}_\alpha$ in the expansion. Using (7) in conjunction with (48), (51) and (54) yields a series of equations that must be satisfied at each order $\mathcal{O}\left( {\varepsilon ^{i}} \right)$, as detailed in Appendix B. In the following we focus on the scenario where the effect of the gravity is of the same order of magnitude of the pressure gradient (Case I). The scenario described by Case II, where the effect of gravity is negligible (for example, in a two-dimensional horizontal domain), is indeed a particular subset of Case I, as will be elucidated in Sect. 2.2. We do not investigate Case III for the reasons illustrated in Appendix B.

From (55) and making use of the state equation at order $\mathcal{O}\left( {\varepsilon ^{0}} \right)$, flow and mass balance satisfy the following equations at order $\mathcal{O}\left( {\varepsilon ^{-1}} \right)$

$$\begin{aligned}&p^{\prime {(0)}}_\alpha =p^{\prime {(0)}}_\alpha \left( x \right) \;; \quad \quad \rho _\alpha ^{\left( 0 \right) } =\rho _\alpha ^{\left( 0 \right) } \left( \mathbf{x }\right) \quad \hbox {with }\; \alpha =\;w,\;o,\;g\end{aligned}$$

(8)

$$\begin{aligned}&\nabla _y \cdot \mathbf{v}_\alpha ^{\left( 0 \right) } =0 \qquad \hbox {with}\; \alpha \;=\;w,\;o,\;g \end{aligned}$$

(9)

where $p^{\prime (0)}_\alpha$, $\rho _\alpha ^{\left( 0 \right) }$ and $\mathbf{v}_\alpha ^{\left( 0 \right) }$ are $\Omega$-periodic in y. From (8) it is clear that pressure and density are constant for each phase within the unit cell (i.e., they do not depend on y), while they vary with x.

Following a similar procedure, one can see that flow and mass balance equations at order $\mathcal{O}\left( {\varepsilon ^{0}} \right)$ can be expressed as [see (56)–(57) in Appendix B]

$$\begin{aligned}&\displaystyle \mu _\alpha \nabla _y^2 \mathbf{v}_\alpha ^{\left( 0 \right) } -\nabla _y p^{\prime (1)}_\alpha -\nabla _x p^{\prime (0)}_\alpha -\rho _\alpha ^{\left( 0 \right) } \mathbf{e}_3 =0 \qquad \hbox {with } \alpha \;=\;w,\;o,\;g\end{aligned}$$

(10)

$$\begin{aligned}&\displaystyle \rho _\alpha ^{\left( 0 \right) } \left( {\nabla _x \cdot \mathbf{v}_\alpha ^{\left( 0 \right) } +\nabla _y \cdot \mathbf{v}_\alpha ^{\left( 1 \right) } } \right) +\mathbf{v}_\alpha ^{\left( 0 \right) } \cdot \left( {\nabla _x \rho _\alpha ^{\left( 0 \right) } +\nabla _y \rho _\alpha ^{\left( 1 \right) } } \right) \;=\;0 \quad \hbox {with } \alpha =w,\;o,\;g\nonumber \\ \end{aligned}$$

(11)

$p^{\prime {(1)}}_\alpha , \quad \rho _\alpha ^{(1)}$ and $\mathbf{v}_\alpha ^{\left( 1 \right) }$ being $\Omega$- periodic in y. Boundary conditions associated with (10)–(11) are obtained through the $i$-th order expansion of the dimensionless counterpart of (3), i.e.,

$$\begin{aligned}&\mathbf{v}_\alpha ^{\left( i \right) } =0\;\;\hbox {on}\;\Gamma _{\alpha s} ; \mathbf{v}_\alpha ^{\left( i \right) } \cdot \mathbf{n}_{\alpha \eta } =0,\;\;\mathbf{v}_\alpha ^{\left( i \right) } =\mathbf{v}_\eta ^{\left( i \right) } \nonumber \\&\mu _\alpha \nabla _y \mathbf{v}_\alpha ^{\left( i \right) } \cdot \mathbf{n}_{\alpha \eta } = \mu _\eta \nabla _y \mathbf{v}_\eta ^{\left( i \right) } \cdot \mathbf{n}_{\alpha \eta } \;\;\hbox {on}\;\Gamma _{\alpha \eta } \quad \hbox {with }\;\alpha ,\quad \eta \;=\;w,\;o,\;g \end{aligned}$$

(12)

upon setting $i$ = 0, 1.

2.2 Closure Equations and Upscaled Formulation

In this section we derive the macro-scale flow equations and the corresponding effective parameters through upscaling of (10)–(11) to the level of the periodic cell, $\Omega$. As already noticed, $p^{\prime (0)}_\alpha$ and $\rho _\alpha ^{\left( 0 \right) }$ are constant within $\Omega$. Therefore, the term $\nabla _x p_\alpha ^{(0)} =\nabla _x p^{\prime {(0)}}_\alpha +\rho _\alpha ^{\left( 0 \right) } \mathbf{e}_3$ (hereinafter termed pressure gradient) appearing in (10) does not depend on the local coordinate y and acts as a forcing term on the pore-scale flow. Note that when Case II is considered the effect of the gravity is negligible and (10)–(11) are still valid with $\nabla _x p_\alpha ^{(0)} =\nabla _x p^{\prime {(0)}}_\alpha$.

Equation (10) is solved together with (9) and the boundary conditions (12) to obtain the zero-order component, $\mathbf{v}_\alpha ^{\left( 0 \right) }$, of velocity. Linearity of the resulting system of partial differential equations leads to

$$\begin{aligned} \mathbf{v}_\alpha ^{(0)} =\;-\mathbf{k}_{\alpha w} \nabla _x p_w^{(0)} -\mathbf{k}_{\alpha o} \nabla _x p_o^{(0)} -\mathbf{k}_{\alpha g} \nabla _x p_g^{(0)} \qquad \hbox {with } \alpha \;=\;w,\;o,\;g \end{aligned}$$

(13)

where $\mathbf{k}_{\alpha \eta } (\eta =w, o, g)$ are second-order tensors depending on y. Introducing (13) into (10) yields the following solution for $p^{\prime (1)}_\alpha$

$$\begin{aligned} p^{\prime {(1)}}_\alpha =-\mathbf{a}_{\alpha w} \cdot \nabla _x p_w^{(0)} -\mathbf{a}_{\alpha o} \cdot \nabla _x p_o^{(0)} -\mathbf{a}_{\alpha g} \cdot \nabla _x p_g^{(0)} +\bar{{p}}^{\prime }_\alpha ; \qquad \hbox {with } \alpha \;=\;w,\;o,\;g\quad \end{aligned}$$

(14)

where $\bar{{p}}^{\prime }_\alpha$ are arbitrary functions of the macroscopic variable x and $\mathbf{a}_{\alpha \eta }$ ($\eta \;\hbox {=}\;w,\;o,\;g)$ are vectors depending on the micro-scale features and satisfying the following property

$$\begin{aligned} \left\langle {\mathbf{a}_{\alpha \eta } } \right\rangle =0;\quad \hbox {where} \left\langle {\bullet } \right\rangle =\frac{1}{\left| \Omega \right| }\int \limits _{\Omega _\alpha } {{\bullet }\,\, d\Omega _\alpha } \end{aligned}$$

(15)

The closure variables $\mathbf{k}_{\alpha \eta }$ and $\mathbf{a}_{\alpha \eta }$ depend on the local scale $\mathbf{y}$ and are obtained by substituting (13) and (14) into (10)

$$\begin{aligned} \mu _\alpha \nabla _y^2 \mathbf{k}_{\alpha \eta } +\delta _{\alpha \eta } \mathbf{I}-\nabla _y \mathbf{a}_{\alpha \eta } =0,\quad \nabla _y \cdot \mathbf{k}_{\alpha \eta } =0 \quad \qquad \hbox { in } \Omega _\alpha \;\;\hbox { with } \alpha , \eta = w,\;o,\;g\quad \end{aligned}$$

(16)

I  being the identity matrix, $\delta _{\alpha \eta }$ = 1 if $\eta$ = $\alpha$, and $\delta _{\alpha \eta }$= 0 otherwise. The system (16) is subject to the following boundary conditions

$$\begin{aligned} \begin{array}{l@{\quad }l} \mathbf{k}_{\alpha \eta } =0 &{}\hbox {on } \Gamma _{\alpha s} , \\ \mathbf{k}_{\alpha \eta } =\mathbf{k}_{\eta \eta } &{}\mu _\alpha \nabla _y \mathbf{k}_{\alpha \eta } \cdot \mathbf{n}_{\alpha \eta } = \mu _\eta \nabla _y \mathbf{k}_{\eta \eta } \cdot \mathbf{n}_{\alpha \eta } \quad \mathbf{k}_{\alpha \eta } \cdot \mathbf{n}_{\alpha \eta } =0 \hbox { on }\;\;\Gamma _{\alpha \eta } \quad \hbox {with}\;\alpha \ne \eta , \\ \mathbf{k}_{\alpha \eta } =\mathbf{k}_{\zeta \eta } \quad &{}\mu _\alpha \nabla _y \mathbf{k}_{\alpha \eta } \cdot \mathbf{n}_{\alpha \eta } =\mu _\zeta \nabla _y \mathbf{k}_{\zeta \eta } \cdot \mathbf{n}_{\alpha \eta } \quad \hbox {on }\; \Gamma _{\alpha \zeta } \hbox {with}\;\alpha \ne \eta \ne \zeta \\ \end{array} \end{aligned}$$

(17)

Integration of (13) over $\Omega _\alpha$ leads to the following upscaled equation

$$\begin{aligned} \left\langle {\mathbf{v}_\alpha ^{(0)} } \right\rangle \;=\;-\mathbf{K}_{\alpha w} \nabla _x p_w^{(0)} -\mathbf{K}_{\alpha o} \nabla _x p_o^{(0)} -\mathbf{K}_{\alpha g} \nabla _x p_g^{(0)} ; \quad \hbox {with } \alpha \;\hbox {=}\;w,\;o,\;g \end{aligned}$$

(18)

where $\mathbf{K}_{\alpha \eta } =\left\langle {\mathbf{k}_{\alpha \eta } } \right\rangle =\int \limits _{\Omega _\alpha } {\mathbf{k}_{\alpha \eta } d\Omega _\alpha } /\left| \Omega \right|$.

It can also be shown (details not reported) that each component, $\left\langle {v_{\alpha ,i}^{(0)} } \right\rangle$, of $\left\langle {\mathbf{v}_\alpha ^{(0)} } \right\rangle$, which is defined as a volume average of the local velocity over $\Omega _\alpha$, coincides with a surface average, i.e.,$\left\langle {v_{\alpha ,i}^{(0)} } \right\rangle =\int \limits _{\Omega _\alpha } {v_{\alpha ,i}^{(0)} } d\Omega _\alpha /\left| \Omega \right| =\int \limits _{\Sigma _{\alpha ,i} } {v_{\alpha ,i}^{(0)} } \left( {\mathbf{x,y}} \right) d\Sigma _{\alpha ,i} /\left| {\partial \Omega _i } \right|$, where $\partial \Omega _i$ is the (solid plus void) surface area of the periodic cell perpendicular to the $y_{i}$-axis and $\Sigma _{\alpha ,i}$ is the part of $\partial \Omega _i$ occupied by the $\alpha$-phase. Note that this definition is completely consistent with the nature of typical laboratory measurements of effective velocities.

We introduce the relative permeability tensors defined as

$$\begin{aligned} \mathbf{K}_{\alpha \eta ,r} ={\mathbf{K}_{\alpha \eta } }/{\mathbf{K}_\alpha } \end{aligned}$$

(19)

where $\mathbf{K}_\alpha$ is the intrinsic permeability associated with phase $\alpha ,$i.e., the permeability of $\Omega$ when its pore space is filled solely by the $\alpha$-phase. Making use of (19), Eq. (18) can also be written as

$$\begin{aligned} \left\langle {\mathbf{v}_\alpha ^{(0)} } \right\rangle \;=\;-\mathbf{K}_\alpha \left( {\mathbf{K}_{\alpha w,r} \nabla _x p_w^{(0)} +\mathbf{K}_{\alpha o,r} \nabla _x p_o^{(0)} +\mathbf{K}_{\alpha g,r} \nabla _x p_g^{(0)} } \right) ,\quad \quad \hbox {with } \alpha \;=\;w,\;o,\;g \end{aligned}$$

(20)

From (20) it is then clear that the zero-order mean velocity of each phase flowing in the system is proportional to the pressure gradients applied to all phases, the coefficients of proportionality being the relative permeability tensors.

3 Analytical Solutions

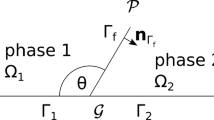
We consider immiscible three-phase flow occurring through the two pore spaces depicted in Fig. 1. The first case (Fig. 1a) is termed Crack model and represents flow within a horizontal plane fracture while the second scenario (Fig. 1b) is termed Capillary tube model and can be seen as a component of a porous medium structure consisting of circular cylindrical pores. The latter configuration has been extensively employed in pore network models (Piri and Blunt 2005). We consider a water-wet system where water flows in contact with the fracture (or the pore) wall while the gas, which is usually the most non wetting phase, occupies the central region of the pore. Albeit both scenarios are simplified configurations of real pore structures and in the Capillary tube model only a very thin film of oil may occur between water and gas (Keller et al. 1997), the two selected pore spaces allow to (i) study key physical processes occurring at the pore scale and the propagation of their effects to the macro-scale, and (ii) derive analytical expressions for upscaled relative permeabilities enabling us to explore the nature of such upscaled quantities.

Fig. 1

Pore structures of the a Crack model and b Capillary tube model

Diverse complex geometries of the pore structure can be treated within the framework illustrated in Sect. 2. In such cases (16)–(17) must be solved numerically. We observe that solving the three systems embedded in (16)–(17) is tantamount to solving three steady-state multi-phase Stokes equations (1) for incompressible fluids, where the forcing term is replaced by a unit body force applied to the $\eta$-phase. Therefore, the numerical solution of (16)–(17) can be obtained through standard available algorithms associated with the treatment of the Stokes problem.

We consider laminar flow which is developing along the $y_{2}$-axis for the Crack model and along the $y_{3}$-axis for the Capillary tube model, as shown in Fig. 1. In this one-dimensional flow configuration the relative permeability tensors reduce to the following set of scalar quantities, $K_{\alpha \eta ,r}$, for the Crack model

$$\begin{aligned}&K_{ww,r} = S_w^3\end{aligned}$$

(21)

$$\begin{aligned}&K_{oo,r} = S_o^3 +3\frac{\mu _o }{\mu _w }S_w S_o^2\end{aligned}$$

(22)

$$\begin{aligned}&K_{gg,r} = S_g^3 +3\left( {\frac{\mu _g }{\mu _o }S_o +\frac{\mu _g }{\mu _w }S_w } \right) S_g^2\end{aligned}$$

(23)

$$\begin{aligned}&K_{w\alpha ,r} = \frac{\mu _w }{\mu _\alpha }K_{\alpha w,r} =\frac{3}{2}S_\alpha S_w^2 \quad \alpha =o,g\end{aligned}$$

(24)

$$\begin{aligned}&K_{go,r} = \frac{\mu _g }{\mu _o }K_{og,r} =3\left( {\frac{\mu _g }{2\mu _o }S_o +\frac{\mu _g }{\mu _w }S_w } \right) S_o S_g \end{aligned}$$

(25)

and for the Capillary tube model

$$\begin{aligned}&K_{ww,r} = S_w^2 -2\left( {1-S_w } \right) \left[ {S_w +\left( {1-S_w } \right) \ln \left( {1-S_w } \right) } \right] \end{aligned}$$

(26)

$$\begin{aligned}&K_{oo,r} = S_o^2 -2\left[ {S_o S_g +S_g^2 \ln S_g +\left( {\frac{\mu _o }{\mu _w }S_o^2 -S_g^2 } \right) \ln \left( {1-S_w } \right) } \right] \end{aligned}$$

(27)

$$\begin{aligned}&K_{gg,r} = S_g^2 -2S_g^2 \left[ {\frac{\mu _g }{\mu _o }\ln \frac{S_g }{1-S_w }+\frac{\mu _g }{\mu _w }\ln \left( {1-S_w } \right) } \right] \end{aligned}$$

(28)

$$\begin{aligned}&K_{w\alpha ,r} = \frac{\mu _w }{\mu _\alpha }K_{\alpha w,r} =2S_\alpha \left[ {S_w +\left( {1-S_w } \right) \ln \left( {1-S_w } \right) } \right] \quad { \alpha } = o, g\end{aligned}$$

(29)

$$\begin{aligned}&K_{go,r} = \frac{\mu _g }{\mu _o }K_{og,r} =2S_g \left[ {\frac{\mu _g }{\mu _o }\left( {S_o +S_g \ln \frac{S_g }{1-S_w }} \right) -\frac{\mu _g }{\mu _w }S_o \ln \left( {1-S_w } \right) } \right] \end{aligned}$$

(30)

where $S_\alpha ={\Omega _\alpha }/\Omega$. As an example of our derivations, Appendix C reports the details of the solution for $K_{oo,r}$ in the Crack model.

Note that (26)–(27) and (29) with $\alpha =o$ coincide with the solutions of Dehghanpour et al. (2011a) which were obtained under the assumption of negligible shear stress at the oil-gas interface. Our derivation considers continuity of velocity and shear stress at the water-oil and gas-oil interfaces. As a consequence and as we show in the following, $K_{og,r}$ may embed a significant contribution of the dragging effect of gas on the oil phase.

Figures 2 and 3 show the dependence of the relative permeability coefficients (21)–(30) on the saturation of each phase for the Crack and for the Capillary tube model, respectively. As reference values, fluid viscosities are set to $\mu _w^{*} = 1.06 \hbox { cP}, \mu _o^{*} = 1.77 \hbox { cP}, \mu _g^{*} = 1.87\times 10^{-2} \hbox {cP}$ (Oak et al. 1990), corresponding to $\mu _o /\mu _w=1.75$, $\mu _g /\mu _o =1.06\;\times 10^{-2}$ and $\mu _g /\mu _w =1.76\;\times 10^{-2}$. The results depicted in Figs. 2 and 3 show that the qualitative pattern of all permeability coefficients in the saturation space is similar for the two models considered, albeit these are associated with diverse pore structures. It can be noted that, as indicated in (21) and (26), $K_{ww,r}$ is only a function of $S_{w}$, it monotonically increases with $S_{w}$ and reaches its maximum (unit) value for $S_{w}$ = 1.

Fig. 2

Relative permeabilities for the Crack model in the saturation space. a $K_{ww,r}$; b $K_{oo,r}$; c $K_{gg,r}$; d $K_{wo,r}$; and $K_{ow,r}$; e $K_{go,r}$ and $K_{og,r}$; f $K_{gw,r}$ and $K_{wg,r}$. Viscosity coefficients are set equal to $\mu _w^*= 1.06 \hbox { cP}, \mu _o^*= 1.77~\hbox { cP}, \mu _g^*= 1.87 \times 10^{-2}\hbox { cP}$

Fig. 3

Relative permeabilities for the Capillary tube model in the saturation space. a $K_{ww,r}$; b $K_{oo,r}$; c $K_{gg,r}$; d $K_{wo,r}$ and $K_{ow,r}$; e $K_{go,r}$ and $K_{og,r}$; f $K_{gw,r}$ and $K_{wg,r}$. Viscosity coefficients are set equal to $\mu _w^*= 1.06 \hbox { cP}, \mu _o^*= 1.77 \,\hbox {cP}, \mu _g^*= 1.87 \times 10^{-2 }\, \hbox {cP}$

The oil relative permeability, $K_{oo,r}$, depends on the saturation of all of the phases and on the ratio between oil and water viscosity. When $\mu _o /\mu _w >1$, the largest values for $K_{oo,r}$ are obtained for $S_g =0.0$ and $S_o=2\left( {3\mu _o /\mu _w -1} \right) \mu _o /\mu _w$ or $S_o=\exp \left[ {0.5\left( {1-\mu _o /\mu _w } \right) /\left( {\mu _o /\mu _w } \right) } \right]$ for the Crack and the Capillary tube model, respectively. Figure 4 depicts the way maximum values of $K_{oo,r}$ depend on $\mu _o /\mu _w$ and the associated oil and water saturations. Results obtained for the Crack and Capillary tube model are plotted with continuous and dashed curves, respectively.

Fig. 4

Maximum values of $K_{oo,r}$ and associated oil ($S_{o})$ and water ($S_{w})$ saturations versus ${\mu _o }/{\mu _w }$. Results obtained with the Crack and Capillary tube model are depicted with continuous and dashed curves, respectively

One can note that maxima of $K_{oo,r}$ tend to increase with $\mu _o /\mu _w$ attaining values which are significantly larger than unity under saturation conditions associated with $S_{o} <$ 1 and $S_{w} >$ 0. This phenomenon has been already observed for two phase flow and is also known as lubrication effect, i.e. in a water wet system $K_{oo,r}$ increases with $S_{w}$ because oil is not in contact with a no-slip boundary when $S_{w} \ne$ 0. Water saturation corresponding to maxima of $K_{oo,r}$ increases with $\mu _o /\mu _w$ and tends asymptotically to a value of 33% and 39%, respectively for the Crack and the Capillary tube model.

Gas relative permeability, $K_{gg,r}$, depends on $S_{g}$, $S_{o}$ (or equivalently $S_{w})$ and on the viscosity ratios $\mu _g /\mu _o$ and $\mu _g /\mu _w$. In the typical setting where these ratio are significantly smaller than unity, $K_{gg,r}$ increases monotonically with $S_{g}$ and the effect of fluid viscosity ratios becomes negligible.

All terms $K_{\alpha \eta ,r}$ (with $\alpha \, \ne \, \eta )$, which account for the viscous coupling between the phases, are in general nonzero. Components $K_{\alpha w,r}$ and $K_{w \alpha ,r}$ (with $\alpha =o$ or $g)$ attain their maximum values when $S_{w}$ = 66 % (and $S_{\alpha }$ = 33 %; $\alpha =o$ or $g)$ for the Crack model and $S_{w}$ = 72 % (and $S_{\alpha }$ = 28 %; $\alpha =o$ or $g)$ for the Capillary tube model, independent of the ratio $\mu _\alpha /\mu _w$. The maximum values of $K_{w \alpha ,r}$ is about 0.2 for both flow configurations. Therefore, oil flow due to pressure gradients applied to water, as described by $K_{ow,r} =K_{wo,r} \mu _o /\mu _w$, can be significant when $\mu _o >\mu _w$. The latter is a typical condition taking place in practical applications, this aspect is further investigated in Sect. 4.

Fluid saturations at which $K_{go,r}$ and $K_{og,r}$ attain their largest values are influenced by the viscosity ratio $\mu _o /\mu _w$ while being independent of $\mu _g/\mu _o$. For the Crack model, $K_{go,r}$ and $K_{og,r}$ reach their respective maxima when $S_{o}$ = 67 % and $S_{g}$ = 33 % for $\mu _o/\mu _w\le 1$ or $S_o=\left( {2\mu _o /\mu _w } \right) /\left( {6\mu _o /\mu _w -3} \right)$ and $S_{g}$ = 33 % for $\mu _o/\mu _w >1$. Figure 5 depicts the dependence of the largest values of $K_{og,r}$ on $\mu _o /\mu _w$ and the associated oil and water saturations. The results related to the Capillary tube model embedded in Fig. 5 have been evaluated numerically through (30). Note that maxima of $K_{og,r}$ increase monotonically with $\mu _o /\mu _w$ for both flow models and can be significantly larger than unity.

Fig. 5

Maximum values of $K_{og,r}$ and associated oil ($S_{o})$ and water ($S_{w})$ saturations versus ${\mu _o }/{\mu _w }$. Results obtained with the Crack and Capillary tube model are depicted with continuous and dashed curves, respectively

Quantification of the relative contribution of each relative permeability term to the total water flow can be deduced by inspection of the results displayed in Fig. 6, which depicts the dependence of $K_{ww,r}$, $K_{wo,r}$ and $K_{wg,r}$ on $S_{w}$ and $S_{g}$ for $S_{o}$ = 15 % (Fig. 6a), 50 % (Fig. 6b), 75 % (Fig. 6c) in the Capillary tube model. Corresponding depictions for oil and gas are shown in Figs. 7 and 8, respectively. Note that the results of Fig. 6 do not depend on fluid viscosities, as described by (26) and (29), while those reported in Figs. 7 and 8 have been computed upon relying on viscosity reference values reported by Oak et al. (1990), as detailed above. Qualitatively similar results can also be obtained with reference to the Crack model as well as by considering diverse viscosity ratios.

Fig. 6

Relative water permeabilities, $K_{ww,r}, K_{wo,r}$ and $K_{wg,r}$, for the Capillary tube model versus $S_{w}$ and $S_{g}$ when a $S_{o}$ = 0.15; b $S_{o}$ = 0.5; c $S_{o}$ = 0.75

Fig. 7

Relative oil permeabilities, $K_{oo,r}$, $K_{ow,r}$ and $K_{og,r}$, for the Capillary tube model tube model versus $S_{w}$ and $S_{g}$ when a $S_{o}$ = 0.15; b $S_{o}$ = 0.5; c $S_{o}$ = 0.75. Viscosity coefficients are set equal to $\mu _w^*= 1.06 \hbox { cP}, \mu _o^*= 1.77 \,\hbox {cP}, \mu _g^*= 1.87 \times 10^{-2}\, \hbox {cP}$

Fig. 8

Relative gas permeabilities, $K_{gg,r}$,$_{ }K_{go,r}$ and $K_{gw,r}$, for the Capillary tube model versus $S_{w}$ and $S_{g}$ when a $S_{o}$ = 0.15; b $S_{o}$ = 0.5; c) $S_{o}$ = 0.75. Viscosity coefficients are set equal to $\mu _w^*= 1.06 \hbox { cP}, \mu _o^*$ $= 1.77 \,\hbox {cP}, \mu _g^*= 1.87 \times 10^{-2} \,\hbox {cP}$

Our results clearly indicate that coupling effects for water and oil flow cannot be neglected because the terms $K_{\alpha \alpha ,r}$ and $K_{\alpha \eta ,r}$ are of the same order of magnitude and $K_{\alpha \eta ,r}$ can also be larger than $K_{\alpha \alpha ,r}$ (see Figs. 6a–c, 7a–c). In particular, note that that the contribution of the gas phase on the oil motion cannot be disregarded and increases as $S_{o}$ decreases (see Fig. 7). Focusing on the flow of the gas phase (see Fig. 8), one can note that $K_{gw,r}$ and $K_{go,r}$ are smaller than $K_{gg,r}$ by several orders of magnitude. This implies that gas flow in these configurations can be characterized upon considering only the effects of the pressure gradient acting on the gas phase.

4 Uncertainty Quantification Through Global Sensitivity Analysis

Fluid viscosity values required for the evaluation of (22)–(25) and (27)–(30) are typically assessed experimentally at the laboratory scale. However, they may vary across several orders of magnitude depending on reservoir conditions in terms of, e.g., temperature and pressure, and/or on gas and oil type (e.g., McGuire et al. 2005), and are therefore to be considered as uncertain parameters under field settings. This Section is devoted to a global sensitivity analysis which has been performed according to the following two steps: (a) evaluation of the way uncertainty in the model output (i.e., relative permeabilities) is impacted by uncertainty associated with fluid viscosities, and (b) quantification of the relative contribution of each of these uncertain viscosity parameters to the total variability of $K_{\alpha \eta ,r}$. As a metric for uncertainty quantification, we consider the variance, $\sigma _{K_{\alpha \eta ,r} }^2$, of $K_{\alpha \eta ,r}$. Note that the relative permeability of water, $K_{w\eta ,r }$ (with $\eta =o$, $w$, $g)$, does not depend on viscosity as shown in (21), (24), (26) and (29) and therefore will not be considered in the following analyses.

It can be shown (Sobol 1993) that if the model response $f(\varvec{\upbeta })$ which is associated with $N$ independent random parameters grouped in vector ${\varvec{\upbeta }} = (\beta _{1},{\ldots },\beta _{N})$ belongs to the space of square integrable functions then the following expansion holds

$$\begin{aligned} f\left( {\varvec{\upbeta }} \right) =f_0 +\sum _{i=1}^N {f_i \left( {\beta _i } \right) } +\sum _{1\le i<j\le N}{f_{ij} \left( {\beta _i ,\beta _j } \right) } +\cdots +f_{1,...,N} \left( {\beta _1 ,...,\beta _N } \right) \end{aligned}$$

(31)

The constant $f_{0}$ is the expected value of $f({\varvec{\upbeta }})$ and $f_{i_{1} ,...,i_{s}} \left( {\left\{ {i_1 ,...,i_s } \right\} \subseteq \left\{ {1,...,N} \right\} } \right)$ are orthogonal polynomials with respect to a probability measure. The total variance, $\sigma _f^2$, of $f({\varvec{\upbeta }})$ can then be written as

$$\begin{aligned} \sigma _f^2 =\sum _{i=1}^N {\sigma _{f,i}^2 } +\sum _{1\le i<j\le N} {\sigma _{f,ij}^2 } +\cdots +\sigma _{f,1,...,N}^2 \end{aligned}$$

(32)

Here, $\sigma _{f,i}^2$ is the contribution to the variance of the model output due to the effect of the uncertain input parameter $\beta _{i}$ when considered individually, and $\sigma _{f,i_1 ,...,i_s }^2$ is due to interaction of the uncertain model parameters belonging to the subset $\left\{ {\beta _{i_{_1 }} ,...,\beta _{i_s } } \right\}$. The Sobol indices are then defined as

$$\begin{aligned} S\left( {f,\beta _{i_1 } ,...,\beta _{i_s } } \right) =\frac{\sigma _{f,i_1 ,...,i_s }^2 }{\sigma _f^2 } \end{aligned}$$

(33)

and express the contribution of a subset of model parameters $\left\{ {\beta _{i _{1 }} ,...,\beta _{i_s } } \right\}$ to the total model variance. One can define 2$^{N}-1$ Sobol indices from (33) such that

$$\begin{aligned} \sum _{i=1}^N {S\left( {f,\beta _i } \right) +\sum _{1\le i<j\le N} {S\left( {f,\beta _i ,\beta _j } \right) } +\cdots +S\left( {f,\beta _i ,\beta _j ,...,\beta _N } \right) =1} \end{aligned}$$

(34)

The principal Sobol indices $S\left( {f,\beta _i } \right)$ in (34) describe the influence of each of the model parameters when considered individually and the mixed terms $S\left( {f,\beta _i ,\beta _j,...} \right)$account for possible interactions between parameters.

In our analysis the relative permeability functions (22)–(25) and (27)–(30) constitute the mathematical models associated with the input parameters $\mu _\alpha$ (with $\alpha =o$, $w$, $g)$ representing the fluid viscosities. We treat these parameters as independent random variables. In the absence of prior knowledge on their probability distribution, we assume that $\mu _\alpha$ (with $\alpha =o$, $w$, $g)$ is uniformly distributed within the interval $\left[ {\mu _\alpha ^m ,\mu _\alpha ^M } \right]$.The variance of each relative permeability term in (22)–(25) and (27)–(30) can then be computed analytically for our settings. The variances of the oil relative permeabilities are given by

$$\begin{aligned} \sigma _{K_{oo,r} }^2 =\frac{3}{4}\left[ {S_{o}^2 S_w} \right] ^{2}{\mathfrak {M}}_1 ; \quad \sigma _{K_{ow,r} }^2 =\frac{3}{16}\left[ {S_o S_w^2 } \right] ^{2}{\mathfrak M}_1 ;\quad \sigma _{K_{og,r} }^2 =\frac{3}{4}\left[ {S_g S_o (S_g +S_o )} \right] ^{2}{\mathfrak M}_1 \end{aligned}$$

(35)

for the Crack model and by

$$\begin{aligned} \sigma _{K_{oo,r} }^2&= \frac{{\mathfrak M}_1 }{3}\left[ {S_o^2 \ln \left( {1-S_w } \right) } \right] ^{2}\nonumber \\ \sigma _{K_{ow,r} }^2&= \frac{{\mathfrak M}_1 }{3}S_o^2 \left[ {S_w +\left( {1-S_w } \right) \ln \left( {1-S_w } \right) } \right] ^{2}\nonumber \\ \sigma _{K_{og,r} }^2&= \frac{{\mathfrak M}_1 }{3}\left[ {S_g S_o \ln \left( {1-S_w } \right) } \right] ^{2} \end{aligned}$$

(36)

for the Capillary tube model.

Each variance in (35)–(36) depends nonlinearly on phase saturations and linearly on ${\mathfrak M}_1$. The latter has the following expression

$$\begin{aligned} {\mathfrak M}_1 =4\frac{(\mu _o^m )^{2}+\mu _o^m \mu _o^M +(\mu _o^M )^{2}}{\mu _w^m \mu _w^M }-3\left[ {\frac{\mu _o^m +\mu _o^M }{\mu _w^m -\mu _w^M }\ln \frac{\mu _w^M }{\mu _w^m }} \right] ^{2} \end{aligned}$$

(37)

and depends only on the lower and upper bounds of the range of variability of oil and water viscosity.

The expressions for the gas relative permeability variances are more complex as shown in Appendix D (70–72). It can be seen that they depend on fluid saturations and on the lower and upper bounds of the range of variability of all three flowing phases. As an example, Fig. 9 depicts the distribution of the relative permeability variances in the ternary saturation phase space for the Capillary tube model when fluid viscosities vary between the following bounds which have been documented in the literature, i.e., $0.2 \hbox {cP}\le \mu _w^*\le 1.4 \hbox {cP}$, $0.5 \hbox {cP}\le \mu _o^*\le 300 \hbox {cP}$ and $0.01 \hbox {cP}\le \mu _g^*\le 0.03 \hbox {cP}$ (e.g., Beal 1946; McGuire et al. 2005). The results associated with the Crack model are qualitatively and quantitatively very similar to those reported in Fig. 9 (details not shown). Note that the coefficient of variation (CV) of each relative permeability is in general non-negligible (i.e., it is larger than 5 %), the only exception being CV of $K_{gg,r}$. Phase saturation values corresponding to values of CV of $K_{gg,r} \ge 5\%$ in Fig. 9b are found within a region characterized by very low values of $S_{g}$ (see the region in the bottom left corner of Fig. 9b, delimited by the dotted line). This result confirms our earlier observation that $K_{gg,r}$ is mainly affected by $S_{g}$ and can be influenced by fluid viscosities only at very small gas saturation levels, as anticipated by inspection of (23) and (28).

Fig. 9

Relative permeability variances for the Capillary tube model. a $\sigma _{K_{oo,r} }^2$; b $\sigma _{K_{gg,r} }^2$; c $\sigma _{K_{ow,r} }^2 ;$ d $\sigma _{K_{go,r} }^2$ and $\sigma _{K_{og,r} }^2$; e $\sigma _{K_{gw,r} }^2$

We conclude our analysis by deriving analytical expressions of the Sobol indices which enable one to investigate the relative contribution (or weight) of each uncertain viscosity parameter to the total variance of $K_{\alpha \eta ,r}$. We indicate with $S\left( {K_{\eta \alpha ,r} ,\mu _\chi } \right)$ the principal Sobol index of $K_{\alpha \eta ,r}$ with respect to $\mu _\chi$ and with $S\left( {K_{\eta \alpha ,r} ,\mu _\chi ,\mu _\xi } \right)$ the term embedding the effects of the interaction between parameters $\mu _\chi$ and $\mu _\xi$. For the oil relative permeabilities we obtain the following results, independent of the flow model considered

$$\begin{aligned} S\left( {K_{o\alpha ,r} ,\mu _w } \right)&= \frac{3(\mu _o^m +\mu _o^M )^{2}}{{\mathfrak M}_1 }\left[ {\frac{1}{\mu _w^m \mu _w^M }-\left( {\frac{1}{\mu _w^m -\mu _w^M }\ln \frac{\mu _w^M }{\mu _w^m }} \right) ^{2}} \right] \end{aligned}$$

(38)

$$\begin{aligned} S\left( {K_{o\alpha ,r} ,\mu _o } \right)&= \frac{1}{{\mathfrak M}_1 }\left[ {\frac{\mu _o^m -\mu _o^M }{\mu _w^m -\mu _w^M }\ln \frac{\mu _w^M }{\mu _w^m }} \right] ^{2}\end{aligned}$$

(39)

$$\begin{aligned} S\left( {K_{o\alpha ,r} ,\mu _w ,\mu _o } \right)&= \frac{(\mu _o^m -\mu _o^M )^{2}}{{\mathfrak M}_1 }\left[ {\frac{1}{\mu _w^m \mu _w^M }-\left( {\frac{1}{\mu _w^m -\mu _w^M }\ln \frac{\mu _w^M }{\mu _w^m }} \right) ^{2}} \right] \end{aligned}$$

(40)

where $\alpha$ = $w$, $o$, $g$. It can be observed that the Sobol indices (38)–(40) do not depend on phase saturations or on the type of pore structure we investigate. Table 1 lists the values of the principal Sobol indices together with the term involving the joint effect of the uncertainty associated with $\mu _w$ and $\mu _o$ on the total variance of $K_{o\alpha ,r}$. The principal Sobol indices are significantly larger than the interaction terms. Note that, even as the interval of variability of $\mu _{o}$ is one order of magnitude larger than that associated with $\mu _{w}$, $S\left( {K_{o\alpha ,r} ,\mu _w } \right)$ is slightly larger than $S\left( {K_{o\alpha ,r} ,\mu _o } \right)$, confirming the marked influence of water viscosity on oil displacement.

Table 1 Sobol indices for $K_{o \alpha ,r}$ (with $\alpha =o, w, g)\,\, \hbox {and}\,\, K_{gw,r}$

Appendix D reports the expressions obtained for the principal Sobol indices associated with the gas relative permeability. We note that Sobol indices associated with $K_{gw,r}$ depend only on water and gas viscosities [see (73)–(74)]. As shown in Table 1, the main contribution to the total variance of $K_{gw,r}$ is due to the variability of $\mu _{w}$ while $\mu _{g}$ has only a marginal effect. On the other hand, the principal Sobol indices associated with $K_{gg,r}$ and $K_{go,r}$ and reported in (75)–(80) depend not only on the bounds of the range of variability of the viscosity parameters but also on fluid phase saturation and pore structure.

Figure 10 depicts the dependence on $S_{o}$ and $S_{g}$ of the principal Sobol indices related to $K_{gg,r}$ for three selected values of $S_{w}$ (i.e., $S_{w}$ = 0.01, 0.2, and 0.4) in the Capillary tube model setting. A corresponding depiction for $K_{go,r}$ is shown in Fig. 11. Qualitatively and quantitatively similar results have been obtained for the Crack model (not reported). We note that the Sobol indices tend to constant values when $S_{w} \ge$ 0.4 (results obtained with $S_{w} >$ 0.4 are not shown). The contribution of $\mu _{o}$ to the total variance of $K_{gg,r}$ and $K_{go,r}$ is significant only for small values of $S_{w}$ and increases with $S_{o}$ (see Figs. 10a, b, 11a, b). Increasing $S_{w}$, the only two key parameters affecting the variability of the results are $\mu _{w}$ and $\mu _{g}$, respectively contributing to about 75% and 18% of the total variances of $K_{gg,r}$ and $K_{go,r}$. The effect of the interaction between parameters $\mu _{\alpha }$ and $\mu _{g,}$ (with $\alpha = w, o$) is less than 7% of the total variance, as shown in Figs. 10 and 11. Interactions between $\mu _{w}$ and $\mu _{o}$ and between $\mu _{w}$,$\mu _{o}$ and $\mu _{g}$ do not contribute to the variability of $K_{gg,r}$ and $K_{go,r}$.

Fig. 10

Sobol indices of $K_{gg}$ for the Capillary tube model versus $S_{o}$ and $S_{g}$ when a $S_{w}$ = 0.01; b $S_{w}$ = 0.2; c $S_{w}$ = 0.4

Fig. 11

Sobol indices of $K_{go}$ for the Capillary tube model versus $S_{o}$ and $S_{g}$ when a $S_{w}$ = 0.01; b $S_{w}$ = 0.2; c $S_{w}$ = 0.4

5 Conclusions

Our work leads to the following major conclusions.

• (1) We upscale steady-state immiscible three-phase flow from the pore- to the Darcy- scale by means of homogenization relying on Multiple Scale Expansion. The mean velocity of each phase flowing in the system is proportional to the pressure gradients applied to all phases, the coefficient of proportionality being the effective relative permeability tensors, $\mathbf{K}_{\alpha \eta ,r}$. Components of $\mathbf{K}_{\alpha \eta ,r}$, can be evaluated once the pore scale geometrical structure of the medium and the distribution of the three phases in the pore space are known. We show that the numerical solution required for the evaluation of $\mathbf{K}_{\alpha \eta ,r}$ can be obtained through standard available algorithms related to the Stokes problem.

• (2) We consider flow taking place at small Reynolds numbers within elementary water wet pore structures corresponding to (a) a plane channel and (b) a capillary tube with circular cross-section. These settings are typical of microfluidics applications and are considered as base examples of multiphase flow processes occurring at the microscale within porous or fractured media. We derive analytical expressions for the relative permeability tensors, $\mathbf{K}_{\alpha \eta ,r}$, which are reduced to scalar quantities, $K_{\alpha \eta ,r}$, for these settings [see (21)–(30)]. These scalars exhibit similar patterns in the phase saturation diagram for the two geometrical settings considered while displaying strong dependence on fluid saturations and viscosities. Upscaled velocities of the water and oil phases are significantly affected by viscous coupling between the three flowing fluids. Our findings show that the coupling effect due to the gas phase, which is usually neglected, can have a remarkable effect on water and oil motion.

• (3) The way the uncertainty associated with fluid viscosities, which are parameters typically hard to characterize under field conditions, propagates to the system and affects the total variability of oil and gas relative permeabilities has been investigated upon relying on the analytical expressions developed in the context of a global sensitivity analysis. Our findings show that uncertainty associated with oil and water viscosity propagates to the oil relative permeability, $K_{o\alpha ,r}$, in a way that does not depend on the flow model considered or on phase saturation values and depends solely on the upper and lower bounds of the selected range of variability for the viscosities of water and oil. Even as the uncertainty of oil viscosity is usually at least one order of magnitude larger than that associated with water viscosity, the variability of $K_{o\alpha ,r}$ is slightly more influenced by the latter than by the former. The variance-based Sobol indices associated with gas relative permeabilities depend on the upper and lower bounds of the range of variability of all the three fluid viscosities and on the saturation of all three phases up to $S_{w} \cong 0.4$.

Appendices

Appendix A: Dimensional Analysis and Dimensionless Stokes Equations

We consider the momentum balance equation (1) for the generic fluid phase $\alpha$. The order of magnitude of the viscous term in (1) is

$$\begin{aligned} \mu _\alpha ^*\left[ {\nabla ^{*2} \mathbf{v}_\alpha ^*+\frac{1}{3}\nabla ^{*}\left( {\nabla ^{*}\cdot \mathbf{v}_\alpha ^*} \right) } \right] \;=\;\mathcal{O}\left( {\frac{\mu _c v_c }{l^{2}}} \right) \end{aligned}$$

(41)

From (1), flow is forced by (a) the macroscopic pressure gradient whose order of magnitude is

$$\begin{aligned} \nabla ^{*}p^{\prime *}_\alpha =\mathcal{O}\left( {\frac{P}{L}} \right) \end{aligned}$$

(42)

and $(b)$ gravity

$$\begin{aligned} \rho _\alpha ^*g^{*} \end{aligned}$$

(43)

We introduce Reynolds, $Re_l$, Froude, $Fr_L$, and Euler, Eu, numbers, respectively defined as

$$\begin{aligned} Re_l =\frac{\rho _c v_c l}{\mu _c };\quad Fr_L =\frac{v_c }{\sqrt{g^{*}L}};\quad Eu=\frac{P}{\rho _c v_c^{2}} \end{aligned}$$

(44)

Making use of (41)–(43), we can consider the following cases:

Case I

In this case flow is forced by both the pressure gradient and gravity. Therefore, the terms (42) and (43) are of the same order of magnitude as the viscous term, i.e.,

$$\begin{aligned} \frac{P}{L}=\mathcal{O}\left( {\frac{\mu _c v_c }{l^{2}}} \right) ;\quad \rho _c g^{*}=\mathcal{O}\left( {\frac{\mu _c v_c }{l^{2}}} \right) \end{aligned}$$

(45)

From the first of (44) one derives the order of magnitude of Eu as

$$\begin{aligned} Eu=\frac{P}{\rho _c v_c ^{2}}=\mathcal{O}\left( {\frac{\mu _c }{\rho _c v_c l}\frac{L}{l}} \right) =\mathcal{O}\left( {\frac{1}{Re_l }\frac{1}{\varepsilon }} \right) =\mathcal{O}\left( {\varepsilon ^{-2}} \right) \end{aligned}$$

(46)

From the second of (45), the order of magnitude of $Fr_L$ is given by

$$\begin{aligned} Fr_L =\frac{v_c }{\sqrt{g^{*}L}}=\mathcal{O}\left( {\sqrt{\varepsilon Re_l }} \right) =\mathcal{O}\left( \varepsilon \right) \end{aligned}$$

(47)

In this case, and making use of the dimensionless quantities defined in (5), Eq. (1) becomes

$$\begin{aligned} \varepsilon ^{2}\mu _{\alpha } \left[ {\nabla ^{2} \mathbf{v}_\alpha +\frac{1}{3}\nabla \left( {\nabla \cdot \mathbf{v}_\alpha } \right) } \right] =\nabla p^{\prime }_\alpha +\rho _\alpha \mathbf{e}_3 ; \quad \nabla \cdot \left( {\rho _\alpha \mathbf{v}_\alpha } \right) =0 \end{aligned}$$

(48)

Case II

In this case flow is forced only by the pressure gradient. Therefore, the term (42) is of the same order of magnitude as the viscous term, while term (43) is much smaller than (41), i.e.,

$$\begin{aligned} \frac{P}{L}=\mathcal{O}\left( {\frac{\mu _c v_c }{l^{2}}} \right) ;\quad \rho _c g^{*}=\mathcal{O}\left( {\varepsilon \frac{\mu _c v_c }{l^{2}}} \right) \end{aligned}$$

(49)

The first of (49) yields the condition (46) on Eu, while from the second of (49) one obtains

$$\begin{aligned} Fr_L =\mathcal{O}\left( {\sqrt{Re_l }} \right) =\mathcal{O}\left( {\sqrt{\varepsilon }} \right) \end{aligned}$$

(50)

Making use of the dimensionless quantities defined in (5), Eq. (1) becomes

$$\begin{aligned} \varepsilon ^{2}\mu _\alpha \left[ {\nabla ^{2} \mathbf{v}_\alpha +\frac{1}{3}\nabla \left( {\nabla \cdot \mathbf{v}_\alpha } \right) } \right] =\nabla p^{\prime }_\alpha +\varepsilon \rho _\alpha \mathbf{e}_3 ;\qquad \qquad \nabla \cdot \left( {\rho _\alpha \mathbf{v}_\alpha } \right) =0 \end{aligned}$$

(51)

Case III

In this case flow is forced only by gravity. Therefore, the term (43) is of the same order of magnitude as the viscous term, while term (42) is much smaller than (41), i.e.

$$\begin{aligned} \frac{P}{L}=\mathcal{O}\left( {\varepsilon \frac{\mu _c v_c }{l^{2}}} \right) ;\quad \rho _c g^{*}=\mathcal{O}\left( {\frac{\mu _c v_c }{l^{2}}} \right) \end{aligned}$$

(52)

The second of (52) yields the condition (47) on Fr $_{L}$, while from the first of (52) one obtains

$$\begin{aligned} Eu=\mathcal{O}\left( {\frac{1}{Re_l }} \right) =\mathcal{O}\left( {\varepsilon ^{-1}} \right) \end{aligned}$$

(53)

In this case, and making use of the dimensionless quantities defined in (5), Eq. (1) becomes

$$\begin{aligned} \varepsilon ^{2}\mu _\alpha \left[ {\nabla ^2 \mathbf{v}_\alpha +\frac{1}{3}\nabla \left( {\nabla \cdot \mathbf{v}_\alpha } \right) } \right] =\varepsilon \nabla p^{\prime }_\alpha +\rho _\alpha \mathbf{e}_3 ; \qquad \qquad \nabla \cdot \left( {\rho _\alpha \mathbf{v}_\alpha } \right) =0 \end{aligned}$$

(54)

Appendix B: Expansion of Dimensionless Stokes Equations

Case I ($Re_l =\mathcal{O}\left( \varepsilon \right) ,Fr_L =\mathcal{O}\left( \varepsilon \right) ,\;Eu=\varepsilon ^{-2})$ and Case II ($Re_l =\mathcal{O}\left( \varepsilon \right) ,Fr_L =\mathcal{O}\left( {\sqrt{\varepsilon }} \right) ,\;Eu=\varepsilon ^{-2})$

Making use of (6)–(7), the dimensionless Stokes equations (48) and (51) respectively for Case I and Case II coincide at order $\mathcal{O}\left( {\varepsilon ^{-1}} \right)$ and become

$$\begin{aligned} \nabla _y p^{{\prime }{(0)}}_\alpha =0; \quad \nabla _y \cdot \left( {\rho _\alpha ^{\left( 0 \right) } \mathbf{v}_\alpha ^{\left( 0 \right) } } \right) =0 \end{aligned}$$

(55)

At order $\mathcal{O}\left( {\varepsilon ^{0}} \right)$ the second of (48) [or equivalently the second of (51)] becomes

$$\begin{aligned} \rho _\alpha ^{\left( 0 \right) } \left( {\nabla _x \cdot \mathbf{v}_\alpha ^{\left( 0 \right) } +\nabla _y \cdot \mathbf{v}_\alpha ^{\left( 1 \right) } } \right) +\mathbf{v}_\alpha ^{\left( 0 \right) } \cdot \left( {\nabla _x \rho _\alpha ^{\left( 0 \right) } +\nabla _y \rho _\alpha ^{\left( 1 \right) } } \right) \;=\;0 \end{aligned}$$

(56)

At the same order $\mathcal{O}\left( {\varepsilon ^{0}} \right)$ the first of (48) (Case I) reads

$$\begin{aligned} \mu _\alpha \nabla _y^2 \mathbf{v}_\alpha ^{\left( 0 \right) } =\nabla _y p^{\prime ( 1 )}_\alpha +\nabla _x p^{\prime ( 0)}_\alpha +\rho _\alpha ^{\left( 0 \right) } \mathbf{e}_3 \end{aligned}$$

(57)

while from the first of (51) (Case II) we derive

$$\begin{aligned} \mu _\alpha \nabla _y^2 \mathbf{v}_\alpha ^{\left( 0 \right) } =\nabla _y p^{\prime {\left( 1 \right) }}_\alpha +\nabla _x p^{\prime {\left( 0 \right) }}_\alpha \end{aligned}$$

(58)

Note also that for incompressible fluids, $\rho _\alpha ^{\left( 0 \right) } =\rho _\alpha$, (56) and (57) simplify as

$$\begin{aligned} \nabla _x \cdot \mathbf{v}_\alpha ^{\left( 0 \right) } +\nabla _y \cdot \mathbf{v}_\alpha ^{\left( 1 \right) } \;=\;0;\;\;\;\;\;\;\;\mu _\alpha \nabla _y^2 \mathbf{v}_\alpha ^{\left( 0 \right) } =\nabla _y p^{\prime {\left( 1 \right) }}_\alpha +\nabla _x p^{\prime {\left( 0 \right) }}_\alpha +\rho _\alpha \mathbf{e}_3 \;\;\; \end{aligned}$$

(59)

Case III ($Re_l =\mathcal{O}\left( \varepsilon \right) ,Fr_L =\mathcal{O}\left( \varepsilon \right) ,\;Eu=\varepsilon ^{-1})$

Making use of (6)–(7), one can note that the first of (54) provides no contribution at order $\mathcal{O}\left( {\varepsilon ^{-1}} \right)$, while the mass conservation law reduces to the second of (55).

At order $\mathcal{O}\left( {\varepsilon ^{0}} \right)$ (54) becomes

$$\begin{aligned}&\mu _\alpha \left[ {\nabla _y^2 \mathbf{v}_\alpha ^{\left( 0 \right) } +\frac{1}{3}\nabla _y \left( {\nabla _y \cdot \mathbf{v}_\alpha ^{\left( 0 \right) } } \right) } \right] =\nabla _y p^{\prime {\left( 0 \right) }}_\alpha +\rho _\alpha ^{\left( 0 \right) } \mathbf{e}_3 ;\nonumber \\&\nabla _x \cdot \left( {\rho _\alpha ^{\left( 0 \right) } \mathbf{v}_\alpha ^{\left( 0 \right) } } \right) +\nabla _y \cdot \left( {\rho _\alpha ^{\left( 1 \right) } \mathbf{v}_\alpha ^{\left( 0 \right) } +\rho _\alpha ^{\left( 0 \right) } \mathbf{v}_\alpha ^{\left( 1 \right) } } \right) =0 \end{aligned}$$

(60)

The second of (55) and the first of (60) with boundary conditions (12) represents a boundary value problem to be solved within the unit cell.

Note that for incompressible fluids and adopting the notation $p_\alpha ^{\left( 0 \right) } =p^{\prime (0)}_\alpha +\rho _\alpha {y_3}$ (60) becomes

$$\begin{aligned} \mu _\alpha \left[ {\nabla _y^2 \mathbf{v}_\alpha ^{\left( 0 \right) } +\frac{1}{3}\nabla _y \left( {\nabla _y \cdot \mathbf{v}_\alpha ^{\left( 0 \right) } } \right) } \right] =\nabla _y p_\alpha ^{\left( 0 \right) };\quad \nabla _x \cdot \mathbf{v}_\alpha ^{\left( 0 \right) } +\nabla _y \cdot \mathbf{v}_\alpha ^{\left( 1 \right) } =0 \end{aligned}$$

(61)

This condition is similar with the non-homogenizable situation described by Ariault et al. (1987, Sect. 7.2.3.1). For this reason we do not pursue further the analysis of this case in Sect. 2.

Appendix C: Oil Relative Permeability for the Crack Model

Three-phase flow between the two parallel plates is one-dimensional along the $y_{2}$-axis (see Fig. 1a). The closure variable tensors, $\mathbf{k}_{\alpha \eta }$, and vectors, $\mathbf{a}_{\alpha \eta }$, in (16) reduce to the scalars $k_{\alpha \eta }$ and $a_{\alpha \eta }$, respectively. As an example, we present here the analytical details to derive the solution of (16) when $\eta$ = $o$. Projecting (16) along directions $y_{1}$ and $y_{2}$ yields

$$\begin{aligned} \begin{array}{l} \partial _{y_1}a_{\alpha o} =0 \\ \mu _\alpha \left( {\partial _{y_1 }^2 k_{\alpha o} +\partial _{y_2 }^2 k_{\alpha o} } \right) +\delta _{\alpha o} -\partial _{y_2 } a_{\alpha o} =0 \quad \hbox { in } \Omega _\alpha \;\;\hbox {with } \alpha \;=\;w,\;o,\;g \\ \end{array} \end{aligned}$$

(62)

where $\delta _{\alpha o} =1$ if $\alpha =o$, $\delta _{\alpha o} =0$ otherwise. The second of (16) allows obtaining $\partial _{y_{2}}k_{\alpha o} =0$ so that the second of (62) simplifies as

$$\begin{aligned} \mu _\alpha \partial _{y_1 }^2 k_{\alpha o} +\delta _{\alpha o} -\partial _{y_2 } a_{\alpha o} =0\quad \hbox { in } \Omega _\alpha \quad \hbox {with,}\quad \alpha \;\hbox {=}\;w,\;o,\;g \end{aligned}$$

(63)

From the first of (62) we obtain that $a_{\alpha o}$ depends solely on $y_{2}$, while $k_{\alpha o}$ is independent of $y_{2}$. Therefore, it follows from (63) that $\partial _{y_2 } a_{\alpha o}$ is constant within the unit cell. Since, by definition, $a_{\alpha o}$ is periodic and $\left\langle {a_{\alpha o} } \right\rangle =0$, it follows that $a_{\alpha o}$ vanishes within $\Omega$. Solving (63) yields

$$\begin{aligned} k_{wo}&= B_1 y_1 +C_1\nonumber \\ k_{oo}&= -\frac{1}{2\mu _o }y_1^2 +B_2 y_1 +C_2 \nonumber \\ k_{go}&= B_3 y_1 +C_3 \end{aligned}$$

(64)

The constants $B_{i}$, and $C_{i}$ ($i$ = 1, 2, 3) can be obtained through the boundary conditions (17), i.e.,

$$\begin{aligned} \begin{array}{l@{\quad }c@{\quad }l} k_{wo} =0 &{} &{}y_1 =c \\ k_{wo} =k_{oo} &{}\mu _w \partial _{y_1 } k_{wo} =\mu _o \partial _{y_1 } k_{oo} \; &{}y_1 =b \\ k_{go} =k_{oo} &{}\;\;\; \mu _g \partial _{y_1 } k_{go} =\mu _o \partial _{y_1 } k_{oo} \;\;&{}y_1 =a \\ \end{array} \end{aligned}$$

(65)

Moreover, the symmetry of the solution with respect to the $y_{2}$-axis allows writing

$$\begin{aligned} \partial _{y_1 } k_{go} =0 \quad y_1 =0 \end{aligned}$$

(66)

Making use of (65)–(66) in (64), we obtain

$$\begin{aligned} \begin{array}{ll} B_1 =-\frac{b-a}{\mu _w }&{}\qquad C_1 =\frac{b-a}{\mu _w }c \\ B_2 =\frac{a}{\mu _o } &{}\qquad C_2 =\frac{b}{\mu _o }\left( {\frac{b}{2}-a} \right) +\frac{b-a}{\mu _w }\left( {c-b} \right) \\ B_3 =0&{}\qquad C_3 =\frac{1}{2\mu _o }\left( {a-b} \right) ^{2}+\frac{b-a}{\mu _w }\left( {c-b} \right) \\ \end{array} \end{aligned}$$

(67)

The oil permeability $K_{oo,}$ defined in (18), is then evaluated as

$$\begin{aligned} K_{oo} =\int \limits _a^b {k_{oo} dy_1 } =\left( {b-a} \right) ^{2}\left[ {\frac{b-a}{3\mu _o }+\frac{c-b}{\mu _w }} \right] \end{aligned}$$

(68)

Recalling that the intrinsic oil permeability, i.e., permeability at $S_{o}$ = 1, is

$$\begin{aligned} K_o =\int \limits _0^c {\frac{1}{2\mu _o }\left( {c^{2}-y_1^2 } \right) dy_1 } =\frac{1}{3\mu _o }c^{3} \end{aligned}$$

(69)

and noting that $\left( {b-a} \right) /c=S_o$ and $\left( {c-b} \right) /c=S_g$, leads directly to (22). All quantities appearing in (21)–(30) can be obtained following a similar procedure.

Appendix D: Gas Relative Permeability Variances and Principal Sobol Indices Associated with $K_{g\eta ,r}$

The variance of $K_{gw,r}, K_{go,r}$ and $K_{gg,r}$ are given respectively by

$$\begin{aligned}&\displaystyle \sigma _{K_{gw,r} }^2 ={\mathfrak M}_1 S_g^2 Q_1 \end{aligned}$$

(70)

$$\begin{aligned}&\displaystyle \sigma _{K_{go,r} }^2 =\frac{1}{12}{\mathfrak M}_2 Q_3^2 +\frac{1}{12}{\mathfrak M}_3 Q_2^2 +\frac{Q_2 Q_3 \left( {\mu _g^M -\mu _g^m } \right) ^{2}}{6(\mu _w^M -\mu _w^m )(\mu _o^M -\mu _o^m )}\ln \frac{\mu _w^M }{\mu _w^m }\ln \frac{\mu _o^M }{\mu _o^m }\end{aligned}$$

(71)

$$\begin{aligned}&\displaystyle \sigma _{K_{gg,r} }^2 =\frac{1}{12}{\mathfrak M}_2 Q_5^2 +\frac{1}{12}{\mathfrak M}_3 Q_4^2 +\frac{Q_4 Q_5 \left( {\mu _g^M -\mu _g^m } \right) ^{2}}{6(\mu _w^M -\mu _w^m )(\mu _o^M -\mu _o^m )}\ln \frac{\mu _w^M }{\mu _w^m }\ln \frac{\mu _o^M }{\mu _o^m } \end{aligned}$$

(72)

The principal Sobol indices for gas relative permeability can be obtained as

$$\begin{aligned}&\displaystyle S\left( {K_{gw,r} ,\mu _w } \right) =\frac{3(\mu _g^M +\mu _g^m )^{2}}{{\mathfrak M}_2 }\left[ {\frac{1}{\mu _w^m \mu _w^M }-\left( {\frac{1}{\mu _w^M -\mu _w^m }\ln \frac{\mu _w^M }{\mu _w^m }} \right) ^{2}} \right] \end{aligned}$$

(73)

$$\begin{aligned}&\displaystyle S\left( {K_{gw,r} ,\mu _g } \right) =-\frac{1}{{\mathfrak M}_2 }\left[ {\frac{\mu _g^M -\mu _g^m }{\mu _w^M -\mu _w^m }\ln \frac{\mu _w^M }{\mu _w^m }} \right] ^{2}\end{aligned}$$

(74)

$$\begin{aligned}&\displaystyle S\left( {K_{go,r} ,\mu _w } \right) =\frac{(\mu _g^M +\mu _g^m )^{2}}{4\sigma _{K_{go,r} }^2 }\left[ {\frac{1}{\mu _w^m \mu _w^M }-\left( {\frac{1}{\mu _w^M -\mu _w^m }\ln \frac{\mu _w^M }{\mu _w^m }} \right) ^{2}} \right] \;\;Q_3^2\end{aligned}$$

(75)

$$\begin{aligned}&\displaystyle S\left( {K_{go,r} ,\mu _o } \right) =\frac{(\mu _g^M +\mu _g^m )^{2}}{4\sigma _{K_{go,r} }^2 }\left[ {\frac{1}{\mu _o^m \mu _o^M }-\left( {\frac{1}{\mu _o^M -\mu _o^m }\ln \frac{\mu _o^M }{\mu _o^m }} \right) ^{2}} \right] \;\;Q_2^2\end{aligned}$$

(76)

$$\begin{aligned}&\displaystyle S\left( {K_{go,r} ,\mu _g } \right) =\frac{1}{12\sigma _{K_{go,r} }^2 }\left( {\mu _g^M -\mu _g^m } \right) ^{2}\left( {\frac{Q_3 }{\mu _w^M -\mu _w^m }\ln \frac{\mu _w^M }{\mu _w^m }+\frac{Q_2 }{\mu _o^M -\mu _o^m }\ln \frac{\mu _o^M }{\mu _o^m }} \right) ^{2}\qquad \quad \end{aligned}$$

(77)

$$\begin{aligned}&\displaystyle S\left( {K_{gg,r} ,\mu _w } \right) =\frac{(\mu _g^M +\mu _g^m )^{2}}{4\sigma _{K_{gg,r} }^2 }\left[ {\frac{1}{\mu _w^m \mu _w^M }-\left( {\frac{1}{\mu _w^M -\mu _w^m }\ln \frac{\mu _w^M }{\mu _w^m }} \right) ^{2}} \right] \;\;Q_5^2\end{aligned}$$

(78)

$$\begin{aligned}&\displaystyle S\left( {K_{gg,r} ,\mu _o } \right) =\frac{(\mu _g^M +\mu _g^m )^{2}}{4\sigma _{K_{gg,r} }^2 }\left[ {\frac{1}{\mu _o^m \mu _o^M }-\left( {\frac{1}{\mu _o^M -\mu _o^m }\ln \frac{\mu _o^M }{\mu _o^m }} \right) ^{2}} \right] \;\;Q_4^2\end{aligned}$$

(79)

$$\begin{aligned}&\displaystyle S\left( {K_{gg,r} ,\mu _g } \right) =\frac{1}{12\sigma _{K_{gg,r} }^2 }\left( {\mu _g^M -\mu _g^m } \right) ^{2}\left( {\frac{Q_5 }{\mu _w^M -\mu _w^m }\ln \frac{\mu _w^M }{\mu _w^m }+\frac{Q_4 }{\mu _o^M -\mu _o^m }\ln \frac{\mu _o^M }{\mu _o^m }} \right) ^{2}\qquad \quad \end{aligned}$$

(80)

Terms $\mathrm{M}_i$ (with $i$ = 2,3) appearing in these equations depend solely on the lower and upper bounds of the range of variability of fluid viscosities, i.e.,

$$\begin{aligned} {\mathfrak M}_2&= 4\frac{\left( {\mu _g^m } \right) ^{2}+\mu _g^M \mu _g^M +\left( {\mu _g^M } \right) ^{2}}{\mu _w^m \mu _w^M }-3\left[ {\frac{\mu _g^m +\mu _g^M }{\mu _w^M -\mu _w^m }\ln \frac{\mu _w^M }{\mu _w^m }} \right] ^{2}\end{aligned}$$

(81)

$$\begin{aligned} {\mathfrak M}_3&= 4\frac{\left( {\mu _g^m } \right) ^{2}+\mu _g^m \mu _g^M +\left( {\mu _g^M } \right) ^{2}}{\mu _o^m \mu _o^M }-3\left[ {\frac{\mu _g^m +\mu _g^M }{\mu _o^M -\mu _o^m }\ln \frac{\mu _o^M }{\mu _o^m }} \right] ^{2} \end{aligned}$$

(82)

while terms $Q_{i}$ ($i$ = 1,...5) depend solely on fluid saturations and pore structure geometry according to

$$\begin{aligned} Q_1 =\frac{3}{16}S_w^4; \quad Q_2 =\frac{3}{2}S_o^2 S_g ;\;\;\;\;Q_3 =3S_w S_o S_g; \quad Q_4 =3S_o S_g^2; \quad Q_5 =3S_w S_g^2\qquad \end{aligned}$$

(83)

for the Crack model and

$$\begin{aligned} Q_1&= \frac{1}{3}\left[ {S_w +\left( {1-S_w } \right) \ln \left( {1-S_w } \right) } \right] ^{2};\qquad \qquad Q_2 =2S_g \left[ {S_o +S_g \ln \left( {S_g /\left( {1-S_w } \right) } \right) } \right] ; \nonumber \\ Q_3&= -2S_g S_o \ln \left( {1-S_w } \right) ;\qquad \qquad Q_4 =2S_g^2 \ln \left( {(1-S_w )/S_g } \right) ;\nonumber \\ Q_5&= -2S_g^2 \ln (1-S_w ) \end{aligned}$$

(84)

for the Capillary tube model.