Abstract
Discounted utility theory and its generalizations (e.g., quasihyperbolic discounting, generalized hyperbolic discounting) use discount functions for weighting utilities of outcomes received in different time periods. We propose a new simple test of convexity–concavity of discount function. This test can be used with any utility function (which can be linear or not) and any preferences over risky lotteries (expected utility theory or not). The data from a controlled laboratory experiment show that about one third of experimental subjects reveal a concave discount function and another one third of subjects reveal a convex discount function (for delays up to two month).
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Intertemporal choice deals with outcomes received in different chronological moments. One of the most popular models of intertemporal choice is discounted utility theory (Samuelson 1937), also known as constant or exponential discounting. This model is derived from the behavioral assumption of stationarity (Koopmans 1960, postulate 4, p. 294): if two streams of intertemporal payoffs yield the same outcomes in the initial period(s) of time then such a common outcome can be discarded without affecting decision maker’s preference between these two streams. Empirical tests of stationarity quickly showed that people often reveal non-constant discounting in the form of the present bias or, occasionally—the future bias. For example, Thaler (1981, p. 202) was one of the first to argue that an individual could choose one apple today over two apples tomorrow and, at the same time, he or she could choose two apples in one year plus one day over one apple in one year. Such a violation of stationarity (known as the present bias) motivated the development of numerous generalized models of intertemporal choice that replaced constant/exponential discounting with a more general convex discount function. Examples of such generalized models include quasihyperbolic discounting (Phelps and Pollak 1968), generalized hyperbolic discounting (Loewenstein and Prelec 1992), liminal discounting (Pan et al. 2015) and rank-dependent discounted utility (Blavatskyy 2016).
Empirical tests of the convexity assumption of discount function are more complicated compared to the empirical tests of stationarity.Footnote 1 Discount function is used for weighting utilities of various intertemporal outcomes. Hence, empirical tests of the shape of discount function may be confounded with the shape of utility function. Early empirical studies often made a simplifying assumption that subjects have linear utility over money. For example, Coller and Williams (1999) confronted subjects with a binary choice between $500 payable in one month and a larger monetary amount payable in three months. Coller and Williams (1999) inferred discount rates assuming a linear Bernoulli utility function. Warner and Pleeter (2001) report the results of a natural experiment from the U.S. military drawdown program. In this program, 11,000 officers and 55,000 enlisted personnel chose between a lump-sum separation benefit (around $50,000 for officers and around $25,000 for enlisted personnel) and an annuity payment. Warner and Pleeter (2001) inferred individual discount rates assuming a linear utility function over money. As Frederick et al. (2002, Sect. 6.1.3, p. 381) pointed out, the conclusions of such studies about the shape of discount function would be biased under conventional microeconomic assumption of diminishing marginal utility of money (concave utility function).
In an alternative approach, several studies (e.g., Chapman 1996; Takeuchi 2011, 2012) deduced the shape of discount function on the assumption that preferences over risky lotteries are represented by expected utility theory. The problem underlying this alternative approach is the need to disentangle risk aversion from intertemporal substitution. Chesson and Viscusi (2003) found that about one third of surveyed business managers preferred alternatives with known time delays over alternatives with risky delays in time (that have the same expected delay), which implies a concave discount function assuming expected utility theory for choice under risk. Onay and Öncüler (2007) documented a similar preference, which implies a concave discount function assuming expected utility theory for choice under risk but may reveal a convex discount function when subjects use non-linear probability weighting in choice under risk.
Attema et al. (2016) propose a direct method for recovering the shape of discount function. Our paper proposes only a simple test whether discount function is convex or concave (or both) without recovering its complete shape. The direct method of Attema et al. (2016) relies on eliciting exact indifferences between streams of intertemporal payoffs. Incentive-compatible elicitation of exact indifferences is complex and requires rounding assumptions (cf. Attema et al. 2016, p. 1480).Footnote 2 The test proposed in our paper employs only two binary choice questions.
In this paper, we propose a new test of convexity–concavity of discount function in intertemporal choice. This test consists of two binary choice questions. The proposed test can be used with any utility function (which can be linear or not) and any preferences over risky lotteries (which can admit expected utility representation or not).
The idea of our test is the following. First, a decision maker chooses between two streams of intertemporal payoffs. Stream A yields a less desirable outcome x right now (t = 0) and a more desirable outcome y later (t = 1). Stream B yields the more desirable outcome y right now as well as the less desirable outcome x—in two periods from now (t = 2).
Second, a decision maker chooses between streams C and D. Stream C (D) is obtained from stream A (B) by delaying the more desirable outcome y by one time period. A decision maker who prefers A in the first question but switches to preferring D in the second question reveals a concave discount function. A decision maker who prefers B in the first question but switches to preferring C in the second question reveals a convex discount function. Consistent decision makers who do not switch between two choice questions can have either convex or concave discount function.
In the next section, we demonstrate that our proposed test relies only on the Jensen’s inequality for discount function and it is independent of the shape of utility function. In fact, the test can be also conducted with non-monetary outcomes. Two binary choice questions in our proposed test involve sure streams of intertemporal payoffs. Thus, the test itself does not require any assumptions about preferences over risky lotteries (which can admit expected utility representation or not).
We implemented our proposed test in a controlled laboratory experiment. We found that about one third of experimental subjects reveal a concave discount function; about one third of subjects reveal a convex discount function. Only few subjects exhibit a choice pattern that is consistent both with concave and convex discount function. Subjects revealing convex discount function slightly outnumber those revealing concave discount function but there is no statistically significant asymmetry between the two groups. These results are robust to order effects and random errors, preference imprecision or noise.
The remainder of the paper is organized as follows: Section 2 describes our proposed test of convexity–concavity of discount function. Section 3 describes how this test was implemented in a laboratory experiment. Section 4 presents the results of this experiment. Section 5 concludes.
2 Convexity–concavity test for a discount function
Let us denote streams of three intertemporal payoffs by three-outcome vectors. The first outcome is the payoff now (at t = 0), the second—at t = 1 and the third—at t = 2. We use two outcomes x > 0 and y > x. For instance, stream \(A\equiv \left(x,y,0\right)\) yields x now and y at t = 1 (nothing at t = 2). Stream \(B\equiv \left(y,0,x\right)\) yields y now and x at t = 2 (nothing at t = 1).
We assume that preferences are represented by an additively separable utility \(U\left({z}_{0},{z}_{1},{z}_{2}\right)=u\left({z}_{0}\right)+D\left(1\right)u\left({z}_{1}\right)+D\left(2\right)u\left({z}_{2}\right)\), where D(.) is a discount function with a conventional normalization D(0) = 1, u(.) is time-invariant utility function with a conventional normalization u(0) = 0 and zt denotes an outcome received at time t. We assume zero background consumption and no intertemporal arbitrage.
Stream A is weakly preferred over stream B if and only if inequality (1) holds.
Inequality (1) can be rearranged as (2).
If discount function D(.) is (strictly) convex, then \(1-D\left(1\right)>D\left(1\right)-D\left(2\right)\) due to Jensen’s inequality. In this case inequality (2) can be rewritten as inequality (3).
Finally, inequality (3) can be rearranged as (4).
The left-hand side of (4) is utility of stream \(C\equiv \left(x,0,y\right)\). The right-hand side of (4) is utility of stream \(D\equiv \left(0,y,x\right)\). Thus, if a decision maker with a convex discount function weakly prefers stream A over stream B then she must strictly prefer C over D. Analogously, we can show that a decision maker with a convex discount function who weakly prefers D over C should strictly prefer stream B over stream A.
On the other hand, a decision maker with a (strictly) concave discount function who weakly prefers C over D should strictly prefer A over B. Whenever a decision maker with a concave discount function weakly prefers B over A, she must prefer D over C.
A decision maker who is indifferent between A and B but prefers D over C reveals a concave discount function. A decision maker who prefers A over B but is indifferent between C and D does the same. A decision maker who is indifferent between A and B but prefers C over D reveals a convex discount function. A decision maker who prefers B over A but is indifferent between C and D does the same. A decision maker who is indifferent between A and B and indifferent between C and D reveals a discount function that is both concave and convex—i.e., a linear function.
3 Experimental design and implementation
We implemented the convexity test described in Sect. 2 with parameters x = €10, y = €20 and a delay t = 1 being one month (t = 2 being two month). Thus, we inferred only the shape of a local discount function (with a delay between now and two month). Subjects faced a binary choice between \(A\equiv \left(\mathrm{10,20,0}\right)\) and \(B\equiv \left(\mathrm{20,0},10\right)\) and a binary choice between \(C\equiv \left(\mathrm{10,0},20\right)\) and \(D\equiv \left(\mathrm{0,20,10}\right)\). These two binary choice questions were intermixed with several other similar intertemporal choice questions analyzed in Blavatskyy and Maafi (2018) and a distractor task.Footnote 3 Each binary choice question was presented to subjects four times (two times with stream A or C appearing as a left-hand side choice option and two times—with stream A or C appearing as a right-hand side choice option). Repetitions of the same question were separated from each other.
Subjects were recruited on the campus of Ecole Polytechnique (France) from the “Laboratoire d’Economie Expérimentale de Saclay” pool. Seventy-five subjects (46 males and 29 females) participated in the experiment. Around half of the subjects (52%) were engineers and half non-engineers. Subjects were aged between 19 and 59, with a mean of 29.84. We ran four sessions with no subject participating in several sessions.
The experiment was computerized. In each session, the experimenter read out written instructions (presented in Appendix B). Each subject was provided with two envelopes for receiving future payments. A white (brown) envelope contained any payment due in one (two) months together with a reminder letter. The letter specified the date of the experiment and the amount (which was filled in at the end of the experiment) of the future payment. The experiment lasted for almost one hour in total.
Figure 1 shows how a binary choice between A and B was presented to subjects. If the subject preferred the right option, she clicked on it and that option was then highlighted in red (see Fig. 1b). The subject had then to confirm her choice to move to the next choice. Raw experimental data are presented in Table 3 in Appendix C.
At the end of the experiment, one question was selected at random. Subjects saw their choice in this question on the screen. Subjects then addressed the envelope(s) to themselves and wrote their future payment(s) in the reminder letter in the corresponding envelope. The payment was made in private. Subjects first announced if they preferred cash or cheque and then received the immediate payment, while experimenter put the earlier (later) future payment in the white (brown) envelope. Subjects earned €37.75 on average, with a minimum of €20 and a maximum of €51.50.
4 Results
Experimental results are presented in Table 1. A subject who consistently chooses B over A reveals a strong preference for B (a choice pattern B ≻ A). A subject who consistently chooses A over B reveals a strong preference for A (a choice pattern A ≻ B). Finally, a subject who chooses A over B on one occasion and chooses B over A on another occasion reveals indifference (a choice pattern A ~ B).
Overall, there are nine possible choice patterns in our experiment, described in the first column of Table 1. The second column of Table 1 shows which discount function (convex, concave, linear or any) corresponds to each choice pattern. The third (fourth) column of Table 1 shows the number of subjects revealing each possible choice pattern when A and C appear as choice options on the left (right) of the screen. The Wilcoxon signed-rank testFootnote 4 rejects the null hypothesis that the observed choice patterns are equal to zero for all observed choice patterns except for one pattern, B ≻ A, D ≻ C, which is consistent with a convex or concave discount function (the p-values are reported in brackets under each observed proportion). We obtain the same results when we consider choices where A and C appear on the right.
There is no apparent order effect—the same result holds through whether streams A and C appear as the left choice options (41% convex, 37% concave, 11% linear, 11% any) or—as the right choice options (45% convex, 35% concave, 13% linear, 7% any). The fifth column of Table 1 tests for order effect and shows no significant order effect (choices where A and C were shown on the left are not significantly different from choices where A and C were shown on the right.
Our experimental results are closest to those reported in Takeuchi (2012, Fig. 4, p. 7) who found that around 40% of subjects reveal a convex discount function and around 30%—a concave discount function for the delay of 49 days (that is most similar to the delays considered in our study). The concavity–convexity test used by Takeuchi (2012), however, relies on the assumption that subjects behave as expected utility maximizers when choosing under risk. In contrast, our proposed test does not require the assumption of expected utility maximization in choice under risk.
There are slightly more subjects revealing a convex discount function than those revealing a concave discount function. Nonetheless, there is no statistically significant asymmetry between those two groups (z = 0.391, p = 0.6961 for choices where A and C are shown on the left; z = 1.033, p = 0.3017 for choices where A and C are shown on the right and z = 0.566, p = 0.5716 for pooled data). Most models of intertemporal choice start with the premise of a convex discount function. Our data support this premise not more than they support a concave discount function (for delays between now and two month). In fact, our data indicate that at least 30% of experimental subjects reveal a concave discount function (cf. Loewenstein 1987; Sayman and Öncüler 2009). This calls for the development of more flexible models of intertemporal choice that allow both for a convex and concave discount function (e.g., Ebert and Prelec 2007; Bleichrodt et al. 2009).
Note that stream B second-order temporally dominates stream A and stream C second-order temporally dominates stream D (cf. Bohren and Hansen 1980, Section III, p. 49).Footnote 5 Thus, any decision maker with a linear utility function and a convex discount function prefers B over A as well as C over D (Bohren and Hansen 1980, proposition 2, p. 50). Consequently, any decision maker with a linear utility function and a concave discount function prefers A over B and D over C.
In summary, any decision maker with a linear utility function can reveal only one of the following three choice patterns: either B ≻ A and C ≻ D (when discount function is convex), or A ≻ B and D ≻ C (when discount function is concave), or A ~ B and C ~ D (when discount function is linear). Only 53% (56% in the poled data) of our experimental subjects reveal these three choice patterns (cf. Table 1). Thus, the assumption of linear utility that is often made for inferring discount factors in experimental studies (cf. Takeuchi 2011, Table 1, p. 458) is violated by at least 44% of our experimental subjects.
One limitation of our proposed test is that subjects exhibiting either A ≻ B and C ≻ D or B ≻ A and D ≻ C remain unclassified (their discount function can be either convex or concave or both). Only 11% (7%) of our experimental subjects exhibit these two choice patterns when streams A and C appear as the left (right) choice options. In the pooled data their share drops to 1%. Thus, only a relative minority of subjects remain unclassified and this does not appear to be a significant limitation of our proposed test. To eliminate this limitation completely, our proposed test should be used with outcomes x and y such that the utility of x is one half of the utility of y. In this case, a decision maker with an additively separable utility cannot exhibit choice patterns A ≻ B and C ≻ D or B ≻ A and D ≻ C. From this point of view, our experimental test (with outcomes €10 and €20) is the ideal theoretical test for a linear utility function (when utility of €10 is exactly one half of utility of €20).
In the pooled data (cf. the sixth column in Table 1) many instances of indifference are observed when subjects choose one stream three out of four times and the other stream—only one out of four times. If we reinterpret such instances as a strict preference for the first stream distorted by one random error or tremble rather than indifference, then we obtain the following results: thirty-five subjects (47%) reveal a convex discount function, 28 subjects (37%) reveal a concave discount function, 3 subjects (4%) reveal a linear discount function, and 9 subjects (12%) cannot be classified (their revealed choice pattern is consistent with any discount function). Therefore, a large number of subjects revealing a linear discount function in the pooled data in Table 1 are caused by instances of indifference when one stream is chosen three out of four times. Reinterpreting such instances as a strict preference distorted by error/tremble brings results for the pooled data close to those when streams A and C appear as the right-hand side choice options (see Table 2 in Appendix A).
5 Conclusion
The existing literature “mechanically” elicits the shape of discount function by retrieving discount factors for various moments of time. Such elicitation is rather complicated since the discount function weights utilities of intertemporal outcomes and various simplifying assumptions on the shape of utility function are often required. For example, many studies simply assume that the utility function over money is linear (see references in Takeuchi 2011, Table 1, p. 458) or that the utility function over risky lotteries is linear in probabilities (e.g., Chapman 1996; Takeuchi 2011, 2012). In this paper, we propose a new test of convexity–concavity of the discount function without laborious elicitation of discount factors for various moments of time. Our proposed test consists of two binary choice questions involving streams of intertemporal payoffs one of which second-order temporally dominates the other. This test is relatively simpler compared to other existing methods. This simplicity comes at a price: the proposed test does not elicit discount factors for specific moments of time—it only characterizes whether a discount function is convex, concave or both (linear).
We collect new experimental data for our proposed test of convexity–concavity of discount function. We find that for a relatively short period (a delay of one and two month) about one third of experimental subjects reveal a convex discount function and about one third reveal a concave discount function. We implemented our test only for one pair of non-zero outcomes (10 and 20 euros). A natural extension of this work is to implement our test with several pairs of non-zero outcomes to test the validity of additively separable utility.
One limitation of our test is that choice patterns A ≻ B and C ≻ D or B ≻ A and D ≻ C remain unclassified (i.e., consistent with both convex and concave discount functions). Any decision maker with an additively separable utility cannot exhibit these two choice patterns if her utility of outcome x is exactly one half of her utility of outcome y. Thus, one possible extension of our test is the following. First, we elicit outcome x that is exactly one half of outcome y in terms of utility. Second, we implement our proposed test with such outcomes x and y. The first stage of this procedure can be implemented by constructing a standard sequence of outcomes that are equally spaced in terms of utility (e.g. Krantz et al. 1971, p. 253, definition 4).
Our proposed test can be also applied to other representations of time preferences beyond the additively separable utility function \({\sum }_{t=0}^{n}D\left(t\right)u\left({x}_{t}\right)\). For example, under rank-dependent discounted utility (Blavatskyy 2016) subjects exhibiting choice pattern A ≻ B and D ≻ C reveal a concave discount function in conjunction with a convex utility function over money and subjects exhibiting choice pattern B ≻ A and C ≻ D reveal a convex discount function in conjunction with a concave utility function over money (cf. Blavatskyy 2018, proposition 4, pp. 369–370). Thus, under rank-dependent discounted utility representation of time preferences, our proposed test becomes a joint test for the curvature of discount function and the curvature of utility function.
Notes
Stationarity is a behavioral axiom that can be directly tested on empirical data since it is formulated in terms of revealed preferences. Convexity of discount function is a property of an unobserved theoretical function that cannot be directly tested on empirical data. From this point of view, the contribution of our paper is to formulate the convexity property (Jensen’s inequality) in terms of revealed preferences so that it can be directly tested on empirical data.
The distractor task was cognitive reflection test (Frederick, 2005) consisting of three questions.
Wilcoxon signed-rank tests were used as normality of distributions was not supported by the data.
An alternative \(L\equiv ({l}_{0},{l}_{1},{l}_{2})\) second-order dominates an alternative \(R\equiv ({r}_{0},{r}_{1},{r}_{2})\) when \({l}_{0}+{l}_{1}+{l}_{2}\ge {r}_{0}+{r}_{1}+{r}_{2}\) as well as \({l}_{0}\ge {r}_{0}\), \({2l}_{0}+{l}_{1}\ge 2{r}_{0}+{r}_{1}\) and \(3{l}_{0}+{2l}_{1}+{l}_{2}\ge {3r}_{0}+{2r}_{1}+{r}_{2}\) and at least one of these inequalities holds as a strict inequality.
References
Attema, A. E., Bleichrodt, H., Rohde, K. I. M., & Wakker, P. P. (2010). Time-tradeoff sequences for analyzing discounting and time inconsistency. Management Science, 56(11), 2015–2030.
Attema, A. E., Han Bleichrodt, Yu., Gao, Z. H., & Wakker, P. P. (2016). Measuring discounting without measuring utility. American Economic Review, 106, 1476–1494.
Blavatskyy, P. (2016). A monotone model of intertemporal choice. Economic Theory, 62(4), 785–812.
Blavatskyy, P. (2018). Temporal dominance and relative patience in intertemporal choice. Economic Theory, 65(2), 361–384.
Blavatskyy, P., & Maafi, H. (2018). Estimating representations of time preferences and models of probabilistic intertemporal choice on experimental data. Journal of Risk and Uncertainty, 56(3), 259–287.
Bleichrodt, H., Rohde, K. I. M., & Wakker, P. P. (2009). Non-hyperbolic time inconsistency. Games and Economic Behavior, 66(1), 27–38.
Bøhren, Ø., & Hansen, T. (1980). Capital budgeting with unspecified discount rates. Scandinavian Journal of Economics, 82(1), 45–58.
Chapman, G. B. (1996). Expectations and preferences for sequences of health and money. Organizational Behavior and Human Decision Processes, 67(1), 59–75.
Chesson, H., & Viscusi, K. W. (2003). Commonalities in time and ambiguity aversion for long-term risk. Theory and Decision, 54, 57–71.
Coller, M., & Williams, M. (1999). Eliciting individual discount rates. Experimental Economics, 2, 107–127.
Ebert, J.E.J. and Drazen Prelec,. (2007). The fragility of time: Time-insensitivity and valuation of the near and far future. Management science, 53(9), 1423–1438.
Frederick, S. (2005). Cognitive reflection and decision making. Journal of Economic Perspectives, 19(4), 25–42.
Frederick, S., Loewenstein, G., & O’Donoghue, T. (2002). Time discounting and time preference: A critical review. Journal of Economic Literature, 40(2), 351–401.
Koopmans, T. (1960). Stationary ordinal utility and impatience. Econometrica, 28, 287–309.
Krantz, D. H., Luce, R. D., Suppes, P., & Tversky, A. (1971). Foundations of measurement, Vol. 1 (Additive and Polynomial Representations). New York: Academic Press.
Loewenstein, G. (1987). Anticipation and the valuation of delayed consumption. Economic Journal, 97(387), 666–684.
Loewenstein, G., & Prelec, D. (1992). Anomalies in intertemporal choice: Evidence and an interpretation. Quarterly Journal of Economics, 107, 573–597.
Onay, S., & Öncüler, A. (2007). Intertemporal choice under timing risk: An experimental approach. Journal of Risk and Uncertainty, 34, 99–121.
Pan, J., Webb, C. S., & Zank, H. (2015). An extension of quasi-hyperbolic discounting to continuous time. Games and Economic Behavior, 89, 43–55.
Phelps, E., & Pollak, R. (1968). On second-best national saving and game-equilibrium growth. The Review of Economic Studies, 35, 185–199.
Rohde, K. I. M. (2010). The hyperbolic factor: A measure of time inconsistency. Journal of Risk and Uncertainty, 41(2), 125–140.
Samuelson, P. (1937). A note on measurement of utility. The Review of Economic Studies, 4, 155–161.
Sayman, S., & Öncüler, A. (2009). An investigation of time-inconsistency. Management Science, 55(3), 470–482.
Takeuchi, K. (2011). Non-parametric test of time consistency: Present bias and future bias. Games and Economic Behavior, 71(2), 456–478.
Takeuchi, K. (2012). Time discounting: the concavity of time discount function: An experimental study. Journal of Behavioral Economics and Finance, 5, 2–9.
Thaler, R. H. (1981). Some empirical evidence on dynamic inconsistency. Economics Letters, 8, 201–207.
Warner, J., & Pleeter, S. (2001). The personal discount rate: Evidence from military downsizing programs. American Economic Review, 91(1), 33–53.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Pavlo Blavatskyy is a member of the Entrepreneurship and Innovation Chair, which is part of LabEx Entrepreneurship (University of Montpellier, France) and funded by the French government (Labex Entreprendre, ANR-10-Labex-11-01).
Appendices
Appendix A
See Table 2.
Appendix B
2.1 Instructions
Thank you for participating in this experiment. The experiment is designed to study individual decisions. You will make your choice on the computer. The computer will communicate your gains at the end of the experiment. Your decisions in the experiment are private. Please do not communicate with others during the experience.
The instructions are simple, if you follow them carefully, you could earn a considerable amount of money. Your winnings will depend on the decisions you make.
The experiment is divided into three parts and a questionnaire:
-
1.
In a first part, we will ask you to choose between two options, and this several times. Each option offers you a given amount of money at three different delays.
-
2.
In a second part, we will ask you respond to three questions of logic.
-
3.
In a third part, we will ask you to choose between two options several times. Each option offers you a given amount of money at three different delays.
-
4.
Finally, you will answer questions about your personal situation.
2.2 Payment
At the end of the experiment, one question of Parts 1 or 3 will be randomly selected and played for real. Part 2 will offer you a bonus per correct answer.
2.3 Detailed instructions
-
Part 1: In this part, you will choose between two options that offer you three amounts of money at three different dates: an amount today, an amount in one month and an amount in 2 months.
Example:
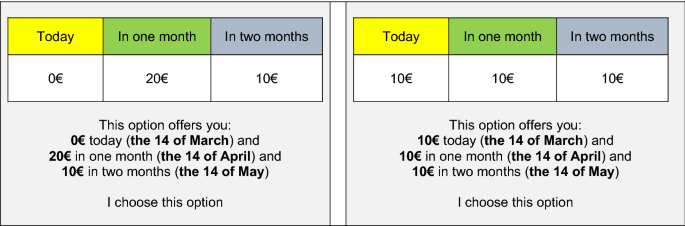
In this question, you will make a choice between two options: a right option and a left option. You save your choices on the computer. Click on the option you prefer. Your preferred option will be highlighted in red, and then click on the bottom OK to confirm your choice.
For this example, if you choose the left option, you will receive nothing today, but you will receive €20 in one month and €10 in two months. If you prefer the right option, you will receive €10 today, €10 in one month and €10 in two months.
In this first part, you are asked to make 100 choices similar to the example above.
To avoid you to come back to receive your future earnings, the amounts you will receive in one month and/or in two months will be deposited in your internal mailbox on the scheduled date or will be sent to you to another address (if you prefer) so that they arrive in your mailboxes on the scheduled date. Please inform the experimenter of what suits you for future payments.
The following text was not printed on the instructions, but was read by the experimenter:
On the right side of your computer, there are two envelopes: one white and one brown. You will receive the white envelope with your earlier payment in one month and the brown envelope with the later payment in two months. Inside each envelope, there is a letter reminding you your participation in the experiment one (two) month(s) ago and your payment. After the payment information at the end of the experiment, you have to address the envelope(s) to yourselves and write your future payment(s) in the reminder letter of the corresponding envelope.
-
Part 2: In this part, you will answer 3 questions of logic. You will receive 0.50 € per correct answer.
-
Part 3: In this part, you will make the same 100 choices similar of Part 1. You will choose between two options that offer you three amounts of money at three different dates: an amount today, an amount in one month and an amount in 2 months.
Do you have any questions?
-
Appendix C
See Table 3 .
Rights and permissions
About this article
Cite this article
Blavatskyy, P.R., Maafi, H. A new test of convexity–concavity of discount function. Theory Decis 89, 121–136 (2020). https://doi.org/10.1007/s11238-020-09747-3
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11238-020-09747-3






