1 Introduction

Congestion control is very important to guarantee specific service quality in communication networks, especially in situations where the availability of resources and the set of competitors change over time unpredictably, yet efficient sharing is expected. Since Jacobson’s work in 1988, congestion control has been associated with the transmission control protocol (TCP) in the Internet, and it has performed remarkably well in the past and was generally believed to have prevented severe congestion as the Internet scaled up by six orders of magnitude in size, speed, load and connectivity [1]. However, it is also well-known that TCP becomes inefficient and prone to instability when the product of bandwidth and latency increases [2, 3].

The explicit control protocol (XCP) is a novel and promising congestion control protocol that outperforms TCP in terms of efficiency, fairness, convergence speed, persistent queue length and packet loss rate [4]. Then, a large amount of works have been made to further analyze and improve the XCP performances. Zhang and Henderson [5] first implemented the XCP stack in Linux, and revealed that the XCP performance can be adversely affected by the data type choice and TCP/IP configurations. In the incremental deployment, XCP behaves improperly, even worse than TCP, because XCP requires the collaboration of routers along the path, which is impossible in an actual scenario. To address this problem, XCP-i model is proposed to make XCP operable on an inter-network consisting of XCP routers and traditional IP routers without loosing the benefit of the XCP control laws [6]. In a multi-bottleneck network, XCP may cause some bottleneck links to be under-utilized, and a flow may not receive its max–min fair allocation. Yang et al. [7] first pinpoint that it is caused by the bandwidth shuffling operation, and an improved version of XCP is proposed, which modifies XCP to shuffle bandwidth only among flows that are bottlenecked at current routers. This modification ensures that the deallocated bandwidth by the shuffling operation will be reused. Therefore, a link can be fully utilized. Hairui et al. [8] proposes another interesting algorithm based on the proportional integral controller to solve the link under-utilization problem, and it also effectively improves XCP performance in a multi-bottleneck topology, the capacity of each link can be optimally utilized, each flow can obtain its max–min fair rate in steady state. According to the operating principle, XCP needs to know the available bandwidth at the output link, which is a tricky business over wireless links, e.g., IEEE 802.11. XCP-b does a nice job of providing a first step toward running XCP on wireless links. It require a few parameters and preserve the good properties of XCP, including high utilization, stable throughput, and reasonable fairness [9]. Barreto [10] proposes XCP-Winf, which relies on the MAC layer information gathered by a new method, rt-Winf, to accurately estimate the available bandwidth and the path capacity over a wireless network path. The evaluation results of XCP-Winf, obtained through simulations, show that the rt-Winf algorithm improves significantly XCP behavior, making it more efficient and stable. The satellite network, as a kind of high bandwidth-delay product network, has recently been paid more and more attention because of its large geographic coverage and cost effectiveness. Long link delay and high bit error rate (BER) are characteristics of satellite networks. Zhou et al. [11] and Sun et al. [12] show that high BER has a seriously negative impact on the XCP performance, and two modified variants of XCP are proposed to solve low throughput under high BER conditions. Liu et al. [13] investigates the Hopf bifurcations in the XCP system. These bifurcation behaviors may cause heavy oscillation of average queue length and induce network instability. Then, a time-delayed feedback control method was proposed for controlling Hopf bifurcations in the XCP system. Additionally, many other efforts have been done on different aspects of the XCP scheme, such as efficiency [14], stability [15, 16], security [17], as well as enhancements for optical packet switched (OPS) networks [18, 19].

Among these concerns, one critical defect in XCP was found. Lachlan et al. [20] reveal that XCP will be instability, when the ratio of maximum to mean round trip time (RTT) is sufficiently large. Their experiments show that large RTT flows cannot obtain their max–min allocations, the aggregate traffic and control interval fluctuate dramatically, and big buffers are required to absorb these oscillations. Therefore, XCP is not globally stable in the presence of heterogeneous delays. Taking into account that the RTT distribution exhibits heavy-tailed characteristics [21, 22], this problem is becoming even more serious owing to the fact that a small number of large RTT flows can significantly reduce the system performance. Based on their analyses, Lachlan et al. propose M-XCP, which reduces the control loop gain with setting the control interval d to be the maximum RTT observed during the last interval, instead of the mean RTT used in the original XCP specification, and shows a strong stability in the face of heterogeneous delays. However, M-XCP needs additional operations for each packet, and then the computing complexity of M-XCP increases dramatically. Most importantly, this modification reduces the system responsiveness significantly and makes the system vulnerable to erroneous RTT attacks.

In this paper, according to the robust control theory, with the help of a recently developed Lyapunov–Krasovskii functional [23], an improved version of XCP, named R-XCP, is proposed to solve the weakness of XCP under heterogeneous delays, and the synthesis problem is reduced to a convex optimization scheme expressed in terms of linear matrix inequalities (LMI) [24]. Extensive simulations have shown that R-XCP significantly decreases the volatilities of the aggregate traffic rate and control time interval, and effectively improves the system stability. Meanwhile, R-XCP sets the control interval d to be the mean RTT, rather than the maximum RTT used as in M-XCP, so it has the same control loop gain with XCP, and is more responsive than M-XCP. Additionally, R-XCP decreases the computational complexity dramatically, and makes the system less sensitive to flows, which contribute little traffic but maliciously report their delays, compared with M-XCP.

The rest of the paper is organized as follows. In Sect. 2, some related works are presented. Section 3 briefly summarizes how XCP works and its weakness in the presence of heterogeneous delays. The main motivations and design guidelines for R-XCP are presented in Sects. 4 and 5 respectively. In Sect. 6, extensive simulations are employed to evaluate the performance of R-XCP, and compare it with XCP and M-XCP. Finally, the conclusion is drawn in Sect. 7.

2 Related works

With the rapid advances in the deployment of high-speed links in the Internet, the requirements for a viable replacement of TCP has become increasingly crucial, and many protocols have been proposed to solve this problem, which can be broadly classified into two categories according to primal–dual modeling [25]. Primal congestion control approach refers to the algorithm executed by source end systems for regulating their sending rates, and is widely used in the current Internet to prevent congestion collapse. TCP and many its variants such as HSTCP [26], STCP [27], HTCP [28], CUBIC [29] and FAST [30] fall into this category, and they are very attractive short-term solutions because the actual barriers to their deployment are very small. However, it is very difficult to achieve high link utilization and fair bandwidth allocation while maintaining small queue length and minimizing packet loss [31].

To address the limitations of pure end-to-end based protocols, active queue management (AQM) [32] was introduced to provide early congestion notification from router sides to end hosts by triggering packet dropping or marking before buffer overflows, which has departed from the strict end-to-end principle. In the past few years, a series of AQM methods, e.g., RED [33], PI [34], BLUE [35], CHOKe [36], AVQ [37], and REM [38] have been proposed, and these AQM schemes can significantly reduce packet loss and achieve some degree of trade-off between queuing delay and flow throughput. However, due to the challenging nature of nonlinear and time-varying behaviors in TCP dynamics, these AQM schemes derived from heuristics ideas or linear models fail to provide satisfactory performance and are not able to guarantee stability over a wide range of network scenarios [39, 40].

In the traditional primal–dual approach, TCP and AQM are designed independently, but should cooperate with each other, causing system performance is obviously restricted. Therefore, it is a natural choice for us to support joint design. Now, many joint design strategies between intermediate nodes and end systems, such as XCP [41], VCP [42], MLCP [43], RCP [44], JetMax [45] and MaxNet [46] have already been proposed. Unlike the primal-dual TCP/AQM distributed algorithm, a flow does not implicitly probe available bandwidth. Instead, a router fairly allocates the spare bandwidth among all flows that share the same link, and quantitatively informs senders how to adjust their rates. Experimental results have shown that joint design based approaches can achieve better network performance compared to pure end-to-end schemes with the addition of simple queue management algorithms.

With the growth of data volumes and variety of Internet applications, data centers have become an efficient and promising infrastructure, and mixing workloads require small predictable latency with others requiring large sustained throughput. In this environment, today’s state-of-the-art TCP protocol fails to satisfy these requirements together within the time boundaries because of impairments such as TCP incast/outcast, buffer pressure and pseudo-congestion effect [47]. And it becomes a new research hotspot. Vasudevan et al. [48] present a practical solution that reducing the minimum retransmission timeout (RTO) from 200 ms to 200 \(\upmu \)s significantly alleviates the problems of TCP in data center networks and improves the overall throughput by several orders of magnitude. Alizadehzy et al. [49] propose DCTCP, which employs a marking scheme at switches that sets the congestion experienced (CE) codepoint in packets as soon as the buffer occupancy exceeds a fixed pre-determined threshold. DCTCP obviously alleviates TCP incast and outcast problems in data center networks, and it is already implemented in latest versions of Microsoft Windows Server operating system. Unlike DCTCP, ICTCP does not require any modifications at the sender side or network elements such as routers, switches, etc. Instead, ICTCP adaptively adjusts the TCP receive window proactively before packet loss occurs. Experimental results demonstrate that ICTCP is effective in avoiding congestion by achieving almost zero timeouts for TCP incast, and it provides high performance and fairness among competing flows [50]. D2TCP uses a distributed and reactive approach for bandwidth allocation and employs a novel deadline-aware congestion avoidance algorithm to vary the sender’s congestion window. D2TCP reduces the fraction of missed deadlines up to 75% as compared to DCTCP [51]. Timeouts lead to dramatic degradation in the network performance and affect the user perceived delay. TCP with guarantee important packets (GIP) can avoid almost all of timeouts and achieve higher goodput for applications with the incast communication pattern [52]. By detecting the unusual spikes, accurately measuring RTT and proper management of RTO, PVTCP is much more effective in addressing incast congestion in virtualized data centers than standard TCP, with requiring no modification to the hypervisor [53]. CONGA splits TCP flows into flowlets, estimates real-time congestion on fabric paths, and allocates flowlets to paths based on feedback from remote switches. This enables CONGA to efficiently balance load and seamlessly handle asymmetry, without requiring any TCP modifications in incast scenarios [54]. Chen et al. [55] builds up an interpretive model which emphasizes particularly on describing qualitatively how various factors affect network performances in incast traffic pattern. With this model, it gives plausible explanations why the various solutions for TCP incast problem can help, but do not solve it entirely.

3 XCP control laws and problem statement

3.1 XCP control laws

In the XCP algorithm, routers explicitly inform sources how to adjust their sending rates. To enable this communication between the network and sources, XCP introduces a congestion header, which allows every packet to carry information about the flow to which the packet belongs, that contains three fields, the sender’s current congestion window size \({ cwnd}\), the estimated round trip time rtt, and the router feedback field \({ feedback}\). Each sender fills its current \({ cwnd}\) and rtt values into the congestion header on a packet departure, and initializes the \({ feedback}\) field to its desired window size.

The core control laws of XCP are implemented at routers. XCP introduces the new concept of decoupling utilization control from fairness control [4]. Each router has two logical controllers, efficiency controller and fairness controller. In each control interval, the efficiency controller calculates the amount of spare bandwidth \(\varphi \) that to be distributed among the flows. The spare bandwidth \(\varphi \) is given by,

$$\begin{aligned} \varphi =\alpha (c-y)-\beta \frac{q}{d} \end{aligned}$$
(1)

where c is the link capacity, y is the aggregate input traffic rate, and q is the persistent queue length. d is the control interval, \(\alpha \) and \(\beta \) are 0.4 and 0.226 respectively, that are chosen to make the system stable [4]. To enable high efficiency, the efficiency controller follows the multiplicative increase multiplicative decrease (MIMD) rule, that allows fast adaptation of y to c.

After calculating \(\varphi \), the fairness controller decides how to distribute \(\varphi \) among all the flows. The fairness controller employs an additive increase multiplicative decrease (AIMD) scheme for this bandwidth allocation, distributing \(\varphi \) equally among all flows when \(\varphi \) is positive, and proportionally to each flow rate when \(\varphi \) is negative. When a link is in the high utilization region, resulting in \(\varphi \thickapprox 0\), which would disable bandwidth redistribution for new data flows. To enable fair redistribution of bandwidth, even when \(\varphi \thickapprox 0\), bandwidth shuffling is performed at each control interval. This operation simultaneously allocates and deallocates the shuffled bandwidth among flows. The shuffled bandwidth is computed as follows,

$$\begin{aligned} h={ max}(0,\gamma y-|\varphi |) \end{aligned}$$
(2)

where \(\gamma \) is a control parameter with default value 0.1.

Fig. 1
figure 1

A simple single bottleneck topology

Full size image
Fig. 2
figure 2

XCP behaves in a noticeably unstable manner when the ratio of maximum to mean RTT is large. The large RTT flow cannot obtain its max–min allocation of 10 Mbps, the aggregate traffic, queue length and control interval fluctuate dramatically, at the 100 Mbps bottleneck

Full size image

3.2 XCP stability problem under heterogeneous delays

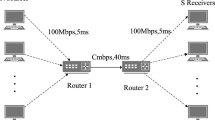
Firstly, we intuitively describe XCP stability problem when the ratio of maximum to average RTT is too large, using the simple single bottleneck topology shown in Fig. 1. In this scenario, there are nine small RTT flows (flow \(i_1\),..., \(i_9\), \({ RTT}_i = \) 20 ms) and only one large RTT flow (flow \(j_1\), \({ RTT}_j = \) 1000 ms) that go through a 100 Mbps bottleneck link. In an ideal case, with a max–min fair allocation, each of the flows gets a bandwidth allocation of 10 Mbps, the aggregate traffic arriving at the bottleneck link and the control interval d will stabilize at 100 Mbps and 118 ms respectively. However, actual simulation results in Fig. 2 show that the large RTT flow cannot obtain its max–min allocation as expected, the aggregate traffic and control interval fluctuate dramatically, therefore, a big buffer is required to absorb these oscillations.

Lachlan et al. first pinpoint that XCP is not globally stable but locally stable in the face of heterogeneous delays, and believe that the instability of XCP is largely due to the nonlinearity encountered when the traffic rate is far from the equilibrium value. Considering that the RTT distribution exhibits heavy-tailed characteristics, this problem is becoming even more serious owing to the fact that a small number of large RTT flows can significantly reduce the system performance. Therefore, this is an urgent problem to be solved or alleviated for making the XCP algorithm more practical. Lachlan et al. [20] further proposes M-XCP, an improved version of XCP, which sets the control interval d to be the maximum RTT observed during the last cycle, instead of the average RTT, and shows a strong stability under heterogeneous delays. However, M-XCP needs additional operations for each packet, the computational complexity of M-XCP increases dramatically, as shown in Sect. 5. Most importantly, M-XCP experiences sluggish system responsiveness. Figure 3 shows that when the control interval d increases, the instability of XCP is removed at the cost of becoming less responsive. Therefore, increasing the value of parameter d is not a good solution, and in-depth theoretical analysis will be given in Sect. 4.

4 Linear analysis and motivation

The dynamic model of XCP behavior was developed in [4]. This model is described by the following coupled, nonlinear differential equations,

$$\begin{aligned} \dot{y}(t)= & {} -\frac{\alpha }{d}(y(t-d)-c)-\frac{\beta }{d^2}q(t-d) \end{aligned}$$
(3)
$$\begin{aligned} \dot{q}(t)= & {} y(t)-c \end{aligned}$$
(4)

where c is the link capacity, y(t) is the aggregate traffic rate, q(t) is the persistent queue length, and d is the control interval. \(\alpha \) and \(\beta \) are system parameters, that are chosen to make the system stable.

In order to analyze the stability of XCP, Katabi et al. [4] employ a variable change \(z(t)=y(t)-c\) to yield a linear system independent of c, and the open-loop transfer function of its corresponding linearized XCP model can be represented as follows, where \(K_1=\frac{\alpha }{d}\) and \(K_2=\frac{\beta }{d^2}\).

$$\begin{aligned} G(s) = \frac{{K_1 \cdot s + K_2 }}{{s^2 }}e^{-ds} \end{aligned}$$
(5)

Further, we can easily get the XCP closed-loop sensitivity function,

$$\begin{aligned} S(s) = \frac{{s^2 }}{{s^2 + K_1 \cdot s \cdot e^{-ds} + K_2 \cdot e^{-ds} }} \end{aligned}$$
(6)
Fig. 3
figure 3

M-XCP converges to the equilibrium rate at around 50 s, which is a long convergence time

Full size image

where \(K_1 = \frac{\alpha }{d}\), \(K_2 = \frac{\beta }{{d^2}}\), \(\beta = \alpha ^2 \sqrt{2}\), \(0< \alpha < \pi / (4\sqrt{2})\) and d is the control interval. With the help of the XCP closed-loop sensitivity function, robustness and responsiveness of the XCP system can be quantitatively analyzed, deduced from its frequency response. Roughly speaking, robustness is inversely proportional to the peak frequency response \(\left\| S \right\| _\infty = \sup _\omega \left| {S(j\omega )} \right| \), while responsiveness is proportional to the unity gain crossover frequency \(\omega _g\) defined by \(\left| {S(j\omega _g )} \right| = 1\), where S is the XCP closed-loop sensitivity function [56]. Since the linearized XCP system is independent of capacity c, robustness and responsiveness are not affected by the link capacity. Thereby, XCP is very suitable for high-speed networks, which has been proven by simulations and experiments [4, 5].

According to Eq. (6), robustness and responsiveness are primarily affected by system parameter \(\alpha (\beta = \alpha ^2 \sqrt{2})\) and control interval d. In order to insure the system stability, Katabi et al. [4] propose a constraint, \(0< \alpha < \pi / (4\sqrt{2}) \approx 0.55\). Due to control interval d is defined as average round trip time of flows passing through the bottleneck link, and vast majority of flows (over 90%) have RTT less than 200 ms [57], we choose \(0< d < 1.0\, \mathrm{s}\). On the basis of these constraints, we quantitatively study their impacts, and plot the robustness and responsiveness as a function of parameter \(\alpha \in (0,0.55)\) and control interval \(d \in (0,1.0)\) in Figs. 4 and  5, respectively.

Fig. 4
figure 4

When system parameter \(\alpha \) increases, XCP becomes less robust (robustness is inversely proportional to the vertical axis in the left figure), but more responsive (responsiveness is proportional to the vertical axis in the right figure)

Full size image
Fig. 5
figure 5

When control interval d increases, XCP becomes less responsive, but robustness is almost completely unaffected by control interval d

Full size image

Figure 4 shows that XCP responsiveness increases while robustness decreases, when parameter \(\alpha \) increases. In original XCP design, \(\alpha \) is set to 0.4, which is an empirical choice. According to Fig. 4, we can see that \(\alpha =0.4\) is a good performance trade-off between robustness and responsiveness. Figure 5 shows that XCP responsiveness decreases dramatically, when control interval d increases. The robustness is almost completely unaffected by control interval d, which is a surprising result. However, Lachlan et al. [20] believe that increasing control interval d can improve the system stability, and demonstrate that XCP is locally stable but globally unstable using NS-2 simulations. This is because XCP is essentially a nonlinear system [15], the linear model is inadequate, and a discrete-time nonlinear system model is required. However, such a nonlinear model is not amenable to straightforward theoretical analysis that is possible with a linear system.

Comparing Figs. 4 and 5, we find that system robustness is sensitive to parameter \(\alpha \) but not sensitive to control interval d, and in contrast system responsiveness is sensitive to control interval d but not sensitive to parameter \(\alpha \). Therefore, it is natural for us to decrease parameter \(\alpha \) for improving system robustness against heterogeneous delays. However, the Internet is a highly dynamic and evolving system of large scale and complex, it is a challenge to choose a reasonable value of \(\alpha \) for each link in such environments. In this paper, according to the robust control theory and Lyapunov–Krasovskii functional, we propose an effective mechanism to adjust parameter \(\alpha \) from an initial value of 0.4 to a reasonable value to improve system robustness against heterogeneous delays, without significantly affecting system responsiveness at the same time.

5 R-XCP protocol

5.1 A modification on XCP system

Experience tells us that congestion control algorithms should be more robust against unpredictable scenarios when aggregate traffic rate y(t) exceeds link capacity c. Corresponding to the XCP system, parameter \(\alpha \) should be decreased when aggregate traffic rate y(t) fluctuates dramatically. More importantly, the control objective is to make \(y(t) = c\), therefore, it is a good choice to choose \(z(t) = y(t)-c\) as the controlled variable. Additionally, Zhang et al. [15] believe that capacity c in XCP efficiency controller, expressed by Eq. (1), is a configurable variable. Therefore, we modify the XCP algorithm by introducing control variable u(t), and expressed via the following nonlinear differential equations,

$$\begin{aligned} \dot{y}(t)= & {} -\frac{\alpha }{d}(y(t-d)-c-u(t))-\frac{\beta }{d^2}q(t-d) \end{aligned}$$
(7)
$$\begin{aligned} \dot{q}(t)= & {} y(t)-c \end{aligned}$$
(8)

Hence, we can dynamically change parameter \(\alpha \) for improving system robustness on the basis of \(z(t) = y(t)-c\). The revised linearized XCP model is depicted in Fig. 6. Please note that, it is not reasonable to disconnect control path and introduce control variable u(t) at these places like place a or b in Fig. 6. At place a, the rate of queue change will become \(\dot{q}(t) = y(t) -c-u(t)\), not being consistent with actual physical system, which is \(\dot{q}(t) = y(t)-c\). In order to analyze the stability of XCP, Katabi et al. [4] ignore the boundary conditions on the queue length q(t), and assumes that q(t) can range from \(-\infty \) to \(+\infty \). In practice, q(t) always has an upper bound of Q, which is the router buffer size, and never goes negative [15]. When the feedback is bounded, the instability caused by this non-linearity is apparent [58]. So it is not reasonable to disconnect control path at place b too.

Fig. 6
figure 6

Block diagram of the revised XCP system

Full size image

5.2 Lyapunov–Krasovskii based controller design

The revised XCP system can be rewritten as follows,

$$\begin{aligned} \dot{x}(t)=Ax(t)+A_dx(t-d)+Bu(t) \end{aligned}$$
(9)

where \(z(t)=y(t)-c\), \(A=\left[ \begin{array}{cc} 0&{}\quad 0\\ 1&{}\quad 0\end{array}\right] \),

\(A_d=\left[ \begin{array}{cc} -\frac{\alpha }{d}&{}\quad -\frac{\beta }{d^2}\\ 0&{} \quad 0\end{array}\right] \), \(B=\left[ \begin{array}{c} \frac{\alpha }{d}\\ 0\end{array}\right] \). \(x(t)=\left[ \begin{array}{c} z(t)\\ q(t)\end{array}\right] \) is the state vector. \(x_0(\theta )=\varphi (\theta )\), \(\theta \in [-d,0]\) is the initial condition.

Since all states are available, we construct the following memoryless state feedback,

$$\begin{aligned} u(t)=Kx(t-d) \end{aligned}$$
(10)

to control system (9). K is the designed feedback gain matrix, corresponding to our controller.

In order to guarantee the asymptotic stability of system (9) under controller (10) for any delay \(d>0\), we applied Lyapunov–Krasovskii functional approach and LMI method to design a suitable feedback gain matrix K.

Theorem 1

System (9) is stabilized by controller (10) for any delay \(d>0\), if there are symmetric positive definite matrices U, V and a matrix X, which satisfy the following matrix inequality,

$$\begin{aligned} \left[ \begin{array}{cc} UA^T+AU+V&{}\quad A_dU+BX\\ UA^T_d+X^TB^T&{}\quad -V\end{array}\right] <0 \end{aligned}$$
(11)

and meanwhile the state feedback gain is given by \(K=XU^{-1}\). \(\square \)

Proof

we propose to employ the well-known Lyapunov–Krasovskii functional,

$$\begin{aligned} V(x_t)=x^T(t)Px(t)+\int ^{t}_{t-d}x^T(\theta )Qx(\theta )d\theta \end{aligned}$$

where matrices P and Q are symmetric and positive definite. The time derivative of this function along trajectory of system (9) under controller (10) is given by,

$$\begin{aligned}&\dot{V}(x_t)=\dot{x}^T(t)Px(t)+x^T(t)P\dot{x}(t)+x^T(t)Qx(t)-x^T(t-d)Qx(t-d)\\&\quad =x^T(t)[A^TP+PA+Q]x(t)+x^T(t)[PA_d+PBK]x(t-d)\\&\qquad + \ x^T(t-d)[A_d^TP+K^TB^TP]x(t)-x^T(t-d)Qx(t-d)\\&\quad =\left[ \begin{array}{c} x(t)\\ x(t-d) \end{array} \right] ^T \left[ \begin{array}{cc} A^TP+PA+Q&{}\quad PA_d+PBK\\ A^T_dP+K^TB^TP&{}\quad -Q\end{array}\right] \left[ \begin{array}{c}x(t)\\ x(t-d)\end{array}\right] \end{aligned}$$

According to the Lyapunov–Krasovskii stability theorem [23], system (9) is stabilized by controller (10) for any delay \(d>0\) if the following inequality holds,

$$\begin{aligned} \left[ \begin{array}{cc} A^TP+PA+Q&{}\quad PA_d+PBK\\ A^T_dP+K^TB^TP&{}\quad -Q\end{array}\right] <0 \end{aligned}$$

Further, the left side of above matrix inequality left and right multiplied by \(diag\{P^{-1},P^{-1}\}\) respectively makes,

$$\begin{aligned} \left[ \begin{array}{cc} P^{-1}A^T+AP^{-1}+P^{-1}QP^{-1}&{}\quad A_dP^{-1}+BKP^{-1}\\ P^{-1}A^T_d+P^{-1}K^TB^T&{}\quad -P^{-1}QP^{-1}\end{array}\right] <0 \end{aligned}$$

Let \(U=P^{-1}\), \(V=P^{-1}QP^{-1}\), \(X=KU\), we can obtain,

$$\begin{aligned} \left[ \begin{array}{cc} UA^T+AU+V&{}\quad A_dU+BX\\ UA^T_d+X^TB^T&{}\quad -V\end{array}\right] <0 \end{aligned}$$

and meanwhile the state feedback gain is given by \(K=XU^{-1}\). \(\square \)

5.3 A better controller

In this subsection, our goal is to design a better controller which takes into account the upperbound of parameter d, to make the system get better performance.

Let us suppose that d has the lowerbound \({h_1} \in {R^ + }\), namely, \({h_1} \le d\), yields \(\frac{1}{d} \le \frac{1}{{{h_1}}}\). Let \({H_1} = \frac{1}{{{h_1}}}\), matrix \({{A}_d}\) can be written as follows,

$$\begin{aligned} {{A}_d} = {{DF}}{{E}_a} \end{aligned}$$
(12)

where \({D} = \left[ {\begin{array}{cccc} { -\alpha {H_1}}&{} 0&{}\ 0&{}{ -\beta H_1^2}\\ 0&{} 0&{}\ 0&{}0 \end{array}} \right] \), \({F} = \left[ {\begin{array}{cc} {\frac{1}{{d{H_1}}} {{I}_2}}&{}0\\ 0&{}{\frac{1}{{dH_1^2}} {{I}_2}} \end{array}} \right] \), \({{E}_1} = \left[ {\begin{array}{c} {{{I}_2}}\\ {{{I}_2}} \end{array}} \right] \), \({{I}_n}\) denotes a unit matrix of n order.

Then, the following inequality is clearly established,

$$\begin{aligned} {{F}^T}{F} < {{I}_4} \end{aligned}$$
(13)

Since all states are measurable, we construct memoryless state feedback \(u(t) = Kx(t-d)\) to control system (9). Then, we have,

$$\begin{aligned} \dot{x}(t) = {A}x(t) + {{\bar{A}}_d}x(t-d) \end{aligned}$$
(14)

where \({{\bar{A}}_d} = {{A}_d} + {BK}\).

Lemma 1

[24] Let define proper matrices D, E and F, if \( {{F}^T}(t){{F }}(t) \le {I} \) is correct, then, for any scalar \( \varepsilon > 0 \), there exists,

$$\begin{aligned} {DEF} + {{E}^T}{{F}^T}{{D}^T} \le \varepsilon {D}{{D}^T} + {\varepsilon ^{-1}}{{E}^T}{E} \end{aligned}$$
(15)

\(\square \)

Using an information on parameter d, we expect a better controller, and propose Theorem 2.

Theorem 2

For \(d \in [{h_1},{h_2}]\), \( {h_2}> {h_1} > 0 \), and scalars \( {\mu _i} (i = 2,3)\), if there exits \( {\varepsilon } > 0\), matrices \( \tilde{P} > 0 \) , \( \tilde{R} > 0 \), Y, \( {\tilde{N}_i}(i = 1,2,3)\), and a nonsingular matrix X, to make LMI (16) is established (\(*\) denotes a matrix block given by matrix symmetry),

$$\begin{aligned} \left[ {\begin{array}{cc} {{{\tilde{\varXi }}_{11}}}&{}\quad \ * \\ {{{\tilde{\varXi }}_{21}}}&{}\quad \ {{{\tilde{\varXi }}_{22}}} \end{array}} \right] < 0 \end{aligned}$$
(16)

where

$$\begin{aligned}&{{{\tilde{\varXi } }}_{11}} = \left[ {\begin{array}{ccc} {{\varGamma _{11}}}&{}\ * &{}\ * \\ {{\varGamma _{21}}}&{}\ {{\varGamma _{22}}}&{}\ * \\ {{\varGamma _{31}}}&{}\ {{\varGamma _{32}}}&{}\ {{\varGamma _{33}}} \end{array}} \right] \\&{{{\tilde{\varXi } }}_{21}} = \left[ {\begin{array}{ccc} {{h_2}\tilde{N}_1^T}&{}{{h_2} \tilde{N}_2^T}&{}{{h_2} \tilde{N}_3^T}\\ 0&{}{\mu {E_a}{X^T}}&{}0 \end{array}} \right] \\&{{{\tilde{\varXi } }}_{22}} = diag \{ {-{h_2}\tilde{R}, -\mu \varepsilon I} \}\\&{\varGamma _{11}} = {\tilde{N}_1} + \tilde{N}_1^T + A{X^T} + X{A^T} + \varepsilon D{D^T}\\&{\varGamma _{21}} = {\tilde{N}_2} -\tilde{N}_1^T + {\mu _2}A{X^T} + {Y^T}{B^T}\\&{\varGamma _{31}} = {\tilde{N}_3} + {\mu _3}A{X^T}-X + {\tilde{P}^T}\\&{\varGamma _{22}} =-{\tilde{N}_2} -\tilde{N}_2^T + {\mu _2}BY + {\mu _2}{Y^T}{B^T} + {\mu _2}\varepsilon D{D^T}\\&{\varGamma _{32}} =-{\tilde{N}_3}-{\mu _2}X + {\mu _3}BY\\&{\varGamma _{33}} =-{\mu _3}X-{\mu _3}{X^T} + {h_2}\tilde{R} + {\mu _3}\varepsilon D{D^T} \\&\mu = 1 + {\mu _2} + {\mu _3} \end{aligned}$$

Then, system (9) will be stabilized with a state feedback \(u(t) = Kx(t-d)\) for \(d \in [{h_1},{h_2}]\). Meanwhile, the state feedback gain is obtained by \(K = Y{X^{-T}} \). \(\square \)

Proof

we propose to employ a novel Lyapunov–Krasovskii functional,

$$\begin{aligned} V(x_t) = {x^T}(t)Px(t) + \int _{t-{h_2}}^t {\int _s^t {{{\dot{x}}^T}(v)R\dot{x}(v)dvds} } \end{aligned}$$

where \( P > 0\) and \(R > 0 \). By taking the derivative of \(V(x_t)\), system (14) and \( x(t)-x(t-d) -\int _{t-d}^t {\dot{x}(s)ds} = 0 \) (Newton–Leibniz Equation [24]) are used, we have,

$$\begin{aligned} \dot{V}(x_t)= & {} 2 {x^T}(t)P\dot{x}(t) \\&+\, 2 [{x^T}(t){N_1} + {x^T}(t-d){N_2} + {{\dot{x}}^T}(t){N_3}] \cdot \\&\quad \ [x(t)-x(t-d) -\int _{t-d}^t {\dot{x}(s)ds} ] \\&+\, 2[{x^T}(t){M_1} + {x^T}(t-d){M_2} + {{\dot{x}}^T}(t){M_3}] \cdot \\&\quad \ [Ax(t) + {{\bar{A}}_d}x(t-d) -\dot{x}(t)] \\&+ \lambda {{\dot{x}}^T}(t)R\dot{x}(t) -\int _{t -\lambda }^t {{{\dot{x}}^T}(s)R\dot{x}(s)ds} \end{aligned}$$

where \( {N_i} \) and \( {M_i} (i = 1,2,3)\) are the free matrixes with corresponding dimensions.

Obviously, the following inequalities are established, where \({\zeta ^{{T}}}(t) = [{{x^{{T}}}(t)},{{x^{{T}}}(t-d)},{{{\dot{x}}^{{T}}}(t)}]\) and \({N^T} = [N_1^T,N_2^T,N_3^T]\).

$$\begin{aligned}&-\int _{t-h_2}^t {{{\dot{x}}^T}(s)R\dot{x}(s)ds} \le -\int _{t-d}^t {{{\dot{x}}^T}(s)R\dot{x}(s)ds}\\&-\, 2[{x^T}(t){N_1} + {x^T}(t-d){N_2} + {{\dot{x}}^T}(t){N_3}]\int _{t-h_2}^t {\dot{x}(s)ds} \\&\quad \le {h_2}{\zeta ^T}(t)N{R^{-1}}{N^T}\zeta (t) + \int _{t-h_2}^t {{{\dot{x}}^T}(s)R\dot{x}(s)ds} \end{aligned}$$

According to the above two inequalities, the following inequality is obtained,

$$\begin{aligned} \dot{V}(x_t) \le \zeta {(t)^T}\left\{ {\left[ {\begin{array}{ccc} {{\varPi _{11}}}&{}\quad \ * &{}\quad \ * \\ {{\varPi _{21}}}&{}\quad \ {{\varPi _{22}}}&{}\quad \ * \\ {{\varPi _{31}}}&{}\quad \ {{\varPi _{32}}}&{}\quad \ {{\varPi _{33}}} \end{array}} \right] + \varTheta } \right\} \zeta \left( t \right) \end{aligned}$$

where

$$\begin{aligned} {\varPi _{11}}= & {} {N_1} + N_1^T + {M_1}A + {A^T}M_1^T\\ {\varPi _{21}}= & {} {N_2}-N_1^T + {M_2}A + {K^T}{\bar{A}_d}^TM_1^T\\ {\varPi _{31}}= & {} {N_3} + {M_3}A-M_{_1}^T + {P^T}\\ {\varPi _{22}}= & {} -{N_2}-N_2^T + {M_2}{\bar{A}_d} + {K^T}{\bar{A}_d}^TM_2^T\\ {\varPi _{32}}= & {} -{N_3}-M_{_2}^T + {M_3}{\bar{A}_d}\\ {\varPi _{33}}= & {} -{M_3}-M_3^T + {h_2}R\\ \varTheta= & {} {h_2}N{R^{-1}}{N^T} \end{aligned}$$

By setting \( \varOmega = \left[ {\begin{array}{ccc} {{\varPi _{11}}}&{}\quad \ * &{}\quad \ * \\ {{\varPi _{21}}}&{}\quad \ {{\varPi _{22}}}&{}\quad \ * \\ {{\varPi _{31}}}&{}\quad \ {{\varPi _{32}}}&{}\quad \ {{\varPi _{33}}} \end{array}} \right] + \varTheta \), if inequality \( \varOmega < 0 \) exits, system (14) will be stabilized based on Lyapunov–Krasovskii stability theorem.

\( \varOmega < 0 \) is equivalent to the following inequality,

$$\begin{aligned} \varOmega = \tilde{\varOmega } + M_d^TF{M_e} + M_e^T{F^T}{M_d} < 0 \end{aligned}$$
(17)

where

$$\begin{aligned}&{{\tilde{\varOmega } }} = \left[ {\begin{array}{cccc} {{\varOmega _{11}}}&{}\quad \ * &{}\quad \ * &{}\quad \ * \\ {{\varOmega _{21}}}&{}\quad \ {{\varOmega _{22}}}&{}\quad \ * &{}\quad \ * \\ {{\varOmega _{31}}}&{}\quad \ {{\varOmega _{32}}}&{}\quad \ {{\varOmega _{33}}}&{}\ * \\ {{h_2}N_1^T}&{}\quad \ {{h_2}N_2^T}&{}\quad \ {{h_2}N_3^T}&{}\quad \ {-{h_2}R} \end{array}} \right] \\&{\varOmega _{11}} = {N_1} + N_1^T + {M_1}A + {A^T}M_1^T\\&{\varOmega _{21}} = {N_2}-N_1^T + {M_2}A + {K^T}{B^T}M_1^T\\&{\varOmega _{31}} = {N_3} + {M_3}A-M_{_1}^T + {P^T}\\&{\varOmega _{22}} =-{N_2}-N_2^T + {M_2}BK + {K^T}{B^T}M_2^T\\&{\varOmega _{32}} =-{N_3}-M_{_2}^T + {M_3}BK\\&{\varOmega _{33}} =-{M_3}-M_3^T + {h_2}R\\&{M_d} = [{{D^{{T}}}M_1^{{T}}} \ \ {{D^{{T}}}M_2^{{T}}} \ \ {{D^{{T}}}M_3^{{T}}} \ \ 0]\\&{M_e} = [0 \ \ {{E_a}} \ \ 0 \ \ 0] \end{aligned}$$

Let \( M = {M_1}\), \( {M_2} = {\mu _2}M \), \( {M_3} = {\mu _3}M \), \( X = {M^{-1}} \), \( Y = K{X^{{T}}}\), \( \tilde{P} = XP{X^{{T}}} \), \( {\tilde{N}_i} = X{N_i}{X^{{T}}} \), \( {\tilde{M}_i} = X{M_i}{X^{{T}}} \), \( \tilde{R} = XR{X^{{T}}} \), and the left side of inequality (17) left and right multiplied by \( diag \{ X,X,X,X \} \) respectively, inequality (16) can be get based on Lemma 1 and Schur Complement Lemma. Thereby, system (9) is asymptotic stable under the control law (10) for \(d \in [{h_1},{h_2}]\), with the feedback gain \(K = Y{X^{-T}} \). \(\square \)

As a numerical example, using Matlab LMI Toolbox [59], when \(d\in [0.1,1.0]\), the state feedback gain \(K = [-6.3707,-0.0001]\) was obtained from Theorem 2.

5.4 Implementation

Like XCP, each R-XCP packet carries a congestion header, which is used to communicate a flow’s state to routers and feedback from the routers on to the receiver. The field \(H\_{ cwnd}\) is the sender’s current congestion window, whereas \(H\_\textit{rtt}\) is the sender’s current RTT estimated value. These are filled in by the sender and never modified in transit. The remaining field, \(H\_{ feedback}\), takes positive or negative values and is initialized by the sender. Routers along the path modify this field to directly control the sender’s congestion windows. \({ pkt}\_{ size}\) is the length of a packet.

Then, implementing an R-XCP router is fairly simple and can be described using the following pseudo code. There are three relevant blocks of code. The first block, which is the same as XCP, is executed at the arrival of a packet and involves updating the estimates (e.g., \({ input}\_{ bytes}\) is the number of input bytes in a control cycle. \({ sum}\_{ rtt}\_{ by}\_{ cwnd}\) and \({ sum}\_{ rtt}\_{ square}\_{ by}\_{ cwnd}\) are two parameters, and their detailed meanings can be found in [4]) maintained by the router.

figure c

The second block is executed when the control timer fires. It involves updating our control variables, reinitializing the estimation variables, and rescheduling the timer. Code lines 1–4 describe the efficiency controller, of which purpose is to maximize link utilization while minimizing drop rate and persistent queues. They are the core of the R-XCP algorithm, where \(y=input\_traffic\) is the aggregate input traffic rate, \(d=avg\_rtt\) is the control interval, \(c=capacity\) is the link capacity, and q is the persistent queue length. u is R-XCP’s control variable, \(\varepsilon _1\) and \(\varepsilon _2\) are the feedback gains, derived from theoretical result \(K = [\varepsilon _1, \varepsilon _2 ]\), and they both have negative values. \(\varphi \) is the amount of spare bandwidth in a control cycle that to be distributed among the flows. \(\alpha \) and \(\beta \) are 0.4 and 0.226 respectively, that are chosen to make the system stable [4].

As can be seen from line 3 and 4, when the control timer expires, R-XCP dynamically adjusts parameter \(\alpha \) online, based on spare bandwidth and persistent queue length. When the link is under-utilized, we have \((input\_traffic-capacity) < 0\) and \(q = 0\), due to \(\varepsilon _1 < 0\) and \(\varepsilon _2 < 0\), we have control variable \(u > 0\), R-XCP indirectly increases parameter \(\alpha \), in turn increasing system responsiveness with the cost of robustness. When the link is congestion, we have \((input\_traffic-capacity) > 0\) and \(q > 0\), due to \(\varepsilon _1 < 0\) and \(\varepsilon _2 < 0\), we have control variable \(u < 0\), R-XCP indirectly decreases parameter \(\alpha \), in turn increasing system robustness.

Code lines 5–9 calculate the control variables of the fairness controller. With Algorithm 3, they jointly implement a complete fairness controller, apportioning the feedback to individual packets to achieve fairness. Since R-XCP does not modify the XCP’s fairness controller, the detailed explanation of the course of fairness computing and involved parameters’ meanings are omitted from this paper, and can be found in [4].

figure d

The third block of code involves computing the feedback and is executed at packets’ departure.

figure e

5.5 Complexity analysis

Like M-XCP, an R-XCP router implementation also has three relevant code blocks, which are executed when a packet arrives, when the control timer expires, and when a packet departs. The statements in each code block are all executed in sequence order, without loop operations. Therefore, each code block has constant time complexity of O(1), and the specific time consumption depends upon the number of statements in each code block. Meanwhile, the R-XCP algorithm uses a small and fixed amount of space which doesn’t depend on the input. Specifically, the input is not taken into account and R-XCP takes the same and constant amount of space for global variables. Therefore, the R-XCP algorithm also has constant space complexity of O(1).

However a detailed analysis found that R-XCP only modifies the second block, i.e., control timer block. It is executed after each control interval d, which is the average RTT of all flows passing through the router. Internet measurement reports that average RTT is roughly 200 ms [57], so the increase of operations is negligible. In contrast, M-XCP requires to operate each packet to observe the maximum RTT during a control interval. Table 1 gives two examples, considering the mean packet size is 400 bytes [60], there are two bottleneck links, each with capacity of 1 and 10 Gbps, the increased operations of M-XCP are at least 312,500 and 3,125,000 ops/s comparing operations respectively (XCP is selected as a common basis for comparison). Under the same scenario, the increased operations of R-XCP are independent of link capacity, and maintains the same level, 5 ops/s. Compared with M-XCP, the increased operations of R-XCP are negligible. Therefore, R-XCP is more suitable for high-speed networks.

Table 1 Additional operations compared with XCP
Full size table
Fig. 7
figure 7

R-XCP is effective in stabilizing XCP when the ratio of maximum to mean RTT is too large

Full size image
Fig. 8
figure 8

The enlarged view of the congestion windows of large RTT flow and small RTT flow, a large RTT flow, b small RTT flow

Full size image

6 Performance evaluation

6.1 Effectiveness validation

First of all, we validate that R-XCP is effective in solving the weakness of XCP when the ratio of maximum to mean RTT is too large, using the same scenario described in Sect. 3. There are nine small RTT flows (flow \(i_1\),..., \(i_9\), \({ RTT}_i = \) 20 ms) and only one large RTT flow (flow \(j_1\), \({ RTT}_j = \)1000 ms) that cross an 100 Mbps bottleneck link. Simulation results in Fig. 7 confirm that R-XCP effectively stabilizes the system, each flow obtains its max–min bandwidth allocation of 10 Mbps, aggregate traffic rate and control interval stabilize at 100 Mbps and 205 ms respectively. Even though fluctuations of per-flow throughput, aggregate traffic rate and control interval are larger than that of M-XCP, however, the convergence time of R-XCP decreases significantly, see Figs. 3 and 7. Further simulations display that R-XCP maintains the same convergence speed (\({<}\)1.0 s) and M-XCP’s convergence time increases continuously, when the bandwidth of a bottleneck link increases. In other words, R-XCP achieves a better balance between robustness and responsiveness, compared with M-XCP. Additionally, control interval d in R-XCP is slightly larger than the average RTT, this is because when parameter \(\alpha \) decreases, system responsiveness decreases slightly, and router buffer is cleared slowly, eventually leading to increased queuing delays and increased cycle length.

The reasons of simulation results in Figs. 2 and 7 can be further understood by looking in more detail at the congestion window \(({ cwnd})\) behavior of each flow. The enlarged view of the flow’s \({ cwnd}\) in Fig. 8 shows that the source of dramatical rate fluctuation is the rapid changes of instantaneous congestion window size, which may significantly differ from the average congestion window over one round trip time, computed by the XCP controller.

In the XCP algorithm, the large RTT flow’s \({ cwnd}\) is highly peaked, and the small RTT flow’s \({ cwnd}\) also changes violently. The reasons can be explained as follows, when the bottleneck congestion occurs, the XCP controller reduces each flow’s rate. Since a large RTT flow has larger congestion window, with more packets in transit, it obtains greater negative feedback, decreasing \({ cwnd}\) significantly. Moreover, when the window size drops below the number of packets outstanding, large RTT flow’s \({ cwnd}\) also becomes zero and stays zero, based on the sliding window method [4]. It is annoying that this peaky behavior is self-sustaining. When the XCP controller finds the link inefficiency, it enlarges each flow’s \({ cwnd}\) at once, leading to a large peak in the queue size. Subsequently, feedbacks become very negative.

This phenomenon can be alleviated by making XCP respond less rapidly to periods of high or low throughput, such as R-XCP by indirectly decreasing \(\alpha \) for improving system robustness against heterogeneous delays. As shown in Fig. 8, R-XCP flow’s \({ cwnd}\) is quite smooth, and generally maintains at steady state value, whether it is large RTT flow or small RTT flow.

Next, extensive NS-2 simulations are used to study the performance of R-XCP for a wide range of network scenarios including varying round trip times of large RTT flows in range [20, 1000 ms], share of large RTT flows in range [0.1, 0.9], and link capacities in range [10, 1000 Mbps]. We evaluate the impact of each network parameter in isolation while retaining the others as basic settings, which are as follows, the round trip times of small RTT flows are fixed at 20 ms. The bottleneck buffer size is set to one bandwidth-delay product. The data packet size is 1000 bytes, while the ACK packet is 40 bytes. To investigate R-XCP’s performance in the presence of variability and burstiness caused by the short-lived, web-like flows arrivals, short-lived traffic are added into the network. These flows arrive according to a Poisson process with an average arrival rate 500/s. The transfer size of these flows is derived from a Pareto distribution with an average of 30 packets, which is consistent with real-world web traffic [61]. Another important issue is seed selection. In order to fully reflect the uncertain behavior of data flows and packets, the parameter defaultRNG value is set to 0. According to NS-2 implementation, the seed value will be changed based on clock and counter, which is a complex problem and is beyond the scope of this paper. Basically, the simulation results tend to be different for every run [62]. However, this non-deterministic behavior has no impact on the statistical characteristics of test items in this paper, this conclusion can be deduced from Sects. 6.2–6.4. Simulation parameters are summarized in Table 2.

Table 2 Simulation parameters
Full size table
Fig. 9
figure 9

The average variances (95% confidence interval) of per-flow’s rate, aggregate traffic rate and control cycle time, with round trip times of large RTT flows ranging from 10 to 1000 ms, a per-flow’s rate, b aggregate traffic rate, c control cycle time

Full size image

In terms of congestion control algorithms, stability is frequently associated with oscillation of per-flow throughput, and measuring rate variations of flows is often used to measure the stability of transport protocols [63,64,65]. In this paper, we specifically use variances of rates and delays observed on the bottleneck link to measure system stability. In order to make results scientific and credible, each experiment is repeated 100 times, and all simulations are run for at least 200 s to ensure that the system has reached its steady state. Meanwhile, the statistics neglect the first 20% of simulation time. Then on the base of these, we present the confidence interval of simulation results. Additionally, please note that only the results of XCP and R-XCP are listed here, because M-XCP is extremely stable, its variances are the smallest in all simulations. However, M-XCP also experiences sluggish system responsiveness as shown in Sects. 3 and 4.

6.2 Varying round trip times

In this experiment, there are 45 small RTT flows as background traffic and five flows with long RTT values. Therefore, the share of large RTT flows is 10%. We fix the bottleneck capacity at 100 Mbps and vary two-way propagation delay of large RTT flows from 10 to 1000 ms. Meanwhile, the web-like traffic is also injected into the network to investigate the protocol’s robustness. Figure 9 gives the average variances of per-flow’s rate, aggregate traffic rate and control cycle time, with 95% confidence interval. As shown in Fig. 9, when the large RTT value is smaller than 100 ms, simulation results of XCP and R-XCP are basically the same. This is because the ratio of maximum RTT to mean RTT is not sufficiently large, XCP remains stable, the stabilizing effects of R-XCP is not clear. When the large RTT value is greater than 100 ms, we find that an order of magnitude decrease in R-XCP, compared with XCP, in terms of aggregate traffic rate variance. We also observe that R-XCP reduces the variance of control interval by at least an order of magnitude, when aggregate traffic rate variance is decreased. That is to say, R-XCP significantly decreases the volatilities of aggregate traffic rate and control interval, and effectively improves the system stability under heterogeneous delays. Additionally, per-flow rate variances of large RTT flows also decrease at the same time. Please note the logarithmic scale of the figures in this and next subsection.

Fig. 10
figure 10

The average variances (95% confidence interval) of per-flow’s rate, aggregate traffic rate and control cycle time, with share of large RTT flows varying from 10 to 90%. a per-flow’s rate, b aggregate traffic rate, c control cycle time

Full size image
Fig. 11
figure 11

The average variances (95% confidence interval) of per-flow’s rate, aggregate traffic rate and control cycle time, with bottleneck capacity varying from 10 to 1000 Mbps, a per-flow’s rate, b aggregate traffic rate, c control cycle time

Full size image

6.3 Varying the share of large RTT flows

With an increase in the share of large RTT flows, aggregate traffic rate and control interval as well as the other performance indicator get more smooth, regardless of which mechanism is applied. But the absolute values of these indicators are significantly reduced, when R-XCP is employed. Figure 10 shows that control interval variance is smaller than \(1\,\hbox {ms}^2\), far less than its mean, when the share of large RTT flows is >0.7. However, when the share of large RTT flows is >0.4, the variance of aggregate traffic rate is less than \(20\,\hbox {Mbps}^2\), the stabilizing effect of R-XCP is not significant. Therefore, we have the following result, when delay uncertainty is within a certain range, XCP can stabilize aggregate traffic rate at the bottleneck link, which shows that it is too conservative to set control interval to maximum RTT, e.g., M-XCP, resulting in low responsiveness.

Fig. 12
figure 12

The convergence dynamics of XCP, R-XCP and M-XCP, from left to right

Full size image

6.4 Varying bottleneck capacity

As shown in Fig. 11, the bottleneck capacity has an amplification effect on the rate variance. When the bottleneck capacity increases, the fluctuations of aggregate traffic rate and per-flow throughput increase significantly, no matter which mechanism is employed. However, R-XCP reduces the variances of aggregate traffic rate and per-flow throughput by about an order of magnitude, compared with XCP, the stabilizing effect of R-XCP is obvious. Meanwhile, R-XCP reduces the variance of control interval significantly, but in each particular mechanism, control interval variance maintains the same across the whole range of bottleneck capacities varying from 10 to 1000 Mbps.

6.5 Convergence dynamics

In this experiment, there are 45 small RTT flows (flow \(a_1 \sim a_{45}\), \({ RTT}_a = \) 20 ms) as background traffic and 5 large RTT flows (flow \(b_1 \sim b_5\), \({ RTT}_b = \) 1000 ms) that share a 100 Mbps bottleneck link. We introduce 5 large RTT flows into the system one after another, with starting times separated by 100 s. The left graph in Fig. 12 illustrates that XCP behaves in a noticeably unstable manner when the ratio of maximum to mean RTT is too large. The middle and right subfigures show that R-XCP and M-XCP both stabilize the system, and fairly reallocate bandwidth to new flows whenever they join the network. Although M-XCP is more smooth than R-XCP, however, M-XCP takes a much longer time than R-XCP to converge to the fair allocation. Additionally, in R-XCP, whenever a new large RTT flow comes in, per-flow throughput becomes smoother, this is because the control cycle becomes larger in this case, leading to a smaller cutoff frequency and more robust levels.

6.6 More security

Additionally, M-XCP makes the system sensitive to erroneous flows which contribute little traffic but report large RTT values. These flows may actually have very large RTTs, overestimate their RTTs due to system jitters, or maliciously overstate their RTTs. Obviously, M-XCP is not an appropriate method under these scenarios, which slows down the entire network dynamics to accommodate a few flows, since it leads to long periods of under-utilization, alternating with periods of overload causing excessive delay and loss [20]. R-XCP can effectively alleviate, but not solve, this problem in M-XCP, due to the fact that it requires the amount of flows with large RTT values is large enough to significantly increase control interval d. To completely solve this problem, access control and other strategies are essentially needed.

7 Conclusions

In this paper, with the aid of Lyapunov–Krasovskii functional, R-XCP is proposed to solve the weakness of XCP under heterogeneous delays based on the robust control theory. R-XCP significantly decreases the volatilities of aggregate traffic rate and per-flow throughput, and effectively improves the system stability when the ratio of maximum to mean RTTs is sufficiently large. Meanwhile, the fluctuation of control interval also decreases dramatically. Compared with M-XCP, R-XCP has a better balance between robustness and responsiveness, and the computing complexity declines significantly at the same time. Besides, R-XCP also makes the system less sensitive to erroneous RTT attacks.