Analysis of secondary user performance in cognitive radio networks with reactive spectrum handoff

Abstract

Cognitive radio networks use dynamic spectrum access of secondary users (SUs) to deal with the problem of radio spectrum scarcity . In this paper, we investigate the SU performance in cognitive radio networks with reactive-decision spectrum handoff. During transmission, a SU may get interrupted several times due to the arrival of primary (licensed) users. After each interruption in the reactive spectrum handoff, the SU performs spectrum sensing to determine an idle channel for retransmission. We develop two continuous-time Markov chain models with and without an absorbing state to study the impact of system parameters such as sensing time and sensing room size on several SU performance measures. These measures include the mean delay of a SU, the variance of the SU delay, the SU interruption probability, the average number of interruptions that a SU experiences, the probability of a SU getting discarded from the system after an interruption and the SU blocking probability upon arrival.

1 Introduction

In wireless communications, radio spectrum is scarce. Traditionally, spectrum regulators use a static spectrum allocation policy to assign spectrum bands to dedicated (licensed) users. The demand for spectrum is constantly increasing due to the increasing number of wireless devices and services, which leads to the fact that the radio spectrum is fully allocated in many countries [1]. However, it has also been shown through several spectrum occupancy measurement studies, see e.g., [2,3,4], that the allocated spectrum is heavily underutilized, which in turn leads to wasted bandwidth of wireless channels.

Cognitive radio networks (CRNs) aim at an efficient use of the scarce spectrum resources [5, 6]. The idea is to allow secondary (unlicensed) users to use the free spectrum gaps without causing any harm to primary (licensed) transmissions. For that purpose cognitive radios should be able to adapt their transmission parameters to the changing spectrum opportunities.

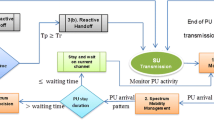
In CRNs, two kinds of spectrum handoff for a secondary user (SU) are distinguished: proactive and reactive spectrum handoff [7]. In proactive spectrum handoff, a SU evacuates its current channel upon the arrival of a primary user (PU) and the interrupted SU switches to a new channel based on a predetermined channel hopping sequence. This sequence is obtained through the analysis of the traffic statistics and the interrupted SU does not perform any spectrum sensing. In reactive spectrum handoff, on the contrary, an interrupted SU is required to sense the spectrum to determine an idle channel for retransmission.

The performance of CRNs has been extensively studied in the last years. A Markovian multiserver queueing model with a preemptive service discipline is presented in [8]. The case of r different user classes is considered where within each user class, customers are served according to their arrival order. The moments of the sojourn time distribution for lower priority customers are derived. An assumption of this model is that higher priority customers can interrupt lower priority customers only when all servers are busy. This means that higher priority customers are aware of the presence of lower priority customers, which does not correctly depict an important aspect of the CRN paradigm where PUs are completely unaware of SU actions. In [9], continuous-time Markov chain (CTMC) models with and without queueing are proposed to analyze the performance of SUs in a CRN. The case where multiple SUs can simultaneously share a spectrum band is considered. A limitation of this work is that it assumes that an interrupted SU should wait on the same channel so as to complete unfinished service when the channel becomes available again.

In [10], a loss model for spectrum access with a finite user population is presented and the delay of SUs is investigated based on a CTMC. In [11], a CTMC model is developed to assess the maximum throughput of SUs in a heterogeneous CRN. The behavior of a CRN system with both PUs and SUs is modeled by a two-dimensional Markov chain in [12,13,14,15]. The throughput and the forced termination probability of SUs are derived in [12], whereas blocking probabilities for PUs and SUs are calculated in [13,14,15]. In [14], spectrum sensing errors are considered. None of the papers discussed above, however, take the sensing time into consideration. In [16, 17], M/G/1 queueing models (with Poisson arrivals, general service times and a single server) are proposed to investigate the case where each SU can transmit on all channels simultaneously. These papers do not take the effect of the handoff processing time into consideration either.

Other studies, see e.g., [18, 19], use the on/off random process to describe the activity behavior of PUs on each channel, where an off period on a channel represents a spectrum opportunity for SUs. In [18], the spectrum utilization and the blocking time are derived, but the effect of the sensing time is not addressed. The influence of the sensing time on the data delivery time is examined in [19]. An assumption of this work is that at least one channel is always available for SUs, and the case where the system is blocked is not investigated.

Some recent analytical models that include sensing time are proposed in [7, 20], but with different sensing time definitions. In [20], the authors refer to in-Band sensing where the sensing delay is the time from a collision moment between a PU and SU until the moment that the collision is detected by the SU. In [7], the sensing time is defined as the time from the moment a SU is interrupted by a PU until the moment an idle channel is found. Both these definitions do not consider the need of a SU to sense upon arrival.

In the present paper, we analyze the performance of SUs in a CRN with reactive spectrum handoff. The sensing time is defined as the time used by a SU to scan the spectrum and detect the first idle channel. Also, each SU performs spectrum sensing every time it attempts to access a channel including the case when a SU has just arrived. Upon the arrival of a PU, the SU instantly evacuates the occupied channel, i.e., no collision between a SU and a PU can happen as in [21]. The contributions of this paper are summarized as follows:

• A CTMC model of a CRN with reactive-decision spectrum handoff is developed. This model, referred to as the “system model” in the sequel, describes the interactions of PUs and SUs where PUs exercise preemptive priority over SUs. Based on this model, a wide range of performance measures are evaluated including the mean SU delay, the SU interruption probability, the SU discard probability and the SU blocking probability.

• A second CTMC model is presented that tracks a specific (tagged) SU from the time it enters the system until it leaves the system. This model, referred to further as the “tagged secondary user model”, allows us to obtain the variance of the SU delay and the mean number of interruptions of a SU. It can be used to obtain higher moments of the SU delay as well.

This paper completes the analysis of [22], where only the system model was studied.

The rest of the paper is structured as follows. In Sects. 2 and 3 we describe the system model and the tagged SU model respectively, together with the associated SU performance measures. Next, the computation methodology is explained in Sect. 4. We provide some numerical examples in Sect. 5. Finally, we draw conclusions in Sect. 6.

2 System model

2.1 Model description

We consider a radio spectrum divided into N frequency bands forming N identical channels, i.e., channels with the same radio characteristics. Each channel can be accessed by PUs and SUs. PUs and SUs arrive according to a Poisson process with rates $\lambda _1$ and $\lambda _2$ respectively.

Upon arrival, a PU is assigned to a channel not occupied by another PU randomly, i.e., no default channel is allocated. The PU transmission time is exponentially distributed with rate $\mu _1$. If all channels are occupied by PUs, a new arriving PU is blocked.

Arriving SUs enter into a sensing state. We assume that a SU senses all channels one by one until it detects the first idle channel. This sensing procedure seems reasonable and has been used in [23, 24]. Also each SU chooses its own sensing order randomly. In this setting, as the sensing time can be different for each SU, and in view of analytical tractability, we assume it is exponentially distributed with rate $\sigma$. In case all channels are busy, a SU stays in the sensing state until at least one channel is detected idle (i.e., not occupied by any PU or other SU). After sensing, a SU enters into a transmission state. The SU transmission time is exponentially distributed with rate $\mu _2$. A SU transmission can be interrupted by the arrival of a PU on the same channel, and in this case the SU is transferred into the sensing state again for retransmission. Thus, and different from [7], the assumptions that a default channel is assigned to SUs upon arrival and the interrupted SU has to stay on its channel if all the other channels are busy, are relaxed. As in [7, 9], we assume that no collisions can occur between SUs trying to transmit on the same channel. Finally, given that SUs only have the free spectrum gaps not in use by PUs at their disposal for transmission, it seems reasonable to consider a maximum number of SUs that are allowed to sense the channels. We thus assume that the number of sensing SUs is limited to K SUs. The parameter K is referred to as the “sensing room size” in the sequel. Arriving and interrupted SUs who find already K sensing SUs in the system, are blocked or discarded from the system, respectively.

In order to analyze this system, we create a CTMC where a state x is given as $x =(x_1,x_2,x_3)$. Here, $x_1$ is the number of transmitting PUs, $x_2$ is the number of transmitting SUs and $x_3$ is the number of sensing SUs. The finite state space S of the Markov chain contains all states such that

$$\begin{aligned} x_1+x_2 \le N \text { and } x_3 \le K\,. \end{aligned}$$

(1)

The row vector $\pi$ of steady-state probabilities of the CTMC can be computed as the solution of the set of balance equations

$$\begin{aligned} \pi Q=0\,, \end{aligned}$$

(2)

where Q is the infinitesimal generator of the CTMC, together with the normalization condition

$$\begin{aligned} \sum \limits _{x \in S} \pi _x = 1 \,, \end{aligned}$$

(3)

where $\pi _x$ denotes the probability that the system is in state x.

In view of the above modeling assumptions, the transition rates $q_{x,y}$ from one state x to another state y ($x\ne y$) are given as

$$\begin{aligned} q_{x,y} = {\left\{ \begin{array}{ll} \lambda _1 \frac{N-x_1-x_2}{N-x_1},&{} \text {if } y=(x_1+1, x_2,x_3),\\ &{} x_1< \ N,\\ \lambda _1 \frac{x_2}{N-x_1},&{} \text {if } y=(x_1+1, x_2-1,x_3+1),\\ &{} x_3< K,\,x_1< N,\\ \lambda _1 \frac{x_2}{N-x_1},&{} \text {if } y=(x_1+1, x_2-1,x_3),\\ &{} x_3 = K,\,x_1< N,\\ \lambda _2,&{}\text {if } y=(x_1, x_2,x_3+1),\, x_3< \ K,\\ x_1\mu _1,&{}\text {if } y=(x_1-1, x_2,x_3),\\ x_2\mu _2,&{}\text {if } y=(x_1, x_2-1,x_3),\\ x_3\sigma ,&{}\text {if } y=(x_1,x_2+1,x_3-1),\\ &{}(x_1+x_2) <N,\\ 0,&{}\text {otherwise}. \end{array}\right. } \end{aligned}$$

(4)

To explain the above equation, we differentiate 8 transition cases. In case 1, an arriving PU does not interrupt a transmitting SU. The rate $\lambda _1 x_2/(N-x_1)$ is the fraction of $\lambda _1$ where a transmitting SU is interrupted by an arriving PU and transferred into the sensing state (case 2) or discarded due to lack of sensing room (case 3). An arriving SU starts to sense if there is a place in the sensing room (case 4). In cases 5 and 6, a PU and a SU finish transmission respectively. In case 7, a SU leaves the sensing state into the transmitting state with rate $x_3\sigma$ if there is at least one idle channel.

2.2 Quasi-birth–death structure

We show next that the above CTMC has a quasi-birth–death (QBD) structure. This allows us to use a specific methodology to efficiently compute steady-state probabilities as described later in the computation methodology section. In order to display the infinitesimal generator Q of the Markov chain in a QBD format, we define the QBD level as the number of sensing SUs $x_3$, whereas the QBD phase corresponds to the pair $(x_1,x_2)$ of transmitting PUs and transmitting SUs. The possible phases are ordered lexicographically for $(x_1, x_2)$, i.e., in the order (0, 0), (0, 1),$\ldots$,(0, N), (1, 0),(1, 1), $\cdots$,$(1,N-1)$,$\ldots$, (i, 0), (i, 1), $\ldots$, $(i,N-i)$,$\ldots ,(N,0)$.

In view of the transition rates of Eq. (4), the generator matrix Q has the following block structure:

(5)

where the submatrices $\varLambda , j\varSigma , Q_{j}$ and $Q_{K}^*$ are derived as follows.

We let the subscripts i, m, j denote the number of PUs $x_1$, transmitting SUs $x_2$ and sensing SUs $x_3$. In the sequel, we also use the concept of horizontal $(\sim )$ and vertical (|) matrix concatenation. Submatrix $\varLambda$ then corresponds to transitions where the level is increased by 1; these are due either to the interruption of a SU by the arrival of a PU (case 2) or the arrival of a new SU (case 4). Matrix $\varLambda$ is therefore given as

(6)

with as component matrices the diagonal matrix $\varLambda _{2,i} =\lambda _2I$, where I is the identity matrix, and $I_i$ defined as

(7)

with elements $\lambda _{i,m}^* = \frac{\lambda _1 m}{N-i}$. Submatrix $j\varSigma$ corresponds to transitions from level j to level $j-1$ due to a SU moving from the sensing to the transmitting state after finding an idle channel (case 7). Matrix $\varSigma$ is therefore structured as follows:

(8)

where $\varSigma _i = (v_1 \sim (\sigma I)) | v_2$, with $v_1$ a column vector of zeros concatenated to the left side of $\sigma I$ and $v_2$ a row vector of zeros concatenated vertically below $v_1 \sim (\sigma I)$. The non-diagonal elements in $Q_j$ correspond to transitions where the level j remains unchanged. For $j<K$, such transitions are due to the arrival of a PU without an interruption of a SU (case 1), the end of a transmission of a PU (case 5) or the end of a transmission of a SU (case 6). Matrix $Q_j$, for $j<K$, and its components are hence given by

$$\begin{aligned} Q_j= & {} \begin{bmatrix} \overline{Q_{0,j}}\,&\varLambda _{1,0}\, \\ M_{1,1}\,&\overline{Q_{1,j}}\,&\varLambda _{1,1}\, \\&2M_{1,2}\,&\overline{Q_{2,j}}\,&\varLambda _{1,2}\, \\&\cdots \,\\&NM_{1,N}\,&\overline{Q_{N,j}}\\ \end{bmatrix}, \end{aligned}$$

(9)

$$\begin{aligned} \varLambda _{1,i}= & {} \begin{bmatrix} \lambda _{i,0}^{**} \, \\&\lambda _{i,1}^{**}\, \\&\cdots \,\\&&\lambda _{i,(N-i-1)}^{**} \\&&0\\ \end{bmatrix}, \end{aligned}$$

(10)

$$\begin{aligned} \overline{Q_{i,j}}= & {} \begin{bmatrix} s_{i,0,j}\,&\\ \mu _2\,&s_{i,1,j}\, \\&2\mu _2\,&s_{i,2,j}\, \\&\cdots \,\\&&(N-i)\mu _2\,&s_{i,N-i,j} \\ \end{bmatrix}, \end{aligned}$$

(11)

$M_{1,i} = (\mu _{1}I) \sim v_3$, where a column vector $v_3$ of zeros is concatenated to the right side of $\mu _{1}I$, and $\lambda _{i,m}^{**} = \lambda _1 (N-i-m)/(N-i)$. The diagonal elements $s_{i,m,j}$ of the matrix $\overline{Q_{i,j}}$ are such that the row sums in the generator matrix Q equal zero. Their values are given in Table 1. A description of the various component matrices is given in Table 2. Finally, the last diagonal block of Q is defined as $Q_{K}^* = Q_{K} +\varLambda$. This is due to case 3, where SUs can still be interrupted while there are already K sensing SUs.

Table 1 Diagonal elements of $\overline{Q_{i,j}}$

Table 2 Component matrices description

2.3 SU performance measures

From this system model, we can compute various performance measures, which we detail below. All these measures are based on the steady-state row vector $\pi$, which we solve from the set of equations $\pi Q=0$. We describe in Sect. 4 how this can be done in an efficient manner.

First, the expected number $E\left[ U_{\text {su2}}\right]$ of transmitting SUs and the expected number $E\left[ U_{\text {su3}}\right]$ of sensing SUs are respectively given by

$$\begin{aligned} E\left[ U_{\text {su2}}\right]= & {} \sum \limits _{x_3=0}^{K} \sum \limits _{x \in S_{x_{3}}} x_2\pi _x \,, \end{aligned}$$

(12)

$$\begin{aligned} E\left[ U_{\text {su3}}\right]= & {} \sum \limits _{x_3=1}^{K} \sum \limits _{x \in S_{x_{3}}} x_3\pi _x \,, \end{aligned}$$

(13)

where $S_{x_{3}}$ is the set of all states within level $x_3$.

The blocking probability $\gamma$ of SUs, i.e., the probability that an arriving SU finds a full sensing room, is given as

$$\begin{aligned} \gamma = \sum \limits _{x \in S_{K}} \pi _x\,. \end{aligned}$$

(14)

With these results and based on Little’s law, the mean delay $E\left[ D_{\text {su}}\right]$ of a SU is then calculated as

$$\begin{aligned} E\left[ D_{\text {su}}\right] = \frac{ E\left[ U_{\text {su2}}\right] + E\left[ U_{\text {su3}}\right] }{\lambda _2 (1 - \gamma )}\,. \end{aligned}$$

(15)

Next, the SU interruption probability $\alpha$, i.e., the probability that a transmitting SU is interrupted upon arrival of a PU, is given as follows:

$$\begin{aligned} \alpha = \sum \limits _{x_3=0}^{K}\sum \limits _{x\in S_{x_3}^{*}} \pi _x\frac{ \lambda _1 x_2/(N-x_1)}{D_1(x)} \,, \end{aligned}$$

(16)

where $\lambda _1 x_2/(N-x_1)$ is the transition rate from state x where a SU gets interrupted due to a PU arrival, $D_1(x)$ denotes the total transition rate from state x, which is given by

$$\begin{aligned} D_1(x) ={\left\{ \begin{array}{ll} x_1\mu _1+x_2\mu _2+ \lambda _1+\lambda _2,\\ \quad \quad \quad \quad \quad \text {if } x_3< K,\, x_1+x_2 = N,\\ x_1\mu _1+x_2\mu _2+ \lambda _1+\lambda _2 +x_3 \sigma ,\\ \quad \quad \quad \quad \quad \text {if } x_3< K, \, x_1+x_2< N,\\ x_1\mu _1+x_2\mu _2+\lambda _1,\\ \quad \quad \quad \quad \quad \text {if } x_3 = K, \, x_1+x_2 = N, \\ x_1\mu _1+x_2\mu _2+\lambda _1+x_3 \sigma ,\\ \quad \quad \quad \quad \quad \text {if } x_3 = K,\, x_1+x_2 < N, \\ \end{array}\right. } \end{aligned}$$

(17)

and $S_{x_3}^{*} = S_{x_3}\setminus \{(N,0,x_3)\}$ denotes the set of all states within level $x_3$ except the state where $x_1=N$. Note that since in the latter state all N channels are occupied by PUs, there are no transmitting SUs to interrupt and a new PU is always blocked.

Similarly, the SU discard probability $\beta$, i.e., the probability that a transmitting SU is interrupted and discarded upon arrival of a PU because of a full sensing room, is computed as

$$\begin{aligned} \beta = \sum \limits _{x\in S_{K}^{*}} \pi _x\frac{ \lambda _1 x_2/(N-x_1)}{D_2(x)} \,, \end{aligned}$$

(18)

where

$$\begin{aligned} D_2(x) ={\left\{ \begin{array}{ll} x_1\mu _1+x_2\mu _2+ \lambda _1,\\ \quad \quad \quad \quad \quad \text {if }x_1+x_2 = N,\\ x_1\mu _1+x_2\mu _2+ \lambda _1+x_3\sigma ,\\ \quad \quad \quad \quad \quad \text {if } x_1+x_2 < N.\\ \end{array}\right. } \end{aligned}$$

(19)

3 Tagged secondary user model

3.1 Model description

In order to further study the system, we use the tagged user approach [25, 26], where a typical user is analyzed while passing through a queueing system. This approach allows us to consider various performance measures pertaining to the expected life time of a single user. To wit, we construct a CTMC that tracks an arbitrary SU throughout its lifetime. As this SU will eventually leave the system, this will necessarily be an absorbing Markov chain. The absorbing state of the Markov chain, denoted by state o, models the exit of the tagged SU, and all the other states are transient. In terms of the transient states, we need to keep track of the number of PUs, transmitting SUs and sensing SUs as before [denoted as $(x_1,x_2,x_3)$], but we also need to keep track of whether the tagged SU is transmitting or sensing. To this end, we introduce a new state variable $x_4$ that takes the values 0 or 1, indicating that the tagged SU is sensing or transmitting respectively.

We now construct the infinitesimal generator $Q_o$ of the absorbing Markov chain, which is represented as follows:

$$\begin{aligned} Q_o = \begin{pmatrix} Q^* &{} q^* \\ \mathbf {0}&{} 0 \end{pmatrix}, \end{aligned}$$

(20)

where $Q^*$ is the infinitesimal subgenerator corresponding to the transient states, $q^*$ is a column vector with rates of transition from transient states to the absorbing state and 0 is a row vector of zeros.

The transition rates $q_{x,y}$ from one transient state x to another transient state y ($x\ne y$) are then given by

$$\begin{aligned} q_{x,y} = {\left\{ \begin{array}{ll} \lambda _1 \frac{N-x_1-x_2}{N-x_1},\quad \text {if } y=(x_1+1, x_2,x_3, x_4),\\ \quad \quad \quad x_1< \ N,\\ \lambda _1 \frac{x_2-1}{N-x_1},\\ \quad \quad \quad \text {if } y=(x_1+1,x_2-1,x_3+1,x_4),\\ \quad \quad \quad x_3< K,\, x_4=1,\, x_1< N,\\ \lambda _1 \frac{x_2-1}{N-x_1},\quad \text {if } y=(x_1+1,x_2-1,x_3,x_4),\\ \quad \quad \quad x_3 = K,\, x_4=1,\, x_1< N,\\ \lambda _1 \frac{x_2}{N-x_1},\\ \quad \quad \quad \text {if }y=(x_1+1, x_2-1, x_3+1,x_4),\\ \quad \quad \quad x_3< K,\,x_4=0,\,x_1< N,\\ \lambda _1 \frac{x_2}{N-x_1},\quad \text {if }y=(x_1+1,x_2-1,x_3,x_4),\\ \quad \quad \quad x_3 = K,\, x_4=0,\, x_1< N,\\ \frac{\lambda _1}{N-x_1},\\ \quad \quad \quad \text {if } y=(x_1+1,x_2-1,x_3+1,x_4-1),\\ \quad \quad \quad x_1< N,\, x_4 =1,\, x_3< K,\\ \lambda _2,\quad \text {if } y=(x_1, x_2,x_3+1,x_4),\,x_3< \ K,\\ x_1\mu _1,\quad \text {if } y=(x_1-1, x_2,x_3,x_4),\\ (x_2-1)\mu _2,\quad \text {if } y=(x_1, x_2-1,x_3,x_4),\\ \quad \quad \quad x_2> 0,\,x_4=1,\\ x_2\mu _2,\quad \text {if } y=(x_1, x_2-1,x_3,x_4),\,x_4=0,\\ x_3\sigma ,\quad \text {if } y=(x_1,x_2+1,x_3-1,x_4),\\ \quad \quad \quad x_1+x_2<N,\, x_4=1,\\ (x_3-1)\sigma ,\quad \text {if }y=(x_1,x_2+1,x_3-1,x_4),\\ \quad \quad \quad x_1+x_2<N,\, x_4=0,\, x_3> 0,\\ \sigma ,\quad \text {if } y=(x_1,x_2+1,x_3-1,x_4+1),\\ \quad \quad \quad x_1+x_2 <N,\,x_4=0,\, x_3 >0,\\ 0,\quad \text {otherwise}. \end{array}\right. } \end{aligned}$$

(21)

This equation is used to construct the infinitesimal subgenerator $Q^*$ where the transitions to the absorbing state o are left out.

The latter transitions correspond to transmission completion of the tagged SU and the tagged SU getting interrupted and discarded from the system because of the arrival of a PU and the lack of sensing room. Therefore, the transition rate from a transient state x to the absorbing state o is given by

$$\begin{aligned} q_{x,o} = {\left\{ \begin{array}{ll} \mu _2, \quad \text {if } x_2 \ge 1,\, x_3 < K,\,x_4 =1,\\ \mu _2+ \frac{\lambda _1}{N-x_1}, \quad \text {if } x_2 \ge 1,\, x_3 = K,\, x_4=1,\\ 0, \quad \text {otherwise}. \end{array}\right. } \end{aligned}$$

(22)

The final ingredient of the tagged user approach is the initial distribution $\pi ^*$ under which the tagged SU enters the system and the absorbing Markov chain is started. Due to the PASTA property [27], we have that this distribution is essentially the same as the steady-state distribution of the model from the previous section, taking into account that (1) the tagged user starts in sensing mode $x_4=0$; (2) we must count the tagged user as well, hence we should increase $x_3$ by one. The vector $\pi ^*$ is obtained by first computing $\pi$ while leaving room for one sensing user in the system. Then $\pi$ is mapped into $\pi ^*$, where the steady-state probabilities corresponding to the tagged SU being in the transmitting state equal zero. Finally, $\pi ^*$ is shifted one level down.

3.2 SU performance measures

The fundamental matrix (see e.g., Chap. 3 of Kemeny and Snell’s classical book [28]) $F=(-Q^*)^{-1}$ of the absorbing Markov chain is the central object from which many performance measures of interest can be obtained. Recall that the element $F_{xy}$ of the fundamental matrix F denotes the average time before absorption that the CTMC spends in transient state y provided that the Markov chain starts from transient state x. Thus, the mean time that the tagged SU spends in the system, i.e., the mean SU delay, is given by the matrix expression:

$$\begin{aligned} E\left[ D_{\text {su}}\right] = \pi ^* F \mathbf{1}, \end{aligned}$$

(23)

where $\mathbf 1$ is a column vector of ones. Note that by Little’s law, $E\left[ D_{\text {su}}\right]$ could also be computed from the system model in Sect. 2 [Eq. (15)], but if nothing else this can serve as a point of reference.

Likewise, the variance of the SU delay is given by

$$\begin{aligned} \mathrm {var}\left[ D_{\text {su}}\right] = 2 \pi ^* F^2 \mathbf{1} - E\left[ D_{\text {su}}\right] ^2. \end{aligned}$$

(24)

Another performance measure of interest is the mean number of interruptions that the tagged SU experiences. For this we need to find an expression for the mean number of times a particular transition from state x to state y is performed. Note that if the random variable $T_x$ denotes the time spent in state x before absorption, the number of transitions from x to y is Poisson distributed with random parameter $q_{x,y} T_x$. The mean number of transitions from x to y is thus $q_{x,y} E\left[ T_x\right] = q_{x,y} [\pi ^* F]_x$. In order to get the mean number of interruptions, we must sum this expression over all transitions that cause the SU to be sent back to sensing mode. If we call this set of transitions $\mathcal{I}$, the mean number of interruptions a SU experiences is given by

$$\begin{aligned} E\left[ N_{\text {int}}\right] = \sum _{(x,y)\in \mathcal{I}} q_{x,y} [\pi ^* F]_x. \end{aligned}$$

(25)

It is clear (as state variables only increase or decrease by one) that this new CTMC also has the block-tridiagonal QBD structure which aids the efficient computation of performance measures (as detailed in the next section). Also, for the various performance measures we never need to compute the entire matrix F, but rather we can suffice solving systems of equations of the form $v Q^* =\nu$, for some vector $\nu$.

4 Computation methodology

Here we show how to solve the equations $\pi Q =0$ and $v Q^* =\nu$ for CTMCs with QBD structure. We solve the first equation for the system model and the second for the tagged secondary user model. Note that the methods described in this section are largely existing techniques (this holds especially true for the first case), which we nevertheless include so as to keep the paper self-contained. Also, in this way we can more carefully describe the more rarely-encountered second case.

The algorithm is essentially a block-structured lower upper (LU) decomposition as described in the classic [29], while the algorithm to compute the equilibrium probabilities (essentially the first case) was detailed in [30, 31].

4.1 Case $\pi Q =0$

To obtain the stationary probability vector $\pi$ for the system model, we employ the Gaussian elimination technique and the concept of censored Markov chains applied to a block-structured tridiagonal QBD using a similar approach as in [32]. To illustrate the major steps of the technique, let a CTMC X(t) have the following generator matrix:

$$\begin{aligned} Q = \begin{bmatrix} L_0&F_0 \\ B_1&L_1&F_1 \\&B_2&L_2&F_2 \\&\ddots&\ddots&\ddots \\&&B_{n-1}&L_{n-1}&F_{n-1} \\&&B_n&L_n \end{bmatrix}. \end{aligned}$$

(26)

Let $L^u_1 = L_1 - B_1 L_0\in v F_0$ be the Schur complement of $L_0$ in Q. Let $Q^{i\rightarrow n}$ denote the generator matrix of the Markov chain censored to the levels i to n, and let $\pi _{i\rightarrow n}$ be the corresponding (partial) distribution. We apply Schur complementation level by level: first eliminating level 0, then level 1, etc. For example, eliminating the level 0 results in

$$\begin{aligned} Q^{1\rightarrow n} = \begin{bmatrix} L^u_1&F_1 \\ B_2&L_2&F_2 \\&\ddots&\ddots&\ddots \\&B_{n-1}&L_{n-1}&F_{n-1} \\&&B_n&L_n \end{bmatrix}. \end{aligned}$$

(27)

We keep folding up the state space in this manner:

$$\begin{aligned} Q^{i\rightarrow n} = \begin{bmatrix} L^u_i&F_i \\ B_{i+1}&L_{i+1}&F_{i+1} \\&\ddots&\ddots&\ddots \\&B_{n-1}&L_{n-1}&F_{n-1} \\&&B_n&L_n \end{bmatrix}, \end{aligned}$$

(28)

where $L^u_i$ is recursively given as

$$\begin{aligned} L^u_i = L_i - B_i {L^u_{i-1}}^{-1} F_{i-1}\,. \end{aligned}$$

(29)

We end up with $Q^{n\rightarrow n} = L^u_n$. We then find the stationary solution by proceeding in a backwards fashion. We have that $\pi _n L^u_n = 0$, and recursively from the first block row of equation $\pi _{i\rightarrow n} Q^{i\rightarrow n} = 0$,

$$\begin{aligned} \pi _i L^u_i + \pi _{i+1} B_{i+1} = 0. \end{aligned}$$

(30)

Finally, we normalize the obtained stationary probability vectors $\pi _i$ corresponding to level i using $\sum _{i=0}^n \pi _i$ 1. This leads to the steady-state vector $\pi$:

$$\begin{aligned} \pi = \frac{1}{\sum _{i=0}^n \pi _i \mathbf 1} \begin{bmatrix} \pi _0&\pi _1&\ldots&\pi _n\end{bmatrix}. \end{aligned}$$

(31)

4.2 Case $v Q^* =\nu$

We solve this equation for v in the context of the tagged SU model to obtain the variance of the SU delay and the number of interruptions of a SU. Here $Q^*$ is the infinitesimal subgenerator defined in Sect. 3. We use the same solution technique described above with the following modifications. Along with computing $L^u_i$, we compute a modified steady-state probability vector as $\nu ^{u}_i= \nu _i - \nu ^{u}_{i-1} {L^u_{i-1}}^{-1} F_{i-1}$, where $\nu ^{u}_0 = \nu _0$. Then, for level n, we solve the following equation for $v_n$: $v_n L^u_n = \nu ^u_n$. Finally, we compute recursively the following equation for $v_i$:

$$\begin{aligned} v_i L^u_i + v_{i+1} B_{i+1} = \nu ^{u}_i. \end{aligned}$$

(32)

5 Numerical results and discussion

In this section, we present some numerical examples in order to investigate the SU performance. We consider a cognitive radio system with $N = 20$ channels. The average transmission time for both PUs and SUs equals $1/\mu _1=1/\mu _2=10$ ms. The offered PU load $\rho _{\text {pu}}$ and the offered SU load $\rho _{\text {su}}$ are defined as $\lambda _1/(N\mu _1)$ and $\lambda _2/(N\mu _2)$ respectively. We consider the case where $\rho _{\text {pu}}=0.3$, as CRNs are expected to operate under light PU load. Of particular interest is the effect of the maximum number of sensing SUs K and the sensing rate $\sigma$ of SUs on the performance measures derived above.

Fig. 1

SU blocking probability $\gamma$ versus $\sigma$ $(\mathrm{s}^{-1})$, for $\rho _{\text {pu}} = 0.3$, $\rho _{\text {su}} = 0.5$, $N=20$, $1/\mu _1=1/\mu _2 =10\$ms and various values of K

Figure 1 shows the SU blocking probability $\gamma$ as a function of the sensing rate $\sigma$ $(\text {in }\mathrm{s}^{-1})$, for $\rho _{\text {su}}=0.5$ and various values of K. We observe from this figure that the blocking probability decreases as K increases, which is intuitively clear since $\rho _{\text {pu}}$ and $\rho _{\text {su}}$ are fixed and for increasing K more SUs are allowed to enter the sensing state and hence less SUs are blocked. The probability $\gamma$ also decreases as the sensing rate $\sigma$ increases. For high K eventually almost no SUs are blocked, as expected.

Fig. 2

SU interruption probability $\alpha$ versus $\sigma$ $(\mathrm{s}^{-1})$, for $\rho _{\text {pu}} = 0.3$, $\rho _{\text {su}} = 0.5$, $N=20$, $1/\mu _1=1/\mu _2 =10\$ms and various values of K

In Fig. 2, the SU interruption probability $\alpha$ is plotted as a function of $\sigma$ $(\text {in }\mathrm{s}^{-1})$, for $\rho _{\text {su}}=0.5$ and various values of K. For an increasing maximum number of sensing users K, we observe an increase of the SU interruption probability. This is because an increase of K will increase the number of SUs that can access the system, and hence (for a given $\sigma$) also the number of transmitting SUs increases, so more SUs can get interrupted by a PU. For higher $\sigma$, sensing SUs enter the transmitting state at a higher rate and get interrupted even more likely. Also we notice that the interruption probability converges to the same value for different $\sigma$ as K increases.

Fig. 3

SU discard probability $\beta$ versus $\sigma$ $(\mathrm{s}^{-1})$, for $\rho _{\text {pu}} = 0.3$, $\rho _{\text {su}} = 0.5$, $N=20$, $1/\mu _1=1/\mu _2 =10\$ms and various values of K

In Fig. 3, the SU discard probability $\beta$ is shown as a function of the sensing rate $\sigma$ $(\text {in }\mathrm{s}^{-1})$, again for $\rho _{\text {su}}=0.5$ and various values of K. From this figure it can be seen that especially for low values of $\sigma$ the SU discard probability first increases and then decreases with increasing K. This observation can be explained intuitively in a similar way as before. For low values of K, an increase of K means that more SUs can get interrupted by a PU, while the probability that an interrupted SU finds a full sensing room still remains high. For high K, however, it is more likely that an interrupted SU will be able to sense again instead of being discarded and therefore $\beta$ decreases with increasing K until eventually no interrupted SUs are discarded. Similarly, it is also clear that for a given K the probability $\beta$ increases and then decreases as $\sigma$ increases. For higher values of K, this behavior is repeated over a smaller range of $\sigma$ and clearly the maximum discard probability is not affected. Comparing Figs. 2 and 3 we see that there is convergence of $\alpha$ upwards values of K and $\sigma$ for which $\beta$ approaches zero.

Fig. 4

Mean SU delay $E\left[ D_{\text {su}}\right]$ (s) versus K, for $\rho _{\text {pu}} = 0.3$, $\rho _{\text {su}} = 0.5$, $N=20$, $1/\mu _1=1/\mu _2 =10\$ms and various values of $t=\sigma /\mu _2$

Figure 4 shows the mean SU delay $E\left[ D_{\text {su}}\right]$ (in s) as a function of the sensing room size K, for $\rho _{\text {su}}=0.5$ and various values of the sensing rate normalized to the SU average transmission rate, i.e., various values of $t=\sigma /\mu _2$. For increasing K, the mean SU delay linearly increases until it reaches some convergence point. Afterwards, a further increase of the maximum number of sensing SUs will not affect the mean SU delay. This convergence is fully in accordance with the observations in Figs. 2 and 3. Also we notice the strong effect of $\sigma$ on the mean SU delay. Increasing the mean sensing time $1/\sigma$ over the given range, we see that the mean delay doubles and sometimes triples.

Fig. 5

Variance of SU delay $\mathrm {var}\left[ D_{\text {su}}\right]$ (s$^2$) versus K, for $\rho _{\text {pu}} = 0.3$, $\rho _{\text {su}} = 0.5$, $N=20$, $1/\mu _1=1/\mu _2 =10\$ms and various values of $t=\sigma /\mu _2$

The corresponding curves for the variance $\mathrm {var}\left[ D_{\text {su}}\right]$ (in s$^2$) of the SU delay are presented in Fig. 5. As expected for M/M/c like queueing systems, the variance has a similar behavior as the mean SU delay.

Fig. 6

SU blocking probability $\gamma$ versus K, for $\rho _{\text {pu}} = 0.3$, $N=20$, $1/\sigma =100$ ms, $1/\mu _1=1/\mu _2 =10\$ms and various values of $\lambda _2$

Fig. 7

SU interruption probability $\alpha$ versus K, for $\rho _{\text {pu}} = 0.3$, $N=20$, $1/\sigma =100 \$ms, $1/\mu _1=1/\mu _2 =10\$ms and various values of $\lambda _2$

Fig. 8

SU discard probability $\beta$ versus K, for $\rho _{\text {pu}} = 0.3$, $N=20$, $1/\sigma =100 \$ms, $1/\mu _1=1/\mu _2 =10\$ms and various values of $\lambda _2$

In Figs. 6, 7 and 8, the SU blocking probability $\gamma$, the SU interruption probability $\alpha$ and the SU discard probability $\beta$, respectively, are plotted versus the maximum number of sensing SUs K, for $1/\sigma =100 \$ms and various values of the SU arrival rate $\lambda _2$. We again see that for increasing values of K (and given values of $\lambda _2$ and $\sigma$) the probability $\gamma$ decreases, the probability $\alpha$ increases and the probability $\beta$ first increases and then decreases, as explained before. Also, we see that the probabilities $\gamma$, $\alpha$ and $\beta$ all increase as $\lambda _2$ increases.

Fig. 9

Mean SU delay $E\left[ D_{\text {su}}\right]$ (s) versus $\lambda _2$ $(\mathrm{s}^{-1})$, for $K = 200$, $\rho _{\text {pu}} = 0.3$, $N=20$, $1/\mu _1=10\$ms and various values of $\mu _2$ and $\sigma$: ($1/\mu _2 =1/\sigma =100\$ms), ($1/\mu _2=50\$ms, $1/\sigma =150\$ms)

Next, we consider a cognitive radio system with a fixed maximum number of sensing SUs $K = 200$ and different values of the average SU transmission time and the average SU sensing time such that the sum of both times is $200\$ms. As before, there are $N=20$ channels, $\rho _{\text {pu}} = 0.3$ and $1/\mu _1=10\$ms. Figure 9 shows the mean SU delay (in s) as a function of the SU arrival rate $\lambda _2$ $(\text {in }\mathrm{s}^{-1})$. This plot can be divided into two parts. In the first part, for an increasing SU arrival rate $\lambda _2$ the mean SU delay increases as the number of SUs (sensing and transmitting) increases. In this part, no SUs are discarded from the system as the sensing room is not full yet. In the second part, the sensing room is almost full and an increase of $\lambda _2$ increases the probability that a SU is discarded from the system before successful completion and consequently decreases the time the SU spends in the system.

Fig. 10

Mean number of SU interruptions $E\left[ N_{\text {int}}\right]$ versus $\lambda _2$ $(\mathrm{s}^{-1})$, for $K = 200$, $\rho _{\text {pu}} = 0.3$, $N=20$, $1/\mu _1=10\$ms and various values of $\mu _2$ and $\sigma$: ($1/\mu _2 =1/\sigma =100\$ms), ($1/\mu _2=50\$ms, $1/\sigma =150\$ms)

Finally, in Fig. 10, the mean number of interruptions $E\left[ N_{\text {int}}\right]$ of a typical (tagged) SU before exiting the system is plotted versus $\lambda _2$ $(\text {in }\mathrm{s}^{-1})$, for the same set of parameters as in Fig. 9. Likewise, this plot can be divided into two parts. In the first part, the mean number of SU interruptions is almost constant as it does not depend on the SU arrival rate when no SUs are discarded. In the second part, for higher $\lambda _2$, the mean number of SU interruptions decreases as more SUs get discarded from the system before completion. The effect of the sensing time on the mean number of SU interruptions has been investigated. The results indicate that the sensing time has a small effect on the mean number of SU interruptions. When increasing the mean sensing time $1/\sigma$ in the range between $5\$ and $100\$ms, for a SU transmission time $1/\mu _2=100\$ms, we observe a decrease of the mean number of SU interruptions of less than 10%. This decrease is due to the higher probability that a SU is discarded from the system. For $1/\sigma > 100\$ms, the mean number of SU interruptions decreases further but preserves the same behavior. Also, an increase of K between 20 and 500 seems not to affect the maximum value of the mean number of SU interruptions and again this measure keeps the same behavior.

6 Conclusions

In this paper, we investigated the impact of different parameters on SU performance measures in a CRN using finite quasi-birth–death CTMCs. It has been shown that an increase of the sensing rate $\sigma$ increases the SU interruption probability, but considerably reduces the mean and variance of the SU delay. Also, the sensing time has a small effect on the mean number of SU interruptions. Future work will focus on further refining the presented models, taking into account e.g., the dependence of the sensing time on the number of idle channels.