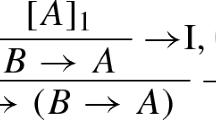Proof-theoretic semantics as a resource for expressing semantic variability

Abstract

The paper highlights proof-theoretic semantics as providing natural resources for capturing semantic variation in natural language. The semantic variations include:

• Distinction between extensional predication and attribution to intensional transitive verbs a non-specific object.

• Omission of a verbal argument in a transitive verb.

• Obtaining sameness of meaning of sentences with transitive verbs with omitted object and existentially quantified object.

• Blocking unwarranted entailments in adjective–noun combinations.

• Capturing quantifier scope ambiguity.

• Obtaining context dependent quantifier domain restriction.

The proof-theoretic resources employed to capture the above semantic variations include:

• The use of different kinds of formal parameters and different ways of binding them to predicates.

• Omission of a premise from a proof-rule.

• Basing meanings (and sameness thereof) on (canonical) derivations in meaning-conferring proof-systems.

• Appealing to substructurality of I/E-rules.

• Controlling the order of rule applications in derivations.

• Controlling the open formulas participating in a context within a sequent.

1 Introduction

The purpose of this paper is to focus on proof-theoretic semantics (PTS), Francez (2015) and Schroeder-Heister (2018), as a resource for the expression and capture of semantic variability in the formal semantics of natural language. PTS was not viewed before from this point of view, and this is the main innovation of the paper, drawing on existing results about the application of PTS to natural language.

I will only consider here variation in sentential meanings, although PTS has a lot to say also on sub-sentential meanings; see Francez (2015) for details.

PTS is an alternative to the more traditional Model-Theoretic Semantics (MTS), as applicable to natural language semantics, which has completely different resources for capturing semantic variability, mainly using the variability of the entities populating models. PTS is a well-established theory of meaning for Logic (e.g., Prawitz (2006)) and has been extended from logic to a theory of meaning for natural language (NL) (to fragments of English). For the benefit of readers unfamiliar with PTS, I include a brief delineation of it in Sect. 2.

In logic, there are well-known examples of semantic variability obtained by proof-theoretic means. Here are some notable examples.

• When logics are defined by means of derivability in sequent calculi (SC), see Gentzen (1935), the connectives receive their intuitionistic meaning (differing from their classical meaning) by imposing a restriction on the size of the succedent of a sequent, ($\le 1$).

• A similar transition from classical to intuitionistic meanings of the connectives is obtained, when using natural-deduction (ND) proof-systems, just by banning the double-negation elimination rule (or some other rule like Reductio-Ad-Absurdum).

• By imposing restrictions on the contexts in SC rules (additive vs. multiplicative), connectives receive substructural meanings.

• By modifying the introduction-rule for the conditional so as to keep track of the use of an assumption in deriving the consequent, thereby banning vacuous discharge, the conditional obtains its relevant meaning (Anderson & Belnap, 1975).

In this paper, I present analogous variations in meaning in natural language. Here are the main variations of meaning obtained by using proof-theoretic means.

• Distinction between extensional predication from attribution of a non-specific argument as an object of an intensional transitive verb. The following is a pair of sentences exhibiting this difference.

  $$\begin{aligned} {\mathsf {A\ man\ kissed\ a\ woman}} \end{aligned}$$

  (1)

  (a specific woman).

  $$\begin{aligned} {\mathsf {\ hospital\ seeks\ a\ nurse}} \end{aligned}$$

  (2)

  (any nurse).

• Omission of the object as a verbal argument of a transitive verb.

  $$\begin{aligned} {\mathsf {Mary\ eats\ an\ apple}} \end{aligned}$$

  (3)
  $$\begin{aligned} {\mathsf {Mary\ eats}} \end{aligned}$$

  (4)

  (eats something).

• Obtaining sameness of meaning of (4) and (5)

  $$\begin{aligned} {\mathsf {Mary\ eats\ something}} \end{aligned}$$

  (5)

• Blocking unwarranted entailments in adjective–noun combinations:

  

  (6)

  but the following inference is incorrect:

  

  (7)

• Capturing quantifier scope ambiguity. A sentence like

  $$\begin{aligned} {\mathsf {Every\ girl\ loves\ some\ boy}}, \end{aligned}$$

  (8)

  in which both the subject and the object contain a determiner, is taken to have two readings, differing in the scopal relationship between its two quantifiers.

• Obtaining context dependent quantifier domain restriction: the universal quantifier every in the sentence (from Stanley and Szabȯ (2000).

  $$\begin{aligned} {\mathsf {every\ bottle\ is\ empty}} \end{aligned}$$

  (9)

  can be made to vary differently depending on a context. For example, every bottle in some room, after a party, is empty.

The actual means employed to obtained the above listed variations in meaning are described below, after PTS and its nomenclature are delineated in Sect. 2.

2 Overview of PTS

In a nutshell, the PTS programme as theory of meaning can be described¹ as follows.

2.1 Sentential meanings

2.1.1 The basic idea

The core idea for defining sentential proof-theoretic meanings is the following.

Replace the received approach of taking sentential meanings as truth-conditions (in arbitrary models of an appropriate format) by taking them as canonical derivability conditions (from suitable assumptions) within a meaning-conferring natural-deduction proof-system in which the derivability conditions are formulated.

In a sense, the proof system should reflect the “use” of the sentences (their inferential roles) in the considered natural language fragments, and should allow recovering pre-theoretic properties of the meanings of sentences such as entailment and consequence drawing (inference).

2.2 Meaning-conferring proof-systems

According to the PTS programme, meaning is determined by a meaning-conferring, most often a natural-deduction, proof-system, say $\mathcal{N}$. Such a system has two kinds of inference rules:

• Introduction rules (I -rules): Those rules have as their conclusion an expression (formula, sentence) governed by an operator said to be introduced by (an application of) the rule. Such rules establish the way the expression governed by the introduced operator can be deduced from the premises of the rule. Such an inference is considered the most direct way to infer the conclusion.

• Elimination rules (E -rules): Those rules have as their major premise an expression (formula, sentence) governed by an operator said to be eliminated by (an application of) the rule. Such rules establish the way a conclusion may be drawn from the expression governed by the eliminated operator. Such an inference is considered the most direct way to infer from the major premise.

Both kind of rules may discharge assumptions when applied, rendering the conclusion independent of some temporarily assumed assumptions.

Example 1

(conjunction) The simplest example of I/E-rules are those introducing and eliminating a conjunction in (propositional) logic, shown below.

(10)

Note that there are two E-rules here. No discharge of assumption is involved in those rules.The I-rule states that a conjunction is inferred from both its conjuncts, while the E-rules state that each of the conjuncts is inferred from a conjunction.

The claim of PTS is, that those rules determine the full meaning of conjunction, independently of the model-theoretic definition using truth-tables (or other models).

Example 2

A simple example involving a discharge of an assumption is the I-rule of the material implication in (propositional) logic.

(11)

The rule ($\supset I$) says that in order to derive a (material) implication $\varphi \supset \psi$, temporarily assume the antecedent $\varphi$, putting around it square brackets to indicate discharge, indexed with i for connecting with a discharging application of the rule indexed by the same index, and derive the consequent $\psi$, potentially using the assumption of the antecedent. Once the consequent has been derived, the assumption of the antecedent is discharged. The E-rule is the familiar modus-ponens.

Once again, according to PTS, those rules tell “the whole story” needed for the meaning of the material implication.

Officially,² the I/E-rules are formulated using sequents of the form $\Gamma : \psi$, where the antecedent $\Gamma$ is a finite collection (most often, a set) of object-language formulas, called a context, the undischarged assumptions, and succedent $\psi$ is also a formula. In this presentation, the dependence of a conclusion on assumptions is made explicit. However, to avoid notational cluttering, often (e.g., in (10) and (11)) the assumptions $\Gamma$ are left implicit. A derivation $\mathcal{D}$ (of $\psi$ from $\Gamma$) is defined recursively by iterating rule applications starting from assumptions $\Gamma$ and reaching a conclusion $\psi$. The derivability (i.e., existence of a derivation) of $\varphi$ from $\Gamma$ in $\mathcal{N}$ is denoted $\vdash _{\mathcal{N}} \Gamma : \varphi$ (where the subscript on ‘$\vdash$’ is often omitted). A variable is called fresh if it does not occur in any assumption on which a conclusion of a rule depends.

I want to stress that according to the PTS programme, the rules proposed are meaning-conferring. That is, they are a definitional tool. They should not be judged against any external yard-stick, in particular not one used in MTS. Completeness proofs as traditionally sought in logic are not a goal here, in spite of being an interesting topic on its own. The main use of model-theory in this connection is for establishing non-derivability by employing counter-models. The rules need, though, meet some proof-theoretic criteria to qualify as meaning-conferring. The two main such conditions are harmony and stability (Dummett, 1993), establishing a balance between I-rules and E-rules, none over-powering the other.

2.3 Canonical derivation and sentential meanings

Definition 1

(Canonical derivation from open assumptions) A $\mathcal{N}$-derivation $\mathcal{D}$ for $\Gamma : \psi$ is canonical iff it satisfies one of the following two conditions.

• The last rule applied in $\mathcal{D}$ is an I-rule (for the main operator of $\psi$).

• The last rule applied in $\mathcal{D}$ is an assumption-discharging E-rule, the major premise of which is some $\varphi$ in $\Gamma$, and its encompassed sub-derivations $\mathcal{D}_{1},\cdots ,\mathcal{D}_{n}$ are all canonical derivations of $\psi$.

Denote by $\vdash _{\mathcal{N}}^{c}$ canonical derivability in $\mathcal{N}$, and by $\mathbf{[}\! [\varphi \mathbf{] \! ]}^{c}_{\Gamma }$ the (possibly empty) collection of canonical derivation of $\varphi$ from a collection of assumptions $\Gamma$.

For $\Gamma$ empty, the definition reduces to the standard definition of a canonical proof. Note the recursion involved in this definition. The important observation regarding this recursion is that it always terminates via the first clause, namely by an application of an I-rule, referred to as an essential application of the rule. In particular, the attribute of canonical proofs that there are none³ for an atomic sentence is preserved by the definition of canonical derivations from open assumptions too. The above mentioned observation justifies the definition of canonicity for derivations from open assumptions $\Gamma$ by preserving the directness of the inference, but the conclusion $\psi$, inferred via the essential application of the I-rule may need to be propagated through application of E-rules to open assumptions in $\Gamma$. This also justifies viewing $\Gamma$ as grounds for assertion of $\psi$.

Example 3

(propagation) As an example of the recursion in the definition of canonical derivations from assumptions and the propagation it involves, consider the following derivation, establishing $\vdash \varphi \vee \psi : \psi \vee \varphi$, the commutativity of disjunction.

The I/E-rules for (classical) disjunction are the following.

The I-rules state that a disjunction is inferable from each disjunct. The E-rule embodies what is known as proof by cases, drawing a conclusion from a disjunction if the conclusion follows from both disjuncts, serving as discharged assumptions.

The canonical derivation of the commutativity of disjunction is the following.

(12)

Both of the sub-derivations

are canonical by the first clause of the definition of canonicity, ending with an application of an I-rule (for disjunction). Those are essential applications of ($\vee I$), deriving $\psi \vee \varphi$. The latter is propagated to the top-level via an application of ($\vee E$) in accordance to the second clause of the definition of canonicity.

Example 4

(canonicity) To realise the role of canonicity in the forthcoming definition of sentential proof-theoretic meanings, consider the following example derivation in, say, classical propositional logic.

(13)

This is a derivation of a conjunction—but not a canonical one, as it does not end with an application of $(\wedge I)$, nor does it have an essential application of it. Thus, the conjunction here was not derived according to its meaning! As far as this derivation is concerned, conjunction could mean anything, e.g., disjunction.

On the other hand, the following example derivation is according to the conjunction’s meaning, being canonical.

(14)

Here, the conjunction is derived in accordance with its meaning, ending with an application of its I-rule.

Next, I turn to defining sentential meanings.

Ever since Gentzen’s casual remark in Gentzen (1935), p. 80

... The introductions represent, as it were, the ‘definitions’ of the symbol concerned, and the eliminations are no more, in the final analysis, than the consequences of these definitions. ...

it is the I-rules that are taken to determine the proof-theoretic meanings, an approach adhered to by mainstream PTS, e.g. Dummett (for example, Dummett (1993)), Prawitz (for example, Prawitz (2006)), Tennant (for example, Tennant (2007)) and many others. For other possibilities, see Francez (2014).

Definition 2

(Sentential meanings) For a compound $\varphi \in L$, its meaning $\mathbf{[}\! [\varphi \mathbf{] \! ]}$ is given as follows.

$$\begin{aligned} \mathbf{[}\! [\varphi \mathbf{] \! ]}= \lambda \Gamma . \mathbf{[}\! [\varphi \mathbf{] \! ]}_{\Gamma }^{c} \end{aligned}$$

(15)

That is, a function mapping collections of sentences $\Gamma$ to the (possibly empty) collection of canonical derivations of $\varphi$ from $\Gamma$.

A useful by-product of this notion of meaning, underlying a natural proof-theoretic consequence definition, is that of grounds for assertion.

Definition 3

(Grounds for assertion)

$$\begin{aligned} GA\mathbf{[}\! [\varphi \mathbf{] \! ]}= \{ \Gamma \ |\ \Gamma \vdash ^{c}_{\mathcal{N}} \varphi \} \end{aligned}$$

(16)

Thus, any $\Gamma$ that canonically derives $\varphi$ serves as grounds for assertion of $\varphi$.

Note that both sentential meanings and grounds for assertion are proof-theoretic (syntactic) objects, not related at all to models and denotations therein. So, those are notions more easily amenable to computational treatment.

For the methodological role of grounds for assertion in the theory of meaning adhered to by PTS, see Dummett (1993). There is another notion of grounds for assertion, though in the same spirit as the current one, but viewed epistemically as a cognitive entity, possibly possessed by an agent, as considered by Prawitz (2012, 2018).

Definition 4

(Proof-theoretic consequences) Let $\Gamma ,\psi \in L$.

$\psi$ is a proof-theoretic consequence of $\Gamma$ ($\Gamma \Vdash _{c} \psi$) iff $GA \mathbf{[}\! [\Gamma \mathbf{] \! ]}\subseteq GA \mathbf{[}\! [\psi \mathbf{] \! ]}$.

That is, the grounds for asserting (all of) $\Gamma$ are already grounds for asserting $\psi$.

Remark 1

Note that the above definitions are brought as background on PTS; they are directly used in what follows. The point here is not to define the PTS of the various constructs and justify it. This was done were the PTS of those constructs was introduced. Rather, the point is to show how this method of defining meaning in NL allows for producing the semantic variability indicated above.

A digression: Inferentialism

A philosophically inclined reader might ask how is PTS, as described above, related to the school in the philosophy of language and logic known as inferentialism (e.g., Brandom (2001); Sellars (1953)). Indeed, the two are related in sharing the same “ideology”, namely the anchoring of meaning in inference rules, the latter originating from “use’ (inferential practices).

However, while inferentialism remains a school in the philosophy of logic and language, PTS goes much further in actually implementing this idea: in devising specific meaning-conferring proof systems with appropriate rules, both for logic and (in my own work) for NL, and investigating the properties of such systems.

This line of development of PTS is in line with Dummett’s “grand programme” for a theory of meaning, starting with logical constant and ultimately encompassing NL too. The reader is referred to Dummett (1993), and in particular to Dummett (1976) (also in Dummett (1993)).

(end of digression)

3 Proof-theoretic semantics and semantic variability

This section surveys some of the applications of PTS as a source of semantic variability in NL. I refer the reader to the original publications of this semantics, and to part II of Francez (2015), for a detailed coverage of the semantic issues involved. Since several of the variations result from sentences built over transitive verbs, the next section presents, as a point of departure, a proof-theoretic semantics for a fragment of English built over such sentences. In the core fragment considered, an I-rule introduces and an E-rule eliminates a determiner-phrase (DP) into (resp. from) the subject or the object positions of a transitive verb.

3.1 PTS for extensional transitive verbs

Extensional transitive verbs (ETVs) occur in sentences like

$$\begin{aligned} \mathsf {Every\ boy\ loves\ some\ girl} \end{aligned}$$

(17)

The pre-theoretical meaning of (17) is that every boy loves (one or more) specific girls, thereby expressing a relation between boys and girls they love. The object some girl is said to have a specific reading.

I start by introducing the meaning-conferring proof-systems, a proof-system with I/E-rules for sentences with transitive rules. As already mentioned, those rules introduce and eliminate determiners (expressing quantifiers) into subjects and objects position of sentences. This semantics was originally presented in Francez and Dyckhoff (2010).

Let the meta-variables R range over extensional verbs. For simplicity, I consider here only two determiners: every and some. See Francez and Ben-Avi (2015) for an extensive coverage of other determiners, including negative ones like no. Let X range over (singular, count) nouns. There are also two kinds of copulas: isa and is being, explained below.

A major ingredient of the proof-system is the use of individual parameters, syntactic objects that can stand in subject and object positions⁴ of transitive verbs. Individual parameters are ranged over by i, j, k. They occur in pseudo-sentences⁵ in the form of $\mathbf{j}\ R\ \mathbf{k}$ and $\mathbf{j}\ \mathsf {isa}\ X$. For example: $\mathbf{j}\ \mathsf {loves}\ \mathbf{k}$, $\mathbf{j}\ \mathsf {loves\ every\ girl}$, $\mathsf {some\ boy\ loves}\ \mathbf{k}$ and $\mathbf{j}\ \mathsf {isa\ girl}$.

Such parameters are a kind of place holders for noun-phrases with determiners that are introduced and eliminated into the positions the parameters are located in.

Pseudo-sentences containing parameters only are ground pseudo-sentences. They play the role of atomic sentences in logic. Their meaning is assumed given from outside⁶ the meaning-conferring system.

As I show below, replacing those parameters by another kind of parameters can serve as resource for capturing variability.

The I/E-rules for the extensional sentences are presented in Fig. 1. In the rules, S ranges over sentences (including pseudo-sentences). $S[\mathbf{j}]$ means S with a distinguished position (here either subject or object positions) filled by j, and $S[\mathsf {every/some}\ X]$ means that j was replaced, in the same distinguished position, by $\mathsf {every/some}\ X$.

Fig. 1

Extensional transitive verbs rules

Remarks about the rules:

e I::

The introduction of $\mathsf {every}\ X$ is similar to the I-rule for universal quantification in 1st-order classical logic. It allows inferring $S[\mathsf {every}\ X]$ from some $\Gamma$ if $S[\mathbf{j}]$ can be inferred from $\Gamma$ and the additional assumption (discharged by the rule upon application) $\mathbf{j}\ \mathsf {isa}\ X$, where the freshness of j (implying j is not mentioned in $\Gamma$) guarantees the arbitrariness of j, thereby assuring that the derivation applies to any X. For example:

e E::

The rule is the usual instantiation rule, allowing to instantiate (in S) $\mathsf {every}\ X$ by any individual parameter (that need not be fresh). For example,

s I::

Again, similarly to the introduction of an existential quantification in 1st-order classical logic, the rule allows inferring $S[(\mathsf {some}\ X)]$ from the proof of $S[\mathbf{j}]$ for a witness j, that has been proved to be an X in the other premise. For example:

s E::

An arbitrary conclusion $S^{\prime }$ can be drawn from $S[(\mathsf {some}\ X)]$ provided it can be drawn from an arbitrary witness for which it is only assumed it is a X.

Example 5

(An exemplary derivation) Below is an example⁷ derivation establishing

$$\begin{aligned} \vdash \mathsf {some}\ U\ \mathsf { isa}\ X,\ \mathsf {every}\ X\ R\ \mathsf {some}\ Y,\ \mathsf {every}\ Y\ \mathsf {isa}\ Z\ : \mathsf {some}\ U\ R\ \mathsf {some}\ Z \end{aligned}$$

To aid the intuition, assume the predicate names abbreviate the following:

• U: Italian

• X: man

• R: loves

• Y: actress

• Z: woman

Thus, the conclusion is some Italian loves some woman.

The derivation is

3.2 Semantic variation: quantifier scope ambiguity

Traditionally, a sentence like

$$\begin{aligned} \mathsf {Every\ girl\ loves\ some\ boy}, \end{aligned}$$

(18)

in which both the subject and the object contain a determiner, is taken to have two readings, differing in the scopal relationship between its two quantifiers. Those reading can be represented by the following 1st-order formulas.

Subject wide-scope (sws):

$$\begin{aligned} \forall x. \mathbf{girl}(x) \rightarrow \exists y. \mathbf{boy}(y)\wedge \mathbf{love}(x,y) \end{aligned}$$

(19)

Subject narrow-scope (sns):

$$\begin{aligned} \exists y. \mathbf{boy}(y) \wedge (\forall x. \mathbf{girl}(x)\rightarrow \mathbf{love}(x,y)) \end{aligned}$$

(20)

For more complicated sentences, for example sentences with relative clauses, more scopal relations among the participating quantifiers are possible.

The question is, how to capture this ambiguity? What generates it?

PTS provides its own explanation and captures this ambiguity in a different way than its traditional captures.

The first step is to complicate a little the I/E-rules, by extending somewhat the proof-language. For any dp-expression D having a quantifier, we extend the previous notation S[D] to $S[(D)_{n}]$, that refers to a sentence S having a designated position filled by D, where n is the scope level (sl) of the quantifier in D. In case D has no quantifier (i.e., it is an individual parameter), $sl=0$. The higher the sl, the higher the scope. For example, $S[(\mathsf {every}\ X)_{1}]$ refers to a sentence S with a designated occurrence of $\mathsf {every}\ X$ of the lowest scope. An example of a higher scope is $S[(\mathsf {some}\ X)_{2}]$, having $\mathsf {some}\ X$ in the higher scope, as in $(\mathsf {every}\ X)_{1}\ \mathsf {loves}\ (\mathsf {some}\ Y)_{2}$, representing the object wide-scope reading of the sentence (8). Thus, we disambiguate ambiguous sentences taking part in derivations. When the sl can be unambiguously determined it is omitted. Finally, I use r(S) to indicate the rank of S, the highest sl on a dp within S.

Now the I/E-rules in Fig. 1 can be reformulated as in Fig. 2 by letting them access the sl, thereby imposing the required scope relationship.

Fig. 2

The scope sensitive extensional I/E-rules

Remarks:

• 1. Both I-rules in Fig. 2 introduce a dp that obtains a higher scope than all the dps already present in $S[\mathbf{j}]$, thereby becoming the highest scoping dp. This is so because the sl it obtained when introduced is higher than the previous rank of $S[\mathbf{j}]$. Thus, the scopal relationships are determined by the order of introduction of the corresponding dps!

• 2. Both E-rules in Fig. 2 eliminate the dp of the highest scope among all the dps present in $S[\mathbf{j}]$.

Example 6

Consider the two derivations below (contexts omitted), capturing the two readings of the sentence (8):

• Subject wide-scope (sws):

  

  (21)

• Subject narrow-scope (sns):

  

  (22)

In (21), the object dp some boy is introduced first, into a ground pseudo-sentence $\mathbf{r}\ \mathsf {loves}\ \mathbf{j}$, obtaining the lower $sl=1$; thereafter, the subject dp is introduced into the pseudo-sentence of rank $r=1$, namely $\mathbf{r}\ \mathsf {loves}\ ({\mathsf {some}\ \mathsf {boy}})_{1}$, thereby obtaining a higher $sl=2$.

On the other hand, in (22) the subject dp every girl is introduced first, into the same ground sentence $\mathbf{r}\ \mathsf {loves}\ \mathbf{j}$, obtaining the lower $sl=1$. Only thereafter is the object dp some boy introduced into the resulting pseudo-sentence of rank $r=1$, namely $(\mathsf {every\ girl})_{1}\ \mathsf {loves}\ \mathbf{j}$, thereby obtaining scope level $s=2$.

According to the definition of meaning in (15), the above two derivations, both canonical, establish that

$$\begin{aligned} \mathbf{[}\! [(\mathsf {every}\ \mathsf {girl})_{2}\ \mathsf {loves}\ (\mathsf {some\ boy})_{1} \mathbf{] \! ]}\ne \mathbf{[}\! [(\mathsf {every\ girl})_{1}\ \mathsf {loves}\ (\mathsf {some\ boy})_{2} \mathbf{] \! ]}\end{aligned}$$

To see that we indeed have a difference in scopal relationship, note that

$$\begin{aligned} \vdash \ (\mathsf {every}\ \mathsf {girl})_{2}\ \mathsf {loves}\ (\mathsf {some\ boy})_{1}, \mathbf{r}\ \mathsf {isa\ girl} : \mathbf{r}\ \mathsf {loves\ some\ boy} \end{aligned}$$

but

$$\begin{aligned} \not \vdash \ (\mathsf {every\ girl})_{1}\ \mathsf {loves}\ (\mathsf {some\ boy})_{2},\mathbf{r}\ \mathsf {isa\ girl} : \mathbf{r}\ \mathsf {loves\ some\ boy} \end{aligned}$$

The elimination rule (E) is applicable in the first case but not in the second; as it can be applied to eliminate the only the dp in the highest scope.Thus, the entailments change, reflecting the scope ambiguity.

This example clearly exemplifies how a semantic fact, the quantifier scope ambiguity, is handled by manipulating order of rule applications—a typical resource of PTS.

3.3 Semantic variation: intensional transitive verbs

3.3.1 Intensional transitive verbs

Intensional transitive verbs (ITVs) occur in⁸ sentences like

$$\begin{aligned} \mathsf {Every\ lawyer\ seeks\ some/a\ secretary} \end{aligned}$$

(23)

The pre-theoretic meaning of (23) is that every lawyer seeks (one or more) unspecific secretaries, thereby expressing a relation between lawyers and some abstract notion, here of a secretary. The object some secretary is said to have an unspecific (or notional) reading.

A semantics for sentences with intensional transitive verbs has to reveal the following three distinguishing characteristics:

• Admittance of non-specific (notional) objects. This difference will be revealed by the corresponding meaning-conferring systems having different I/E-rules.

• Resistance to substitutability of coextensives. This difference can be exemplified by the following two similarly looking arguments,⁹ where (24) is valid while (25) is not.

  

  (24)
  

  (25)

• Suspension of existential commitment. This difference is manifested by (17) presupposing the existence of girls, allowing the passivisation inference

  

  (26)

while

$$\begin{aligned} \mathsf {John\ seeks\ a\ unicorn} \end{aligned}$$

(27)

does not carry a presupposition of the existence of unicorns, invalidating

(28)

Digression: The question of what populates models suitable for specifying adequate truth-conditions for ITVs is quite complicated, and there is no consensus about it within the community; not even regarding the semantic type of the object of the intensional verb, e.g., a quantifier (Zimmermann, 1993), a property (Moltmann, 2013), or a minimal situation (Moltmann, 1997). There is also an indirect interpretation via decomposition¹⁰ of the intensional verb (Quine, 1956; Larson, 2001). Another approach (Forbes, 2000) appeals to Davidsonian event semantics and its thematic roles. A dynamic semantics for ITVs was proposed in Sznajder (2012), where an update via ITVs is proposed.

(end of digression)

3.3.2 PTS for intensional transitive verbs

Let $\hat{R}$ range over transitive verbs lexically specified as admitting intensional reading. The central proof-theoretics tools used for formulating a PTS for ITVs are two:

• 1. Introduce an additional kind of parameters (in addition to individual parameters used for extensional transitive verbs), called notional parameters.

• 2. Introduce an additional copula is being, expressing a different way of binding a predicate to an argument, different than predication (isa).

Notional parameters are ranged over by ${\mu , \nu }$. They occur in pseudo-sentences like $\nu \ \mathsf {is\ being\ a}\ X$ and $\mathbf{j}\ \hat{R}\ \nu$. For example, $\nu \ \mathsf {is\ being\ a\ secretary}$ and $\mathbf{j}\ \mathsf {seeks\ a\ secretary}$.

Recall that pseudo-sentences containing parameters only (now of both kinds), are ground pseudo-sentences. They fill the role of atomic sentences in logic. Their meaning is assumed given from outside the meaning-conferring system.

The distinction between two kind of parameters replaces the distinction of unqualified entities and whatever is taken as denotation of notions in the model-theoretic approach mentioned above, however, with no ontological burden! They just have different deductive roles in the meaning-conferring system, as seen by the rules below.

The I/E-rules for the intensional sentences are presented in Fig. 3.

Fig. 3

Intensional transitive verbs rules

Remarks about the rules The remarks both explain the intensional rule and relate to the difference from the corresponding extensional rules.

• First, note that according to the ($s_{n} I$)-rules only $\mathsf {some}\ X$ (or, more colloquially, $\mathsf {a}\ X$) can be introduced notionally, and only into the object position, as known from the ITV theory.

• $s_{n} I$: It is simpler here to replace the $S[\cdots ]$ notation by an explicit $\hat{R}$ (and its arguments), since no notional introduction into a subject position is allowed. Consider now the characteristics of ITVs, that shed light over the difference between the extensional (sI) and intensional ($s_{n} I$) rules

• $s_{n} E$: Here, too, an arbitrary conclusion $S^{\prime }$ can be drawn from a notional sentence provided it can be drawn from an arbitrary notional witness. Note that $\mathbf{j}\ \mathsf {seeks}\ \mathbf{k}$ cannot be deduced from $\mathbf{j}\ \mathsf {seeks\ a\ secretary}$ and $\mathbf{k}\ \mathsf {isa\ secretary}$, as expected from non-specificity of the object in an ITV sentence.

• non-specificity: The non-specificity of $\mathsf {some}\ X$ in the conclusion of ($s_{n} I$) is reflected by the absence, in that rule, of a predicative premise of the form $\mathbf{j}\ \mathsf {isa}\ X$ (with an individual parameter j), the latter replaced, in contrast, with a non-predicative premise $\nu \ \mathsf {is\ being\ a}\ X$ (with a notional parameter $\nu$).

For example:

Thus, the difference of interpretation of the transitive verbs resides in the way parameters are associated with nouns.

• 1. in j isa X, the notation is just a sugaring of the standard first-order logic notation P(a), which model-theoretically would imply that a is referring and P has an extension containing the object referred to by a.

• 2. On the other hand, $\nu \ \mathsf {is\ being\ a}\ X$ is not first-order expressible. Rather, it might correspond to a second-order variable bound to a predicate name. Model theoretically, there is no reference involved to an element of the domain.

• absence of existential commitment: Existential commitment here is expressed via a use of an individual parameter in the second premise of ($s_{n} I$). So, suspension of existence is manifested directly by the form of the ($s_{n} I$)-rule introducing a non-specific indefinite determinate-phrase into the object position, that does not have a premise involving an individual parameter. Suppose secretaries exist and unicorns do not exist. This would be embodied at the level of ground (i.e., atomic) sentences, so that $\mathbf{k}\ \mathsf {is\ a} {\ secretary}$ could surface as a possible premise, while $\mathbf{k}\ \mathsf {is\ a\ unicorn}$ will not. This difference between secretaries and unicorns has no bearing on the notions being a secretary and being a unicorn. At the atomic level, there is no difference in the status of $\nu \ \mathsf {is\ being\ a\ secretary}$ and $\nu \ \mathsf {is\ being\ a\ unicorn}$ as premises. Associating a name to a notion has no existential commitment. As a result, j seeking a (non-specific) secretary and j seeking a (non-specific) unicorn are derived (with $\Gamma$ omitted) in exactly the same way:

  

  This can be contrasted with the derivation of j finds a unicorn, which needs a premise appealing to an individual parameter.

  

  Under the supposition about unicorns, the premises $\mathbf{k}\ \mathsf {isa\ unicorn}$ and $\mathbf{j}\ \mathsf {finds}\ \mathbf{k}$ will not be simultaneously derivable from any grounds $\Gamma$.

The lack of existential commitment is also manifested by the inference

(30)

being valid.

I would like to stress once again that j is a secretary and j isa unicorn are atomic sentences, the meaning of which is given from outside the meaning-conferring rules. This externally given difference in meaning would presumably originate from from the lexical semantics of the relevant nouns.

• resistance to substitutivity: This is obtained by introducing different equality theories for the two ind of parameters. I refer the reader to Francez (2016) for the technical details.

3.4 Semantic variation: implicit objects

3.4.1 Implicit objects of (extensional) transitive verbs

Extensional transitive verbs come with two kinds of objects.

• Expressed (explicit) object: Sentence with an explicit object are the “regular” kind of transitive sentences, of the same kind we saw before when considering the extensional verbs.

  $$\begin{aligned} \mathsf {Every\ girl\ ate\ an\ apple} \end{aligned}$$

  (31)

  with a pre-theoretic meaning as described above for extensional transitive verbs.

• Implicit object: In contrast, some (lexically specified) transitive verbs allow omission of their object, like

  $$\begin{aligned} \mathsf {every\ girl\ ate} \end{aligned}$$

  (32)

  Standardly, the pre-theoretic meaning of (32) is taken to be identical to that of

  $$\begin{aligned} \mathsf {every\ girl\ ate\ something} \end{aligned}$$

  (33)

A semantics for sentences with transitive verbs has to reveal the following distinguishing characteristics of verbs of those two kinds.

• How is the existentially quantified reading of the missing object of (32) obtained?

• What is the basis of the sameness of meaning of (32) and (33)?

The MTS supporting the above distinction appeals to “filler elements” in domains of denotation of arbitrary semantic types (Blom et al., 2012; Giorgolo and Asudeh, 2012). The extra-theoretic interpretation of such “filler elements” is non-obvious, as is the presence of such elements in lexical meaning assignments of NL words. They cary an ontological commitment which is left unexplained. See Francez (2017) for further difficulties involved with the filler value semantics.

The major point in this section is to show how the above distinction between two kinds of extensional transitive verbs, expressed object vs. implicit object verbs, complicated to make in MTS, is conveniently made in PTS.

The distinction is accounted for by the presence or absence of a premise of the I-rule of the object.

3.4.2 A PTS for implicit objects of extensional transitive verbs

For the expressed object, the rules are those in Fig. 1, to which I add rules for a nominally-unqualified object something.

The nominally-unqualified existential quantification in object position is governed by the following I/E-rules.¹¹

(34)

The difference between those two I/E-rules and the I/E-rules for nominally-qualified nps ((sI) and (sE) above) is the absence of a nominally-qualifying premise $\mathbf{k}\ \mathsf {isa}\ X$ (for some noun X) in the I-rule, and the absence of a corresponding discharged assumption in the E-rule.

For example,

For the implicit object, the main ideas on which the PTS for implicit arguments is based is the following:

• The reduction of an argument is reflected proof-theoretically by omission of a premise in I-rules. In this case, the omission of an object is obtained in exactly the same way as having a nominally-unqualified object.

• Sameness of meaning is based on sameness of I-rules, implying sameness of canonical derivations.

• object reduction: Let $R^{u}$ range over transitive verbs lexically specified as permitting object reduction. The I/E-rules are the following.

  

  (35)

  Here only a sentence with an $R^{u}$-verb can be used. Note the “missing” premise $\mathbf{k}\ \mathsf {isa}\ X$ (for some X), leaving the object nominally-unqualified, hence omittable. It is crucial to note that the subject of $R^{u}$ has to be an individual parameter, assuring the meaning-identity with the explicit existentially case below. The parameter j is a basis for introduction of a universally quantified subject with a higher scoping quantifier.

For example, with $R^{u}=\mathsf {ate}$ (with contexts omitted):

(36)

Note that no similar (uI)-application can be used to derive, for example, j smiled, under the assumption that smiled is lexically specified as a proper intransitive verb.

Example 7

As an example, I show that

$$\begin{aligned} \vdash \ \mathsf {every\ girl\ ate\ some\ apple}\ : \mathsf {every\ girl\ ate} \end{aligned}$$

(37)

The derivation is shown in Fig. 4.

Fig. 4

Derivation of every girl ate

So, the “essence” of the derivation is not using the premise $\mathbf{k}\ \mathsf {isa\ apple}$ for (uI), later discharged by the application of (sE), in deriving $\mathbf{j}\ \mathsf {ate}$.

• Sameness of meaning: the following proposition, expressing the equality of meaning between intransitive $R^{u}$-headed pseudo-sentence and explicitly existentially-quantified R-headed pseudo-sentences is a simple consequence of those rules.

Proposition 1

$$\begin{aligned} \mathbf{[}\! [\mathbf{j}\ R^{u} \mathbf{] \! ]}= \mathbf{[}\! [\mathbf{j}\ R\ \mathsf {\mathrm{something}} \mathbf{] \! ]}\end{aligned}$$

(39)

and in particular

$$\begin{aligned} \mathbf{j}\ R^{u} \equiv _{GA} \mathbf{j}\ R\ \mathsf {\mathrm{something}} \end{aligned}$$

(40)

Proof

immediate, as there is a one-one correspondence between canonical derivations on both sides of the equality, because the premises of the respective I-rules are the same.

A consequence of Proposition 1 is the following theorem,¹² establishing that the sameness of meaning for ground pseudo-sentences with $R^{u}$-verbs extends to a congruence of sameness of meaning for arbitrary sentences with $R^{u}$-verbs in the fragment (namely, arbitrary quantified nps as subject). As we have here only two possible subjects, I state the theorem for both, explicitly.

Theorem 1

$$\begin{aligned}&\mathbf{[}\! [\mathsf {\mathrm{every}}\ X\ R^{u} \mathbf{] \! ]}= \mathbf{[}\! [\mathsf {every}\ X\ R\ \mathsf {\mathrm{something}} \mathbf{] \! ]}\end{aligned}$$

(41)

$$\begin{aligned}&\mathbf{[}\! [\mathsf {\mathrm{some}}\ X\ R^{u} \mathbf{] \! ]}= \mathbf{[}\! [\mathsf {some}\ X\ R\ \mathsf {\mathrm{something}} \mathbf{] \! ]}\end{aligned}$$

(42)

The easy proof can be found in Francez (2017).

4 Semantic variations in adjective–noun combinations

In this section I point out a semantic variation not related to transitive verbs; rather, it is related to variability in adjective–noun combination.

4.1 Adjective–noun combination

The language fragment is extended with sentences such as

$$\begin{aligned}&\mathsf {\mathbf{j}\ isa\ beautiful\ girl} \end{aligned}$$

(43)

$$\begin{aligned}&\mathsf {...\ loves\ every/some\ beautiful\ girl} \end{aligned}$$

(44)

The main task of the semantics it support the well-known typological distinction between three (main) kinds of adjective–noun combination (cf. Morzycki (2015)): intersective, subsective and privative. This distinction is achieved without employing models at all, no scales or yardsticks (what are a yardstick or scale for skill? for beauty?) The MTS literature is very vague on those formal matters concerning what populates models.

A common property of all the adjective–noun combinations, for which I/E-rules are provided below, is that they relate to compound nouns only. In order to derive a sentence with a dp, a determiner needed to be added, and then one of the dp I/E-rules is used. For example, to deduce some beautiful girl smiles (from some $\Gamma$), the adjectival modification rules will be used to derive the compound noun meaning j is a beautiful girl (according to the class to which beautiful belongs), and then the rule (sI), introducing some beautiful girl into the subject position of - smiles is used.

4.1.1 A PTS for adjective–noun combination

The adjective–noun combination is characterized proof-theoretically as a covert conjunction-like operation, via I/E-rules that make use of substructurality, allowing a distinction between projecting from both conjuncts together, or from each one of them separately, and in all cases either unconditionally or conditionally.

• intersective adjectives: The rules are modeled after the additive conjunction (the classical/intuitionistic conjunction).

  

  (45)

  Since grey is assumed (lexically) intersective, the following inferences are valid:

  

  (46)
  

  (47)

• subsective adjectives: The meaning of the modification by means of adjectives in this class depends on the meaning of the modified noun. To reflect this dependence, the I-rule uses the meaning of the noun as a discharged assumption. The discharged assumption is “recorded” in the conclusion in the modified noun.

  

  (48)

  For $X=\mathsf {elephant}$ and $A=\mathsf {small}$, the conclusion $\mathbf{j}\ \mathsf {isa\ small\ elephant }$ is obtained from a derivation of $\mathbf{j}\ \mathsf {is\ small}$ provided $\mathbf{j}\ \mathsf {isa\ elephant}$ is assumed (and then discharged). Similarly, for $X = \mathsf {mouse}$ and $A = \mathsf {small}$, the conclusion $\mathbf{j}\ \mathsf {isa\ small\ mouse}$ is obtained from a derivation of $\mathbf{j}\ \mathsf {is\ small}$ provided $\mathbf{j}\ \mathsf {isa\ mouse}$ is assumed (and then discharged). The elimination rules are:

  

  (49)

Thus, there are two ways of drawing a conclusion from $\mathbf{j}\ \mathsf {isa}\ A\ X$ for a subsective A:

• 1. The conclusion $\mathbf{j}\ \mathsf {isa}\ X$ (as for the intersective case).

• 2. $\mathbf{j}\ \mathsf {is}\ A$ can be used as a discharged assumption only jointly with $\mathbf{j}\ \mathsf {isa}\ X$ to derive $S^{\prime }$.

However, if A is subsective, then $\not \vdash \mathbf{j}\ \mathsf {isa}\ A\ X : \mathbf{j}\ \mathsf {is}\ A$.

For example, the two ways of drawing a conclusion from $\mathbf{j}\ \mathsf {isa\ small\ elephant}$ are:

• 1. $\mathbf{j}\ \mathsf {is\ small}$ can be used only jointly with $\mathbf{j}\ \mathsf {isa\ elephant}$ to derive an arbitrary $S^{\prime }$.

• 2. The conclusion $\mathbf{j}\ \mathsf {isa\ elephant}$.

• privative adjectives: Here we meet a dual dependence: the meaning of the modification depends on the meaning of the (privative) adjective. A fake gun is a gun only under the assumption of being fake. This is ensured by having the adjective as a discharged assumption in the derivation of the combination.

  

  (50)
  

  (51)

Thus, there are again two ways of drawing a conclusion from $\mathbf{j}\ \mathsf {isa}\ A\ X$ for a privative A:

• 1. $\mathbf{j}\ \mathsf {isa}\ X$ can be used only jointly with $\mathbf{j}\ \mathsf {is}\ A$ to derive $S^{\prime }$.

• 2. The conclusion $\mathbf{j}\ \mathsf {is}\ A$.

However, if A is privative, then $\not \Vdash \; \mathbf{j}\; \mathsf {isa}\; A\; X: \;\mathbf{j}\; \mathsf {isa}\; X$.

The two ways of drawing a conclusion from $\mathbf{j}\ \mathsf {isa\ fake\ gun}$ are:

• 1. $\mathbf{j}\ \mathsf {isa\ gun}$ can be used only jointly with $\mathbf{j}\ \mathsf {is\ fake}$ to derive an arbitrary $S^{\prime }$.

• 2. The conclusion $\mathbf{j}\ \mathsf {is\ fake}$.

To summarise:

• intersective adjectival modification: projects each component (i.e., the adjective and the noun) unconditionally, on its own.

• subsective adjectival modification: projects unconditionally either both components jointly, or the second component (the noun) on its own, and projects the adjective conditionally.

• privative adjectival modification: project both components jointly unconditionally, projects the adjective unconditionally on its own and projects the noun conditionally.

Thus, a major proof-theoretic feature of rules, their optional substructurality, is made use of in the meaning-conferring system for adjective–noun combination (see Francez (2017) for full details, and Francez (2016) for the underlying mathematical treatment).

4.2 Semantic variation: contextual meaning variation

4.2.1 Background: quantifier domain restriction

From Stanley and Szabȯ (2000):

The problem of context dependence is the problem of explaining how context contributes to interpretation ...

See Stanley and Szabȯ (2000) for a discussion of a variety of special cases of the general problem of meaning variation with context. In Francez (2014) a proof-theoretic semantics for a special case of the general context dependence problem, is provided namely quantifier domain restriction (QDR). I concentrate here on universal quantification only.

To explain the QDR-problem itself, consider the following example sentence (from (Stanley & Szabȯ, 2000)).

$$\begin{aligned} \mathsf {every\ bottle\ is\ empty} \end{aligned}$$

(52)

The literal model-theoretic meaning of (52), involving quantification and predication, attributes the property of emptiness to every entity in a model falling under the extension¹³ of bottle. The general consent is, however, that in different circumstances, to be captured by contexts, the domain of quantification is not over the whole extension of bottle (all bottles in the universe); rather, it is over a restriction of this extension to one determined by a context, e.g., every bottle in a room where some party takes place in one context, or bottles in some chemistry laboratory in another context.

The general semantic problem faced in an attempt to model the variance of literal meaning with context has, according to Stanley and Szabȯ (2000), two facets.

• Descriptive: Deriving the interpretation of some phrase relative to a context, given prior characterization of what features of a context have a bearing on the meaning of that phrase.

• Fundamental: Specifying the above mentioned characterization, namely what it is about a context in virtue of which the derivation of the interpretation yields the correct meaning in that context. This specification involves some explicit definition of a context.

Thus, for (52), the descriptive meaning is the proper derivation of the restricted domain of quantification given a context, while the fundamental issue is what in the structure of a context determines the appropriate domain restriction.

In general, MTS has many difficulties in adequately solving the foundational aspect of contextual variance of truth-condition. See Francez (2014) for a critical survey. A major contribution of the current approach is the provision of a solution, within the PTS programme, of the foundational problem. In particular, PTS offers a natural candidate for a an explication of contexts: incorporation (of an open formula) to the context $\Gamma$ of a sequent.

It is important to realize what is not the semantic problem discussed here, namely the determination of which context is the “right” context for any given token of a contextually-dependent meaning of a sentence. The latter issue is always determined by extra-linguistic means, independently of whether MTS or PTS are employed as the theory of meaning. Rather, the issue is how to handle contextual meaning variation once a context has been determined.

Finally, the consequences that can be drawn from the contextually-varying meaning of an (affirmative) sentence, namely (affirmative) sentences entailed by a sentence with contextually-varying meaning, which themselves have meanings varying with context, are hardly ever considered in MTS-based discussions. In the proposed PTS, they are expressed via E-rules in the meaning-conferring ND-system.

4.2.2 Modification

In order to formulate the PTS, relative clauses are added to the fragment. Typical sentences include the following.

$$\begin{aligned}&\mathsf {every\ some/boy\ loves\ every/some\ girl\ who(m)\ smiles/loves\ every/some\ flower/}\nonumber \\&\mathsf { whom\ some\ girl\ loves} \end{aligned}$$

(53)

$$\begin{aligned}&\mathsf {every/some\ girl\ is\ a\ girl\ who\ loves\ every/some\ boy} \end{aligned}$$

(54)

$$\begin{aligned}&\mathsf {some\ boy\ loves\ every/some\ girl\ who\ loves\ every}\nonumber \\&\mathsf { boy\ who\ smiles}\ \ {({ nested\; relative \;clause})} \end{aligned}$$

(55)

So, girl who smiles and girl who loves every boy are compound nouns. The notation is extended with $S[-]$, that denotes, for S including an individual parameter in some distinguished position, the result of removing that parameter, leaving that position unoccupied. Examples are loves every girl (a parameter removed from subject position in j loves every girl), and every girl loves (a parameter removed from object position in every girl loves k ).

The corresponding meaning-conferring ND-system is extended by adding the following I/E-rules.

(56)

(57)

The familiar conjunctive behavior of relative clauses is exhibited here by its rules, resembling the rules for logical conjunction.

As an example of a derivation in this fragment, consider

$$\begin{aligned} \vdash \mathsf {every\ girl\ sings} : \mathsf {every\ girl\ who\ smiles\ sings} \end{aligned}$$

(58)

exhibiting the downward monotonicity of every in its first argument.

4.2.3 Back to quantifier domain restriction

Now the proof-theoretic semantics for QDR can be presented. for simplicity, quantifier scope ambiguity, discussed above, is ignored here.

Definition 5

An NLDR-context (NL domain restricting context) c is a finite collection $\Gamma _{c}$ of pseudo-sentences with one individual parameter only. Let CNL (NL contexts) be the collection of all NLDR-contexts.

The NLDR-contexts $\Gamma _{c}(\mathbf{j})$ can be of one of the forms $\mathbf{j}\ \mathsf {isa}\ X$ (X a noun), $\mathbf{j}\ \mathsf {is}\ A$ (A an adjective) and $\mathbf{j}\ P$ (P a verb-phrase). Note that compound contextual restrictions can also be imposed. For example, $\Gamma _{c} (\mathbf{j}) = \mathsf {\mathbf{j}\ isa\ man\ whom\ every\ girl\ loves}$. Since the fragment has only modification by means of (intersective) adjectives and relative clauses, all the examples will be restricted to such modification. Extension, for example, to incorporate preposition phrases are not an obstacle in principle, just that it has not been done yet.

This definition provides an explicit notion of a context, compatible with the general proof-theoretic notion of a context as an antecedent of a sequent.

A NLDR-context c provides a discharged assumption for imposing its restriction.

(59)

(60)

Again, a family of I/E-rules is employed, for all possible NLDR-contexts. Note that ‘$:_{c}$’ that records that the provability is in the context c.

Returning to the ‘empty bottles’ sentence in (52), instead of the unrestricted

we have the contextual restriction by c to, say, a party:

Thus, an explicit way is provided for explaining how does an NLDR-context modify the domain of quantification to require satisfaction of the context.

Example 8

Below is a derivation establishing

$$\begin{aligned}&\vdash \mathsf {every\ Italian\ woman\ smiles},\mathsf {every\ woman\ who\ smiles\ is\ beautiful}\nonumber \\&\quad :_{c}\ \mathsf {every\ woman\ is\ beautiful} \end{aligned}$$

(61)

in an NLDR-context c with $\Gamma _{c}(\mathbf{k}) = \mathbf{k}\ \mathsf {is\ Italian}$, intended to restrict the universal quantification on women to a universal quantification on Italian women. For typographical reasons, I abbreviate in the derivation Woman, Italian, Beautiful and Smiles to W, I, B and S, respectively.

Example 9

The following example from Stanley and Szabȯ (2000) is pointed out as being difficult for MTS-handling, as it seemingly requires context-shift during meaning evaluation.

$$\begin{aligned} \mathsf {every\ sailor\ waved\ to\ every\ sailor} \end{aligned}$$

(63)

where the context imposes the restriction that the quantification in the subject is restricted to one “kind” of sailors, say sailors on the ship, while the object quantification is restricted, say, to sailors on the shore. Under the current approach, such examples pose no problem whatsoever. Suppose that j is the parameter used to introduce every sailor in the subject, while k is the parameter used to introduce every sailor in the object. Then, all we have to do is consider a context $c_{sailors}$, with $\Gamma _{c_{sailors}}(\mathbf{j})= \mathbf{j}\ \mathsf {is-on-the-ship}$, and $\Gamma _{c_{sailors}}(\mathbf{k})= \mathbf{k}\ \mathsf {is-on-the-shore}$. No context shift is involved. As a full derivation is somewhat lengthy, I skip the details.

5 Conclusions

In this paper, I focused on proof-theoretic semantics, a theory of meaning for natural language alternative to the traditional model theoretic semantics, viewing it as a resource for capturing semantic variation, a view not proposed before.. The main methodological difference between the two approaches is replacing the conception of meaning as truth-conditions in suitable, usually fairly complicated, models (bearing not always obvious ontological commitments), by canonical derivability conditions in meaning-conferring proof systems (expressing grounds for assertion). Those meaning-conferring proof-systems where shown to provide resources naturally supporting meaning variation.

Here are the main variations presented in this survey.

• The use of different sorts of syntactic parameters to distinguish extensional predication from attribution of intensional non-specific “notionality”.

• Omission of a (predicative) premise in a rule to express omission of a verbal argument.

• Rooting the sameness of meaning on equality of grounds for assertion.

• Using substructurality to block unwarranted conclusions.

• Using the order of applications of I-rules to capture quantifier scope ambiguity.

• The use of an open assumption (with a free variable) as an explication of a context, employed to express a quantifier domain restriction.

Presumably, there are more semantic variations that can be captured by proof-theoretic resources once a PTS for the constructs exhibiting those variation has been devised.