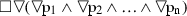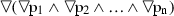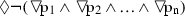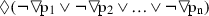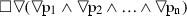Not ignorance, but ignorance of ignorance, is the death of knowledge.
Alfred North Whitehead
But there are also unknown unknowns. These are things we don’t know we don’t know.
Donald Rumsfeld
Abstract
I discuss the question of when knowledge of higher order ignorance is possible and show in particular that, under quite plausible assumptions, knowledge of second order ignorance is impossible.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
It is good to know when one is ignorant. But sometimes one is ignorant of one’s ignorance. One might think that, in that case, it would be good to know of one’s second order ignorance. But it can be shown, under quite plausible assumptions, that it is impossible to know of one’s second order ignorance. Second order ignorance is inevitably third-order ignorance. Likewise, third-order ignorance is inevitably fourth order ignorance and so on, indefinitely, through all the orders of ignorance. When one is second order ignorant one enters a black hole from which there is no epistemic escape.Footnote 1
What goes for ignorance also goes for indeterminacy or being borderline. In a sorites series, there may be borderline cases. It is often supposed that between the borderline and the definite cases, there may be borderline borderline cases. But again, it can be shown that, under plausible assumptions, it can never be correct to assert that a given case is borderline borderline. Any second order borderline case is inevitably third-order. Likewise, any third-order borderline case is inevitably fourth order and so on, indefinitely, through all the orders of being borderline.
These result are surprising and, although they are implicit in the earlier literature on contingency, they have, as far as I know, never been made explicit or further developed.Footnote 2
Let me give an informal proof of the result, leaving a formal treatment of this and related results to the appendix. We presuppose the modal system S4, in which whatever is necessarily the case is both the case and is necessarily necessarily the case. Thus under the epistemic interpretation, we presuppose that whatever is known to be the case is both in fact the case and is known to be known to be the case (positive introspection) and, under the indeterminacy interpretation, we presuppose that whatever is definitely the case is both in fact the case and is definitely definitely the case.
-
First, let us fix on terminology. Say that:
-
one is ignorantthat p if one does not know that p \((\lnot \mathrm{Kp})\);
-
it is (epistemically) possible that p if one is ignorant that not-p (Mp \(=\,_\mathrm{df} \lnot \mathrm{K}\lnot \mathrm{p})\)
-
one is ignorant of the fact that p if p is the case and one is ignorant that p (p \(\wedge \lnot \mathrm{Kp}\));
one is (first-order) ignorantwhether p if one is both ignorant that p and ignorant that not-p (Ip \(=\,_\mathrm{df} \lnot \mathrm{Kp} \wedge \lnot \mathrm{K}\lnot \mathrm{p}\));
one is Rumsfeldignorantof p if one is ignorant of the fact that one is ignorant whether p (Ip \(\wedge \lnot \mathrm{KIp}\)); and
one is second-orderignorantwhether p if one is ignorant whether one is ignorant whether p (IIp).
Note that first-order ignorance whether p amounts to its being epistemically possible that p and epistemically possible that not-p (Mp \(\wedge \mathrm{M} \lnot \mathrm{p}\)).
We now establish various claims (all within the context of the system S4):
(1) Second-order ignorance implies first-order ignorance.
For suppose that one is not first-order ignorant. Then either one knows p (Kp) or ones know not-p \((\mathrm{K}\lnot \mathrm{p}\)). Suppose the former (the other case is similar). Then since one knows that p, one knows that one knows that p (KKp) and hence one knows that one is not ignorant whether p (Lemma 3).
(2) Second-order ignorance implies Rumsfeld ignorance.
For second order ignorance implies first order ignorance by (1) and ignorance whether one is ignorant whether p implies ignorance that one is ignorant whether p.
Let us note that the converse also holds:
(2*) Rumsfeld ignorance implies second-order ignorance.
For suppose one is Rumsfeld ignorant. Then one does not know that one is first-order ignorant. But given that one is first-order ignorant, one also does not know that one is not first-order ignorant.
(3) One does not know that one is Rumsfeld ignorant.
For suppose one knows that one is Rumsfeld ignorant \((\mathrm{K}(\mathrm{Ip} \wedge \lnot \mathrm{KIp})\)). Then one knows, in particular, that one is first-order ignorant (KIp) and, it follows from the truth of what one knows \(((\mathrm{K}(\mathrm{Ip} \wedge \lnot \mathrm{KIp})\)), that one does not know that one is first-order ignorant \((\lnot \mathrm{KIp}\)). A contradiction.
From (2) and (3) it follows that:
(4) One does not know that one is second-order ignorant.
For if one knew one were second-order ignorant whether p, one would know that one was Rumsfeld ignorant of p by (2), which is impossible by (3).
(4) is a theorem of the modal system S4. We have therefore established the logical impossibility—at least relative to system S4—of knowing that one is second-order ignorant (Theorem 4).
Let us make a number of observations.
Why surprising?
We should perhaps first consider why this result is so surprising even though, from a technical point of view, it is relatively trivial. Suppose one does not know certain propositions. Assuming negative introspection (that one knows what one does not know), it follows that one knows that one does not know each of these propositions. As is well-known, negative introspection does not follow from positive introspection. But there would appear to be no good reason why positive introspection should preclude one’s knowing that one does not know each of these proposition.
Indeed, suppose one were to list all of the propositions that one knows:
This is something one should in principle be able to do, whilst knowing that one knows each of the propositions on the list. Given that the list is exhaustive, then even though it is not guaranteed that one would know that the list is exhaustive, there would appear to be nothing to prevent one from knowing that it is exhaustive, that there was nothing else left to know; and so if one failed to know any proposition, one would know that it was not known since one could see that it did not appear on the list.
Our result shows that this line of reasoning is mistaken. For if one is second order ignorant whether p, then the fact that one does not know that p and the fact that one does not know that not-p will not appear on the list. But one could not know that they do not appear on the list, since this would amount to knowledge of second order ignorance.
Thus the result shows that what might appear to be a plausible model for achieving knowledge of what one does not know is not something that will always work. The content of everything that one knows might prevent one from seeing that it is the content of everything that one knows.
Orders of ignorance
If one suffers from second-order ignorance then one does not know that one suffers from second-order ignorance and, of course, if one suffers from second-order ignorance then one does not know that one does not suffer from second-order ignorance, since it is impossible to know what is false. So second-order ignorance implies third-order ignorance (ignorance whether one is second-order ignorant). Likewise third-order ignorance implies fourth order ignorance and so on, indefinitely, through all the orders of ignorance.
Moreover, as we have seen, second-order ignorance implies first-order ignorance. Consequently, third-order ignorance implies second-order ignorance and so on, indefinitely, through all the orders of ignorance. Thus any form of higher order ignorance (beyond the first) will imply all orders of ignorance (including the first).
Although knowledge of second-order ignorance is impossible, knowledge of first-order ignorance certainly is possible and, indeed, would appear to be commonplace. I am ignorant of whether is it raining in London right now, for example, and I certainly know that I am ignorant since I know that I do not have the evidence required to settle the question.
Second-order ignorance would also appear to be possible, even though knowledge of second-order ignorance is not. Indeed, let us suppose that there is a counter-example to the characteristic axiom 5 of S5, i.e. a case in which one is ignorant that p \((\lnot \mathrm{Kp})\) but ignorant that one is ignorant that p \((\lnot \mathrm{K}\lnot \mathrm{Kp}\)). Given that one is ignorant that one is ignorant that p \((\lnot \mathrm{K}\lnot \mathrm{Kp}\)), it follows that one is ignorant that not-p \((\lnot \mathrm{K}\lnot \mathrm{p})\) and hence that one is ignorant whether p (Ip). But also one is ignorant that one is ignorant that p \((\lnot \mathrm{K}\lnot \mathrm{Kp}\)) and hence ignorant that is one ignorant whether p \((\lnot \mathrm{KIp})\). (The converse also holds: any case of second-order ignorance will be a counter-example to axiom 5. For second-order ignorance implies Rumseldian ignorance—\((\lnot \mathrm{Kp} \wedge \lnot \mathrm{K}\lnot \mathrm{Kp}) \vee (\lnot \mathrm{K}\lnot \mathrm{p} \wedge \lnot \mathrm{K}\lnot \mathrm{K}\lnot \mathrm{p}\))—and either disjunct will then serve as a counter-example to axiom 5).
We therefore see, when we look at the series of ignorance claims:
-
(I1)
one is ignorant (i.e. first-order ignorant) whether p
-
(I2)
one is second-order ignorant whether p
-
(I3)
one is third-order ignorant whether p
\(\vdots \)
that there are only three possible distributions of truth-value (Theorem 6). Either all of the ignorance claims are false—one is not ignorant whether p and consequently one does not suffer from any form of higher order ignorance (since that would require that one be first-order ignorant); or the first claim is true and all the others are false—one knows one is ignorant whether p and consequently one does not suffer from any higher order of ignorance since that would imply that one suffers from second-order ignorance; or all of the ignorance claims are true—one is second-order ignorant and hence ignorant at every order. Thus either one is not ignorant or one is knowingly ignorant or one is thoroughly ignorant. Ignorance of ignorance, rather than ignorance, is indeed the death of knowledge, though perhaps not in the sense that Whitehead intended.
I have so far only looked at the modalities which can be formed from the ignorance operator: ignorance whether p; ignorance whether ignorance whether p; and so on. One might also bring in the operators for knowledge and epistemic possibility, thereby allowing ourselves to talk of ignorance whether one knows that p, for example, or ignorance whether one knows that it is epistemically possible that p. But even if one allows the use of these other epistemic operators in the formation of the prefix to p, one’s ‘epistemic profile’ will peter out at the third level: once told how things are under a threefold iteration of these operators, there will be nothing else of this sort to be told (Theorem 12).Footnote 3
Fitch The present result is closely related to the famous result of Fitch (1963).Footnote 4 He pointed out that ignorance of the fact that q (q \(\wedge \lnot \mathrm{Kq}\)) could not itself be known. Although second order ignorance is not itself a form of Fitchean ignorance, it is equivalent (within S4) to Rumsfeld ignorance, which is a form of Fitchean ignorance, in which the base state q is constituted by ignorance whether p for some given state p.
The present case of Fitch-style unknowability is of interest for a number of different reasons. In the first place, there is perhaps special interest attaching to the state of second-order ignorance and to how, in particular, it may differ from first-order ignorance (with the former being unknowable and the latter not).
In the second place, second-order ignorance may be regarded as a purely mental state, not consisting in a connection between something non-mental (the base state q) and something mental \((\lnot \mathrm{Kq}\)). Indeed, it might even be thought that ignorance of ignorance could be an internal mental state in that it could be grounded in something completely internal to the mind (as given, let us say, by the lack of evidence under an internalist conception of evidence).
Fitchean states may, of course, be purely mental or internal in this sense. Indeed, Rumsfeld ignorance may well be a mental state of this sort. But second order ignorance has a quite special status. For it may be shown to be the weakest purely mental state that is incapable of being known. If a purely mental state concerning a given proposition p is incapable of being known then it will imply a state of second order ignorance concerning p (Theorem 10). In other words, the unknowability of a purely mental state is always attributable to second order ignorance; given that the purely mental state requires second order ignorance, we can always see its unknowability as arising from the unknowability of second order ignorance.
This is in marked contrast to the unknowability of states which may not be purely mental, as with one’s not knowing p, when p itself is not a mental state . In this case, without the restriction to purely mental states, it may be shown that there is no weakest unknowable state and hence no common source for the unknowability (Theorem 11).
Other systems The proofs of the above results all presuppose the principles of the system S4; and the characteristic 4 axiom of S4 is, of course, somewhat controversial—both for knowledge and for definiteness. Suppose we drop the characteristic 4 axiom of S4 (\(\square \mathrm{A} \supset \square \square \mathrm{A}\)), thereby obtaining the system T. Then it can no longer be shown that knowledge of second-order ignorance is impossible.
Indeed, we can establish a strong result to the contrary. For consider the series of ignorance claims (I1), (I2), (I3), \(\ldots \) above and any possible assignment of truth-values to each claim in the series. Thus it might be supposed that one is n-th order ignorant for each even n and not n-th order ignorant for each even n or that one is n-th order ignorant for prime n and not n-th order ignorant for composite n. It can then be shown that each such supposition is consistent within the system T, i.e. that there is no logical basis, within T, for ruling it out (Theorem 15).
A related result can also be established. Say that one absolutely knows the proposition p if one knows that p, knows that one knows that p, knows that one knows that p, and so on (Kp, KKp, KKKp, \(\ldots \)). Of course, within S4 one absolutely knows whatever one knows but, within T, this need not be so. It can then be shown that each order of ignorance is absolutely knowable. In other words, for each order n, one may consistently suppose that one has absolute knowledge of one’s n-th order ignorance (corollary 16). Thus, somewhat paradoxically, the failure to know certain kinds of things (in particular, what one knows) may enable one to know other kinds of things (such as second order ignorance) which one would otherwise be incapable of knowing.
Moving in the other direction, stronger systems than S4 may narrow the possibility of knowledgeable ignorance. We previously noted that S4 left open three consistent assignments of truth values to the series of ignorance claims (I1), (I2), (I3), \(\ldots \): no ignorance; knowledgeable first-order ignorance; and thorough-going ignorance. Within the system S5 (whose additional axiom is \({\mathrm{A}} \supset \square \lozenge \mathrm{A}\)), all ignorance will be known, thereby excluding the possibility of thorough-going ignorance. On the other hand in the system S4M (whose additional axiom is \(\lozenge \square \mathrm{A} \vee \lozenge \square \lnot \mathrm{A}\)), all ignorance will be thorough-going, thereby excluding the possibility of knowledgeable ignorance.Footnote 5
Finally, note that the negative result on second order ignorance does not depend upon having axiom T. The result can also be establishing using axiom \(\mathrm{D} (= \lozenge \top )\) in place of T (observation to Theorem 4). This means that there are also plausible tense-logical, doxastic and proof-theoretic analogues of the result, where contingency corresponds to A sometimes but not always being the case under a tense logical reading, to suspension of belief under a doxastic reading, and to undecidability under a proof-theoretic reading.
General ignorance The ignorance we have so far dealt with concerns specific ignorance, i.e. ignorance concerning a specific proposition. But one may also be ignorant about some subject matter. One may be ignorant, for example, about which candidates will be elected to the senate.
We might think of the subject matter as given by a set of propositions \(\mathrm{p}_{1}, \mathrm{p}_{2}, \ldots , \mathrm{p}_\mathrm{n}\). Thus in the case of the senatorial contest, the propositions might be that John McCain is elected, that Elizabeth Warren is elected, and so on.
Ignorance about a given subject matter can then take two forms. It can be complete ignorance or partial. In the case of complete ignorance, one is ignorant whether p for each of the propositions constituting the subject matter and, in the case of partial ignorance, one is ignorant whether p for at least one of the propositions constituting the subject matter.
One might think that one could escape the barrier to knowledgeable second order ignorance when the ignorance in question concerns some subject matter rather than a specific proposition. But this is not so. It is impossible to know of one’s ignorance of one’s ignorance concerning some subject matter or to know of one’s second order ignorance concerning some subject-matter. And these results hold whether the ignorance be complete or partial (Theorem 7).
Indeterminacy
The notion of being borderline is the analogue of the notion of contingency in the modal sphere and of the notion of ignorance in the epistemic sphere. Where D is used for the definitely operator (it is definitely the case that), we may define it being borderline that A (BA) in terms of its being neither definitely the case that A nor definitely the case that not-A \((\lnot \mathrm{DA} \wedge \lnot \mathrm{D}\lnot \mathrm{A}\)), in analogy to the definition of contingency in terms of necessity and to the definition of ignorance in terms of knowledge.
The above results are relevant to the phenomenon of vagueness, when characterized in terms of the property of being borderline, in a number of different ways (indeed, it was my interest in vagueness which originally motivated my interest in these results). In the first place, it is often supposed that just as one may be in a position to assert that a case is borderline without being in a position to assert that it is an actual case of the given predicate, so one may be in a position to assert that a case is borderline borderline without being in a position to assert that it is a borderline case of the predicate.
But this line of thought is misguided for two separate reasons. For even though a borderline case of a predicate need not be an actual case of a predicate, a borderline borderline case of a predicate must be a borderline case of the predicate (or, at least, within the context of S4). Moreover, one never is in a position to assert that a case is borderline borderline (again, in the context of S4) if one can only properly assert what is definitely true. For even though a case can be borderline borderline, it can never be definitely borderline borderline.
In the second place, it is often supposed that the familiar cases of vagueness are thoroughgoing in the sense of not simply requiring the presence of borderline cases but also the presence of borderline borderline cases. But if vagueness is thoroughgoing, one is never in a position to assert its existence. For its existence would require that one of the cases to which the predicate applies be borderline borderline; and, as we have seen, this is not something that can definitely be the case. This, in my opinion, is one reason among others for being skeptical as to whether one can even characterize vagueness in terms of the notion of borderline case (Fine 2008).
Formal appendix
We adopt the usual symbolism of propositional modal logic  and standard results and terminology will be taken for granted.
and standard results and terminology will be taken for granted.  A (it is contingent that A) is an abbreviation for (\(\lozenge \)A \(\wedge \,\lozenge \lnot \mathrm{A}\)). Under an epistemic interpretation of the modalities, \(\square \)A means that
A (it is contingent that A) is an abbreviation for (\(\lozenge \)A \(\wedge \,\lozenge \lnot \mathrm{A}\)). Under an epistemic interpretation of the modalities, \(\square \)A means that  one knows that A, \(\lozenge \)A that it is possible for all one knows that A, and
one knows that A, \(\lozenge \)A that it is possible for all one knows that A, and  A that one is ignorant whether or not A. Under the vagueness-theoretic interpretation, \(\square \)A means that it is definitely the case that A, \(\lozenge \)A that it is indefinite that A, and
A that one is ignorant whether or not A. Under the vagueness-theoretic interpretation, \(\square \)A means that it is definitely the case that A, \(\lozenge \)A that it is indefinite that A, and  A that it is indefinite whether or not A. We use numerical superscripts in an obvious way for iterations of a modality. Thus \(\square ^{2}\) is short for \(\square \square \) and
A that it is indefinite whether or not A. We use numerical superscripts in an obvious way for iterations of a modality. Thus \(\square ^{2}\) is short for \(\square \square \) and  for
for  .
.
We show how to simplify formulas of the form  A within the modal systems T and S4. But first:
A within the modal systems T and S4. But first:
For n \(= 1, 2, \ldots ,\)
-
(i)
\(\square (\square \mathrm{A } \vee \square \lnot \mathrm{A}\)) is provably equivalent in T to \(\square ^{2}\mathrm{A }\vee \square ^{2}\lnot \mathrm{A};\) and
-
(ii)
\(\lozenge (\lozenge \mathrm{A }\wedge \lozenge \lnot \mathrm{A}\)) is provably equivalent in T to \(\lozenge ^{2}\mathrm{A }\wedge \lozenge ^{2}\lnot \mathrm{A}\).
(ii) follows from (i) given the duality of \(\square \) and \(\lozenge \).
As for the right-to-left direction of (i), \(\square \mathrm{A}\)\(\vdash \)\(\square \mathrm{A} \vee \square \lnot \mathrm{A}\) and so \(\square ^{2}\mathrm{A} = \square \square \mathrm{A}\)\(\vdash \)\(\square (\square \mathrm{A} \vee \square \lnot \mathrm{A}\)). Similarly, \(\square ^{2}\lnot \mathrm{A}\)\(\vdash \)\(\square (\square \mathrm{A} \vee \square \lnot \mathrm{A}\)); and so, putting together these two results, \(\square ^{2}\mathrm{A} \vee \square ^{2}\lnot \mathrm{A}\)\(\vdash \)\(\square (\square \mathrm{A} \vee \square \lnot \mathrm{A}\)).
In proving the left-to-right direction of (i), it will be convenient to employ a natural deduction style of reasoning. Suppose \(\square (\square \mathrm{A} \vee \square \lnot \mathrm{A}\)); and make the temporary supposition of A. Since \(\square \mathrm{A} \vee \square \lnot \mathrm{A}\) (given \(\square (\square \mathrm{A} \vee \square \lnot \mathrm{A})\)) and since A is inconsistent with \(\square \lnot \mathrm{A}\), we may infer \(\square \)A. But then from \(\square (\square \mathrm{A} \vee \square \lnot \mathrm{A}\)) and \(\square \)A, we may infer \(\square (\mathrm{A} \wedge (\square \mathrm{A} \vee \square \lnot \mathrm{A})\)); and since A is inconsistent with \(\square \lnot \mathrm{A}\), we may infer \(\square \square \mathrm{A}\). Similarly, under the supposition of \(\lnot \mathrm{A}\), we may infer \(\square ^{2}\lnot \mathrm{A}\); and so from the main supposition, we may infer \(\square ^{2}\mathrm{A} \vee \square ^{2}\lnot \mathrm{A}\), as required. \(\square \)
We now have:
-
(i)
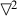 A is provably equivalent in T to \((\lozenge ^{2}\mathrm{A}\,\wedge \,\lozenge \square \lnot \mathrm{A}) \vee (\lozenge ^{2}\lnot \mathrm{A}\,\wedge \,\lozenge \square \mathrm{A})\)
A is provably equivalent in T to \((\lozenge ^{2}\mathrm{A}\,\wedge \,\lozenge \square \lnot \mathrm{A}) \vee (\lozenge ^{2}\lnot \mathrm{A}\,\wedge \,\lozenge \square \mathrm{A})\) -
(ii)
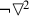 A is provably equivalent in T to
A is provably equivalent in T to 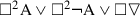 A
A -
(iii)
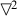 A is provably equivalent in S4 to \((\lozenge \mathrm{A} \wedge \lozenge \square \lnot \mathrm{A}) \vee (\lozenge \lnot \mathrm{A} \wedge \lozenge \square \mathrm{A})\)
A is provably equivalent in S4 to \((\lozenge \mathrm{A} \wedge \lozenge \square \lnot \mathrm{A}) \vee (\lozenge \lnot \mathrm{A} \wedge \lozenge \square \mathrm{A})\) -
(iv)
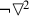 A is provably equivalent in S4 to
A is provably equivalent in S4 to 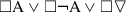 A
A
- (i):
-
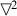 A
A - -||-:
-
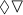 A
A 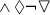 A by definition of
A by definition of 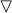
- -||-:
-
\(\lozenge (\lozenge \mathrm{A }\wedge \lozenge \lnot \mathrm{A}) \wedge \lozenge \lnot (\lozenge \mathrm{A }\wedge \lozenge \lnot \mathrm{A}\)) by definition of
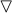
- -||-:
-
\(\lozenge ^{2}\mathrm{A }\wedge \lozenge ^{2}\lnot \mathrm{A }\wedge \lozenge \lnot (\lozenge \mathrm{A }\wedge \lozenge \lnot \mathrm{A}\)) by Lemma 1(ii)
- -||-:
-
\(\lozenge ^{2}\mathrm{A} \wedge \lozenge ^{2}\lnot \mathrm{A} \wedge \lozenge (\square \lnot \mathrm{A} \vee \square \mathrm{A}\)) by simplification in T
- -||-:
-
\(\lozenge ^{2}\mathrm{A } \wedge \lozenge ^{2}\lnot \mathrm{A} \wedge (\lozenge \square \lnot \mathrm{A} \vee \lozenge \square \mathrm{A}\)) by simplification in T
- -||-:
-
(\(\lozenge ^{2}\mathrm{A } \wedge \lozenge ^{2}\lnot \mathrm{A } \wedge \lozenge \square \lnot \mathrm{A}) \vee (\lozenge ^{2}\mathrm{A } \wedge \lozenge ^{2}\lnot \mathrm{A} \wedge \lozenge \square \mathrm{A}\)) by truth-functional (tf) logic
- -||-:
-
(\(\lozenge ^{2}\mathrm{A }\wedge \lozenge \square \lnot \mathrm{A})\vee (\lozenge ^{2}\lnot \mathrm{A} \wedge \lozenge \square \mathrm{A}\)) since \(\lozenge \square \lnot \mathrm{A}\) implies \(\lozenge \lozenge \lnot \mathrm{A}\) and \(\lozenge \square \mathrm{A}\) implies \(\lozenge \lozenge \lnot \mathrm{A}\).
- (ii):
-
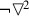 A
A - -||-:
-
\(\lnot [(\lozenge ^{2}\mathrm{A }\wedge \lozenge \square \lnot \mathrm{A}) \vee (\lozenge ^{2}\lnot \mathrm{A} \wedge \lozenge \square \mathrm{A}\))] by (i)
- -||-:
-
\((\lnot \lozenge ^{2}\mathrm{A} \vee \lnot \lozenge \square \lnot \mathrm{A}) \wedge (\lnot \lozenge \lnot \mathrm{A} \vee \lnot \lozenge \square \mathrm{A}\)) by tf logic
- -||-:
-
(\(\square ^{2}\lnot \mathrm{A} \vee \square \lozenge \mathrm{A}) \wedge (\square ^{2}\mathrm{A} \vee \square \lozenge \lnot \mathrm{A}\)) by simplification in T
- -||-:
-
(\(\square ^{2}\lnot \mathrm{A} \wedge \square ^{2}\mathrm{A}) \vee (\square ^{2}\lnot \mathrm{A} \wedge \square \lozenge \lnot \mathrm{A}) \vee (\square \lozenge \mathrm{A} \wedge \square ^{2}\mathrm{A}) \vee (\square \lozenge \mathrm{A }\wedge \square \lozenge \lnot \mathrm{A}\)) by tf logic
- -||-:
-
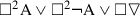 A
A
since
- (a):
-
(\(\square ^{2}\lnot \mathrm{A }\wedge \square ^{2}\mathrm{A}\)) -||- \(\square ^{2} (\lnot \mathrm{A} \wedge A\)) -||- \(\bot \),
- (b):
-
(\(\square ^{2}\lnot \mathrm{A} \wedge \square \lozenge \lnot \mathrm{A}\)) -||- \(\square ^{2}\lnot \mathrm{A}\) given that \(\square ^{2}\lnot \mathrm{A} \vdash \)\(\square \lozenge \lnot \mathrm{A}\),
- (c):
-
(\(\square ^{2}\mathrm{A } \wedge \square \lozenge \mathrm{A}\)) -||- \(\square ^{2}\)A similarly, and
- (d):
-
(\(\square \lozenge \mathrm{A} \wedge \square \lozenge \lnot \mathrm{A}\)) -||- \(\square (\lozenge \mathrm{A }\wedge \lozenge \lnot \mathrm{A}\)) -||-
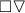 A.
A. - (iii):
-
& (iv). From (i) and (ii) by the properties of S4.\(\square \)
 A provably implies
A provably implies  A in S4.
A in S4.
 A -||- \((\lozenge \mathrm{A }\,\wedge \, \lozenge \square \lnot \mathrm{A}) \,\vee \, (\lozenge \lnot \mathrm{A}\, \wedge \, \lozenge \square \mathrm{A}\)) by Lemma 2(i). But \(\lozenge \square \lnot \mathrm{A} \vdash \)\(\lozenge \lozenge \lnot \mathrm{A} \vdash \)\(\lozenge \lnot \mathrm{A}\); and so (\(\lozenge \mathrm{A }\wedge \lozenge \square \lnot \mathrm{A}) \vdash \)\(\lozenge \mathrm{A }\wedge \lozenge \lnot \mathrm{A}\) =
A -||- \((\lozenge \mathrm{A }\,\wedge \, \lozenge \square \lnot \mathrm{A}) \,\vee \, (\lozenge \lnot \mathrm{A}\, \wedge \, \lozenge \square \mathrm{A}\)) by Lemma 2(i). But \(\lozenge \square \lnot \mathrm{A} \vdash \)\(\lozenge \lozenge \lnot \mathrm{A} \vdash \)\(\lozenge \lnot \mathrm{A}\); and so (\(\lozenge \mathrm{A }\wedge \lozenge \square \lnot \mathrm{A}) \vdash \)\(\lozenge \mathrm{A }\wedge \lozenge \lnot \mathrm{A}\) =  A. Similarly, (\(\lozenge \lnot \mathrm{A} \wedge \lozenge \square \mathrm{A}\)) \(\vdash \)
A. Similarly, (\(\lozenge \lnot \mathrm{A} \wedge \lozenge \square \mathrm{A}\)) \(\vdash \) A; and so
A; and so  A \(\vdash \)
A \(\vdash \) A.\(\square \)
A.\(\square \)
Say that the formula A is boxablein the system S if \(\square \)A is consistent in S and that otherwise A is unboxable. (Any inconsistent formula is trivially unboxable and so our interest is only in the consistent unboxable formulas).
FormalPara Theorem 4The formula  A is unboxable in S4.
A is unboxable in S4.
By Lemma 3,  A \(\vdash \)
A \(\vdash \) A. Also:
A. Also:
-
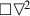 A
A -
\(\vdash \)
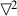 A
A -
\(\vdash \) (\(\lozenge \mathrm{A} \wedge \lozenge \square \lnot \mathrm{A}) \vee (\lozenge \lnot \mathrm{A} \wedge \lozenge \square \mathrm{A}\)) by Lemma 2(i)
-
\(\vdash \)\(\lozenge \square \lnot \mathrm{A} \vee \lozenge \square \mathrm{A}\).
So  A \(\vdash \) (
A \(\vdash \) ( A)
A)  A). But (
A). But ( A) \(\vdash \)
A) \(\vdash \) A) \(\vdash \)\(\bot \) and (
A) \(\vdash \)\(\bot \) and ( A) \(\vdash \)
A) \(\vdash \) A) \(\vdash \)\(\bot \); and so
A) \(\vdash \)\(\bot \); and so  A \(\vdash \)\(\bot \).\(\square \)
A \(\vdash \)\(\bot \).\(\square \)
Let us observe that it can also be shown that  A is unboxable in K4[D], where K4[D] is the non-normal extension of K4 with the axiom \(\mathrm{D} = \lozenge \top \). So this result includes certain unimodal tense logics, certain logics of belief, and the logic of provability (with the understanding that its theorems should be true but not necessarily provable).Footnote 6
A is unboxable in K4[D], where K4[D] is the non-normal extension of K4 with the axiom \(\mathrm{D} = \lozenge \top \). So this result includes certain unimodal tense logics, certain logics of belief, and the logic of provability (with the understanding that its theorems should be true but not necessarily provable).Footnote 6
For \(m, n > 1,\)A -||-  A in S4.
A in S4.
 A \(\vdash \)
A \(\vdash \) A by Lemma 3; and so, substituting
A by Lemma 3; and so, substituting  A for A,
A for A,  A \(\vdash \)
A \(\vdash \) A. By Theorem 4, \(\vdash \)
A. By Theorem 4, \(\vdash \) A \(\vdash \)
A \(\vdash \) A; and so
A; and so  A \(\vdash \)
A \(\vdash \) A
A  A \(\vdash \)
A \(\vdash \) A. Hence
A. Hence  A -||-
A -||-  A. Appropriately substituting for A,
A. Appropriately substituting for A,  A -||-
A -||-  , \(\hbox {k} >1\), from which the result follows.
, \(\hbox {k} >1\), from which the result follows.
By a contingency profile\(\upalpha \) is meant an infinite sequence \(\upalpha _{1}\upalpha _{2}\upalpha _{3 }\ldots \) of T’s and F’s. Corresponding to a contingency profile \(\upalpha \) is the set  = \(\{\mathrm{A}_{1}, \mathrm{A}_{2}, \mathrm{A}_{3}, \ldots \}\), where \(\mathrm{A}_{\mathrm{k}}\) is
= \(\{\mathrm{A}_{1}, \mathrm{A}_{2}, \mathrm{A}_{3}, \ldots \}\), where \(\mathrm{A}_{\mathrm{k}}\) is  \(\mathrm{p}\) when \(\upalpha _\mathrm{k }\) is T and \(\mathrm{A}_\mathrm{k}\) is
\(\mathrm{p}\) when \(\upalpha _\mathrm{k }\) is T and \(\mathrm{A}_\mathrm{k}\) is  p when \(\upalpha _\mathrm{k }\) is F. A contingency profile \(\upalpha \) is said to be consistent in the system S if the corresponding set
p when \(\upalpha _\mathrm{k }\) is F. A contingency profile \(\upalpha \) is said to be consistent in the system S if the corresponding set  is consistent in S. \(\square \)
is consistent in S. \(\square \)
A contingency profile \(\upalpha \) is consistent in S4 iff it is of the form FFF \(\ldots \) or TFF \(\ldots \) or TTT \(\ldots \).
FormalPara ProofBy Corollary 5, a consistent contingency profile must be of the form \(\upalpha _{1}\)FF \(\ldots \) or \(\upalpha _{1}\)TT \(\ldots \). But it is readily shown that if \(\upalpha _{1} = \mathrm{F}\) then each \(\upalpha _{k} =\mathrm{F}\).
The consistency of FFF \(\ldots \) is established by the model:
the consistency of TFF \(\ldots \) by the model:
and the consistency of TTT \(\ldots \) by the model:
\(\square \)
We may establish some somewhat more general results:
FormalPara Theorem 7For \(n > 0\), the formulas \(), \) and  are unboxable in S4.
are unboxable in S4.
Let us deal with the formula  (the proof for the second formula is similar).
(the proof for the second formula is similar).
-
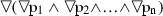
-
\(\vdash \)\(\lozenge (\lozenge \mathrm{p}_{1} \wedge \lozenge \lnot \mathrm{p}_{1} \wedge \lozenge \mathrm{p}_{2} \wedge \lozenge \lnot \mathrm{p}_{2} \wedge \)...\( \wedge \lozenge \mathrm{p}_{\mathrm{n}} \wedge \lozenge \lnot \mathrm{p}_{\mathrm{n}})\) by def. of
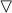 and the system T
and the system T -
\(\vdash \)\(\lozenge \lozenge \mathrm{p}_{1} \wedge \lozenge \lozenge \lnot \mathrm{p}_{1} \wedge \lozenge \lozenge \mathrm{p}_{2} \wedge \lozenge \lozenge \lnot \mathrm{p}_{2}\,\wedge \,\)...\(\,\wedge \,\lozenge \lozenge \mathrm{p}_{\mathrm{n}} \wedge \lozenge \lozenge \lnot \mathrm{p}_{\mathrm{n}}\) by T
-
\(\vdash \)\(\lozenge \mathrm{p}_{1} \wedge \lozenge \lnot \mathrm{p}_{1} \wedge \lozenge \mathrm{p}_{2} \wedge \lozenge \lnot \mathrm{p}_{2}\,\wedge \,\)...\(\,\wedge \,\lozenge \mathrm{p}_{\mathrm{n}} \wedge \lozenge \lnot \mathrm{p}_{\mathrm{n}})\) by S4.
Hence:
(*)  \(\square [\lozenge \mathrm{p}_{1} \wedge \lozenge \lnot \mathrm{p}_{1} \wedge \lozenge \mathrm{p}_{2} \wedge \lozenge \lnot \mathrm{p}_{2}\,\wedge \,\)...\(\,\wedge \, \lozenge \mathrm{p}_{\mathrm{n}} \wedge \lozenge \lnot \mathrm{p}_{\mathrm{n}}\)].
\(\square [\lozenge \mathrm{p}_{1} \wedge \lozenge \lnot \mathrm{p}_{1} \wedge \lozenge \mathrm{p}_{2} \wedge \lozenge \lnot \mathrm{p}_{2}\,\wedge \,\)...\(\,\wedge \, \lozenge \mathrm{p}_{\mathrm{n}} \wedge \lozenge \lnot \mathrm{p}_{\mathrm{n}}\)].
Also:
-
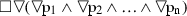
-
\(\vdash \)
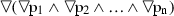
-
\(\vdash \)
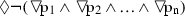
-
\(\vdash \)
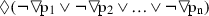
-
\(\vdash \lozenge (\square \mathrm{p}_{1} \vee \square \lnot \mathrm{p}_{1}\vee \square \mathrm{p}_{2} \vee \square \lnot \mathrm{p}_{2 }\,\vee \,\ldots \,\vee \, \square \mathrm{p}_{\mathrm{n}} \vee \square \lnot \mathrm{p}_{\mathrm{n}})\).
But then, given (*) above, it follows that:
-
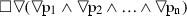
-
\(\vdash \)\(\lozenge [(\square \mathrm{p}_{1} \vee \square \lnot \mathrm{p}_{1} \vee \square \mathrm{p}_{2} \vee \square \lnot \mathrm{p}_{2 }\,\vee \,\)...\(\,\vee \,\, \square \mathrm{p}_{\mathrm{n}} \vee \, \square \lnot \mathrm{p}_{\mathrm{n}}) \wedge (\lozenge \mathrm{p}_{1} \wedge \lozenge \lnot \mathrm{p}_{1} \wedge \lozenge \mathrm{p}_{2} \wedge \lozenge \lnot \mathrm{p}_{2}\,\wedge \,\)...\(\,\wedge \, \lozenge \mathrm{p}_{\mathrm{n}} \wedge \lozenge \lnot \mathrm{p}_{\mathrm{n}})\)],
which is readily shown to be contradictory.
The proof for the formula  is straightforward since if
is straightforward since if  were boxable then
were boxable then  would also be boxable.
would also be boxable.
The final case is the formula  . We prove
. We prove  inconsistent in S4 by induction on n. The case n = 1 is Theorem 4. Consider the case n = k +1. Suppose, for reduction,
inconsistent in S4 by induction on n. The case n = 1 is Theorem 4. Consider the case n = k +1. Suppose, for reduction,  . Then
. Then  and so (\(\lozenge \mathrm{p}_{1} \,\wedge \lozenge \square \lnot \mathrm{p}_{1})\, \vee \) (\(\lozenge \lnot \mathrm{p}_{1} \wedge \lozenge \square \mathrm{p}_{1}) \vee \) (\(\lozenge \mathrm{p}_{2} \wedge \lozenge \square \lnot \mathrm{p}_{2})\, \vee \) (\(\lozenge \lnot \mathrm{p}_{2} \wedge \lozenge \square \mathrm{p}_{2})\,...\) \(\vee \) (\(\lozenge \mathrm{p}_{\mathrm{n}} \wedge \lozenge \square \lnot \mathrm{p}_{\mathrm{n}})\,\, \vee \) (\(\lozenge \lnot \mathrm{p}_{\mathrm{n}} \wedge \lozenge \square \mathrm{p}_{\mathrm{n}})\). Without loss of generality, suppose (\(\lozenge \mathrm{p}_{1} \wedge \lozenge \square \lnot \mathrm{p}_{1})\) and so, in particular, \(\lozenge \square \lnot \mathrm{p}_{1}\). Given \(\square \)(
and so (\(\lozenge \mathrm{p}_{1} \,\wedge \lozenge \square \lnot \mathrm{p}_{1})\, \vee \) (\(\lozenge \lnot \mathrm{p}_{1} \wedge \lozenge \square \mathrm{p}_{1}) \vee \) (\(\lozenge \mathrm{p}_{2} \wedge \lozenge \square \lnot \mathrm{p}_{2})\, \vee \) (\(\lozenge \lnot \mathrm{p}_{2} \wedge \lozenge \square \mathrm{p}_{2})\,...\) \(\vee \) (\(\lozenge \mathrm{p}_{\mathrm{n}} \wedge \lozenge \square \lnot \mathrm{p}_{\mathrm{n}})\,\, \vee \) (\(\lozenge \lnot \mathrm{p}_{\mathrm{n}} \wedge \lozenge \square \mathrm{p}_{\mathrm{n}})\). Without loss of generality, suppose (\(\lozenge \mathrm{p}_{1} \wedge \lozenge \square \lnot \mathrm{p}_{1})\) and so, in particular, \(\lozenge \square \lnot \mathrm{p}_{1}\). Given \(\square \)( and so \(\lozenge \square (\square \lnot \mathrm{p}_{1} \wedge \) (
and so \(\lozenge \square (\square \lnot \mathrm{p}_{1} \wedge \) ( . But \(\square \lnot \mathrm{p}_{1}\) is inconsistent with
. But \(\square \lnot \mathrm{p}_{1}\) is inconsistent with  and so
and so  , which is inconsistent by the inductive hypothesis.\(\square \)
, which is inconsistent by the inductive hypothesis.\(\square \)
A p-formula is any formula whose sole sentence letter is p. The formula A is modalized if every sentence letter of A occurs within the scope of a model operator.
Any p-formula \(\square \)B, for B non-modal, is equivalent in T to: \(\top \), \(\bot \), \(\square \)p, or \(\square \lnot \mathrm{p}\).
FormalPara ProofAny non-modal p-formula B is equivalent to \(\top \), \(\bot \), p, or \(\lnot \mathrm{p}\); and from this it is readily shown that any p-formula \(\square \mathrm{B}\), for B non-modal, is equivalent to \(\top \), \(\bot \), \(\square \mathrm{p}\), or \(\square \lnot \mathrm{p}\).\(\square \)
Say that the formula A is completefor a class of formulas \(\Delta \)in the modal system S if for any formula B of \(\Delta \) either A \(\vdash \)\(_{\mathrm{S}}\) B or A \(\vdash \)\(_{\mathrm{S}} \lnot \mathrm{B}\).
FormalPara Lemma 9In S4, each of the formulas \(\square \)p, \(\square \lnot \mathrm{p}\) and  A is complete for the class of modalized p-formulas.
A is complete for the class of modalized p-formulas.
We first show by inspection that each of the formulas \(\square \mathrm{p}\), \(\square \lnot \mathrm{p}\) and  is complete for the class of formulas \(\{\top , \bot , \square \mathrm{p}, \square \lnot \mathrm{p}\}\) and hence, by the previous lemma, is complete for the class of all p-formulas of the form \(\square \mathrm{B}\), for B non-modal.
is complete for the class of formulas \(\{\top , \bot , \square \mathrm{p}, \square \lnot \mathrm{p}\}\) and hence, by the previous lemma, is complete for the class of all p-formulas of the form \(\square \mathrm{B}\), for B non-modal.
It is easy to show that completeness is preserved under negation and conjunction, i.e. that if A is complete for \(\Delta \) then it is complete for \(\{\lnot \mathrm{C}: \mathrm{C} \in \Delta \}\) and for \(\{\mathrm{C}\,\wedge \,\mathrm{D}: \mathrm{C},\mathrm{D }\in \Delta \}\). It therefore suffices to show that completeness is preserved under necessitation, i.e. that if A is complete for \(\Delta \) then it is complete for \(\{\square \mathrm{C}:\mathrm{C }\in \Delta \}\). But it is readily shown that completeness is preserved under necessitation for any formula of the form \(\square \mathrm{B}\). For suppose \(\square \mathrm{B}\) is complete for the class of formulas \(\Delta \). Take now any formula of the form \(\square \mathrm{C}\) for C \(\in \Delta \). Then either \(\square \mathrm{B} \vdash \)\(\mathrm{C}\,\mathrm{or }\, \square \mathrm{B} \vdash \)\(\lnot \mathrm{C}\). In the former case, \(\square \square \mathrm{B} \vdash \)\(\square \mathrm{C}\) and so \(\square \mathrm{B} \vdash \)\(\square \mathrm{C}\) given that, in S4, \(\square \mathrm{B} \vdash \)\(\square \square \mathrm{B}\). In the latter case, \(\square \square \mathrm{B} {\vdash }\)\(\square \lnot \mathrm{C}\) and so \(\square \mathrm{B} \vdash \)\(\square \square \mathrm{B} {\vdash }\)\(\square \lnot \mathrm{C} \vdash \)\(\lnot \square \mathrm{C}\).\(\square \)
It can be shown that, in contrast to the case for S4, there is no consistent p-formula of T that is complete for the class of modalized p-formulas.
FormalPara Theorem 10In the system S4, the modalized p-formula A is unboxable iff it implies  p.
p.
The right to left direction follows from Theorem 4. For the other direction, suppose that A does not imply  . Then A is consistent with
. Then A is consistent with  and hence, by Lemma 2(iv), consistent with
and hence, by Lemma 2(iv), consistent with  . But then A is consistent with \(\square \mathrm{p}\) or \(\square \lnot \mathrm{p}\) or
. But then A is consistent with \(\square \mathrm{p}\) or \(\square \lnot \mathrm{p}\) or  . So by Lemma 9, one of these three formulas of the form \(\square \mathrm{B}\) implies A. But then \(\square \mathrm{B}\) implies \(\square \mathrm{A}\) and, since \(\square \mathrm{B}\) is consistent then so is \(\square \mathrm{A}\).\(\square \)
. So by Lemma 9, one of these three formulas of the form \(\square \mathrm{B}\) implies A. But then \(\square \mathrm{B}\) implies \(\square \mathrm{A}\) and, since \(\square \mathrm{B}\) is consistent then so is \(\square \mathrm{A}\).\(\square \)
This result does not hold when the requirement that the formula A be modalized is dropped. For consider the Fitch formula p \(\wedge \, \lozenge \lnot \mathrm{p}\). As is well known, this is unboxable (in T and not just S4). However, it does not imply  (even in S4) since it is compatible with
(even in S4) since it is compatible with  .
.
Indeed, it may be shown that:
FormalPara Theorem 11In S4, there is no weakest unboxable p-formula, i.e. no unboxable p-formula implied by all unboxable formulas.
FormalPara Proofp \(\wedge \, \lozenge \lnot \mathrm{p} {\mathrm{and}} \lnot \mathrm{p}\, \wedge \, \lozenge \mathrm{p}\) are both unboxable. Now if there were a weakest unboxable formula A, it would be implied by both p \(\wedge \lozenge \lnot \mathrm{p}\) and \(\lnot \mathrm{p}\,\wedge \,\lozenge \mathrm{p}\) and hence implied by their disjunction (p \(\wedge \,\lozenge \lnot \mathrm{p}) \vee (\lnot \mathrm{p} \wedge \lozenge \mathrm{p}\)), which is equivalent in T to  . But
. But  is consistent in S4 and hence so is \(\square \mathrm{A}\) and A would be boxable after all.\(\square \)
is consistent in S4 and hence so is \(\square \mathrm{A}\) and A would be boxable after all.\(\square \)
It should be noted that any unboxable formula A (in T) will imply a Fitch formula of the form B \(\wedge \, \lozenge \lnot \mathrm{B}\) for, since \(\lozenge \lnot \mathrm{A}\) is a theorem, A will imply and, indeed, be equivalent to A \(\wedge \,\lozenge \lnot \mathrm{A}\). However, this is not a case in which we can attribute the unboxability of A to that of A \(\wedge \,\lozenge \lnot \mathrm{A}\), since the unboxability of A is already presupposed. I do not know if there is a meaningful result in which we are able to attribute the unboxability of p-formulas in T to a common source.
An (affirmative) modality is a (possibly empty) string of \(\square \)’s and \(\lozenge \)’s; and an extended (affirmative) modality is a (possibly empty) string of \(\square \)’s, \(\lozenge \)’s and  ’s. Two modalities \(\upvarphi \) and \(\uppsi \) are equivalent in a given system if \(\upvarphi \mathrm{p}\) is provably equivalent to \(\uppsi \mathrm{p}\) in the system; and similarly, for when one modality implies another.
’s. Two modalities \(\upvarphi \) and \(\uppsi \) are equivalent in a given system if \(\upvarphi \mathrm{p}\) is provably equivalent to \(\uppsi \mathrm{p}\) in the system; and similarly, for when one modality implies another.
It is well known that are are exactly 7 non–equivalent modalities in S4. Using \(\wedge \) for the empty string, any modality is equivalent in S4 to one of: \(\wedge \), \(\square \), \(\lozenge \), \(\lozenge \square \), \(\square \lozenge \), \(\lozenge \square \lozenge \) and \(\square \lozenge \square \). Using the easy direction of Theorem 10 and some of our earlier results, we can extend this result to the extended modalities.
FormalPara Theorem 12Any extended modality is equivalent in S4 either to an unextended modality or to one of the following:  .
.
Show that the result of prefixing \(\square \), \(\lozenge \) or  to any modality on the list is equivalent to a modality on the list. We do not go into details but let us note that Theorem 10 is useful in that if we can show that a modality of the form \( \ldots \) implies
to any modality on the list is equivalent to a modality on the list. We do not go into details but let us note that Theorem 10 is useful in that if we can show that a modality of the form \( \ldots \) implies  then it follows that \( \ldots \) is equivalent to \( \ldots \) (since
then it follows that \( \ldots \) is equivalent to \( \ldots \) (since  is equivalent to \()\), that \( \ldots \) is equivalent to
is equivalent to \()\), that \( \ldots \) is equivalent to  , which is equivalent to \(\bot \), and that \( \ldots \) is equivalent to \(\ldots \). \(\square \)
, which is equivalent to \(\bot \), and that \( \ldots \) is equivalent to \(\ldots \). \(\square \)
Thus, as with unextended modalities, any extended modality will be equivalent to one of length at most 3. It may be verified that all of the modalities listed under the corollary are non-equivalent. I do not know if there are any normal modal systems that have only finitely many non-equivalent modalities but infinitely many non-equivalent extended modalities.
We turn finally to the possibilities for contingency within T and other logics. But first we review a familiar result on modal degree. The modal degree md(A) of a formula A is the maximum number of nested occurrences of \(\square \) within the formula. It may be recursively defined by:
-
md(p) = 0
-
md\((\lnot \mathrm{A})\) = md(A)
-
md((A \(\vee \) B)) = max(md(A), md(B))
-
md(\(\square \)A) = md(A) + 1.
Given a binary relation R on a set W, we take \(wR^\mathrm{n}v\) to hold, for w, \(v \in W\) and \(\mathrm{n} \ge 0\), if there is a sequence of elements \(w_{0}, w_{1}, \ldots , w_{\mathrm{n}}\) for \(w_{0}=w\), \(w_{\mathrm{n}}=v\) and \(w_{\mathrm{k}}\,Rw_{\mathrm{k+1}}\) for \(\mathrm{k} = 0, 1, \ldots , \mathrm{n-1}\); and given a Kripke model \({\varvec{M}} = (W, R, \upvarphi , w)\), we let \({\varvec{M}}^\mathrm{n}\), for \(\mathrm{n} \ge 0\), be the model (\(W^\mathrm{n}, R^\mathrm{n}, \upvarphi ^\mathrm{n}, w)\), where \(W^\mathrm{n} = \{v \in W: wR^\mathrm{k}v\) for \(\mathrm{k} \le \mathrm{n}\}\) and \(R^\mathrm{n}\) and \(\upvarphi ^\mathrm{n}\) are the restriction of R and \(\upvarphi \) to \(W^\mathrm{n}\).
FormalPara Lemma 13Given any formula A of modal degree \(\le \) n and any model \({\varvec{M}} = (W, R, \upvarphi , w)\):
A is true at \({\varvec{M}}\) iff A is true at \({\varvec{M}}^\mathrm{n}\).
FormalPara ProofBy a straightforward induction on n.\(\square \)
Use of the lemma will often be implicit.
By a strip model of order n, n \(\ge \) 0, is meant a Kripke-model of the form \({\varvec{{M}}} = (W, R, \upvarphi , 0\)), where:
-
(i)
\(W = \{0, 1, 2, \ldots , \hbox {n}\}\);
-
(ii)
\(R = \{<\mathrm{k}, \mathrm{k+1}>: \mathrm{k} = 0, 1, 2, \ldots , \hbox {n -1}\} \cup \{<\mathrm{k}, \mathrm{k}>: \mathrm{k} \in \mathrm{W}\}\)
Note that the valuation \(\upvarphi \) is left undetermined; and, since our only interest is in the single sentence letter p, \(\upvarphi \) will be determined by an assignment of truth-values to each of the worlds 0, 1, 2, ..., n. We may therefore represent \(\upvarphi \) by a sequence \(\hbox {p}_{0}\mathrm{p}_{1} \ldots \hbox {p}_{\mathrm{n}}\) of length n + 1, where \(\hbox {p}_{\mathrm{k}}\) is p should p be true at k and \(\hbox {p}_\mathrm{k}\) is should p be false at k. Thus a strip model will look like so:
We say that the strip model \({{\varvec{M}}} = (W^{+}, R^{+}, \upvarphi ^{+}, 0\}\) of order n+1 extends the strip model \({\varvec{{M}}} ^{+} = (W, R, \upvarphi , 0\)) of order n if \(\upvarphi \) is the restriction of \(\upvarphi ^{+ }\) to W, i.e. if the truth-values of p at the worlds 0, 1, 2, ..., n are the same in each model. Let us use ±A ambiguously for A or \(\lnot \mathrm{A}\). \(\square \)
FormalPara Lemma 14For each strip model \({{\varvec{M}}} = (W, R, \upvarphi , 0\)) of order n and each formula  , there is an extension \({{\varvec{M}}}^{+} = (\mathrm{W}^{+}, \mathrm{R}^{+}, \upvarphi ^{+}, 0\)) of \({{\varvec{M}}} = (W, R, \upvarphi , 0\)) at which
, there is an extension \({{\varvec{M}}}^{+} = (\mathrm{W}^{+}, \mathrm{R}^{+}, \upvarphi ^{+}, 0\)) of \({{\varvec{M}}} = (W, R, \upvarphi , 0\)) at which  is true.
is true.
By induction on n. For each n, there are two cases to consider: when  and when
and when  .
.
n = 0 The given model \({{\varvec{M}}} = (W, R, \upvarphi , 0\)) is of the form \((\{0\}, R, \upvarphi , 0\)) and the associated sequence is either p or \({\bar{\mathrm{p}}}\).
Suppose first that  . If the associated sequence is p, we may let the sequence associated with \({{\varvec{M}}}^{+}\) be \(\hbox {p}{\bar{\mathrm{p}}}\); and if the associated sequence is, we may let the sequence associated with \({{\varvec{M}}}^{+}\) be \({\bar{\mathrm{p}}}\)p.
. If the associated sequence is p, we may let the sequence associated with \({{\varvec{M}}}^{+}\) be \(\hbox {p}{\bar{\mathrm{p}}}\); and if the associated sequence is, we may let the sequence associated with \({{\varvec{M}}}^{+}\) be \({\bar{\mathrm{p}}}\)p.
Now suppose that  . If the associated sequence is p, we may let the sequence associated with \({{\varvec{M}}}^{+}\) be pp; and if the associated sequence is \(({\bar{\mathrm{p}}})\), we may let the sequence associated with \({{\varvec{M}}}^{+}\) be \({\bar{\mathrm{p}}}{\bar{\mathrm{p}}}\).
. If the associated sequence is p, we may let the sequence associated with \({{\varvec{M}}}^{+}\) be pp; and if the associated sequence is \(({\bar{\mathrm{p}}})\), we may let the sequence associated with \({{\varvec{M}}}^{+}\) be \({\bar{\mathrm{p}}}{\bar{\mathrm{p}}}\).
\(\underline{\mathrm{n = k+1}}\) The given model \({{\varvec{M}}} = (W, R, \upvarphi , 0\)) is of the form \((\{0, 1, \ldots , \hbox {k+1}\}, R, \upvarphi , 0\)).
Suppose first that  . There are two subcases. (a)
. There are two subcases. (a)  is true at \({{\varvec{M}}}\). Consider the model \({{\varvec{N}}} = (W, R, \upvarphi , 1\)). By IH, there is an extension \({{\varvec{N}}}^{+}\) of \({{\varvec{N}}}^\mathrm{k}\) (which no longer contains the point 0) at which
is true at \({{\varvec{M}}}\). Consider the model \({{\varvec{N}}} = (W, R, \upvarphi , 1\)). By IH, there is an extension \({{\varvec{N}}}^{+}\) of \({{\varvec{N}}}^\mathrm{k}\) (which no longer contains the point 0) at which  is true. Let \({{\varvec{M}}}^{+}\) be the corresponding extension of \({{\varvec{M}}}\) (in which the point 0 is restored). Then
is true. Let \({{\varvec{M}}}^{+}\) be the corresponding extension of \({{\varvec{M}}}\) (in which the point 0 is restored). Then  will be true at 0 in \({{\varvec{M}}}^{+}\) and
will be true at 0 in \({{\varvec{M}}}^{+}\) and  false at 1 in \({{\varvec{M}}}^{+}\); and so
false at 1 in \({{\varvec{M}}}^{+}\); and so  will be true at \({{\varvec{M}}}^{+}\). (b)
will be true at \({{\varvec{M}}}^{+}\). (b)  is false at \({{\varvec{M}}}\). The proof is similar to that for (a) but with the role of
is false at \({{\varvec{M}}}\). The proof is similar to that for (a) but with the role of  and
and  reversed.
reversed.
Now suppose  . Again, there are two subcases. (a)
. Again, there are two subcases. (a)  is true at \({{\varvec{M}}}\). By IH, there is an extension \({{\varvec{N}}}^{+}\) of \({{\varvec{N}}}^\mathrm{k}\) at which
is true at \({{\varvec{M}}}\). By IH, there is an extension \({{\varvec{N}}}^{+}\) of \({{\varvec{N}}}^\mathrm{k}\) at which  is true (with \({{\varvec{N}}}\) as before). Let \({{\varvec{M}}}^{+}\) be the corresponding extension of \({{\varvec{M}}}\). Then
is true (with \({{\varvec{N}}}\) as before). Let \({{\varvec{M}}}^{+}\) be the corresponding extension of \({{\varvec{M}}}\). Then  will be true at 0 in \({{\varvec{M}}}^{+}\) and
will be true at 0 in \({{\varvec{M}}}^{+}\) and  true at 1 in \({{\varvec{M}}}^{+}\); and so
true at 1 in \({{\varvec{M}}}^{+}\); and so  and hence
and hence  will be true at \({{\varvec{M}}}^{+}\). (b)
will be true at \({{\varvec{M}}}^{+}\). (b)  is false at \({{\varvec{M}}}\). By IH, there is an extension \({{\varvec{N}}}^{+}\) of \({{\varvec{N}}}^\mathrm{k}\) at which
is false at \({{\varvec{M}}}\). By IH, there is an extension \({{\varvec{N}}}^{+}\) of \({{\varvec{N}}}^\mathrm{k}\) at which  is true. Let \({{\varvec{M}}}^{+}\) be the corresponding extension of \({{\varvec{M}}}\). Then
is true. Let \({{\varvec{M}}}^{+}\) be the corresponding extension of \({{\varvec{M}}}\). Then  will be true at 0 in \({{\varvec{M}}}^{+}\) and also true at 1 in \({{\varvec{M}}}^{+}\); and so
will be true at 0 in \({{\varvec{M}}}^{+}\) and also true at 1 in \({{\varvec{M}}}^{+}\); and so  and hence
and hence  will be true at \({{\varvec{M}}}^{+}\).\(\square \)
will be true at \({{\varvec{M}}}^{+}\).\(\square \)
Each set of formulas  is consistent in the system T.
is consistent in the system T.
By Lemma 14, there will be a strip model \({{\varvec{M}}}_{1}\) (of order 1) at which  , an extension \({{\varvec{M}}}_{2}\) of \({{\varvec{M}}}_{1}\) at which
, an extension \({{\varvec{M}}}_{2}\) of \({{\varvec{M}}}_{1}\) at which  and
and  are true; and so on. The union \({{\varvec{M }}}\) of the models \({{\varvec{M}}}_{1}\), \({{\varvec{M}}}_{2}, \ldots \) will then be a model for
are true; and so on. The union \({{\varvec{M }}}\) of the models \({{\varvec{M}}}_{1}\), \({{\varvec{M}}}_{2}, \ldots \) will then be a model for  since each of \({{\varvec{M}}}_{1}, {{\varvec{M}}}_{2}\), ...are generated submodels of \({{\varvec{M}}}\) and hence will agree with \({{\varvec{M}}}\). \(\square \)
since each of \({{\varvec{M}}}_{1}, {{\varvec{M}}}_{2}\), ...are generated submodels of \({{\varvec{M}}}\) and hence will agree with \({{\varvec{M}}}\). \(\square \)
For each formula A, let \(\square ^{\infty }\)A be the set of formulas \(\{\mathrm{A}, \square \mathrm{A}, \square ^{2}\mathrm{A}, \square ^{3}\mathrm{A}, \ldots \}\).
FormalPara Corollary 16For each \(\hbox {n} = 1, 2, \ldots ,\) is consistent in T.
is consistent in T.
By the theorem,  is consistent in T. But it is then readily shown that each of the formulas
is consistent in T. But it is then readily shown that each of the formulas  , \(\ldots \) is a consequence of
, \(\ldots \) is a consequence of  .\(\square \)
.\(\square \)
The strip models (and their unions) satisfy the condition that wRv and wRu implies \(w=v \) or \(w=u\) or \(u=v\). The various results will therefore also hold in the system obtained by adding the ‘linearity’ axiom \(\hbox {A} \vee \square (\hbox {A } \supset \hbox { B) }\vee \square \hbox {(A }\supset \lnot {\mathrm{B}}\)) to T. The corollary can also be established for the system B.
Notes
I am grateful to Eli Alshanetsky, Tom Donaldson, Tim Williamson, the participants in an Academia discussion session and two referees for helpful comments.
The critical observation that second order ignorance implies first order ignorance (Remark (1) below and Lemma 3 of the appendix) goes back to Montgomery and Routley (1966). The earlier literature also deals with some related issues. Montgomery and Routley (1968), Humberstone (1995) and Kuhn (1995) investigate the question of axiomatizing a modal logic with a contingency (or non-contingency) operator as primitive; Cresswell (1988) and Humberstone (1995) consider the question of when necessity can be defined in terms of contingency; and Montgomery and Routley (1966, 1969) and Mortensen (1976) study logics obtained by adding various special non-contingency axioms to a base logic of non-contingency. Hoek and Lomuscio (2004) is a more recent treatment of some of these questions, though apparently written in ignorance of the earlier literature.
I have talked in this section on ‘orders’ in an informal way. See Williamson (1999) for a more formal discussion of the notion.
See Brogaard and Salerno (2013) for a survey of recent work on the topic.
The system S4M, in which all continency is contingent, features prominently in Suzanne Bobzien’s work on vagueness, as in Bobzien (2010) for example.
Thanks to Martin Pleitz for pointing me in the direction of this observation.
References
Bobzien, S. (2010). Higher-order vagueness, radical unclarity and absolute agnosticism. Philosophers’ Imprint, 10(10), 1–30.
Brogaard, B., & Salerno, J. (2013) Fitch’s paradox of unknowability. In Stanford encyclopedia of philosophy. https://plato.stanford.edu/entries/fitch-paradox/.
Cresswell, M. J. (1988). Necessity and contingency. Studia Logica, 47, 145–149.
Fine, K. (2008). The impossibility of vagueness. Philosophical Perspectives, 22(1), 111–136.
Fitch, F. (1963). A logical analysis of some value concepts. The Journal of Symbolic Logic, 28, 135–142.
Humberstone, I. L. (1995). The logic of non-contingency. Notre Dame Journal of Formal Logic, 36(2), 214–229.
Kuhn, T. S. (1995). Minimal non-contingency logics. Notre Dame Journal of Formal Logic, 36, 230–234.
Montgomery, H., & Routley, R. (1966). Contingency and non-contingency bases for normal modal logics. Logique et Analyse, 9, 318–328.
Montgomery, H., & Routley, R. (1968). Non-contingency axioms for S4 and S5. Logique et Analyse, 11, 422–424.
Montgomery, H., & Routley, R. (1969). Modalities in a sequence of normal non-contingency modal systems. Logique et Analyse, 12, 225–227.
Mortensen, C. (1976). A sequence of normal modal systems with non-contingency bases. Logique et Analyse, 19, 341–344.
Van der Hoek, W., & Lomuscio, A. (2004). A logic for ignorance. Electronic Notes in Computer Science, 85(2), 1–17.
Williamson, Timothy. (1999). On the structure of higher-order vagueness. Mind, 108, 127–142.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Fine, K. Ignorance of ignorance. Synthese 195, 4031–4045 (2018). https://doi.org/10.1007/s11229-017-1406-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11229-017-1406-z




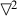 A is provably equivalent in T to
A is provably equivalent in T to 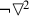 A is provably equivalent in T to
A is provably equivalent in T to 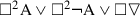 A
A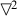 A is provably equivalent in S4 to
A is provably equivalent in S4 to 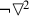 A is provably equivalent in S4 to
A is provably equivalent in S4 to 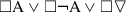 A
A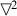 A
A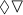 A
A 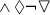 A by definition of
A by definition of 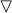
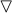
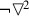 A
A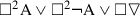 A
A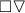 A.
A.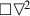 A
A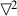 A
A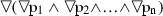
 and the system T
and the system T