1 Introduction

The problems of enumerating structures such as circuits, paths, trees and cliques in graphs and networks are of fundamental importance. This kind of tasks is usually hard to deal with, due to its challenging time/space complexity. Indeed, even a small graph may contain a huge number of such structures. In the enumeration process, it is important to point that counting and finding are two different processes: Finding is the construction of elements, and counting is determining their number. Generally, knowing the count is rarely useful in finding the objects and even if we are able to count the elements in polynomial time, we might not be able to find all of them due to an exponential number of elements and huge memory requirements. In the following, we will use enumeration and finding interchangeably.

Our interest is in finding the elementary circuits of a directed graph, which is a fundamental problem of graph theory. A circuit is a loop through which information propagates and it is widely used in real-world applications. For example, circuits can reveal money laundering in the financial system [1]. They represent fragile ecosystem dependencies in food webs [2]. Finding circuits is also interesting in fraud detection [3]. Circuits serve as a method for social network analysis and modeling [4] and are used to evaluate networks balance [5]. Finding circuits is also important in biology [6,7,8], and Internet systems [9].

The first algorithms proposed for finding elementary circuits of a directed graph require either a lot of memory or have exponential running time [10, 11]. As a result, they become impractical as the graph size increases. The algorithm by Johnson [12] is one of the most efficient algorithms for finding elementary circuits. It is still the best state of art algorithm, yet it may fail to handle some large graphs. To deal with larger graphs, Lu et al. [13] introduce a parallel algorithm based on Johnson’s algorithm aiming to reduce the execution time. Their algorithm is based on first splitting the job into small ones and then applying Johnson’s algorithm on each one in parallel. Giscard et al. [14] proposed an algorithm that counts the circuits of a graph without enumerating them. It gives the number of circuits for a length l, but it is tested for a limit of \(l=10\). In [15] the authors present an algorithm that deals with large graphs but only finds circuits of length less than or equal to k. The limit in their tests is \(k=6\).

In this paper, we present parallel approaches for finding all circuits of a directed graph. We first detect whether the graph contains circuits by searching for the strongly connected components, then we start exploring the graph to find all the circuits. Our algorithms proceed by a massive exploration of paths. We present two approaches based on the initial set used for exploration: The first uses vertices of the graph to which we assign a search area, while the second uses triplets to reduce the search space of exploration. Our algorithms permit to find circuits of a given length l and circuits with a specific vertex or edge. We develop a parallel implementation of the proposed approaches in a graphics processing unit (GPU) environment that is better suited for massive exploration. Our algorithms can find millions of circuits in a reduced time. We provide, to the best of our knowledge, the first GPU-based algorithms for finding elementary circuits of directed graphs.

The remaining of this paper is organized as follows. In Sect. 2 we present the background and related work. In Sect. 3, we introduce some preliminary definitions. The parallel algorithms are explained in Sect. 4. Details of the GPU implementation and examples are given in Sect. 5. Section 6 describes the experimental tests and results. Conclusion and future work are discussed in Sect. 7.

2 Related work

Finding cyclic structures in a graph has been largely studied in the literature because of its many potential application scenarios. Some existing works have been interested in detecting circuits of directed or undirected graphs [16,17,18,19]. Other studies focused on finding the shortest circuit [20,21,22] or the longest circuits of a graph [23,24,25,26]. In this paper, we are interested in finding all the elementary circuits of a directed graph. It is a classical problem whose most efficient solutions date back to the 1970s.

Tiernan [10] was the first to propose the idea of blocking visited vertices. The algorithm is based on a backtracking procedure. It generates all elementary paths \(p = (v_{1}, v_{2}, \ldots , v_{k})\) with \(v_{1} < v_{i}\) for all \(i \in \{2, \ldots , k\}\). Starting from some vertex \(v_{1}\), it chooses an edge to traverse to some vertex \(v_{2}\) such that \(v_{2} > v_{1}\) and continue this way. Whenever no vertex can be reached, the procedure backs up one vertex and chooses a different edge to traverse. If \(v_{1}\) is adjacent to \(v_{k}\) the algorithm lists an elementary circuit \((v_{1}, v_{2}, \ldots , v_{k}, v_{1})\). This approach examines more simple paths than necessary, making the worst-case time bound exponential in the number of elementary circuits and in the graph size.

Tarjan’s algorithm [11] is based on Tiernan’s depth-first method but it is faster. It lists all the cycles in \(O((|V |+ |E |) |C |)\) time. It uses backtracking procedure to avoid unnecessary work. Two stacks are needed, the point stack for storing the path currently being examined, and a Boolean vector called marked stack to indicate whether a vertex is used in a path or not. Whenever a new circuit is found, all vertices in the current point stack will eventually be unmarked when popped from this stack. If no circuit is found involving a vertex, it will be deleted from the point stack, but continue to be marked. Some of the unnecessary work in Tiernan’s algorithm is avoided by the condition that a vertex can be added to the point stack only if it is unmarked.

The algorithm by Weinblatt [27] begins processing the graph by eliminating vertices which cannot belong to any circuits. Next, it selects a starting vertex and chooses an edge to follow. Circuits are found when a path is cyclic or by combining parts of previously discovered circuits with a part of the path that is being processed. However, this requires more storage and the time saved by efficient search is lost in searching the constructed circuits and paths.

Of all the algorithms analyzed, the algorithm of Johnson [12] is the fastest algorithm having an upper time bound of \(O((|V |+ |E |) |C |)\). The success of this backtrack algorithm is due to an effective pruning technique which avoids much of the fruitless search present in earlier algorithms. For each start vertex s, a recursive backtracking procedure is invoked and its computation is similar to that of Tarjan’s algorithm, except for the marking system, which was considerably enhanced. A vertex is blocked each time it enters the stack. It remains blocked until we backtrack from a vertex v that belongs to the last enumerated circuit. The unblock process recursively unblocks the vertices that have a path to v.

In 2006, an algorithm by Liu and Wang [28] present a way to enumerate circuits in directed and undirected graphs. It uses \(k-1\) paths to generate k circuits by exploring adjacent vertices of the tail (the last vertex in the path), this way it can enumerate circuits by length. Compared to Johnson’s and Tiernan’s algorithms, their algorithm is slower and not efficient.

In [29], the authors propose a parallelizable algorithm into \(|V - 1 |\) parts. They use a backtracking strategy using pointers allowing to backtrack more than one vertex at a time, jumping directly to the vertex from which further path extensions are possible.

The algorithm by Lu et al. [13] is capable of handling large-scale graphs. The idea is to split the job into subroutines depending on the number of edges. Then apply Johnson’s algorithm to find all elementary circuits including an edge in parallel for each subroutine. Every subroutine has a search area that consists of the graph after deleting all the edges in inputs for previous subroutines. For this, they grade the edges, by estimating the number of all elementary paths from a vertex v to a vertex u. The edge with higher Id will have smaller search area. This approach is implemented on Hadoop using the MapReduce technique. Compared to previous approaches, this algorithm reduces the running time for finding elementary circuits of a graph but it uses depth-first search (DFS) sequential algorithm of Johnson. Theoretically, DFS has been proven by Reif [30] to be inherently sequential. It is considered to be a challenging problem for parallelization. Recently, algorithms that find length-constrained circuits have been proposed. In [15], the authors find circuits bounded by length \(k = 6\). Another work by [31] finds bounded circuits from a source vertex s in undirected graphs in parallel, with a maximum length of \(k = 8\).

The algorithms we propose in this paper exploit the massive parallelism of the multi-cores GPU by running multiple searches simultaneously which makes it capable of finding millions of circuits in a short time. The exploration process is based on the breadth-first search (BFS) algorithm that is better suited to parallel implementation. Details are given in the following.

3 Preliminaries

In this section, we present formal definitions [32] that support our approaches to enumerate all elementary circuits of a graph. Let \(G = (V, E)\) be a finite directed simple graph with vertex set V and edge set E. Let Id(v) denote the number associated with the vertex v.

Definition 1

(Elementary path) A simple path p in a graph \(G = (V, E)\) is a finite sequence of vertices \(p = \langle v_{1}, v_{2}, \ldots , v_{k}\rangle\), such that \((v_{i}, v_{i+1}) \in E\) for \(i \in \{1, 2, \ldots , k-1\}\). A path is elementary if no vertex appears twice.

Definition 2

(Elementary circuit) A circuit is a path in which the first and the last vertices are identical. An elementary circuit is a circuit where no vertex appears twice except the first and the last vertices.

Two elementary circuits are distinct if one is not a cyclic permutation of the other. Note that, in this paper we represent a circuit as a sequence of vertices \(c = \langle v_{1}, v_{2}, \ldots , v_{k} \rangle\) without writing the redundant vertex twice.

Definition 3

(Strongly Connected Component) A strongly connected component (SCC) in a directed graph is defined as a subgraph in which every vertex is reachable from every other vertex. That is, for any two vertices u and v in a strongly connected component, there exists a path from u to v, and a path from v to u.

We define In-edges(v), the set of incoming edges of a vertex v such that:

$$\begin{aligned} In{-}edges(v) = \{ (u,v) |(u,v) \in E \} \end{aligned}$$

Similarly, we define Out-edges(v) the set of outgoing edges of v:

$$\begin{aligned} Out{-}edges(v) = \{ (v,u) |(v,u) \in E \} \end{aligned}$$

We name the destination vertex of the outgoing edge of v the out-neighbor of v. Likewise, the origin vertex of the incoming edge of v is called the in-neighbor.

For the sake of introducing the approaches below, we define the set of triplets as follows:

Definition 4

(Triplets) We denote by T(G) the set of triplets of \(G = (V, E)\) defined as:

$$\begin{aligned} T(G) = \{ \langle x,v,y \rangle |x, y, v \in V \qquad with \qquad&(x,v) \in In\text{- }edges(v), \\&(v,y) \in Out\text{- }edges(v), \\&Id(v)< Id(x), \\&Id(v) < Id(y)\} \end{aligned}$$

A triplet is a sequence of vertices that initiate a path of length greater than two. We name v the source-vertex and x the in-vertex for a triplet \(\langle x,v,y \rangle\). Using triplets allows to find every circuit only once and reduce the search space, as we shall see in the sequel.

In the following, we present our algorithms for finding all elementary circuits.

4 Parallel algorithms for finding elementary circuits

We present here our parallel approaches for finding elementary circuits of directed graphs. Circuits are constructed starting from a source-vertex s. We build elementary paths by iteratively exploring adjacent vertices.

To avoid visiting vertices that do not belong to any circuit, we first find all the SCCs of the graph as a preprocessing task. Definition 3 shows that an SCC consisting of more than one vertex must contain circuits and that all vertices in any circuit should be in the same SCC. Decomposing the graph into SCCs reduces the number of initial source vertices and the number of neighbors to be visited. Only neighbors that are in the same SCC are considered, hence, reducing the number of paths to be explored. In this work, we use the algorithm by Tarjan [33] for finding SCCs of the graph. The algorithm’s running time is linear in the number of edges and vertices in G, it finds SCCs in \(O(|V |+ |E |)\) time.

Once the graph has been partitioned into SCCs, we move to the exploration phase. A straightforward approach to obtain all circuits is to enumerate all combinations of distinct edges and check if the path may construct a circuit. On this basis, we propose two algorithms: Vertex-based algorithm for finding elementary circuits (V-FEC) and triplets-based algorithm for finding elementary circuits (T-FEC). Our algorithms are based on a massive exploration of paths. For each SCC found, we run a parallel breadth-first search (BFS) starting from a set of initial source vertices and build exploration trees. The detailed algorithm V-FEC is presented in Sect. 4.1.

To reduce the search space and filter out some unnecessary combinations, we propose algorithm T-FEC that uses triplets instead of vertices as initial set. As with the precedent algorithm, V-FEC, we first find SCCs of the graph. Then, we generate the set of initial triplets and begin exploration. The same process of exploration is used. It is interesting to note that using triplets helps to balance exploration trees. The detailed algorithm is presented in Sect. 4.2.

For the following, C denotes the set of circuits found. Set P is used to contain the explored paths.

4.1 A vertex-based approach V-FEC

As explained above, the first algorithm is vertex-based. We begin by finding the SCCs of the graph. Then, we initialize the set of paths P with vertices of the SCCs: \(P = \{\langle s_{1} \rangle\), \(\langle s_{2} \rangle\),..., \(\langle s_{k} \rangle \}\).

We define the search area (SA) of a vertex s by the subgraph induced by s and vertices with Id greater than the Id of s which are in the same SCC: \(SA(s) = \{u \in V |SCC(u) = SCC(s) \hbox {~and~} Id(u) > Id(s)\}\), SCC(v) denotes the identifier of the SCC where vertex v belongs. In other words, for a vertex s we only consider vertices in the same SCC with Id greater than Id of s. Comparably, in Johnson’s algorithm, we consider vertex s to be the smallest vertex in the SCC. When all circuits from s are found, we remove s, In-edges(s) and Out-edges(s), and then, we explore the rest of the SCC in a similar manner.

In the exploration phase, for every vertex \(s_{i}\) in P, we only explore vertices in its search area. We start by visiting the out-neighbors of \(s_{i}\). Then, we iteratively explore the visited vertices until no more vertices can be visited. The above-mentioned process is outlined in Algorithm 1.

figure a

4.1.1 Exploration

Now we detail the exploration phase.

Our algorithm is based on running multiple BFS graph exploration simultaneously from every initial paths \(p_{i} \in P\). (P has been already initialized with vertices of the SCCs found.) We construct exploration trees for every source-vertex \(s_{i}\) of \(p_{i}\) by visiting the out-neighbors of the last vertex v of path \(p_{i}\). For any neighbor u of v, one of the following situations occurs:

  • Vertex u is the source-vertex \(s_{i}\): \(p_{i}\) is an elementary circuit. Add \(p_{i}\) to C,

  • u is not visited and belongs to the search area of \(s_{i}\): \(p_{i}\) is extended. We add \(\langle p_{i},u \rangle\) to the set of paths P.

  • u is already visited: the path \(\langle p_{i},u \rangle\) cannot constitute an elementary circuit.

The algorithm proceeds iteratively by visiting the last visited vertex of each resulting path until no path can be found \((P = \varnothing )\). At the end of the exploration phase, we would have listed all the circuits ordered by their length. A pseudo-code of the explained process is presented in Procedure 1.

figure b
Fig. 1
figure 1

Graph decomposition into SCCs

Full size image

Example 1

To better explain the proposed algorithm we run an example on graph \(G = (V,E)\), \(|V |= 12\) and \(|E |= 22\) shown in Fig. 1a. We begin with a search for the SCCs of the graph to eliminate unnecessary vertices and edges. Graph G contains three strongly connected components, a large SCC: \(SCC_{0}\) and two trivial ones: \(SCC_{1}\) and \(SCC_{2}\), illustrated in Fig. 1b. We remove all the trivial SCCs and the edges going to or from them and begin processing the remaining graph.

We initialize the set P of paths with the vertices of \(SCC_{0}\) (l = 0 in Fig. 2). Then we start constructing exploration trees for each source-vertex s. We visit out-neighbors of s that are in its search area. We recall that a vertex u is in the search area of vertex s if the two vertices are in the same SCC and \(Id(u) > Id(s)\). Consider vertex s, \(Id(s) = 1\). Vertex s has three out-neighbors: vertex 0, 2 and 4. Vertex 0 is not in SA(s) since 0 < 1. In this case, vertex 0 is not considered. If a vertex has no visited neighbors, the path is removed, e.g., paths: \(\langle 8 \rangle\) and \(\langle 9 \rangle\) have no visited neighbors, so they are removed. (l = 0 in Fig. 2).

Fig. 2
figure 2

Exploration trees from different source vertices: V-FEC approach

Full size image

4.2 A triplets approach T-FEC

We aim to reduce the search space for the exploration phase by generating triplets using direct neighbors of each vertex. The idea is to construct what can constitute potential circuits by joining incoming and outgoing edges of a given vertex. We divide the process into two stages and define a parallel algorithm for each one of them. As a first step, (1) we generate the set of triplets T(G), and then, (2) we run a parallel breadth-first search (BFS) for each resulting triplet in a likewise strategy as in the V-FEC approach. Algorithm 2 outlines the proposed approach.

figure c

4.2.1 Triplets generation

The idea of using triplets to begin exploration helps reducing the search space and avoids redundant circuits. Triplets also permit to have more balanced exploration trees, thus, a more balanced work charge. We build the set of triplets by making every possible combination \(\langle x,v,y \rangle\) of the in-neighbors and out-neighbors of vertex v such as:

  • x is the in-neighbor of v with \(x \in SA(v)\), i.e., \(Id(v) < Id(x)\) and v and x are in the same SCC.

  • Similarly, y is the out-neighbor of v with \(y \in SA(v)\).

If \(x = y\), \(c = \langle v,y \rangle\) is a 2-length circuit. The generation process is presented in Procedure 2.

figure d

4.2.2 Exploration

The exploration phase for algorithm T-FEC is similar to the exploration in algorithm V-FEC. Initially we visit the out-neighbors of y for every triplet \(\langle x,v,y \rangle \in T\). Only neighbors in SA(v) are considered. Then, we iteratively visit the out-neighbors of the last visited vertex \(v_{k}\) of every path \(p_{i}\) \(\in P\). We recall that for a triplet \(\langle x,v,y \rangle\), v denote the source-vertex and x is the in-vertex. For any neighbor u of vertex \(v_{k}\), the exploration goes as follows:

  • u is the in-vertex (\(u = x\)): \(p_{i}\) is an elementary circuit. Add \(p_{i}\) to C,

  • u is not visited and \(u \in SA(v)\): \(p_{i}\) is extended, its an elementary path. We add \(\langle p_{i}, u \rangle\) to P.

  • u is already visited: \(\langle p_{i}, u \rangle\) is not an elementary path.

The exploration is over when no path can be expanded \((P = \varnothing )\). The exploration process is described in Procedure 3.

figure e

4.3 Proof of correctness

In the following, we will prove that Algorithms V-FEC and T-FEC find every elementary circuit of a graph exactly once.

We start by showing that both algorithms find only elementary circuits of a graph.

Lemma 1

Algorithms V-FEC and T-FEC find elementary circuits only.

Proof

In algorithm V-FEC, every vertex in a path is marked as visited and a new vertex is added to a path if it is not already visited. If a vertex is visited we do not visit it again (line 10 of Procedure 1). Hence, a path cannot contain redundant vertices. Let a path \(p =\langle v_{1}, \dots , v_{i}, \dots , v_{k} \rangle\) to be expanded, and let vertices \(v_{l}\) and \(v_{i}\) be in out-neighbors of vertex \(v_{k}\). Suppose that vertex \(v_{l}\) is not visited yet. If \(v_{l} \in SA(v_1)\), it will be added to p and marked as visited. However, since vertex \(v_{i}\) is previously visited, it will not be explored again. This confirms that algorithm V-FEC finds only elementary circuits.

Similarly, for algorithm T-FEC, in Procedure 3 exploreT-FEC, in line 9, visited vertices are not explored again, thus, the resulting circuits are elementary. \(\square\)

Theorem 1

Algorithms V-FEC and T-FEC find all the elementary circuits of a graph exactly once.

Proof

The correctness of this lemma can be verified by the following: (1) Algorithms V-FEC and T-FEC find any elementary circuit exactly once, (2) all the elementary circuits of the graph are found.

To prove the first property, we suppose a circuit is found more than once. Let \(\langle v_{1}, v_{i}, \dots , v_{l} \rangle\) be a circuit, such that \(Id(v_{i}) = i\), \(\forall v_{i} \in V\), and vertex \(v_{1}\) has the smallest Id. Many permutations of the same circuit can be found by starting from different source vertices. A circuit can be expressed in a permuted form as many times as the number of vertices it has: \(\langle v_{1}, v_{i}, \dots , v_{l} \rangle\), \(\langle v_{i}, \dots , v_{l}, v_{1} \rangle\), \(\dots\), \(\langle v_{l}, v_{1}, v_{i}, \dots \rangle\).

In algorithm V-FEC, during the exploration phase every vertex of each SCC starts building its exploration tree by visiting its out-neighbors. A new vertex is added to a path if its Id is greater than the Id of the source-vertex (line 10 in Procedure 1: see the definition of SA(s) in Sect. 4.1). As a consequence, the first vertex in a path is always the vertex with the smallest Id.

Consider a circuit \(c = \langle v_{1}, v_{i}, \dots ,v_{l} \rangle\) and two cyclic permutations of c: \(c' = \langle v_{i}, \dots v_{l}, v_{1} \rangle\) and \(c'' = \langle v_{l}, v_{1}, v_{i}, \dots \rangle\). Following Procedure 1 exploreV-FEC, we try to construct circuit c and its permutations starting from different source vertices \(v_{1}\), \(v_{i}\),..., and \(v_{l}\). Each time we visit a neighbor we check if its Id is greater than the Id of the source-vertex of the path. Since \(Id(v_{1}) < Id(v_{i})\) and \(Id(v_{1}) < Id(v_{l})\), in both cases, \(\langle v_{i}, \dots v_{l}, v_{1} \rangle\) and \(\langle v_{l}, v_{1}, v_{i}, \dots \rangle\), vertex \(v_{1}\) is not explored, thus, circuits \(c'\) and \(c''\) cannot be constructed. Hence, no circuit can be found more than once.

In a similar way, when generating triplets for a vertex v in algorithm T-FEC, we only consider neighbors that have Ids greater than Id(v), and likewise for the exploration phase, this guarantees that circuits are not duplicated. We come to the conclusion that both algorithms find each circuit exactly once.

Now we prove the second property: Algorithms V-FEC and T-FEC find all the elementary circuits of a graph. We know from the definition of SCC that every SCC with more than one vertex must have circuits, and that all vertices in any circuit belong to the same SCC. Finding all elementary circuits of a graph is equivalent to finding all elementary circuits starting from a vertex, for every vertex of the graph.

In algorithm V-FEC, Procedure exploreV-FEC finds for a vertex s all the elementary circuits starting from s such that Id(s) is the smallest, by visiting every neighbor of every vertex within SA(s) not visited yet in the same SCC, making every possible combination of possible paths (follows directly from Lemma 1 and the proof of property(1)). Thus, for every elementary circuit of the graph, with all vertices in SA(s), its cyclic permutation starting by vertex s is returned at the end of the algorithm. Since Procedure exploreV-FEC, is called for every vertex of every SCC of the graph, every elementary circuit is found.

Similarly for T-FEC, in the triplets generation phase, we consider all neighbors of vertex v having Id greater than Id(v). Procedure exploreT-FEC visits every neighbor of every vertex within SA(v) not visited yet in the same SCC. It finds for a triplet \(\langle x,v,y \rangle\) all the elementary circuits starting from v and including vertices x and y, such that Id(v) is the smallest. The procedure is called for every generated triplet; thus, every elementary circuit is found. We conclude that the proposed algorithms find all the elementary circuits of a graph exactly once. This completes the proof. \(\square\)

4.4 Circuits and paths given a source vertex

For some applications, we are interested in the enumeration of circuits that goes through a certain vertex v. The proposed approaches can be easily adapted to only find circuits that contains vertex v.

To achieve this, we make an adjustment in the initialization phase. In the vertex-based approach, we initialize the set of paths to v and then call Procedure 1 exploreV-FEC, which only runs for vertex v. For the triplets approach, we generate triplets for vertex v by calling Procedure 2 generateTriplets and omit the condition about considering only vertices greater than v, which was mainly put to avoid enumerating circuits that are enumerated in the exploration process of other vertices. Since we just list circuits of v, circuits containing vertices of inferior Id are not found if we do not consider all vertices of the graph. That means, the set of triplets is generated using all of v’s neighbors and there will be no redundant circuits. For both approaches, the exploration procedure remains the same, except for the condition about vertices Ids for the same reason explained above. In this case, the entire graph is considered.

In a similar manner, we can find circuits with a given edge (u, v) by initializing Paths to \(\langle u,v \rangle\) in the vertex based approach. Or by generating triplets of form \(\langle x_{i},u,v \rangle\) with \(x_{i} \in\) in-neighbors of u, for the triplet based approach. It is also possible to enumerate existing paths from a given source vertex s to a destination vertex d by searching circuits containing the edge (d, s) or Using triplets \(\langle d,s,y_{i} \rangle\) where \(y_{i} \in\) out-neighbors of s.

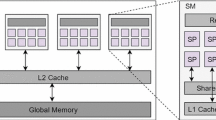
5 GPU implementation

A GPU is a highly parallel architecture that adopts the single instruction multiple data (SIMD) processing model. A GPU program consists of sequential segments and parallel segments of codes. The sequential codes run on the CPU, and the parallel codes, called kernels, run on the GPU. When a kernel is invoked, a large number of threads are launched to exploit data parallelism. Threads are grouped into blocks and blocks can be grouped into a grid. Thus, the kernel configuration has a significant effect on the degree of parallelism and hence influences the computing efficiency.

In this section, we present a GPU implementation of the proposed approaches. We proceed in parallel, multiple BFS explorations. This model fits the multi-threaded GPU architecture.

The SCC decomposition algorithm was not parallelized due to the low impact in the processing time of the algorithm. A GPU-kernel is used to implement the exploration phase of the vertex-based version. For T-FEC two kernels are used: The first kernel generates the set of initial triplets, the second one explores the graph.

Developing efficient graph processing algorithms in GPU is a challenging task. A GPU has limitations such as a relatively small memory size. Thus, the choice of data structures and strategies employed to take advantage of the characteristics of the different types of GPU memories is important to overcome these limitations. In our implementation, we use data structures that are best suited to the GPU. We also take advantage of the GPU global, local and shared memories.

In the following we discuss our choices for data structures and detail the implementation of our algorithms.

5.1 Data structures

5.1.1 Graph representation

Compressed adjacency list is the most common data structure for graph representation in GPU. It provides compact storage for large sparse graphs and regular memory access. It uses two arrays to store the graph \(G = (V,E)\) and only requires \(O(|V |+ |E |)\) memory space. Adjacency lists of all vertices are packed into a single large array that we name the edge array. We store the starting position of the adjacency list in the edge array for each vertex [34]. When outgoing edges are used in the edge array, we name this adjacency list format, the compressed sparse row (CSR). If incoming edges are used in the edge array, it is called compressed sparse column (CSC) [35]. To generate triplets both CSR and CSC representations are used, since we need to access both incoming and outgoing edges of each vertex. Once the triplets are generated we no longer need the incoming edges, CSC arrays are deleted. An example of the CSR and CSC representations of the graph in Fig. 1a is represented in Fig. 3.

Fig. 3
figure 3

Data structure for graph representation

Full size image

5.1.2 Intermediate data storage and results

When searching for circuits, a number of paths is generated in every iteration. We keep track of them by using a global integer array. Initially, it contains the initial vertices or generated triplets. Another array stores the circuits. Since the GPU do not allow dynamic memory allocation, every memory that becomes necessary must be previously allocated. We declare two static structures Circuits and Paths larger enough for the purpose they were intended to.

During exploration, previously visited vertices in a path must not be visited again. This guarantees that circuits found are elementary. A single bit indicating whether or not the vertex is in the path is sufficient. Accordingly, a bitmap (bit array) Visited is employed to mark the already visited vertices. This map is defined by a bi-dimensional matrix that contains a row for each path and \(|V |\) columns of bits, one for each vertex of the graph. In terms of bytes, the number of columns is \(\lceil \frac{|V |}{8} \rceil\), e.g., in a graph G with \(|V |= 12\) a path storage occupy only 2 bytes. A Vertex \(v_{j}\) belongs to path i if and only if, bit j of row i is set to 1. Figure 4 shows an example of these arrays. The Paths matrix stores the vertices of an explored path in the order in which they are discovered. In the Visited matrix, each row contains a combination of bits that corresponds to the visited vertices of a path.

In addition to the small occupied space, adding a vertex or checking if it is already in the solution is done using a simple logical operation in the desired position. Because the bit-level operations are among the least computationally expensive, this method of storage contributes to improve the algorithm running time.

5.2 Parallel implementation

Now we detail the parallel implementations of V-FEC and T-FEC algorithms. We first describe the triplets generation process for T-FEC; then, we detail the exploration phase for both V-FEC and T-FEC.

5.2.1 Triplets generation

We begin by creating the set T(G) of initial triplets \(\langle x,v,y \rangle\). Such a set is created by selecting vertex \(v \in V\) and analyzing all pairs of its adjacent vertices: x in the in-neighbors of v and y in out-neighbors of v. Procedure 2 generateTriplets describes the process of generating triplets. We launch a kernel generateTriplets and we assign a thread to every vertex v in the SCC. Each thread takes a vertex x from the edge array \(E_{in}\) and another vertex y from the edge array \(E_{out}\) and verify that they are in SA(x). When this condition is satisfied the thread adds the combination \(\langle x,v,y \rangle\) to the set of triplets. Another pair of neighbors is analyzed until all neighbors are checked. In the case where vertex x equals vertex y, \(\langle x,v\rangle\) is a 2-length circuit and is added to the set C.

At the end of the triplets generation phase, the set of incoming edges is no longer needed. We free memory used by deleting \(V_{in}\) and \(E_{in}\) arrays. We only keep the set of outgoing edges: \(V_{out}\) and \(E_{out}\) arrays, for the graph representation.

5.2.2 Exploration

The exploration kernels, exploreV-FEC and exploreT-FEC, are quite similar. Kernel exploreV-FEC launches a number of threads equal to the number of initial vertices. Kernel exploreT-FEC launches a number of threads equal to the number of generated triplets. Each thread is assigned a vertex/triplet and starts exploring. During exploration, it is important to save:

  • for V-FEC: the source-vertex and the last visited vertex.

  • for T-FEC: the source-vertex, the in-vertex and the last visited vertex of a path.

These data are essential for exploration. The last visited vertex of a path permits to expand the set of paths with new paths. At each iteration, a thread visits the out-neighbors of the last visited vertex of the path it is assigned to. In V-FEC, the source-vertex determines when a circuit is found. If the new vertex is the source-vertex, it is a circuit. For T-FEC, it is the in-vertex that determines a circuit. We use an atomic operation to add the discovered circuits by copying the current path to Circuits. If the new vertex do not constitute a circuit, the path can be expanded when the two following conditions are met: we first check if the explored vertex is not visited using a simple bit-wise operation, then, we check if the vertex is in the search area of the source-vertex. Considering these data are used by a thread for as many out-neighbors there is to explore, it is more appropriate to copy data to shared memory because it is faster. In V-FEC, we use two vectors \(V_{source}\) and \(V_{last}\) to store the source-vertex and the last visited vertex of a path, respectively. Another vectors \(V_{in}\), that stores in-vertices, is necessary for the triplet based approach. The number of copied paths equals the number of threads per block. Chunks of the Visited array corresponding to copied paths are also transferred to shared memory.

Each thread uses a local array called frontier array to store the newly visited vertices to be copied back in global memory as new paths for the next iteration. We use a shared array frontierOffsets, set to 0, to compute the number of new paths. Each thread increments the value corresponding to its Id when it founds a new path. These values are used to copy the results of each thread in parallel to global memory. We first compute offsets for each thread on a block level by applying a parallel scan [34] on the frontierOffsets array. We use another array blockOffsets array to store the offsets of the blocks. Since there is no synchronization between blocks of threads, we use atomic operations to calculate the offsets of blocks. These two indices (frontierOffsets and blockOffsets) are used to compute the global memory address for each thread to copy its result. The schema represented in Fig. 4 encapsulates the process.

Compared to the V-FEC algorithm, the exploration process in T-FEC requires less iterations considering that two vertices are already explored for each path, when generating triplets. Moreover, the triplets approach exposes more parallelism in early iterations, since there is more initial triplets than initial vertices which results in more thread occupancy.

Fig. 4
figure 4

A schema for paths exploration process

Full size image

Example 2

(Using triplets) Consider the same graph \(G = (V,E)\) in Fig. 1a. In the T-FEC algorithm we start by initializing triplets and its corresponding Visited bitmap. A thread is mapped to a vertex, e.g., thread 2 generates triplets corresponding to vertex 2. We generate combinations of in-neighbors and out-neighbors of vertex 2. The in-neighbors of vertex 2 are vertex 1 and vertex 3. Vertex 1 is not considered since \(1 < 2\). For vertex 3, \(3 > 2\), so vertex 3 is considered. The out-neighbors of vertex 2 are vertex 0 and 9. \(0 < 2\) vertex 0 is not considered as well. We are left with two valid vertices: vertex 3 as in-neighbor and vertex 9 as out-neighbor. As a result the triplet \(\langle 3,2,9 \rangle\) is generated. Triplets from all SCCs are generated before starting exploration. The visited vertices of each triplet are marked as visited in the Visited array. Array Visited is an array of bytes (unsigned integers of length = 8 bits), we only use one bit to mark the visited vertices. Thus, \(\lceil \frac{n}{8} \rceil\) columns are needed. In this example \(n = 12\), as a consequence, Visited is a two columns array. During exploration, if a circuit is found, it is added to the Circuits array next to the circuits already found at earlier iterations. We take as an example triplet \(\langle 2,0,1 \rangle\), vertex 2 is the in-vertex, vertex 0 is the source-vertex and vertex 1 is the last vertex of the path. We explore out-neighbors of vertex 1 that are vertices 0, 2 and 4. Vertex 0 is already visited so it is not added to Paths. Vertex 2 is the in-vertex, path \(\langle 2,0,1,2 \rangle\) is a circuit, we add it to Circuits. \(Circuits {} = Circuits {} \cup \{\langle 2,0,1 \rangle \}\). Vertex 4 is not visited and is in SA(0): the new path \(\langle 2,0,1,4 \rangle\) is added to Paths.

6 Experimental results

In this section, we present the results obtained by the CUDA implementation of the two proposed algorithms and the CPU multi-core implementation of algorithm V-FEC using Posix Threads library in C++. We compare the results to those of Johnson’s algorithm. We use the Python implementation of Johnson’s algorithm in the NetworkX packageFootnote 1.

6.1 Experiment settings

Experiments were conducted on a GPU station with 32 GB RAM, with an Intel Xeon Silver 4216 2.10GHz CPU. The GPU card is an Nvidia GeForce RTX 2080 Ti with 11GB of GDDR6 VRAM and 4,352 CUDA cores, CUDA Version 11.0.

6.2 Results

Table 1 Experimental comparison of V-FEC, T-FEC, mCore-V-FEC (using 8 CPU cores) and the algorithm by Johnson for synthetic graphs
Full size table
Table 2 Experimental comparison of V-FEC, T-FEC and the algorithm by Johnson for real-world graphs
Full size table
Table 3 The results per level showing the maximum depth for each algorithm, the maximum number of circuits and the number of circuits for each level
Full size table
Fig. 5
figure 5

Experimental comparison of Johnson’s algorithm and mCore-V-FEC with V-FEC and T-FEC algorithms

Full size image

We use two sets of data. The first set contains synthetic graphs generated using the R3MAT graph generator [36]. It generates graphs that resemble the properties observed in real-world graphs following a power law distribution. The description of these graphs and the execution times of our implementation compared with the execution times of Johnson’s algorithm and the parallel multi-core implementation of V-FEC are presented in Table 1.

Column \(|C |\) represents the number of elementary circuits found by the compared algorithms. For each graph, we ran the algorithms 20 times and calculate the average time taken. The execution times are presented in milliseconds.

For the graph "graph-80-1-1-0," algorithm T-FEC could not enumerate all circuits of the graph. This is due to the large number of intermediate results (paths) that could not fit in the GPU memory. As an alternative, we succeeded to list all the circuits of size equal or less than 16.

For some graphs, where the number of circuits is very important, it is not possible to enumerate all the circuits, due to memory limitations. The search for elementary circuits with Johnson’s algorithm for these graphs result in an out of memory error (OOM). On the other hand, our algorithms proceed by levels. At each iteration, circuits of length l are found. This gives the possibility to enumerate circuits of a given length without having to enumerate all the circuits of the graph. For such graphs it is possible to proceed by enumerating the circuits until a maximum depth is reached. Table 3 shows these results.

In addition to the synthetic graphs generated by the R3MAT model [36], we use real-world datasets from four different sources: Konect [37] (moreno_taro, moreno_sheep), SNAP Library [38] (p2p-Gnutella04, p2p-Gnutella08 and email-Eu-core), networkrepository [39] (EPA) and Pajek [40] (Baywet). Characteristics of these graphs are given in Table 2.

We adapt our algorithms to count circuits without enumerating them. This significantly reduces the memory storage needed since we do not keep track of all the visited vertices. The Paths matrix is replaced by vectors that stores the source-vertex and the last vertex for each path (in addition to the in-vertex in the triplets approach). This permits to explore larger graphs and to explore more levels as shown in Table 3.

Table 4 Experimental results for the impact of the SCC graph decomposition in V-FEC
Full size table
Table 5 Experimental results for the impact of the SCC graph decomposition in T-FEC
Full size table

6.3 Analysis

Table 6 Results of the impact of the graph degree distribution on execution time
Full size table

The results presented in Tables 1, 2, and 3 show that our algorithms can significantly reduce the running time to find all elementary circuits compared to Johnson’s algorithm and the multi-core implementation of V-FEC. The speed-ups over the algorithm of Johnson vary from 8.13 (graph-40-1-1-0), to 190.23 (graph-80-1-1-0), and increase with the number of circuits. The recorded speed-ups for the parallel multi-core implementation are between 1.15 (graph-40-1-1-0) and 19.32 (graph-100-1-1-1). Figure 5 shows the speed-ups achieved by V-FEC and T-FEC compared to the algorithm by Johnson.

We analyze the effect of the SCC decomposition phase on the overall processing time by comparing the execution time of both approaches with and without decomposing the graph into SCCs. Detailed results for V-FEC and T-FEC algorithms are listed in Tables 4 and 5. V-FEC + SCC and T-FEC + SCC present execution times of V-FEC and T-FEC using SCC decomposition, while V-FEC - SCC and T-FEC - SCC present the execution times of the algorithms without the SCC decomposition phase. The results show that the decomposition of the graph into SCCs can reduce processing time compared to when the graph is not decomposed into SCCs. In fact, finding the SCCs of the graph can reduce the number of vertices to be explored and avoid fruitless paths, thus, minimizing the time of the exploration phase, which justify the use of the preprocessing phase in our algorithms. Experiments demonstrate that time achieved by the decomposition phase is negligible compared to the overall running time, as presented in Fig. 6.

Fig. 6
figure 6

Experimental results for the impact of the SCC graph decomposition

Full size image
Fig. 7
figure 7

Results of the impact of the graph degree distribution

Full size image
Fig. 8
figure 8

Results of the impact of the degree distribution order

Full size image

We note that while V-FEC algorithm performs better in some graphs, T-FEC gives better results in others. In an attempt to identify what variables affect the results, we run a series of experiments on synthetic graphs, using the R-Mat graph generator model [41]. The generator takes as an input \(|V |\), \(|E |\) and the parameters a b c and d which represents the probabilities of an edge falling into partitions. We fix \(|V |= 64\) and vary \(|E |\) and the values of a, b, c and d and observe the behavior of both V-FEC and T-FEC approaches. The results are presented in Table 6. We observe that the degree distribution of the graph is a relevant parameter in the algorithms’ performance. We divide Table 6 into three sets based on the degree distribution. We represent the execution times of both approaches on these graphs in Fig. 7. The second set in the table represent graphs where the degrees of vertices are almost uniform. For these graphs, we remark that V-FEC and T-FEC algorithms are equivalent (Fig. 7c). The first and the third set are graphs with few vertices having higher degree than other vertices with a difference in the ordering of these vertices. In the first set the high degree vertices are processed in the end, while in the last set they are processed in the beginning. We observe that V-FEC algorithm outperforms the T-FEC algorithm for the graphs in the last set of the table (Fig. 8b). In this case, the number of triplets that are generated is important for those vertices with high degree. Indeed, a lot of combinations are generated, which means more paths to be explored and some of them are fruitless. On the contrary, the triplets approach outperforms the vertex-based one for the first set of graphs (Fig. 7a).

To further analyze the impact of the distribution order of the vertices’ degree, we use a graph labeling function based on the in and out degrees of the vertices of the graph. We know that the more in-neighbors and out-neighbors a vertex has the more probable it is to belong to circuits. Based on that, we order the vertices according to the product of their in and out degrees. We use two graph labeling functions: the first one \(l_{Asc}\) organizes the vertices in an increasing order of in-degree * out-degree. The second function \(l_{Desc}\), lists the vertices in a decreasing order of the vertices’ in-degree * out-degree. We apply this labeling to some of the graphs in Table 6 and run algorithm V-FEC. We compare the results with and without the labeling functions. The results are represented in Fig. 8. We observe that algorithm V-FEC gives better results when the \(l_{desc}\) label is applied. Indeed, by visiting vertices with more neighbors in early iterations we have higher probability to find circuits earlier and without exploring much of the fruitless paths. Experimentally observing, we can tell that the degree distribution order is a crucial parameter in the algorithm execution.

7 Conclusion

In this paper, we proposed parallel algorithms for enumerating all elementary circuits of a directed graph. Algorithms V-FEC and T-FEC first detect whether a circuit exists, by searching for strongly connected components, then, explore possible paths in parallel to find elementary circuits. In addition, they enumerate circuits of a given length and circuits going through a given vertex. We have provided theoretical guarantees on the correctness of V-FEC and T-FEC. The presented algorithms were implemented and tested in a GPU environment. To the best of our knowledge, these are the first parallel GPU-based algorithms for finding all the elementary circuits of a graph. Conducted experiments showed a significant improvement in execution times of V-FEC and T-FEC compared with the algorithm by Johnson, due to the massive parallelism offered by the GPU. The speed-up over the sequential algorithm was from \(\approx\) 8 to 190 times.

We should note that the size of the GPU memory can be a limiting factor that prevents from handling large graphs with millions of circuits. For future work, we intend to scale to larger graphs by working on multi-GPU approaches and parallel strategies on cluster of GPUs.