1 Introduction

In 4G LTE networks, it is necessary to maintain the location of the user equipment (UE), so that incoming calls are connected to the UE. The network keeps track of the location of the UE using a mobility management scheme, which consists of location registration and paging processes. The location registration, also known simply as registration, is a procedure whereby the UE registers its location in the network databases each time it enters a new location. On the other hand, the paging process is a procedure that the network uses to determine the UE’s current cell in the registered location, in order to connect incoming calls to the UE.

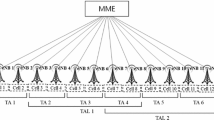
The LTE network consists of non-overlapped tracking areas (TAs), or a group of cells, while several TAs constitute a TA list (TAL). Mobility management entity (MME) is responsible for initiating paging and authenticating the mobile device. Additionally, it retains location information at the TA level for each user and then, during the initial registration process, selects the appropriate gateway [1]. Figure 1 shows that MME connects to the evolved Node Bs (eNBs), whose radio coverage is a cell.

Fig. 1
figure 1

TA and TAL in the LTE network

Full size image

In TAL-based registration, the UE registers every time it exits the current TAL to enter a new TAL. If a UE enters a cell that is not in its current TAL, the UE informs MME of its new location, and the MME allocates a new TAL to the UE.

Considering the simple configuration in Fig. 1, if the UE in cell 10 enters cell 13 and the received TA id (TA 4) is not in TAL 1, then the UE registers its new TAL. The MME then allocates TAL 2 to the UE where TAL 2 = {TA 3, TA 4, TA 5}.

Various studies have considered TAL-based registration. Chung [2] proposed movement-based TAL forming, based on the assumption that a TA consists of a single cell. Deng et al. [3] proposed to form the TAs as a set of rings, and change adaptively, based on the users’ mobility. Grigoreva et al. [4] proposed the dynamic formation of TALs, based on variable TAL forms, and mobility prediction to reduce signaling. Chen et al. [5] proposed a new green field TA planning model using multi-objective optimization with constraints, which aimed to find a better trade-off between the two conflicting objectives. In addition, some paging schemes for TAL-based mobility management have been proposed [6, 7], and research results on how to apply TAL-based registration to not only 4G, but also 5G, have recently been presented [8,9,10]. However, because of their complex procedure, these were difficult to implement. In this situation, it is essential to study how to implement TAL-based mobility management to optimize performance on radio channels.

References [6, 7, 11, 12] presented a significant TAL allocation known as central policy. Under this policy, the TA in which the UE registers its location becomes the central TA of the new TAL. This policy can lessen the possibility of the UE quickly exiting the new TAL [6, 7, 11, 12]. This type of central policy is known as a TA-based central policy.

Compared to the traditional static mobility management scheme, such as zone-based registration [13], the TAL-based registration can reduce the ping-pong effect by adopting the central policy. The performance of the TAL-based registration is affected by the allocation of the TAL. Inadequate allocation of TAL may lead to TAL-based registration causing side effects. As a result, real implementation of the TAL-based registration with TA-based central policy is difficult, since for actual network architecture, gradual increase in the TAL size cannot be guaranteed.

In this study, we consider TAL-based registration with central policy. We propose a cell-based central policy to mitigate the problem of the rapid increase in the TAL size in current TA-based central policy. Under the cell-based central policy, the cell in which a UE registers its location becomes the central cell of the new TAL. Under this policy, since the TAL can have any number of TAs, it is possible to implement TAL-based registration with cell-based central policy (TbRcc) in actual network architecture. In addition, in this study, we also propose a scheme to further improve the performance of TAL-based registration with cell-based central policy and analyze its performance.

The main contributions of this paper are fourfold: (1) The cell-based central policy is proposed to guarantee gradual stepwise increase in the TAL size. (2) TAL-based registration with cell-based central policy and single-cell TA (TbRcc1c) is also proposed, in order to reduce the registration cost and make up the optimum TAL. (3) We develop a semi-Markov process model to properly analyze the performance of the proposed scheme. (4) Lastly, comparison of the performance of our scheme with those of classical TAL-based registration and distance-based registration shows that the performance of our proposed scheme is better.

The contents of the paper are as follows: Sect. 2 introduces TAL-based registration with central policy and proposes TAL-based registration with cell-based central policy and single-cell TA (TbRcc1c) to make up the optimal TAL. Section 3 analyzes the signaling cost of the proposed scheme by using semi-Markov process model. Section 4 describes our numerical study to investigate the performance of the proposed scheme. Finally, Sect. 5 concludes the paper.

2 TAL-based registration with cell-based central policy and single-cell TA

First, we introduce TAL-based registration with central policy and then propose TAL-based registration with cell-based central policy and single-cell TA (TbRcc1c), in order to make up the optimal TAL, and also consider an implicit registration to reduce the total cost of TAL-based registration.

2.1 TAL-based registration and central policy

In TAL-based registration, if the UE enters a TA that is not in its TAL, the UE registers its TAL, so as to inform MME of its new location.

Figure 2 shows the 2-D hexagonal cell configuration [11, 14] that is considered in this study to analyze its exact performance. A small hexagon represents a cell, and the area marked by bold lines (composed of seven cells) represents a TA. In this 2-D hexagonal cell configuration, every cell borders six neighboring cells. Our study also assumes a random walk mobility model [11, 14,15,16]. In this model, the UE enters the six neighboring cells with equal probability (= 1/6).

Fig. 2
figure 2

A TAL in a 2-D hexagonal cell configuration (NT = 7)

Full size image

Considering the TA-based central policy, let NC be the number of cells in a TA and NT be the number of TAs in a TAL.

Figure 2 shows a TAL in a 2-D hexagonal cell, where NT = 7. Figure 2b shows that, for example, if a UE exits the current TAL from cell (7, 3), then the UE registers its new TAL, such that its new TA is the central TA of the new TAL. This central policy can avoid the possibility of the UE quickly exiting the TAL.

Figure 2 shows the ring structure of TA that most of the previous studies on TA-based central policy assumed [3, 7, 11, 13]. Under this TA-based central policy, the TAL should have TAs of \(1 + \mathop \sum \nolimits_{i = 1}^{n} 6i\), n = 1, 2, …, in order to set the TA in which a UE registers its location as the central TA of the new TAL. For example, the TAL only has 1, 7, 19, … TAs, and then, the TAL only has 7, 49, 133, … cells. As a result, real implementation of the TAL-based registration with TA-based central policy is difficult, since for actual network architecture, gradual increase in the TAL size cannot be guaranteed.

2.2 TAL-based registration with cell-based central policy

To provide more diverse TAL size, mitigation of the condition of the central TA may be considered. We consider the cell structure of TA in which TA can be composed of any number of cells. For example, in the case of NC = 4, the TAL of NT = 9 can be defined as shown in Fig. 3a, which can be termed TAL with TA-based central policy and four-cell TA. However, even in this case, the most basic TAL of NC = 4 and NT = 1 cannot be defined by the TA-based central policy, since there is no central TA.

Fig. 3
figure 3

A TAL with central policy (NC = 4)

Full size image

Incidentally, in the case of TAL of NC = 4 and NT = 4 as shown in Fig. 3b, even though there is no exact central TA, it seems that cells 1 and 2 approximately correspond to the center of the TAL. Similarly, Fig. 3c shows that in the case of TAL of NC = 4 and NT = 1, even though there is no exact central TA, it seems that cells 1 and 2 approximately correspond to the center of the TAL. If a UE exits cell 2 of the current TAL to enter cell 5, then the UE registers its new TAL such that cells 5 and 2 are the (pseudo) central cells of the new TAL, which can be termed TAL with cell-based central policy and four-cell TA. This is the basic concept of the cell-based (pseudo) central policy. Figure 3b and c shows that cells 1 and 2 are not the exact central cells of the TAL, but are pseudo-central cells of the TAL. However, from now on, we will simply term even this cell-based pseudo-central policy ‘cell-based central policy,’ unless a particular distinction is needed.

In summary, in this study, the cell-based central policy is proposed to mitigate the constraint of the TA-based central policy. Under the cell-based central policy, the cell in which a UE registers its location is the central cell of the new TAL. Figure 4 shows the central cells of the TAL with cell-based central policy for NT = (2 and 4) when NC = 4. Consider, for example, Fig. 4a, in which NT is 2, and NC is 4. In this case, there is no unique central TA, but 2 cells marked as ‘0′ will constitute the central cells of the TAL. Under the cell-based central policy, when a UE exits the current TAL, it registers its new TAL, such that the cell in which it registers is one of the central cells of the new TAL, as shown in Fig. 4a. Similarly, even in the case of TAL of NC = 4 and NT = 4, a UE registers its new TAL such that the cell in which it registers is one of the central cells of the new TAL, as shown in Fig. 4b.

Fig. 4
figure 4

A TAL with cell-based central policy (NC = 4)

Full size image

Under this policy, the TAL can have any number of TAs. As a result, it is possible to implement TAL-based registration with cell-based central policy for actual network architecture.

Note that TAL-based registration with cell-based central policy includes TAL-based registration with TA-based central policy. For example, when NC = 7, TAL-based registration with TA-based central policy is a special case of TAL-based registration with cell-based central policy for NT = 1 + \(\mathop \sum \nolimits_{i = 1}^{n} 6i\), n = 1, 2, …

2.3 TAL-based registration with cell-based central policy and single-cell TA

Incidentally, what is the optimal NC of TAL-based registration with cell-based central policy that offers the minimum total cost? In this section, we suggest that the optimal NC is 1.

For explanation, consider the case of NC = 3, as shown in Fig. 5. Also assume that NT = 3 (the total number of cells in the TAL is 9) shows the minimum total cost. However, in the case of NC = 3, since as the NT increases, the number of cells that make up the entire TAL increases by 3, the actual minimum total cost should be obtained by changing the total number of cells in the TAL from 7 to 11 (natural numbers that are greater than 6, and less than 12).

Fig. 5
figure 5

A TAL with cell-based central policy (NC = 3)

Full size image

When the total number of cells in the TAL is either 7 or 11, it would be most appropriate to configure the TAL as NC = 1, NT = 7 or NC = 1, NT = 11, respectively. As a result, we consider that NC = 1, in order to obtain the actual minimum total cost by changing the total number of cells in the TAL from 7 to 11.

Consider Fig. 6 as another example, which shows the possible configurations when NC⋅ NT = 8. Considering the case of NC⋅ NT = 8, there are three possible configurations: (a) NC = 4, NT = 2, (b) NC = 2, NT = 4, and (c) NC = 1, NT = 8.

Fig. 6
figure 6

A TAL with cell-based central policy (NC⋅ NT = 8)

Full size image

Figure 6a shows the optimal configuration for NC = 4, NT = 2, and the two shaded cells in the center part are the center cells of this TAL, since they have the same characteristics. Figure 6b shows the optimal configuration for NC = 2, NT = 4, and one shaded cell in the center part is the center cell of this TAL. Finally, Fig. 6c shows the optimal configuration for NC = 1, NT = 8, and the single shaded cell in the center part is the center cell of this TAL. Among them, as shown in Fig. 6c NC = 1, NT = 8 would provide the lowest cost, compared to (a) NC = 4, NT = 2, or (b) NC = 2, NT = 4, since (a), (b), and (c) have (22, 24, and 20) edges, respectively.

Figure 7 shows the total costs for the various TAL structures in Fig. 6, assuming that the calls are generated according to the Poisson processes with the rate λc = 1, and the staying time in a cell follows a gamma distribution with shape parameter α = 2. It is also assumed that the registration cost for one registration, U, is 10, and the paging cost for the single cell, P, is 1.

Fig. 7
figure 7

Total costs for the TAL structures in Fig. 6

Full size image

Figure 7 shows that the TAL structure (c) NC = 1 has the least cost, compared to any other NC. From the figure, TAL structure (a) NC = 4 has more cost than TAL structure (b) NC = 2, which has more cost than TAL structure (c) NC = 1. Given NC⋅NT, the smaller the NC of a TAL structure, the less the cost. Therefore, the TAL structure adopting NC = 1 has less cost than any other TAL structure adopting NC = (2, 3, 4 and so on) has, since the TAL structure adopting NC = 1 constructs the TAL that has the least registrations.

Therefore, in our study, we assumed NC = 1 to determine the number of cells that make up the optimum TAL. With this assumption, there is no restriction on the number of cells that make up the TAL, and any value is possible.

Figure 8 shows cases of NT = (10 and 14). In Fig. 8a, the upper-left 10 cells constitute TAL of NT = 10 (and NC = 1), in which the two shaded cells in the center part of TAL are center cells. In the figure, there are four kinds of cells: (0, 1, 2, and 3), in which cells with the same number have the same characteristic. If the UE exits the current TAL, then the exited cell and the entered cell (two dotted cells) constitute the center cells of the new TAL, as shown in Fig. 8a. Similarly, in Fig. 8b, the upper-left 14 cells constitute TAL of NT = 14 (and NC = 1), in which the two shaded cells in the center part of the TAL are center cells. In the figure, there are five kinds of cells: (0, 1, 2, 3, and 4), in which cells with the same number have the same characteristic. If the UE exits the current TAL, then the exiting cell and the entered cell (two dotted cells) constitute the center cells of the new TAL, as shown in Fig. 8b.

Fig. 8
figure 8

A TAL with cell-based central policy and single-cell TA (NC = 1)

Full size image

2.4 TAL-based registration with implicit registration

Referring to the system requirements [1], if the UE successfully sends a Page Response Message or an Origination Message, the cell can know the UE’s location. This is known as implicit registration (IR) [1, 6, 14]. If a call from or to the UE occurs, the network can identify the UE’s cell by the Page Response Message or the Origination Message, without registration messages. This means that if a network uses a TAL-based registration and IR simultaneously, the network can know the UE’s cell without registration process. If IR is adopted, the registration cost of the TAL-based registration can be reduced. Therefore, our study considers the TAL-based registration with IR, an improved scheme of the original TAL-based registration.

3 Modeling and performance analysis

The following notations are defined to analyze the total cost on radio channels:

CP: Paging cost in one hour.

CU: Location registration cost in one hour.

U: The location registration cost for one registration.

P: The paging cost for one cell.

NC: Number of cells in a TA.

NT: Number of TAs in a TAL.

Tc: Interval between two calls (r. v., Tc ~ Exp[1/λc], E(Tc) = 1/λc).

Tm: Staying time in a cell (r. v., E(Tm) = 1/λm).

Rm: Time between the arrival of the call, and the time when the UE moves out of the cell (r.v.)

\(f_{{\text{m}}}^{*} \left( s \right)\): The Laplace–Stieltjes transform for \(T_{{\text{m}}} \left( { = \mathop \smallint \nolimits_{t = 0}^{\infty } e^{{ - {\text{st}}}} f_{{\text{m}}} \left( t \right)dt} \right)\).

We also assume the following to obtain the total cost on radio channels:

  • When the UE enters a neighboring cell, the probability of selecting one of the neighboring cells is 1/6.

  • The incoming and outgoing calls are generated with the rates λi and λo, respectively, according to the Poisson processes and the staying time in a cell, while Tm follows a general distribution with the mean 1/λm.

Note that by the additional property of the Poisson processes, the incoming calls with the rate λi and outgoing calls with the rate λo form total calls with the rate λc (= λi + λo) [17].

3.1 Semi-Markov process model

An analytical model for the proposed scheme is presented using 2-D random walk mobility and semi-Markov process model. When the values of NT and NC are given, it is also possible to draw the state–transition diagram, and calculate the total cost on radio channels. This paper does not present simulation results, since the mathematical model proposed in this study is so clear that it is not necessary to verify it again by simulation.

An embedded Markov chain model is considered to consider the general cell-staying time and the IR effect of the calls. Assuming NC = 1, a Markov chain model for the consideration of the registration is explained. In our proposed model, the state i is defined as the state in which the UE resides in the cell i.

For example, in the case NC = 1, NT = 4, only three states are necessary to analyze the registration cost, as shown in Fig. 9a:

Fig. 9
figure 9

State transition diagram (NC = 1)

Full size image

State 0: The state that UE is in central cells marked as ‘0.’

State 1: The state that UE is in outer cells marked as ‘1.’

State 0′: The state that a call occurred to/from the UE, and the cell changed to central cell.

Note that state 0′ is related to implicit registration. UE in state 0 can enter state 1 with a probability of 1/3P[Tc > Tm], move to a neighboring state 0 with a probability of 1/6P[Tc > Tm], or move to a new TAL (and still be in state 0) with a probability of 1/2P[Tc > Tm]. When a call is generated, the UE in state 0 can transit to state 0′ (in other words, with probability P[Tc < Tm]). Similarly, the UE in state 1 can enter state 0 with a probability of 1/3P[Tc > Tm], or move to a new TAL (and be in state 0) with a probability of 2/3P[Tc > Tm]. When a call is generated, the UE in state 1 can also transit to state 0′ (in other words, with probability P[Tc < Tm]).

The UE in state 0′ can enter state 1 with a probability of 1/3P[Tc > Rm], move to a neighboring state 0 with a probability of 1/6P[Tc > Rm], or move to a new TAL (and to be in state 0) with a probability of 1/2P[Tc > Rm]. Finally, when a call is generated, the UE in state 0′ can transit to state 0′ (in other words, with a probability of P[Tc < Rm]).

Figure 9b and c shows that a Markov chain model for other cases can be similarly obtained:

$$m = P\left[ {T_{{\text{c}}} > T_{{\text{m}}} } \right], m^{\prime} = P\left[ {T_{{\text{c}}} > R_{{\text{m}}} } \right]$$

The probability that a UE enters other cells before a call occurs can be calculated as follows [14]:

$$m = P\left[ {T_{{\text{c}}} > T_{{\text{m}}} } \right] = \mathop \int \limits_{0}^{\infty } \mathop \int \limits_{{t_{{\text{m}}} }}^{\infty } \lambda_{{\text{c}}} e^{{ - \lambda_{{\text{c}}} t_{{\text{c}}} }} f_{{\text{m}}} \left( {t_{{\text{m}}} } \right)dt_{{\text{c}}} dt_{{\text{m}}} = f_{{\text{m}}}^{*} \left( {\lambda_{{\text{c}}} } \right)$$
(1)

Now, let us derive m′ = P[Tc > Rm], which is the probability of a UE, whose state is changed due to the call occurrence, moving to the neighboring cell before another call from/to the UE occurs.

The density function of Rm, fr(t) is from the random observer property [17],

$$f_{{\text{r}}} \left( t \right) = \lambda_{{\text{m}}} \mathop \int \limits_{\tau = t}^{\infty } f_{{\text{m}}} \left( \tau \right)d\tau = \lambda_{{\text{m}}} \left( {1 - F_{{\text{m}}} \left( t \right)} \right)$$
(2)

The Laplace–Stieltjes transform for the distribution is as follows:

$$\begin{aligned} f_{{\text{r}}}^{*} \left( s \right) = \mathop \int \limits_{t = 0}^{\infty } e^{{ - {\text{st}}}} f_{{\text{r}}} \left( t \right)dt = \mathop \int \limits_{t = 0}^{\infty } e^{{ - {\text{st}}}} \lambda_{{\text{m}}} \left( {1 - F_{{\text{m}}} \left( t \right)} \right)dt = \frac{{\lambda_{{\text{m}}} }}{s} - \mathop \int \limits_{t = 0}^{\infty } e^{{ - {\text{st}}}} \lambda_{{\text{m}}} F_{{\text{m}}} \left( t \right)dt \\ & \quad \quad \,\,\, = \frac{{\lambda_{{\text{m}}} }}{s} + \left[ {\frac{{\lambda_{{\text{m}}} }}{s}e^{{ - {\text{st}}}} \lambda_{{\text{m}}} F_{{\text{m}}} \left( t \right)} \right]_{t = 0}^{\infty } - \frac{{\lambda_{{\text{m}}} }}{s}\mathop \int \limits_{t = 0}^{\infty } e^{{ - {\text{st}}}} f_{{\text{m}}} \left( t \right)dt = \frac{{\lambda_{{\text{m}}} }}{s}\left( {1 - f_{{\text{m}}}^{*} \left( s \right)} \right) \\ \end{aligned}$$
(3)

This gives:

$$m\prime = P\left[ {T_{{\text{c}}} > R_{{\text{m}}} } \right] = \mathop \int \limits_{0}^{\infty } \mathop \int \limits_{{t_{{\text{c}}} = r_{{\text{m}}} }}^{\infty } \lambda_{c} e^{{ - \lambda_{{\text{c}}} t_{{\text{c}}} }} f_{{\text{r}}} \left( {r_{{\text{m}}} } \right)dt_{{\text{c}}} dr_{{\text{m}}} = \mathop \int \limits_{0}^{\infty } f_{{\text{r}}} \left( {r_{{\text{m}}} } \right)e^{{ - \lambda_{{\text{c}}} t_{{\text{c}}} }} dr_{{\text{m}}} = \frac{{\lambda_{{\text{m}}} }}{{\lambda_{{\text{c}}} }}\left( {1 - f_{{\text{m}}}^{*} \left( {\lambda_{{\text{c}}} } \right)} \right)$$
(4)

The UE’s staying time in a cell, Tm, affects the transition probability. If Tm follows a gamma distribution, the mean is 1/λm and the variance is V. Then, P[Tc > Tm] is:

$$m = P\left[ {T_{{\text{c}}} > T_{{\text{m}}} } \right] = \left( {\frac{{\lambda_{{\text{m}}} \gamma }}{{\lambda_{{\text{m}}} \gamma + \lambda_{{\text{c}}} }}} \right)^{\gamma } {\text{where}}\,\gamma = \frac{1}{{V\lambda_{{\text{m}}}^{2} }}$$
(5)

In this case, the staying time in state 0′ is different from the staying time in other states. The staying time in state 0′ is the interval from the time a call to/from a UE occurs in a cell, until the time it transits (moves to a neighboring cell, or generates a call again). On the other hand, the staying time in other states, except state 0′, is the interval from the time the UE enters a cell, until the time it transits (moves to a neighboring cell, or generates a call).

It needs to be considered that to evaluate the accurate performance, the staying time in each state is different. First, the staying time in state 0′ can be expressed as:

$$T_{{\text{c}}} , {\text{if}}\; T_{{\text{c}}} \le R_{{\text{m}}}$$

\(R_{{\text{m}}} , \,{\text{if}} \;T_{{\text{c}}} > R_{{\text{m}}}\).

Its mean can be obtained as follows:

$$\begin{gathered} \tau_{{0^{\prime}}} = \mathop \int \limits_{0}^{\infty } \mathop \int \limits_{0}^{{r_{{\text{m}}} }} t_{{\text{c}}} f_{{\text{c}}} \left( {t_{{\text{c}}} } \right)dt_{{\text{c}}} f_{{\text{r}}} \left( {r_{{\text{m}}} } \right)dr_{{\text{m}}} + \mathop \int \limits_{0}^{\infty } \mathop \int \limits_{{r_{{\text{m}}} }}^{\infty } r_{{\text{m}}} f_{{\text{c}}} \left( {t_{{\text{c}}} } \right)dt_{{\text{c}}} f_{{\text{r}}} \left( {r_{{\text{m}}} } \right)dr_{{\text{m}}} \hfill \\ \quad = \mathop \int \limits_{0}^{\infty } \left[ {\mathop \int \limits_{0}^{{r_{{\text{m}}} }} t_{{\text{c}}} f_{{\text{c}}} \left( {t_{{\text{c}}} } \right)dt_{{\text{c}}} + \mathop \int \limits_{{r_{{\text{m}}} }}^{\infty } r_{{\text{m}}} f_{{\text{c}}} \left( {t_{{\text{c}}} } \right)dt_{{\text{c}}} } \right]f_{{\text{r}}} \left( {r_{{\text{m}}} } \right)dr_{{\text{m}}} = \frac{1}{{\lambda_{{\text{c}}} }}\left( {1 - \frac{{\lambda_{{\text{m}}} }}{{\lambda_{{\text{c}}} }}\left[ {1 - f_{{\text{m}}}^{*} \left( {\lambda_{{\text{c}}} } \right)} \right]} \right) \hfill \\ \end{gathered}$$
(6)

Next, the staying time in other states, except state 0′, can be expressed as:

$$T_{{\text{c}}} , {\text{if}}\; T_{{\text{c}}} \le T_{{\text{m}}}$$
$$T_{{\text{m}}} , {\text{if}}\; T_{{\text{c}}} > T_{{\text{m}}}$$

Its mean τi (i = 0, 1, 2, …) can be derived as follows:

$$\begin{gathered} \tau_{i} = { }\mathop \int \limits_{0}^{\infty } \mathop \int \limits_{0}^{{t_{{\text{m}}} }} t_{{\text{c}}} f_{{\text{c}}} \left( {t_{{\text{c}}} } \right)dt_{{\text{c}}} f_{{\text{m}}} \left( {t_{{\text{m}}} } \right)dt_{{\text{m}}} + \mathop \int \limits_{0}^{\infty } \mathop \int \limits_{{t_{{\text{m}}} }}^{\infty } t_{{\text{m}}} f_{{\text{c}}} \left( {t_{{\text{c}}} } \right)dt_{{\text{c}}} f_{{\text{m}}} \left( {t_{{\text{m}}} } \right)dt_{{\text{m}}} \hfill \\ = \mathop \int \limits_{0}^{\infty } \left[ {\mathop \int \limits_{0}^{{r_{{\text{m}}} }} t_{{\text{c}}} f_{{\text{c}}} \left( {t_{{\text{c}}} } \right)dt_{{\text{c}}} + \mathop \int \limits_{{r_{{\text{m}}} }}^{\infty } r_{{\text{m}}} f_{{\text{c}}} \left( {t_{{\text{c}}} } \right)dt_{{\text{c}}} } \right]f_{{\text{r}}} \left( {r_{{\text{m}}} } \right)dr_{{\text{m}}} = \frac{1}{{\lambda_{{\text{c}}} }}\left( {1 - \frac{{\lambda_{{\text{m}}} }}{{\lambda_{{\text{c}}} }}\left[ {1 - f_{{\text{m}}}^{*} \left( {\lambda_{{\text{c}}} } \right)} \right]} \right) \hfill \\ \end{gathered}$$
(7)

In order to obtain the steady-state probability \(\tilde{\pi }\), first calculate the steady-state probability π for the usual Markov chain with transition probability P by using the balanced equations, as follows [17]:

$$\pi P = \pi , \, \mathop \sum \limits_{{\text{j}}} \pi_{{\text{j}}} = 1$$
(8)

Then, considering the different staying time, the final steady-state probability of the semi-Markov process can be obtained as follows [17]:

$$\tilde{\pi }_{i} = \frac{{\pi_{i} \tau_{i} }}{{\mathop \sum \nolimits_{{\text{j}}} \pi_{{\text{j}}} \tau_{{\text{j}}} }}$$
(9)

3.2 Total cost on radio channels

The registration and the paging costs constitute the total cost on radio channels.

The registration cost per hour, Cu, can be given as follows:

$$C_{{\text{U}}} = U\lambda_{{\text{m}}} \sum\nolimits_{{{\text{j}} \in {\text{B}} }} {\left[ {\tilde{\pi }_{{\text{j}}} \cdot p_{{\text{U}}} \left( {\text{j}} \right)} \right]}$$
(10)

where B is the set of states for the boundary cells in a TAL, and \(p_{{\text{U}}} \left( j \right)\) is the probability that a UE in state j enters a neighboring cell to perform location registration. For example, in Fig. 9a, \(C_{{\text{U}}} = U\lambda_{{\text{m}}} \sum\nolimits_{{{\text{j}} \in {\text{B}}}} {\tilde{\pi }_{{\text{j}}} \cdot p_{{\text{U}}} \left( j \right) = U\lambda_{{\text{m}}} \left[ {\left( \frac{1}{2} \right)\left( {\tilde{\pi }_{0} + \tilde{\pi }_{0^{\prime}} } \right) + \left( \frac{2}{3} \right)\tilde{\pi }_{1} } \right]}\), since B = {0, 1, 0′}, \(p_{{\text{U}}} \left( 0 \right)\) = \(p_{{\text{U}}} \left( {0^{\prime}} \right)\) = 1/2, and \(p_{{\text{U}}} \left( 1 \right)\) = 2/3.

Assuming the mobile network adopts simultaneous paging [14, 15] the paging cost per hour is as follows:

$$C_{P} = P\lambda_{i} \left[ {N_{{\text{T}}} \cdot N_{{\text{C}}} } \right]$$
(11)

Finally, the total cost on radio channels may be obtained, as follows:

$$C_{T} = C_{U} + C_{P}$$
(12)

4 Numerical results

To obtain the numerical results for TAL-based registration with cell-based central policy and single-cell TA, the following assumptions are made [14, 15, 18]:

U = 10, P = 1, λm = 5, λc = λi + λo = 1 + 1 = 2.

Both incoming call and outgoing call are generated according to the Poisson processes with the rates λi and λo, respectively. The staying time in a cell follows a gamma distribution with mean 1/λm.

4.1 Performance of TAL-based registration with cell-based central policy and single-cell TA

Figure 10 shows the total costs for various numbers of TAs in a TAL. Generally, as the number of TAs in a TAL increases, the registration cost decreases due to the infrequency of the registrations; however, because of the large paging area, the paging cost increases. Finally, in this case, the optimal number of TAs in a TAL that minimizes the total cost is 7:

Fig. 10
figure 10

Total costs for various numbers of TAs in a TAL

Full size image

The optimal number of TAs in a TAL that results in the minimal total cost can be obtained for any other situation. Figure 11 shows the total costs and the optimal number of TAs in a TAL for various E(Tm). Generally, the lower the E(Tm), the greater the total cost. This is because of the increase in the location registrations. As a result, as E(Tm) decreases, the optimal number of TAs in a TAL increases, since the location area (TAL) must be large to reduce location registrations.

Fig. 11
figure 11

Total costs for various E(Tm)

Full size image

Figure 12 shows the total costs and the optimal number of TAs in a TAL for various call-to-mobility (CMR) ratios. CMR is defined as λc/λm, i.e., the higher the CMR, the more the call generation compared to cell entrance. Consequently, the higher the CMR, the greater the paging cost due to increase in paging. Therefore, as CMR increases, the optimal number of TAs in a TAL decreases, since the location area (TAL) must be small to reduce paging cost. In the examples, the optimal number of TAs in a TAL is 7, which when CMR = 1, minimizes the total cost. On the other hand, when CMR = 1.15, the optimal number of TAs in a TAL is 5; and when CMR = 1.35, the optimal number of TAs in a TAL is 4:

Fig. 12
figure 12

Total costs for various CMRs

Full size image

Through many numerical results for various circumstances, the proposed TAL-based registration with cell-based central policy yields better performance than the TAL-based registration with TA-based central policy in every case.

4.2 Effect of implicit registration

Figure 13 shows the effect of implicit registration in total costs. In general, if implicit registration is implemented, the registration cost decreases. Figure 13 shows that when CMR = 1 and implicit registration is not implemented, the optimal number of TAs in a TAL would be 5, and the total cost is 9.106. On the other hand, if implicit registration is implemented, the optimal number of TAs in a TAL would be 7, and the total cost is 6.023. In this case, because of the effect of implicit registration, total cost decreases by 33.9%.

Fig. 13
figure 13

Effect of implicit registration on total costs

Full size image

4.3 Comparison with distance-based registration

Figure 14 shows the total costs of various numbers of TAs in a TAL for single-cell TA (NC = 1), compared to distance-based registration (DBR) that shows good performance [14, 15, 18]. Note that DBR is a special case of TAL-based registration with single-cell TA. In these circumstances, TAL-based registration with single-cell TA reached a minimum value of 8.536 at 5 TAs, while DBR had a minimum value of 8.779 at 7 TAs (i.e., distance threshold = 2). In Fig. 14, it is evident that TAL-based registration with single-cell TA is superior to DBR in every case.

Fig. 14
figure 14

Comparison with distance-based registration

Full size image

5 Conclusion

This study investigated TAL-based registration with central policy for LTE networks. This policy can lessen the possibility of the UE quickly exiting the new TAL. However, considering the actual network architecture, it makes TAL-based registration a challenge to implement. Thus, a cell-based central policy was proposed to mitigate this challenge. TAL-based registration with cell-based central policy and single-cell TA (TbRcc1c) was also proposed to reduce the registration cost and make up the optimal TAL.

Furthermore, an improved analytical model for the proposed scheme was proposed that uses 2-D random walk mobility and semi-Markov process model to consider the effect of implicit registration of calls and obtain exact cost. Finally, comparison of the performance of TbRcc1c with those of the classical TAL-based registration and distance-based registration shows that the performance of the proposed scheme is improved.

Finally, the TAL-based registration with cell-based central policy is shown to be superior to TAL-based registration with TA-based central policy in every case, and that TAL-based registration with single-cell TA is superior to distance-based registration (DBR), which is known to show good performance.

Under the proposed policy, the TAL can have any number of TAs; as a result, it is possible to easily implement the proposed TbRcc1c in any real network architecture. The results of this study can be used in research on the mobility management of next-generation networks [8,9,10], as well as LTE networks. In further study, the 5G-related matters will be investigated to implement the proposed method in 5G network.