Introduction. Elastic-plastic deformation of structural elements in zones of their increased loading (stress and strain concentration zones) is accompanied by the accumulation of scattered damage at micro- and mesolevels [1,2,3]. It was demonstrated in [4] that the endurance limit of a structural material (SM) acts as a threshold stress at which local microdamages in the form of micropores, microcracks, and other microfractures start to manifest themselves. To solve technological problems of the theory of plasticity, an important aspect is to specify the process of damage accumulation kinetics within the range from the yield stress limit to the strength limit (the stage of macrocrack nucleation in a representative material element).

The accumulation of scattered damage in SM is, in fact, a complex multistage process, the final result of which is the macrocrack initiation. In order to describe this process as correctly as possible, it is necessary that the defining criterion at the first stage of fracture should take into account the time and path of complex loading as one of the main parameters. The above criterion should be closely related to the basic equations that describe elastic-plastic deformation processes.

The analysis of the existing criteria presented in works [5,6,7,8,9,10] allows one to conclude that, from the point of view of reliability of description of the processes that occur in a material during its elastic-plastic deformation, the energy criterion is the most promising. The energy criteria, which are based on the basic principles of thermodynamics of irreversible processes and continuum mechanics of damage, are currently the most widely used in describing various processes of elastic-plastic deformation and the damageability of SMs [3, 8, 11]. As a rule, they take into account the character of thermomechanical loading and the type of the stress state, as well as the influence of the first and second invariants of the stress tensors on the characteristics of static and cyclic strength of SMs and structural elements.

The aim of the presented work is to develop and substantiate the limits of application of the generalized fracture criterion at the stage of SM macrocrack nucleation under complex stress state conditions taking into account the main provisions of continuum mechanics of damageability. At this longest stage of the fracture process, from the phenomenological point of view, we will consider as successively alternating two processes: (1) the nucleation of microdefects (in the form of micropores and microcracks) and (2) their growth and merging with the appearance of a macrocrack (incubation period). It is described, as a rule, in the form of a kinetic equation of change in the damageability parameter depending on the conditions of elastic-plastic deformation of SM. A scalar, vector or tensor, which is characterized by one of the types of thermodynamic potential, can be considered as the damage parameter.

The Method of Substantiation of the Damage Criterion in a Complex Stressed State. As a first approximation, we choose the damageability parameter in the form of a scalar, which is characterized by the potential F, which takes into account the rate of release of a part of the elastic strain energy Y. In this case, the variation rate of the scalar parameter of the damageability D will be determined by [3, 12]

$$ \dot{D}=\frac{\partial {F}_D\left(Y,{\upvarepsilon}_i^{(p)},D,\dots \right)}{\partial Y}, $$
(1)

where \( {\upvarepsilon}_i^{(p)} \) is the intensity of irreversible constitutive strain in the representative element of the material.

Based on the general view of the damage potential [3] and replacement of the equivalent von Mises stress by the equivalent stress according to the Pisarenko–Lebedev criterion [5], with its further integration, the equations describing the damage accumulation in a complex stress state were obtained [13]:

$$ D={\left(\frac{A^2R}{2 EB}\right)}^b\frac{1}{n}\left[{\left({\upvarepsilon}_i^p\right)}^n-{\left({\upvarepsilon}_{iD}^p\right)}^n\right], $$
(2)

where A, B, b, and n = 2mb +1 are the material constants under isothermal active loading, m is strengthening parameter of the deformation diagram of SM, \( {\upvarepsilon}_{iD}^{(p)} \) is threshold value of plastic strain intensity, and E is elastic modulus of the first kind (i.e., the Young modulus).

The stress state type function R is defined as follows:

$$ R=\frac{2}{3}\left(1+v\right){\left[\upchi +\left(1-\upchi \right)\frac{\upsigma_1}{\upsigma_i}\right]}^2+3\left(1-2v\right){K}^2, $$
(3)

where v is Poisson’s ratio, χ is the Pisarenko–Lebedev parameter, σi is stress intensity, and K is stiffness parameter of the stress state type.

For uniaxial tension conditions, we have D = D1 and R = 1. The experimental D1 = f(ε(p)), which is the damage capacity under uniaxial tensile conditions, is determined from the basic experiment. At present, for metallic SMs, the most widespread is the method of determination of damage accumulation behavior for uniaxial tension conditions, which is based on the assessment of elastic modulus E degradation or change in the specific electrical resistance (resistivity) ρ [14]:

$$ {D}_1=1-\frac{\tilde{E}}{E_0}, $$
(4)
$$ {D}_1=\frac{1}{2}1\mathrm{n}\frac{\tilde{E}}{E_0}, $$
(5)
$$ {D}_1=1\sqrt{\frac{\tilde{E}}{E_0},} $$
(6)
$$ {D}_1=\frac{\tilde{\uprho}\hbox{-} {\uprho}_0}{\uprho_0}, $$
(7)

where \( \tilde{E},{E}_0,\tilde{\uprho}, \) and ρ0 are the current and initial values of the elastic modulus and resistivity, respectively.

Equations (4) and (5) were obtained based on the hypothesis of deformation equivalence of intact and damaged SM [15], while Eq. (6) was derived according to the hypothesis of elastic energy equivalence [16]. Numerous experiments [13, 17, 18] demonstrated that the use of dependence via Eq. (7) makes it possible to take into account most accurately all the changes in metallic SM that take place in a representative element of the specimen working area volume during its elastic-plastic deformation. Therefore, the method of damage assessment via the resistivity variation was chosen in the work as the most reliable one.

Figure 1 depicts the experimental damage accumulation curves for metallic SMs, which were obtained according to dependences (4)–(7) for uniaxial tension.

Fig. 1.
figure 1

Kinetics of damage accumulation: (1) experiment; (2), (3), (4), and (5) are dependences (7), (4), (5), and (6), respectively.

Full size image

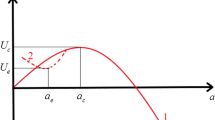
The analysis of experimental results demonstrates that the kinetics of damage accumulation in relatively brittle materials (D16T and VT22 alloys) has a linear pattern, while that in more plastic materials (30KhGSA and 12Kh18N10T steels) is non-linear, which coincides with the conclusions of Rabotnov and Kachanov [1, 2]. The regularities of damage and strain accumulation depicted in Fig. 1 made it possible to establish the relationship between their current values D1 and ε1 and limit values D1R and ε1R at the stage of macrocrack nucleation, respectively, in the form of

$$ {D}_1={D}_{1R}{\left(\frac{\upvarepsilon_1}{\upvarepsilon_{1R}}\right)}^{\upalpha}. $$
(8)

Equation (8) allows one to present the damage accumulation patterns in the form of a function, which depends on the level of plasticity of metallic SM. Graphically, the influence of the parameter α on the curve shape described via Eq. (8) is demonstrated in Fig. 2.

Fig. 2.
figure 2

Kinetics of damage accumulation depending on the parameter α.

Full size image

Based on the statistical processing of experimental results for D16T and VT22 alloys, as well as 30KhGSA and 12Kh18N10T steels by the regression analysis, the dependence of the parameter α on the mechanical properties of metal SM was established as

$$ \upalpha =\frac{\upsigma_u}{\upsigma_R}\left[10.3{E}_0\cdot {10}^{-5}{\upvarepsilon}_{1R}-2.4\frac{\upsigma_u}{\upsigma_R}+4.3\right]{\upvarepsilon}_{1R}\left[9.1{\upvarepsilon}_{1R}+11.5\right]-{E}_0\cdot {10}^{-5}, $$
(9)

where σu and σR are strength limit and fracture stress according to the conditional strain diagram (which ignores the cross-sectional area reduction of tested specimens), respectively (MPa).

Similarly, the dependence for the limiting value of the scalar damage parameter D1R on the mechanical properties of metallic SMs was obtained:

$$ {D}_{1R}=\frac{1}{100}\left\{\frac{\sigma_u}{\sigma_R}\left[25\frac{\sigma_u}{\sigma_R}-2{E}_0\cdot {10}^{-5}{\upvarepsilon}_{1R}-7\right]+{E}_0\cdot {10}^{-5}\left[9{E}_0\cdot {10}^{-5}-20\right]+{\upvarepsilon}_{1R}\left[43{\upvarepsilon}_{1R}-4\right]\right\}. $$
(10)

Figure 3 shows the calculated curves of damage accumulation kinetics according to Eq. (8) with regard Eqs. (9) and (10), in comparison with the experimental curve obtained via Eq. (7).

Fig. 3.
figure 3

Kinetics of damage accumulation: (1) calculated curve; (2) experimental curve.

Full size image

In general, the SM fracture involves the interaction of two fracture mechanisms: tear and shear [19, 20]. To specify the parameters of the defining equations of state and fracture criteria, a basic tensile and torsional test of SM specimens is usually performed. In this case, as demonstrated in Fig. 4, the limiting values of scalar parameters of damageability DR (by tear D1R and shear DRK) are different and depend on the level of the limiting strain of metallic SM and on the yield stress σY.

Fig. 4.
figure 4

Dependence of damage limit value on the level of plasticity of metallic SMs (T = 293 K): (1) tension; (2) torsion; (3) yield stress σY in tension.

Full size image

The main methodology used to determine the kinetics of SM damage accumulation during torsion is based on tests of thin-walled tubular specimens [5], which are very complicated in terms of manufacturing and processing. However, it is possible to simplify this methodology.

The damage accumulation \( {\tilde{D}}_{\upgamma\ \max }, \)which takes place during torsion of a thin-walled tubular specimen, is determined via the resistivity variation of the SM specimen depending on its torsion angle γ, using the equation similar to Eq. (8), which can be written in the form

$$ {\tilde{D}}_{\upgamma}={\tilde{D}}_{RK}{\left(\upgamma /{\upgamma}_R\right)}^{\tilde{\upbeta}}, $$
(11)

where \( {\tilde{D}}_{RK} \) is the true value of the torsional damage limit, which takes into account the non-uniform distribution in the section, \( \tilde{\upbeta} \) is the plasticity parameter of SM, and γR is the torsional angle’s limit value.

The torsional test of solid cylindrical specimens in strain-controlled loading mode yields the conditional diagram of damage accumulation kinetics Dγ , i.e., the value averaged over the specimen’s cross-section radius. This makes it possible to derive the equation similar to Eq. (11) by replacing true values of \( {\tilde{D}}_{\upgamma\ \max },{\tilde{D}}_{RK}, \) and \( \tilde{\upbeta} \)by conditional ones (Dγ, DRK, and βγ), which disregard the non-uniformity of value distribution in the cross-section. Schematically, the regularities of distribution of shear stresses τ, shear strains γ, and damages Dγ over the cross-section during elastic-plastic deformation of a solid cylindrical specimen are shown in Fig. 5.

Fig. 5.
figure 5

Distribution patterns of shear strains γ, stresses τ, and damages Dγ during elastic-plastic deformation of continuous cylindrical specimens.

Full size image

In case of torsion, according to the linear law of variation of the twisting angle γ = γ(r) (see Fig. 5), Eq. (11) can be reduced to the following form:

$$ \tilde{D}\left({\upgamma}_{\mathrm{max}},r\right)={\tilde{D}}_{RK}{\left(\frac{\upgamma_{\mathrm{max}}r}{R{\upgamma}_R}\right)}^{\tilde{\upbeta}}. $$
(12)

Dependence (12) determines the damage area of the ring of the average radius r and width dr in the solid specimen. Then, the total area of microdamage in the ring \( {\tilde{S}}_n \) can be derived as follows:

$$ {\tilde{S}}_n=2\uppi rdr{\tilde{D}}_{RK}{\left(\frac{\upgamma_{\mathrm{max}}}{R\ {\upgamma}_R}\right)}^{\tilde{\upbeta}}. $$
(13)

After integration, we obtain the total theoretical area of microdamages of the cross-section of a solid specimen with radius R:

$$ {\tilde{S}}_n=\frac{2\uppi {\tilde{D}}_{RK}{\left(\frac{\upgamma_{\mathrm{max}}}{\upgamma_R}\right)}^{\tilde{\upbeta}}{R}^2}{\tilde{\upbeta}+2}. $$
(14)

The experimental value of the microdamage area Sne is defined through the conditional damage:

$$ {S}_{ne}=\uppi {R}^2{D}_{RK}{\left(\frac{\upgamma_{\mathrm{max}}}{\upgamma_R}\right)}^{\upbeta_y}. $$
(15)

According to the condition \( {\tilde{S}}_n\left({\upgamma}_{\mathrm{max}}\right)={S}_{ne}\left({\upgamma}_{\mathrm{max}}\right), \) we get

$$ {\tilde{D}}_{RK}=\frac{1}{2}{D}_{RK}\left(\tilde{\upbeta}+2\right){\left(\frac{\upgamma_{\mathrm{max}}}{\upgamma_R}\right)}^{\upbeta_y-\tilde{\upbeta}}. $$
(16)

Equation (12) is a theoretical dependence of damage accumulation kinetics for a thin-walled tubular specimen. When integrating Eq. (13), it is necessary to substitute the inner and outer radii of the tubular specimen as integration boundaries, taking into account the homogeneity of the stress-strain state in its wall.

The validity of Eq. (16) was verified by comparing the experimental results obtained for solid and tubular specimens made of D16T aluminum alloy. The outer and inner diameters were 12 and 10 mm, respectively.

The experimental procedure is described in detail in [19]. The results are shown in Fig. 6, where: 1 and 2 are experimental curves constructed via Eq. (7) for cylindrical solid and tubular specimens, respectively; 3 and 4 are curves calculated via Eq. (11) for the actual and infinitesimal wall thickness values of the tubular specimen, respectively; 5 and 6 are curves constructed via Eqs. (4) and (5), respectively, for the tubular specimen, with the elastic modulus E being replaced by the shear modulus G; εi is the strain intensity. The analysis of the results demonstrates the possibility of using the developed technique to estimate the value of torsional damage.

Fig. 6.
figure 6

Kinetics of damage accumulation for alloy D16T at T = 293 K.

Full size image

The limiting value of the scalar damage parameter DR depends on the type of stress state, which can be taken into account by the third invariant of the stress tensor:

$$ \upeta =\frac{\upsigma_0}{\upsigma_i},\xi =\frac{27{I}_3}{2{\upsigma}_i}, $$
(17)

where σ0 is the mean stress, \( {\upsigma}_0=\frac{1}{3}{\updelta}_{ij}{\upsigma}_0,{\upsigma}_i \) is stress intensity, \( {\upsigma}_i=\sqrt{\frac{3}{2}{S}_{ij}{S}_{ij},}\ {I}_3 \) is the third invariant of the stress tensor, \( {I}_3=\frac{1}{3}{S}_{ij}{S}_{j\overline{K}}{S}_{\overline{K}l}, \) and Sij is stress deviator, Sij = σij = δijσ0.

The above parameters η i ξ are sufficient to determine the limit state for any point on the von Mises surface. According to the Davidenkov–Fridman fracture model [5, 6, 20], the failure process of SM is carried out by two mechanisms: tear and shear (Fig. 4). Let us denote the limiting value of the damage parameter for tear as D1R , that for shear by DRK , and the limiting value of the damage, which is realized under other types of stress state, by D1R, D𝜇R. Consider the case where DKR ≤ DμR ≤ D1R. Three possible curves (1–3) of the limit state of SM, depending on the type of the stressed state (type of failure) are plotted in Fig. 7.

Fig. 7.
figure 7

Possible variation patterns of the limit state value of the damage parameter according to the type of failure.

Full size image

The Nadai–Lode parameter in stresses was chosen as an argument of the stress state type function f (μ):

$$ \upmu =\frac{2{\upsigma}_2-{\upsigma}_1-{\upsigma}_3}{\upsigma_i-{\upsigma}_3},\kern0.5em {\upsigma}_1\ge {\upsigma}_2\ge {\upsigma}_3, $$
(18)

where σ1, σ2 , and σ3 are the principal stresses.

It is known that for uniaxial tension μ = -1, in torsion μ = 0, and in compression μ =1. Then, the stress state type function can be written in the form

$$ f\left(\upmu \right)=\operatorname{arccos}\left(-\upmu \right). $$

For other types of stress state, when the failure mechanisms of tear and shear are realized simultaneously, the limit value of the damage parameter DμR falls within the following ranges:

$$ \left\{\begin{array}{l}{D}_{KR}\le {D}_{\upmu R}\le {D}_{1R}\kern0.5em \mathrm{for}\kern0.5em \upmu \le 0,\\ {}{D}_{KR}\le {D}_{\upmu R}\le {D}_{-1R}\kern0.5em \mathrm{for}\kern0.5em \upmu \ge 0,{D}_{KR}\le {D}_{-1R},\\ {}{D}_{KR}\ge {D}_{\upmu R}\ge {D}_{-1R}\kern0.5em \mathrm{for}\kern0.5em \upmu \ge 0,{D}_{KR}\ge {D}_{-1R},\end{array}\right. $$
(20)

where D-1R is the limit value of damage for uniaxial compression, D−1R = hD1R, h is healing parameter, which is determined experimentally. For metallic SMs, h ≈ 0.4–0.6, according to [3, 4, 13].

According to the system of inequalities (20), the limit curve 3 (Fig. 7) satisfies all requirements. Then, the critical value of damage DμR depending on the function of the type of stress state f (μ) can be defined as follows:

$$ {D}_{\upmu R}=\frac{D_{\pm 1R}{D}_{KR}}{\sqrt{D_{KR}^2{\cos}^2f\left(\upmu \right)+{D}_{\pm 1R}^2{\sin}^2f\left(\upmu \right)}}. $$
(21)

In Eq. (21), under the condition μ ≤ 0, the value of D1R is used in the numerator uses, while at μ > 0 the value of D-1R is alternatively used. Graphically, the dependence of the limit value can be described by a combination of two ellipses, which is shown by the solid line in Fig. 8.

Fig. 8.
figure 8

Dependence of the limit value of the damage parameter DμR on the function of the type of stress state f (μ).

Full size image

Taking into account the healing parameter h and the sign of the Nadai–Lode parameter, Eq. (21) will take the following form:

$$ {D}_{\upmu R}=\frac{D_{\pm 1R}{D}_{KR}}{\sqrt{D_{KR}^2{\cos}^2\mathrm{ar}\cos \mathrm{s}\left(-\upmu \right)+{D}_{\pm 1R}^2{\sin}^2\ \mathrm{ar}\cos \mathrm{s}\left(-\upmu \right)}}. $$
(22)

Equation (22) describes the dependence of the damage limit value of an initially isotropic metallic SM on the type of stress state and the two failure mechanisms (tear and shear).

The limit values (at the stage of macrocrack nucleation) of the damage parameter for metallic SMS, namely D16T alloy and 12Kh18N10T steel are listed in Table 1.

Table 1. Experimental Values of the Damage Limit Parameter for Metallic SMs at T = 293 K
Full size table

The dependences of the damage parameter limit values on the type of stress state are plotted in Fig. 9, where the dots indicate the experimental results.

Fig. 9.
figure 9

Kinetics (paths 1 and 2) and limit values (curve 3) of the SM damage parameter depending on the type of stress state.

Full size image

The experimental results obtained prove that the accumulation of microdamages in the material during its elastic-plastic deformation occurs in accordance with two main failure mechanisms – tear and shear. In this case, the prevailing mechanism is tear.

Thus, the proposed methodology makes it possible to reliably determine the critical value of the damage parameter for metallic SMs at the stage of macrocrack initiation, taking into account the type of stress state.

Conclusions

  1. 1.

    The accumulation of scattered damages occurs simultaneously with the processes of elastic and elastic-plastic deformation of structural materials in the zones of their increased loading, starting from the threshold level of equivalent stresses, which correspond to the endurance limit of metal SM [4].

  2. 2.

    Under active loading (deformation), the damage accumulation process is realized according to a model that takes into account two failure mechanisms (tear and shear) and depends on the type of stress state.

  3. 3.

    It is demonstrated that for engineering calculations the most accurate approach is based on determining the damage parameter by estimating the change in the electrical resistivity of a metal SM specimen. The simplest approach is the one that takes into account the change in the elastic modulus of the specimen during its elastic-plastic deformation.

  4. 4.

    It was found that, in order to perform basic experiments to determine the damage parameter, it is necessary to use equations (4) and (6) for brittle and plastic materials, respectively.

  5. 5.

    A generalized fracture criterion for SM in the form of a criterial equation at the stage of macrocrack nucleation was developed based on the results of tensile and torsional tests of solid cylindrical specimens.

  6. 6.

    Using the effect of specific electrical resistance variation in metallic SMs during their elastic-plastic deformation, an experimental-and-calculation method for estimating the kinetics of damage accumulation by shear using cylindrical specimens was developed. The proposed method allows one to take into account the non-uniform strain distribution along the specimen radius.

  7. 7.

    It is demonstrated and substantiated that the critical value of the damage parameter for metallic SMs is always less than unity and depends on the level of ultimate plasticity of the material and the type of stress state.