Microstructure-Based Model for Sharp Stress Raiser-Related Fatigue Stage Length Assessment

A model for evaluating the fatigue life of specimens/structure elements with sharp stress raisers/defects is presented. The model permits of computing the number of cycles to fatigue crack initiation and its growth from a sharp stress raiser to failure at a constant stress span with the only application of characteristics of static strength and microstructure of the initial material. The model can be used to assess the fatigue life of components that contain structural stress raisers and defects stemming from their manufacturing technique (surface roughness, surface cuts, scratches, and microcracks). The model reliability was verified with experimental results taken from the literature, calculations appeared to be in good agreement with experimental data. Fatigue curves to a grain-size crack initiation and to fracture of smooth specimens and those with a chemically-notched blunt raiser that simulates the casting defects in aircraft components were calculated. The two sets of specimens from a Ti–6Al–4V titanium alloy differing in the cross-section (rectangular and cylindrical) and in microstructure (different grain sizes). Smooth specimens exhibited the test surface roughness R_v = 10 and 19 μm (average dent depth), which was assumed to be a sharp raiser for calculations. The model need not long-term and labor-consuming high-cycle fatigue tests to construct the fatigue curve.

Introduction. Structure elements that operate under cyclic loading suffer from fatigue damages, which could give rise to the nucleation of fatigue cracks, their propagation, and at last to failure. The fatigue crack originates, as a rule, on the surface, in stress raiser locations caused by component designs (openings, fillets, slots, sharp ribs, etc.), manufacturing defects of the material (inclusions, insoluble precipitates, pores, microcracks, etc.) used for the production of the components, or defects formed in machining or in operation (surface roughness, dents, scratches, corrosion cracks, etc.). Structure elements are most often functioning under load cycle asymmetry. Until recently, scientists involved in the realm of fatigue were strongly convinced that fatigue life (number of load cycles) or a fatigue curve cannot be computed without fatigue or fatigue crack resistance tests of the specimens. However, in the last few years, they were shaken in their confidence due to considering microstructural factors of the fatigue process. The fatigue fracture of the materials and structure elements is assumed to be divided into the two stages: crack nucleation and its extension to fracture. With regard to such division, the life to fracture N_total was proposed to be assessed as the sum of lives to crack initiation N_i and its growth N_FCG [1]

$$ {N}_{total}={N}_i+{N}_{FCG}. $$

(1)

For evaluating the fatigue life to initiation of a surface crack a grain deep under regular cyclic symmetrical uniaxial loading of smooth specimens from titanium alloys, the following equation was derived [1]:

$$ {N}_i={\left(\frac{\upbeta}{\upsigma_a-{\upsigma}_{-1,e}}\right)}^2, $$

(2)

where

$$ \upbeta =\frac{ME}{{\left(1+v\right)}^3\sqrt{\uppi \left(1-v\right)}}, $$

M is the mean value of the Taylor factor, which is determined from crystallographic texture analysis of the initial material, E is the elastic modulus and v is Poisson’s ratio that are evaluated from the data on tensile tests of standard specimens, σ_1,e is the endurance limit of smooth specimens at the symmetrical cycle (calculated parameter), σ _a is the stress amplitude, and N_i is the number of load cycles.

The endurance limit can be defined from the phenomenological relation of σ _1,e against the grain size d [2]

$$ {\upsigma}_{-1,e}=\frac{E\sqrt{b}}{\sqrt{l_c}}, $$

(4)

$$ {l}_c={E}^2b{\left(A+B\arctan \left(\left(E\sqrt{\frac{b}{4d}}-A\right)/B\right)\right)}^{-2}, $$

(5)

where A = (σ_f + σ_p)/2, B = (σ_p − σ_f)/π, σ_f is the stress of internal friction in the crystal lattice, σ_f ≅ ME[2(1 + v)]⁻¹ ⋅ 10⁻³, σ_p is the proportionality limit evaluated from tensile tests, d is the average grain size, obtained from microstructure analysis of the initial material, and b is the Burgers vector module.

The model was also advanced to assess the crack growth stage length N_FCG from the initial crack depth (l = d) to its final depth (l = l_i ), which is taken as the fatigue fracture criterion gained with the same initial data as for the N_i evaluation [1].

For evaluating the fatigue stage length in view of stress concentrations, the procedure was proposed to calculate the life to fatigue crack initiation from the blunt stress raiser root/blunt root-notch and on its further growth to fracture in the specimens under symmetrical tension–compression (or symmetrical bending) at the constant stress cycle span [3]. The notches with the theoretical stress intensity factor K_t ≤ 4 are considered the blunt ones. The procedure is based on the concept originating from Eq. (2). As is seen from analysis of life equation (2) in terms of Eq. (3), the coefficient β is determined via the elastic parameters E and v and the texture parameter M, while σ _a is the stress amplitude that is applied at a distance from the notch, if one present, and is the amplitude of nominal stresses over the cross-section with the notch root. In the general case, the exponent is dependent on the energy of the packing defect and slippage morphology and, as was experimentally established by many researchers, its value of 2 gives satisfactory fit for titanium and many other structural alloys [4]. Hence, such factors as grain sizes and stress concentrations should be accounted for in the N_i calculations by the parameter, being the endurance limit. Thus, the life assessment (or fatigue curves) should be based on the evaluation of the endurance limit in terms of the above factors.

The endurance limit assessment for the blunt notch was built upon the concept of critical distance and the statement that the fatigue strength of notch-containing specimens is defined by a minimum local stress at the critical distance from the notch root necessary for initiation of the fatigue crack near its root, which equals the endurance limit of smooth specimens [3]. It was also shown that the critical distance, i.e., the distance from the notch root in the direction perpendicular to the applied tensile stress was equal to the parameter l_c from Eq. (2) [3]. This parameter in Eq. (2) characterizes the thickness of the surface layer with the mechanical properties differing from those of the rest of the material where local plastic strains are developing under cyclic loading. So, on the basis of the Lukáš–Klesnil empirical equation for approximation of the distribution of local tensile stresses [5], the formula was advanced to assess fatigue strength in view of the microstructure and the blunt notch of the ρ radius in the root [3]

$$ {\upsigma}_{-1}=\frac{E\sqrt{b}}{K_t}\sqrt{1/{l}_c+4.5/\uprho .} $$

(3)

The life on the fatigue crack growth from the blunt notch root is defined with the same equation as for smooth specimens [1], only instead of the constant amplitude of nominal stress σ_a , the amplitude of local stress should be applied that is changing with the crack extension.

The object of the present study is to elaborate the procedure for evaluating the fatigue stage length of specimens/structure elements with sharp-root notches (K_t > 4) under regular cyclic uniaxial loading. The above characteristics of static strength (E, v, σ_p ) and microstructure (d, M, b), sharp-root notch depth D and its form in terms of the geometrical factor Y would serve as the initial data for such assessment.

Background. The approaches based on the Kitagawa–Takahashi diagram (KT-diagram) are proposed to analyze the fatigue strength for the case of a sharp-root notch (K_t > 4) [6]. Previously [7], known KT-diagram modifications [8, 9] were used to elaborate the microstructure-based model for the assessment of fatigue strength of specimens/structure elements with sharp-root notches or surface defects that can be taken as the initial cracks. So, the distribution of local stresses from the root of such a notch is suggested to be similar to their distribution ahead of the crack tip. It is also considered that cyclic loading of the above specimens/structure elements at the level of their endurance limit σ_th initiates the crack from the sharp-root notch, which penetrates to a certain depth l and is arrested through a gradually growing effect of its closure. The equation for the boundary curve of threshold stresses σ_{−1, th} = f(l) in terms of the maximum stress under symmetrical cyclic loading for the notch D deep is proposed as [7]:

$$ {\upsigma}_{-1, th}=E\sqrt{b/{l}_c}{Y}_1\sqrt{d}\frac{1+\left(\sqrt{l_s/d}-1\right)\left\{1-\exp \left[\left(d-l\right)/\left(\left(\sqrt{l_s/d}-1\right){l}_c\right)\right]\right\}\kern1em \mathrm{at}\ l\ge d,}{Y\sqrt{D+l}} $$

(7)

where ls is the material characteristic, viz the length parameter that describes the depth of a surface half-penny physically small crack (PSC) with the maximum level of its closure near the tip, which is consistent with the level of the long crack (LC) closure at the motive force equivalent to the threshold SIF span for LC ∆K_th,LC and at the leve lof applied stress span equivalent to the endurance limit of smooth specimens ∆σ _e . On the other hand, l_s is the additional size to the size of a surface half-penny short crack for evaluating SIF near its tip by the form traditional for linear-elastic fracture mechanics [10].

As was shown in [11], this parameter can be assessed with the equation

$$ {l}_s=\frac{8^2\uppi d{\left(1+v\right)}^2h}{12{M}^2b}, $$

(8)

where h is the distance between neighboring parallel slip planes in the crystal lattice according to which the slip system is activated in terms of the Taylor factor M, h is determined from the crystal lattice parameters: for bcc-metals h = 0.707|b| and for fcc-metals h = 0.866|b| [12], for hcp-metals with the most susceptible slip systems: basic h = c and prizmatic $h=a\sqrt{3}$ (a and c are the hcp crystal lattice parameters [11]).

In Eq. (7), the two parameters Y₁ and Y are added that are the geometrical factors (SIF corrections): Y₁ for the surface plane microstructurally short crack (MSC) a grain deep d and Y for the sharp notch with a crack that propagates from its root. For the deepest point of the half-penny front of a surface plane crack located relative to the tensile stress direction against M, Y₁ is calculated by the formula [3]:

$$ {Y}_1={Y}_2\left(2\sqrt{1/\left(d/{l}_s+1\right)}-1\right), $$

(9)

where Y₂ is the geometrical factor for the deepest point of the half-penny front of a surface plane crack located perpendicularly to the tensile stress direction. For instance, for the crack on the surface of infinite half-space, Y₂ = 0.73, for a grain with the most susceptible slippage orientation (i.e., at M = 2), Y₂ = 0.67 [3]. Depending on the geometry of a notch and structure element and the method of loading, the formula for defining Y or its value in the form of the constant can be taken from [13].

Procedure of Calculating the Fatigue Stage Length with a Sharp-Root Notch. The life N_i at the crack initiation stage with a sharp-root notch is proposed to be calculated with Eq. (2) in view of (3) where σ_{−1, th} calculated by Eq. (7) for l = d should be substituted for σ_{−1, e}. Thus, at the symmetrical load cycle and different stress amplitudes σ_a, the fatigue curve ${\upsigma}_a=\upbeta {N}_i^{-1/2}+{\upsigma}_{-1, th}$ (d ) to the initiation of a crack l = d from the sharp notch root is obtained (Fig. 1).

Fig. 1.

Scheme of plotting the model-calculated fatigue curves to MSC initiation l = d deep (1) and to fracture (2) of sharp-root notch specimens. To the left-boundary threshold stress curve [Eq. (7)].

Then, at the crack growth stage, its initial size is a_in = D + d, where D is the notch depth. It is also suggested that such a crack still does not exhibit any effect of closure, which will be increasing after further crack growth. Thus, the kinetic diagram of crack propagation at the fixed stress span Δσ should originate from the kinetic diagram of long crack growth for the effective SIF span and terminate with the kinetic diagram of long crack growth for the SIF span, which accounts for the total effect of crack closure. The equation for the Paris portion of the kinetic diagram of LC growth for the effective SIF span (Fig. 2, curve 1) can be presented as [14]:

Fig. 2.

Scheme of the model for evaluating the LC growth rate without regard (1) and with regard (2) to the crack closure effect and PSC on the first (3) and second (4) portions in smooth specimens, geometrical location of points, defining the initiation of PSC growth [15] (5).

$$ \frac{da}{dN}=b{\left(\frac{\Delta K}{\Delta {K}_{th, eff}}\right)}^3, $$

(10)

where a is the notch-containing crack size, a = D + l, ΔK is the SIF span,

$$ \Delta K=\Delta \upsigma Y\sqrt{\uppi a}, $$

(11)

ΔK_{th, eff} is the effective threshold SIF span, which can be evaluated by the formula [14]

$$ \Delta {K}_{th, eff}=E\sqrt{b}. $$

(12)

The equation for the Paris portion of the kinetic diagram of LC growth, which considers the total effect of crack closure (Fig. 2, curve 2) is given as [15]

$$ \frac{da}{dN}=b{\left(\frac{\Delta K}{\Delta {K}_{th, LC}}\right)}^m, $$

(13)

where ΔK_{th, LC} is the threshold SIF span for LC, which is calculated for the symmetrical cycle as

$$ \Delta {K}_{th, LC}={\upsigma}_{-1,e}{Y}_2\sqrt{\uppi {l}_s}, $$

(14)

the exponential m is calculated from the scheme (Fig. 2)

$$ m=3\frac{\log \Delta {K}_{th, eff}-\log {K}_f}{\log \Delta {K}_{th, LC}-\log {K}_f}, $$

(15)

$$ \log {K}_f=\frac{1}{3}\left(3\log E+\log \sqrt{b}-5\right). $$

(16)

The construction of the model scheme (Fig. 2) is based on the hypothesis that for a single alloy, the kinetic LC growth diagram for the effective SIF span and for the SIF span with the account of crack closure are brought to a point at high growth rates [15]. This hypothesis was experimentally supported for alloys of different classes [14].

Thus, the equation for the kinetic diagram of the crack propagating from the sharp notch root D deep at the fixed stress span Δσ can be written in the following way:

$$ \frac{da}{dN}=b{\left(\frac{\Delta \upsigma Y\sqrt{\uppi a}}{\Delta {K}_{th}}\right)}^3, $$

(17)

where ΔK_th is the threshold SIF span, which is gradually increasing with the effect of closure of a growing crack

$$ \Delta {K}_{th}=\Delta {K}_{th, eff}+\left(\Delta {K}_{th, LC}-\Delta {K}_{th, eff}\right)\left[1-{e}^{-k\prime \left(a-D-d\right)}\right], $$

(18)

$$ k^{\prime }=\frac{\Delta {K}_{th, eff}}{l_c\left(\Delta {K}_{th, LC}-\Delta {K}_{th, eff}\right)}. $$

(19)

The plots of Eqs. (10), (13), and (17) in the coordinates of the crack growth rate da/dN vs crack size with the notch a for the two fixed stress span levels Δσ₂ > Δσ₁, are presented in Fig. 3. As is seen, the plots of Eq. (17) intersect those of Eq. (13) at the points with the abscissae a_x . The a_x values for different Δσ levels are defined from the equation

Fig. 3.

Scheme of plotting the kinetic diagrams of fatigue crack growth from the sharp notch root for the two fixed stress spans Δσ₂ > Δσ₁ (heavy solid lines), 1.1 and 1.2 – plots of Eq. (17), 2.1 and 2.2 – plots of Eq. (13), 3.1 and 3.2 – plots of Eq. (10).

$$ {\left(\frac{\Delta \upsigma Y\sqrt{\uppi {a}_x}}{\Delta {K}_{th}}\right)}^3={\left(\frac{\Delta \upsigma Y\sqrt{\uppi {a}_x}}{\Delta {K}_{th, LC}}\right)}^m, $$

(20)

which was obtained as the difference between Eqs. (17) and (13), substituting a_x for a. Thus, the crack growth kinetics from a_in to a_x and from a_x to a_t are described with Eqs. (17) and (13), respectively.

Hence, the length of stage 2 N_FCG is evaluated with the equation

$$ {N}_{FCG}=\frac{1}{b}\underset{a_{in}}{\overset{a_x}{\int }}{\left(\frac{\Delta {K}_{th}}{\Delta \upsigma Y\sqrt{\uppi a}}\right)}^3 da+\frac{1}{b}\underset{a_x}{\overset{a_t}{\int }}{\left(\frac{\Delta {K}_{th, LC}}{\Delta \upsigma Y\sqrt{\uppi a}}\right)}^m da, $$

(21)

where a_t is the final crack size with the notch, a_t = D + l_t.

In the above model (21), the sharp notch with the crack that grows from its root is considered to be a long crack, i.e., it can be used to predict the length of stage 2 for sharp-root notches deeper than 1 mm. For small sharp-root notches (D < 1mm), instead of ∆K (11), traditional for linear-elastic fracture mechanics, which determines the moving force of a long crack, short crack calculations should include the Dagdale correction for plasticity F [16] or the additional size l_D to the size of a short crack in the El Haddad equation [10]. Then the first alternative of the life equation at stage 2 would have the form

$$ {N}_{FCG}=\frac{1}{b}\underset{a_{in}}{\overset{a_x}{\int }}{\left(\frac{\Delta {K}_{th}}{\Delta \upsigma \left(2\uppi {Fr}_e+Y\sqrt{\uppi Fa}\right)}\right)}^3 da+\frac{1}{b}\underset{a_x}{\overset{a_t}{\int }}{\left(\frac{\Delta {K}_{th, LC}}{\Delta \upsigma Y\sqrt{\uppi a}}\right)}^m da, $$

(22)

where the denominator of the first term is ∆K for short cracks, and the Dagdale correction for plasticity F is defined by the formula [16]

$$ F=\frac{1}{2}\left[\sec \left(\frac{\uppi}{2}\frac{\upsigma_{\mathrm{max}}}{\upsigma_Y}\right)+1\right], $$

(23)

σ_max is the maximum cycle stress (for the symmetrical cycle σ_max = Δσ/2 = σ_a ), σ_Y is the yield stress (may be replaced with σ_p or σ_0.2 ), r_e is calculated from ∆K for a short crack of d size, equivalent to ΔK_{th, eff} at the stress, equivalent to σ_{−1, e} [16]. In view of (4) and (12), we have

$$ {r}_e=\frac{{\left(\sqrt{l_c}-Y\sqrt{\uppi Fd}\right)}^2}{2\uppi F}. $$

(24)

The second alternative results in

$$ {N}_{FCG}=\frac{1}{b}\underset{a_{in}}{\overset{a_x}{\int }}{\left(\frac{\Delta {K}_{th}}{\Delta \upsigma Y\sqrt{a+{l}_D}}\right)}^3 da+\frac{1}{b}\underset{a_x}{\overset{a_t}{\int }}{\left(\frac{\Delta {K}_{th, LC}}{\Delta \upsigma Y\sqrt{\uppi a}}\right)}^m da, $$

(25)

where

$$ {l}_D={l}_s{\left({Y}_2/Y\right)}^2. $$

(26)

The corresponding corrections should be made in Eq. (17) and in the left side of Eq. (20).

Then the fatigue curve to fracture σ_a = f(N_i + N_FCG) with the sharp-root notch would have the form, shown in Fig. 1. Calculating the maximum of function (7) σ_{th, max}, the inflection point of the fatigue curve to fracture from the sloping-down portion to the horizontal one at the level of the endurance limit can be found.

It should be noted that the above calculations are applied to the symmetrical load cycle (R = -1). Thus, it is assumed that ΔK = K_max, i.e., the crack penetrates only within the tensile half-cycle, and in Eqs. (10)–(25) the maximum cycle values K, K_th , K_th,LC , σ_a can be substituted for ∆K, ∆K_th , ∆K_th,LC , Δσ, respectively.

Load Cycle Asymmetry. The models for predicting fatigue fracture stage lengths and endurance limits, constructed and presented in the above section, are applied to alternating symmetrical loading. However, the majority of structure elements is functioning under alternating asymmetric loading. Below the approach is advanced, providing the employment of the models in terms of the load cycle asymmetry.

Fatigue life calculations with the load cycle asymmetry are proposed to be based on the same approach as the notch case. The cycle asymmetry effect is accounted for in the life equation to crack initiation via the effect of mean cycle stress on the endurance limit, which is expressed in terms of the stress span or maximum cycle stress. At the stage of crack growth, the effect of cycle asymmetry should be considered in the growth rate equations by changing both parameters: threshold SIF span and maximum threshold SIF of the cycle.

At present, the fatigue strength at the asymmetric load cycle is defined by the stress span Δσ_R or maximum cycle stress σ_{max, R} as the empirical exponential function of the endurance limit at the symmetrical cycle Δσ₋₁ and mean cycle stress σ_m. This relation for smooth specimens has the form [17]

$$ {\Delta \upsigma}_{R,e}={\Delta \upsigma}_{-1,e}\left(1-{\left(\frac{\upsigma_m}{\upsigma_L}\right)}^n\right), $$

(27)

where

$$ {\upsigma}_m=\frac{\upsigma_{\mathrm{max}}+{\upsigma}_{\mathrm{min}}}{2}, $$

(28)

σ_L is the boundary condition, being the ultimate strength σ_u or yield stress σ_0.2.

For titanium alloys, it is assumed that n = 1 and σ_L = σ_0.2. Then, in view of Δσ₋₁ = 2σ₋₁, R = σ_min/σ_max and (28), from (27) we have the expression for calculating the endurance limit of smooth specimens at different stress ratios R

$$ {\Delta \upsigma}_{R,e}=\frac{2{\upsigma}_{-1,e}}{1+\frac{\upsigma_{-1,e}\left(1+R\right)}{\upsigma_{0.2}\left(1+R\right)}} $$

(29)

and

$$ {\upsigma}_{\max, R,e}={\Delta \upsigma}_{R,e}/\left(1-R\right). $$

(30)

For evaluating the endurance limit with the cycle asymmetry and sharp-root notch σ_{max, R, th}, σ_{max, R, e} should be substituted for σ_{−1, e} in Eq. (7) as follows:

$$ {\upsigma}_{\max, R, th}={\upsigma}_{\max, R,e}{Y}_1\sqrt{d}\frac{1+\left(\sqrt{l_s/d}-1\right)\left\{1-\exp \left[\left(d-l\right)/\left(\left(\sqrt{l_s/d}-1\right){l}_c\right)\right]\right\}}{Y\sqrt{D+l}}. $$

(31)

With this, the parameter l_s that is defined with the threshold SIF – endurance limit ratio is the constant value for a single material and is independent of the cycle asymmetry, which is traced in some studies [18, 19].

So, the life equation to crack initiation of size d in view of the cycle asymmetry would have the form

$$ {N}_1={\left(\frac{\upbeta}{\upsigma_{\mathrm{max}}-{\upsigma}_{\max, R, th}(d)}\right)}^2 $$

(32)

or

$$ {N}_i={\left(\frac{\left(1-R\right)\upbeta}{\Delta \upsigma -{\Delta \upsigma}_{R, th}(d)}\right)}^2, $$

(33)

where β is defined by Eq. (3).

For calculating the stage length of crack growth from a sharp-root notch, Eq. (21) for D > 1 mm and Eqs. (22) or (25) for D < 1 mm are used. At R ≥ 0, the threshold SIF span for LC ∆K_th,LC is defined by Eq. (14), where Δσ_{R, e} is substituted for σ_{−1, e} , which is calculated by Eq. (29). Moreover, Eq. (24) for evaluating the parameter r_e would have the form

$$ {r}_e=\frac{1}{2\uppi F}{\left(\frac{E\sqrt{b}}{\upsigma_{\max, R,e}}-Y\sqrt{\uppi Fd}\right)}^2. $$

(34)

Model Verification. Fatigue life calculations by the above procedure and their comparison with experimental data were based on fatigue test results for Ti–6Al–4V titanium alloy specimens in the form of fatigue curves to fracture [20]. The two types of specimens were used: rectangular cross-section of 5 × 15 mm (FL specimens) and circular cross-section of 5 mm diameter (CY specimens). Tensile test results were also cited: E = 115·10⁵. MPa, σ_{0 2} = 800 and 920 MPa for FL and CY specimens, respectively.

The alloy possesses a duplex, β-transformed, lamellar microstructure differing in the sizes of its elements for FL and CY specimens since they were cut from the blanks of different types. Mean thicknesses of α-lamellae for FL and CY specimens are d = 3.5 and 7.0 μm, respectively, which were evaluated from micrographs in Fig. 4. Just this parameter is responsible for the fatigue strength of (α + β) titanium alloys, Ti–6Al–4V in particular, with a similar type of microstructure [2]. Under cyclic loading, slippage, and thus, fatigue crack initiation proceeds along the basic plane parallel to the α-lamella cross-section with the Burgers vector $\overrightarrow{b}=\overrightarrow{a}$. So, we have b = 2.5 ⋅ 10⁻¹⁰m and h = 4.5 ⋅ 10⁻¹⁰m [15]. In those microstructures, α-lamellae are accumulated in clusters and similarly oriented within one cluster, and the clusters themselves are arbitrarily oriented within one β-grain. Thus, the specimen exhibits a nondescript blurred texture in its volume, as a result, the fatigue crack initiation should occur in the α-lamellae cluster with the most susceptible slippage orientation. So the smallest Taylor factor value M = 2 may be taken for calculations, accordingly Y₁ = 0.67 [15].

Fig. 4.

Microstructure of FL (a) and CY (b) Ti–6Al–4V specimens [20].

High-cycle fatigue tests were carried out under uniaxial tension–tension loading with R = 0.1 and a 100-Hz frequency. Since the specimens 5 mm thick were tested to failure, the finite crack size a_t = 4 mm was adopted for calculations, considering that the remaining 1 mm is due to instantaneous final fracture.

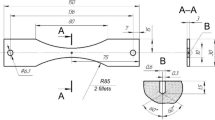
Smooth specimens and those artificially notched on their surface have been put to experimental tests. In [20], the data on the surface roughness of smooth specimens measured by the parameter R_v that characterizes the depth of dents were also cited. As the studies on crack initiation nuclei demonstrated, the crack started just from the dent root. The mean R_v values for smooth FL and CY specimens eaqual 10 and 19 μm, respectively. Thus, such a dent may be considered a sharp-root micronotch in the form of a surface semi-elliptical crack D = R_v deep. The geometrical factor Y for the deepest front point of this crack [13] makes up 0.75. In contrast to this, the surfaces of artificial notches may be assumed smooth since they were chemically prepared (Fig. 5). These notches possess the two sizes: depth D and root radius ρ (Fig. 6). They were taken from Fig. 5, the theoretical concentration coefficients K_t were calculated by the Inglis formula ${K}_t=1+2\sqrt{D/\uprho}$.

Fig. 5.

Fatigue fractures of artificially-notched specimens: (a) FL and (b) CY [20].

Fig. 6.

Scheme of an artificial notch.

As a result, we have for the artificially-notched FL and CY specimens D = 800 μm, ρ = 500 μm, K_t = 3.53 and D = 750 μm, ρ = 200 μm, K_t = 4.87, respectively. As is seen from K_t calculation results, the this notches can be considered blunt according to conventional classification, however, K_t for CY specimens somewhat exceeds the conventional limit for the blunt ones (K_t = 4). Therefore, for those specimens, the two calculations of the fatigue curve to fracture were performed (for sharp and blunt notches). For evaluating the endurance limit σ _max,R for the blunt notch, formula (6) was used

$$ {\upsigma}_{\max, R}=\frac{\upsigma_{\max, R,e}}{K_t}\sqrt{1+4.5\frac{l_c}{\uprho}}, $$

(35)

where σ_{max, R, e} was defined by Eq. (30) in view of (29), and the life at the crack growth stage N_FCG was obtained from Eq. (25), assuming the blunt notch with MSC initiated from its root as an initial surface semi-elliptical PSC with Y = 0.75.

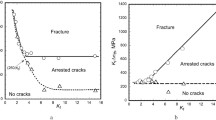
Calculated fatigue curves to fatigue crack initiation of l = d size and to fracture by the criterion a_t = 4 mm for the four above sets of specimens from a Ti–6Al–4V titanium alloy are compared with experimental data [20] (Fig. 7). The life at the crack growth stage was calculated by Eq. (25). As is seen, the calculated fatigue curves to fracture interpret satisfactorily experimental results, which corroborates the validity of the advanced model. Fatigue curves for artificially-notched CY specimens calculated by different alternatives [Eqs. (31) and (35)] give equally good fit of experimental data in the range of low loads close to the endurance limit (Fig. 7d). While at higher loads, these curves diverge, and lack of experimental data makes it difficult to identify a better alternative for this notch. On the other hand, a satisfactory agreement between the fatigue curve and experimental data points to an adequate application of the model to the life assessment at the stage of crack growth from the sharp-root notch for the case of the blunt one (Fig. 7c). The discrepancy between the procedures of fatigue curve assessment for different notch types consists only in the application of different models for evaluating the endurance limit, and thus, different procedures of plotting the fatigue curve to fracture.

Fig. 7.

Comparison of calculated fatigue curves with experimental results for fatigue tests of Ti–6Al–4V specimens [20]: (1) to crack initiation and (2, 2′) to fracture.

It should also be noted that the application of the geometrical factor Y against the growing semi-elliptical crack size a and geometrical sizes of specimen cross-section to the life assessment at the crack growth stage does not essentially change the result in comparison with the use of the constant value Y = 0.75. The fatigue curves to fracture for CY specimens calculated with Y = 0.75 and with Y , defined by the equation [13]

$$ Y=g\left[0.752+2.02\left(\frac{a}{2r}\right)+0.37{\left\{1-\sin \left(\frac{\uppi a}{4r}\right)\right\}}^3\right], $$

(36)

$$ g=\frac{1}{\cos \left(\frac{\uppi a}{4r}\right)}\frac{1.84}{\uppi}{\left\{\tan \left(\frac{\uppi a}{4r}\right)/\left(\frac{\uppi a}{4r}\right)\right\}}^{0.5} $$

(37)

are compared in Fig. 8, where r is the radius of the “critical” specimen cross-section.

Fig. 8.

Comparison of fatigue curves to fracture calculated with Y = 0.75 (1) and Y calculated by Eq. (36) in view of (37) (2).

As is seen in Fig. 8, curve 2 at low load levels demonstrates more conservative life assessment than curve 1, while at high load levels, it is vice versa.

The results show that the fatigue strength and life assessment for smooth specimens should take account of their surface roughness. Considering this roughness as sharp dents with crack initiation from their root at the endurance limit, its penetration to a certain size (larger than a grain size) and arrest of further extension, we obtain the fatigue curve, having a horizontal portion that starts at N ≈ 5 ⋅ 10⁵ cycles (Fig. 7a, b). The existence of a horizontal portion on the fatigue curves of smooth specimens for some materials and its absence for others are probably explained by that result. If the surface roughness of smooth specimens exceeds a grain size, such specimens cannot be taken as the smooth ones. On the other hand, this result can also provide an explanation for the differences, met in the literature, in the mode of thought as to the crack sizes at the endurance limit of smooth specimens. These issues would require of investigations.

Conclusions

1. The advanced microstructure-based fatigue life model provides calculations of the number of cycles to fatigue crack initiation and its growth from the notch root to fracture of specimens/structure elements at the constant stress span, with the only use of characteristics of static strength and microstructure of the initial material.

2. The model can be applied to fatigue life assessment of components that contain structural notches and defects stemming from their manufacturing technique (surface roughness, surface cuts, scratches, pores, and microcracks). Differences in the fatigue curve assessment procedures for different notch types (sharp or blunt) consist only in the use of different models for evaluating the endurance limit, and thus, different procedures of plotting the fatigue curve to fracture. The fatigue curves for Ti–6Al–4V specimens with a sharp-root notch exhibit a horizontal portion starting at N ≈ 5 ⋅ 10⁵ cycles, and on the fatigue curve for the specimens with a blunt-root notch, such a portion is absent.

3. The model need not long-term and labor-consuming fatigue and fatigue resistance tests to construct fatigue curves and kinetic diagrams of fatigue crack growth.

4. The model reliability was verified with experimental results, taken from the literature for Ti–6Al–4V specimens. Calculated fatigue curves were found to be in good agreement with experimental data.