Introduction. Fatigue crack growth (FCG) process is associated with the formation of new crack faces. Formation of new crack surfaces need the activation energy. During fatigue process, this energy can be delivered to the process zone due to work of external loading. The dissipated damage energy is responsible for “jump like” fatigue crack growth. This concept is reflected in several formulas and ideas of fatigue crack growth [1,2,3,4,5,6,7,8], where the fatigue crack growth process is treated as a discrete process where the local fatigue crack growth is associated with a specified “unit” of fatigue crack growth (see Fig. 1):

Fig. 1.
figure 1

Discrete nature of fatigue fracture process.

Full size image
$$ \frac{da}{dN}=\frac{d^{\ast }}{N_f}. $$
(1)

Generally, the fatigue crack growth can be postulated as a process involving the following assumptions [2, 4, 5, 7, 8]:

  1. (i)

    the material is composed of simple particles of a finite dimension, , which represents the elementary material block size, below which material cannot be regarded as a continuum (Fig. 1);

  2. (ii)

    ahead crack tip exist two plastic zones; static and cyclic (Fig. 1);

  3. (iii)

    the fatigue crack tip is supposed to be equivalent to a notch with radius, ρ;

  4. (iv)

    the fatigue crack growth process is considered as representing successive crack increments (after Nf cycles) due to crack re-initiations over the distance, d*, ρ.

The mentioned assumptions are already reflected in several fatigue crack propagation models based on low-cycle fatigue (LCF) data [9,10,11,12,13,14].

Another relevant aspect in these local approaches is the calculation of local stresses and strains at the crack tip. The most commonly used local approaches are based on Coffin–Manson & Morrow relationships [15,16,17] with or without the influence of the mean stress effects. Glinka [2], Peeker and Niemi [18], Noroozi et al. [7, 8], Hurley and Evans [19], among others, used in their studies the strain fatigue damage parameter. More recently, Correia et al. [20], Hafezi et al. [21], and De Jesus and Correia [22] have used the Smith–Watson–Topper (SWT) local damage parameter [23]. The equivalent stress amplitude damage parameter, σar, has been used for the fatigue crack growth modeling based on local approaches by Correia and Huffman [12, 13].

In this paper, probabilistic fatigue crack initiation and propagation fields are presented based on strain energy approach proposed by Huffman [24] and considering the generalized probabilistic fatigue model suggested by Correia et al. [25]. The Huffman fatigue crack growth model based on strain energy density is analyzed considering several fatigue damage parameter such as strain, Smith–Watson–Topper (SWT), and equivalent stress amplitude. An analysis of results from the application of the fatigue crack growth model proposed by Huffman using the different damage parameters and experimental data is done. The generalized probabilistic fatigue model is used aiming at generating probabilistic FCG fields, for the fatigue damage parameters under consideration. In this analysis, experimental fatigue data of the P355NL1 steel from the low-cycle fatigue and fatigue crack growth tests are used [26,27,28].

1. Huffman Fatigue Crack Initiation and Growth Model. The fatigue crack growth relations are established with the linear elastic fracture mechanics (LEFM) to evaluate the stress distributions in a material. The variables such as the geometry and loading are considered to obtain the fatigue crack growth rates. Glinka [2] was pioneer to relate the local stress and strain at the crack tip, by relating the strain energy distribution with the LEFM approach, and the fatigue failure of the material ahead the crack tip. This so called local approach is used to generate the fatigue crack growth for several crack lengths and calculating the stress or strain lives at the crack tip. These stresses and strains are used to obtain the number of cycles to failure, Nf , leading to the crack growth extension, Δa.

Huffman [24] proposed a fatigue damage parameter, D, based on strain energy density concepts and calculated it from cyclic stress-strain properties as given by

$$ \left(\frac{U_e}{U_d{\uprho}_c}\right)\left(\frac{U_p^{\ast }}{U_d{\uprho}_c}\right)=D=\frac{2N}{2{N}_f}, $$
(2)

where Ue is the elastic strain energy density, \( {U}_p^{\ast } \) is the complementary plastic strain energy density, ρc is the critical dislocation density, and Ud is the strain energy density that can be estimated by

$$ {U}_d=\left(\frac{E}{2\left(1+\upnu \right)}\right)\cdot {\left|\overrightarrow{b}\right|}^2, $$
(3)

where ν is Poisson’s ratio and \( \overrightarrow{b} \)_ is the Burgers vector. The value of \( \mid \overrightarrow{b}\mid \) is equal to 2 52 · 1010. m for iron, steel or similar metals as can be found in [24]. Finding the strain energy density by integrating the Ramberg–Osgood stress-strain relationship results the damage equation in terms of material parameters:

$$ \left(\frac{2}{U_d^2{\uprho}_c^2}\right)\left(\frac{n^{\hbox{'}}}{1+{n}^{\hbox{'}}}\right)\left(\frac{1}{K^{\hbox{'}}}\right)\left({\upsigma}_{\mathrm{max}}^2\right){\left({\upsigma}_a\right)}^{\frac{1+{n}^{\hbox{'}}}{n^{\hbox{'}}}}=D=\frac{1}{2{N}_f}, $$
(4)

where σmax is the maximum stress and σa is the stress amplitude. This equation can be used to generate the stress–life, strain–life, and fatigue crack growth curves from cyclic stress-strain properties.

The strain-life or Morrow parameters can be assessed via Eq. (3)as follows:

$$ \upsigma {\hbox{'}}_f=E{\left(\frac{2}{U_d^2{\uprho}_c^2}{\left(\frac{1}{K^{\hbox{'}}}\right)}^{1/n\hbox{'}}\left(\frac{n^{\hbox{'}}}{1+{n}^{\hbox{'}}}\right){E}^{\left(1+2n\hbox{'}\right)/n\hbox{'}}\right)}^{\frac{-{n}^{\hbox{'}}}{1+3{n}^{\hbox{'}}}}, $$
(5)
$$ b=\frac{-{n}^{\hbox{'}}}{1+3{n}^{\hbox{'}}}, $$
(6)
$$ \upvarepsilon {\hbox{'}}_f=E{\left(\frac{2{\left(K\hbox{'}\right)}^3}{U_d^2{\uprho}_c^2E}\left(\frac{n^{\hbox{'}}}{1+{n}^{\hbox{'}}}\right)\right)}^{\frac{-1}{1+3{n}^{\hbox{'}}}}, $$
(7)
$$ c=\frac{-1}{1+3{n}^{\hbox{'}}}, $$
(8)

where σ'f is the fatigue strength coefficient, E is the elastic modulus, K' and n' nare the cyclic Ramberg–Osgood parameters [29], b is the fatigue strength exponent, ε'f is the fatigue ductility coefficient, c is the fatigue ductility exponent, and the ρc parameter can be determined by fitting the resultant strain–life curve to low-cycle strain–life data by solving the Eq. (4):

$$ {\uprho}_c=\sqrt{\left(\frac{2\left(2{N}_f\right)}{U_d^2 EN}\right)\left(\frac{n^{\hbox{'}}}{1+{n}^{\hbox{'}}}\right){\left(\frac{1}{K^{\hbox{'}}}\right)}^{\left(1/n\hbox{'}\right)}\left({\upsigma}_{\mathrm{max}}^2\right){\left({\upsigma}_a\right)}^{\left(\frac{1+{n}^{\hbox{'}}}{n^{\hbox{'}}}\right)}}. $$
(9)

According to [24], this parameter has been found between 1 ⋅ 1015 ≤ ρc ≤ 3 ⋅ 1016 m−2. The Huffman fatigue crack growth rates using the Δa calibrator can be given by

$$ \left(\frac{\varDelta a}{U_d^2{\uprho}_c^2}\right)\left(\frac{n^{\hbox{'}}}{1+{n}^{\hbox{'}}}\right)\left(\frac{1}{K^{\hbox{'}}}\right)\left({\upsigma}_{\mathrm{max}}^2\right){\left({\upsigma}_a\right)}^{\left(\frac{1+{n}^{\hbox{'}}}{n^{\hbox{'}}}\right)}=\frac{\varDelta a}{N_f-0}\approx \frac{da}{dN}. $$
(10)

In Eq. (10), the stresses, σa and σmax, are the local stresses near the crack tip that can be related to the load, geometry and fatigue crack growth parameters as proposed by Noroozi et al. [7, 8]. The fatigue crack growth rate considering the driving force is given by the following expression:

$$ \frac{da}{dN}=C{\left(\varDelta \upkappa \right)}^{\upgamma}, $$
(11)

where γ is the fatigue crack growth rate exponent, Δκ is the fatigue crack growth driving force, and C is the fatigue crack growth rate coefficient that is given by

$$ C=\left(\frac{\varDelta a}{U_d^2{\uprho}_c^2}\right)\left(\frac{n^{\hbox{'}}}{1+{n}^{\hbox{'}}}\right){\left(K\hbox{'}\right)}^{\frac{2}{1+{n}^{\hbox{'}}}}{(E)}^{-\left(\frac{4{n}^{\hbox{'}}+2}{n^{\hbox{'}}+1}\right)}{\left(\frac{1}{2}\right)}^{\frac{1}{n^{\hbox{'}}}}{\left(\frac{1}{2\uppi x}\right)}^{\frac{1+3{n}^{\hbox{'}}}{1+{n}^{\hbox{'}}}}. $$
(12)

The fatigue crack growth driving force can be calculated as

$$ \varDelta \upkappa ={K}_{\mathrm{max}}^p{\left(\varDelta K\right)}^{1-p}, $$
(13)
$$ {K}_{\mathrm{max}}={K}_{\max, applied}+{K}_r, $$
(14)
$$ \varDelta K=\varDelta {K}_{applied}+{K}_r, $$
(15)
$$ p=\frac{2{n}^{\hbox{'}}}{1+3{n}^{\hbox{'}}}, $$
(16)
$$ \upgamma =\frac{2+6{n}^{\hbox{'}}}{1+{n}^{\hbox{'}}}=\frac{-2}{b+c}, $$
(17)

where ΔK is the total stress intensity factor range, ΔKapplied is the applied stress intensity factor range, Kmax,applied is the maximum applied stress intensity factor, and Kr is the residual stress intensity factor. The adjustment of the Huffman fatigue crack growth model to the experimental results is made using the values of Δa and x as calibrators.

Several authors such as Correia et al. [20, 26, 27], Hafezi et al. [21], and De Jesus and Correia [22] proposed the use of the finite element method to obtain the stresses and strains fields based on linear-elastic and elastoplastic analyses. These numerical analyses to calculate the stresses and strains ahead of the crack tip can be used for fitting the fatigue crack growth model proposed by Huffman [24] to the experimental FCG data.

2. Probabilistic Fatigue Damage Fields. The probabilistic fatigue damage fields can be obtained using the generalized probabilistic model for several fatigue damage parameters proposed by Correia et al. [25]. Originally, the probabilistic model was proposed by Castillo and Fernández-Canteli [30] for stress- and strain-based fatigue damage parameters using the Weibull or Gumbel distributions. These probabilistic distributions satisfy the statistical and physical requirements of the fatigue data. Correia et al. [25] proposed the generalization of the fatigue probabilistic model for several damage parameters, considering the similarity between the power relations used for the deterministic damage representation and the hyperbolic probabilistic fields proposed by Castillo and Fernández-Canteli [30]:

$$ \uppsi =q\left({N}_f\right), $$
(18)
$$ \uppsi =\upkappa {\left(2{N}_f\right)}^{\upalpha}+{\uppsi}_0, $$
(19)

where ψ is a fatigue damage parameter, ψ0 is the fatigue (endurance) limit, κ and α are material constants, q is the decreasing function of total fatigue life, and finally, 2Nf or Nf represent the reversals to failure and the number of cycles to failure, respectively.

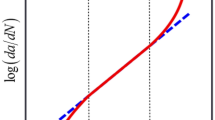
The deterministic power-law model is shown in Fig. 2. Several fatigue damage parameters based on stress, strain or energy criteria, describing the same schematic representation of Fig. 2, can be used in Eqs. (18) and (19).

Fig. 2.
figure 2

Schematic representation of the deterministic power-law fatigue failure criterion [25].

Full size image

Thus, fatigue damage parameters such as strain amplitude, εa, walker-like strain, εw, Smith–Watson–Topper, SWT, as well as the equivalent stress amplitude, σar, among others, can be described by the generalized fatigue damage parameter, ψ:

$$ \uppsi ={\upvarepsilon}_a, $$
(20)
$$ \uppsi ={\upvarepsilon}_w={\upvarepsilon}_a{\left(\frac{2}{1-{R}_{\upsigma}}\right)}^{1-{\upgamma}_w}, $$
(21)
$$ \uppsi = SWT={\upsigma}_{\mathrm{max}}{\upvarepsilon}_a, $$
(22)
$$ \uppsi ={\upsigma}_{ar}={\left({\upsigma}_{\mathrm{max}}\right)}^{1-{\upgamma}_w}{\left({\upsigma}_a\right)}^{\upgamma_w}, $$
(23)

where the Walker exponent is defined as

$$ {\upgamma}_w=\frac{1+{n}^{\hbox{'}}}{1+3{n}^{\hbox{'}}}. $$
(24)

According to [31], the main advantage of the γw parameter is to describe the material mean stress fatigue

behavior sensitivity, where for the SWT-life model, this parameter is equal to 0.5.

In this way, the generalized probabilistic model to describe the fatigue failure criterion for several damage parameters was proposed by Correia et al. [25], based on Castillo and Fernández-Canteli probabilistic model [30], is given by

$$ P=F\left({N}_f^{\ast };{\upsigma}_{ar}^{\ast}\right)=1-\exp \left\{-{\left[\frac{\log \left({N}_f/{N}_0\right)\log \left(\uppsi /{\uppsi}_0\right)-\uplambda}{\updelta}\right]}^{\upbeta}\right\}, $$
(25)
$$ \log \left({N}_f/{N}_0\right)\log \left(\uppsi /{\uppsi}_0\right)\ge \uplambda . $$
(26)

where P is the probability of failure, N0 and ψ0 are values for normalizing, and β, δ, and λ are the dimensionless Weibull parameters. The normalizing parameters N0 and ψ0 are the threshold value for life and the corresponding value for the equivalent stress, respectively. The maximum likelihood method is used to estimate the Weibull parameters, where the details can be found in [30].

3. Application of the Strain Energy Density Based Crack Propagation Model to Generate Probabilistic Fatigue Crack Initiation and Propagation Data.

3.1. Procedure to generate Probabilistic Fatigue Crack Initiation and Propagation Fields. The procedure proposed to generate probabilistic fatigue crack initiation and propagation fields may be summarized in the following steps:

3.1.1. Probabilistic Fatigue Crack Initiation Fields:

  1. (i)

    estimation of the Weibull parameters for the generalized probabilistic fatigue model based on strain, stress or energy damage parameters (Section 2), using experimental strain-life data from smooth specimens;

  2. (ii)

    application of the Huffman fatigue crack initiation model to estimate the Morrow constants (Section 1);

  3. (iii)

    computation of the probabilistic Huffman fatigue crack initiation models for several fatigue damage parameters.

3.1.2. Probabilistic Fatigue Crack Propagation Fields:

  1. (i)

    the first step considered in probabilistic fatigue crack initiation fields (Section 2);

  2. (ii)

    application of the Huffman fatigue crack propagation model based on strain energy density with probabilistic fatigue damage models (Section 1);

  3. (iii)

    computation of the P – da/dN – ΔK – R fields.

3.2. Probabilistic Fatigue Crack Initiation Data. The parameters of the cyclic elastoplastic stress–strain curves and elastic properties of the P355NL1 steel were collected in references [26,27,28]. These parameters were obtained based on experimental low-cycle fatigue tests of smooth specimens performed under strain controlled conditions carried out according the ASTM E606 standard. In Table 1 the cyclic stress-strain properties for the P355NL1 steel are shown.

Table 1. Cyclic Stress-Strain Properties for P355NL1 Steel [26,27,28]
Full size table

The Morrow constants obtained using the Coffin–Manson & Morrow relation [15,16,17] are presented in Table 2. In this table, Morrow constants’ estimates, according to the assumption in the Huffman model [24] presented in Section 1, are also shown. This model allows evaluating the fatigue crack initiation phase based on strain energy. Equations (5)–(8) were used to estimate the Morrow constants and Eq. (9) used to obtain the critical dislocation density. A good agreement for the Morrow strain-life constants between the Huffman model and the Coffin–Manson & Morrow relation is verified (see Table 2). The critical dislocation density, ρc, estimated and presented in Table 2, is similar to that of other materials with identical mechanical properties (see [24]).

Table 2. Morrow Constants for P355NL1 Steel Calculated as per Eqs. (5)–(8)
Full size table

In Fig. 3, the stress–life, strain–life, and SWT–life curves are presented, being compared the experimental results with the Huffman fatigue crack initiation model predictions. In these figures, a good agreement between the experimental results and the fatigue crack initiation model predictions by Huffman [24] can be observed.

Fig. 3.
figure 3

Stress–life (a), strain–life (b), and SWT–life (c) curves of P355NL1 steel.

Full size image

Figure 4 shows the probabilistic fields for such fatigue damage parameters as strain amplitude, SWT, and equivalent stress amplitude, using the generalized probabilistic model [Eqs. (25) and (26)] presented in Section 1 and proposed by Correia et al. [25]. The Walker exponent for the P355NL1 steel is equal to 0.79 and used to generate the probabilistic field (Fig. 4c). These probabilistic fields are used to generate the probabilistic Huffman fatigue crack growth fields

Fig. 4.
figure 4

Probabilistic εa – Nf (a), SWT Nf (b), and σar – Nf (c) fields of P355NL1 steel.

Full size image

3.3. Probabilistic Fatigue Crack Propagation Data. The fatigue crack propagation data of the P355NL1 steel collected in [26,27,28] were used to evaluate the fatigue crack growth model based on strain energy proposed by Huffman [24].

Fatigue crack growth (FCG) rates for several stress R-ratios under constant amplitude loading conditions were obtained using the ASTM E647 standard and considering the Paris law [32]. The CT specimens of P355NL1 steel were built with a width W = 40 mm and a thickness B = 4.5 mm. For the P355NL1 steel, the FCG tests were carried out for stress R-ratios, Rσ = 0, 0.5, and 0.7. All FCG tests were carried out for stress R-ratios, Rσ = 0, 0.5, and 0.7, in air at room temperature under a sinusoidal waveform at a maximum frequency of 20 Hz.

In this study, the results of linear-elastic and elastoplastic finite element analyses for a zone ahead of the crack tip of the CT geometry are required. These were obtained by De Jesus and Correia [20, 22, 27]. In those analyses, the cyclic elastoplastic curve obtained experimentally was considered by De Jesus and Correia [20, 22, 27]. The residual stress intensity factor results, Kr, are presented in Fig. 5 against the applied stress intensity factor range, ΔKapplied, for CT specimen built in P355NL1 steel, which were calculated by De Jesus and Correia [20, 22, 27]. The numerical model of the CT specimen was highly refined at the crack tip region in order to estimate the crack increment, Δa. De Jesus and Correia [20, 22, 26, 27] estimated the Δa parameter as equal to 45 · 10−3 m. This value was used in this research.

Fig. 5.
figure 5

Residual stress intensity factor Kr as a function of ΔKapplied for the CT geometry made in P355NL1 steel.

Full size image

The fatigue crack growth model based on strain energy proposed by Huffman [24] with the generalized probabilistic model for several fatigue damage parameters was applied to CT specimen geometry made of P355NL1 steel. The fatigue crack growth rate constants for several fatigue damage parameters, such as, strain amplitude, SWT, and Walker stress amplitude, were obtained from Eqs. (10) and (11)–(17) are shown in Table 3.

Table 3. Fatigue Crack Growth Rate Constants from Eqs. (10)–(17) for P355NL1 Steel
Full size table

The probabilistic Huffman fatigue crack growth rates based on strain, SWT, and Walker stress amplitude fatigue damage parameters for the P355NL1 pressure vessel steel taking into account several stress R-ratios, are shown in Figs. 6–8. Figure 9 shows that the models appear to be more sensitive to stress ratio effects compared to the measured fatigue crack growth rates. It can be seen that models which demonstrate high levels of stress ratio sensitivity show particularly poor correlation at high stress R-ratios, Rσ , for materials which seem insensitive to stress R-ratio effects. As compared to the stress-life or strain-life, however, these models provide more accurate estimations Although the P355NL1 steel was tested at two strain R-ratios, Rε, the stress R-ratios, Rσ, were not drastically different. Because of this, differences in the stress-strain behavior of the material at different stress R-ratios may not have been observed even if they exist. If the material demonstrates stress ratio-sensitive stress-strain behavior, it could make a difference in how the residual stress would be calculated at a crack tip. A difference in the behavior of the residual stress would influence the residual stress intensity factor, Kr, and therefore would influence the calculated stress ratio dependent fatigue crack growth rates. This would appear as a lack of stress-ratio effect in a material, while could be the same stress ratio effect as far as what the material itself goes through at the crack tip. However, this would be disguised by a change in cyclic stress-strain behavior influencing the residual stress profile differently at various stress R-ratios.

Fig. 6.
figure 6

Probabilistic prediction of the fatigue crack growth for P355NL1 steel based on Huffman FCG model and P – εa – N field for Rσ = 0 (a), 0.5 (b), and 0.7 (c).

Full size image
Fig. 7.
figure 7

Probabilistic prediction of the fatigue crack growth for P355NL1 steel based on Huffman FCG model and P – SWT – N field for Rσ = 0 (a), 0.5 (b), and 0.7 (c).

Full size image
Fig. 8.
figure 8

Probabilistic prediction of the fatigue crack growth for P355NL1 steel based on Huffman FCG model and P – σar – N field for Rσ = 0 (a), 0.5 (b), and 0.7 (c).

Full size image
Fig. 9.
figure 9

Fatigue crack growth rates for the probability of failure equal to 50% based on Huffman model and P – εa – N (a), P – SWT – N (b), and P – σar – N (c) fields for several stress R-ratios.

Full size image

It is noteworthy that the strain amplitude probability field appears to be less sensitive to stress ratio. This could be evidence in support of using strain-life based calculations preferentially over stress-life based calculations under certain circumstances, though much further investigation would be necessary to determine that. These results are also evidence that care should be taken when selecting a mean stress effect, as overly sensitive models can lead to over-designed structures or under-designed structures depending on the expected load cases.

Conclusions

  1. 1.

    The strain energy based fatigue crack initiation model proposed by Huffman can be used to estimate the Morrow constants giving good results when compared to the experimental results.

  2. 2.

    The fatigue crack propagation model based on strain energy density proposed by Huffman can be used with results from the linear-elastic and elastoplastic numerical analyses and a good agreement is observed.

  3. 3.

    The Huffman model uses the calibration parameters, Δa and x, which are required for the fit of the Huffman FCG model to the experimental FCG data.

  4. 4.

    The combination of the Huffman fatigue crack growth model with the generalized probabilistic model allowed to generate the probabilistic fields for the fatigue crack propagation rates.

  5. 5.

    The probabilistic crack propagation fields generated using several fatigue damage parameters such as strain, SWT, and equivalent stress amplitude, allowed to conclude that the strain damage parameter is the most suitable for the P355NL1 steel, taking into account the comparison that is made with the experimental crack propagation data, showing that this material is not sensitive to the mean stress effects.