Formation of the First Stars and Black Holes

Haemmerlé, L.; Mayer, L.; Klessen, R. S.; Hosokawa, T.; Madau, P.; Bromm, V.

doi:10.1007/s11214-020-00673-y

Formation of the First Stars and Black Holes

Published: 21 April 2020

Volume 216, article number 48, (2020)
Cite this article

Download PDF

Access provided by Autonomous University of Puebla

Space Science Reviews Aims and scope Submit manuscript

Formation of the First Stars and Black Holes

Download PDF

L. Haemmerlé¹,
L. Mayer²,
R. S. Klessen³,
T. Hosokawa⁴,
P. Madau⁵ &
…
V. Bromm⁶

1031 Accesses
48 Citations
10 Altmetric
1 Mention
Explore all metrics

Abstract

We review the current status of knowledge concerning the early phases of star formation during cosmic dawn. This includes the first generations of stars forming in the lowest mass dark matter halos in which cooling and condensation of gas with primordial composition is possible at very high redshift ($z > 20$), namely metal-free Population III stars, and the first generation of massive black holes forming at such early epochs, the so-called black hole seeds. The formation of black hole seeds as end states of the collapse of Population III stars, or via direct collapse scenarios, is discussed. In particular, special emphasis is given to the physics of supermassive stars as potential precursors of direct collapse black holes, in light of recent results of stellar evolution models, and of numerical simulations of the early stages of galaxy formation. Furthermore, we discuss the role of the cosmic radiation produced by the early generation of stars and black holes at high redshift in the process of reionization.

The numerical frontier of the high-redshift Universe

Article Open access 28 March 2015

A universal minimal mass scale for present-day central black holes

Article 19 June 2017

The origins of massive black holes

Article 20 September 2021

Use our pre-submission checklist

Avoid common mistakes on your manuscript.

1 First Stars

The first generation of stars, the so-called Population III (or Pop. III) built up from truly metal-free primordial gas. They have long been thought to live short, solitary lives, with only one extremely massive star forming in each dark matter halo with about 100 solar masses or more (Omukai 2001; Abel et al. 2002; Bromm et al. 2002; O’Shea and Norman 2007). The idea was that first star formation is simple and one only needs to know the initial Gaussian density perturbations of material at very high-redshift which are very well understood, e.g. from measuring cosmic microwave background (CMB) anisotropies (Planck Collaboration et al. 2016a), the growth of cosmological structures, and the heating and cooling processes in the primordial gas. However, this simple picture has undergone substantial revision in recent years, and we now understand that stellar birth in the early Universe is subject to similar complexity as star formation at present days. Numerical simulations indicate that fragmentation is a wide-spread phenomenon in first star formation (Clark et al. 2011a; Greif et al. 2012), and consequently that Pop. III stars form as members of multiple stellar systems with separations as small as the distance between the Earth and the Sun (e.g. Turk et al. 2009; Clark et al. 2011b; Greif et al. 2011; Smith et al. 2011; Stacy and Bromm 2013). Studies that do include radiative feedback (Hirano et al. 2014, 2015; Hosokawa et al. 2016), magnetic fields (Machida et al. 2006, 2008; Schleicher et al. 2009, 2010; Sur et al. 2010, 2012; Turk et al. 2012; Schober et al. 2012b,a; Bovino et al. 2013), dark matter annihilation (Smith et al. 2012; Stacy et al. 2014), as well as the primordial streaming velocities (Tseliakhovich and Hirata 2010; Greif et al. 2011; Maio et al. 2011a; Stacy et al. 2011) add further levels of complexity. It turns out that all of these processes are relevant and need to be incorporated in our theoretical models. There is agreement now that primordial star formation is equally dynamic and difficult to understand as stellar birth at present days (e.g. Mac Low and Klessen 2004; McKee and Ostriker 2007; Klessen and Glover 2016)

In this section we investigate how star formation progresses once the combination of gravitational collapse and cooling leads to a strong accretion flow into the center of a high-redshift halo, and we discuss the most important physical processes that govern stellar birth on small scales. We focus on the standard pathway to Pop. III star formation. We argue that the accretion disk that forms around the first object is likely to fragment, which typically results in the formation of a cluster of stars with a wide range of masses rather than the built-up of a single high-mass object. We then speculate about how stellar feedback, the presence of magnetic fields, the potential energy input from dark matter annihilation and the possible existence of large-scale streaming velocities between baryons and dark matter may influence this picture. Supermassive stars and the possible seeds for supermassive black holes will be discussed in Sects. 2 and 3, respectively. The implications on the reionization of the Universe are addressed in Sect. 4

1.1 Spherical Collapse Models

The simplest model for primordial star formation is the run-away collapse of a spherically symmetric halo with mass exceeding the critical value for the cooling instability to set in (Glover 2005, 2013). This was studied extensively in the early 2000’s (Abel et al. 2002; Bromm et al. 2002; Bromm and Larson 2004; Yoshida et al. 2003, 2006, 2008). Figure 1 adopted from Clark et al. (2011b) shows a typical example of such a system. And from the numbers provided, we can obtain a crude estimate of the accretion rate onto the center of the halo as

$$ \dot{M} = \zeta \dfrac{M_{\mathrm{J}}}{\tau _{\mathrm{ff}}} \propto \dfrac{c_{\mathrm{s}}^{3}}{G}, $$

(1)

where $M_{\mathrm{J}} \approx 50~{\mathrm{M}}_{\odot } \,\mu ^{-2} n^{-1/2} T^{3/2}$ is the Jeans mass with number density $n$ measured in particles per cubic centimeter, temperature $T$ in Kelvin, and mean molecular weight $\mu $ being ${\sim }1.22$ for primordial atomic and ${\sim} 2.33$ for primordial molecular gas, where $\tau _{\mathrm{ff}} \approx 52~\mathrm{{Myr}\, \mu ^{-1/2} n^{-1/2}}$ is the free-fall time, and where $c_{\mathrm{s}} = (k_{\mathrm{B}}T/\mu m_{\mathrm{H}})^{1/2}$ is the sound speed with the Boltzmann constant $k_{\mathrm{B}}$ and the proton mass $m_{\mathrm{H}}$. Because of $\dot{M} \propto T^{3}$, warmer gas leads to higher accretion rates. The factor $\zeta $ can take values of up to several tens depending on the actual density profile and by how much the actual gas mass $M$ exceeds the Jeans mass $M_{\mathrm{J}}$ (for classical studies, see Shu 1977; Larson 1969; Penston 1969; Whitworth and Summers 1985). With a typical gas temperature of $T\sim 1500$ K we get accretion rates of $\dot{M} \approx 2 \times 10^{-3}$ M_⊙ yr⁻¹.

1.2 Disk Fragmentation

These early calculations typically stopped when the object in the center reached number densities of $n \approx 10^{16}\text{ cm}^{-3}$ or more, because then the computational timestep became prohibitively small. At this time the protostar has a mass of only ${\sim} 10^{-3}$ M_⊙. However, as more and more gas falls to the center it also carries along more and more angular momentum. Eventually this gas settles into a rotationally supported disk rather than being consumed by the central protostar. Theoretical and numerical models that follow the build-up and longer-term evolution of this disk show that the system is prone to fragmentation.

Disk fragmentation on various spatial and temporal scales is reported by various authors (Machida et al. 2008; Clark et al. 2011b; Greif et al. 2011, 2012; Dopcke et al. 2013; Susa 2013; Susa et al. 2014; Hosokawa et al. 2016; Stacy and Bromm 2013; Stacy et al. 2016; Turk et al. 2009; Wollenberg et al. 2020). Under typical conditions of Pop. III star formation the mass load onto the disk by accretion from the infalling envelope exceeds its capability to transport this material inwards by gravitational or magnetoviscous torques, that is by spiral arms (Binney and Tremaine 1987) or by the magnetorotational instability (Balbus and Hawley 1998). Consequently the disk becomes Toomre unstable and fragments. This preferentially occurs at the outer edge of the disk. The instability region moves outwards as the disk grows larger by accretion of higher angular momentum material, and the formation of new protostars occurs at larger and larger radii as the evolution progresses. This is indicated in Fig. 1, adopted from Clark et al. (2011b), which shows the build-up of altogether four protostars within only about hundred years after the formation of the first object.

Disk fragmentation has important consequences for the resulting stellar mass spectrum. As matter flows through the disk towards the center, it first encounters the Hill volume of secondary protostars further out and preferentially gets swallowed by these objects. Otherwise, this gas would have continued to move inwards and would eventually be accreted by the central object. Clearly, disk fragmentation limits the mass growth of the primary star in the center, and so this process has been termed ‘fragmentation-induced starvation’ in the context of present-day star formation (Kratter and Matzner 2006; Peters et al. 2010; Girichidis et al. 2011, 2012a,b). Some of these protostars may get ejected by dynamical encounters with other protostars or fragments while some may move inwards to get accreted by the central object (Clark et al. 2011a; Greif et al. 2012; Smith et al. 2012; Stacy et al. 2016). As a consequence of these stochastic behavior, the mass spectrum of Pop. III stars is expected be very broad, possibly reaching down into the substellar regime. We conclude that the standard pathway of Pop. III star formation leads to a stellar cluster with a wide distribution of masses rather than the build-up of one single high-mass object.

1.3 Radiative Feedback

Massive Pop III stars are expected to enter the hydrogen burning main sequence while still accreting (Zinnecker and Yorke 2007; Maeder 2009). For accretion rates below $\dot{M} \approx 10^{-3}$ M_⊙ they are thought to be compact and very hot at their surface (Hosokawa and Omukai 2009; Hosokawa et al. 2010, 2012), implying that they emit large numbers of ionizing photons (Schaerer 2002) that can significantly influence their birth environment. For rates much larger than $\dot{M} \gtrsim 10^{-2}$ M_⊙ stellar evolution calculations suggest that stars remains bloated and fluffy (Hosokawa et al. 2013; Umeda et al. 2016; Woods et al. 2017; Haemmerlé et al. 2018b). In this case, the surface temperature is relatively low, and although very luminous, these stars do not emit much ionizing radiation and could be able to maintain this high accretion flow for a very long time. In the right environment this could possibly lead to the formation of supermassive stars as we discuss in Sect. 2.

Compact and hot Pop. III stars create HII regions which eventually break out of the parental halo and may affect stellar birth in neighboring systems (see, e.g. Kitayama et al. 2004; Whalen et al. 2004; Alvarez et al. 2006; Abel et al. 2007; Yoshida et al. 2007; Greif et al. 2008; Wise et al. 2012b,a; Jeon et al. 2014). The question is when this happens and how radiative feedback influences the immediate birth environment. When addressing this problem, we can seek guidance from models of stellar birth at present days. Recent simulations (Yorke and Sonnhalter 2002; Krumholz et al. 2009; Kuiper et al. 2010, 2011; Peters et al. 2010, 2011; Commerçon et al. 2011; Rosen et al. 2016) indicate that once a protostellar accretion disk has formed, it quickly becomes gravitationally unstable and so material in the disk midplane flows inwards along dense filaments, whereas radiation escapes through optically thin channels above the disk. Even ionized material can be accreted, if the accretion flow is strong enough (Keto 2007; Peters et al. 2010). Radiative feedback is found not to be able to shut off the accretion flow, instead it is the dynamical evolution of the disk material that controls the mass growth of individual protostars.

Due to the lack of metals and dust, protostellar accretion disks around Pop. III stars can cool less efficiently and are much hotter than disks at present days (Tan and McKee 2004). Furthermore, the stellar radiation field couples less efficiently to the surrounding because the opacities are smaller. It is thus not clear how well the above results can be transferred to the primordial case. Numerical simulations in two dimensions by Hosokawa et al. (2011), Hirano et al. (2014) and Hirano et al. (2015) find that radiative feedback can indeed stop stellar mass growth and quickly remove the remaining accretion disk, resulting in final stellar masses from a few 10 M_⊙ up to about 1000 M_⊙. However, these calculations cannot capture disk fragmentation and the formation of multiple stellar systems. Three-dimensional calculations by Stacy et al. (2012), Susa (2013, 2014), or Hosokawa et al. (2016) on the other hand find widespread fragmentation with a wide range of stellar masses down to ${\sim} 1$ M_⊙. All calculations have limitations and shortcomings, either in terms of resolution or in the number of physical processes included. High resolution is essential for correctly computing the recombination rate in ionized or partially ionized gas. It goes quadratic with the density, and consequently, not resolving the high-density shell of gas swept up by the expanding ionized gas can result in incorrect HII region expansion rates and sizes (see, e.g. Rahner et al. 2017, 2019). By a similar token, treating only ionizing radiation and neglecting the impact of Lyman-Werner wavebands can lead to large errors in the overall photon escape fraction (Schauer et al. 2015). Consequently, any firm conclusions about the resulting mass spectrum of Pop. III stars in the presence of radiative feedback seems premature at this stage.

1.4 Magnetic Fields

Also the presence of dynamically important magnetic fields will influence disk evolution and fragmentation. Unfortunately, we know very little about magnetic fields in the high-redshift universe. Theoretical models predict that magnetic fields could be produced in various ways, for example via the Biermann battery (Biermann 1950), the Weibel instability (Lazar et al. 2009; Medvedev et al. 2004), or thermal plasma fluctuations (Schlickeiser and Shukla 2003). Other models invoke phase transitions that occur during cosmic inflation (Sigl et al. 1997; Grasso and Rubinstein 2001; Banerjee and Jedamzik 2003; Widrow et al. 2012). In each case, the inferred field strengths are very small. The only way to obtain dynamically significant magnetic fields is through the small-scale turbulent dynamo, which is very efficient in amplifying even extremely small primordial seed fields to the saturation level. This process is very fast and acts on timescales much shorter than the dynamical free-fall time. An analytic treatment is possible in terms of the Kazantsev model (Kazantsev 1968; Subramanian 1998; Schober et al. 2012b,a). Once backreactions become important, the growth rate slows down, and saturation is reached within a few large-scale eddy-turnover times (Schekochihin et al. 2002, 2004; Schober et al. 2015).

Depending on the properties of the turbulent flow, the magnetic energy density at saturation is thought to lie between 0.1% and a few 10% of the kinetic energy density (Federrath et al. 2011, 2014). Fields this strong affect the evolution of protostellar accretion disks: They remove angular momentum from the star-forming gas (Machida et al. 2008; Machida and Doi 2013; Bovino et al. 2013; Latif et al. 2013b, 2014b), drive protostellar jets and outflows (Machida et al. 2006), and they reduce the level of fragmentation in the disk (Turk et al. 2011; Peters et al. 2014). Altogether, we expect Pop. III clusters to have fewer stars with higher masses than predicted by purely hydrodynamic simulations. However, a full assessment of these differences still needs to be worked out in detail.

1.5 Streaming Velocity

Prior to recombination, baryons are tightly coupled to photons resulting in a standing acoustic wave pattern (Sunyaev and Zel’dovich 1970). This results in oscillations between baryons and dark matter with relative velocities of about $30\text{ km}$ s⁻¹ and coherence lengths of several 10 Mpc to 100 Mpc (Silk 1986) at $z \approx 1000$. After recombination, baryons are no longer tied to photons, their sound speed drops to ${\sim} 6\text{ km}$ s⁻¹, and the velocity with respect to the dark matter component becomes supersonic with Mach numbers of ${\mathcal{M}} \approx 5$ (Tseliakhovich and Hirata 2010). In the subsequent cosmic evolution, the relative streaming velocity decays linearly with $z$, and reaches ${\sim }1$ km $\text{s}^{-1}$ at the onset of first star formation at $z \approx 30$. Numerical simulations with streaming velocities suggest a reduction of the baryon overdensity in low-mass halos, a delay of the onset of cooling, and a larger critical mass for collapse (Greif et al. 2011; Stacy et al. 2011; Maio et al. 2011b; Naoz et al. 2012, 2013; O’Leary and McQuinn 2012; Latif et al. 2014a; Schauer et al. 2017b). This can have substantial impact on the resulting $21\text{ cm}$ emission (Fialkov et al. 2012; McQuinn and O’Leary 2012; Visbal et al. 2012, see also Sect. 4). Gas in halos which are located in regions of large streaming velocities will be more turbulent than in more quiescent systems, and so we expect more fragmentation and a bias towards smaller stellar masses (Clark et al. 2008). However, this process has not yet been modeled with sufficient resolution, and so a reliable prediction of the stellar mass spectrum in regions with large streaming velocities is still outstanding.

1.6 Dark Matter Annihilation

Despite its importance for cosmic evolution and structure formation, the true physical nature of dark matter is unknown and so the studies of the impact of dark matter annihilation on first star formation are still highly speculative. As baryons collapse in the centers of primordial halos, they may drag along dark matter particles in a processes termed ‘adiabatic contraction’ (Blumenthal et al. 1986). It can lead to a density increase of several orders of magnitude, and as the annihilation rate scales quadratically with the density the corresponding energy input and ionization rate may become large enough to influence the dynamics of the gas. Spolyar et al. (2008) and Freese et al. (2009) suggest that this process could potentially overcome the cooling provided by H₂ and eventually halt further collapse. They call the resulting object ‘dark star’. It has a size of few astronomical units and is powered by dark matter annihilation rather than by nuclear fusion. If dark matter particles also scatter weakly on baryons this could lead to a structure that is stable for a long time (Freese et al. 2008; Iocco 2008; Iocco et al. 2008; Yoon et al. 2008; Hirano et al. 2011).

There are several concerns that have been raised in this context. First, it is not clear whether collapse stalls once the energy input from dark matter annihilation becomes comparable to the cooling rate, because the larger heating rate may catalyze further H₂ formation and lead to a correspondingly larger cooling rate (Ripamonti et al. 2010). Second, the underlying assumption of perfect alignment between dark matter cusp and gas collapse is most likely violated in realistic star formation conditions. For example, Stacy et al. (2012, 2014) find that non-axisymmetric perturbations lead to a separation between dark matter cusp and collapsing gas and causes the annihilation energy input to be too small for dark star formation. Similarly, Smith et al. (2012) see no evidence for the build-up of dark stars in their simulations. However, they find that dark matter annihilation has the potential to modify the dynamics of the accretion disk and reduce the level of disk fragmentation. As before, more work is required before we are able to draw firm conclusions.

2 Supermassive Stars

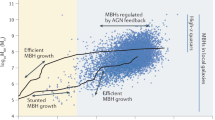
Motivated by recent discoveries of supermassive black holes (SMBHs) exceeding $10^{9}~{\mathrm{M}_{\odot }}$ at high redshifts $z \gtrsim 6$, the formation of supermassive stars (SMSs) in the early universe has drawn great attention for recent years. A possible formation pathway of the SMSs is the direct collapse (DC) model (e.g., Bromm and Loeb 2003), where the SMSs gain the huge mass via very rapid mass accretion, typically 0.1–10 $\mathrm{M}_{\odot }$ yr⁻¹ expected in atomic cooling primordial haloes.

Although the evolution and final fates of the SMSs had been investigated in the literature for past decades (e.g., Hoyle and Fowler 1963; Osaki 1966; Unno 1971; Fricke 1973; Fuller et al. 1986), the actual formation process had been ignored in such previous studies (‘monolithic’ models); a SMS in the stable nuclear burning phase was assumed initially, and then the subsequent evolution was followed. However, considering the formation process is critically important. For instance, the stellar radiative feedback against the accretion flow is a potential obstacle in forming massive stars. Even in the normal primordial star formation, where the typical stellar mass is thought to be ${\sim} 100~{\mathrm{M}_{\odot }}$, the stellar UV feedback may be strong enough to halt the mass accretion onto the stars (e.g., McKee and Tan 2008; Hosokawa et al. 2011; Sugimura et al. 2020). In the DC model, where the stellar mass is supposed to become much higher, the more tremendous UV radiative feedback may prevent the SMS formation early on. Solving the evolution of accreting SMSs from their birth stage is necessary to evaluate the strength of the UV feedback. In the same vein, the earlier evolution with the rapid mass accretion also affects the final fate of the SMS, i.e., at which point it collapses into a BH. This determines how massive SMBH seeds are finally provided in the DC scenario.

2.1 Numerical Modeling of Accreting Stars

Numerical modeling of accreting stars has been developed in some different contexts, including the binary evolution (e.g., Kippenhahn and Meyer-Hofmeister 1977; Neo et al. 1977), present-day star formation (e.g., Stahler et al. 1980; Stahler 1988; Palla and Stahler 1991; Behrend and Maeder 2001; Hosokawa and Omukai 2009; Haemmerlé et al. 2016), and primordial star formation (e.g., Stahler et al. 1986; Omukai and Palla 2003). In parallel with the emergence of the DC model, the similar method has been applied for the evolution of SMSs with extremely high accretion rates exceeding $10^{-2}~{ \mathrm {M}_{\odot } }\,{\mbox{yr}}^{-1}$.

Regardless of such different contexts, the above studies basically solve the same governing equations to construct stellar models,

$$ \left ( \frac{\partial r}{\partial M} \right )_{t} = \frac{1}{4 \pi \rho r^{2}}, $$

(2)

$$ \left ( \frac{\partial P}{\partial M} \right )_{t} = - \frac{\mathit{GM}}{4 \pi r^{4}}, $$

(3)

$$ \left ( \frac{\partial L}{\partial M} \right )_{t} = \epsilon - T \left ( \frac{\partial s}{\partial t} \right )_{M} , $$

(4)

$$ \left ( \frac{\partial s}{\partial M} \right )_{t} = \frac{G M}{4 \pi r^{4}} \left ( \frac{\partial s}{\partial p} \right )_{T} \left ( \frac{L}{L_{s}} - 1 \right ) C , $$

(5)

where $M$ is the mass coordinate, $\epsilon $ the energy production rate via nuclear fusion, $s$ the specific entropy, $L_{s}$ the radiative luminosity with adiabatic temperature gradient, $C$ the coefficient determined by the mixing-length theory when $L > L_{s}$ ($C=1$ otherwise), and the remaining quantities have ordinary meanings. Effects of the mass accretion are incorporated in the term $T (\partial s / \partial t)_{M}$ in Eq. (4), which is approximately discretized as

$$ \left ( \frac{\partial s}{\partial t} \right )_{M} = \left ( \frac{\partial s}{\partial t} \right )_{m} + \dot{M}_{\ast }\left ( \frac{\partial s}{\partial m} \right )_{t} , $$

(6)

where $m$ is the inverse mass coordinate measured from the surface, $m \equiv M_{\ast } - M$. An evolutionary calculation begins with an initial model with small mass, and advances with updating models by adding the accreting gas mass $\dot{M}_{*}\Delta t$, where $\Delta t$ is the time step.

2.1.1 Accretion-Induced “Inflation” of Stars

Figure 2 summarizes the results by Hosokawa et al. (2012), who have numerically followed the evolution of protostars accreting at various constant rates including high rates exceeding $10^{-2}~{ \mathrm {M}_{\odot } }\,{\mbox{yr}}^{-1}$. The black curve in panel (a) represents the case with $\dot{M}_{*}= 10^{-3}~{ \mathrm {M}_{\odot } }\,{\mbox{yr}}^{-1}$, a relatively low accretion rate typical for the normal primordial star formation. A striking feature for this case is the stellar contraction occurring for $6~{\mathrm{M}_{\odot }}\lesssim M_{*} \lesssim 30~{ \mathrm{M}_{\odot }}$. This is the so-called Kelvin-Helmholtz (KH) contraction stage, during which the star loses its energy by radiating away. The stellar effective temperature and emissivity of ionizing photons substantially rises during this, and the UV feedback against the accretion flows begins to operate. The presence of the KH contraction thus marks the onset of the stellar UV feedback. Since the central temperature gradually rises, the hydrogen burning starts just after the stellar mass exceeds $30~{\mathrm{M}_{\odot }}$. After this point, the stellar radius turns to rise following the mass-radius relation for zero-age main-sequence (ZAMS) stars.

By contrast, the above evolution drastically changes with the more rapid accretion. Panel (a) shows that the KH contraction stage only spans the narrower mass range for such cases. The contraction turns to the expansion with the accretion rates $6 \times 10^{-3}~{ \mathrm {M}_{\odot } }\,{\mbox{yr}}^{-1}$ and $0.03~{ \mathrm {M}_{\odot } }\,{\mbox{yr}}^{-1}$. With the highest rate $0.06~{ \mathrm {M}_{\odot } }\,{\mbox{yr}}^{-1}$, the contraction never occurs and the stellar radius monotonically increases as the star accretes the gas. The stellar radius finally reaches $\simeq 7000~{\mathrm{R}_{\odot }}$ (or nearly 30 AU) when the stellar mass is $\sim 1000~{\mathrm{M}_{\odot }}$. Panel (b) summarizes the evolution with the even higher accretion rates, $0.06~{ \mathrm {M}_{\odot } }\,{\mbox{yr}}^{-1}\leq \dot{M}_{*}\leq 1~{ \mathrm {M}_{\odot } }\,{\mbox{yr}}^{-1}$, showing further intriguing features, i.e., the curves corresponding to the different accretion rates represent the same mass-radius relation for $M_{*} \gtrsim 300~{\mathrm{M}_{\odot }}$. The radius at $M_{*} \simeq 1000~{\mathrm{M}_{\odot }}$ is consequently ≃ 30 AU for all the cases.

The above behavior is well interpreted with the following analytic argument. Let us begin with the general expression of the stellar luminosity

$$ L_{*} = 4 \pi R_{*}^{2} \sigma T_{\mathrm{eff}}^{4}, $$

(7)

where $\sigma $ is the Stefan-Boltzmann constant. As for very massive stars, the luminosity is very close to the Eddington value,

$$ L_{*} \simeq L_{\mathrm{Edd}} \propto M_{*} . $$

(8)

In the current cases with the high accretion rates, a stellar surface layer inflates because it always traps a part of the heat released from the contracting interior. The effective temperature accordingly decreases to several ×1000 K, where H⁻ bound-free absorption mostly contributes the opacity. Since the H⁻ opacity has a very strong temperature-dependence, the effective temperature is almost fixed at a constant value. Substituting equation (8) and $T_{\mathrm{eff}} \simeq 5000$ K into equation (7), we derive the mass-radius relation

$$ R_{*} \simeq 2.6 \times 10^{3}~R_{\odot }\left ( \frac{M_{*}}{100~M_{\odot }} \right )^{1/2} , $$

(9)

which is indicated by the thin green lines in Fig. 2. The above derivation includes no dependence on the accretion rate, which explains why the different lines in Fig. 2 eventually converge into the same mass-radius relation.

2.1.2 Birth of Accreting SMSs

Hosokawa et al. (2013) have further followed the later evolution until the stellar mass reaches $10^{4} \sim 10^{5}~{\mathrm{M}_{\odot }}$. Figure 3 illustrates the evolution of the stellar interior structure with the constant accretion rate $1~{ \mathrm {M}_{\odot } }\,{\mbox{yr}}^{-1}$. We see that the monotonic increase of the stellar radius continues after the stellar mass exceeds $1000~{\mathrm{M}_{\odot }}$. The analytic formula given by equation (9) still provides a good fit for the evolution of the stellar radius, though it only slightly overestimates the radius for $M_{*} \gtrsim 3 \times 10^{4}~{\mathrm{M}_{\odot }}$. The similar evolution has been reported by the different authors (e.g., Umeda et al. 2016; Haemmerlé et al. 2018b).

Figure 3 shows that a surface layer which only has a small fraction of the total mass significantly inflates to cover a large part of the stellar radial extent. The star has a bloated envelope and compact core like red giants. Most of the stellar mass is contained in the central core, which gradually contracts as the star accretes the gas. The central temperature rises during this, as in the ordinary KH contraction. As a result, the nuclear burning starts just after the total stellar mass exceeds ${\simeq} 4000~{\mathrm{M}_{\odot }}$. The central convective core gradually extends after that, owing to the heat input caused by the nuclear fusion. The outer convective layer remains bloated as long as the rapid mass accretion continues, so that the stellar radius is much larger than the ZAMS stars with the same masses.

As described above, SMSs under the very rapid mass accretion greatly inflate. Their effective temperatures are only ${\simeq} 5000$ K, and the UV emissivity is much smaller than that of non-accreting stars. The resulting UV feedback is thus too weak to disturb the accretion flow toward the stars, so that the rapid growth of the stellar mass should continue as far as the high accretion rates exceeding ${\sim} 10^{-2}~{ \mathrm {M}_{\odot } }\,{\mbox{yr}}^{-1}$ are maintained. In the standard DC model, SMSs exceeding $10^{5}~{\mathrm{M}_{\odot }}$ may appear in less 0.1 Myr since the birth of the initial embryonic protostar, and they provides massive SMBH seeds once the gravitational collapse occurs via the general relativistic instability (Sect. 2.1.4).

2.1.3 Accretion at $\dot{M}>10$ $\mathrm{M}_{\odot }$ yr⁻¹

Beside the usual DC scenario based on atomic cooling haloes, an alternative formation route for massive BH seeds has been proposed, relying on the merger of massive, gas-rich galaxies (Mayer et al. 2010, 2015; Mayer and Bonoli 2019), as we describe in more details in Sect. 3. In this scenario, inflows as high as $10^{5}$ $\mathrm{M}_{\odot }$ yr⁻¹ are found on subparsec scales.

The evolution of SMSs under accretion at $\dot{M}>10$ $\mathrm{M}_{\odot }$ yr⁻¹, up to 1000 $\mathrm{M}_{\odot }$ yr⁻¹, has been simulated in Haemmerlé et al. (2019). The main qualitative difference compared to models at lower rates is that for such rates the accretion timescale $M/\dot{M}$ becomes similar to or shorter than the dynamical time of the star. Thus, above a limit in the accretion rate, the evolution proceeds hydrodynamically. This limit is an increasing function of the stellar mass $M$, since the perturbation to equilibrium induced by a given amount of mass added at the surface becomes relatively weaker as the stellar mass grows.

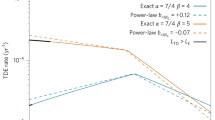
The curve of $\dot{M}(M)$ is shown on Fig. 4. Rates of ${\gtrsim} 100$ $\mathrm{M}_{\odot }$ yr⁻¹ become consistent with equilibrium only when the accretor is supermassive ($M \gtrsim 10^{4}$ $\mathrm{M}_{\odot }$). If the conditions for equilibrium are satisfied, the star evolves in a qualitatively similar way as for lower rates: the envelope is inflated and the evolutionary track follows the Hayashi limit upwards. Most of the star is radiative, and hydrogen burns in the centre, driving convection in a core that contains a few percent of the total stellar mass. For $\dot{M}=1000$ $\mathrm{M}_{\odot }$ yr⁻¹, the mass fraction of the convective core can be as low as 1% at the endpoint of the evolution.

If lower mass objects accrete at rates $\gtrsim 100$ $\mathrm{M}_{\odot }$ yr⁻¹, their evolution proceeds dynamically, since the pressure and temperature gradients required for equilibrium cannot build. The further evolution in the dynamical regime is not known. In particular, the possibility for dark collapse (Mayer and Bonoli 2019) shall be addressed with hydrodynamical simulations.

2.1.4 The Final Collapse of SMSs

SMSs end their life through the general relativistic (GR) instability, which is a radial pulsation instability that reflects photon’s contribution to gravity (Chandrasekhar 1964). GR effects impact negligibly the properties of stable SMSs, but they are critical for their stability, since these stars are always close to the Eddington limit. For $M>10^{4}$ $\mathrm{M}_{\odot }$, the ratio $\beta $ of the gas pressure to the total pressure is of the order of a few percent. The first adiabatic exponent can be developed as

$$ \varGamma _{1}=\left .\frac{{\mathrm{dln}}P}{{\mathrm{dln}}\rho }\right \vert _{ \mathrm{ad}}=\frac{4}{3}+\frac{\beta }{6}+\mathcal{O}(\beta ^{2}). $$

(10)

Thus, $\varGamma _{1}$ exceeds its classical critical value $\varGamma _{\mathrm{crit}}=4/3$ by typically a percent. In these conditions, the small corrections to $\varGamma _{\mathrm{crit}}$ arising from GR effects can trigger the collapse. For polytropic models, the first order post-Newtonian correction to $\varGamma _{\mathrm{crit}}$ is

$$ \varGamma _{\mathrm{crit}}=\frac{4}{3}+K\frac{r_{S}}{r}+\mathcal{O}\left (\frac{r_{S}^{2} }{r^{2}}\right ), $$

(11)

where $r_{S}=2\mathit{GM}_{r}/c^{2}$ is the local Schwarzschild radius and $K$ is a constant that takes a value of 1.12 for a polytrope $n=3$, i.e. for an isentropic star in the limit $\beta \rightarrow 0$. As one considers increasing masses, the gas correction to $\varGamma _{1}$ decreases while the GR correction to $\varGamma _{\mathrm{crit}}$ increases, until

$$ \frac{\beta }{6}< K\frac{r_{S}}{r} \quad \Longrightarrow \quad \varGamma _{1}< \varGamma _{\mathrm{crit}} $$

(12)

and the star becomes GR unstable.

The limit in mass above which accreting SMSs become GR unstable has been investigated in numerical simulations (Umeda et al. 2016; Woods et al. 2017; Haemmerlé et al. 2018b), and are shown on Fig. 5. Discrepancies appear between the various studies (see Woods et al. 2019 for a detailed discussion), but all the models indicate a limit of several $10^{5}$ $\mathrm{M}_{\odot }$ for a range in accretion rate that covers two orders of magnitudes. Models accreting at 100–1000 $\mathrm{M}_{\odot }$ yr⁻¹ suggest that this limit remains always below $10^{6}$ $\mathrm{M}_{\odot }$ even for such extreme rates (Haemmerlé et al. 2019).

Hydrodynamical simulations of the final collapse of SMSs indicate that the bulk of the stellar mass at the onset of instability forms a black hole in a dynamical time (Saijo et al. 2002; Saijo 2004; Liu et al. 2007; Shibata et al. 2016b; Sun et al. 2017, 2018; Li et al. 2018; Uchida et al. 2017). In spherical symmetry, the whole mass is swallowed by the black hole, but rotation allows for a few percent of the stellar mass to orbit outside the horizon as a torus. Such asymmetries could trigger detectable gravitational wave (GW) emission. In the presence of a magnetic field, relativistic jets are found to form, which could trigger ultra-long gamma-ray bursts (ULGRBs). Thus the final collapse of SMSs might allow for multi-messenger signatures of DC. Thermonuclear explosion could occur in the presence of metals (Fuller et al. 1986; Montero et al. 2012), or in a narrow mass-range around 55 000 $\mathrm{M}_{\odot }$ (Chen et al. 2014).

2.2 Rotation in SMSs

Rotation is key in the evolution of SMSs, for positive and negative reasons. The negative reasons rely on the angular momentum problem, which is general to star formation: the contraction from interstellar to stellar densities require mechanisms to extract angular momentum, in order to avoid break-up by centrifugal forces (Spitzer 1978; Bodenheimer 1995). This angular momentum barrier is particularly strong in massive star formation, due to the importance of radiation pressure, the lack of magnetic fields, and the short evolutionary timescales (e.g. Lee and Yoon 2016, Takahashi and Omukai 2017, Haemmerlé et al. 2017). It constitutes also a strong bottleneck for the efficient mass growth of SMBHs once formed (Sugimura et al. 2018). The positive reasons rely on the possibility for the final collapse of SMSs to trigger GWs and ULGRBs (Sect. 2.1.4). Rotation is required in both cases, in order to break spherical symmetry and to allow for the formation of collimated jets.

The effect of rotation on SMSs has been studied in details in the context of monolithic models, i.e. neglecting accretion (Fowler 1966; Bisnovatyi-Kogan et al. 1967; Appenzeller and Kippenhahn 1971; Baumgarte and Shapiro 1999b,a; New and Shapiro 2001; Shibata et al. 2016a; Butler et al. 2018; Dennison et al. 2019). In general, these studies assume the star is rotating as a solid body, with a surface velocity corresponding to the Keplerian value. The assumption of solid rotation relies on convection, which dominates in monolithic models. The idea of Keplerian rotation follows from the argument of angular momentum conservation during the formation process. As a consequence of Keplerian rotation, the star is expected to loose mass at the equator as it further contracts, and this configuration is called the mass-shedding limit (Baumgarte and Shapiro 1999b). The most striking result of these studies is the possibility for stars of $10^{8}$–$10^{9}$ $\mathrm{M}_{\odot }$ to be stabilised by rotation against GR (Fowler 1966; Bisnovatyi-Kogan et al. 1967). Moreover, the rotational properties of monolithic SMSs at collapse are found to be universal, in the sense that their spin parameter is

$$ a=\frac{cJ}{\mathit{GM}^{2}}=0.97, $$

(13)

according to numerical computations (Baumgarte and Shapiro 1999a). This parameter is key for the outcome of the collapse, since a value $<1$ allows for the whole mass to form a black hole without angular momentum loss.

Monolithic models have been used as initial conditions to simulate the final collapse of SMSs (Saijo et al. 2002; Saijo 2004; Liu et al. 2007; Shibata et al. 2016b; Sun et al. 2017, 2018; Li et al. 2018; Uchida et al. 2017). A black hole is found to form, containing 90–95% of the stellar mass, and a typical spin parameter $a\sim 0.7$. The remaining gas is maintained outside the horizon by the centrifugal force and takes the geometry of a torus, before relativistic jets are launched. Interestingly, relaxing the constraint of solid rotation allows for more angular momentum to be contained in the star, which results in more massive torus and more energetic jets (New and Shapiro 2001; Sun et al. 2018).

When accretion at ${\gtrsim} 0.1$ $\mathrm{M}_{\odot }$ yr⁻¹ is accounted for, the rotational properties of SMSs are at the opposite extreme of those of monolithic models (Haemmerlé et al. 2018a; Haemmerlé and Meynet 2019). First, since accretion stabilises the star against convection, solid-body rotation is not ensured, and the highly non-homologous contraction of the stellar interior leads to strong differential rotation, with a core rotating $10^{4}\mbox{--}10^{5}$ times faster than the surface in terms of frequency. Second, building a supermassive hydrostatic object by accretion requires its surface to rotate always at less than 10–20% of the Keplerian velocity (Fig. 6). Thus, accreting SMSs must be slow rotators.

This result is a consequence of the $\varOmega \varGamma $-limit (Maeder and Meynet 2000), i.e. the fact that the break-up velocity of massive stars is lowered by the effect of their strong radiation pressure, compared to Keplerian velocity. Break-up is reached when any contribution from gas pressure would destroy the star. For low-mass stars, this condition translates into the equality between gravity and the centrifugal force, which corresponds to the Keplerian limit:

$$ \frac{\mathit{GM}}{{R^{2}_{\mathrm{eq},\mathrm{crit}}}}=\frac{{ {\mathrm{v}}^{2}_{\mathrm{crit},\mathrm{1}}}}{{ R_{\mathrm{eq},\mathrm{crit}}}} \quad \Longleftrightarrow \quad { {\mathrm{v}}_{\mathrm{crit},\mathrm{1}}}=\sqrt{\frac{\mathit{GM}}{{ R_{\mathrm{eq},\mathrm{crit}}}}}=\sqrt{\frac{2}{3}\frac{\mathit{GM}}{R}}={ {\mathrm{v}}_{\mathrm{Kep}}}, $$

(14)

where $R_{\mathrm{eq},\mathrm{crit}}$ is the equatorial radius at break-up, which according to the Roche model is 1.5 times the polar radius $R$, nearly unchanged by rotation. The Roche model is always accurate for SMSs, thanks to the large density contrasts in their interiors. For massive stars, one has to account for the effect of radiation pressure in the mechanical equilibrium, and the condition for break-up becomes

$$ \frac{\mathit{GM}}{{R^{2}_{\mathrm{eq},\mathrm{crit}}}}=\frac{{ {\mathrm{v}}^{2}_{\mathrm{crit},\mathrm{2}}}}{{ R_{\mathrm{eq},\mathrm{crit}}}}-\frac{1}{\rho }\frac{{\mathrm{d}}{ P_{\mathrm{rad}}}}{{\mathrm{d}}r}, $$

(15)

where $P_{\mathrm{rad}}$ is the radiation pressure. If we neglect the deformation of the star and use the equation of radiative transfer $F=-\frac{c}{\kappa \rho }\frac{{\mathrm{d}}{P_{\mathrm{rad}}}}{{ \mathrm{d}}r}$, this condition gives a break-up velocity

$$ {{\mathrm{v}}_{\mathrm{crit},\mathrm{2}}}={ {\mathrm{v}}_{\mathrm{crit},\mathrm{1}}}\sqrt{1-\frac{\kappa L }{4\pi \mathit{cGM}}}={{\mathrm{v}}_{\mathrm{Kep}}}\, \sqrt{1-{\varGamma }}, $$

(16)

where $\varGamma $ is the Eddington factor. This expression shows that in the limit ${\varGamma }\rightarrow 1$ (Eddington limit), the corrected critical velocity goes to 0, i.e. stars that are nearly Eddington must be slow rotators. When accounting for the anisotropy of the flux, in the limit ${\varGamma }\rightarrow 1$, the expression becomes

$$ {{\mathrm{v}}_{\mathrm{crit},\mathrm{2}}}=\frac{3}{2}\,{ {\mathrm{v}}_{\mathrm{crit},\mathrm{1}}}\sqrt{1-{ \varGamma }} $$

(17)

Interestingly, for ${\varGamma }\lesssim 0.6$, one has ${{\mathrm{v}}_{\mathrm{crit},\mathrm{2}}}>{ {\mathrm{v}}_{\mathrm{crit},\mathrm{1}}}$. This is a consequence of the von Zeipel theorem (von Zeipel 1924), i.e. the reduction of the flux at the equator (where the centrifugal force is the strongest) due to the decrease of effective gravity. But for ${\varGamma }\gtrsim 0.6$, we see that ${{\mathrm{v}}_{\mathrm{crit},\mathrm{2}}}<{ {\mathrm{v}}_{\mathrm{crit},\mathrm{1}}}={ {\mathrm{v}}_{\mathrm{Kep}}}$, i.e. the break-up velocity is lowered compared to the Keplerian limit.

Forming a supermassive hydrostatic object by accretion requires the constraint from the $\varOmega \varGamma $-limit to be satisfied all along the accretion phase, for the in-falling gas to be incorporated by the star. As an extreme case of the $\varOmega \varGamma $-limit, accreting SMSs cannot rotate faster than 10–20% of their Keplerian velocity (Fig. 6). It follows that their structure is not impacted by rotation. In addition, rotational mixing (shear diffusion and meridional circulation) remains negligible due to the short evolutionary timescales.

The constraint on the surface velocity translates into a constraint on the accreted angular momentum, which cannot exceed significantly a percent of the Keplerian angular momentum. The angular momentum barrier is thus particularly strong for SMSs. Two mechanisms might allow for efficient angular momentum loss in the accretion process: gravitational torques (Begelman et al. 2006; Wise et al. 2008; Hosokawa et al. 2016) and magnetic fields (Pandey et al. 2019; Haemmerlé and Meynet 2019; Deng et al. 2019, 2020). Supermassive accretion discs are highly gravitationally unstable, and departures from axial symmetry are pronounced. It results in strong gravitational torques that enhance accretion by removing angular momentum from the in-falling gas (Hosokawa et al. 2016). In addition, the turbulence driven by gravitational instability are found to generate strong magnetic fields, in a much more efficient way than magneto-rotational instability (Deng et al. 2019, 2020). These processes might be self-regulating, since any cut in accretion due to the centrifugal barrier will result in the accumulation of mass in the disc, which shall enhance fragmentation and turbulence. In this picture, the star will adjust on the fastest rotation velocity compatible with the $\varOmega \varGamma $-limit, and the curve of Fig. 6 would give the expected rotation velocity of SMSs as a function of the mass, not only the upper limit. Magnetic fields might play a role at all the stages of the SMBH formation process. In the early phase of the collapse of the mini-halo, magnetic fields of 0.1 nG are strong enough to avoid break-up (Pandey et al. 2019). Such fields are consistent with primordial fields whose flux was kept frozen during the formation of the halo. During the main accretion phase onto the star, magnetic coupling between the stellar surface and its winds could remove the 99% of the Keplerian angular momentum provided the magnetic field at the stellar surface is about 10 kG (Haemmerlé and Meynet 2019). Such fields are too large to be driven by a convective dynamo, but they are consistent with primordial origins and correspond to the upper limit of detected magnetic fields on massive stars, which are suspected to be fossil fields (Townsend et al. 2005; Rivinius et al. 2010; Grunhut et al. 2012).

3 Formation of Massive Black Hole Seeds

Here we cover the different flavours of direct collapse scenarios that have been proposed in the literature. The formation of massive BH seeds from metal-free Population III stars is covered in Sect. 1. In this section we will also briefly discuss the growth, by accretion, of black hole seeds formed from Pop III stars and from direct collapse routes in light of the observational constraints currently posed by observations of bright QSOs at $z > 5$.

3.1 The Rapid Rise of High-z QSOs and the Challenge for Light Black Hole Seed Models

The existence of extremely bright QSOs up to $z > 7$ (Fan et al. 2006; Wu et al. 2015; Bañados et al. 2018) is in tension with BH formation scenarios in which BH seeds start out light, of order a hundred solar masses as natural for the Pop III scenario (Sect. 1), and then grow gradually by Eddington-limited accretion. At $z > 7$, assuming the standard LCDM cosmology, simply the lookback time is too short for a light BH seed to grow to $10^{9}$ $\mathrm{M}_{\odot }$, the BH mass inferred by assuming that the source radiates at the Eddington limit (note that if accretion occurs at a fraction of Eddington, as suggested by other constraints for lower z QSOs, the timescale problem is further exacerbated). We briefly recall here the arguments that support the need for a massive BH seed in order to explain the rapid emergence of the bright high-z quasars. The time $t(M_{\mathit{BH}})$ required for a black hole of initial mass $m_{\mathit{seed}}$ to reach a mass $M_{\mathit{BH}}$, assuming Eddington-limited and continous accretion, is given by:

$$ t(M_{\mathit{BH}}) = \frac{t_{\mathit{Edd}}}{f_{\mathit{edd}}} \frac{\epsilon _{r}}{(1-\eta )} \ln \left ( \frac{M_{\mathit{BH}}}{m_{\mathit{seed}}}\right ), $$

(18)

where $t_{\mathit{Edd}} \equiv c \sigma _{T}/(4 \pi G \mu m_{p})$ is the Eddington time ($\sim 0.45$ Gyr for a pure hydrogen gas, with $\mu =1$), $f_{\mathit{edd}}$ expresses at which fraction of the Eddington limit the black hole is accreting, and $\epsilon _{r}$ and $\eta $ are, respectively, the radiative efficiency and accretion efficiency.^{Footnote 1} Assuming a radiatively-efficient accretion event, we assume $\epsilon _{r} = \eta = 0.1$, a typical average value for Shakura-Sunyaev thin disks (Shakura and Sunyaev 1973). Adopting a more realistic molecular weight per electron for a plasma at zero metallicity with cosmic abundance of hydrogen ($X = 0.75$) and helium ($Y = 0.25$), $\mu = 1/(1 - Y/2) = 1.14$, the Eddington time lowers to $t_{\mathit{Edd}} \sim 0.39$ Gyr. Note that the precise value of the metallicity is marginal in this calculation, as metallicity has only a minor effect on the value of the molecular weight (e.g., for a gas at solar metallicity, $\mu =1.18$ instead of the value $\mu =1.14$ assumed here). The mass of the supermassive black holes powering the most luminous high-z quasars is typically of the order of $M_{\mathit{BH}} = 10^{9}~\mathrm{M}_{\odot }$, so that this is the value we assume for the target mass. Note that this is a conservative choice as there is at least one known high-z QSO with black hole mass of ${\sim} 10^{10}~\mbox{M}_{\odot }$, see Wu et al. (2015). Further assuming that the seed black hole is able to accrete continuously at the Eddington limit ($f_{\mathit{edd}} = 1$), the timescale necessary to reach the target mass is $t_{(M_{\mathit{BH}})} = 0.4$ Gyr for a seed of $10^{5}~\mbox{M}_{\odot }$, while is $t_{(M_{\mathit{BH}})} \sim 0.7$ Gyr for a black holes starting from $10^{2}~\mbox{M}_{\odot }$, the average value for light seeds produced by Pop III stars (see next paragraph and Sect. 2). In this latter case the growth timescale is comparable to the age of the universe at $z = 7$ (assuming the Planck cosmology of Ade et al. 2015).

There are two alternative solutions, which are being extensively studied since a few years. In the first one, the light BH seed is allowed to accrete above the Eddington limit, continuously or episodically. Pop III remnants can form black hole seeds with masses up to ${\sim} 1000$ $\mathrm{M}_{\odot }$ (see Sect. 1). The environments where Pop III BH seeds may form at $z \sim 15\mbox{--}30$ have been extensively studied with numerical simulations, which agree on the fact that such seeds grow too slow, at Sub-Eddington rates, as the gas in their host mini-halo is efficiently photoionized, and eventually expelled, owing to radiative feedback from the massive stellar progenitor (eg., Johnson and Bromm 2007, Wise et al. 2008). In particular, primordial stars in the mass range $140\mbox{--}260~\mbox{M}_{\odot }$ explode as pair-instability supernovae (Heger et al. 2003), liberating enough energy to effectively empty the mini-halos of gas. Lower-mass Pop III stars would still damp energy, having a significant impact on the ambient medium if they form in clusters, as it is likely (Greif 2015), owing to the shallow potential wells of mini-halos. X-ray radiative feedback also suppresses further fueling of gas, leading effectively to accretion rates as small as ${\sim} 1\%$ of the Eddington rate, and thus stifling the growth of the BH seed well below the expectations from the Eddington-limited accretion model considered above (Alvarez et al. 2009; Jeon et al. 2012).

Only later, when star formation has led to metal enrichment, increasing the cooling rate, and the original host halo has grown significantly in mass to allow atomic cooling via Ly-$\alpha $ radiation, accretion can in principle restart (see also the recent review by Inayoshi et al. 2019).

Super-Eddington accretion onto light seeds could then be achieved, in principle, in radiatively inefficient accretion disks or in accreting envelopes emitting highly anisotropically (see Mayer and Bonoli 2019 for a review, and Inayoshi et al. 2019, Takeo et al. 2018). Several studies, both at the level of radiation hydrodynamics and MHD simulations of various accretion flow configurations (e.g. Sadowski et al. 2013), and at the level of larger scale models at nuclear (proto) galactic scales with parametrized analytical accretion models, such as the SLIM disk model, have been developed in the last decades. Alternatively, the formation of a much heavier BH seed, with mass ${>} 10^{4}~\mbox{M}_{\odot }$ can be invoked, which could then grow in the required time to billion solar masses in an Eddington-limited regime. This second route is what we will discuss thoroughly in the remainder of this section, and goes by the name of direct collapse. Direct collapse is a general scenario rather than a specific model. There are indeed various models proposed to generate a massive BH seed without starting from a conventional stellar progenitor, as recently reviewed in detail by Woods et al. (2019). Two of the models examined in the literature are covered in the next subsection.

3.2 Direct Collapse Scenarios for the Origin of Massive BH Seeds

In direct collapse scenarios the initial BH is not resulting from the collapse of an ordinary star. Note that, at high redshift ($z>20$), for ordinary stars we mean Population III stars as described in the first section of this review. Population III stars would produce a light BH seed with mass in the range from a few tens to of order thousand solar masses, according to the mass distribution of such early population of metal-free stars. In direct collapse scenarios the BH seeds that arise have a mass of at least $10^{4}$ $\mathrm{M}_{\odot }$, but can be even as large as $10^{8}$ $\mathrm{M}_{\odot }$ in the most extreme models including rotation (Sect. 2.2) or through dark collapse (Mayer and Bonoli 2019). The formation of a SMS is usually postulated for the precursor stage, which then collapses into a massive BH seed, by the GR radial instability, or because the SMS progenitor can never achieve a global hydrostatic equilibrium (see Sect. 2.1.3).

3.2.1 A Crucial Aspect: Angular Momentum Transport in Protogalaxies

The first stage in the direct collapse scenarios involves gas skipping conventional star formation and reaching, instead, extremely high densities, collecting a gravitationally bound mass large enough to generate a supermassive precursor object. Note that we will assume this all happens in the galactic nucleus since QSOs are associated to galactic nuclei, but most of our considerations are not necessarily restricted to the nuclear region only. In order to generate a supermassive precursor, irrespective on whether or not the object will remain in a protostellar-like regime before collapsing, or will shine, even briefly, as an SMS, enormous quantities of interstellar gas have to be delivered to the galactic nucleus from galactic scales. This gas then has to become gravitationally bound and produce the precursor. These steps, necessary for the precursor stage, are a crucial aspect of direct collapse models and, while various propositions have been made, the jury is still on what is the actual mechanism that prevails, if any.

If there is general consensus on one aspect that is on the broad scenario for how angular momentum can be lost in protogalaxies. This is believed to happen primarily via gravitational torques in primordial gas-rich galaxies (e.g. Begelman et al. 2006, Lodato and Natarajan 2006), perhaps boosted by violent phenomena such as galaxy mergers (Mayer et al. 2010, 2015). In order for such torques to be effective at removing angular momentum from gas the galactic disks, and in particular their nuclear regions, need to be in a marginally self-gravitating state. This corresponds to a regime in which the Toomre Q parameter (Toomre 1964), which measures the susceptibility of the disk to become unstable to its own self-gravity, must hover just above unity. In an entirely gaseous disk the Toomre parameter is defined as $Q = c_{s} \kappa /\pi G \varSigma $, where $c_{s}$ is the sound speed, $\kappa $ is the epicyclic frequency of gas motion, $\varSigma $ is the gas surface mass density, and $G$ is the gravitational constant. The definition is strictly local, although it is customary to use it also globally or expressing it using average properties in the disk. If Q drops below unity in most of the disk, gas will fragment copiously, producing substructure (clouds, and then stars from clouds possibly), thus interrupting the large scale global torquing action of spiral density waves by breaking their coherence. If, by heating or mass loss, it increases comfortably above unity ($Q > 2$) the disk will become gravitationally stable, and thus not capable anymore to transfer angular momentum and re-shuffle mass. If $Q$ remains low enough to allow self-gravity to excite non-axisymmetric structures, such as bars and spiral arms, efficient angular momentum transport can occur as gravitational torques by such structures behave as an effective viscous drag acting on the gas flow. Numerical simulations of protogalaxies have indeed shown that gas inflow rates are triggered by non-axisymmetric instabilities, such as spiral arms (Latif et al. 2013a) and bars-in-bars instabilities (Shlosman 2011; Choi et al. 2013). Examples are shown in Fig. 7 and 8.

Neglecting gas accretion, the stability of a gas-dominated protogalactic disk will be determined by the two conditions valid for any self-gravitating gas disk. Namely, its surface density must be low enough to maintain the Toomre Q above unity, and the cooling time has to be longer than the local orbital time (Gammie 2001). For the latter condition, to so-called Gammie criterion, simulations using improved numerical resolution have demonstrated convergence as a function of resolution after a decade of discordant results (Deng et al. 2017). If the cooling time drops below the local orbital time the Toomre Q will decrease and eventually drop below unity, entering the fragmentation regime.

Models of direct collapse have thus focused on ways to avoid rapid cooling of the protogalactic disk in order to maintain sustained gas inflows as opposed to fragmentation. At sufficiently high redshift ($z > 15\mbox{--}20$) gas in typical dark matter halos was still metal-free (with the exception of rare high density peaks), and radiative cooling was occurring either via molecular lines, predominantly via roto-vibrational transitions of the $H_{2}$ molecule, or, in sufficiently massive halos ($M_{\mathit{vir}} >10^{7}~\mbox{M}_{ \odot }$), via atomic hydrogen line cooling. If $H_{2}$ cooling is suppressed, the protogalactic disk would not cool below a temperature of ${\sim} 10^{4}$ K, thus evolving isothermally and remaining stable to fragmentation, as found in the semi-analytical model of Lodato and Natarajan (2006). Achieving suppression of molecular cooling has thus become the main objective in direct collapse models.

3.2.2 Routes to Direct Collapse: Metal-Free Atomic Cooling Halos and Mergers of Most Massive Metal-Enriched Primordial Galaxies

In the last couple of years the community has made progress in studying both the conventional route to direct collapse, which involves gas inflows in metal-free atomic cooling halos (e.g. Latif et al. 2013a, Regan and Haehnelt 2009, Regan et al. 2017) and other scenarios, such as the merger-driven model (Mayer et al. 2010; Bonoli et al. 2014; Mayer and Bonoli 2019), or models whereby colliding streams in proto-halos at very high-z (Hirano et al. 2017) or streaming velocities (Schauer et al. 2017a) play a role in providing favourable conditions.

The most conventional route to suppress $H_{2}$ cooling has been to invoke nearby sources of Lyman-Werner photons, which can efficiently dissociate $H_{2}$. This could happen by invoking a proximity condition, as a sufficiently nearby star forming (proto)galaxy could be responsible for a high dissociating flux. The idea was proposed originally by Dijkstra et al. (2008), and explored first assuming a constant local dissociating Lyman-Werner background, to find out the required level in order to accomplish $H_{2}$ dissociation (e.g. Latif et al. 2013a), and, lately, computing self-consistently the spatially and temporally dependent dissociating flux from sources in galaxies forming within hydrodynamical cosmological simulations of the early Universe before the reionization epoch (Regan et al. 2017, 2019; Wise et al. 2019). A large body of theoretical and numerical work has led to the notion that the required Lyman-Werbner flux is roughly 1000 times higher than the reference intensity value $J_{21} = 1 \times 10^{-21}$ erg s⁻¹ cm⁻² Hz⁻¹ sr⁻¹ (see review by Latif 2019), orders of magnitude above the expected mean background flux value (e.g. Ahn et al. 2009).

Current state-of-the-art simulations, such as Renaissance (Wise et al. 2019, see Fig. 9), showed that the mechanism can be successful in very rare objects forming relatively late, at $z < 20$, as it requires that, in addition to the proximity requirement, on one hand, sufficient metal-pollution to power gas cooling and intense star formation in the neighboring galaxy, and, on the other end, that the target system is still metal-free by that time. In the Renaissance cosmological volume, nearly 40 Mpc on a side, out of which subvolumes encompassing high density regions were re-sampled at higher resolution, a few tens of candidate systems that remain star-free and metal-free by the onset of the atomic cooling halo phase were found (Regan et al. 2019). Most importantly, the Renaissance runs also showed that dynamical heating by mergers and accretion is contributing significantly to maintain a warm nearly isothermal core in the protogalaxy, hence relaxing the requirement on the critical Lyman-Werner flux. The few tens of atomic cooling halos that remain metal-free and star-free by the end of the simulation have indeed been exposed to a mean Lyman-Werner flux just comparable to $J_{21}$, yet the simulations are not conclusive as they lack the resolution to exclude fragmentation of the protogalactic cores into clusters of Pop III stars (Regan et al. 2019). In addition, even if fragmentation would not be an issue, the formation of a direct collapse BH seed would require sustained nuclear accretion rates at ${>} 0.1$ $\mathrm{M}_{\odot }$ yr⁻¹ in the protogalactic nucleus to produce an SMS (see Sect. 2), or even a quasi-star (Begelman 2010), for timescales ${>} 10^{6}$ yr (namely at least longer than the expected lifetime of the SMS or quasi-star). In at least two of the highest resolution re-simulations of selected rare high density peaks in the Renaissance volume, such high inflow rate conditions seem indeed to be fulfilled towards the end of the simulation, almost 1 Myr after the beginning of gas collapse in the halo (Wise et al. 2019). However, gas accumulation occurs on separate gravitationally bound clumps that, by the same time, achieve a mass only an order of magnitude higher than that of Pop III stars, between 1000 and $10^{4}$ $\mathrm{M}_{\odot }$. With such the latter mass range for the precursors the resulting massive BH seed would still be too light to explain the most massive of the high-z QSOs ($M_{\mathit{BH}} \sim 10^{10}~\mbox{M}_{\odot }$) by Eddington limited accretion.

Mergers can also temporarily enhance gas inflow rates by removing angular momentum via strong tidal torques and gas shocking, these being considerably more intense than internal torques due to disk instabilities. The effect of dynamical heating brings us to the other proposed mechanism, namely heating by gas accretion and shocking induced mergers of much more massive and more mature galaxies at somewhat later epochs, $z \sim 8\mbox{--}10$. At this stage the first massive galaxies residing in halos with $M_{\mathit{vir}} \sim 10^{12}$ $\mathrm{M}_{\odot }$ do appear (Mayer et al. 2010). This mass scale is interesting since it is consistent with the virial mass expected for the hosts of the high-z QSOs given their clustering amplitude and low abundance (Volonteri et al. 2008).

In this second scenario, since it occurs much later, gas is already metal-enriched, yet simulations have shown that cooling is still inefficient as compressional heating and shocks in equal mass mergers are sufficient to counteract cooling by maintaining the temperature of the pc-scale disky core emerging in the merger remnant at 5000–8000 K, allowing only sporadic fragmentation at its outskirts (Mayer et al. 2015, see Fig. 8). Most importantly, in this case radial gas inflows, and thus gas accretion rates onto the core, occur at the phenomenal rate in the range 1000–$10^{4}$ $\mathrm{M}_{\odot }$ yr⁻¹ for nearly $10^{5}$ yr after the merger (Fig. 10), allowing the formation of an ultra-compact supermassive rotating gas core that thus meets naturally the conditions to become an SMS (see Sect. 2.1.3). This allows the central core to reach a mass of ${\sim} 10^{9}~\mbox{M}_{\odot }$ in less than $10^{5}$ yr. The central core is fast rotating and gravitationally bound, and with such a high mass it can form, in principle, a supermassive BH seed which would have no problem in reaching the mass of the brightest QSOs in less than hundred million years even with accretion sustained at a fraction of Eddington (Bonoli et al. 2014; Mayer and Bonoli 2019).

The reason why inflow rates are so much higher in the merger-driven collapse is partially because major mergers produce the strongest tidal torques and shocks, as they give rise to the largest displacement of mass, and partially because the halos involved in this scenario are, by construction, much more massive than atomic cooling halos. Indeed, to zeroth order, neglecting residual angular momentum in the flow, the radial gas flow will displace mass with amplitude $\dot{M} \sim V_{\mathit{vir}}^{3}/G \sim M_{\mathit{vir}}$ (where $M_{\mathit{vir}}$ and $V_{\mathit{vir}}$ are the virial mass and virial velocity of the host halo, respectively), with $M_{\mathit{vir}}$ increasing by more than a factor of 1000 between atomic cooling halos ($M_{\mathit{vir}} \sim 10^{9\mbox{--}10}~\mbox{M}_{ \odot }$) and high-sigma peaks at $z \sim 8\mbox{--}10$ possessing $M_{\mathit{vir}} \sim 10^{12}~\mbox{M}_{\odot }$ (see Bonoli et al. 2014, Mayer and Bonoli 2019 for details). New multi-scale merger simulations of high density peaks reaching parsec resolution with fully cosmological initial conditions (from the previously published MassiveBlack runs of Feng and Soria 2011) appear to confirm the existence of such prominent gas inflows (Capelo, Mayer et al., in preparation). With such extreme conditions it is also possible that the SMS stage is skipped, and rather a BH seed nearly as massive as the entire supermassive gas core could form either because it becomes compact enough to collapse due to the General Relativistic radial instability (Mayer and Bonoli 2019), or because it can never find an hydrostatic equilibrium configuration (see Sect. 2.1.3), a route refereed to as dark collapse. In this latter case an ultra-massive BH seed would arise, as massive as nearly the entire precursor core of ${\sim} 10^{9}~\mbox{M}_{\odot }$, since numerical relativity simulations of rotating polytropic SMS/clouds reaching a critical compactness show that the radial GR instability triggers a global collapse of about half of the total mass into a central black hole (e.g. Shibata and Shapiro 2002), or even into a binary system of two black holes if the massive precursor becomes bar unstable and fragments (Reisswig et al. 2013).

Observationally, both the conventional direct collapse scenario based on $H_{2}$ dissociation in metal-free atomic cooling halos and the merger-driven scenario gives rise to a number of direct collapse BHs that, while low in absolute sense, it is still high enough to accomodate the abundance of high-z QSOs (Mayer and Bonoli 2019; Latif 2019). However, a sensible quantitative comparison with observations will have to take into account the detailed mechanism of BH seed formation from the precursor, eg whether an SMS, a quasi-star, or neither of the two, will form prior to collapse (see Woods et al. 2019), and the duty-cycle of the resulting AGN.

4 Reionization After Planck and Before JWST

The transformation of cold neutral intergalactic hydrogen into a highly ionized warm plasma marks the end of the dark ages and the beginning of the age of galaxies. In popular cosmological scenarios, massive stars within early protogalaxies, aided perhaps by a population of accreting seed black holes, generated the UV and X-ray radiation that reheated and reionized the Universe. Observations of resonant absorption in the spectra of distant quasars show that hydrogen reionization was still ongoing at $z\sim 6$ and fully completed by redshift 5.5 (Fan et al. 2006; Becker et al. 2015). An early onset of reionization appears to be disfavored by the final, full-mission Planck CMB anisotropy analysis, which yields an integrated Thomson scattering optical depth of $\tau _{\mathrm{es}}=0.054\pm 0.007$ (Planck Collaboration et al. 2018). And while the evolution of the ionization and thermal state of the $z\gtrsim 6$ Universe is being constrained by a number of direct probes, from the damping wing absorption profiles in the spectra of quasars (e.g., Bañados et al. 2017), through the luminosity function (LF) and clustering properties of Ly$\alpha $ emitting galaxies (Ouchi et al. 2010; Schenker et al. 2014), to the flux power spectrum of the Ly$\alpha $ forest (Oñorbe et al. 2017), many pivotal aspects of this process remain highly uncertain.

Over the last few years, HST deep optical and NIR imaging data have led to the discovery and study of some of the earliest-known galaxies at redshifts $z=\mbox{7--}10$, corresponding to a period when the Universe was only ${\gtrsim} 500$ Myr old (e.g., Finkelstein et al. 2015; Livermore et al. 2017; Oesch et al. 2017; see Fig. 11). The faint-end slope of the rest-frame UV LF of these high-redshift sources has been measured to be very steep ($\alpha \approx -2$), such that the integrated UV luminosity density is contributed equally by each decade in galaxy luminosity, and therefore may depend on whatever physics regulates star formation in the faintest dwarfs (see, e.g., Bouwens et al. 2012; Atek et al. 2015; Ishigaki et al. 2017, and references therein). The importance of star-forming galaxies for reionization further depends on the Lyman-continuum (LyC) photon yield per unit UV luminosity and on the fraction of these photons that can escape into the IGM (Madau et al. 1999; Robertson et al. 2010). Galaxy-dominated scenarios that satisfy many of the observational constraints can be constructed if one extrapolates the UV LF to sufficiently faint magnitudes ($M_{\mathrm{UV}} \sim -13$) assuming a time- and luminosity-averaged escape fraction of ∼15% at $z\gtrsim 6$ (e.g., Haardt and Madau 2012; Robertson et al. 2015; Bouwens et al. 2015; Madau 2017). The presence of moderate- and low-luminosity AGNs at early times can change inferences on the role of galaxies in reionization (e.g., Madau and Haardt 2015; Giallongo et al. 2019), and the differing effective temperature of the radiation between stars and AGN can impact the thermal history of the reionized IGM (D’Aloisio et al. 2017). At low metallicity, stellar populations in early galaxies may be characterized by an increased LyC photon production from binary stars compared to the present-day Universe (Stanway et al. 2016). The enhanced LyC photon yield may boost the equivalent width of nebular emission lines ([O III], H$\alpha $, H$\beta $) (e.g., Smit et al. 2014), which are redshifted into the rest-frame wavelength range relevant for the James Webb Space Telescope (JWST) NIRSpec instrument. The impact of nebular emission on the spectra of galaxies is also regulated by the escape fraction, and forthcoming measurements of the rest-frame UV continuum slope with the equivalent width of the H$\beta $ emission line may allow the identification of galaxies with extreme LyC leakage up to redshift 9 (Zackrisson et al. 2017).

Figures 12 and 13 depict some of the available observational probes of the epoch of reionization. These include observations of the Gunn-Peterson absorption troughs indicating that the Universe was mostly reionized by $z\sim 6$ (Fan et al. 2006; Becker et al. 2015), the evolution of the cosmic SFR density at high redshift (Oesch et al. 2017), and the evolution of the IGM mean temperature at $z\lesssim 5.5$ (Walther et al. 2019). In addition, the sensitivity of Ly$\alpha $ emission to intervening neutral gas is also being used to explain the dearth of Ly$\alpha $ emitters (LAEs) observed at $z>6.5$ (Ouchi et al. 2010; Schenker et al. 2014). Recent Planck CMB anisotropy data together with measurements of the kinetic Sunyaev-Zel’dovich effect by the Atacama Cosmology and the South Pole Telescopes constrain the redshift where the volume-averaged neutral fraction drops below 50% to lie between $z=7.3$ and 10.5 ($2\sigma $), and yield an upper limit to the width of the reionization period of $\Delta z <2.8$ (Planck Collaboration et al. 2016b).

4.1 The Reionization Equation

Cosmic reionization involves a complex interplay between the abundance, clustering, spectrum, and LyC radiation leakage of photoionizing sources, and the density, clumpiness, and temperature of intergalactic gas. Detailed simulations of reionization must be informed by insight from semi-empirical modeling and theoretical calculations that provide a proper accounting of the volume-averaged production and absorption of ionizing radiation in an expanding medium. Below, we give an example of how theory informs computation.

The general idea of a gradual reionization process driven by a steadily increasing UV photon production rate can be cast into a simple quantitative framework by integrating the “reionization equation” (Madau 2017)

$$ \frac{d\langle x_{\mathrm{HII}}\rangle }{dt} = \frac{\langle \dot{n}_{\gamma } \rangle }{\langle n_{\mathrm{H}}\rangle (1+\langle \kappa ^{\mathrm{LLS}}_{ \nu _{L}}\rangle /\langle \kappa ^{\mathrm{IGM}}_{\nu _{L}}\rangle )} -\frac{ \langle x_{\mathrm{HII}}\rangle }{\bar{t}_{\mathrm{rec}}}. $$

(19)

for the time evolution of the volume-averaged hydrogen ionized fraction $x_{\mathrm{HII}}$. Here, $\langle {\dot{n}}_{\gamma } \rangle $ is the emission rate into the IGM of ionizing photons per unit proper volume, $\langle n_{\mathrm{H}}\rangle $ is the cosmological mean proper density of hydrogen, $\langle \kappa ^{\mathrm{LLS}}\rangle ^{-1}$ and $\langle \kappa ^{\mathrm{IGM}}\rangle ^{-1}$ are the photon proper mean free path at the hydrogen Lyman edge caused by the Lyman-limit systems (LLSs) and the diffuse IGM, respectively, and $\bar{t}_{\mathrm{rec}}$ is an effective recombination timescale in a clumpy IGM.^{Footnote 2} The above equation assumes a photon mean free path that is much smaller than the horizon size (so that the mean specific intensity relaxes to the source function), and an early IGM that is organized in three main phases – a uniform ionized medium, a uniform neutral medium, and the LLSs (Madau 2017).

It is this ODE that statistically describes the transition from a neutral universe to a fully ionized one, turning reionization into a photon-counting exercise in which the growth rate of H $\scriptstyle\mathrm {II}$regions is equal to the rate at which ionizing photons are produced minus the rate at which they are consumed by radiative recombinations in the IGM. Before reionization, at $z>6$, UV photons carve out cosmological H $\scriptstyle\mathrm {II}$regions in the uniform component that expand in an otherwise largely neutral phase. At $z < 6$, however, the diffuse IGM is observed to be highly ionized, with only a small residual amount of neutral hydrogen set by the balance between radiative recombinations and photoionizations from a nearly uniform UV radiation background, and provides negligibly small H $\scriptstyle\mathrm {I}$photoelectric absorption. The continuum opacity is instead dominated by the optically thick (to ionizing radiation) LLSs, high density regions that trace non-linear and collapsed structures, occupy a small portion of the volume, and are able to keep a significant fraction of their hydrogen in neutral form (e.g. Miralda-Escudé et al. 2000; Gnedin and Fan 2006; Furlanetto and Mesinger 2009; Haardt and Madau 2012). The integration of Equation (19) therefore provides a link between the pre-overlap and post-overlap phases of the reionization process.

Figure 14 shows the reionization history obtained by numerically integrating Equation (19) assuming a constant emission rate of ionizing photons per hydrogen atom, $\langle \dot{n}_{\gamma }\rangle /\langle n_{\mathrm{H}}\rangle =3$ phot Gyr⁻¹. The theoretical curve is consistent with a number of observational constraints on the ionization state of the $z>5$ universe, from the redshift-dependent prevalence of LAEs in narrow band surveys at $z=$7–8 (Schenker et al. 2014), to the damping wing absorption profiles measured in the spectra of $z=6.3$ (Schroeder et al. 2013) and $z=7.1$ quasars (Greig et al. 2017). While the pre-overlap stages extend over a considerable range of redshift, the phase of overlap, indicated by the sudden drop in the neutral gas fraction at $z\simeq 6$, is clearly defined even in the presence of the LLSs: $\langle x_{\mathrm{HI}}\rangle $ decreases by more than 2 orders of magnitude over a fraction of the then Hubble time. Such a dramatic transition marks the epoch when the photon mean free path becomes determined by the LLSs rather than by the typical size of H $\scriptstyle\mathrm {II}$regions. Note how current state-of-the-art radiation-hydrodynamic simulations of reionization produce a poor fit to the observations of the Gunn-Peterson optical depth in the spectra of Sloan Digital Sky Survey (SDSS) quasars at $5< z<61$ (Fan et al. 2006), as well as to estimates of the ionized fraction at $z=5$ and 6 based on a combination of hydrodynamical simulations with measurements of the Ly$\alpha $ forest opacity (Bolton and Haehnelt 2007). The disagreement is an artifact of current reionization simulations underestimating the amount of UV absorption in the post-reionization Universe, as LLSs remain effectively unresolved.

5 Concluding Remarks

We have reviewed our current understanding of early structure formation, from first stars to the first black holes emerging at high redshift, and have addressed the impact of early star forming galaxies and early accreting massive black holes on the reionization of the Universe. We have highlighted the importance of radiative feedback in determining various key aspects of first objects, such as the masses of first stars and the growth rate of the black holes arising from them. Radiative feedback, in particular dissociation of molecular hydrogen by the Lyman-Werner radiation produced by early star forming galaxies, plays a key role also in models for massive black hole seed formation ($M_{\mathit{BH}} >10^{4}~\mbox{M}_{\odot }$ by direct collapse in metal-free atomic cooling halos. Likewise, thermodynamical feedback from accretion and mergers could provide the required heating to avoid fragmentation in the most rapidly growing atomic cooling halos. Alternative models for direct collapse, such as from major mergers of the first metal-enriched massive galaxies at $z \sim 8\mbox{--}10$, actually rely exclusively on thermodynamical feedback from shocks and compressional heating to stifle widespread fragmentation, and can give rise to much larger black hole seeds, of order a billion solar mass. In direct collapse models, a paramount role is played by the physics of their likely precursors, accreting supermassive stars (SMS). We have thus covered in detail the latest developments in modeling SMSs, including rotation and the different regimes arising with accretion rates varying by orders of magnitude, according to either the atomic cooling halo scenario and the galaxy merger-driven scenario. In doing so, we have reported on the possibility that collapse into a massive black hole seed, at the highest accretion rates, occurs without prior formation of a SMS, the so-called dark collapse route. The reionization of hydrogen during the first billion years of cosmic history is the last major phase transition of baryonic matter in the Universe and involves the early production, propagation, and absorption of LyC radiation. The full reionization of helium is believed to have occurred at a later time, when hard UV-emitting bright quasars and other AGN became sufficiently abundant. While it is generally agreed that star-forming galaxies and the first accreting seed black holes in their nuclei are the best candidates for providing the required ionizing power, there are still many uncertainties on the relative contributions of these sources as a function of epoch. The resolution of such uncertanties feels overdue and may soon be achieved by the large wavelength coverage, unique sensitivity, and spectroscopic and imaging capabilities of the JWST together with ongoing and future experiments aimed at measuring the redshifted 21-cm signal from neutral hydrogen during the epoch of first light.

Notes

The accretion efficiency $\eta $ directly depends on the spin of the black hole, and reaches the maximum value of $\eta \sim 0.42$ for maximally rotating Kerr black holes. The radiative efficiency $\epsilon _{r}$ depends both on the type of accretion and on the accretion efficiency: for radiatively efficient accretion events, one can assume $\epsilon _{r} = \eta $.
Photon losses by LLSs are also due to radiative recombinations. In analytical models it is standard practice, however, to include the effect of LLSs as a reduction in the source term through the finite mean free path of ionizing radiation. Three different quantities – the escape fraction, the gas clumping factor, and the mean free path – are then used to describe what are essentially radiative recombinations in the ISM, the IGM, and the LLSs. Numerical simulations of cosmic reionization show that such a separation into distinct regimes may indeed be reasonable (Kaurov and Gnedin 2015).

References

T. Abel, G.L. Bryan, M.L. Norman, The formation of the first star in the universe. Science 295, 93–98 (2002)
ADS Google Scholar
T. Abel, J.H. Wise, G.L. Bryan, The H II region of a primordial star. Astrophys. J. Lett. 659, 87–90 (2007)
ADS Google Scholar
P.A.R. Ade, Y. Akiba, A.E. Anthony, et al., A measurement of the cosmic microwave background B-mode polarization with POLARBEAR. Publ. Korean Astron. Soc. 30(2), 625–628 (2015)
ADS Google Scholar
K. Ahn, P.R. Shapiro, I.T. Iliev, et al., The inhomogeneous background of H2-dissociating radiation during cosmic reionization. Astrophys. J. 695, 1430–1445 (2009)
ADS Google Scholar
M.A. Alvarez, V. Bromm, P.R. Shapiro, The H II region of the first star. Astrophys. J. 639, 621–632 (2006)
ADS Google Scholar
M.A. Alvarez, J.H. Wise, T. Abel, Accretion onto the first stellar-mass black holes. Astrophys. J. Lett. 701, 133–137 (2009)
ADS Google Scholar
I. Appenzeller, R. Kippenhahn, General relativistic secular instability of supermassive stars. Astron. Astrophys. 11, 70 (1971)
ADS Google Scholar
H. Atek, J. Richard, M. Jauzac, et al., Are ultra-faint galaxies at $z = 6$–8 responsible for cosmic reionization? Combined constraints from the Hubble Frontier Fields clusters and parallels. Astrophys. J. 814, 69 (2015)
ADS Google Scholar
S.A. Balbus, J.F. Hawley, Instability, turbulence, and enhanced transport in accretion disks. Rev. Mod. Phys. 70, 1–53 (1998)
ADS Google Scholar
E. Bañados, B.P. Venemans, C. Mazzucchelli, et al., An 800 million solar mass black hole in a significantly neutral universe at redshift 7.5. ArXiv e-prints (2017)
E. Bañados, B.P. Venemans, C. Mazzucchelli, et al., An 800-million-solar-mass black hole in a significantly neutral Universe at a redshift of 7.5. Nature 553, 473–476 (2018)
ADS Google Scholar
R. Banerjee, K. Jedamzik, Are cluster magnetic fields primordial? Phys. Rev. Lett. 91(25), 251301 (2003)
ADS Google Scholar
R. Barnett, S.J. Warren, G.D. Becker, et al., Observations of the Lyman series forest towards the redshift 7.1 quasar ULAS J1120+0641. Astron. Astrophys. 601, 16 (2017)
Google Scholar
T.W. Baumgarte, S.L. Shapiro, Evolution of rotating supermassive stars to the onset of collapse. Astrophys. J. 526, 941–952 (1999a)
ADS Google Scholar
T.W. Baumgarte, S.L. Shapiro, Luminosity versus rotation in a supermassive star. Astrophys. J. 526, 937–940 (1999b)
ADS Google Scholar
G.D. Becker, J.S. Bolton, P. Madau, et al., Evidence of patchy hydrogen reionization from an extreme Ly$\alpha $ trough below redshift six. Mon. Not. R. Astron. Soc. 447, 3402–3419 (2015)
ADS Google Scholar
M.C. Begelman, Evolution of supermassive stars as a pathway to black hole formation. Mon. Not. R. Astron. Soc. 402, 673–681 (2010)
ADS Google Scholar
M.C. Begelman, M. Volonteri, M.J. Rees, Formation of supermassive black holes by direct collapse in pre-galactic haloes. Mon. Not. R. Astron. Soc. 370, 289–298 (2006)
ADS Google Scholar
R. Behrend, A. Maeder, Formation of massive stars by growing accretion rate. Astron. Astrophys. 373, 190–198 (2001)
ADS Google Scholar
L. Biermann, Über den Ursprung der Magnetfelder auf Sternen und im interstellaren Raum (miteinem Anhang von A. Schlüter). Z. Naturforsch. Teil A 5, 65 (1950)
ADS MathSciNet MATH Google Scholar
J. Binney, S. Tremaine, Galactic Dynamics (Princeton University Press, Princeton, 1987)
MATH Google Scholar
G.S. Bisnovatyi-Kogan, Y.B. Zel’dovich, I.D. Novikov, Evolution of supermassive stars stabilized by large-scale motions. Sov. Astron. 11, 419 (1967)
ADS Google Scholar
G.R. Blumenthal, S.M. Faber, R. Flores, et al., Contraction of dark matter galactic halos due to baryonic infall. Astrophys. J. 301, 27–34 (1986)
ADS Google Scholar
P. Bodenheimer, Angular momentum evolution of young stars and disks. Annu. Rev. Astron. Astrophys. 33, 199–238 (1995)
ADS Google Scholar
J.S. Bolton, M.G. Haehnelt, The observed ionization rate of the intergalactic medium and the ionizing emissivity at $z >= 5$: evidence for a photon-starved and extended epoch of reionization. Mon. Not. R. Astron. Soc. 382, 325–341 (2007)
ADS Google Scholar
S. Bonoli, L. Mayer, S. Callegari, Massive black hole seeds born via direct gas collapse in galaxy mergers: their properties, statistics and environment. Mon. Not. R. Astron. Soc. 437, 1576–1592 (2014)
ADS Google Scholar
R.J. Bouwens, G.D. Illingworth, P.A. Oesch, et al., Lower-luminosity galaxies could reionize the Universe: very steep faint-end slopes to the UV luminosity functions at $z >= 5$–8 from the HUDF09 WFC3/IR observations. Astrophys. J. Lett. 752, 5 (2012)
ADS Google Scholar
R.J. Bouwens, G.D. Illingworth, P.A. Oesch, et al., Reionization after Planck: the derived growth of the cosmic ionizing emissivity now matches the growth of the galaxy UV luminosity density. Astrophys. J. 811, 140 (2015)
ADS Google Scholar
S. Bovino, D.R.G. Schleicher, J. Schober, Turbulent magnetic field amplification from the smallest to the largest magnetic Prandtl numbers. New J. Phys. 15(1), 013055 (2013)
ADS Google Scholar
V. Bromm, R.B. Larson, The first stars. Annu. Rev. Astron. Astrophys. 42, 79–118 (2004)
ADS Google Scholar
V. Bromm, A. Loeb, Formation of the first supermassive black holes. Astrophys. J. 596, 34–46 (2003)
ADS Google Scholar
V. Bromm, P.S. Coppi, R.B. Larson, The formation of the first stars. I. The primordial star-forming cloud. Astrophys. J. 564, 23–51 (2002)
ADS Google Scholar
S.P. Butler, A.R. Lima, T.W. Baumgarte, et al., Maximally rotating supermassive stars at the onset of collapse: the perturbative effects of gas pressure, magnetic fields, dark matter, and dark energy. Mon. Not. R. Astron. Soc. 477, 3694–3710 (2018)
ADS Google Scholar
S. Chandrasekhar, The dynamical instability of gaseous masses approaching the Schwarzschild limit in general relativity. Astrophys. J. 140, 417 (1964)
ADS MathSciNet MATH Google Scholar
K.-J. Chen, A. Heger, S. Woosley, et al., The general relativistic instability supernova of a supermassive Population III star. Astrophys. J. 790, 162 (2014)
ADS Google Scholar
J.-H. Choi, I. Shlosman, M.C. Begelman, Supermassive black hole formation at high redshifts via direct collapse: physical processes in the early stage. Astrophys. J. 774, 149 (2013)
ADS Google Scholar
P.C. Clark, S.C.O. Glover, R.S. Klessen, The first stellar cluster. Astrophys. J. 672, 757–764 (2008)
ADS Google Scholar
P.C. Clark, S.C.O. Glover, R.S. Klessen, et al., Gravitational fragmentation in turbulent primordial gas and the initial mass function of Population III stars. Astrophys. J. 727, 110 (2011a)
ADS Google Scholar
P.C. Clark, S.C.O. Glover, R.J. Smith, et al., The formation and fragmentation of disks around primordial protostars. Science 331, 1040 (2011b)
ADS Google Scholar
B. Commerçon, P. Hennebelle, T. Henning, Collapse of massive magnetized dense cores using radiation magnetohydrodynamics: early fragmentation inhibition. Astrophys. J. Lett. 742, 9 (2011)
ADS Google Scholar
A. D’Aloisio, P.R. Upton Sanderbeck, M. McQuinn, et al., On the contribution of active galactic nuclei to the high-redshift metagalactic ionizing background. Mon. Not. R. Astron. Soc. 468, 4691–4701 (2017)
ADS Google Scholar
H. Deng, L. Mayer, F. Meru, Convergence of the critical cooling rate for protoplanetary disk fragmentation achieved: the key role of numerical dissipation of angular momentum. Astrophys. J. 847(1), 43 (2017)
ADS Google Scholar
H. Deng, L. Mayer, H. Latter, et al., Local simulations of MRI turbulence with meshless methods. Astrophys. J. Suppl. Ser. 241(2), 26 (2019)
ADS Google Scholar
H. Deng, L. Mayer, H. Latter, Global simulations of self-gravitating magnetized protoplanetary disks (2020). arXiv:2001.08693
K.A. Dennison, T.W. Baumgarte, S.L. Shapiro, Maximally Rotating Supermassive Stars at the Onset of Collapse: Effects of Gas Pressure (2019). arXiv:1906.04190
M. Dijkstra, Z. Haiman, A. Mesinger, et al., Fluctuations in the high-redshift Lyman-Werner background: close halo pairs as the origin of supermassive black holes. Mon. Not. R. Astron. Soc. 391, 1961–1972 (2008)
ADS Google Scholar
G. Dopcke, S.C.O. Glover, P.C. Clark, et al., On the initial mass function of low-metallicity stars: the importance of dust cooling. Astrophys. J. 766, 103 (2013)
ADS Google Scholar
A. Doussot, H. Trac, R. Cen, SCORCH. II. Radiation-Hydrodynamic simulations of reionization with varying radiation escape fractions. ArXiv e-prints (2017)
X. Fan, M.A. Strauss, R.H. Becker, et al., Constraining the evolution of the ionizing background and the epoch of reionization with $z\sim 6$ quasars. II. A sample of 19 quasars. Astron. J. 132, 117–136 (2006)
ADS Google Scholar
C. Federrath, S. Sur, D.R.G. Schleicher, et al., A new jeans resolution criterion for (M)HD simulations of self-gravitating gas: application to magnetic field amplification by gravity-driven turbulence. Astrophys. J. 731, 62 (2011)
ADS Google Scholar
C. Federrath, J. Schober, S. Bovino, et al., The turbulent dynamo in highly compressible supersonic plasmas. Astrophys. J. Lett. 797, 19 (2014)
ADS Google Scholar
H. Feng, R. Soria, Ultraluminous X-ray sources in the Chandra and XMM-Newton era. Nature 55, 166–183 (2011)
Google Scholar
A. Fialkov, R. Barkana, D. Tseliakhovich, et al., Impact of the relative motion between the dark matter and baryons on the first stars: semi-analytical modelling. Mon. Not. R. Astron. Soc. 424, 1335–1345 (2012)
ADS Google Scholar
S.L. Finkelstein, R.E. Ryan Jr., C. Papovich, et al., The evolution of the galaxy rest-frame ultraviolet luminosity function over the first two billion years. Astrophys. J. 810, 71 (2015)
ADS Google Scholar
W.A. Fowler, The stability of supermassive stars. Astrophys. J. 144, 180 (1966)
ADS Google Scholar
K. Freese, P. Bodenheimer, D. Spolyar, et al., Stellar structure of dark stars: a first phase of stellar evolution resulting from dark matter annihilation. Astrophys. J. Lett. 685, 101 (2008)
ADS Google Scholar
K. Freese, P. Bodenheimer, P. Gondolo, et al., Dark stars: a new study of the first stars in the Universe. New J. Phys. 11(10), 105014 (2009)
ADS Google Scholar
K.J. Fricke, Dynamical phases of supermassive stars. Astrophys. J. 183, 941–958 (1973)
ADS Google Scholar
G.M. Fuller, S.E. Woosley, T.A. Weaver, The evolution of radiation-dominated stars. I—nonrotating supermassive stars. Astrophys. J. 307, 675–686 (1986)
ADS Google Scholar
S.R. Furlanetto, A. Mesinger, The ionizing background at the end of reionization. Mon. Not. R. Astron. Soc. 394, 1667–1673 (2009)
ADS Google Scholar
S. Gallerani, A. Ferrara, X. Fan, et al., Glimpsing through the high-redshift neutral hydrogen fog. Mon. Not. R. Astron. Soc. 386, 359–369 (2008)
ADS Google Scholar
C.F. Gammie, Nonlinear outcome of gravitational instability in cooling, gaseous disks. Astrophys. J. 553, 174–183 (2001)
ADS Google Scholar
E. Giallongo, A. Grazian, F. Fiore, et al., Space densities and emissivities of active galactic nuclei at $z>4$. Astrophys. J. 884(1), 19 (2019)
ADS Google Scholar
P. Girichidis, C. Federrath, R. Banerjee, et al., Importance of the initial conditions for star formation—I. Cloud evolution and morphology. Mon. Not. R. Astron. Soc. 413, 2741–2759 (2011)
ADS Google Scholar
P. Girichidis, C. Federrath, R. Allison, et al., Importance of the initial conditions for star formation—III. Statistical properties of embedded protostellar clusters. Mon. Not. R. Astron. Soc. 420, 3264–3280 (2012b)
ADS Google Scholar
P. Girichidis, C. Federrath, R. Banerjee, et al., Importance of the initial conditions for star formation—II. Fragmentation-induced starvation and accretion shielding. Mon. Not. R. Astron. Soc. 420, 613–626 (2012a)
ADS Google Scholar
S. Glover, The formation of the first stars in the Universe. Space Sci. Rev. 117, 445–508 (2005)
ADS Google Scholar
S. Glover, The first stars, in The First Galaxies, ed. by T. Wiklind, B. Mobasher, V. Bromm Astrophys. Space Sci. Library, vol. 396, 2013, p. 103
Google Scholar
N.Y. Gnedin, X. Fan, Cosmic reionization redux. Astrophys. J. 648, 1–6 (2006)
ADS Google Scholar
D. Grasso, H.R. Rubinstein, Magnetic fields in the early Universe. Phys. Rep. 348, 163–266 (2001)
ADS Google Scholar
T.H. Greif, The numerical frontier of the high-redshift Universe. Comput. Astrophys. Cosmol. 2, 3 (2015)
ADS Google Scholar
T.H. Greif, J.L. Johnson, R.S. Klessen, et al., The first galaxies: assembly, cooling and the onset of turbulence. Mon. Not. R. Astron. Soc. 387, 1021–1036 (2008)
ADS Google Scholar
T.H. Greif, S.D.M. White, R.S. Klessen, et al., The delay of Population III star formation by supersonic streaming velocities. Astrophys. J. 736, 147 (2011)
ADS Google Scholar
T.H. Greif, V. Bromm, P.C. Clark, et al., Formation and evolution of primordial protostellar systems. Mon. Not. R. Astron. Soc. 424, 399–415 (2012)
ADS Google Scholar
B. Greig, A. Mesinger, Z. Haiman, et al., Are we witnessing the epoch of reionisation at $z=7.1$ from the spectrum of J1120+0641? Mon. Not. R. Astron. Soc. 466, 4239–4249 (2017)
ADS Google Scholar
J.H. Grunhut, T. Rivinius, G.A. Wade, et al., HR 5907: discovery of the most rapidly rotating magnetic early B-type star by the MiMeS collaboration. Mon. Not. R. Astron. Soc. 419, 1610–1627 (2012)
ADS Google Scholar
F. Haardt, P. Madau, Radiative transfer in a clumpy universe. IV. New synthesis models of the cosmic UV/X-ray background. Astrophys. J. 746, 125 (2012)
ADS Google Scholar
L. Haemmerlé, G. Meynet, Magnetic braking of supermassive stars through winds. Astron. Astrophys. 623, 7 (2019)
ADS Google Scholar
L. Haemmerlé, P. Eggenberger, G. Meynet, et al., Massive star formation by accretion. I. Disc accretion. Astron. Astrophys. 585, 65 (2016)
ADS Google Scholar
L. Haemmerlé, P. Eggenberger, G. Meynet, et al., Massive star formation by accretion. II. Rotation: how to circumvent the angular momentum barrier? Astron. Astrophys. 602, 17 (2017)
Google Scholar
L. Haemmerlé, T.E. Woods, R.S. Klessen, et al., On the rotation of supermassive stars. Astrophys. J. Lett. 853, 3 (2018a)
ADS Google Scholar
L. Haemmerlé, T.E. Woods, R.S. Klessen, et al., The evolution of supermassive Population III stars. Mon. Not. R. Astron. Soc. 474, 2757–2773 (2018b)
ADS Google Scholar
L. Haemmerlé, G. Meynet, L. Mayer, et al., Maximally accreting supermassive stars: a fundamental limit imposed by hydrostatic equilibrium. Astron. Astrophys. 632, 2 (2019)
ADS Google Scholar
A. Heger, C.L. Fryer, S.E. Woosley, et al., How massive single stars end their life. Astrophys. J. 591, 288–300 (2003)
ADS Google Scholar
S. Hirano, H. Umeda, N. Yoshida, Evolution of primordial stars powered by dark matter annihilation up to the main-sequence stage. Astrophys. J. 736, 58 (2011)
ADS Google Scholar
S. Hirano, T. Hosokawa, N. Yoshida, et al., One hundred first stars: protostellar evolution and the final masses. Astrophys. J. 781, 60 (2014)
ADS Google Scholar
S. Hirano, T. Hosokawa, N. Yoshida, et al., Primordial star formation under the influence of far ultraviolet radiation: 1540 cosmological haloes and the stellar mass distribution. Mon. Not. R. Astron. Soc. 448, 568–587 (2015)
ADS Google Scholar
S. Hirano, T. Hosokawa, N. Yoshida, et al., Supersonic gas streams enhance the formation of massive black holes in the early universe. Science 357, 1375–1378 (2017)
ADS MathSciNet MATH Google Scholar
T. Hosokawa, K. Omukai, Evolution of massive protostars with high accretion rates. Astrophys. J. 691, 823–846 (2009)
ADS Google Scholar
T. Hosokawa, H.W. Yorke, K. Omukai, Evolution of massive protostars via disk accretion. Astrophys. J. 721, 478–492 (2010)
ADS Google Scholar
T. Hosokawa, K. Omukai, N. Yoshida, et al., Protostellar feedback halts the growth of the first stars in the Universe. Science 334, 1250 (2011)
ADS Google Scholar
T. Hosokawa, K. Omukai, H.W. Yorke, Rapidly accreting supergiant protostars: embryos of supermassive black holes? Astrophys. J. 756, 93 (2012)
ADS Google Scholar
T. Hosokawa, N. Yoshida, K. Omukai, et al., Protostellar feedback and final mass of the second-generation primordial stars. Astrophys. J. Lett. 760, 37 (2012)
ADS Google Scholar
T. Hosokawa, H.W. Yorke, K. Inayoshi, et al., Formation of primordial supermassive stars by rapid mass accretion. Astrophys. J. 778, 178 (2013)
ADS Google Scholar
T. Hosokawa, S. Hirano, R. Kuiper, et al., Formation of massive primordial stars: intermittent UV feedback with episodic mass accretion. Astrophys. J. 824, 119 (2016)
ADS Google Scholar
F. Hoyle, W.A. Fowler, On the nature of strong radio sources. Mon. Not. R. Astron. Soc. 125, 169 (1963)
ADS Google Scholar
K. Inayoshi, E. Visbal, Z. Haiman, The Assembly of the First Massive Black Holes (2019). arXiv:1911.05791
F. Iocco, Dark matter capture and annihilation on the first stars: preliminary estimates. Astrophys. J. Lett. 677, 1 (2008)
ADS Google Scholar
F. Iocco, A. Bressan, E. Ripamonti, et al., Dark matter annihilation effects on the first stars. Mon. Not. R. Astron. Soc. 390, 1655–1669 (2008)
ADS Google Scholar
M. Ishigaki, R. Kawamata, M. Ouchi, et al., Full-Data Results of Hubble Frontier Fields: UV Luminosity Functions at $z\sim 6-10$ and a Consistent Picture of Cosmic Reionization. ArXiv e-prints (2017)
M. Jeon, A.H. Pawlik, T.H. Greif, et al., The first galaxies: assembly with black hole feedback. Astrophys. J. 754, 34 (2012)
ADS Google Scholar
M. Jeon, A.H. Pawlik, V. Bromm, et al., Radiative feedback from high-mass X-ray binaries on the formation of the first galaxies and early reionization. Mon. Not. R. Astron. Soc. 440, 3778–3796 (2014)
ADS Google Scholar
J.L. Johnson, V. Bromm, The aftermath of the first stars: massive black holes. Mon. Not. R. Astron. Soc. 374, 1557–1568 (2007)
ADS Google Scholar
A.A. Kaurov, N.Y. Gnedin, Cosmic reionization on computers. III. The clumping factor. Astrophys. J. 810, 154 (2015)
ADS Google Scholar
A.P. Kazantsev, Enhancement of a magnetic field by a conducting fluid. Sov. Phys. JETP 26, 1031 (1968)
ADS Google Scholar
E. Keto, The formation of massive stars: accretion, disks, and the development of hypercompact H II regions. Astrophys. J. 666, 976–981 (2007)
ADS Google Scholar
R. Kippenhahn, E. Meyer-Hofmeister, On the radii of accreting main sequence stars. Astron. Astrophys. 54, 539–542 (1977)
ADS Google Scholar
T. Kitayama, N. Yoshida, H. Susa, et al., The structure and evolution of early cosmological H II regions. Astrophys. J. 613, 631–645 (2004)
ADS Google Scholar
R.S. Klessen, S.C.O. Glover, Physical processes in the interstellar medium, in Star Formation in Galaxy Evolution: Connecting Numerical Models to Reality, Saas-Fee Advanced Course, vol. 43. (Springer, Berlin, 2016), p. 85
Google Scholar
K.M. Kratter, C.D. Matzner, Fragmentation of massive protostellar discs. Mon. Not. R. Astron. Soc. 373, 1563–1576 (2006)
ADS Google Scholar
M.R. Krumholz, R.I. Klein, C.F. McKee, et al., The formation of massive star systems by accretion. Science 323, 754 (2009)
ADS Google Scholar
R. Kuiper, H. Klahr, H. Beuther, et al., Circumventing the radiation pressure barrier in the formation of massive stars via disk accretion. Astrophys. J. 722, 1556–1576 (2010)
ADS Google Scholar
R. Kuiper, H. Klahr, H. Beuther, et al., Three-dimensional simulation of massive star formation in the disk accretion scenario. Astrophys. J. 732, 20 (2011)
ADS Google Scholar
R.B. Larson, Numerical calculations of the dynamics of collapsing proto-star. Mon. Not. R. Astron. Soc. 145, 271 (1969)
ADS Google Scholar
M.A. Latif, Black hole formation via gas-dynamical processes, ed. by M. Latif, D. Schleicher (2019), pp. 99–113
M.A. Latif, D.R.G. Schleicher, W. Schmidt, et al., High-resolution studies of massive primordial haloes. Mon. Not. R. Astron. Soc. 430, 588–598 (2013a)
ADS Google Scholar
M.A. Latif, D.R.G. Schleicher, W. Schmidt, et al., The small-scale dynamo and the amplification of magnetic fields in massive primordial haloes. Mon. Not. R. Astron. Soc. 432, 668–678 (2013b)
ADS Google Scholar
M.A. Latif, J.C. Niemeyer, D.R.G. Schleicher, Impact of baryonic streaming velocities on the formation of supermassive black holes via direct collapse. Mon. Not. R. Astron. Soc. 440, 2969–2975 (2014a)
ADS Google Scholar
M.A. Latif, D.R.G. Schleicher, W. Schmidt, Magnetic fields during the formation of supermassive black holes. Mon. Not. R. Astron. Soc. 440, 1551–1561 (2014b)
ADS Google Scholar
M. Lazar, R. Schlickeiser, R. Wielebinski, et al., Cosmological effects of Weibel-type instabilities. Astrophys. J. 693, 1133–1141 (2009)
ADS Google Scholar
H. Lee, S.-C. Yoon, On the role of the $\varOmega $$\varGamma $ limit in the formation of Population III massive stars. Astrophys. J. 820, 135 (2016)
ADS Google Scholar
J.-T. Li, G.M. Fuller, C.T. Kishimoto, Neutrino burst-generated gravitational radiation from collapsing supermassive stars. Phys. Rev. D 98(2), 023002 (2018)
ADS Google Scholar
Y.T. Liu, S.L. Shapiro, B.C. Stephens, Magnetorotational collapse of very massive stars to black holes in full general relativity. Phys. Rev. D 76(8), 084017 (2007)
ADS Google Scholar
R.C. Livermore, S.L. Finkelstein, J.M. Lotz, Directly observing the galaxies likely responsible for reionization. Astrophys. J. 835, 113 (2017)
ADS Google Scholar
G. Lodato, P. Natarajan, Supermassive black hole formation during the assembly of pre-galactic discs. Mon. Not. R. Astron. Soc. 371, 1813–1823 (2006)
ADS Google Scholar
M.-M. Mac Low, R.S. Klessen, Control of star formation by supersonic turbulence. Rev. Mod. Phys. 76, 125–194 (2004)
ADS Google Scholar
M.N. Machida, K. Doi, The formation of Population III stars in gas accretion stage: effects of magnetic fields. Mon. Not. R. Astron. Soc. 435, 3283–3305 (2013)
ADS Google Scholar
M.N. Machida, K. Omukai, T. Matsumoto, et al., The first jets in the Universe: protostellar jets from the first stars. Astrophys. J. Lett. 647, 1–4 (2006)
ADS Google Scholar
M.N. Machida, T. Matsumoto, S.-i. Inutsuka, Magnetohydrodynamics of Population III star formation. Astrophys. J. 685, 690–704 (2008)
ADS Google Scholar
P. Madau, Cosmic reionization after Planck and before JWST: an analytic approach. Astrophys. J. 851, 50 (2017)
ADS Google Scholar
P. Madau, F. Haardt, Cosmic reionization after Planck: could quasars do it all? Astrophys. J. Lett. 813, 8 (2015)
ADS Google Scholar
P. Madau, F. Haardt, M.J. Rees, Radiative transfer in a clumpy universe. III. The nature of cosmological ionizing sources. Astrophys. J. 514, 648–659 (1999)
ADS Google Scholar
A. Maeder, Physics, Formation and Evolution of Rotating Stars (Springer, Berlin, 2009)
Google Scholar
A. Maeder, G. Meynet, Stellar evolution with rotation. VI. The Eddington and Omega-limits, the rotational mass loss for OB and LBV stars. Astron. Astrophys. 361, 159–166 (2000)
ADS Google Scholar
U. Maio, S. Khochfar, J.L. Johnson, et al., The interplay between chemical and mechanical feedback from the first generation of stars. Mon. Not. R. Astron. Soc. 414, 1145–1157 (2011b)
ADS Google Scholar
U. Maio, L.V.E. Koopmans, B. Ciardi, The impact of primordial supersonic flows on early structure formation, reionization and the lowest-mass dwarf galaxies. Mon. Not. R. Astron. Soc. 412, 40–44 (2011a)
ADS Google Scholar
L. Mayer, S. Bonoli, The route to massive black hole formation via merger-driven direct collapse: a review. Rep. Prog. Phys. 82(1), 016901 (2019)
ADS Google Scholar
L. Mayer, S. Kazantzidis, A. Escala, et al., Direct formation of supermassive black holes via multi-scale gas inflows in galaxy mergers. Nature 466, 1082–1084 (2010)
ADS Google Scholar
L. Mayer, D. Fiacconi, S. Bonoli, et al., Direct formation of supermassive black holes in metal enriched gas at the heart of high-redshift galaxy mergers. Astrophys. J. 810, 51 (2015)
ADS Google Scholar
I.D. McGreer, A. Mesinger, V. D’Odorico, Model-independent evidence in favour of an end to reionization by $z\approx 6$. Mon. Not. R. Astron. Soc. 447, 499–505 (2015)
ADS Google Scholar
C.F. McKee, E.C. Ostriker, Theory of star formation. Annu. Rev. Astron. Astrophys. 45, 565–687 (2007)
ADS Google Scholar
C.F. McKee, J.C. Tan, The formation of the first stars. II. Radiative feedback processes and implications for the initial mass function. Astrophys. J. 681, 771–797 (2008)
ADS Google Scholar
M. McQuinn, R.M. O’Leary, The impact of the supersonic baryon-dark matter velocity difference on the $z \sim 20\ 21$ cm background. Astrophys. J. 760, 3 (2012)
ADS Google Scholar
M.V. Medvedev, L.O. Silva, M. Fiore, et al., Generation of magnetic fields in cosmological shocks. J. Korean Astron. Soc. 37, 533–541 (2004)
ADS Google Scholar
J. Miralda-Escudé, M. Haehnelt, M.J. Rees, Reionization of the inhomogeneous universe. Astrophys. J. 530, 1–16 (2000)
ADS Google Scholar
P.J. Montero, H.-T. Janka, E. Müller, Relativistic collapse and explosion of rotating supermassive stars with thermonuclear effects. Astrophys. J. 749, 37 (2012)
ADS Google Scholar
S. Naoz, N. Yoshida, N.Y. Gnedin, Simulations of early baryonic structure formation with stream velocity. I. Halo abundance. Astrophys. J. 747, 128 (2012)
ADS Google Scholar
S. Naoz, N. Yoshida, N.Y. Gnedin, Simulations of early baryonic structure formation with stream velocity. II. The gas fraction. Astrophys. J. 763, 27 (2013)
ADS Google Scholar
S. Neo, S. Miyaji, K. Nomoto, et al., Effect of rapid mass accretion onto the main-sequence stars. Publ. Astron. Soc. Jpn. 29, 249–262 (1977)
ADS Google Scholar
K.C.B. New, S.L. Shapiro, Evolution of differentially rotating supermassive stars to the onset of bar instability. Astrophys. J. 548, 439–446 (2001)
ADS Google Scholar
P.A. Oesch, R.J. Bouwens, G.D. Illingworth, et al., The Dearth of $z\sim10$ Galaxies in all HST Legacy Fields – the Rapid Evolution of the Galaxy Population in the First 500 Myr. ArXiv e-prints (2017)
R.M. O’Leary, M. McQuinn, The formation of the first cosmic structures and the physics of the $z \sim 20$ universe. Astrophys. J. 760, 4 (2012)
ADS Google Scholar
K. Omukai, Primordial star formation under far-ultraviolet radiation. Astrophys. J. 546, 635–651 (2001)
ADS Google Scholar
K. Omukai, F. Palla, Formation of the first stars by accretion. Astrophys. J. 589, 677–687 (2003)
ADS Google Scholar
J. Oñorbe, J.F. Hennawi, Z. Lukić, et al., Constraining reionization with the $z \sim 5$-6 Ly$\alpha$ forest power spectrum: the outlook after Planck. Astrophys. J. 847, 63 (2017)
ADS Google Scholar
Y. Osaki, The pulsation and evolution of super-massive stars. Publ. Astron. Soc. Jpn. 18, 384 (1966)
ADS Google Scholar
B.W. O’Shea, M.L. Norman, Population III star formation in a $\varLambda $CDM universe. I. The effect of formation redshift and environment on protostellar accretion rate. Astrophys. J. 654, 66–92 (2007)
ADS Google Scholar
M. Ouchi, K. Shimasaku, H. Furusawa, et al., Statistics of 207 Ly$\alpha $ emitters at a redshift near 7: constraints on reionization and galaxy formation models. Astrophys. J. 723, 869–894 (2010)
ADS Google Scholar
F. Palla, S.W. Stahler, The evolution of intermediate-mass protostars. I—basic results. Astrophys. J. 375, 288–299 (1991)
ADS Google Scholar
K.L. Pandey, S.K. Sethi, B. Ratra, Cosmological magnetic braking and the formation of high-redshift, super-massive black holes. ArXiv e-prints (2019)
M.V. Penston, Dynamics of self-gravitating gaseous spheres-III. Analytical results in the free-fall of isothermal cases. Mon. Not. R. Astron. Soc. 144, 425 (1969)
ADS Google Scholar
T. Peters, M.-M. Mac Low, R. Banerjee, et al., Understanding spatial and spectral morphologies of ultracompact H II regions. Astrophys. J. 719, 831–843 (2010)
ADS Google Scholar
T. Peters, R. Banerjee, R.S. Klessen, et al., The interplay of magnetic fields, fragmentation, and ionization feedback in high-mass star formation. Astrophys. J. 729, 72 (2011)
ADS Google Scholar
T. Peters, D.R.G. Schleicher, R.J. Smith, et al., Low-metallicity star formation: relative impact of metals and magnetic fields. Mon. Not. R. Astron. Soc. 442, 3112–3126 (2014)
ADS Google Scholar
R. Adam, N. Aghanim, et al. (Planck Collaboration), Planck intermediate results. XLVII. Planck constraints on reionization history. Astron. Astrophys. 596, 108 (2016b)
Google Scholar
P.A.R. Ade, N. Aghanim, et al. (Planck Collaboration), Planck 2015 results. XIII. Cosmological parameters. Astron. Astrophys. 594, 13 (2016a)
Google Scholar
Planck Collaboration, N. Aghanim, Y. Akrami, et al., Planck 2018 results. VI. Cosmological parameters. ArXiv e-prints (2018)
D. Rahner, E.W. Pellegrini, S.C.O. Glover, et al., Winds and radiation in unison: a new semi-analytic feedback model for cloud dissolution. Mon. Not. R. Astron. Soc. 470(4), 4453–4472 (2017)
ADS Google Scholar
D. Rahner, E.W. Pellegrini, S.C.O. Glover, et al., WARPFIELD 2.0: feedback-regulated minimum star formation efficiencies of giant molecular clouds. Mon. Not. R. Astron. Soc. 483(2), 2547–2560 (2019)
ADS Google Scholar
J.A. Regan, M.G. Haehnelt, The formation of compact massive self-gravitating discs in metal-free haloes with virial temperatures of ∼13000–30000 K. Mon. Not. R. Astron. Soc. 393, 858–871 (2009)
ADS Google Scholar
J.A. Regan, E. Visbal, J.H. Wise, et al., Rapid formation of massive black holes in close proximity to embryonic protogalaxies. Nat. Astron. 1, 0075 (2017)
Google Scholar
J.A. Regan, T.P. Downes, M. Volonteri, et al., Super-Eddington accretion and feedback from the first massive seed black holes. Mon. Not. R. Astron. Soc. 486(3), 3892–3906 (2019)
ADS Google Scholar
C. Reisswig, C.D. Ott, E. Abdikamalov, et al., Formation and coalescence of cosmological supermassive-black-hole binaries in supermassive-star collapse. Phys. Rev. Lett. 111(15), 151101 (2013)
ADS Google Scholar
E. Ripamonti, F. Iocco, A. Ferrara, et al., First star formation with dark matter annihilation. Mon. Not. R. Astron. Soc. 406, 2605–2615 (2010)
ADS Google Scholar
T. Rivinius, T. Szeifert, L. Barrera, et al., Magnetic field detection in the B2Vn star HR 7355. Mon. Not. R. Astron. Soc. 405, 46–50 (2010)
ADS Google Scholar
B.E. Robertson, R.S. Ellis, J.S. Dunlop, et al., Early star-forming galaxies and the reionization of the Universe. Nature 468, 49–55 (2010)
ADS Google Scholar
B.E. Robertson, R.S. Ellis, S.R. Furlanetto, et al., Cosmic reionization and early star-forming galaxies: a joint analysis of new constraints from Planck and the Hubble Space Telescope. Astrophys. J. Lett. 802, 19 (2015)
ADS Google Scholar
A.L. Rosen, M.R. Krumholz, C.F. McKee, et al., An unstable truth: how massive stars get their mass. Mon. Not. R. Astron. Soc. 463, 2553–2573 (2016)
ADS Google Scholar
A. Sadowski, R. Narayan, R. Penna, et al., Energy, momentum and mass outflows and feedback from thick accretion discs around rotating black holes. Mon. Not. R. Astron. Soc. 436, 3856–3874 (2013)
ADS Google Scholar
M. Saijo, The collapse of differentially rotating supermassive stars: conformally flat simulations. Astrophys. J. 615, 866–879 (2004)
ADS Google Scholar
M. Saijo, T.W. Baumgarte, S.L. Shapiro, et al., Collapse of a rotating supermassive star to a supermassive black hole: post-Newtonian simulations. Astrophys. J. 569, 349–361 (2002)
ADS Google Scholar
D. Schaerer, On the properties of massive Population III stars and metal-free stellar populations. Astron. Astrophys. 382, 28–42 (2002)
ADS Google Scholar
A.T.P. Schauer, D.J. Whalen, S.C.O. Glover, et al., Lyman-Werner UV escape fractions from primordial haloes. Mon. Not. R. Astron. Soc. (2015)
A.T.P. Schauer, B. Agarwal, S.C.O. Glover, et al., Lyman-Werner escape fractions from the first galaxies. Mon. Not. R. Astron. Soc. 467, 2288–2300 (2017a)
ADS Google Scholar
A.T.P. Schauer, J. Regan, S.C.O. Glover, et al., The formation of direct collapse black holes under the influence of streaming velocities. Mon. Not. R. Astron. Soc. 471, 4878–4884 (2017b)
ADS Google Scholar
A.A. Schekochihin, S.C. Cowley, G.W. Hammett, et al., A model of nonlinear evolution and saturation of the turbulent MHD dynamo. New J. Phys. 4, 84 (2002)
ADS Google Scholar
A.A. Schekochihin, S.C. Cowley, S.F. Taylor, et al., Saturated state of the nonlinear small-scale dynamo. Phys. Rev. Lett. 92(8), 084504 (2004)
ADS Google Scholar
M.A. Schenker, R.S. Ellis, N.P. Konidaris, et al., Line-emitting galaxies beyond a redshift of 7: an improved method for estimating the evolving neutrality of the intergalactic medium. Astrophys. J. 795, 20 (2014)
ADS Google Scholar
D.R.G. Schleicher, D. Galli, S.C.O. Glover, et al., The influence of magnetic fields on the thermodynamics of primordial star formation. Astrophys. J. 703, 1096–1106 (2009)
ADS Google Scholar
D.R.G. Schleicher, R. Banerjee, S. Sur, et al., Small-scale dynamo action during the formation of the first stars and galaxies. I. The ideal MHD limit. Astron. Astrophys. 522, 115 (2010)
MATH Google Scholar
R. Schlickeiser, P.K. Shukla, Cosmological magnetic field generation by the Weibel instability. Astrophys. J. Lett. 599, 57–60 (2003)
ADS Google Scholar
J. Schober, D. Schleicher, C. Federrath, et al., Magnetic field amplification by small-scale dynamo action: dependence on turbulence models and Reynolds and Prandtl numbers. Phys. Rev. E 85(2), 026303 (2012a)
ADS Google Scholar
J. Schober, D. Schleicher, C. Federrath, et al., The small-scale dynamo and non-ideal magnetohydrodynamics in primordial star formation. Astrophys. J. 754, 99 (2012b)
ADS Google Scholar
J. Schober, D.R.G. Schleicher, C. Federrath, et al., Saturation of the turbulent dynamo. Phys. Rev. E 92(2), 023010 (2015)
ADS Google Scholar
J. Schroeder, A. Mesinger, Z. Haiman, Evidence of Gunn-Peterson damping wings in high-$z$ quasar spectra: strengthening the case for incomplete reionization at $z \sim 6$-7. Mon. Not. R. Astron. Soc. 428, 3058–3071 (2013)
ADS Google Scholar
N.I. Shakura, R.A. Sunyaev, Black holes in binary systems. Observational appearance. Astron. Astrophys. 24, 337–355 (1973)
ADS Google Scholar
M. Shibata, S.L. Shapiro, Collapse of a rotating supermassive star to a supermassive black hole: fully relativistic simulations. Astrophys. J. Lett. 572, 39–43 (2002)
ADS Google Scholar
M. Shibata, Y. Sekiguchi, H. Uchida, et al., Gravitational waves from supermassive stars collapsing to a supermassive black hole. Phys. Rev. D 94(2), 021501 (2016b)
ADS Google Scholar
M. Shibata, H. Uchida, Y.-i. Sekiguchi, Stability of rigidly rotating supermassive stars against gravitational collapse. Astrophys. J. 818, 157 (2016a)
ADS Google Scholar
I. Shlosman, Galactic bars in cosmological context. Mem. Soc. Astron. Ital. Suppl. 18, 175 (2011)
ADS Google Scholar
F.H. Shu, Self-similar collapse of isothermal spheres and star formation. Astrophys. J. 214, 488–497 (1977)
ADS Google Scholar
G. Sigl, A.V. Olinto, K. Jedamzik, Primordial magnetic fields from cosmological first order phase transitions. Phys. Rev. D 55, 4582–4590 (1997)
ADS Google Scholar
J. Silk, The cosmic microwave background radiation, in Implications for galaxy formation, ed. by E.W. Kolb, M.S. Turner, D. Lindley, et al. (University of Chicago Press, Chicago, 1986), pp. 143–158
Google Scholar
R. Smit, R.J. Bouwens, I. Labbé, et al., Evidence for ubiquitous high-equivalent-width nebular emission in $z \sim 7$ galaxies: toward a clean measurement of the specific star-formation rate using a sample of bright, magnified galaxies. Astrophys. J. 784, 58 (2014)
ADS Google Scholar
R.J. Smith, S.C.O. Glover, P.C. Clark, et al., The effects of accretion luminosity upon fragmentation in the early universe. Mon. Not. R. Astron. Soc. 414, 3633–3644 (2011)
ADS Google Scholar
R.J. Smith, T. Hosokawa, K. Omukai, et al., Variable accretion rates and fluffy first stars. Mon. Not. R. Astron. Soc. 424, 457–463 (2012)
ADS Google Scholar
L. Spitzer, Physical Processes in the Interstellar Medium (Wiley-Inter science, New York, 1978)
Google Scholar
D. Spolyar, K. Freese, P. Gondolo, Dark matter and the first stars: a new phase of stellar evolution. Phys. Rev. Lett. 100(5), 051101 (2008)
ADS Google Scholar
A. Stacy, V. Bromm, Constraining the statistics of Population III binaries. Mon. Not. R. Astron. Soc. 433, 1094–1107 (2013)
ADS Google Scholar
A. Stacy, V. Bromm, A. Loeb, Effect of streaming motion of baryons relative to dark matter on the formation of the first stars. Astrophys. J. Lett. 730, 1 (2011)
ADS Google Scholar
A. Stacy, T.H. Greif, V. Bromm, The first stars: mass growth under protostellar feedback. Mon. Not. R. Astron. Soc. 422, 290–309 (2012)
ADS Google Scholar
A. Stacy, A.H. Pawlik, V. Bromm, et al., The mutual interaction between Population III stars and self-annihilating dark matter. Mon. Not. R. Astron. Soc. 441, 822–836 (2014)
ADS Google Scholar
A. Stacy, V. Bromm, A.T. Lee, Building up the Population III initial mass function from cosmological initial conditions. Mon. Not. R. Astron. Soc. 462, 1307–1328 (2016)
ADS Google Scholar
S.W. Stahler, Deuterium and the stellar birthline. Astrophys. J. 332, 804–825 (1988)
ADS Google Scholar
S.W. Stahler, F.H. Shu, R.E. Taam, The evolution of protostars. I—global formulation and results. Astrophys. J. 241, 637–654 (1980)
ADS Google Scholar
S.W. Stahler, F. Palla, E.E. Salpeter, Primordial stellar evolution—the protostar phase. Astrophys. J. 302, 590–605 (1986)
ADS Google Scholar
E.R. Stanway, J.J. Eldridge, G.D. Becker, Stellar population effects on the inferred photon density at reionization. Mon. Not. R. Astron. Soc. 456, 485–499 (2016)
ADS Google Scholar
K. Subramanian, Can the turbulent galactic dynamo generate large-scale magnetic fields? Mon. Not. R. Astron. Soc. 294, 718 (1998)
ADS Google Scholar
K. Sugimura, T. Hosokawa, H. Yajima, et al., Stunted accretion growth of black holes by combined effect of the flow angular momentum and radiation feedback. Mon. Not. R. Astron. Soc. 478(3), 3961–3975 (2018)
ADS Google Scholar
K. Sugimura, T. Matsumoto, T. Hosokawa, et al., The Birth of a Massive First-Star Binary (2020). arXiv:2002.00012
L. Sun, V. Paschalidis, M. Ruiz, et al., Magnetorotational collapse of supermassive stars: black hole formation, gravitational waves, and jets. Phys. Rev. D 96(4), 043006 (2017)
ADS Google Scholar
L. Sun, M. Ruiz, S.L. Shapiro, Simulating the magnetorotational collapse of supermassive stars: incorporating gas pressure perturbations and different rotation profiles. Phys. Rev. D 98(10), 103008 (2018)
ADS Google Scholar
R.A. Sunyaev, Y.B. Zel’dovich, Small-scale fluctuations of relic radiation. Astrophys. Space Sci. 7, 3–19 (1970)
ADS Google Scholar
S. Sur, D.R.G. Schleicher, R. Banerjee, et al., The generation of strong magnetic fields during the formation of the first stars. Astrophys. J. Lett. 721, 134–138 (2010)
ADS Google Scholar
S. Sur, C. Federrath, D.R.G. Schleicher, et al., Magnetic field amplification during gravitational collapse—influence of turbulence, rotation and gravitational compression. Mon. Not. R. Astron. Soc. 423, 3148–3162 (2012)
ADS Google Scholar
H. Susa, The mass of the first stars. Astrophys. J. 773, 185 (2013)
ADS Google Scholar
H. Susa, K. Hasegawa, N. Tominaga, The mass spectrum of the first stars. Astrophys. J. 792, 32 (2014)
ADS Google Scholar
S.Z. Takahashi, K. Omukai, Primordial protostars accreting beyond the $\varOmega $$\varGamma $-limit: radiation effect around the star-disc boundary. Mon. Not. R. Astron. Soc. 472, 532–541 (2017)
ADS Google Scholar
E. Takeo, K. Inayoshi, K. Ohsuga, et al., Rapid growth of black holes accompanied with hot or warm outflows exposed to anisotropic super-Eddington radiation. Mon. Not. R. Astron. Soc. 476, 673–682 (2018)
ADS Google Scholar
J.C. Tan, C.F. McKee, The formation of the first stars. I. Mass infall rates, accretion disk structure, and protostellar evolution. Astrophys. J. 603, 383–400 (2004)
ADS Google Scholar
A. Toomre, On the gravitational stability of a disk of stars. Astrophys. J. 139, 1217–1238 (1964)
ADS Google Scholar
R.H.D. Townsend, S.P. Owocki, D. Groote, The rigidly rotating magnetosphere of $\sigma $ Orionis E. Astrophys. J. Lett. 630, 81–84 (2005)
ADS Google Scholar
D. Tseliakhovich, C. Hirata, Relative velocity of dark matter and baryonic fluids and the formation of the first structures. Phys. Rev. D 82(8), 083520 (2010)
ADS Google Scholar
M.J. Turk, T. Abel, B. O’Shea, The formation of Population III binaries from cosmological initial conditions. Science 325, 601 (2009)
ADS Google Scholar
M.J. Turk, B.D. Smith, J.S. Oishi, et al., yt: A multi-code analysis toolkit for astrophysical simulation data. Astrophys. J. Suppl. Ser. 192, 9 (2011)
ADS Google Scholar
M.J. Turk, J.S. Oishi, T. Abel, et al., Magnetic fields in Population III star formation. Astrophys. J. 745, 154 (2012)
ADS Google Scholar
H. Uchida, M. Shibata, T. Yoshida, et al., Gravitational collapse of rotating supermassive stars including nuclear burning effects. Phys. Rev. D 96(8), 083016 (2017)
ADS Google Scholar
H. Umeda, T. Hosokawa, K. Omukai, et al., The final fates of accreting supermassive stars. Astrophys. J. Lett. 830, 34 (2016)
ADS Google Scholar
W. Unno, Physical state and stability of super-massive objects. Publ. Astron. Soc. Jpn. 23, 123 (1971)
ADS Google Scholar
E. Visbal, R. Barkana, A. Fialkov, et al., The signature of the first stars in atomic hydrogen at redshift 20. Nature 487, 70–73 (2012)
ADS Google Scholar
M. Volonteri, G. Lodato, P. Natarajan, The evolution of massive black hole seeds. Mon. Not. R. Astron. Soc. 383, 1079–1088 (2008)
ADS Google Scholar
H. von Zeipel, The radiative equilibrium of a rotating system of gaseous masses. Mon. Not. R. Astron. Soc. 84, 665–683 (1924)
ADS Google Scholar
M. Walther, J. Oñorbe, J.F. Hennawi, et al., New constraints on IGM thermal evolution from the Ly$\alpha $ forest power spectrum. Astrophys. J. 872(1), 13 (2019)
ADS Google Scholar
D. Whalen, T. Abel, M.L. Norman, Radiation hydrodynamic evolution of primordial H II regions. Astrophys. J. 610, 14–22 (2004)
ADS Google Scholar
A. Whitworth, D. Summers, Self-similar condensation of spherically symmetric self-gravitating isothermal gas clouds. Mon. Not. R. Astron. Soc. 214, 1–25 (1985)
ADS MATH Google Scholar
L.M. Widrow, D. Ryu, D.R.G. Schleicher, et al., The first magnetic fields. Space Sci. Rev. 166, 37–70 (2012)
ADS Google Scholar
J.H. Wise, M.J. Turk, T. Abel, Resolving the formation of protogalaxies. II. Central gravitational collapse. Astrophys. J. 682, 745–757 (2008)
ADS Google Scholar
J.H. Wise, T. Abel, M.J. Turk, et al., The birth of a galaxy—II. The role of radiation pressure. Mon. Not. R. Astron. Soc. 427, 311–326 (2012a)
ADS Google Scholar
J.H. Wise, M.J. Turk, M.L. Norman, et al., The birth of a galaxy: primordial metal enrichment and stellar populations. Astrophys. J. 745, 50 (2012b)
ADS Google Scholar
J.H. Wise, J.A. Regan, B.W. O’Shea, et al., Formation of massive black holes in rapidly growing pre-galactic gas clouds. ArXiv e-prints (2019)
K.M.J. Wollenberg, S.C.O. Glover, P.C. Clark, et al., Formation sites of Population III star formation: the effects of different levels of rotation and turbulence on the fragmentation behaviour of primordial gas. Mon. Not. R. Astron. Soc. (2020). https://doi.org/10.1093/mnras/staa289
Article Google Scholar
T.E. Woods, A. Heger, D.J. Whalen, et al., On the maximum mass of accreting primordial supermassive stars. Astrophys. J. Lett. 842, 6 (2017)
ADS Google Scholar
T.E. Woods, B. Agarwal, V. Bromm, et al., Titans of the early Universe: the Prato statement on the origin of the first supermassive black holes. Publ. Astron. Soc. Aust. 36, 027 (2019)
ADS Google Scholar
X.-B. Wu, F. Wang, X. Fan, et al., An ultraluminous quasar with a twelve-billion-solar-mass black hole at redshift 6.30. Nature 518, 512–515 (2015)
ADS Google Scholar
S.-C. Yoon, F. Iocco, S. Akiyama, Evolution of the first stars with dark matter burning. Astrophys. J. Lett. 688, 1 (2008)
ADS Google Scholar
H.W. Yorke, C. Sonnhalter, On the formation of massive stars. Astrophys. J. 569, 846–862 (2002)
ADS Google Scholar
N. Yoshida, T. Abel, L. Hernquist, et al., Simulations of early structure formation: primordial gas clouds. Astrophys. J. 592, 645–663 (2003)
ADS Google Scholar
N. Yoshida, K. Omukai, L. Hernquist, et al., Formation of primordial stars in a $\varLambda $CDM universe. Astrophys. J. 652, 6–25 (2006)
ADS Google Scholar
N. Yoshida, S.P. Oh, T. Kitayama, et al., Early cosmological H II/He III regions and their impact on second-generation star formation. Astrophys. J. 663, 687–707 (2007)
ADS Google Scholar
N. Yoshida, K. Omukai, L. Hernquist, Protostar formation in the early universe. Science 321, 669 (2008)
ADS Google Scholar
E. Zackrisson, C. Binggeli, K. Finlator, et al., The spectral evolution of the first Galaxies. III. Simulated James Webb Space Telescope spectra of reionization-epoch galaxies with Lyman-continuum leakage. Astrophys. J. 836, 78 (2017)
ADS Google Scholar
H. Zinnecker, H.W. Yorke, Toward understanding massive star formation. Annu. Rev. Astron. Astrophys. 45, 481–563 (2007)
ADS Google Scholar

Download references

Acknowledgements

The authors thank ISSI for the organisation of the conference at the origin of this review.

Author information

Authors and Affiliations

Département d’Astronomie, Université de Genève, chemin des Maillettes 51, 1290, Geneva, Switzerland
L. Haemmerlé
Center for Theoretical Astrophysics and Cosmology, Institute for Computational Science, University of Zurich, Winterthurerstrasse 190, 8057, Zurich, Switzerland
L. Mayer
Zentrum für Astronomie, Institut für Theoretische Astrophysik, Universität Heidelberg, Albert-Ueberle-Str. 2, 69120, Heidelberg, Germany
R. S. Klessen
Department of Physics, Kyoto University, Kyoto, 606-8502, Japan
T. Hosokawa
Department of Astronomy and Astrophysics, University of California, 1156 High Street, Santa Cruz, CA, 95064, USA
P. Madau
Department of Astronomy, The University of Texas at Austin, Austin, TX, 78712, USA
V. Bromm

Authors

L. Haemmerlé
View author publications
You can also search for this author in PubMed Google Scholar
L. Mayer
View author publications
You can also search for this author in PubMed Google Scholar
R. S. Klessen
View author publications
You can also search for this author in PubMed Google Scholar
T. Hosokawa
View author publications
You can also search for this author in PubMed Google Scholar
P. Madau
View author publications
You can also search for this author in PubMed Google Scholar
V. Bromm
View author publications
You can also search for this author in PubMed Google Scholar

Additional information

Publisher’s Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Star Formation

Edited by Andrei Bykov, Corinne Charbonnel, Patrick Hennebelle, Alexandre Marcowith, Georges Meynet, Maurizio Falanga and Rudolf von Steiger

Rights and permissions

Reprints and permissions

About this article

Cite this article

Haemmerlé, L., Mayer, L., Klessen, R.S. et al. Formation of the First Stars and Black Holes. Space Sci Rev 216, 48 (2020). https://doi.org/10.1007/s11214-020-00673-y

Download citation

Received: 13 March 2020
Accepted: 09 April 2020
Published: 21 April 2020
DOI: https://doi.org/10.1007/s11214-020-00673-y

Keywords

Use our pre-submission checklist

Avoid common mistakes on your manuscript.

Formation of the First Stars and Black Holes

Abstract

Similar content being viewed by others

The numerical frontier of the high-redshift Universe

A universal minimal mass scale for present-day central black holes

The origins of massive black holes

1 First Stars

1.1 Spherical Collapse Models

1.2 Disk Fragmentation

1.3 Radiative Feedback

1.4 Magnetic Fields

1.5 Streaming Velocity

1.6 Dark Matter Annihilation

2 Supermassive Stars

2.1 Numerical Modeling of Accreting Stars

2.1.1 Accretion-Induced “Inflation” of Stars

2.1.2 Birth of Accreting SMSs

2.1.3 Accretion at \(\dot{M}>10\) \(\mathrm{M}_{\odot }\) yr⁻¹

2.1.4 The Final Collapse of SMSs

2.2 Rotation in SMSs

3 Formation of Massive Black Hole Seeds

3.1 The Rapid Rise of High-z QSOs and the Challenge for Light Black Hole Seed Models

3.2 Direct Collapse Scenarios for the Origin of Massive BH Seeds

3.2.1 A Crucial Aspect: Angular Momentum Transport in Protogalaxies

3.2.2 Routes to Direct Collapse: Metal-Free Atomic Cooling Halos and Mergers of Most Massive Metal-Enriched Primordial Galaxies

4 Reionization After Planck and Before JWST

4.1 The Reionization Equation

5 Concluding Remarks

Notes

References

Acknowledgements

Author information

Authors and Affiliations

Additional information

Publisher’s Note

Rights and permissions

About this article

Cite this article

Keywords

Navigation

Formation of the First Stars and Black Holes

Abstract

Similar content being viewed by others

The numerical frontier of the high-redshift Universe

A universal minimal mass scale for present-day central black holes

The origins of massive black holes

1 First Stars

1.1 Spherical Collapse Models

1.2 Disk Fragmentation

1.3 Radiative Feedback

1.4 Magnetic Fields

1.5 Streaming Velocity

1.6 Dark Matter Annihilation

2 Supermassive Stars

2.1 Numerical Modeling of Accreting Stars

2.1.1 Accretion-Induced “Inflation” of Stars

2.1.2 Birth of Accreting SMSs

2.1.3 Accretion at \(\dot{M}>10\) \(\mathrm{M}_{\odot }\) yr−1

2.1.4 The Final Collapse of SMSs

2.2 Rotation in SMSs

3 Formation of Massive Black Hole Seeds

3.1 The Rapid Rise of High-z QSOs and the Challenge for Light Black Hole Seed Models

3.2 Direct Collapse Scenarios for the Origin of Massive BH Seeds

3.2.1 A Crucial Aspect: Angular Momentum Transport in Protogalaxies

3.2.2 Routes to Direct Collapse: Metal-Free Atomic Cooling Halos and Mergers of Most Massive Metal-Enriched Primordial Galaxies

4 Reionization After Planck and Before JWST

4.1 The Reionization Equation

5 Concluding Remarks

Notes

References

Acknowledgements

Author information

Authors and Affiliations

Additional information

Publisher’s Note

Rights and permissions

About this article

Cite this article

Share this article

Keywords

Search

Navigation

2.1.3 Accretion at \(\dot{M}>10\) \(\mathrm{M}_{\odot }\) yr⁻¹