Improved Approach in the Coupling Function Between Primary and Ground Level Cosmic Ray Particles Based on Neutron Monitor Data

Abstract

In this work an improved approach of existing approximations on the coupling function between primary and ground-level cosmic-ray particles is presented. The proposed coupling function is analytically derived based on a formalism used in Quantum Field Theory calculations. It is upgraded compared to previous versions with the inclusion of a wider energy spectrum that is extended to lower energies, as well as an altitude correction factor, also derived analytically. The improved approximations are applied to two cases of Forbush decreases detected in March 2012 and September 2017. In the analytical procedure for the derivation of the primary cosmic-ray spectrum during these events, we also consider the energy spectrum exponent $\gamma$ to be varied with time. For the validation of the findings, we present a direct comparison between the primary spectrum and the amplitude values derived by the proposed method and the obtained time series of the cosmic-ray intensity at the rigidity of 10 GV obtained from the Global Survey Method. The two sets of results are found to be in very good agreement for both events as denoted by the Pearson correlation factors and slope values of their scatter plots. In such way we determine the validity and applicability of our method to Forbush decreases as well as to other cosmic-ray phenomena, thus introducing a new, alternative way of inferring the primary cosmic-ray intensity.

1 Introduction

The primary cosmic-ray (CR) particles that manage to penetrate Earth’s geomagnetic field undergo various interactions with the atmospheric components. These interactions/collisions result in the production of showers of secondary particles, some of which might have sufficient lifetime and energy to reach ground level and be detected by neutron monitor detectors (NM) (see, for example, Simpson, 2000). In this work we focus only on the production of secondary neutrons as they are the main contributor of the recorded NM hits. The necessity of an accurate coupling function between primary and secondary CR particles has been discussed in various studies (e.g., Clem and Dorman, 2000; Mavromichalaki, 2012), especially for the study of many interesting and important CR phenomena, such as Forbush decreases (FDs), Ground Level Enhancements (GLEs) etc., the understanding of which is crucial for the rapidly developing field of Space Weather and its applications (Mavromichalaki, 2012).

In this work we focus mainly on the case of the Forbush decreases of CR intensity that were first introduced by Forbush (1937). These events become evident as a rapid decrease of the CR intensity by at least 2% (Forbush, 1954; Cane, 2000; Belov, 2008). The typical duration of a FD event is of the order of a few hours (reaching up to 2 days) with a recovery time of up to one week. FDs are generally thought to be due to interplanetary coronal mass ejections (CMEs) from the Sun (Lockwood, 1971; Venkatesan and Badruddin, 1990; Cane, 2000; Kumar and Badruddin, 2014; Belov et al., 2014; Lingri et al., 2016; Papaioannou et al., 2020), the fastest of which form shock waves that, propagating toward Earth, interact with and modulate the ambient galactic cosmic-ray background, resulting to its decreased intensity.

After Neutron Monitors were invented by Simpson (1948), the introduction of the response function that relates the primary CR spectra with the detected secondary ones was followed by Fonger (1953), Brown (1957) and Dorman (1957). Since then, coupling functions have been the object of ongoing studies through different approaches (analytical, computational etc.) by many researchers (Villoresi et al., 2000; Flückiger et al., 2008; Maurin et al., 2015; Usoskin et al., 2015). We mention below some of the most widely used functions of this kind:

• i) The function of Clem and Dorman (2000) that was derived numerically through Monte Carlo simulations.

• ii) The function of Caballero-Lopez and Moraal (2012) that takes into account muons, Cherenkov and stratospheric balloon detectors response functions.

• iii) The function of Dorman et al. (2000) that was computed from an analytical approach using appropriate parameterization techniques.

• iv) The function of Mishev et al. (2020) that was computed using the PLANETOCOSMICS simulation tool (Desorgher et al., 2005) based on the GEANT 4 package (Agostinelli et al., 2003), a fully integrated particle physics Monte Carlo simulation package.

Here, we extend the formalism of Xaplanteris et al. (2020) that relies on QFT. The obtained results are applied to two observed Forbush decreases and are directly compared with the results obtained by means of Dorman’s coupling function (Clem and Dorman, 2000). The main finding of this study is the satisfactory results reached by this approach.

In this work we improve this coupling function of Xaplanteris et al. (2020) in two distinct and critical aspects:

First, the expansion to lower-energy regions. More specifically, the previous version was applicable only for energy spectra above 3 GeV that correspond to a cut-off rigidity of 3.8 GV. Here we extend the coupling function down to energies starting from 1 GeV and translating to a cut-off rigidity of 1.69 GV. This extended energy spectrum allows us to use data from several NM stations in the cut-off rigidity range 1.6–3.8 GV that could not be included in the previous study, thus improving significantly the data sample and allowing a more credible evaluation.

Second, the use of an altitude (atmospheric depth) correction factor based on analytical calculations. We note that an altitude correction factor was also included in the previous study, but was computed using a rather rough approximation, by means of a model of atmospheric particle concentration proportional to altitude. This time, it is derived by assuming that the concentration of atmospheric particles follows a Boltzmann distribution with the altitude (Seinfeld and Pandis, 2006).

After the above two improvements, our upgraded coupling function is applied to the two FDs of March 2012 and of September 2017, similarly to Xaplanteris et al. (2020). The results obtained for the primary CR spectrum during these events are directly compared to the corresponding ones using the Global Survey Method (GSM). This technique uses ground-level data of cosmic rays of rigidity 10 GV from all neutron monitor stations in different geomagnetic coordinates simultaneously, thus deriving the main characteristics of CR variations outside Earth’s atmosphere (Belov et al., 2018).

This work is structured as follows: the data selection from different NM stations is presented in Section 2. The events studied in this work are briefly discussed alongside the main characteristics of all considered NM stations. In Section 3 we present the analytical calculations that lead to the upgraded version of the coupling function, in terms of both extension to lower energies and the altitude correction factor. Then results for the two FDs are shown in Section 4. Following the necessary computations, the spectrum of the primary cosmic rays is deduced and is then directly compared with the primary spectrum obtained from the GSM method. Finally, our results are verified and discussed in Section 5, where we discuss the benefits of the new coupling function and an outlook of future actions.

2 Data Selection

Two FD cases, using cosmic-ray data corrected for pressure and efficiency, are considered: those of March 2012 and of September 2017. The data were obtained by the high-resolution real-time Neutron Monitor Database (NMDB, http://www.nmdb.eu) (Mavromichalaki et al., 2011). The selection of the NM stations was based on the cut-off rigidity of each station that had to fulfill the energy requirement of $E_{\mathrm{cut}} \geq 1~\text{GeV}$, which translates to a rigidity requirement $R_{\mathrm{cut}} \geq 1.6~\text{GV}$, as well as their altitude. The selected stations cover a wide energy spectrum with $R_{\mathrm{cut}}$ ranging from 1.60–8.53 GV, as well as a wide range of stations’ altitudes, from sea level to 3.500 meters above. The main characteristics of the considered NM stations, such as geographic coordinates, cut-off energy and rigidity, altitude, mean atmospheric pressure and the altitude correction factor are given in Table 1.

Table 1 Characteristics of the neutron monitor stations considered for the study of the Forbush decreases of March 2012 and September 2017.

In the following, we provide a short description of the two selected FDs:

i) The Event of March 2012: In early March 2012, during the maximum phase of Solar Cycle 24, an array of significant solar X-ray flares were recorded. The FD starting on 7 March 2012 was associated with activity from the solar region AR 11429 (Livada, Mavromichalaki, and Plainaki, 2018) as identified from the National Oceanic and Atmospheric Administration (NOAA). This event consists of two distinct decreases. The Coronal Mass Ejection (CME) of 4 of March 2012 at 11:00 UT was the first of a series of CMEs that were observed between March 4 and 12. The strongest of them was associated with a NOAA GOES X-class flare (X 5.4) occurring on 7 March 2012 at 00:02 UT. The first CME was recorded by SOHO/LASCO on 7 March 2012 at 00:24 UT reaching a maximum plane-of-sky speed of 2684 km/s and a second one followed shortly thereafter at 01:30 UT, with plane-of-sky speed peaking at 1825 km/s. The shock produced from these two CMEs arrived at geospace on 8 March 2012 at 11:05 UT causing a severe geomagnetic storm (Patsourakos et al., 2016).

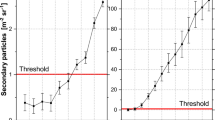
The average value of the FD amplitude (minimum recorded value of the CR intensity) reached 12%. The corrected for pressure and efficiency hourly cosmic-ray data, were normalized to the mean intensity of the 5 March 2012, two days before the event. The time profile of the normalized cosmic-ray intensity from all NM stations considered is presented in Figure 1. We note that the recorded amplitude from the stations of ATHN, ROME and BKSN (the ones with the largest cut-off rigidities) has a smaller value compared to the amplitude recorded from the remaining six stations (JUNG, LMKS, KIEL, IRKT, NEWK and YKTK).

Figure 1

Time profile of the normalized cosmic-ray intensity decrease recorded at nine neutron monitor stations during the time period 6–18 March 2012. The mean value of the interval 5–6 March 2012 was used for normalization.

It should be noted that the Yakutsk station (YKTK), considered here, has a cut-off rigidity of 1.65 GV which corresponds to an energy cut-off of 0.96 GeV. While this value is technically borderline outside the energy spectrum of our coupling function ($E_{\mathrm{cut}} \geq 1~\text{GeV}$), we chose to include the station in order to test the behavior of the coupling function even in the case that the lowest energy limit is slightly exceeded.

ii) The Event of September 2017: For the second event under study, we consider the FD occurring between 6–13 of September 2017. It is worth mentioning that September 2017 was by far the most active month concerning proton flux and intensities that originated from solar eruptions in Solar Cycle 24 (Mavromichalaki et al., 2018). More specifically, 23 M- and 4 X-Class flares, along with and 3 fast CMEs, took place and were recorded by SOHO/LASCO and GOES instruments. All X-Class flares originated from the active region NOAA AR 12673. The solar events associated with the FD are two of the aforementioned X-Class flares. The first one was a GOES X2.2 flare at 08:57 UT on 6 September 2017, followed by a GOES X9.3 flare at 11:53 UT on the same day. These flares were associated with a CME with plane-of-sky speed peaking at 1238 km/s (Mavromichalaki et al., 2018; Kurt et al., 2019; Livada and Mavromichalaki, 2020).

For the study of this event, hourly cosmic ray corrected for pressure and efficiency data from eight (8) NM stations were processed. We note that acquisition of the BKSN station data during this period was not possible. These data were normalized to the mean value of the quiet interval 5–6 September 2017. The average amplitude of this FD was calculated to about 7%. The time profile of the secondary cosmic-ray intensity of each station is illustrated in Figure 2. We again note that the amplitude recorded from the stations ATHN, CALM, ROME with high cut-off rigidity, is smaller than the one recorded by the remaining five stations: JUNG, LMKS, NEWK, IRKT and YKTK. We also note that the largest amplitude (9.48%) is recorded at the YKTK NM station that has the lowest cut-off rigidity (1.65 GV) of all stations considered here.

Figure 2

Time profile of the normalized cosmic-ray intensity for the time period 6–13 September 2017. The mean value of the interval 5–6 September 2017 has been used for normalization.

3 Improvements of the Coupling Function

Many of the calculations of this section are identical to those of Xaplanteris et al. (2020), meaning the choice of the same Lagrangian density, $L$, as the initial point of the computations (Peskin and Schroeder, 1995; Srednicki, 2007; Bilal, 2011):

$$ L = \frac{1}{2} ( \partial _{\mu } \Phi _{1} )^{2} + \frac{1}{2} ( \partial _{\mu } \Phi _{2} )^{2} + \frac{1}{2}m_{1}^{2} \Phi _{1}^{2} + \frac{1}{2}m_{2}^{2} \Phi _{2}^{2} - \frac{\lambda }{2!2!}\Phi _{1}^{2}\Phi _{2}^{2}, $$

(1)

where $\Phi _{1}$, $\Phi _{2}$ are the scalar fields describing the proton and neutron, respectively, $m_{1}$, $m_{2}$ their corresponding masses and $\lambda$ is the coupling constant of our calculations.

Assuming also the same form for the counter terms with the previous work (see also Peskin and Schroeder, 1995; Weinberg, 1995), we deduce the same analytical form for the 4-point function, which represents the probability amplitude for the interaction of two incoming and two outgoing particles:

$$ G^{(4)} = - i(2\pi )^{4}\frac{\hat{\lambda }_{0}}{1 - \frac{3\hat{\lambda }_{0}}{8\pi ^{2}}\ln ( \frac{E}{E_{\mathrm{cut}}} )}, $$

(2)

where $\hat{\lambda } _{0}$ is a constant to be determined by the normalization condition and $E_{\mathrm{cut}}$ is the energy cut-off above which this function is valid.

3.1 Energy Spectrum

The first improvement attempted here is a change in the assumed model for the particle interactions that result in neutron production. In more detail, the primary protons that penetrate Earth’s atmospheric layers move towards the surface. In their path they interact with atmospheric particles (O₂, N₂ etc.) resulting in the production of secondary neutrons (among other particles). In our previous work the interaction model that was taken into account was of the form

$$ p^{ +} \rightarrow p^{ +} + n + \bar{n}, $$

(3)

meaning that a primary proton produces a new proton of lower energy and neutron-antineutron pair.

In spite of its simplicity, the major disadvantage of this model is that the primary proton has to have sufficient energy to give rise to three particular products. This further resulted in a very large energy cut-off of $E_{\mathrm{cut}} \geq 3~\text{GeV}$.

In this work we adopt a generalized secondary particles production model of the form

$$ p^{ +} + X \rightarrow p^{ +} + A + n, $$

(4)

meaning that the collision of a primary proton with a large atmospheric particle-target $X$ (atmospheric molecule) results in the production of a new proton (again with lower energy that the initial one), a neutron and another large particle $A$. It is practically as if we assume that the secondary neutron escapes from the X-target particle as a result of the collision. We also assume that after the collision the produced proton and neutron continue their motion towards the surface (Dorman, 1974).

For the remainder of our calculations the two large atmospheric particles $X$, $A$ will be assumed to remain at rest due to their large masses compared to nucleon mass. With this assumption the new energy cut-off is computed as

$$ E_{p} + M = E_{p}' + M' + E_{n}, $$

(5)

where $M$, $M'$ are the masses of the atmospheric particles $X$, $A$, respectively.

If we assume that the produced secondary neutron escapes from particle $X$ after the collision then the atmospheric particle masses $M$, $M'$ will differ by 1 GeV: $M = M' + 1$.

Also If we further assume that the secondary proton and neutron are produced at rest, then $E'_{p} = E_{n} =1~\text{GeV}$. So, after substitution of the above to Equation 5 we find the new upgraded energy cut-off to be 1 GeV under our new model.

Our changed interaction model will cause further modifications in our previous calculations, particularly in the Lehmann, Symmanzik, Zimmermann (LSZ) formula which provides the scattering amplitude of the interaction (which now consists of five particles) (Weinberg, 1995; Griffiths, 2008). The scattering amplitude formula is given by

$$ S_{fi} = \prod_{i = 1}^{2} \biggl(\frac{1}{\sqrt{2E_{i}}} \frac{1}{ ( 2\pi )^{3/2}}\biggr)G^{(4)}\prod _{j = 1}^{3} \biggl(\frac{1}{\sqrt{2E_{j}}} \frac{1}{ ( 2\pi )^{3/2}}\biggr), $$

(6)

where $i$, $j$ correspond to the primary and secondary particles, respectively.

We further assume that the two atmospheric particles are practically at rest because of their large masses, so Equation 6 reduces to

$$ S_{fi} = \frac{1}{2^{3/2}}\frac{1}{ ( 2\pi )^{15/2}} \frac{1}{\sqrt{0.24}} \frac{1}{\sqrt{4M'M}} \frac{1}{E^{3/2}}G^{(4)}, $$

(7)

where $E$ is the energy of the primary proton and we have also assumed that the secondary proton is left with 60% of its initial energy (Dorman, 1974) and that the remaining energy is appointed to the secondary neutron and the produced (still) particle $A$.

Thus, the new coupling function is determined as

$$ W(E) = \vert S_{fi} \vert ^{2} = 1.65\times 10^{ - 2}\frac{1}{E^{3}} \biggl[ \ln \biggl( \frac{E}{E_{\mathrm{cut}}} \biggr) \biggr]^{2} \biggl[ \frac{5}{1 - 0.095\ln ( \frac{E}{E_{\mathrm{cut}}} )} \biggr]^{2}, $$

(8)

where $E_{\mathrm{cut}} = 1~\text{GeV}$, the new energy cut-off.

We note that the value of $M$ used for the determination of Equation 8 was that of nitrogen, meaning: $M = 14m_{p} = 14~\text{GeV}$.

We should also note that normally the coupling function would be given by Equation 8 with integrations over the possible energy values of all particles involved (except for the energy of the incident proton which would remain the only free parameter): $\int|S_{fi}|^{2}dE_{X}dE_{A}dE_{n}dE_{p'}$. Since in our assumed interaction the atmospheric particles are considered to be at rest and the energies of the secondary neutron and proton are specifically defined in relation to the energy of the incident proton (40% and 60% of its energy, respectively), the integrations are omitted (analytically we have included appropriate delta functions of the form, $\int dE_{X}\delta(E_{X} - M)/E_{X} = 1/M$ for each particle). So the constant in front of Equation 8 has to carry dimensions of $\text{GeV}^{2}$ in order for the coupling function $W(E)$ to have the desired dimensions of 1/GeV.

Moreover the value of $\hat{\lambda}_{0}$ constant from Equation 2 was chosen as $\hat{\lambda}_{0} =5$. This would normally by determined by the normalization condition of our function, namely

$$ \int _{0}^{\infty } W(E) dE = 1 $$

(9)

but since our function is valid only for the energy region $E \geq 1~\text{GeV}$, it was chosen so that it fits with other widely used coupling functions, as can be seen in Figure 3 above.

Figure 3

Direct comparison of the newly computed coupling function with other widely used coupling functions.

From Figure 3 it becomes evident that the newly derived coupling function, although it is in good agreement with the Dorman function (Dorman et al., 2000), it differs in shape with the other two, especially in the lower energy region. In order to assess the level of agreement between the newly derived function and the Caballero–Lopez (C–L) and Moraal function we present in Figure 4 a scatter plot between the values of both functions for energies from 1 GeV up to 50 GeV with step of 1 GeV. In this plot we have used a fit function of the form

$$ f(x)=ax\exp(-x/b), $$

(10)

with $a,b$ the fit parameters.

Figure 4

Scatter plot between the newly derived coupling function and the one of C–L & Moraal for energies from 1–50 GeV with step of 1 GeV.

In order to assess the goodness of the fit we compute the Spearman rank correlation coefficient, which is given by

$$ r_{s} =1- \frac{6 \sum_{i}d_{i}^{2}}{n(n^{2}-1)}, $$

(11)

where $n$ is the number of data values considered (in our case 50, energies from 1 GeV up to 50 GeV with step 1 GeV) and di is the difference of the ranks between each pair of values.

For our case we find that the Spearman coefficient is, $r_{s}=0.887$. As we can see from Figure 4 the value of $R$ is, $R = 0.856$. These two parameters suggest good agreement between the values of the two functions in general. It should be noted that the marker points on the far right, the ones that deviate the most, are the ones that correspond to energy of 1, 2, 3 GeV and so on (from right to left). Meaning that the deviation between the two coupling functions is mostly evident in the lower energies, whereas in higher energies the two functions are in satisfactory agreement (marker points on the left). The reason for this deviation in the lower energies is the fact that in our assumed model we are accounting only one possible process, namely production of secondary neutrons, which are the main contributor to NM hits. On the contrary, C–L and Moraal function takes into account muons, Cherenkov and stratospheric balloon detectors. The fact that other important processes, such as deep inelastic processes, thermalization and diffusion of the secondary neutrons etc, are not considered in our calculations means that our theory is not normalized, as mentioned above, in Equation 9, thus leading to differences in the lower energy region. Another reason for the different behavior in the lower energy region is of course the different technique followed for the derivation of each function. C–L and Moraal function are derived using a Monte Carlo simulation tool whereas our function is derived purely analytically.

3.2 Altitude Correction

The second major improvement in our theoretical computations is the determination of an altitude correction factor based on a realistic model of atmospheric structure. We note that this factor, while included in our calculations in our previous work (Xaplanteris et al., 2020), was derived by means of a fairly simplistic approach, namely that the atmospheric particle concentration is proportional to altitude. Here we assume that the atmospheric particle concentration follows a Boltzmann distribution:

$$ n = n_{0}\exp \biggl( - \frac{U - U_{0}}{kT} \biggr) = n_{0}\exp \biggl( - \frac{mgh}{kT} \biggr), $$

(12)

where $n_{0}$ is the concentration of atmospheric particles at ground level, $m$ is the (an average) mass of atmospheric particles, $g$ is the gravitational acceleration, $h$ is the altitude, measured from sea level upward, $k$ the Boltzmann constant and $T$ the absolute temperature (K).

For the absolute temperature we use the relation (NACA Report, 3182)

$$ T(h) = T_{0} - ah, $$

(13)

where $T_{0} = 296~\text{K}$, is the sea level temperature, $\alpha = 0.008~\text{m/K}$ and $h$ is the altitude.

Assuming the atmospheric particles follow Equation 12, then, for a NM station at altitude $H$, the percentage of particles that are above this altitude, thus contributing to this station’s counts, is given by

$$ F'(h) = \frac{\int _{H}^{h_{u}} n_{0}\exp ( - \frac{mgh}{kT(h)} ) dh}{\int _{0}^{h_{u}} n_{0}\exp ( - \frac{mgh}{kT(h)} ) dh}, $$

(14)

where $h_{u}$ is the upper limit of the atmosphere for the geomagnetic coordinates of this NM station. This is taken as follows:

• i) For high latitude NM stations (ATHN, ROME, CALM, NEWK), $h_{u} = 18.000~\text{m}$

• ii) For middle latitude NM stations (BKSN, JUNG, LMKS, IRKT), $h_{u} = 15.000~\text{m}$

• iii) For low latitude NM stations (KIEL, YKTK), $h_{u} = 8.000~\text{m}$.

We note that in the computations that follow in Section 4 we will actually use the inverse of the factor given in Equation 14. As a result, the values of the altitude’s correction factor that are given in Tables 1 and 2 are determined by

$$ F_{al}(h) = \frac{1}{F'(h)}. $$

(15)

In Figure 5 below we present the coupling function, given by Equation 8 for four different atmospheric depths. The change in variables can be done using the barometric equation (NACA Report, 3182):

$$ p(h) = p_{0} \biggl( \frac{T_{0} - ah}{T_{0}} \biggr)^{n}, $$

(16)

where $p_{0}$ is the pressure at sea level and $n = 5.2561$, the dimensionless exponent.

Figure 5

Coupling function of a neutron monitor for different atmospheric depths.

Table 2 The recorded FD amplitude and the calculated one of the primary CRs for each NM station for the event of March 2012.

4 Application to Forbush Decreases

After the computation of the coupling function $W(E)$, Equation 8, as well as the altitude correction factor, Equation 15, we proceed with the application of these results to the case of the two Forbush decreases discussed in Section 2.

The initial point of the application will be the relation between secondary and primary Cosmic Ray intensities (Clem and Dorman, 2000):

$$ \frac{\delta N(t)}{N} = \int _{E_{\mathrm{cut}}}^{\infty } W(E)\frac{\delta D(E,t)}{D} dE, $$

(17)

where $W(E)$ is the calculated coupling function, Equation 8, $\delta N(t)/N$ is the secondary CR intensity spectrum as a function of time provided by NMDB data and $\delta D(E,t)/D$, is the primary CR intensity spectrum as a function of both energy and time, which will be determined.

This relation between primary and secondary CR intensities is determined by the coupling coefficients method, introduced by Dorman (1974), which is one of the most frequently used methods for the derivation of the primary cosmic-ray spectrum.

Following the same assumption as in the previous work (Xaplanteris et al., 2020), we express the primary CR spectrum as a product of two different parts:

$$ \frac{\delta D(E,t)}{D} = \int _{0}^{t} \frac{\delta D_{I}(t)}{D}dt \int _{E_{\mathrm{cut}}}^{\infty } \frac{\delta D_{II}(E)}{D} dE. $$

(18)

The main difference from our previous work will be in the assumed form of the energy dependent part of the primary spectrum, meaning $\delta D_{II}(E)$. More specifically, in our previous study we assumed a rather simple form of a power law:

$$ \frac{\delta D_{II}(E)}{D} = kE^{ - \gamma }, $$

(19)

with a constant value for $\gamma$, the energy spectrum exponent.

This time we will attempt to use a potentially more realistic form with a variable exponent $\gamma$ as a function of time:

$$ \frac{\delta D_{II}(E)}{D} = \int _{E_{\mathrm{cut}}}^{\infty } \biggl( \frac{E}{E_{\mathrm{cut}}} \biggr)^{ - \gamma (t)}dE. $$

(20)

The time dependent values for $\gamma$ are taken from (Livada, Mavromichalaki, and Plainaki, 2018; Livada and Mavromichalaki, 2020). For the FD of March 2012 daily values for $\gamma$ are given whereas for the event of September 2017, 12-hour values of the exponent $\gamma$ are used.

With the use of the energy spectrum exponent $\gamma$ as a function of time, the primary Cosmic Rays spectrum as a function of time is determined by

$$ J(t) = \frac{\delta D_{I}(t)}{D} = \frac{1}{I}\frac{1}{C}F_{\mathrm{al}} \frac{\delta N(t)}{N}, $$

(21)

where $I = \int _{E_{\mathrm{cut}}}^{\infty } W(E) dE$ and $W(E)$ is given by Equation 8,

$$ C = \int _{E_{\mathrm{cut}}}^{\infty } \biggl( \frac{E}{E_{\mathrm{cut}}} \biggr)^{ - \gamma (t)}dE, $$

is the energy dependent part of the primary CR intensity, $F_{\mathrm{al}}$ is the altitude correction factor given by Equation 15, $\delta N(t)/N$ is the secondary CR intensity spectrum given directly by NMDB data.

After the application of our results we determine the primary CR intensity spectra which are presented in Figures 6 and 7. The final results regarding the amplitude of the two Forbush decreases for the secondary and primary CRs are also summarized in Tables 2 and 3, respectively.

Figure 6

Time profile of the CR intensity from nine stations in the heliosphere using the new coupling function (upper panel) for the FD of March 2012. A direct comparison of the mean value of CR intensity with the corresponding one of CRs of 10 GV taken from the GSM technique is given in the lower panel.

Figure 7

Time profile of the CR intensity in the heliosphere using the new coupling function (upper panel) for the FD of September 2017. A direct comparison of the mean value of intensity with the corresponding one of CRs of 10 GV taken from the GSM technique (lower panel) is attempted.

Table 3 The recorded FD amplitude and the calculated one of the primary CRs for each NM station for the event of September 2017.

As a first qualitative comment of the results for the primary CR spectrum we see that the time profiles follow the corresponding time profiles for the secondary CR spectrum in both cases. Moreover, the computed time profiles from each NM station are in good agreement with one another as expected, since outside Earth’s atmosphere the effects that modulate the secondary CR intensities and amplitudes (such as air concentration, meteorological conditions etc) are absent. As a result, the computed values for the primary spectrum from each NM station should be significantly close.

c) Comparison of the two methods

For a more quantitative evaluation of the results, the time profiles of the primary CR spectrum for the two FDs under study, Figures 6 and 7 (upper panels), are compared with the corresponding ones using the GSM technique (lower panels). This method was first introduced in 1970 and uses the worldwide NM network as a multi-directional device, taking into account the different geographical characteristics of each station (Belov et al., 2018). This approach makes it possible to determine the first two angular moments of the distribution function of CRs in the interplanetary space on an hourly basis. The values for the FD amplitude of the primary cosmic rays of the two events by the two techniques are given in Table 4.

Table 4 Primary FD amplitude values obtained by the newly computed coupling function as well as by the GSM technique for the two studied events.

We note that the time profiles of the primary CRs for the two FDs under study follow the same general behavior, meaning that the minimum values and the recovery periods are very similar, particularly for the event of March 2012. However, the most important result is the agreement of the amplitude values of the primary CR spectrum for both events, especially for the case of September 2017 (Table 4). The scatter plots for the two studied FDs given in the corresponding Figures 7 and 8 reveal the level of the correlation between the CR values outside the atmosphere derived using the GSM technique and the mean values of the primary CR spectrum calculated by the new updated function.

Figure 8

Scatter plot of the CRs of rigidity 10 GV obtained from the GSM method and the mean value of primary CR intensity by the newly computed function for the FD of March 2012.

As we can see from Figures 8 and 9 there is good agreement between the values of the primary CR spectrum derived by the two methods. More specifically for the FD of March 2012 we see from Figure 8 that the values of the slope as well as the Pearson correlation coefficient are significantly close to unity, $p1 = 1.154(\pm 0.055)$ and $R = 0.956$, suggesting a strong agreement between the two sets of results. The same result is also outlined from Figure 9 for the event of September 2017, where the corresponding values are $p1 = 1.018(\pm 0.077)$ and $R = 0.946$, suggesting once again a very good agreement between the two used different methods.

Figure 9

Scatter plot of the CRs of rigidity 10 GV obtained from the GSM method and the mean value of primary CR intensity by the newly computed function for the FD of September 2017.

5 Discussion and Conclusions

In this work a coupling function between primary and secondary cosmic-ray particles is derived based on analytical calculations with the purpose of proposing a new, fully analytical method of deriving the primary CR spectrum. The basis of the analytical computations is the previous, approximate version of the coupling function that appeared in Xaplanteris et al. (2020), which made use of fundamental Quantum Field Theory tools and techniques, such as Feynman graphs and renormalization phenomena. The improvements discussed in this work include:

• i) A widened energy spectrum in which the coupling functions are valid and applicable. More specifically, this newer version of the new coupling function is valid for energies of the primary protons above 1 GeV ($E_{\mathrm{cut}}=1~\text{GeV}$), as opposed to $E_{\mathrm{cut}}=3~\text{GeV}$ in the previous version. This improvement was achieved by the assumption of a new more realistic interaction model for the production of the secondary neutrons, given by Equation 5.

• ii) The inclusion of a more accurate and precise altitude correction factor in our calculations, given by Equation 13. This correction factor was also deduced analytically, under the assumption that the concentration of atmospheric particles follows a Boltzmann distribution as a function of altitude. In the previous study, the altitude correction factors were determined approximately.

• iii) The use of variable cosmic-ray energy spectrum exponent $\gamma$, as a function of time. In the previous work the value of the energy spectrum exponent was assumed to be constant during the studied Forbush decreases. This time the exponent $\gamma$ was treated as time-variable in the calculations, with values taken from the work of Livada and Mavromichalaki (2020).

It is noteworthy that the finalized version of the newly derived coupling function given by Equation 8 and presented in Figure 3 compares well with some of the most widely used coupling functions in cosmic-ray studies. As can be seen, our results are in very good agreement with those of Caballero-Lopez and Moraal (2012), Clem and Dorman (2000) and especially Dorman et al. (2000), despite using a completely new analytical approach. In more detail, the major difference between the newly derived function and the one of C–L and Moraal becomes evident in the lower energy region as can be seen in Figure 4. The difference between the two functions is due to the fact that in our analytical model we focused solely on the production of secondary neutrons, which is the dominant process for NM hits whereas C–L and Moraal function takes into account more contributing processes. Moreover, the expansion of the previous results to lower energy regions (from 1 GeV to 3 GeV) for different atmospheric depths given in Figure 5 seems to be satisfactory, yielding valid results.

After the calculation of the three crucial improvements discussed above, the newly derived coupling function is applied to two Forbush decreases, on March 2012 and September 2017. We find that the primary CR spectrum that is obtained from the application of Equation 19 (Figures 6 and 7), shows the same form as the one of the secondary cosmic rays (Figures 1 and 2), meaning that the minimum values of the FD amplitude appear at the same time and the recovery periods are also similar in both cases. Moreover, the calculated amplitudes for the primary spectrum from each NM station are significantly close as can be seen from the amplitude deviation values (Tables 2 and 3), which is also an expected result (Livada and Mavromichalaki, 2020) due to the absence of atmospheric modulation effects. For a more valid confirmation of our results, a direct comparison between them and the corresponding results for the primary CR spectrum derived from the GSM technique is also presented in Figures 6 and 7 as well as in the corresponding scatter plots, Figures 8 and 9. The plots determined by both methods appear to agree significantly (lower panels in Figures 6 and 7), especially for the Forbush decrease of March 2012. Also the Forbush decrease amplitudes for the primary spectrum computed by both techniques appear to be in a very satisfactory agreement (Table 4), especially for the case of September 2017. The strong agreement between the two sets of results for the primary CRs also becomes evident from the correlation coefficients of the two scatter plots (Figures 8 and 9).

Further improvement of this coupling function could involve the extrapolation of these results to energies lower than 1 GeV. This will render this coupling function applicable for all Neutron Monitor stations of the NMDB global network without any exceptions or limitations. Moreover, the applicability of these results and methodology for the case of Ground Level Enhancements (GLEs) is another possible direction of our study (Mavromichalaki et al., 2010). If the application of the updated coupling function to this different category of cosmic-ray phenomena yields again satisfactory results, meaning significantly similar primary CR spectra from different NM stations as well as strong agreement with the corresponding results from other methods (e.g. GSM technique), then the validity of these results will be further expanded. Lastly, inclusion of different processes, such as deep inelasticity, thermalization and diffusion of the secondary neutrons etc, in our model will be also attempted although in a fully analytical way. All these studies will be very useful to Space Weather applications.