Automated Detection of Chromospheric Swirls Based on Their Morphological Characteristics

Abstract

High-resolution observations have revealed that rotating structures known as “chromospheric swirls” are ubiquitous in the solar chromosphere. These structures have circular or spiral shapes, are present across a broad range of spatial and temporal scales and are considered as viable candidates for providing an alternative mechanism for the heating of the chromosphere and corona. Therefore, an accurate determination of their number and a statistical study of their physical properties are deemed necessary. In this work we present a novel, automated swirl detection method, which utilizes image pre-processing, curved structure tracing and machine learning techniques that allow for the detection of swirling events based on their morphological features as they appear in chromosphere filtergrams. The method is applied to H$\alpha$ chromospheric spectral line images obtained by the CRisp Imaging Spectropolarimeter (CRISP) at the Swedish 1-m Solar Telescope (SST). It is also tested on grayscale images of vortical sea current flows represented/visualized by synthetic streamlines from the NASA/Goddard Space Flight Center Scientific Visualization Studio. The results are rather encouraging since swirling events are successfully identified. Further improvements of the algorithm, its prospects for the detection and statistical studies of the properties of these events using a wide range of imaging data and its potential application in other scientific fields for the detection of rotating motions are discussed.

1 Introduction

Quiet-Sun vortical motions of various scales have been extensively detected in solar high-resolution observations. The existence of these type of motions had already been predicted by theory (e.g. Stenflo, 1975; Spruit, Nordlund, and Title, 1990) and were found in numerical simulations (Stein and Nordlund, 2000; Shelyag et al., 2011; Kitiashvili et al., 2012; Wedemeyer-Böhm et al., 2012). They are driven by convective processes and are formed as a direct consequence of the conservation of angular momentum carried by the plasma. They are localized at the downdrafts of intergranular lanes where cooled plasma sinking towards the solar interior undergoes a forced rotation. At the photosphere they were identified either by the derived local velocity field behavior or by the swirling motion of small-scale magnetic field concentrations known as bright points (BPs). After the first detection of a vortex flow at the photospheric level (Brandt et al., 1988) several observations of vortices have been reported over the last years. Bonet et al. (2008) following the logarithmic spiral trajectories of BPs in high-resolution G-band images obtained with the Swedish 1-m Solar Telescope (SST; Scharmer et al., 2003) reported an occurrence rate of 1.8$\times 10^{-3}$ vortices Mm⁻² min⁻¹, with a mean radius of ∼0.5 Mm and a mean lifetime of ∼5 minutes. Bonet et al. (2010) updated the previous estimations, by visual inspection of magnetograms obtained by the Imaging magnetograph eXperiment (IMaX) on the 1-m balloon-borne SUNRISE telescope, to an occurrence rate of ≃ 3.1$\times 10^{-3}$ vortices Mm⁻² min⁻¹ with a mean duration of ∼7.9 minutes. Further studies of small-scale photospheric vortex flows by Balmaceda et al. (2010) and Vargas Domínguez et al. (2011) provided similar, small scale radii of 1 Mm and 0.25 Mm, respectively, while the latter by studying two datasets of SST G-band observations derived occurrence rates of 1.4$\times 10^{-3}$ vortices Mm⁻² min⁻¹ and 1.6$\times 10^{-3}$ vortices Mm⁻² min⁻¹. Large-scale photospheric vortex flows with diameters of ∼15.5 – 21 Mm and lifetimes longer than 1 h residing at quiet-Sun supergranular junctions, have been revealed by Attie, Innes, and Potts (2009). Requerey et al. (2018) detected a similar vortex flow at supergranular junctions which consisted of three recurrent vortices lasting for ∼7 h each and having diameters of ∼5 Mm.

Photospheric vortical motions often force co-localized magnetic fields within intergranular lanes, which penetrate the solar atmosphere from the photosphere upwards, to rotate thus producing co-rotating structures which are observed in the chromosphere as “chromospheric swirls” and in the corona as “magnetic tornadoes” (Wedemeyer and Steiner, 2014). Chromospheric swirls were initially detected by Wedemeyer-Böhm and Rouppe van der Voort (2009) while studying high-resolution images obtained in the Ca ii 8542 Å spectral line from the CRisp Imaging Spectropolarimeter (CRISP; Scharmer et al., 2008) at the SST. They appeared as dark rings, arcs or spiral-like rotating structures with diameters estimated at ∼1.5 Mm and upward flows of 2 to 7 kms⁻¹. Wedemeyer-Böhm et al. (2012) studied a number of 14 chromospheric swirls observed with CRISP/SST in the same line and derived typical diameters of ∼1.5 Mm, lifetimes of 12.7±4.0 min and an occurrence rate up to 3$\times 10^{-3}$ swirls Mm⁻² min⁻¹. Simultaneous observations with the Atmospheric Imaging Assembly (AIA; Lemen et al., 2012) onboard the Solar Dynamics Observatory (SDO; Pesnell, Thompson, and Chamberlin, 2012) at several energy channels mapping the transition region and the corona revealed the signature of such swirls higher up. Park et al. (2016) were the first to report a chromospheric swirl observed with the CRISP/SST in the H$\alpha$ absorption line wavelengths. This swirl was simultaneously observed in the Ca ii 8542 Å spectral line and higher up in the Mg ii K and Mg ii strong UV lines observed with the Interface Region Imaging Spectrograph (IRIS; De Pontieu et al., 2014). Examining the same set of observations, Tziotziou et al. (2018) revealed a quiet-Sun, persistent (of at least 1.7 h duration) small-scale “tornado” with a radius of ∼2.2 Mm which had a significant substructure in the form of several smaller swirls. Recently, a multiwavelength study of chromospheric swirls in the H$\alpha$ and Ca ii 8542 Å lines, as well as in the photospheric Fe i line from Shetye et al. (2019) revealed structures with typical radii of 2 Mm and 10 min durations.

As rotating features are ubiquitous in the solar atmosphere their detection, their number, as well as a statistical analysis of their properties, such as lifetimes and radii, is a fundamental issue. In order to take advantage of the large amount of the available observations an automated detection technique is needed to reliably identify them in the solar images without manual intervention. In recent years several techniques have been proposed for the automated detection of vortex flows observed at the photospheric level in an attempt to avoid previous commonly used methods based on visual inspection (Bonet et al., 2008; Balmaceda et al., 2010; Wedemeyer-Böhm et al., 2012). Almost all these automated detection methods are based on the estimation of the horizontal velocity field of the vortical flows by using the Local Correlation Tracking (LCT; November and Simon, 1988) or the Fourier Local Correlation Tracking (FLCT; Fisher and Welsch, 2008) techniques applied on 2D intensity maps obtained from observations or numerical simulations. Once the velocity field is estimated a method established by Graftieaux, Michard, and Grosjean (2001) for the study of turbulence in fluid dynamics is very often used for vortex detection. According to this method two functions $\Gamma _{1}$ and $\Gamma _{2}$ are defined, which are used to identify the centers and boundaries of vortices. Giagkiozis et al. (2017) made use of LCT before applying the $\Gamma$ functions for the identification of centers and boundaries of vortices in CRISP observations, while Liu, Nelson, and Erdélyi (2019) made use of FLCT before applying this method to synthetic data, numerical simulations and observations. Kato and Wedemeyer (2017) used an LCT input velocity field obtained from 3D numerical simulations and the concept of the “vorticity strength” or “swirling strength” (Zhou et al., 1999), which is the imaginary part of the eigenvalues of the velocity gradient tensor, to automatically find swirling features in flows projected on a two-dimensional plane of view. These techniques, however, do not determine precisely or objectively the boundaries of vortices and do not convey on the true long-term swirling motions on a time-varying field. Quite recently, the Lagrangian-averaged vorticity deviation (LAVD) technique, which was developed by Haller et al. (2016) for turbulent fluids, has been introduced to objectively identify vortex boundaries. It takes into account the variance of the examined quantities and makes use of the invariant Lagrangian-averaged vorticity deviation parameter, in order to objectively (i.e. invariantly under time-dependent rotations and translations of the observer) determine the borders of the vortex flow in two or even three dimensions (de Souze e Almeida Silva et al., 2018). Rempel et al. (2017) and de Souze e Almeida Silva et al. (2018) applied this technique to detect vortices in plasmas. A novel dynamical equation of the swirling strength has been more recently introduced by Canivete Cuissa and Steiner (2020). The evolution equation was applied on radiative magneto-hydrodynamical simulations of the solar atmosphere produced with the CO⁵BOLD code. It is found that the swirling strength and its evolution equation are very important for the identification of vortices and for obtaining precise information about their formation, dynamics and evolution.

The vortex detection methods proposed so far have their strengths and weaknesses. Results from applying them to observational or simulated data show that vortex flows are very abundant in the solar surface with a continuous distribution of diameters and lifetimes. All methods, however, give small mean values for both parameters (i.e. of some decades of km and some decades of seconds, respectively). This probably means that these methods fail to detect longer lived and larger vortex flows. Another important weakness is that they have as an input the horizontal velocity field, which should be estimated with sufficient accuracy. The horizontal velocity field, however, is usually estimated utilizing LCT (or similar techniques), which has several limitations (Verma, Steffen, and Denker, 2013) and must be used with caution.

As mentioned before, swirling events are found to be quite common in the solar chromosphere. As they link the lower solar layers with the corona they may play an important role in the energy channeling to the upper solar layers by the transport of Poynting flux (Wedemeyer-Böhm et al., 2012) and/or by the dissipation of various types of MHD waves (Tziotziou, Tsiropoula, and Kontogiannis, 2020). However, given the complexity of the chromospheric pattern, estimation of the horizontal velocity field using LCT is rather impossible at this level. It is thus imperative to have a method that unambiguously detects them allowing the accurate estimation of their abundance in the solar chromosphere. Their detection will also permit the determination of their physical properties, such as radii and lifetimes, which is an important step towards the estimation of their contribution to the energy transport in the solar atmosphere.

The aim of this work is to introduce a novel automated detection method for the identification of chromospheric swirls which is based on their morphology as revealed in chromospheric H$\alpha$ filtergrams. In contrast to other methods, our method avoids the limitations of the LCT, which is hardly applicable to chromospheric images and is based on the identification of the features solely from their shapes. This paper is organized as follows: In Section 2 we give a short description of the observations used, in Section 3 the different stages of the methodology and the corresponding results are presented, in Section 4 the conclusions and the prospects for future work are given, while in Appendix A the flow chart of the method is provided and in Appendix C the results of the application of the proposed methodology to synthetic data are shown.

2 Observations

The developed chromospheric swirl detection algorithm is tested and applied to quiet-Sun CRISP/SST observations recorded on June 7, 2014 with a 4 s cadence at seven wavelengths along the H$\alpha$ and Ca ii 8542 Å spectral line profiles resulting in ∼700 images per wavelength per spectral line. The field-of-view (FOV) roughly covers a $60^{\prime\prime} \times 60^{\prime\prime}$ (1017×1017 pixels on the CRISP FOV) area. We refer the reader to Park et al. (2016), Tziotziou et al. (2018) and Tziotziou, Tsiropoula, and Kontogiannis (2019) for further details concerning the observations acquisition, the CRISP data reduction pipeline and the preparation of the datacubes.

For the implementation of the algorithm the 100 to 200 H$\alpha -$0.26 Å filtergrams of the time series of the first observing interval were used. This particular H$\alpha$ wavelength was chosen because according to Tziotziou et al. (2018) it is in this wavelength that swirling motions are best visible, while the particular subset of images was chosen due to the clarity of the swirls during the corresponding time interval and the existence of less low quality images compared to other time intervals of the time series. It has to be noted that no swirl detection method has been applied so far on H$\alpha$ observations due to the extreme complexity of the chromosphere when observed in the center and near-line center wavelengths of this line. Nonetheless, we note that the applicability of the method is not restricted only to the H$\alpha$ observations, as further discussed in Section 4.

In order to examine both the applicability and the reliability of the proposed method in other scientific fields where turbulence forms swirling flows, a synthetic image produced by a model that simulates ocean flows is used. More information on the synthetic image used and the obtained results are presented and discussed in Appendix C.

3 Methodology and Results

The main goal of the entire procedure is to automatically identify swirling events in solar images based on their morphological characteristics. In order to detect potential swirling phenomena in space and simultaneously track them in time, a solar image datacube of specified time interval is required. The designed methodology/algorithm outputs the coordinates of the detected swirls by adopting a parametrization based on current knowledge concerning physical properties of chromospheric swirls, such as radii, velocities and lifetimes. However, because even the most significant physical properties of swirls are not yet known in a definitive way, the algorithm was designed in a parametrized form, so as the different parameters could be easily modified. The proposed method can be divided in a series of standalone stages that represent the basic steps of the entire procedure. These stages can be summarized as follows:

• i) Image pre-processing. It includes filtering, scaling and thresholding and is applied individually to each of the original images. It outputs thresholded images with dark structures that will be the objects of further processing.

• ii) Tracing of highly dark curved structures. To attack this problem, a method is developed oriented to the tracing of dark structures (due to the fact that chromospheric swirls appear dark in H$\alpha$ and Ca ii IR solar images) with high curvature in the thresholded images. Again this stage is applied individually to each image.

• iii) Selecting and combining traced, curved segments. To this end, a method is developed for the selection of curved segments of interest and the estimation of their centers of curvature. It uses certain exclusion criteria that are based on physical quantities, such as, curvature degree, maximum velocities, minimum swirl lifetime and minimum expected radius. The selected traced segments along with their centers of curvature are combined over a specified time interval containing a number of consecutive images.

• iv) Clustering of the calculated centers of curvature in space and time. A two-level clustering process is adopted here. The first level utilizes the Density-Based Spatial Clustering of Applications with Noise (DBSCAN) method to cluster together the centers of curvature encountered in a set of consecutive images over the specified (narrow) time interval. The clustered centers are then associated with their respective segments providing swirl candidate areas. Then, a second level clustering is performed over the centers of swirl candidates from the entire image sequence, or a selected subset of it, to characterize the most persistent swirl candidates, which are also consistent with the prescribed physical parameters, as swirls.

A schematic description of the developed algorithm for the swirls detection is given in Appendix A as a flow chart, while a detailed description is provided in the following subsections.

3.1 Image Pre-Processing

The aim of the image pre-processing stage is to improve the quality of the images of the dataset under study by e.g. enhancing specific features for further analysis, detecting sharp discontinuities, which help to locate the boundaries of these features, suppressing noise and/or undesired distortions, etc., so that the features that will be beneficial for the solution of the problem at hand are highlighted.

3.1.1 Image Filtering

As a first step, the pre-processing stage involves the application of an edge enhancement method. The operator used in the present study is based on the difference of 2D Gaussian filters (kernels) with different smoothing radii. It is applied in each one of the original images of the dataset (Figure 1, top row). This operation results to an image with a scaled histogram, of uniformly distributed intensities around zero which correspond to intensities of dark and bright structures (Figure 1, bottom row). This particular filtering technique, often referred to as Difference of Gaussians (DoG), is frequently used to enhance/detect edges and is similar to the Laplacian to Gaussian (LoG) and the Difference of Boxes (DoB) edge enhancement techniques which are, however, less effective for the features of interest in the present study. This operator is essentially a bandpass filter constructed by the subtraction of two low-pass (Gaussian blurring) filters. In the two-dimensional case, the convolution between the DoG operator and the intensity function $z_{i}(x,y)$ at the $(x,y)$ pixel of the $n\times m$ field-of-view of the $i$th image of a dataset of $N$ images is defined as:

$$\begin{aligned} F_{i}(x,y)=\hat{DoG}\cdot z_{i}(x,y) =& (G_{\sigma _{1}}-G_{\sigma _{2}})* z_{i}(x,y), \end{aligned}$$

(1)

where the pair $x=0,1,\ldots,n-1$, $y=0,1,\ldots,m-1$, stands for the spatial coordinates of a pixel in an image and $G_{\sigma _{1}}$, $G_{\sigma _{2}}$ are the Gaussian functions with standard deviations $\sigma _{1}$ and $\sigma _{2}$, respectively. The value of the standard deviation of the above Gaussian kernels ($\sigma _{1}$ and $\sigma _{2}$, respectively) determines the level of blurring for each of the two convolutions occurred in the original image and is related to the blurring radius $r$ of the respective Gaussian convolution kernel. The choice of values for $r_{\sigma {1}}$ and $r_{\sigma {2}}$ depends both on the spatial resolution and the size of the smallest traced structure of the investigated dataset and should guarantee that details and compact dark structures with well-defined borders are maintained, while undesired pixel or subpixel level blurring is avoided. In our case their values are optimally set to 4 and 5 pixels, respectively, which roughly corresponds to half of the radius (in pixels) of the minimum traced circle. We furthermore note that the DoG operation removes a significant amount of noise which usually translates to artifacts, since it removes high frequency details (Figure 1, right column).

Figure 1

Top row: An original image from the H$\alpha$ dataset (left) and the corresponding histogram of the intensity values (right). Bottom row: The same image after the application of the Difference of Gaussians (DoG) operator (left) and the resulting symmetrical across zero histogram (right), where the high frequency values have been removed by the operator.

3.1.2 Image Scaling

The low quality of a significant number of images in the dataset, which translates to high levels of blurring and/or distortion due to seeing effects, led us to include an additional step in the pre-processing stage that involves an automated scaling of the filtered images.

It is known that for any set of measurements that follows the Gaussian distribution, 99.7% of them reside within the interval $[\mu -3\sigma ,\mu +3\sigma ]$ where $\mu$ is the mean and $\sigma$ the standard deviation of the distribution. We choose to exploit the fact that the distribution of the intensities of each DoG filtered H$\alpha$ image $i$ exhibits a Gaussian-like histogram (Section 3.1.1). Fitting a Gaussian probability density function to each histogram (Figure 2, top panel) provides an estimation of the respective $\mu _{i}$ and $\sigma _{i}$ of the intensity values for the $i$th image. We note that this is a working approach for this image scaling step, as the Gaussian of a 2D distribution is calculated differently resulting in two sigmas ($\sigma _{x},\sigma _{y}$) and that $\sigma _{i}$ should not be confused with $\sigma _{1}$ and $\sigma _{2}$ of the Gaussian kernels discussed in the previous subsection. Using the extracted parameters we automatically scale the ${i}$th image between a slightly wider interval, i.e. $[\mu _{i}-4\sigma _{i},\mu _{i}+4\sigma _{i}]$, to include the majority of the histogram values. This scaled, single-channeled, grayscale image (Figure 3, bottom left panel) is more suitable for the application of the contrast-dependent adaptive thresholding technique that follows (Section 3.1.3). This automated image scaling step does not involve any additional parameters that need to be estimated, while it demands negligible computational time.

Figure 2

Top: The histogram of a single filtered image where the fit of the Gaussian to the distribution (light blue line) is used to determine the scaling interval ($[\mu _{i}-4\sigma _{i},\mu _{i}+4 \sigma _{i}]$, found between the red dashed lines). Bottom: Barplot of the FWHMs of the Gaussians of 40 H$\alpha$ filtered images of the dataset (images 7 – 46 of the time series) divided by the mean value of these 40 FWHMs (red dashed line corresponds to a ratio of 1), providing an estimation of their relative quality. From the barplot we can immediately deduce, for reference, the highest (24) and lowest (38) quality images of this particular set. The latter image was used as an example for the scaling plot provided in Figure 3. This information is useful since the quality of an image affects the final detection outcome.

Figure 3

Top row: A filtered image selected from the time series (left) and the corresponding binary image created by the application of the adaptive thresholding technique (right). Bottom row: The same filtered image as in the top row after the application of the scaling process (left) and the significantly improved adaptive thresholding-generated binary mask (middle). At the right panel the final image is presented as a combination of the filtered image and the binary mask, where negative-valued structures (dark areas) reside between zero-valued borders (white areas). The uniformly illuminated stripe at the bottom of the images is part of the FOV observed by the CRISP/SST instrument and deliberately included here, in order to demonstrate the effect of such artifacts on the pre-processing steps of filtering and adaptive thresholding.

This approach additionally provides an immediate evaluation of the quality of each image of the dataset, without actually displaying it, by using the Full-Width at Half-Maximum (FWHM) of its Gaussian distribution that is roughly $\simeq 2.355\sigma$. Low quality images result in narrow histograms with low FWHM values. To characterize automatically an image $i$ of the dataset under study as a low quality image, we simply compare the ratio of its FWHM$(i)$ value to the mean FWHM value computed over all images of the examined dataset (Figure 2, bottom panel). This enables us to decide whether a lack of detected vortex-like structures or a wide gap in the time evolution of the detected ones is due to a series of consecutive low quality images, or is not.

3.1.3 Image Thresholding

Thresholding is a process of partitioning an image into segments based on the values of pixels. There are several thresholding techniques (Sezgin and Sankur, 2004) that are widely used in various scientific fields, including solar physics. When varying illumination images are considered local thresholding techniques should be used, since they estimate a different threshold for every pixel in the image, based on the grayscale information of its neighboring pixels (Sauvola and Pietikäinen, 2000; Romen Singh et al., 2012; Roy et al., 2014).

Our method of choice after converting every filtered and scaled image of the dataset, represented by the function $F_{i}(x,y)$, $i=0,1,\ldots,N-1$, into an 8-bit grayscale image $f_{i}(x,y)$ with values between 0 – 255, is the local adaptive thresholding technique. In particular, the simple method of the mean weighted averaging is used, where the local threshold $T_{i}(x,y)$ for the $(x,y)$ pixel of the $i$th image is determined as the mean of the intensity values of the surrounding pixels. For each one of the $N$ filtered images an associated $n\times m$ mask (binary) image:

$$ B_{i}(x,y)=\textstyle\begin{cases} 1, \quad \mbox{if } f_{i}(x,y) > T_{i}(x,y), \\ 0, \quad \mbox{if } f_{i}(x,y)\leq T_{i}(x,y). \end{cases} $$

(2)

The binary image is then applied to the filtered image by keeping the negative values of $F_{i}(x,y)$ for pixels with $B_{i}(x,y)=0$ while setting the rest equal to zero. The result is an image $Z_{i}(x,y)$ with negative values that are associated with enhanced dark structures in our original image, and zero as an upper limit. Figure 3 demonstrates the effect of the adaptive thresholding technique on the filtered (top row) and the filtered and scaled images (bottom row). $Z_{i}(x,y)$ provides compact areas to the dark structure-oriented tracing algorithm (to be described in Section 3.2), but also facilitates their tracing as they are restricted within zero-valued borders (see Figure 3, bottom right panel). The adopted technique seems more suitable for images with varying illumination, such as the images used in the present study, when compared to other ones (e.g. global, Otsu, etc.)

3.2 Tracing of Curved Structures

As stated in the introduction, chromospheric swirls appear as rings, arcs, or spirals, i.e. they feature high curvature. In order to identify them, we perform tracing of the dark, curved structures encountered in the filtered and thresholded images produced by the pre-processing stage (Section 3.1). For isolating curved, vortex-related features based on spatial information, a one-dimensional tracing approach is used that results in locating centers of curvature of vortex-related segments. In terms of computational complexity and time, one-dimensional tracing is far less demanding than two-dimensional tracing approaches. Moreover, as we search for high-curvature structures, this further restricts our study of feature/segment tracing to methods that use local curvature and oriented segment connectivity/directivity. These methods perform structure segmentation in 2D images by exploiting a physical constraint. Such algorithms have been widely used for the detection of coronal loops and are based on general pattern recognition methods, such as the Hough transform, the wavelet transform etc. or on more application-dependent methods, such as the direction of the coronal loop’s modeled magnetic field (Lee, Newman, and Gary, 2004), where the physical constraint of the segment connectivity is associated with the local orientation of an extrapolated solar magnetic field. For an overview of image processing techniques and automated feature recognition algorithms applied to solar data the reader is referred to the review by Aschwanden (2010).

In the present study, we develop an automated tracing algorithm for identifying highly-curved structures. We use as a basis the Oriented Coronal Loop Tracing (OCCULT-2) algorithm, developed by Aschwanden, De Pontieu, and Katrukha (2013) for automated tracing of coronal loops, in which, however, we introduce very important modifications dictated by the problem under study. The modifications were applied on the latest version of the original OCCULT-2 software included in the Solar SoftWare (SSW) packages.¹ Since as already mentioned, chromospheric swirls appear darker than their background in images taken in the H$\alpha$ and Ca ii IR lines (Wedemeyer et al., 2013; Park et al., 2016; Tziotziou et al., 2018) we modified the OCCULT-2 algorithm, which oriented to the automated tracing of bright coronal loops, into a dark-structure high-curvature-oriented tracing algorithm. The original algorithm performs a bidirectional iterative detection of coronal loops in a lowpass–highpass-filtered image by searching the location of the maximum flux of a selected structure, which is also part of the brightest loop. It then uses an oriented directivity criterion to determine the local ridge and proceeds to the next loop point until it reaches a base level threshold or a faint loop point. Once the bidirectional tracing is completed, the loop is erased from the residual image and the code proceeds to the next peak of the image flux, repeating the process. Many of the basic concepts of the original algorithm such as the bidirectional tracing and the oriented directivity are kept but major modifications were implemented in several other of its aspects. These modifications have as follows:

• i) The pre-processing stage of filtering, scaling and adaptive thresholding described in Section 3.1, which leads to the $Z_{i}(x,y)$ image, replaced the entire pre-processing stage of the original algorithm.

• ii) The coordinate $(x_{min},y_{min})$ with the minimum flux value is searched instead of the maximum value in the entire $Z_{i}(x,y)$ image.

• iii) The initial (only) angle (direction) of each segment which is about to be traced, is determined by rotating a linear segment of bidirectionally increasing length centered at the pixel with the minimum flux $(x_{min},y_{min})$, up to the point that it reaches zero values at both ends. This process is repeated over a range of angles from 0 to 180^∘, with respect to the horizontal (Figure 4, bottom right). The angle $\phi (x_{min},y_{min})$ of the segment with the minimum length, thus the minimum thickness of the structure’s adaptive border, determines the initial directional angle of the structure’s tracing (see Figure 4).

  Figure 4

  

  Left panel: An image from the timeseries used to show the tracing stage of the algorithm. This image is the result of the entire pre-processing stage as a combination of the filtered and scaled image and the binary mask (created by the application of the adaptive thresholding technique). Right column: Close up visualization of the initial direction determination process (see text). The algorithm locates the minimum flux point and determines the initial direction iteratively (top panel). At the bottom panel a more detailed visualization of the iterative process for specific angles ($35^{\circ},60^{\circ},90^{\circ},120^{\circ},150^{\circ}$ with respect to the horizontal dashed line) around the initial minimum flux point (green cross) is shown. Each of the light blue lines represents the calculated length at the respective angle. The angle of the segment with the minimum length, which in this case was found at $35^{\circ}$, defines the initial direction.

• iv) The dark structure is sequentially traced between the mask border using an oriented directivity criterion based on the negative flux of the structure, until a zero value of the image is reached, with the process repeated bidirectionally. In each iteration, a local curvature criterion is applied and the linear parts of the traced segment are excluded (see Section 3.3).

• v) At the end of the tracing of each segment further global selection criteria are applied in each traced structure in order to exclude any remaining linear structures or cases that exceed the restrictions implied for the physical parameters (see Section 3.3).

This process is repeated for every $Z_{i}(x,y)$, $i=0,1,\ldots,N-1$, image of the dataset produced in the pre-processing stage (Section 3.1), providing a number of $N_{i}$ curved segments of the traced dark structures in every $i$ image. The relative quality of each image of the dataset affects the tracing results which further depend on the image pre-processing described in Section 3.1. Detailed adaptive thresholding-generated binary masks lead to more accurate tracing. In turn, the quality of the adaptive mask itself depends on the relative quality of the image, since the adaptive thresholding technique works better on high-quality and high-contrast images. Therefore, the scaling stage of the image pre-processing step, described in Section 3.1.2, as Figure 5 clearly demonstrates, is extremely important for the entire tracing procedure.

Figure 5

The effect of the quality of the image on the tracing and selection results. Example of traced and selected structures (orange line segments) from an image of relatively low quality (image 38 of the H$\alpha$ image dataset, Figure 3) before (left panel) and after (right panel) the automated scaling.

3.3 Criteria for Curved Segments Selection

The criteria for selecting the curved structures in the images, are based on the current information regarding specific physical properties of chromospheric swirls. Although these properties are kept fixed during the entire process, they can be easily modified to accommodate any updated relevant information. Currently, chromospheric swirls are generally considered to be small-scale structures with radii $\lesssim 1.5$ Mm (Wedemeyer-Böhm et al., 2012). In order to maintain the possibility of detecting swirls (or segments of swirls) with larger radii, we did not restrict the tracing algorithm by including a maximum radius criterion. Nevertheless, considering the fact that swirls are not likely to have a radius $< 200$ km we set the minimum curvature radius to be traced to $r_{min}=400$ km. The image scale of the CRISP/SST instrument is 0.059$''/$pixel in the H$\alpha$ line (see Section 2), which means that a conversion to pixel units yields $r_{min}\simeq 9$ pixels.

We seek to establish a lower limit of curvature levels above which the traced segment is acceptable (i.e. it exhibits a sufficient degree of curvature). To this end, we choose to make use of the easily calculated standard deviation $\sigma _{\alpha }$ of the angles $\alpha (s)$ of each traced segment $s$ with an assumed constant radius $R$ and length $L$. Then this standard deviation is equal to

$$ \sigma _{\alpha }=\sigma [\alpha (s)]=\frac{1}{2R}\sqrt{ \frac{L(L+1)}{3}} .$$

(3)

The detailed mathematical derivation of Equation 3 is presented in Appendix B. The derived equation is essentially an approximation that helps to establish the threshold of the standard deviation of the segments’ calculated discrete angles, which, in turn, indicates the accepted level of curvature. For reference, the $\sigma _{\alpha }$ of the fully closed circle of any radius $R$ with $L=2\pi R$ is $\sim 1.8$ with an angle of curvature $D_{\alpha }=180L/\pi R=360^{\circ }$ and the $\sigma _{\alpha }$ of a segment of length $l_{test}=4$ and radius $r_{max}=50$ pixels is 0.026 with an angle of curvature 4.6^∘. We note that $r_{max}$ is chosen for reference calculations of $\sigma _{\alpha }$ and it is not embedded in the algorithm as a restriction.

The geometrical characteristics of a random segment are presented in Figure 6. If the curved segment reaches during the tracing process a length greater than $3l_{test}=l_{c}=12$ pixels we confine the local curvature by including a local $\sigma _{\alpha }$ criterion. Hence, between the iteration of each $j$ and $j+1$ points with $j\ge 12$, the local, already traced part of the segment with length $l_{c}$, which corresponds to $N_{l_{c}}=13$ points, is kept if

$$ \sigma [\alpha (s_{l_{c}})]\geq 0.02\mbox{,} \quad s_{l_{c}}\in [s(j)-l_{c},s(j)] .$$

(4)

Using the local curvature criterion only the linear parts of an overall curved traced structure can be excluded (Figures 6 and 7). Following the tracing of a segment, a global curvature criterion is applied. Applying different $\sigma _{\alpha }$ values in the range $[\sigma _{\alpha }(r_{max},l_{test}), \sigma _{\alpha }(r_{min},\pi r_{min})]=[0.026,0.92]$ with the higher value corresponding to the $\sigma _{\alpha }$ of minimum semicircle, we concluded that a traced segment of length $L$ and mean curvature radius $R$ is kept if

$$ \sigma [\alpha (s_{l})]=\sigma _{\alpha }(R_{l},l)\geq 0.4\mbox{,} \quad s_{l}\in [L/5,4L/5], $$

(5)

where $s_{l}$ denotes (the length coordinates of) the central region, whose length and mean radius are $l=3L/5$ and $R_{l}$, respectively. The effect of both $\sigma _{\alpha }$ criteria is demonstrated in Figure 6. This global $\sigma _{\alpha }$ criterion is applied in the central region of the segment in order to exclude linear structures with highly curved edges that, for example, may result from tracing obscurities or segments with varying shape that survive the local $\sigma _{\alpha }$ criterion (see Figure 7 and blue region of Figure 6).

Figure 6

A schematic representation explaining the effect of the local and global curvature criteria on a random segment (black thick line) that consists of both linear and curved parts (regions inside colored rectangles). The segment length coordinates are measured in pixels and the distance between the points is considered equal to $\Delta S=1$ pixel. Green circles denote the physical coordinates of a segment point with segment coordinate $s(j)$, while thin black continuous straight lines show the direction $a_{j}$ of each point’s local curvature radius with respect to the horizontal (purple lines). Dotted lines represent large curvature radii exceeding the diagram borders, while colored rectangles denote three regions, hereafter red, green and blue region, of the segment with different standard deviation $\sigma _{\alpha }$ values. Finally, black circled green crosses show the centers of curvature for a number of points within the green region. The red region is excluded by the local curvature criterion due to its small $\sigma _{\alpha }$ value (see text for details), while the remaining green and blue regions survive both local and global curvature criteria. If the blue region was a separate segment, it would probably be excluded by the global curvature criterion.

Figure 7

Example of the effect of the local curvature criterion on the centers of curvature and the shape of the traced structures. In the left panel only the global curvature criterion is applied. Despite the fact that all linear structures have been excluded, some of the curved segments contain linear parts. After the inclusion in the algorithm of the local curvature criterion the linear parts disappear (right panel). Moreover, use of the local curvature criterion also helps to keep curved parts of largely linear structures, which would otherwise be excluded by the global curvature criterion (black rectangles). In addition, the centers of curvature seem to be almost intact, since we use the median value of all centers of curvature of each segment (Section 3.4).

By the end of the tracing and selection stage we have determined the segments of adequate curvature that are likely to constitute parts of a vortex formation. At this point, each of these segments has a number of centers of curvature equal to the number of its points. A choice of a single meaningful center of curvature serves as a representative of the segment and leads to less computationally expensive processes in the upcoming stage. Therefore, we consider the median center of curvature for each of the curved segments since, unlike the case of the mean center, it is hardly affected by outliers. Consequently, the final output of this stage consists of the median center of each (adequately curved) $s_{k}$, $k=0,1,\ldots,N_{i}$, segment in each $i$ image, hence $\lbrace [x_{c}(s_{k}),y_{c}(s_{k})]_{i}\rbrace$.

3.4 Two-Tier Clustering

3.4.1 Clustering of Curved Structures in Space and Identification of Swirl Candidates

The tracing and selection processes provide curved segments (see left panel of Figure 8), as well as the median center of curvature for each segment. However, not every traced segment is part of a circular or spiral swirling structure as in chromospheric images several other curved structures, such as mottles and dark chromospheric lanes may also appear. In order to group together traced segments that is more likely to represent vortical structures, we search for areas of high center-of-curvature concentrations by clustering together the derived centers of curvature.

Figure 8

Left panel: Traced curved segments over a 5-time-step interval window (i.e. i image$\pm 2$ images separated by a 4 s cadence) centered at image 33 of the dataseries. The traced and selected segments are gathered between the areas of linear chromospheric structures. The time of origin for each segment is represented by a red-purple color table scaled over the $T=5$ time step with red-colored segments originating from the first image, while deep purple from the last one. Right panel: The differently colored clusters of centers of curvature over the $T$ interval around image 33 define the Swirl Candidates. Colored markers with larger radii represent the core cluster points of each group, whereas the ones with the smaller radii are the corresponding border points. Black points do not meet the desired conditions, therefore they are labeled by the clustering algorithm as noise.

Clustering is a wide-spread machine learning technique that involves grouping of data points, based on specific similarity properties and is used for statistical analyses in several scientific fields. Having checked different clustering algorithms based on a variety of concepts, we found that the Density-Based Spatial Clustering of Applications with Noise algorithm (DBSCAN, Ester et al., 1996), which is based on the notion of the data points’ local density, is the most suitable option. DBSCAN, unlike other clustering methods, does not require the number of clusters to be known a priori, since the clusters are defined sequentially, as the algorithm evolves. Moreover, DBSCAN is able to identify and remove outliers, i.e. clusters with very few points that lie in low density regions of the feature space such as centers of curvature computed from swirl-unrelated curved segments produced by the tracing algorithm.

The acquired results depend on two key parameters: the parameter $\epsilon$, which defines the radius of the local circle around a data point, and the parameter $MinPts$, which defines the minimum number of points that must lie in the neighborhood of a data point so that this is considered as a core point of a cluster. The points that lie in the neighborhood of a core point but do not, however, satisfy the $MinPts$ requirement around their own neighborhood, are labeled as border points of the cluster. Every point that is neither a core nor a border point corresponds to lower density regions in the data space and is characterized as noise.

In our case, input data in the DBSCAN algorithm are the median centers of the curved segments encountered in a number of $T$ consecutive images (corresponding to a temporal interval of the datacube). This is deemed necessary due to the high temporal variability of the chromosphere, as well as to the existence in the dataset of a number of low quality images due to seeing effects. Specifically, for any $i$ image of the datacube, the set of coordinates given to the clustering algorithm consists of the $\sum _{m} N_{m}$ median centers $x_{c}$, $y_{c}$ of every segment within the considered time step $T$, with $N_{m}$ being the number of curved segments traced for the $m$th image, where $m=i-(T-1)/2,\ldots,i-1,i,i+1,\ldots,i+(T-1)/2$. Hence, with $s_{k}$ defining the segment length coordinates and $k=0,1,\ldots,N_{m}-1$, the considered for clustering data points set is $\lbrace [x_{c}(s_{k}),y_{c}(s_{k})]_{m}\rbrace$. The value of $T$ depends on the cadence of the dataset and must be an odd number as we should investigate the same number of images before and after the $i$th image. For example, in the present CRISP/SST H$\alpha$ dataset with a 4 s cadence we choose $T=5$ that corresponds to a 20 s temporal interval. The left panel of Figure 8 shows the superposed curved segments of images 31–35 from which the clusters of image 33 are created. The choice of a $T>1$ provides two major advantages: (i) a curved area in an image $i$ is more likely to be traced even if the image is blurred and (ii) potential short-lived swirling phenomena ($<20$ s) are more likely to be detected as well. However, $T$ should be low enough to ensure that the field has not changed significantly during this time interval. Hence, in general for any H$\alpha$ datacube

$$ max[cadence\cdot T]\leq 20s,\qquad T\in 2\mathbb{N}+1, $$

(6)

with the cadence being ≤20 s, as is the usual case for observations obtained from modern solar observatories. The combination of $T$ and other major physical restrictions set in Section 3.3 leads to the selection of the $\epsilon$ and $MinPts$ key clustering parameters. The first one is set equal to twice the minimum radius of the tracing algorithm, hence, $\epsilon =18$ in our case, whereas the second one is determined by the expected number of centers of curvature within that radius. A curved segment that preserves its shape throughout the interval $T$ should produce at least a number of $T$ (median) centers of curvature located within the $\epsilon$ radius circle. As a result

$$ \epsilon =2r_{min},\qquad MinPts=T .$$

(7)

As an example, the obtained curvature center clusters for image 33 are shown in Figure 8. These clusters along with the segments that generated them, are labeled as Swirl Candidates (SCs) and further processing is needed in order to label them as swirls. Figure 9 shows the derived SCs for a $T=5$ time interval centered around image 33 of the datacube, where we have kept the clusters with a number of core points greater than two in order to further reduce the possibility of a random curved structure detection. Each SC of the total $S_{c,i}$ of the $i$th image is denoted with $sc_{k}$, with $k=0,1,\ldots,S_{c,i}$, and represented in the FOV by a median center calculated from the centers of curvature of its associated segments, producing an output of $\lbrace [X_{c}(sc_{k}),Y_{c}(sc_{k})]_{i}\rbrace$ centers of SCs.

Figure 9

The clusters with a number of core points greater than two are associated with the corresponding curved segments providing the Swirl Candidates (SCs) for each image of the dataset. The SCs are plotted over image 33 of the H$\alpha -$0.26 Å datacube which is the central image of the 5-image time interval of the clustering procedure shown in Figure 8. The SCs seem to reside between linear chromospheric structures.

3.4.2 Clustering of Curved Segments in Time and Swirl Detection

The characterization of the SCs as swirls involves a second level clustering process, now in the time dimension. Once more the DBSCAN algorithm is adopted. The SCs that survive this process, thus the most persistent ones, are finally labeled as swirls.

Using the swirl properties, which are currently prevailing in the literature, we accept as a swirl every SC that preserves a center of curvature for at least (a total of) $t_{sc,min}=1.5$ min throughout a dataseries with a 5 min minimum duration, within the $2r_{min}$ radius. It has to be noted that the resulting characterization is somewhat subjective since, as mentioned already, swirl properties are not definitely known. The set of coordinates provided as input to the second level clustering consists of the median center $X_{c},Y_{c}$ of every $sc_{k}$ swirl candidate, hence, $\lbrace [X_{c}(sc_{k}),Y_{c}(sc_{k})]_{m}\rbrace$, with $m=0,1,\ldots,T_{sb}-1$ and $k=0,1,\ldots,S_{c,m}-1$, where $S_{c,m}$ is the maximum number of SCs of the $m$th image of an examined subset of the initial dataset consisting of a number $T_{sb}\le N$ images. The selection of a subset from the initial dataset is optional and can be used for the exclusion of images at a specific time interval of the sequence due to e.g. the existence of a large number of consecutive low quality images. The $MinPts$ parameter of the DBSCAN part of the algorithm is now associated with the $t_{sc,min}$ assumption made earlier as

$$ T_{sc}=\lfloor t_{sc,min}/cadence \rfloor , $$

(8)

where “⌊ ⌋” denotes integer division, leading to the second level clustering parametrization:

$$ \epsilon =2r_{min},\qquad MinPts=T_{sc}. $$

(9)

The requirement set earlier i.e. preservation of an SC for at least 1.5 min within a radius of $2r_{min}$ leads to the formation of the clusters as a result of the second level clustering and their characterization as swirls. In accordance with the results of the previous sections, the output consists of a representative center in the FOV for each of the detected swirls (clusters). This center is defined as the mean value of the coordinates of each detected swirl in the FOV leading to the output set of swirl centers $\lbrace [X_{s},Y_{s}]\rbrace$, $s=1,\ldots,S$, where $S$ is the number of the detected swirls.

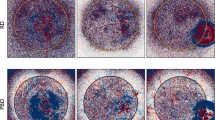
Having described so far in detail all the necessary steps for processing our dataset of choice to find SCs and finally swirls within it, we present and discuss below the acquired collective final results. The constructed algorithm, that is also shown as a flow chart in Appendix A (see Figure 13) was applied, as already mentioned in Section 2, in the wavelength close to line center (i.e. −0.26 Å) H$\alpha$ CRISP/SST dataset areas. A number of $T_{sb}=100$ images ($\simeq 6.5$ min) was given to the algorithm, while according to Equations 8 and 9, $\epsilon =18$ and $MnPts=23$ for the 4 s cadence. This particular parametrization of choice revealed the existence of $S=10$ swirls within the examined time interval (see Figures 10 and 11) in the particular FOV. In the left panel of Figure 10 several other areas of high point density can also be seen. These areas would probably be characterized as swirls, as well, if we accept as swirls structures with $t_{sc,min}<1.5$ min, therefore with $T_{sc}<23$ in the second level clustering process, or if we examine a set of $T_{sb}>100$ images.

Figure 10

The second level clustering of the overall centers (median center of each cluster) of each SC. The markers follow the same notation as in Figure 8. The cluster centers are projected on the entire FOV (left panel) providing the centers of the detected swirls. The vertical lines represent the mean center of each swirl in space and time. These lines reveal the shift of the swirl’s center in space throughout the examined time interval.

Figure 11

Left panel: Time evolution of the 10 detected swirls within the examined time interval as a projection to the z-x plane, with x restricted in the range of 400 to 995 pixels where all detected swirls are concentrated (see Figure 10). The vertical lines represent the mean center $X_{s}$, $Y_{s}$ of each cluster. The colored number at the top of each cluster represents the number of the corresponding detected swirl shown in Figure 12. Right panel: The superposed segments of the detected “swirl 2” (green lines) over the examined time interval, distributed around its mean center (orange cross). The time of origin for each segment is represented by a green color table scaled over the examined time interval, with the darkest (lightest) shade indicating the earliest (latest) segment.

Figures 10 (right panel) and 11 (left panel) depict the temporal and spatial evolution, as well as the consistency of swirl centers during the examined time interval, while Figure 12 shows snapshots of the detected 10 swirls. Visual inspection was performed to each one of these detected swirls to test the reliability of the algorithm. The results are promising as 7 out of 10 of the detected swirls (swirls 1, 2, 3, 4, 5, 7, 10 of Figure 12) clearly present swirling motion throughout the examined time interval, while the remaining 3 out of 10 (swirls 6, 8, 9 of Figure 12), despite the fact that they are associated with spiral or spiral-like persistent structures, cannot be positively characterized as swirls. In particular, the detected structure labeled as swirl 2 in Figures 12 and 11 (right panel) is one of the already known and studied swirls in the examined FOV. Tziotziou et al. (2018) reported the existence of a smaller swirl within the larger investigated vortex flow area that here coincides with swirl 2. As noted by these authors the exact location and general shape, however, varies throughout the 1.7 h duration of the observations. Such a behavior can also be seen in the snapshot of swirl 2 in Figures 12 where a second circular structure resides within the vortex flow area centered in the swirl center calculated by the algorithm. Additionally, despite the fact that the center of swirl 7 is located within the same vortex flow area, it was labeled as a different swirl due to the persistence and consistency of its center throughout the examined 6.5 min interval.

Figure 12

Snapshots of the final H$\alpha$ swirls detected by the algorithm over the field of view of the observations provided by the CRISP/SST instrument. The detected swirls reside between linear chromospheric structures and present swirling motions within the examined time interval of 6.5 min. The orange cross in each snapshot represents the mean center of the swirl (see text).

It is obvious that application of the method in a longer time interval or even in the entire time series will give clues on the intermittent or persistent character of the detected swirls. It will also help to determine in a more definitive way some of their properties, such as lifetimes and radii. In addition, the relative shift in space of the swirl centers during their time evolution, as it is revealed in the examined time interval, could suggest e.g. interaction with nearby structures, loss of the spiral-like shape, and widening of the rotating magnetic structures. It could also be directly related to photospheric vortex motions. A study of these issues is planned for the future.

4 Discussion

In this work we presented a novel automated chromospheric swirl detection method. In contrast to recently presented methods which detect vortex flows based on the evolution of photospheric horizontal velocity fields, extracted with Local Correlation Tracking (LCT) techniques, which are hardly applicable in the dynamical chromosphere, the designed method focuses on the morphological characteristics of swirling structures that appear in images obtained in the H$\alpha$ chromospheric line.

The designed algorithm is divided into four standalone stages: (i) image pre-processing; (ii) tracing of highly curved structures; (iii) selecting and combining traced dark, curved segments; (iv) two-tier clustering (a) in space providing the swirl candidates and (b) in time providing the detected, persistent swirls. The algorithm accepts as an input a datacube of H$\alpha$ filtergrams obtained at line center or near line-center wavelengths where these features are best visible (datacubes of other chromospheric lines in which these structures are observed can also be used). After the pre-processing stage, the automated tracing of highly curved structures/segments with a bidirectional tracing and an oriented directivity approach is performed in each image of the dataset. The curved segments are selected and combined over a specified time interval according to some criteria related to the physical parameters of swirls (i.e. curvature degree, minimum lifetime and radius, etc.). As a result, the algorithm produces an output of coordinates in the examined FOV that correspond to and are characterized by some predetermined parameters as swirls. The high center-of-curvature concentrations are grouped together using a first-level clustering in space, which provides the SCs. Finally, a second level clustering procedure, which labels as swirls those SCs that are considered more persistent, i.e. have lifetimes of at least 1.5 min, provides their centers, the time follow-up of which gives clues about their time evolution.

The novel automated algorithm was applied to observations obtained by the CRISP/SST instrument in the H$\alpha$ line. It resulted to the detection of 10 structures in the entire ($60^{\prime\prime} \times 60^{\prime\prime}$) FOV characterized as swirls throughout an examined 6.5 min time interval of the 4 s cadence dataseries. The detected swirls seem to preserve their circular-like or spiral-like shape throughout the whole duration of the examined time interval or at least, during the most part of it. These swirls would be hardly identified through visual inspection of the images. The high abundance of swirls in the chromosphere that was revealed in recent work (Wedemeyer-Böhm et al., 2012; Wedemeyer and Steiner, 2014) is also demonstrated in the current work: (i) The detected swirls were the result of a conservative parametrization in order to detect the most conspicuous cases (e.g. use of small $\epsilon$ and large $MinPts$ parameters in the clustering processes), and (ii) both the SCs and the final swirls are distributed over the entire FOV and occupy areas between linear fibril-like structures. In particular, point (ii) suggests that numerous undetected small-scale swirls potentially reside below the dynamical linear magnetic structures observed in the CRISP/SST FOV under study. This indication further encourages the application of the presented method on different H$\alpha$ datasets, as well as in different chromospheric lines (e.g. Ca ii 8542 Å), in which these features are observed.

We note that the final number of detected swirls depends mainly on the number of SCs resulting from the algorithm and the choice of the right physical properties for defining an SC as a swirl that, as already discussed, remains quite arbitrary. Point taken, the algorithm has been constructed and structured in such a way that one should be able to easily alter the criteria in order to derive more SC cases, therefore, possibly leading to a larger number of detected swirls within the examined datacube. For example, an increase of the overall accuracy of the SC detection algorithm occurs by applying it in a smaller field of view, or a region of interest within a wider field of view. Such a choice, the filtering and the adaptive thresholding remain exactly the same, whereas the tracing part of the algorithm is expected to be more accurate. This scenario would result to a greater number of traced and selected curved segments, thus a greater number of centers of curvature, which, in turn, means that the clustering parameter $MinPts$ should be optimized in both clustering levels. A similar outcome should be expected if the sensitive $\sigma _{\alpha }$ parameter is changed. A decrease of the $\sigma _{\alpha }$ criteria would increase the number of accepted traced segments of lower curvature degree simultaneously leading to a greater number of produced centers of curvature and the proper modification of $MinPts$. Although an increase of the SCs seemingly leads to a better outcome, it also favors the detection of a large number of random-curved structures, along with the desired SCs, that finally do not constitute real swirls.

The purpose of this work was the development and implementation of an algorithm for the automated detection of chromospheric swirls and the evaluation of its efficiency. It is for this reason that the time interval for the application of the method was selected to be relatively small, i.e. ≃ 4$t_{sc,min}$ (or 100 images from the total 700 of the dataset). However, the algorithm could be applied in any time interval with no need for further parametrization. As these swirling structures are considered to be potential candidates for contributing to the mass transfer and heating of the chromosphere and corona, reliable values and a systematic statistical analysis of their properties are required. As a future research direction, we plan to apply the algorithm in a longer time interval, in order to obtain reliable information and a meaningful statistical analysis on the number, location, lifetime, radius, etc. of swirling events in the solar chromosphere. The estimation of these parameters will allow the quantification of the turbulence by investigating of the power-law slopes in the corresponding power spectra.

The vortex flow and swirl automated detection methods proposed so far focus on the detection of vortex flows using observations and numerical simulations of the photosphere or numerical simulations of the chromosphere. The presented method is based, for the first time, on chromospheric observations and could serve as a complementary method in an overall photospheric vortex flow–chromospheric swirl co-validation process. Such a process would be a very significant step forward, because it is very important to understand how many vortices rooted in the photosphere manage to finally reach the chromosphere and appear as chromospheric swirls or reach even higher altitudes and appear as tornadoes. Moreover, further benchmarking and the potential of the algorithm to expand on a wide range of applications in other scientific fields, where turbulence is known to form vortex flows (e.g. oceanography and meteorology) is demonstrated by the detection of SCs in synthetic streamline images, which demanded only a slight change of the key parameters (see Appendix C for details). This potential stems from the structure of the pre-processing stage which utilizes techniques, such as the combination of adaptive thresholding and FWHM-oriented image scaling that is proved to be rather effective in any application involving high-contrast images with varying illumination, especially if a convolution with an edge enhancement kernel has been used before.

We note that the proposed method with some modifications can also be applied to the automated detection of linear or quasi-linear fibrillar structures which are abundant in the FOV. These structures that are observed in quiet and active regions of the Sun, on the solar disk and at the limb, are the subject of intensive studies (see the review of Tsiropoula et al., 2012) and the accurate determination and statistical analysis of their properties are very important. Some necessary modifications for such an implementation would most likely involve the initial thresholding part and the physical restrictions set in the tracing and selection part of the algorithm, e.g. by reversing/modifying the $\sigma _{\alpha }$ criterion in order to exclude curved instead of linear structures. Naturally, in this case the clustering part would be obsolete. In addition, future plans include the improvement of the algorithm itself, e.g. the increase of the overall accuracy of the detection method, its application in different datasets, the inclusion of detailed spatial and temporal information for the detected swirls as a part of the output information and the modification of the tracing part to a less flux dependent version.

Appendices

Appendix A: Flow Chart of the Method

A schematic representation of the proposed automated chromospheric swirl detection method is shown in the following flow chart (Figure 13).

Figure 13

Flow chart of the automated chromospheric swirl detection method.

Appendix B: Derivation of Curvature Criteria

Considering a certain segment, the algorithm calculates the directional angle for each point of a segment:

$$ \alpha _{j}=\alpha _{j-1}+\Delta \alpha _{j}, $$

(10)

with $j=1,\ldots,N_{L}$, where $N_{L}$ is the number of points of the segment, $\alpha_{0}$ is the angle of the first segment point that results from the tracing algorithm, $\Delta \alpha _{j}=\frac{\Delta S}{r_{j}}$ is the local curvature angle, $\Delta S$ is the length of the arc and $r_{j}$ the local curvature radius. Since we use a step of $\Delta S=1$ pixel in the iterative tracing the resulting angle for each segment point is

$$ \alpha _{j}=\alpha _{j-1}+\frac{1}{r_{j}}. $$

(11)

Assuming a constant radius $r_{j}=R$ along a segment of $N_{L}$ points with length coordinates along the segment $s(j)=j$ (in pixels, since $\Delta S=1$ pixel), Equation 11 becomes

$$ \alpha _{j}=\alpha _{0}+\frac{j}{R}. $$

(12)

We denote with $s$ the segment length coordinates $s_{k}$ of each, $k=0,1,\ldots,N_{i}-1$ segment of the $i$th image in order to simplify the analysis. The calculation of the mean angle of such a segment yields $\overline{\alpha }=\frac{\sum _{j=1}^{N_{L}} \alpha _{j}}{N_{L}}= \alpha _{0}+\frac{N_{L}+1}{2R}$, leading to a standard deviation of $N_{L}$ discrete angles:

$$ \sigma _{\alpha }=\sigma [\alpha (s)] = \sqrt{ \frac{\sum _{j=1}^{N_{L}} (\alpha _{j}-\overline{\alpha })^{2}}{N_{L}-1}}= \frac{1}{2R}\sqrt{\frac{N_{L}(N_{L}+1)}{3}} .$$

(13)

As the segment’s length $L=N_{L}\Delta S \stackrel{\Delta S=1}{\Longrightarrow } N_{L}=L$, Equation 13 becomes

$$ \sigma _{\alpha } (R,L) =\frac{1}{2R}\sqrt{\frac{L(L+1)}{3}} .$$

(14)

Appendix C: Application of the Method to Synthetic Data

In order to further demonstrate/examine the effectiveness of the designed chromospheric swirl detection algorithm in other scientific fields, we applied it to a high-contrast image of synthetic vortex flows. It was obtained by the NASA/Goddard Space Flight Center Scientific Visualization Studio, from a movie representing Gulf Stream Sea Surface Currents² that are depicted by synthetic streamlines as single, grayscale image (snapshot) with dimensions 1024×576 pixels. Since no time evolution is involved, the algorithm is only applied up to the first-level clustering and the determination of SCs (see Figure 13). During the application of the algorithm only the first-level clustering parameters required proper modification. Naturally, since in this case $T=1$, we set $MinPts=2$ requiring at least two points within $\epsilon =2r_{min}$ in order to form an SC. The minimum radius was determined simply by the radius of the smallest visually-resolved vortex in the synthetic image, hence, $r_{min}\simeq 8$ pixels, which led to $\epsilon =16$ (see Section 3.4.1 for definitions of the parameters). The acquired results are presented in Figure 14. The results are quite promising since the detected vortex-like structures that are labeled as “Swirl Candidates” represent more than 90% of all visually resolved vortices within the field of view. Visual inspection shows that the algorithm fails to detect (i) elongated vortex-like structures, (ii) faint vortices at the edges of the image, and (iii) vortices with extremely small radii. Point (i) suggests that the automated swirl detection algorithm would probably fail to provide all swirling structures of solar images in which large projections effects are important i.e. of images taken close to the solar limb.

Figure 14

The grayscale image obtained from the NASA/Goddard Space Flight Center Scientific Visualization Studio (https://svs.gsfc.nasa.gov/3913) with the synthetic streamlines representing sea surface currents (top panel) and the same image after the application of the swirl detection algorithm up to the first level clustering and the determination of the “SCs” (bottom panel). Each SC is represented by a different color and depicted by its traced segments and their corresponding centers of curvature. Apart from the circular and spiral shaped SCs, several other obscure clusters of, probably short-lived, curved structures are found, as well as, probably persistent, highly curved parts of elongated vortices.