Dependence of Major Geomagnetic Storm Intensity ($\mathrm{Dst}\le -100$ nT) on Associated Solar Wind Parameters

Abstract

We investigate the influence of various solar wind parameters on the intensity of the associated major geomagnetic storm. SYM-H_min was used to indicate the intensity of major geomagnetic storms, while $I(B_{s})$, $I(E_{y})$ and $I(Q)$ were used to indicate the time integrals of the southward interplanetary magnetic field component ($B_{s}$), the solar wind electric field ($E_{y}$), and Q, which is the combination of $E_{y}$ and the solar wind dynamic pressure, during the main phase of a major geomagnetic storm, respectively. We have found that the correlation coefficient (CC) between the time integral of solar wind parameters and the intensity of an associated major geomagnetic storm has a physical meaning, while the CC between the peak value of a given solar wind parameter and the intensity of an associated major geomagnetic storm has no physical meaning. We used 67 major geomagnetic storms that occurred between 1998 and 2006 to calculate the CC between SYM-H_min and $I(B_{s})$, the CC between SYM-H_min and $I(E_{y})$, and the CC between SYM-H_min and $I(Q)$. The derived CC between $I(B_{s})$ and SYM-H_min is 0.33, while the CC between $I(E_{y})$ and SYM-H_min is 0.57, and the CC between $I(Q)$ and SYM-H_min is 0.86, respectively. These values indicate that $I(B_{s})$, $I(E_{y})$ and $I(Q)$ contribute in a small, moderate, and crucial way to the intensity of a major geomagnetic storm, respectively. For the solar wind to have a strong geoeffectiveness $B_{s}$ plays a role, together the solar wind speed and density, but also the dynamic pressure > 3 nPa. Large and long duration $B_{s}$ or $E_{y}$ cannot ensure a major geomagnetic storm, if the solar wind dynamic pressure is much lower than 3 nPa.

1 Introduction

A geomagnetic storm is a significant disturbance of the Earth’s magnetic field (e.g. Gonzalez et al. 1994) due to the continuous interaction between the solar wind with a southward magnetic field and the magnetosphere. It is generally accepted that a large and long duration southward interplanetary magnetic field ($B_{s}>10$ nT for more than 3 h) or large and long duration solar wind electric field ($E_{y}>5$ mV/m for more than 3 h) will lead to a major geomagnetic storm (Gonzalez and Tsurutani 1987) with the contribution of both solar wind speed and density or solar wind density alone (not mentioned in the previous work). To investigate the effects of various solar wind parameters on the associated geomagnetic storms, many researchers usually calculated the CCs between the peak values of various solar wind parameters and the intensities of such geomagnetic storms (e.g. Choi et al. 2009; Kane, 2005, 2010; Echer et al. 2008; Ji et al. 2010; Richardson and Cane 2011; Wu and Lepping 2002; Wu and Lepping 2016). Of the various solar wind parameters, peak values of $B_{s}$ and $E_{y}$ usually have good correlation with the intensity of the associated geomagnetic storm, while the solar wind speed, dynamic pressure or density alone usually have a poor correlation with it (e.g. Wu and Lepping 2002; Echer et al. 2008). The CC between the intensity of a super geomagnetic storm and the peak of $B_{s}$, as well as the CC with the peak of $E_{y}$ have been calculated using solar wind data and 11 super geomagnetic storms that occurred during Solar Cycle 23 (Echer, Gonzalez, and Tsurutani 2008). The CC with the $B_{s}$ peak was found to be 0.23, and the CC with $E_{y}$ was also 0.23. However, the CC between $B_{s}$ and the intensity of the associated super geomagnetic storm was 0.93 by Meng, Tsurutani, and Mannucci (2019). The CC between the $B_{s}$ peak and the intensity of the associated super geomagnetic storm is very high, implying that the peak magnitude of $B_{s}$ determines the strength of the superstorm to a large extent (Meng, Tsurutani, and Mannucci 2019). However, the contribution made by the solar wind speed and density have not been investigated, yet.

A geomagnetic storm comprises a main phase and a recovery phase. The development of a geomagnetic storm depends on the injection term and the decay term of the ring current. The injection term is larger than the decay term during the main phase. Some researchers proposed that the injection term is only a linear function of the solar wind electric field with solar wind density making little contribution (Burton, McPherron, and Russell 1975; Fenrich and Luhmann 1998; O’Brien and McPherron 2000b). Statistical results reported by O’Brien and McPherron (2000a) suggested that the solar wind density does not independently drive the ring current. According to solar wind data and the minimum of Dst indices of the 11 super geomagnetic storms ($\mathrm{Dst}\le -250$ nT) that occurred during Solar Cycle 23, the CC between $I(E_{y})$ and the minimum Dst is 0.62, which is much larger than that the CC between the $E_{y}$ peak and the intensity of the super geomagnetic storm (Echer, Gonzalez, and Tsurutani 2008). We note that the effect of the solar wind dynamic pressure or density on the intensity of a super geomagnetic storm was not investigated by Echer, Gonzalez, and Tsurutani (2008).

Wang, Chao, and Lin (2003) found that the injection term of the ring current, $Q$, not only depends on the solar wind electric field, but also depends on the solar wind dynamic pressure, which is a function of speed and density. Case studies (Kataoka et al. 2005; Chen, Le, and Zhao 2020), global MHD simulations (Lopez et al. 2004), and an impulse response function model (Weigel 2010) suggest that the solar wind density is an important parameter modulating the transfer of solar wind energy to the magnetosphere during the main phase of a storm.

There are two different views with regard to the injection term of the ring current of a geomagnetic storm at present. One of the perspectives is that the injection term of the ring current is a linear function of the solar wind electric field (Burton, McPherron, and Russell 1975; Fenrich and Luhmann 1998; O’Brien and McPherron 2000b). Alternatively, the injection term of the ring current can also be, as mentioned before, a function of solar wind dynamic pressure (Wang, Chao, and Lin 2003). To shed light on this discrepancy, the effects of two different kinds of injection terms on the intensity of the associated major geomagnetic storm will be studied separately and then compared to each other. This is one of the objectives of the present study.

To investigate the influence of some kind of solar wind parameters on the intensity of an associated major geomagnetic storm, researchers usually calculate the correlation coefficient (CC) between the peak value of that solar wind parameter and the intensity of the associated major geomagnetic storm (e.g. Echer et al. 2008; Meng, Tsurutani, and Mannucci 2019). Is the calculation method for the CC used in these articles correct? To answer the question, we will find a correct method to calculate the CC between a solar wind parameter and the major geomagnetic storm intensity. After that, the influence of the southward component of the interplanetary magnetic field (IMF), solar wind speed and density on the associated major geomagnetic storm intensity will be investigated using a correct method. Whether large and long duration $B_{s}$ alone or $E_{y}$ can guarantee a major geomagnetic storm will be checked. This is also the motivation of the present study. The organization of this article is as follows. The data analysis is presented in Section 2, the discussion in Section 3, and the summary in Section 4.

2 Data Analysis

2.1 Solar Wind Data and Geomagnetic Storm Data

The time resolution of the Dst index is 1 hour, while the time resolution of the SYM-H index is 1 minute. The study conducted by Wanliss and Showalter (2006) suggests that the SYM-H index can be used as a high time resolution Dst index. The SYM-H index was obtained from the World Data Center for Geomagnetism, Kyoto (at http://wdc.kugi.kyoto-u.ac.jp/aeasy/index.html). In this study, the solar wind data observed by the Advanced Composition Explorer (ACE) from 1998 to 2006 (at ftp://mussel.srl.caltech.edu/pub/ace/level2/magswe) with time resolution of 64 s are used. Major geomagnetic storms that occurred during the period from 1998 to 2006 were used in the present study. Because of the solar wind data gap for some major geomagnetic storms, only the main phases of 67 of them have solar wind data. Therefore, these storms are used to study the effects of solar wind parameters on the intensity.

2.2 Time Integrals of Solar Wind Parameters

We use $I(B_{s})$ to indicate the time integral of $B_{s}$ during the main phase of a storm, which is calculated as follows:

$$ I({B}_{s}) = \int _{t_{s}}^{t_{e}}B_{z}\, \mathrm{d}t. $$

(1)

If $B_{z}$ is northward, then $B_{z}$ is set as zero in the calculation of $I(B_{s})$. $t_{s}$ and $t_{e}$ indicate the start and end times of the associated major geomagnetic storm main phase, respectively.

The solar wind electric field is calculated as $E_{y}=V_{sw}B_{z}$, where $V_{sw}$ is solar wind speed, and $B_{z}$ is the $z$-component of IMF. We use $I(E_{y})$ to indicate the time integral of $E_{y}$ during the main phase of a storm, which is calculated as follows:

$$ I(E_{y}) = \int _{t_{s}}^{t_{e}}E_{y}\, \mathrm{d}t = \int _{t_{s}}^{t_{e}}V_{sw}B_{{z}} \,\mathrm{d}t. $$

(2)

If $B_{z}$ is northward, then $B_{z}$ is set as zero in the calculation of $I(E_{y})$.

Burton, McPherron, and Russell (1975) proposed a linear function of the dawn-to-dusk component of the solar wind electric field to describe the changes of the pressure-corrected Dst index caused by the energy injection from the solar wind into the ring current as well as the ring current decay,

$$ \mathrm{d} \text{Dst}^{*}/\mathrm{d}t = Q(t)- \text{Dst}^{*}/{\tau }, $$

(3)

where Dst^∗ is the pressure-corrected Dst index and the contribution made by the magnetopause current has been subtracted in Equation 3. We directly use SYM-H to substitute Dst in Equation 3. $\tau$ and Q are the decay time and the injection term of the ring current, respectively. Q has the following form:

$$ Q = \left \{ \textstyle\begin{array}{l@{\quad }l} 0 & B_{z} \ge 0, \\ \left |V_{sw}{B}_{z}\right | & B_{z} < 0. \end{array}\displaystyle \right . $$

(4)

Fenrich and Luhmann (1998) proposed that Q is a linear function of the solar wind electric field with some difference from the Q described in the article by Burton, McPherron, and Russell (1975).

The injection term of the ring current described by Wang, Chao, and Lin (2003) is calculated as follows:

$$ Q = \left \{ \textstyle\begin{array}{l@{\quad }l} 0 & V_{sw}{B}_{s} \le 0.49~\text{mV}/\text{m,} \\ -4.4(V_{sw}{B}_{s}-0.49)(\textit{P}_{sw}/3)^{0.5} & V_{sw}{B}_{s} > 0.49~\text{mV}/\text{m}. \end{array}\displaystyle \right . $$

(5)

$P_{sw}$ is the solar wind dynamic pressure. It is evident that Q not only depends on the solar wind electric field, but also depends on the solar wind dynamic pressure. $I(Q)$, which indicates the time integral of Q during the main phase of a geomagnetic storm, is calculated by

$$ I(Q) = \int _{t_{s}}^{t_{e}} \textit{Q}\,\mathrm{d}t. $$

(6)

2.3 The Calculation of the CCs Between Solar Wind Parameters and SYM-H_min

When we want to know the effect of some solar wind parameters on the intensity of the storm, we usually calculate the CC between the solar wind parameter and the intensity of an associated geomagnetic storm. It is very important to calculate the CC correctly.

According to Equation 3, we have

$$ \int _{t_{s}}^{t_{e}}\mathrm{d}( \text{SYM-H}^{*})=\int _{t_{s}}^{t_{e}} ( Q(t)-\text{SYM-H}^{*}/\tau )\,\mathrm{d}t. $$

(7)

Assuming that the time integral of injection term is much larger than the time integral of the decay term during the main phase of a major geomagnetic storm, then we have

$$ \int _{{t}_{s}}^{{t}_{e}}\mathrm{d}( \text{SYM-H}^{*})\simeq \int _{{t}_{s}}^{{t}_{e}} {Q(t)}\, \mathrm{d}t. $$

(8)

We use

$$ \int _{t_{s}}^{t_{e}}\mathrm{d}( \text{SYM-H}^{*})=\text{SYM-H}^{\ast }_{\mathrm{min}}\bigg|^{ t_{e}}_{t_{s}}, $$

(9)

$$ \text{SYM-H}^{\ast }_{\mathrm{min}}\bigg|^{t_{e}}_{t_{s}}= \text{SYM-H}_{\mathrm{min}}\bigg|_{t_{e}}-7.26P_{sw}^{1/2} \bigg|_{t_{e}}-\text{SYM-H}_{\mathrm{min}}\bigg|_{t_{s}}+7.26P_{sw}^{1/2} \bigg|_{t_{s}}, $$

(10)

and

$$ \text{SYM-H}_{\mathrm{min}}\bigg|_{t_{e}}-\text{SYM-H}_{ \textrm{min}}\bigg|_{t_{s}}\simeq \text{SYM-H}_{\mathrm{min}}. $$

(11)

For a major geomagnetic storm,

$$ \left ( {7.6\sqrt{{{\left . {{\textit{P}_{sw}}} \right |}_{{t_{s}}}}} - 7.6\sqrt{{{\left . {{\textit{P}_{sw}}} \right |}_{{t_{e}}}}} } \right ) $$

is much smaller than SYM-H_min, Therefore,

$$ \text{SYM-H}_{\mathrm{min}}\approx \int _{t_{s}}^{t_{e}} Q(t)\,\mathrm{d}t $$

(12)

$Q$ can be only a linear function of the solar wind electric field (Burton, McPherron, and Russell 1975; Fenrich and Luhmann 1998; O’Brien and McPherron 2000b) or the combination of the solar wind electric field and dynamic pressure as found by Wang, Chao, and Lin (2003).

For convenience, we use CC$(X, Y)$ to indicate the CC between two parameters X and Y. To investigate the effect of a southward component of the IMF alone on the intensity of an associated major geomagnetic storm, CC($I(B_{s})$, SYM-H_min) is calculated. To investigate the effect of the solar wind electric field, CC($I(E_{y})$, SYM-H_min) is also calculated. Finally, to investigate the effect of Q, CC($I(Q)$, SYM-H_min) is calculated and compared with CC($I(E_{{y}})$, SYM-H_min), so that we can judge whether the solar wind dynamic pressure is an important factor for the intensity of a major geomagnetic storm.

2.4 Results

The CC between SYM-H_min and $I(B_{s})$ for the 67 major storms is shown in the upper panel of Figure 1. CC(SYM-H_min, $I(B_{s})$) is only 0.33, suggesting that $I(B_{s})$ contributes little to SYM-H_min.

Figure 1

The CC between SYM-H_min and $I(B_{z})$ (upper panel) and the CC between SYM-H_min and $I(E_{y})$ (lower panel).

The CC between SYM-H_min and $I(E_{y})$ is shown in the lower panel of Figure 1. CC(SYM-H_min, $I(E_{y})$) is 0.57. Obviously, CC(SYM-H_min, $I(E_{y})$) is much larger than CC(SYM-H_min, $I(B_{s})$), indicating that $I(E_{y})$ is much more important than $I(B_{s})$ for the intensity of a major geomagnetic storm. Because $E_{y}=V_{sw}B_{s}$, the solar wind speed is an important parameter as well. The derived statistical significance (ss) of CC(SYM-H_min, $I(B_{s})$) is 99.7%, while the ss of CC(SYM-H_min, $I(E_{y})$) is 99.9%.

The CC between SYM-H_min and $I(Q)$ is shown in Figure 2. CC(SYM-H_min, $I(Q)$) is 0.86. The derived ss of CC(SYM-H_min, $I(Q)$) is 100%. CC(SYM-H_min, $I(Q)$) is much larger than CC(SYM-H_min, $I(E_{y})$), indicating that Q is much more important than $E_{y}$ for the intensity of the associated major geomagnetic storm. According to Equation 5, we can easily judge that the solar wind dynamic pressure is an important parameter affecting the intensity of a major geomagnetic storm.

Figure 2

The CC between SYM-H_min and I(Q).

3 Discussion

We know that the basic condition to trigger a geomagnetic storm is that the solar wind has a southward IMF component. Our study shows that CC(SYM-H_min, $I(B_{s})$) is only 0.33, indicating that $B_{s}$ alone can hardly trigger a major geomagnetic storm. The comparison between CC(SYM-H_min, $I(B_{s})$) and CC(SYM-H_min, $I(E_{y})$) tells us that $V_{sw}$ is important for the intensity of a major geomagnetic storm, while the comparison between CC(SYM-H_min, $I(E_{y})$) and CC(SYM-H_min, $I(Q)$) tell us that $P_{sw}$ is also an important parameter. $P_{sw}$ is the combination of $V_{sw}$ and density $(N_{p})$, indicating that both $V_{sw}$ and $N_{p}$ are important as well.

When the solar wind reaches the magnetosphere, three solar wind parameters, $B_{z}$, $V_{sw}$ and $N_{p}$, will interact with the magnetosphere simultaneously. This may be the reason why only $I(Q)$ makes a crucial contribution to the intensity of a major geomagnetic storm, while $I(B_{s})$ and $I(E_{y})$ make a small and moderate one, because any solar wind parameter cannot be removed from the interaction between the solar wind and the magnetosphere. As previously stated, only $I(Q)$ makes a crucial contribution to the intensity of a major geomagnetic storm, indicating that such intensity is only related to $I(Q)$. In this context, the CC between the time integral of any single solar wind parameter during the main phase of a major geomagnetic storm and its intensity will be small. Equation 12 implies that the CC between the peak value of a solar wind parameter and a major geomagnetic storm intensity has no physical meaning.

According to Equation 5, if P$_{sw}$ is equal to 3 nPa during the main phases of major geomagnetic storms, CC(SYM-H_min, $I(E_{y})$) will be equal to CC(SYM-H_min, $I(Q)$). We find that $P_{sw}$ during the main phases for most major geomagnetic storms studied in this article is larger than 3 nPa. This may be the reason why CC(SYM-H_min, $I(Q)$) is much larger than CC(SYM-H_min, $I(E_{y})$), which implies that a solar wind with a strong geoeffectiveness requires $P_{sw}>3$ nPa. Because $P_{sw}=N_{p}V_{sw}^{2}$, $P_{sw}> 3$ nPa demands that N_p should satisfy the condition $N_{p}>3~\mbox{nPa}/\mbox{V}_{sw}^{2}$, indicating that $N_{p}$ is dependent on $V_{\mathit{sw}}$. Lower $V_{sw}$ will requires higher $N_{p}$ so that $P_{{sw}}$ can be larger than 3 nPa. The results of the present study show that CC(SYM-H_min, $I(Q)$) is much larger than CC(SYM-H_min, $I(E_{y})$) providing statistical evidence that the injection term of the ring current in the article by Wang, Chao, and Lin (2003) is more accurate than those proposed by Burton, McPherron, and Russell (1975), Fenrich and Luhmann (1998), and O’Brien and McPherron (2000b).

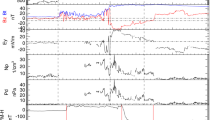
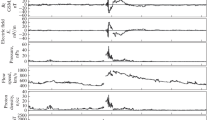
The example shown in Figure 3 is used to help us understand the results obtained in the present study. An interplanetary shock indicated by the first vertical red solid line in Figure 3 was observed by ACE spacecraft at 19:00 UT on 18 October 1998. When the shock reached the magnetosphere at 19:52 UT, it caused a storm sudden commencement, which is indicated by the first vertical red dashed line. The solar wind between the second and third vertical solid lines is a sheath, while the solar wind between the third and fourth vertical solid red lines is a magnetic cloud (MC), which is the interplanetary structure associated with enhanced magnetic field strength. An MC presents a long and smooth rotation of the magnetic field vector and low proton temperature (Burlaga et al. 1981). We can see from Figure 3 that the SYM-H index decreased quickly due to the sheath. The average $B_{s}$ and $E_{y}$ of the MC between the third and fourth vertical solid lines are 16.8 nT and 6.8 mV/m, respectively, and the time duration between the third and fourth vertical solid lines is longer than 10 h. According to the criteria proposed by Gonzalez and Tsurutani (1987), the MC should trigger a very intense geomagnetic storm. However, as shown in Figure 3, the MC has a weak geoeffectiveness. The averaged $B_{s}$ and $E_{y}$ of the sheath are 13.8 nT and 5.9 mV/m, respectively, and the duration of the sheath is slightly more than 2 h. The time duration of the sheath is much shorter than that of the MC, and the average $B_{s}$ and $E_{y}$ in the sheath are smaller than those in the MC. However, the geoeffectiveness of the sheath is much stronger than that of the MC. Why? We find that the averaged $P_{sw}$ of the MC is 1.43 nPa, while the averaged $P_{sw}$ in the sheath is 18.5 nP, which is much larger than that of the MC. The case shown in Figure 3 supports the concept that $P_{sw}$ is an important factor in determining the intensity of a geomagnetic storm. Figure 3 gives evidence that a large and long duration $B_{s}$ or even $E_{y}$ cannot guarantee a major geomagnetic storm, if $P_{sw}$ is much lower than 3 nPa.

Figure 3

The solar wind parameters observed by ACE spacecraft during 18–19, October 1998. Form top to bottom, we depict the solar wind speed, density, magnetic field strength, $z$-component of the magnetic field, solar wind electric field, solar wind dynamic pressure, proton $\beta$ and SYM-H index, respectively.

4 Summary

The results from the present study can be summarized as follows:

We have found that the CC between the time integral of solar wind parameters and the intensity of the associated major geomagnetic storm has a physical meaning, while the CC between the peak value of solar wind parameters and the intensity of the associated major geomagnetic storm has no physical meaning.

$I(B_{s})$, $I(E_{y})$ and $I(Q)$ made a small, moderate, and crucial contribution to the intensity of the associated major geomagnetic storm, respectively, indicating that $I(B_{s})$, $I(E_{y})$, and $I(Q)$ have a poor, moderate, and good correlation with it, respectively. The results of the present study provide statistical evidence that $E_{y}$ is a much more important parameter for the intensity of a major geomagnetic storm than $B_{s}$, while Q is a much more important parameter than $E_{y}$. The present study indicates that both $E_{y}$ and $P_{sw}$ are important for the intensity of a major geomagnetic storm, namely that $B_{s}$, $V_{sw}$, and $N_{p}$ are all important. The solar wind that has a strong geoeffectiveness not only demands that $B_{s}$ works together with $V_{sw}$, and $N_{p}$, but also demands $P_{sw}> 3$ nPa.