Active Region Photospheric Magnetic Properties Derived from Line-of-Sight and Radial Fields

Abstract

The effect of using two representations of the normal-to-surface magnetic field to calculate photospheric measures that are related to the active region (AR) potential for flaring is presented. Several AR properties were computed using line-of-sight ($B_{\mathrm{los}}$) and spherical-radial ($B_{r}$) magnetograms from the Space-weather HMI Active Region Patch (SHARP) products of the Solar Dynamics Observatory, characterizing the presence and features of magnetic polarity inversion lines, fractality, and magnetic connectivity of the AR photospheric field. The data analyzed correspond to ${\approx\,}4{,}000$ AR observations, achieved by randomly selecting 25% of days between September 2012 and May 2016 for analysis at 6-hr cadence. Results from this statistical study include: i) the $B_{r}$ component results in a slight upwards shift of property values in a manner consistent with a field-strength underestimation by the $B_{\mathrm{los}}$ component; ii) using the $B_{r}$ component results in significantly lower inter-property correlation in one-third of the cases, implying more independent information as regards the state of the AR photospheric magnetic field; iii) flaring rates for each property vary between the field components in a manner consistent with the differences in property-value ranges resulting from the components; iv) flaring rates generally increase for higher values of properties, except the Fourier spectral power index that has flare rates peaking around a value of $5/3$. These findings indicate that there may be advantages in using $B_{r}$ rather than $B_{\mathrm{los}}$ in calculating flare-related AR magnetic properties, especially for regions located far from central meridian.

1 Introduction

It is well known that the energy that powers solar flares and coronal mass ejections (CMEs) is slowly built up in the magnetically structured coronae of active regions (ARs) and then quickly released via the reconfiguration of the magnetic field (Aschwanden et al., 2017). In the absence of direct measurements of the coronal magnetic field (or uniquely defined non-potential reconstructions), flare forecasting has relied on photospheric information instead. In particular, flare prediction has given great importance to the normal-to-surface field component, $B_{\mathrm{n}}$, for several reasons. First, because the normal component can be assumed from the line-of-sight (LOS) component under certain circumstances (i.e., close to disk centre). Second, the normal component provides the positive- and negative-polarity areas in the photosphere where the 3D magnetic field – which extends into the corona – is rooted. In this sense, the normal component should provide information as regards the magnetic energy flux that flows from the photosphere into the coronal volume occupied by the AR.

Previous studies have focussed on quantifying spatial patterns of the photospheric field using the LOS component restricted to regions near disk centre. In terms of the physical characteristic or process to be analyzed, these studies can be grouped into a few categories:

• i) those detecting and parameterizing magnetic polarity inversion lines (MPILs) as proxies of current-carrying magnetic structures emerging through the photosphere (e.g. Falconer, Moore, and Gary, 2003; Schrijver, 2007);

• ii) those quantifying the complex spatial patterns of the photospheric field in terms of the field’s multi-scale behaviour (e.g. Abramenko, 2005; Hewett et al., 2008; Guerra et al., 2015) and fractal properties (e.g. Conlon et al., 2008, 2010; Ermolli et al., 2014; McAteer, Gallagher, and Ireland, 2005);

• iii) those characterizing the field connectivity based on photospheric information (e.g. Georgoulis and Rust, 2007; Ahmed et al., 2010; Zuccarello et al., 2014; Barnes and Leka, 2006).

For ARs away from disk centre, some considerations need to be taken into account when using LOS data. As ARs move away from disk centre, the observing angle, $\theta'$, increases and the contributions of the magnetic vector magnitude and direction to the LOS component change (Leka, Barnes, and Wagner, 2017). In addition, the LOS component samples an increasing portion of the parallel-to-surface component, resulting in artefacts like unphysical limb-effect MPILs in magnetic structures such as ARs. The common $\mu$-angle correction, $B_{\mathrm{n}} = B_{\mathrm{los}}/\mu$ where $\mu=\cos (\theta' )$, assumes the whole photospheric field is normal and therefore results in enhancement of such artefacts. Thus, it seems reasonable to assume that a more sophisticated approximation of the normal component of the magnetic field will represent more consistently any property calculated far from disk centre.

Before the launch of the Solar Dynamics Observatory (SDO; Pesnell, Thompson, and Chamberlin, 2012), some statistical studies of flaring-related magnetic properties of ARs employed a more realistic normal component measured from space- and ground-based vector magnetograms (see e.g. Leka and Barnes, 2007). These studies contributed greatly to the understanding of flaring active regions, but the regular use of vector-magnetic field in flare forecasting was not practical until the Heliospheric Magnetic Imager (HMI; Scherrer et al., 2012) on board SDO started providing near-realtime full-disk vector magnetograms. The HMI vector data preparation pipeline provides the $B_{\mathrm{los}}$ component from the Mharp series and the surface-normal component in the form of the spherical-radial field, $B_{r}$ from the Milne–Eddington (ME) inversion series. Therefore, a statistical study focussing on the difference between AR properties calculated from $B_{\mathrm{los}}$ and $B_{r}$ seems appropriate and timely. In Section 2, the data sample used and pre-processing methods are described, while Section 3 describes the AR properties investigated. Section 4 presents the results, focussing on the difference in properties calculated using the $B_{\mathrm{los}}$ and $B_{r}$ data (Section 4.1), their variation with AR longitudinal position (Section 4.2), the correlation between properties (Section 4.3), and their flare association (Section 4.4). Finally, Section 5 presents concluding remarks.

2 Data Sample

The AR properties included in this study were calculated from the Space-weather HMI Active Region Patch (SHARP; Bobra et al., 2014) data products from SDO. SHARP data products contain AR magnetograms derived from the HMI full-disk magnetograms. Vector and LOS maps are derived from the hmi.ME_720s_fd10 and hmi.Mharp_720s series, respectively. ARs are detected as a group of pixels exceeding a threshold value of 100 G in the unsigned LOS field. These strong-field pixels are then separated into individual HMI Active Region Patches (HARPs; Hoeksema et al., 2014), each uniquely identified by a HARP number and the observation time. SHARP data contain, amongst other information, the disambiguated photospheric magnetic field in two sampling systems: field magnitude, azimuth and inclination angles (with respect to the LOS) in native image-plane sampling; spherical radial, longitudinal and latitudinal components of the field in cylindrical equal area (CEA) de-projected sampling. A near-realtime (NRT) version of the SHARP data is created and made available with short delay from the observation time. In this version the selected HARP field-of-view (FOV) varies according to the AR evolution.

For this study, CEA NRT data were accessed from the hmi.sharp_cea_720s_nrt series. A robust sample of the entire SHARP repository was selected to perform a significant statistical study of flare-related AR properties. This sample corresponds to 25% of the days between 15 September 2012 and 17 May 2016, selected from a random uniform distribution. The distribution of the selected days is displayed in the left panel of Figure 1. For each selected day, four time stamps are analyzed, which correspond to a cadence of 6 hr (i.e. times closest to 00:00, 06:00, 12:00, and 18:00 UT). On average there are approximately ten SHARP regions on disk at any time in the sample. Thus 12,733 SHARPs were analyzed, with the right panel of Figure 1 displaying the spatial distribution of heliographic (HG) coordinates ($\phi$ and $\theta$ for longitude and latitude, respectively). It can be seen that SHARP locations are distributed uniformly over the two hemispheric active latitude bands and across all longitudes.

Figure 1

Graphic representation of the of the data sample analyzed. Sample corresponds to 25% of days randomly selected between 15 September 2012 and 17 May 2016. Distribution of the selected days by year (left panel) and solar disk locations of SHARPs (right panel).

Data quality selection is done before calculating the properties. In the pre-processing stage, first NRT SHARP data are checked for bad-quality images (images containing mostly null values), missing header information, or failing of the world coordinate system (WCS; Thompson, 2006) calculation. If any of these problems are encountered, the HARP is considered as bad data and no properties are calculated from it. HARP FOVs can contain off-limb pixels when the patches are detected near the solar limb. Thus, HARPs are pre-processed in order to exclude off-limb pixels from subsequent calculations. An edge-detection procedure was implemented to detect the solar limb in CEA de-projected images. First, the gradient of the image is calculated by convolving the image with a Sobel filter (see e.g. Al-Ghraibah, Boucheron, and McAteer, 2015). Then using the WCS, the HG location can be assigned to each pixel on the limb. Finally, the lowest value of the longitudinal distance is selected as the new maximum longitude for the HARP FOV. The result of this process is an image trimmed in the horizontal (i.e. longitudinal) direction.

3 Active Region Magnetic Properties

The quantities considered here correspond to AR magnetic field properties for most of which the significance in flare prediction has been shown (see e.g. Barnes and Leka, 2008). Each feature described below can provide one or more properties to the study. However, properties presented here correspond to a subgroup selected for the purpose of illustrating differences between $B_{\mathrm{los}}$- and $B_{r}$-calculated properties. This subgroup covers different aspects of ARs, from photospheric features of interest such as MPILs, to the entire AR flux distribution.

3.1 Magnetic Polarity Inversion Line (MPIL) Properties

MPILs, or neutral lines, in the photosphere of ARs separate distinct patches of positive and negative flux and several studies have related the flare occurrence to MPIL properties (e.g. Schrijver, 2007; Mason and Hoeksema, 2010; Falconer et al., 2012). A subset of MPILs have also been identified as strong MPILs (or $^{\star }\mbox{MPILs}$) based on:

• i) strong horizontal gradients in the vertical-field component across the MPIL;

• ii) strong horizontal-field component over the MPIL.

$^{\star}\mbox{MPILs}$ can be considered as photospheric evidence of the emergence of highly twisted fields and the place in ARs where flux cancellation is likely to take place. Bokenkamp (2007) developed an algorithm to define $^{\star}\mbox{MPILs}$ using a three-stage process based on the original $^{\star}\mbox{MPIL}$ detection routine of Falconer, Moore, and Gary (2003). First, MPILs are identified as contours of zero field in a strongly smoothed $B_{\mathrm{n}}$. Then a vector-magnetic field map is calculated from the smoothed $B_{\mathrm{n}}$ image using a potential-field model (e.g. Alissandrakis, 1981). $^{\star}\mbox{MPILs}$ are then extracted from the detected MPILs by thresholding: i) the gradient of the vertical magnetic field; ii) the strength of the horizontal magnetic field in the potential-field model. Second, the same process of detection is repeated for a less-smoothed $B_{\mathrm{n}}$ image. $^{\star}\mbox{MPILs}$ are determined by comparing between $^{\star}\mbox{MPILs}_{1}$ and $^{\star}\mbox{MPILs}_{2}$ identified in the first and second stages, respectively; retained $^{\star}\mbox{MPILs}$ correspond to portions of $^{\star}\mbox{MPILs}_{2}$ that are separated from $^{\star }\mbox{MPILs}_{1}$ by distances less than a specified threshold of 11 Mm. Finally, this comparison method is applied between $^{\star}\mbox{MPILs}$ identified from an unsmoothed image and the newly identified $^{\star }\mbox{MPILs}$ with the same distance threshold of 11 Mm. Note that in ARs with complicated magnetic configurations, the $^{\star}\mbox{MPIL}$ detection algorithm usually identifies multiple $^{\star}\mbox{MPILs}$ within one magnetogram FOV.

In this study, a modification of the Bokenkamp (2007) detection algorithm was implemented by skipping the final stage in the three-stage process to reduce computation time. A comparison between original- and modified-algorithm results shows very little difference between the detected $^{\star}\mbox{MPILs}$. Therefore, the modified two-stage process is used here to find $^{\star}\mbox{MPILs}$ using $B_{\mathrm{n}}=B_{r}$ and $B_{\mathrm{n}}$ = $\mu$-corrected $B_{\mathrm{los}}$, with smoothing factors of 6 and 3 pixels used in the first and second stages of the calculation, respectively. Flux threshold values used to define the strong segments of MPILs are 120 and $100~\mbox{Mx}\,\mbox{cm}^{-2}$ in each stage, correspondingly. From the determined $^{\star}\mbox{MPILs}$, several properties can be obtained such as maximum and total lengths of $^{\star }\mbox{MPIL}$ segments ($L_{\mathrm{max}}$ and $L_{\mathrm{tot}}$, respectively), and the total unsigned flux $\Phi_{\mathrm{MPIL}}$ near $^{\star}\mbox{MPILs}$. In this paper, only the total length is reported.

3.2 Decay Index

The horizontal-field decay index, $n_{\mathrm{hor}}$, is a quantity related to the onset of the torus instability for current-carrying flux ropes in ARs. The torus instability has been extensively studied in relation to the success or failure of ARs in producing CMEs (e.g. Liu, 2008b; Zuccarello et al., 2014; Zuccarello, Aulanier, and Gilchrist, 2015). However, a statistical study of how the decay index relates to flare occurrence has not been conducted. In order to determine $n_{\mathrm{hor}}$, a 3D vector-magnetic field is required to be derived from the photospheric field using a field extrapolation. In the coronal volume of an AR, $n_{\mathrm{hor}}$ is defined as the localized gradient of the logarithmic horizontal magnetic field with logarithmic height,

$$ n_{\mathrm{hor}} = - \frac{\mathrm{d}\log (B_{\mathrm{hor}} )}{\mathrm{d}\log (h )}, $$

(1)

where $B_{\mathrm{hor}}$ is the horizontal component of the magnetic field and $h$ is the height above the photosphere. In order to derive the 3D vector-magnetic field above the AR, a potential-field model is implemented (e.g. Alissandrakis, 1981), using $B_{r}$ or $\mu$-corrected $B_{\mathrm{los}}$ as photospheric lower boundary input. After a 3D array of localized $n_{\mathrm{hor}}$ values is determined from this model, several $^{\star}\mbox{MPIL}$-related decay index properties can be derived. Included here are: i) the minimum height of critical decay index ($n_{\mathrm{cr}} = 1.5$) above $^{\star}\mbox{MPILs}$, $h_{\mathrm{min}}$; ii) the maximum ratio of $^{\star}\mbox{MPIL}$ length to $h_{\mathrm{min}}$ from each $^{\star}\mbox{MPIL}$ in an AR, $(L/h_{\mathrm{min}} )_{\mathrm{max}}$. A decay index calculation based on a potential field provides an estimate of how quickly the horizontal component of the field due to sources (e.g. overlying arcade fields in active regions), external to a current-carrying non-potential field, decreases with height. There have been several studies (Török and Kliem, 2005; Kliem and Török, 2006; Fan and Gibson, 2007; Liu, 2008a) establishing the gradient of a magnetic field overlying an erupted flux rope as important to understanding kink and torus instabilities for solar eruptions.

3.3 Schrijver’s $R$ Value

The $R$ value quantifies the unsigned photospheric magnetic flux near (i.e. within ${\approx\,}15$ Mm of) strong-field high-gradient MPILs within active regions. This property and its usefulness in forecasting was first investigated by Schrijver (2007). The presence of such MPILs indicates that twisted magnetic structures which carry electrical currents (associated with the potential for flare activity) have emerged into the active region through the solar surface. Therefore, $R$ represents a proxy for the free magnetic energy that is available for release in a flare.

The algorithm for calculating $R$ is relatively simple, computationally inexpensive, and was developed using $B_{\mathrm{los}}$ magnetograms from the Michelson Doppler Imager (MDI; Scherrer et al., 1995) on board the Solar and Heliospheric Observatory (SOHO: Domingo, Fleck, and Poland, 1995). First, a bitmap is constructed for each polarity in a magnetogram, indicating where the absolute magnitude of the magnetic flux density exceeds the threshold value of $150~\mbox{Mx}\,\mbox{cm}^{-2}$. These bitmaps are then dilated by a square kernel of $3 \times3$ pixels and the areas where the bitmaps overlap are defined as strong-field MPILs. This combined bitmap is then convolved with a Gaussian filter of 15 Mm FWHM, which corresponds to the peak value of the distribution of flare ribbon distance (as observed in EUV images) from MPILs (see Schrijver, 2007 for further details). Finally, the Gaussian-convolved bitmap is multiplied with the absolute flux value of the $B_{\mathrm{los}}$ magnetogram and $R$ is calculated as the sum over all pixels.

For calculating $R$ values from the magnetogram sample, it is necessary to pre-process the data and implement some changes in the corresponding algorithms. First, SHARP magnetograms are resampled from $0.03^{\circ}~\mbox{pixel}^{-1}$ to $0.12^{\circ}~\mbox{pixel}^{-1}$ (i.e. equivalent to MDI resolution in a CEA de-projection) to match the definition in Schrijver (2007). Second, to calculate $R$ using the $B_{r}$ component it is necessary to use a different (and higher) threshold of $300~\mbox{Mx}\,\mbox{cm}^{-2}$ in defining strong-field MPILs. This is because the $B_{r}$ component has increasing levels of noise at increasing distances from disk centre, due to larger contributions from the linear Stokes polarization (which has a higher noise level than the circular Stokes polarization, which provides the $B_{\mathrm{los}}$ component). This value was determined by making a series of test calculations of $R$ for HARP/AR full-disk passage for threshold values in the range $150\,\mbox{--}\,500~\mbox{Mx}\,\mbox{cm}^{-2}$. The chosen value of $300~\mbox{Mx}\,\mbox{cm}^{-2}$ corresponds to the threshold making $\log [R (B_{r} ) ]$ closest to $\log [R (B_{\mathrm{los}} ) ]$ when the regions are located within $45^{\circ}$ of central meridian.

3.4 Fourier Spectral Power Index

The spectral power index, $\alpha$ (also referred to as an exponent), corresponds to the power-law exponent achieved in fitting the function $E (k ) \propto k^{-\alpha}$ to the 1D power spectral density $E (k )$ in magnetograms. This field-fractality-related property parameterizes the power contained in magnetic structures at spatial scales $l = k^{-1}$ belonging to the inertial range of magnetohydrodynamic turbulence. Empirically, ARs with high spectral power index display an overall high productivity of flares (see e.g. Abramenko, 2005; Guerra et al., 2015). Historically, $\alpha$ has been calculated using $B_{\mathrm{los}}$ under the assumption that it represents the normal-field component at small distances from disk centre. First, a magnetogram is processed using a FFT to yield $E (k_{x}, k_{y} )$, the 2D power spectral density (PSD), that is, the squared absolute value of the FFT. To convert 2D PSD from wave numbers $k_{x}$ and $k_{y}$ to the 1D PSD $E (k )$ with isotropic wave number $k = (k_{x}^{2} + k_{y}^{2} )^{0.5}$, it is necessary to integrate $E (k_{x}, k_{y} )$ over angular direction in Fourier space and multiply by a factor of $2 \pi k$. Finally, a power-law fit is performed as a linear fit to the log-log representation of $E (k )$ vs. $k$ and the slope (i.e. $\alpha$) is obtained over the inertial range corresponding to $2\,\mbox{--}\,20~\mbox{Mm}$ (i.e. $k=0.05\,\mbox{--}\,0.5~\mbox{Mm}^{-1}$). Power spectral indices are calculated for both $B_{\mathrm{los}}$ and $B_{r}$ as described here – no changes were necessary between the two data formats.

3.5 Effective Connected Magnetic Field Strength

The effective connected magnetic field strength, $B_{\mathrm{eff}}$, is a morphological proxy that aims to quantify strong MPILs at the photosphere of an AR. It was first introduced by Georgoulis and Rust (2007) and modified by Georgoulis (2010, 2013). $B_{\mathrm{eff}}$ is based on the idea that an AR may be represented by a dipole with foot-point separation equal to the magnetogram pixel size and total flux equal to the total connected flux of the AR. First, patches of both magnetic polarities are identified using the partitioning method of Barnes, Longcope, and Leka (2005), producing a set of non-overlapping areas with known outlines, magnetic flux content, and flux-weighted centroid positions. Second, a connectivity matrix is defined for the fluxes $\Phi _{ij}$ committed to opposite-polarity partition pairs $ij$. Each connection is given a length, $L_{ij}$, that is, the distance between the flux-weighted centroids of the partition pair. Fluxes in the connectivity matrix are found via a simulated annealing method designed to emphasize MPILs. This is achieved through preferably connecting closest opposite-polarity fluxes by minimizing

$$ \sum_{ij} \biggl( \frac{|\mathbf{\mathit{r_{i}}}-\mathbf{\mathit {r_{j}}}|}{l_{\mathrm{max}}} + \frac{|\Phi_{i}+\Phi_{j}|}{|\Phi_{i}|+|\Phi _{j}|} \biggr), $$

(2)

where $r$ and $\Phi$ are the position vector and flux of each partition, $i$ and $j$ indicate positive- and negative-flux partitions, respectively, $l_{\mathrm{max}}$ is the diagonal length of the magnetogram, and the sum is performed over all opposite-polarity pairs.

For flux-balanced ARs, a connectivity matrix contains only opposite-polarity connections after the annealing process. However, ARs are rarely flux balanced, mostly due to large-scale connections to flux beyond the FOV. To rectify this, a ring of “mirror flux” is placed a large distance from the AR. Connections between excess AR flux and the mirror flux are treated as open and not included in $B_{\mathrm{eff}}$. From the connectivity matrix, $B_{\mathrm{eff}}$ is measured in magnetic intensity units as

$$ B_{\mathrm{eff}}=\sum_{i}\sum _{j}\frac{\Phi_{ij}}{L^{2}_{ij}}. $$

(3)

To calculate $B_{\mathrm{eff}}$, the entire AR must be taken into account, while partitions belonging to the quiet Sun or small isolated partitions (which do not contribute to flare activity) must be excluded. To this end, minimum thresholds are imposed on flux density ($100~\mbox{Mx}\,\mbox{cm}^{-2}$), partition area (40 pixels, ${\approx\,}5.3~\mbox{Mm}^{2}$ from SHARP CEA pixel size of $0.03^{\circ}$), and enclosed flux ($5\times10^{19}$ Mx), with values chosen following AR time-series tests. Threshold selection also affects the calculation speed; lower thresholds include larger portions of magnetic flux, producing more partitions at the expense of slower calculations. Since $B_{\mathrm{eff}}$ is a quantity calculated from the normal-field component, the same thresholds are used for both $B_{r}$ and $B_{\mathrm{los}}$ to compare the values produced, keeping in mind that in principle $B_{r}$ values are higher than the corresponding $B_{\mathrm{los}}$ when considering ARs far from disk centre. According to Barnes and Leka (2008), $B_{\mathrm{eff}}$ can be seen as an $R$-value with the flux-weighting given by the connectivity matrix. Therefore some correlation between these two properties can be expected.

3.6 Ising Energy

The term Ising energy originates from the solid state physics Ising model. This model is used to characterize the state of magnetic systems in which opposite polarities can have short and long range interactions, such as ferromagnetic materials. This quantity was proposed as a measure of AR magnetic complexity in MDI LOS magnetograms by Ahmed et al. (2010) and corresponds to interaction energy between pairs of magnetic polarities. First, flux values are byte-scaled to $0\,\mbox{--}\,255$. Second, low values ($0\,\mbox{--}\,30$) represent strongest negative fields and are flagged with −1, while high values ($230\,\mbox{--}\,255$) represent strongest positive fields and are flagged with $+1$; intermediate values ($31\,\mbox{--}\,229$) represent lower absolute field strength and are set to 0 and ignored. Finally, the Ising energy is calculated as

$$ E_{\mathrm{Ising}}=-\sum_{ij}\frac{S_{i}S_{j}}{d^{2}}, $$

(4)

where $S_{i}=+1$ and $S_{j}=-1$ for positive and negative pixels, respectively, and $d$ is the distance between opposite-polarity pixel pairs $ij$. $E_{\mathrm{Ising}}$ correlates with AR flare productivity according to Ahmed et al. (2010), but it has not been implemented in the forecasting literature. For the calculation of the Ising energy, it is necessary to define ranges that correspond to strong positive and negative pixels. Unlike the byte-scaling applied in Ahmed et al. (2010), an absolute flux threshold is used here; only pixels of absolute value greater than $100~\mbox{Mx}\,\mbox{cm}^{-2}$ are considered, and they are flagged with $+1$ (−1) if their value is positive (negative).

$E_{\mathrm{Ising}}$ and $B_{\mathrm{eff}}$ show a similar functional form. However, in the former, unipolar magnetic elements correspond to strong pixels (field strength ${>\,}100~\mbox{Mx}\,\mbox{cm}^{-2}$), while, for the latter, the same are represented by non-overlapping partitions. For the Ising energy, the connectivity accounts for all possible connections between strong pixels pairs, without, however, taking into account the magnetic flux of these pixels. Some degree of correlation between $E_{\mathrm{Ising}}$ and $B_{\mathrm{eff}}$ is expected. Thus, by definition, the Ising energy is a non-zero quantity as long as there are at least two strong opposite-polarity pixels within a HARP but at least two sizeable, non-overlapping opposite-polarity magnetic partitions are required for a non-zero $B_{\mathrm{eff}}$.

4 Results

A total of $12{,}773$ SHARP magnetograms were available in the selected sample. This sample was then filtered to leave only those HARP numbers that were associated to (one or more) NOAA-numbered regions at any time during the HARP disk passage. A total of $3{,}999$ SHARPs (31.3%) are included in the results presented in this section. On occasion, the dynamic evolution of active regions within a HARP associated to multiple NOAA regions can lead to the splitting of the HARP into two or more patches. This particular scenario is important to consider if the full-disk passage of HARPs is studied at any cadence. However, the data sample in this study was randomly selected, and therefore the evolution of any particular region is unlikely to be included.

Results from this statistical study are shown with emphasis on four aspects: differences in property values from using $B_{\mathrm{los}}$ or $B_{r}$ data (Section 4.1); variation of properties with AR longitudinal position (Section 4.2); correlations between properties (Section 4.3); flaring association of individual properties (Section 4.4).

4.1 LOS- versus Radial-Field Comparison

Most properties studied here are strictly speaking defined in terms of the surface-normal ($B_{\mathrm{n}}$) component of the photospheric field. In their original implementations, properties are calculated either using only $B_{\mathrm{los}}$ (if restricted to disk centre) or $\mu$-angle corrected $B_{\mathrm{los}}$. The availability of $B_{r}$ (equivalent to $B_{\mathrm{n}}$) and $B_{\mathrm{los}}$ in the SHARP data products allows direct comparison between the resulting properties that each produces. However, SHARP $B_{\mathrm{los}}$ and $B_{r}$ magnetograms are derived from different polarization signals (i.e. different detectors) and therefore the LOS component from the ME inversion ($|B|\cos(\gamma)$; $|B|$ is the field strength, $\gamma$ the inclination angle with respect to the LOS) does not necessarily match $B_{\mathrm{los}}$. Therefore, a comparison between $|B|\cos(\gamma)$ and $B_{\mathrm{los}}$ in the plane-of-sky coordinate system should be done before proceeding with the AR-property calculations. Figure 2a presents the density histogram from a pixel-by-pixel comparison of all HARP regions on 6 August 2014 at 00:00 UT. This date was chosen because multiple regions of different sizes are present and more or less distribute all over the solar disk. Figure 2b, on the other hand, shows the average percentage difference between the two signals as a function of $|B|\cos(\gamma)$, for each polarity separately. Figure 2a shows that, for pixels with ${>\,} 500$ G, $B_{\mathrm{los}}$ underestimates the field strength. Positive and negative polarities (black and red curves in Figure 2b, respectively) show similar average differences between $B_{\mathrm{los}}$ and $|B|\cos(\gamma)$ values, up to ${\approx\,} 1.5$ kG, where negative polarities are observed to have larger difference. At the highest common value, positive and negative polarities are, on average, underestimated by $B_{\mathrm{los}}$ by 25% and 30%, respectively. However, in Figure 2a it is observed that such big differences display a density of only about $10^{-5}$.

Figure 2

Pixel-by-pixel comparative density histogram (a) between the SHARP $B_{\mathrm{los}}$ signal and the LOS signal recovered from the Milne–Eddington inversion, $|B|\cos(\gamma)$. Average absolute difference percentage (b) as a function of $|B|\cos(\gamma)$ for each polarity separately. Data used to produce these plots correspond to all HARPs present on 6 August 00:00 UT. $B_{\mathrm{los}}$ seems to systemically underestimate the field in pixels with absolute strength greater than 500 G. The maximum observed difference between the two signals for strong-field pixels (${\approx\,}1.8$ kG) is 25% and 30% for positive- and negative-polarity pixels, correspondingly. Error bars correspond to the $1\sigma$ values.

Thus, the relatively small difference between the two LOS signals allows for the use of the readily available SHARP $B_{\mathrm{los}}$ in this study. In addition, the well-known lower noise level (5 – 10 G; compared to 60 – 150 G of the ME inversion LOS) and the difficulty to recover the LOS component from the CEA fields, make the SHARP $B_{\mathrm{los}}$ more useful in real-time forecasting applications. Figure 3 contains six panels displaying the distribution of values for all properties calculated. In all panels of Figure 3, grey-scale shading displays the distributions from $B_{\mathrm{los}}$ (light grey) and from $B_{r}$ (mid-grey), while regions of distribution overlap are indicated in dark grey.

Figure 3

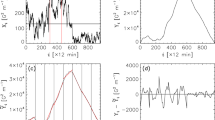
Frequency distributions of AR properties: (a) total $^{\star }\mbox{MPIL}$ length, $L_{\mathrm{tot}}$; (b) maximum ratio of $^{\star}\mbox{MPIL}$ length to minimum height of critical decay index, $(L/h_{\mathrm{min}} )_{\mathrm{max}}$; (c) Schrijver’s $R$ value; (d) Fourier spectral power index, $\alpha$; (e) effective connected field strength, $B_{\mathrm{eff}}$; (f) Ising energy, $E_{\mathrm{Ising}}$. In all panels, the grey-scale shading displays the distributions from $B_{\mathrm{los}}$ (light grey) and from $B_{r}$ (mid-grey), while regions of distribution overlap are indicated in dark grey.

Figure 3a – 3c presents the histograms for the MPIL-related properties. Distributions of the total length of strong-gradient MPILs ($L_{\mathrm{tot}}$; Figure 3a) show that a very similar behaviour is found from $B_{\mathrm{los}}$ and $B_{r}$ – both distributions cover a similar range of values. A lower occurrence at high values of $L_{\mathrm{tot}}$ reflects the drop-off in observation of large/complex ARs, while the decrease in occurrence for small values appears to be related to the fact that strong MPILs are rarely found in only one or two magnetogram pixels. For $(L/h_{\mathrm{min}} )_{\mathrm{max}}$, the maximum ratio of MPIL length to minimal height of critical decay index (Figure 3b), as with $L_{\mathrm{tot}}$, both $B_{\mathrm{los}}$ and $B_{r}$ show similar shape and span similar ranges of values. Both distributions for this property are slightly skewed to higher values. This skewness implies that the most probable value of this property comes from ARs that display $L > h_{\mathrm{min}}$. This property combines two AR measures ($^{\star}\mbox{MPIL}$ length and minimum height of critical decay index), so it is difficult to assess the variation between $B_{\mathrm{los}}$ and $B_{r}$ as both properties vary between data types. In the distributions of Schrijver’s $R$ (Figure 3c) the main observed difference is the $B_{r}$ distribution being slightly shifted towards higher values in comparison to the $B_{\mathrm{los}}$ distribution. This difference results from the higher flux threshold used with $B_{r}$, which removes some of the low R values ($\log(R) = 1\,\mbox{--}\,2.5$), and from the systematic underestimation of field strength by $B_{\mathrm{los}}$ (Figure 2), which affects those regions producing larger values ($\log(R) > 3$).

In Figure 3d, the $\alpha$ (Fourier power spectral index) distributions are shown. Notably, the range of values from $B_{\mathrm{los}}$ data is reduced when using $B_{r}$ data. Guerra et al. (2015) reported values of $\alpha>2.5$ from $B_{\mathrm{los}}$ data as AR NOAA 11158 approached the limb, implying that the values of $\alpha$ which are most different when using $B_{r}$ likely correspond to ARs far from disk centre. This can be verified in Section 4.2, since the property dependence on AR location will be analyzed. The modification of such values appears to cause a slight shift to lower values in the $B_{r}$ distribution, although both distributions display a relatively well-defined peak in the bin 1.55 – 1.70. This property-value range includes $\alpha = 1.67 \approx 5/3$, the Kolmogorov exponent (Kolmogorov, 1941), implying that a large portion of studied HARPs correspond to ARs of which the photospheric plasma is in (or close to) a fully developed hydrodynamical turbulence.

Figures 3e and 3f display the histograms of the magnetic-connectivity properties, respectively. The distributions of the effective connected magnetic field strength, $B_{\mathrm{eff}}$, display a similar behaviour to Schrijver’s $R$ value in Figure 3c (i.e. a slight shift to larger values when using $B_{r}$ data). This behaviour is in correspondence with the field-strength underestimation of $B_{\mathrm{los}}$ and puts in evidence the correlation between $B_{\mathrm{eff}}$ and $R$. For the Ising energy, $E_{\mathrm{Ising}}$, the distributions from $B_{\mathrm{los}}$ and $B_{r}$ span the same range and show a similar distinctive shape, unlike any other properties. First, there is a clear tendency of the occurrence to increase with the $E_{\mathrm{ising}}$ value – most NOAA-numbered HARPs show complex connectivity dominated by strong (i.e. ${>\,}100~\mbox{Mx}\,\mbox{cm}^{2}$) opposite-polarity pixels pairs close to each other. On the other hand, the presence of a peak at low values of $0.1\,\mbox{--}\,1.0~\mbox{pixel}^{-2}$ is due to the definition of $E_{\mathrm{ising}}$ – unlike $B_{\mathrm{eff}}$, only the distance separating pixels are used and not magnetic flux. Therefore, some of the HARPs containing early stages of AR formation (i.e. small numbers of significant-flux pixels that separate during spot formation, before additional flux emergence partially fills the AR interior) can produce the number of low-value regions observed in that peak.

4.2 Variation with AR Longitudinal Position

One objective of this study is to investigate the dependence of derived properties on SHARP Heliographic (HG) position. Since AR evolution shows very little variation in latitudinal position, more emphasis is given to the variation of properties with the HG longitude, $\phi$. Figures 4 and 5 present differences between $B_{\mathrm{los}}$- and $B_{r}$-derived properties in two forms. First, panels (a), (c), and (e) show scatter plots of property values derived from $B_{\mathrm{los}}$ versus $B_{r}$, where the diagonal black line is unity and data points are colour-coded to represent three groups of SHARP longitudes: $|\phi| < 60^{\circ}$ (black); $60^{\circ} \leqslant|\phi| < 75^{\circ}$ (blue); $|\phi| \geqslant75^{\circ}$ (red). Second, panels (b), (d), and (f) present locations and magnitudes of the difference in $B_{\mathrm{los}}$- and $B_{r}$-derived properties, with each data point at the SHARP centroid position at the observation time and colour representing magnitude of difference between property values from the field components. The difference is defined as $X (B_{r} ) - X (B_{\mathrm{los}} )$ where $X$ can be any of the properties studied, such that when $B_{r}$ yields a larger property value than $B_{\mathrm{los}}$ the difference is positive. In all cases except $\alpha$, the differences are calculated after taking the logarithm of the property, in order to better visualize the differences. In addition, Table 1 presents maximum and minimum values and the first four moments (mean, standard deviation, kurtosis, and skewness) for the distributions of the differences (all $\phi$ groups included). Mean and $\pm\sigma$ values are depicted in Figures 4 and 5a, 5c, and 5e as solid and dotted grey diagonal lines, correspondingly.

Figure 4

Differences between $B_{\mathrm{los}}$- and $B_{r}$-derived properties: (a) – (b) $L_{\mathrm{tot}}$, (c) – (d) $(L/h_{\mathrm{min}} )_{\mathrm{max}}$; (e) – (f) $\log (R )$. Left-hand panels ((a), (c), and (e)) show scatter plots of properties derived from $B_{\mathrm{los}}$ vs. $B_{r}$, where the diagonal line is unity and data points are colour-coded to represent three longitude groups: $|\phi| < 60^{\circ}$ (black); $60^{\circ} \leqslant|\phi| < 75^{\circ}$ (blue); $|\phi| \geqslant75^{\circ}$ (red). Right-hand panels ((b), (d), and (f)) present locations and magnitude differences between $B_{r}$- and $B_{\mathrm{los}}$-derived properties, with each data point at the SHARP centroid position at the observation time and colour representing magnitude of difference between property values from the field components.

Figure 5

As Figure 4, but for properties: (a) – (b) $\alpha$, (c) – (d) $B_{\mathrm{eff}}$; (e) – (f) $E_{\mathrm{Ising}}$.

Table 1 Distribution moments of the difference between property values from the field components $B_{\mathrm{los}}$ and $B_{r}$.

The $L_{\mathrm{tot}}$ scatter plot in Figure 4a displays a linear log–log correlation between values calculated from $B_{\mathrm{los}}$ and those from $B_{r}$. The distribution of points around the unity diagonal shows a small positive mean, implying that $B_{r}$ values are larger on average. This correlation shows a low level of dispersion, with $2/3$ of points ($2\sigma$ is the distance between dotted grey lines) spanning ${\approx\,} 0.7$, less than an order of magnitude. There appears to be no systematic dependence on longitude as blue and red symbols ($60^{\circ} \leqslant|\phi| < 75^{\circ}$ and $|\phi| \geqslant75^{\circ}$, respectively) appear to fall within the scatter of black symbols ($|\phi | < 60^{\circ}$). In Figure 4b, the majority of points have differences close to zero (green symbols) and few non-zero values are found for $|\phi| < 30^{\circ}$. At greater $\phi$, $L_{\mathrm{tot}}$ values from $B_{r}$ are marginally larger than those from $B_{\mathrm{los}}$ (yellow symbols). Overall the largest differences are on the order of tens of Mm, with these magnitudes restricted to $B_{r}$ resulting in larger values than $B_{\mathrm{los}}$ (red symbols). The $^{\star}\mbox{MPIL}$ detection process is identical for both field components, so larger $B_{r}$ values are due to more pixels passing the $^{\star}\mbox{MPIL}$ flux threshold, as a consequence of field-strength underestimation of $B_{\mathrm{los}}$. In addition, two characteristics are clearly identified in Figure 4b: i) a systematically larger $B_{r}$ values (positive differences) with increasing $|\phi|$, and ii) asymmetric distribution of values over the disk, with higher differences achieved for western longitudes. These two observations seem to be consistent with the spatial and temporal variations of noise levels in the HMI inverted magnetic field data (Hoeksema et al., 2014). The noise in the vector-field strength exhibits a centre-to-limb variation (${\approx\,} 60\,\mbox{--}\,150$ G) that also varies with the satellite orbital velocity. This variation produces an east–west asymmetry in the noise pattern which appears periodically around 1:00, 7:00, 13:00, and 19:00 UT (see Figures 6 and 7 in Hoeksema et al., 2014). These times are close to the daily sampling times used in this study. Furthermore, the $^{\star}\mbox{MPIL}$ detection algorithm uses a flux threshold of $100\,\mbox{--}\,120~\mbox{Mx}\,\mbox{cm}^{-2}$, which is not high enough for eliminating these noise contributions to the calculated property values.

In Figure 4c, a linear log–log correlation is observed for $(L/h_{\mathrm{min}} )_{\mathrm{max}}$. Points show a very small negative mean value and seem to be almost symmetrically distributed around it. This correlation shows a larger scatter in comparison to $L_{\mathrm{tot}}$ – most points are distributed over almost an order of magnitude around the mean. Figure 4d shows a slightly different scenario to $L_{\mathrm{tot}}$: near-zero differences (green symbols) dominate for $(L/h_{\mathrm{min}} )_{\mathrm{max}}$ over all $\phi$ values, but some large-magnitude differences (predominantly blue symbols) also occur. There seems to be no obvious indication that non-zero values dominate over any longitudes, with the larger scatter attributed to this property being the combination of two independent AR properties. The largest differences between $B_{r}$- and $B_{\mathrm{los}}$-derived $(L/h_{\mathrm{min}} )_{\mathrm{max}}$ are on the order of hundreds of gauss and seem to occur mostly when using $B_{\mathrm{los}}$. Again, it is difficult to assess the differences between $B_{\mathrm{los}}$ and $B_{r}$ as both $^{\star}\mbox{MPIL}$ length and $h_{\mathrm{min}}$ above these MPILs vary between field components.

The scatter plot for $\log (R )$ in Figure 4e shows a reasonable linear correlation for data points from $|\phi| < 60^{\circ}$ (black symbols). The linear correlation shifts above the unity diagonal for $60^{\circ} \leqslant |\phi| < 75^{\circ}$ (blue symbols) and more so for $|\phi| \geqslant 75^{\circ}$ (red symbols), indicating that $B_{\mathrm{los}}$ gives systematically lower values compared to $B_{r}$ further from disk centre. All points are more or less equally distributed around the unity diagonal with the smallest mean value of all properties and with most points distributed over ${\approx\,} 1.3$ orders of magnitude. However, visualization of the data in Figure 4f shows that property differences for $|\phi | < 60^{\circ}$ are a mixture of negative ($B_{\mathrm{los}}$ yielding larger $R$ values; blue symbols) and near-zero values (green symbols). This behaviour, in locations where both property values should be essentially the same (disk centre), can be attributed to the different magnetic flux thresholds applied in determining $R$-value MPILs. For $|\phi| \geqslant60^{\circ}$, $\log [R (B_{r} ) ]$ becomes larger than $\log [R (B_{\mathrm{los}} ) ]$ (yellow–red symbols), with differences increasing at $|\phi| \geqslant 75^{\circ}$. Since in this case, both flux thresholds used are above the typical noise levels (150 and 300 G for $B_{\mathrm{los}}$ and $B_{r}$, respectively), larger $B_{r}$ values with increasing $|\phi|$ must arise from a better definition of the MPILs, specially at far distances from the central meridian.

Figure 5a presents the scatter plot for the Fourier spectral power index, $\alpha$, which has a mostly linear relationship over low values (i.e. 0.5 – 2.0). Beyond that range, $\alpha (B_{r} )$ appears to saturate while $\alpha (B_{\mathrm{los}} )$ continues increasing, with the divergence from linearity and scatter increasing progressively with $|\phi|$ (blue and red symbols). The distribution of all differences is clearly skewed towards $B_{\mathrm{los}}$ values with a mean value lying below the unity diagonal and negative large skewness. In this case, the $2\sigma$ spread is only ${\approx\,} 0.6$, since most points come from a region with $|\phi| < 60^{\circ}$. This location dependence is easily observed in Figure 5b, where most data points for $|\phi| < 45^{\circ}$ have near-zero differences (green symbols) and those for $|\phi| > 45^{\circ}$ are dominated by negative differences ($B_{\mathrm{los}}$ yielding larger $\alpha$ values; blue symbols). Although $B_{\mathrm{los}}$ and $B_{r}$ are equally affected by foreshortening effects that cut off small size scales at greater $|\phi |$, differences in the structure of magnetic features with differing sizes will affect $B_{\mathrm{los}}$ spatial-frequency sampling another way. While small-scale mostly vertical flux tubes (i.e. network/plage fields) experience the usual diminishing of $B_{\mathrm{los}}$ field strength by viewing angle, large-scale fields contained in AR sunspots will experience less diminishing of $B_{\mathrm{los}}$ in comparison to small-scale fields. This unbalanced decrease of LOS signal occurs because when viewed obliquely, large-scale (sunspot) fields include horizontal-field strength components which are not detectable by HMI in the small-scale fields. Therefore this effect produces systematic diminishing of Fourier power at small scales (i.e. large $k$) more than at large scales (i.e. small $k$), hence increasing the $\alpha$ calculated from $B_{\mathrm{los}}$.

For $B_{\mathrm{eff}}$, Figure 5c shows a generally linear log–log relation between $B_{\mathrm{los}}$- and $B_{r}$-derived values. Similar to $L_{\mathrm{tot}}$, the majority of data points (and therefore the difference mean) lie above the unity diagonal – $B_{\mathrm{eff}} (B_{r} )$ is typically greater than $B_{\mathrm{eff}} (B_{\mathrm{los}} )$, as a consequence of the $B_{\mathrm{los}}$ field-strength underestimation. The distribution of all points around the unity diagonal shows a spread of $2\sigma= 0.9$, almost an order of magnitude. The correlation weakens for $60 \leqslant|\phi| < 75^{\circ}$ (blue symbols) and practically disappears for $|\phi| \geqslant75^{\circ}$ (red symbols), but these data points still fall within the scatter for $|\phi| < 60^{\circ}$ (black symbols). As shown in Figure 5d, $B_{r}$ yields values almost equal to or slightly larger than those from $B_{\mathrm{los}}$ for $|\phi| < 30^{\circ}$ (yellowish–green symbols) with a higher frequency of large differences starting at $|\phi| \geqslant30^{\circ }$. As explained for the $L_{\mathrm{tot}}$ case, the flux threshold value of $100~\mbox{Mx}\,\mbox{cm}^{-2}$ used for $B_{\mathrm{eff}}$ does not remove the effects of vector-field noise spatio-temporal patterns, and therefore the asymmetric increasing difference with $|\phi|$ appears.

Finally, Figures 5e and 5f present $E_{\mathrm{Ising}}$ as showing a similar behaviour to $B_{\mathrm{eff}}$; a generally linear log–log relation with large scatter ($2\sigma\approx 1.15$ orders of magnitude) and data points lying almost exclusively above the unity diagonal (positive mean). In contrast to $B_{\mathrm{eff}}$, there is a very wide range of values for $E_{ \mathrm{Ising}} (B_{r} )$ over the smallest values of $E_{ \mathrm{Ising}} (B_{\mathrm{los}} )$, which correspond to the secondary (low-frequency) peaks in Figure 3f. Values of $E_{ \mathrm{Ising}} (B_{\mathrm{los}} ) < 1.0$ result from SHARPs containing small ARs in the early stages of formation (i.e. a small number of quite separated opposite-polarity pixels). Correspondingly larger values of $E_{ \mathrm{Ising}} (B_{r} )$ (observed at many longitudes) arise from the underestimation of the field strength by $B_{\mathrm{los}}$. Although $E_{ \mathrm{ising}}$ uses a pixel-consideration threshold of $100~\mbox{Mx}\,\mbox{cm}^{-2}$ – lower than the maximum noise level in $B_{r}$ – no longitudinal variation and/or east–west asymmetry is observed, likely due to contributions from noisy pixels being few and small (opposite-polarity pixels separated by large distances).

On one hand, the LOS component is well known to be less noisy (${\approx\,}5\,\mbox{--}\,10$ G) but it also presents issues related to the viewing-angle obliqueness: not only a field-strength decrease but also, in extreme cases, the presence of false MPILs in complex sunspot ARs. The former issue is particularly clear in the behaviour of $\alpha$ with the longitudinal distance. The effect of false MPILs in MPIL-related properties could be difficult to observe, since properties such as $L_{\mathrm{tot}}$ and $R$ sum the contributions of all $^{\star}\mbox{MPIL}$ segments and their contributions will be small in comparison to the real MPILs present in NOAA-numbered regions. On the other hand, the effect of noise patterns seen in $B_{r}$-calculated properties can be alleviated by choosing a high enough flux threshold or, alternatively, by performing statistical corrective analysis such as in Falconer et al. (2016). However, using $B_{r}$ data should result in more consistent property representation with AR disk position.

No property in this study was observed to have a significant variation with the HG latitudinal position. However, the longitudinal variation of properties here found might not apply to ARs located at higher latitudes than those included in this study.

4.3 Property–Property Correlations

In addition to exploring the behaviour between $B_{\mathrm{los}}$- and $B_{r}$-derived values of a given property, it is worth investigating correlations between different properties for a given field component. This is presented in Figure 6 in the form of scatter plots for all pair-wise combinations of the six properties derived from $B_{\mathrm{los}}$ (panels A1 – 15) and $B_{r}$ (panels B1 – 15). Data points are colour-coded in the same way as those in the left-hand panels of Figures 4 and 5: $|\phi| < 60^{\circ}$ (black); $60^{\circ} \leqslant|\phi| < 75^{\circ}$ (blue); $|\phi| \geqslant 75^{\circ}$ (red). For practical purposes, a random 25% of data points from $|\phi| < 60^{\circ}$ are provided in each plot. Property self-correlation panels (i.e. on the diagonal) are omitted. Linear (Pearson) and nonlinear-rank (Spearman) correlation coefficients (CC) for each property pair are given in Tables 2 and 3 of the Appendix for $B_{\mathrm{los}}$ and $B_{r}$ data, respectively. Uncertainty estimates for CC values are given in Figure 8.

Figure 6

Property–property plots for values calculated using $B_{\mathrm{los}}$ (A panels; below diagonal) and $B_{r}$ (B panels; above diagonal). All panels in a given row share a common abscissa (left for panels A, right for panels B), while all panels in a given column share a common ordinate (bottom for panels A, top for panels B). In the $B_{\mathrm{los}}$ case, from top to bottom (and left to right) properties are displayed in the order: $L_{\mathrm{tot}}$; $(L/h_{\mathrm{min}} )_{\mathrm{max}}$; $\log (R )$; $\alpha$; $B_{\mathrm{eff}}$; $E_{\mathrm{Ising}}$. For $B_{r}$, property order is reverse of the order for $B_{\mathrm{los}}$. As in the left-hand panels of Figures 4 and 5, data points are colour-coded to represent three longitude groups: $|\phi| < 60^{\circ}$ (black); $60^{\circ} \leqslant|\phi| < 75^{\circ}$ (blue); $|\phi| \geqslant75^{\circ}$ (red). In comparing the effect of $B_{\mathrm{los}}/B_{r}$ for the same property pair, match the same number in panels A and B.

Table 2 Linear (Pearson) and nonlinear-rank (Spearman) correlation coefficients for $B_{\mathrm{los}}$-derived properties.

Table 3 Linear (Pearson) and nonlinear-rank (Spearman) correlation coefficients for $B_{r}$-derived properties.

Relationships between $B_{\mathrm{los}}$-derived properties in Figure 6 (A panels) and Table 2 span the full range of correlations from very weak to very strong. As expected, properties related to the same features correlate well – e.g. correlations between the MPIL-related property pairs $L_{\mathrm{tot}}$–$(L/h_{\mathrm{min}} )_{\mathrm{max}}$ and $L_{\mathrm{tot}}$–$R$ are very strong ($| \mathrm{CC}| \geqslant0.8$) and that for the magnetic-connectivity pair $B_{\mathrm{eff}}$–$E_{\mathrm{Ising}}$ is strong ($0.6 \leqslant|\mathrm{CC}| < 0.8$). However, a good correlation is observed between pairs of different property types – e.g. $B_{\mathrm{eff}}$ and $E_{\mathrm{Ising}}$ show at least strong correlation ($|\mathrm{CC}| \geqslant0.6$) with $L_{\mathrm{tot}}$ and $R$. This is due to the magnetic-connectivity properties scaling with the amount and proximity of opposite-polarity flux; defining features of strong/long MPILs. CCs decrease with increasing $|\phi|$ for all property pairs, while the fractality-related property $\alpha$ shows at most moderate correlation ($|\mathrm{CC}| < 0.6$) with all properties.

Comparative $B_{r}$-derived property–property correlations are given in Figure 6 (B panels) and Table 3, with results generally similar to the $B_{\mathrm{los}}$ case. Differences include most $B_{r}$-derived CCs being lower than those from $B_{\mathrm{los}}$ (although less clear in pairs with a magnetic-connectivity property) and the CC decrease with increasing $|\phi|$ being smaller in magnitude than for $B_{\mathrm{los}}$. The variation of linear and nonlinear CCs from $B_{\mathrm{los}}$ to $B_{r}$ can be understood in terms of the more consistent property representation from $B_{r}$. As shown in Section 4.2, using $B_{r}$ to calculate properties results in the reduction of viewing-angle bias in $B_{\mathrm{los}}$, such that CCs between some viewing-angle sensitive and insensitive property pairs increase for $|\phi| \geqslant75^{\circ}$ with $B_{r}$. This is expected for some property pairs as one property influences the calculation of the other – e.g. $L_{\mathrm{tot}}$–$R$, where the MPIL location (and hence the length) is used to determine the spatial region within which flux is integrated into $R$. Without the common bias in $B_{\mathrm{los}}$, CCs between property pairs that are sensitive to viewing angle decrease for $|\phi| \geqslant75^{\circ}$ with $B_{r}$ (e.g. $R$–$B_{\mathrm{eff}}$, $R$–$E_{\mathrm{Ising}}$, and $B_{\mathrm{eff}}$–$E_{\mathrm{Ising}}$).

From a total of 90 property-pair correlations (45 linear/45 nonlinear), 59 (29/30) decreased when $B_{\mathrm{los}}$ was replaced by $B_{r}$ in property calculations. Only 33 (13/20) of those correlations decreased by values larger than their associated standard errors (see Figure 8 in the Appendix for details). Such decreases in CC indicate that these properties may have a greater degree of independence than previously thought from $B_{\mathrm{los}}$ data. However, only about 37% of the studied properties showed a significant decrease.

4.4 Flaring Association

For the purposes of flare forecasting it is necessary to know the relation between the calculated properties and observed flaring activity. As mentioned before, most of these properties have been reported as having useful association with occurrence of flares/CMEs in the AR they represent. Attention is paid here to the overall differences in flaring rates associated with $B_{\mathrm{los}}$- and $B_{r}$-derived properties. Figure 7 presents average flaring rates observed in a 24-hr window after the property observation time. In each panel, rates are displayed for flares of C-class and greater for $B_{\mathrm{los}}$ (light grey, top plot), $B_{r}$ (dark grey, bottom plot), with error bars indicating Poisson uncertainties (i.e. $N^{-1/2}$, where $N$ is the number of HARPs in a property-value bin). It is very important to note that $B_{\mathrm{los}}$- and $B_{r}$-derived flaring rates for the same property-value bin do not relate to the same HARPs, due to the differences between $B_{\mathrm{los}}$ and $B_{r}$ property values presented in the scatter plots of Figures 4 and 5.

Figure 7

Average C-class and greater flaring rates in the subsequent 24 hr, with error bars indicating Poisson uncertainties (i.e. $N^{-1/2}$, where $N$ is number of SHARPs in a property-value bin). In each panel, grey-scale shading displays the flaring rates for properties calculated from $B_{\mathrm{los}}$ (light grey) and from $B_{r}$ (dark grey), while regions of overlap are indicated in mid-grey.

The general behaviour of most panels in Figure 7 (i.e. except panel (d), which represents $\alpha$) is that average flaring rates increase with increasing property value. This tendency is a good indicator that those properties might capture good statistical association of future flaring activity levels in ARs. In addition, although properties like $R$ and $B_{\mathrm{eff}}$ span different dynamic ranges between $B_{r}$ and $B_{\mathrm{los}}$ values, $B_{r}$ distributions appear to show a different (i.e. slower) rate in increase in comparison to the $B_{\mathrm{los}}$ distributions. The difference between $B_{r}$- and $B_{\mathrm{los}}$-associated flaring rates is due to many of the HARPs being corrected upwards into the higher-valued property bins. A distinctly different behaviour is displayed by $\alpha$ in Figure 7d, where a restriction of values to $\alpha< 2.5$ presented in Figures 3d and 5a and 5b is again evident. Folding of $B_{\mathrm{los}}$-derived values into the smaller $B_{r}$ range yields a slight increase in most $B_{r}$ flaring rates in that range, enhancing the peak around $\alpha= 5/3 \approx1.67$. However, the maximum rate achieved by $\alpha$ is lower than all other properties by at least a factor of 2. This implies that there is a much greater mixture of flaring and non-flaring populations in all $\alpha$ property-value bins, indicating that, although better determined by $B_{r}$, it is less useful as flare predictor than other properties here studied. In order to determine the forecasting advantage of using $B_{r}$ data over $B_{\mathrm{los}}$, proper forecasting and verification analysis must be performed, which lies beyond the scope of this investigation.

5 Conclusions

This work presents a statistical study of differences in AR properties calculated from different components of the magnetic field, focussing on six properties that have been claimed to quantify the AR potential to produce flares/CMEs: total length of strong MPILs, $L_{\mathrm{tot}}$; maximum ratio of strong MPIL length to minimum height of critical decay index, $(L/h_{\mathrm{min}} )_{\mathrm{max}}$; Schrijver’s $R$ value; Fourier spectral power index, $\alpha$; effective connected magnetic field strength, $B_{\mathrm{eff}}$; and Ising energy, $E_{\mathrm{Ising}}$. All six properties were calculated from SDO/HMI SHARP CEA NRT LOS ($B_{\mathrm{los}}$) and spherical-radial ($B_{r}$) magnetograms, with the dependence on longitudinal position, inter-property correlations, and associated flaring rates studied.

Overall, property-value distributions calculated from $B_{\mathrm{los}}$ and $B_{r}$ are similar. Differences in observed ranges indicate that $B_{r}$ typically yields marginally larger values than $B_{\mathrm{los}}$ for all properties except $(L/h_{\mathrm{min}} )_{\mathrm{max}}$ (which shows a scatter of values from $B_{\mathrm{los}}$ sometimes larger than those from $B_{r}$) and $\alpha$ (which shows a constraining of values from $B_{r}$ to ${<\,} 2.5$, compared to those from $B_{\mathrm{los}}$ spreading out to 3.3). Properties such as $L_{\mathrm{tot}}$, $(L/h_{\mathrm{min}} )_{\mathrm{max}}$, and $E_{\mathrm{Ising}}$ do not show a strong dependence on longitudinal position, while $\log (R )$ ($B_{r}$ greater), $\alpha$ ($B_{\mathrm{los}}$ greater), and $B_{\mathrm{eff}}$ ($B_{r}$ greater) display progressively increasing differences between $B_{\mathrm{los}}$ and $B_{r}$ with increasing absolute longitude. Although $B_{r}$ data contain higher levels of noise with complex spatio-temporal patterns, considering the difficulty that the LOS component has in estimating the normal-to-surface field at increasing longitudinal distance from the central meridian, and the systematic field-strength underestimation, the results here presented support the conclusion that $B_{r}$-derived properties are a more consistent representation of the AR properties.

The properties considered here show a wide range of correlations, with linear (Pearson) and nonlinear-rank (Spearman) correlation coefficients similar in value for all cases. All property-pair correlations become weaker with increasing longitudinal distance from the central meridian, with decreases for $B_{\mathrm{los}}$ more pronounced than those for $B_{r}$. While most property pairs show lower correlation levels from $B_{r}$ than from $B_{\mathrm{los}}$, only approximately a third of them show significantly lower values when compared to their associated errors. This implies that some properties calculated from $B_{r}$ data may provide more independent information as regards the physical state of the AR photospheric magnetic field than the same properties calculated from $B_{\mathrm{los}}$.

Binned property-value 24-hr flaring rates from $B_{\mathrm{los}}$ and $B_{r}$ differ, due to each SHARP resulting in different values for a given property. However, the differences in flaring rate distributions between these two forms of magnetogram data are consistent with the redistribution of properties to values that are typically larger for $B_{r}$ than for $B_{\mathrm{los}}$ (except $\alpha$, which is folded into a more constrained property range). Notably, flaring rates for most properties increase with increasing property values, apart from $\alpha$ where they peak for values close to $5/3$.

Although $B_{r}$ data seem to provide a more consistent determination of AR properties across the solar disk, there is an additional aspect of these data to consider. While it appears that $B_{r}$ should be preferentially considered over $B_{\mathrm{los}}$ for locations with significant viewing-angle bias, the less noisy $B_{\mathrm{los}}$ data may be more suitable towards disk centre. However, to determine the real utility of $B_{r}$ data for flare forecasting, the AR properties calculated from both field components should be compared using a variety of forecast methods (e.g. discriminant analysis, machine learning, etc.) Definitive statements on the forecasting advantage of using $B_{r}$-derived properties over those from $B_{\mathrm{los}}$ can only then be made after forecast verification.

Appendix: Correlation Coefficients

Tables 2 and 3 each contain values of linear (Pearson) and nonlinear-rank (Spearman) correlation coefficients (CC) for all AR property-pair combinations for $B_{\mathrm{los}}$ and $B_{r}$, respectively. The coefficients are calculated separately for the three groups of SHARP longitudes with data points colour-coded in Figures 6 and 7: $|\phi| < 60^{\circ}$ (black); $60 \leqslant|\phi| < 75^{\circ}$ (blue); $|\phi| \geqslant 75^{\circ}$ (red). Figure 8 presents the errors for correlation coefficients contained in Tables 2 and 3. In both panels, plots of standard error versus CC value for linear (filled circles) and nonlinear (open circles) correlations in all three longitudinal-position groups (same colour code applies). The left panel corresponds to $B_{\mathrm{los}}$-calculated properties and the right panel corresponds to $B_{r}$-calculated properties. The standard error for a (linear/nonlinear) correlation coefficient is estimated as

$$ \mathrm{SE}_{r} = \sqrt{\frac{1-r^{2}}{n-2}}; $$

(5)

where $r$ can be the Pearson or the Spearman CC, and $n$ is the number of points used in their calculations. The dotted lines in the plots of Figure 8 mark ranges for expressing the standard errors in percentage of the CC value.

Figure 8

Error analysis for correlation coefficients displayed in Tables 2 and 3. The left and right panels correspond to property-pair (linear and nonlinear) correlations calculated from $B_{\mathrm{los}}$ and $B_{r}$, correspondingly. The colour code corresponds to Figure 6.