Acceleration and Storage of Energetic Electrons in Magnetic Loops in the Course of Electric Current Oscillations

Abstract

A mechanism of electron acceleration and storage of energetic particles in solar and stellar coronal magnetic loops, based on oscillations of the electric current, is considered. The magnetic loop is presented as an electric circuit with the electric current generated by convective motions in the photosphere. Eigenoscillations of the electric current in a loop induce an electric field directed along the loop axis. It is shown that the sudden reductions that occur in the course of type IV continuum and pulsating type III observed in various frequency bands (25 – 180 MHz, 110 – 600 MHz, 0.7 – 3.0 GHz) in solar flares provide evidence for acceleration and storage of the energetic electrons in coronal magnetic loops. We estimate the energization rate and the energy of accelerated electrons and present examples of the storage of energetic electrons in loops in the course of flares on the Sun or on ultracool stars. We also discuss the efficiency of the suggested mechanism as compared with the electron acceleration during the five-minute photospheric oscillations and with the acceleration driven by the magnetic Rayleigh–Taylor instability.

1 Introduction

We present an explanation for some long-lived radio events on the Sun and stars, for example, for type IV solar radio bursts with a rather high brightness temperature, which last for tens of minutes and frequently reveal fine structural details, such as type III bursts, zebra patterns, and sudden reductions (e.g. Slottje, 1972; Chernov 2006). Aurass et al. (2003) concluded that the fine structure in the type IV burst on 25 October 1994, including more than 100 broadband radio pulsations at 110 – 600 MHz that have been identified as repeated type III bursts, and the zebra patterns at 120 – 250 MHz are caused by numerous injections of fast electrons into the magnetic loop. Observations of repetitive particle accelerations in HXR, microwave, and the group of type III radio bursts with a period of about three minutes observed in the metric and decimetric frequencies (25 – 180, 245, and 610 MHz) in the flare on 23 – 24 September 2011 were presented by Kumar, Nakariakov, and Cho (2016). Note that Kumar, Nakariakov, and Cho (2015) did not observe type III radio bursts in the interplanetary medium in the pulsation events related to the flare on 20 July 2013. This fact is consistent with possible confinement of the accelerated electrons in coronal magnetic loops. Quasi-periodic type III bursts with a period of 270 s and a positive frequency drift that covered the range 0.7 – 3 GHz in the flare on 19 July 2012 were investigated by Huang et al. (2016).

Stellar flares also display long-lived radio events with high brightness temperatures. Red dwarfs reveal such events with a fine structure similar to the solar type (Bastian et al. 1990). In particular, in AD Leo, quasi-periodic pulsations and sudden reductions are detected. YZ CMi also produces broadband radio emission with rich fine structures that include sudden reductions. In ultracool stars, intriguing intense radio emission that lasts for several rotation periods is observed (e.g. Hallinan et al. 2007; Berger et al. 2008). However, the extremely efficient mechanism of electron acceleration in the atmospheres of ultracool dwarfs is still unknown.

Sudden reductions in the solar and stellar flaring radio emission indicate the possibility of accumulation of energetic electrons in coronal magnetic loops. Indeed, if we assume that the continuum emission of type IV events is caused by the loss-cone instability in a loop (a magnetic trap), the sudden reductions can occur as a result of injection of accelerated electron beams into the trap. The injected particles fill the loss-cone, and thereby the loss-cone instability is quenched (Zaitsev and Stepanov 1975; Benz and Kuijpers 1976). Wave-particle interaction changes the pitch-angle distribution of injected electrons; this increases the number of energetic particles trapped in a loop. It is estimated that the threshold ratio of $n _{2}$ (the number density of fast electrons responsible for the sudden reduction) to $n _{1}$ (the number density of those responsible for continuum emission) is $n_{2}/n_{1} \ge 6 \times 10^{ - 2}$ (Zaitsev and Stepanov 1975). Fleishman, Stepanov, and Yurovsky (1994) presented the example of fragmented particle injection into a coronal loop. From the analysis of microwave solar bursts on 17 November 1991, these authors concluded that the origin of sudden reductions can be upward injections of ${\approx}\,100~\mbox{keV}$ electron beams filling the loss-cone of the coronal loop.

As a result of the multiple injections of accelerated electrons into the continuum source, the radio emission can become long lived. Periodic type III bursts also promote accumulation of fast particles in coronal loops. Zlotnik et al. (2003) showed that the broadband radio pulsations in the flare of 25 October 1994 resulted from periodic injections of fast electrons into the coronal loop. Plasma waves are generated by the beams of these electrons that propagate along the magnetic field of the loop. The pulses revealed a negative frequency drift similar to type III bursts that is associated with electron beams with a velocity of $c/3$ ($c$ is the speed of light) propagating from dense to rarefied plasma in the solar atmosphere. Interestingly, zebra pattern emission in the flare on 25 October 1994 arose 2.5 min after the broadband pulsations. If the sources of both fine structures are located in the same magnetic loop, this time delay means that the zebra pattern starts after about a hundred injections of energetic electrons into the loop. This is because the instability threshold at the double plasma resonance needed for the zebra pattern exceeds the threshold of the beam instability needed for the type III bursts. The minimum rate of electron acceleration was estimated as $\dot{N}_{2} \approx 7\times10^{29}~\mbox{s}^{-1}$ (Zlotnik et al. 2003), which is 5 – 7 orders of magnitude lower than the rate of electron acceleration in powerful flares (Miller et al. 1997).

It should be noted that the problem of the energetic particle storage in solar magnetic loops has been discussed by many authors. For example, Wentzel (1976) and Bespalov, Zaitsev, and Stepanov (1991) suggested that energetic electrons can be stored through the turbulent diffusion of electrons on whistler waves. The typical timescale of this process does not exceed tens of seconds, however. The idea of energetic electrons stored in magnetic loops in the course of electric current oscillations was initially suggested by Zlotnik et al. (2003). It was also demonstrated that about a two-percent modulation of the magnetic field of a coronal loop is sufficient for this modulation to work as a periodic electron accelerator. Here, we develop the idea of acceleration and accumulation of energetic particles in magnetic loops by electric current oscillations.

2 Electron Acceleration by the Induced Electric Field in a Magnetic Loop as an RLC Circuit

2.1 Excitation of the Induced Electric Field

Convective motions of the photosphere interacting with the magnetic field near the loop legs generate the electric current inside the loop. This current flows through the coronal part of the loop from one of its footpoints to the other and closes inside the photosphere, where isotropic conductivity is realized. Hence, the current-carrying coronal loop can be presented as an equivalent electric (RLC) circuit whose eigenfrequency depends on the magnitude of the constant component of the electric current $I_{0}$, on the electron number density $n$, the loop radius $r_{0}$, and the length $l$ of the coronal part of the loop (Khodachenko et al. 2009):

$$\begin{aligned} \nu _{\mathrm{RLC}}= \frac{c}{2\pi \sqrt{LC(I_{0})}} \approx \frac{1}{2\pi \sqrt{2\pi \zeta}} \frac{I_{0}}{cr_{0}^{2}\sqrt{nm_{i}}} . \end{aligned}$$

(1)

Here $L = 2l\zeta$ is the loop inductance, $\zeta = \ln ( 4l/\pi r_{0} ) - (7/4)$, and $C(I_{0}) \approx c^{4}\rho_{0}\pi r_{0}^{4} /( I_{0}^{2}l )$ is the effective capacitance depending on the current in the loop, and $\rho_{0} = nm_{i}$ is the electron density. The basic contribution to the capacity of an equivalent circuit is made by the coronal part of the loop.

Electric current oscillations in the RLC circuit are connected with the oscillations of the azimuthal component of the magnetic field $B_{\varphi} (r,t) = 2rI_{z}(t)/cr_{0}^{2}$. These oscillations, in turn, in accordance with the Maxwell–Faraday equation $\operatorname{curl} \boldsymbol{E} = - (1/c)\partial \boldsymbol{B} /\partial t$, generate an electric field directed along the flux tube axis. This electric field is parallel to the component of the magnetic field $B_{z}$, and therefore it should efficiently accelerate charged particles. Assuming $I _{{z}}(t) = I _{0} + \Delta I \sin(2 \pi \nu _{\mathrm{RLC}}t)$ and averaging over the half-period of the oscillations, we find the relation of the electric field with the loop radius $E_{z}(r)$, the maximum value $E_{\max}$ reached near the loop surface, and the mean value along the loop radius $\overline{E}$:

$$E_{\mathrm{z}}(r)=\frac{4{\nu }_{\mathrm{RLC}}{I}_0}{c^2}\frac{\mathrm{\Delta }I}{I_0}{\left(\frac{r}{r_0}\right)}^2,E_{max}=\frac{4{\nu }_{\mathrm{RLC}}{I}_0}{c^2}\frac{\mathrm{\Delta }I}{I_0},\overline{E}=\frac{4}{3}\frac{{\nu }_{\mathrm{RLC}}{I}_0}{c^2}\frac{\mathrm{\Delta }I}{I_0}.$$

(2)

Thus, the accelerating electric field depends on the amplitude of electric current oscillations $\Delta I$ in the electric circuit. In the self-consistent equation for the equivalent electric circuit, the resistance and the capacitance are dependent on the electric current (Khodachenko et al. 2009):

$$\begin{aligned} \frac{1}{c^{2}}L\frac{\mathrm{d}^{2}y}{\mathrm{d}t^{2}} + \biggl[ R(I_{0}) (1 + y)^{2} - \frac{ \vert V_{ {r}} \vert l_{1}}{c^{2}r_{1}} \biggr] \frac{\mathrm{d}y}{\mathrm{d}t} + \frac{1}{C(I_{0})} \biggl(1 + \frac{3}{2}y + \frac{1}{2} y^{2}\biggr)y = 0. \end{aligned}$$

(3)

Here, $y = (I - I_{0})/I_{0}$, $V _{ {r}}$ is the radial component of the convergent flow of the photospheric matter in the loop legs, and the effective resistance of a loop, $R(I_{0})$, can be represented as

$$ R(I_{0}) \approx \frac{F_{1}^{2}I_{0}^{2}l_{1}}{(2 - F_{1})c^{4}n_{1}m_{i}\nu_{\mathrm{ia}}^{\prime}\pi r_{1}^{4}}, $$

(4)

where $l_{1}, r_{1}, n_{1}$, and $F _{1}$ are the scale of the loop along the height, the loop radius, the plasma density, and the relative density of neutral particles in the area of the photospheric electromotive force (EMF), respectively, and $\nu_{\mathrm{ia}}^{\prime}$ is the frequency of electron–atom collisions. The right term in the square brackets in Equation 3 denotes the EMF in the footpoint of the loop and can be considered as a negative resistance. The horizontal flow of plasma into the loop is driven by the photosphere convection that occurs, for example, when the footpoints of the loop are in the node of several supergranulation cells. The footpoints of the loop as an RLC circuit primarily contribute to the whole loop resistance due to their comparatively low conductivity determined by ion-atom collisions (the so-called Cowling conductivity Cowling 1976).

Equation 3 suggests that electric field oscillations must be in-phase at all points of the loop (the lumped circuit approach). On the other hand, the electric current variations propagate along the loop with the Alfvén speed. Therefore, for the in-phase condition, the Alfvén time $\tau_{\mathrm{A}} = l/V_{\mathrm{A}}$ must be less than the period of RLC oscillations $T_{\mathrm{RLC}} = 1/ \nu _{\mathrm{RLC}}$. The Biot–Savart law suggests $I_{0} \approx cr_{0}B_{\varphi 0}(r_{0})/2$, and thus the twist of the loop magnetic field should be quite low (Stepanov, Zaitsev, and Nakariakov 2012).

Equation 1 corresponds to the frequency of Alfvén oscillations in a coronal magnetic loop with a wave vector $| \boldsymbol{k} | \approx r_{0}^{ - 1}$ directed almost perpendicular to the axis of the magnetic flux tube at an angle $\cos \theta \approx (B_{\varphi} /B_{z})$ to the magnetic field $\boldsymbol{B}$. In such a case, the frequency of Alfvén oscillations coincides with Equation 1 up to a coefficient of the order of unity (Stepanov, Zaitsev, and Nakariakov 2012).

From Equation 3 it also follows that the excitation of the oscillations of the coronal magnetic loop as an RLC circuit occurs if the negative resistance of the photospheric EMF exceeds the loop resistance:

$$ R(I_{0}) \le |V_{ {r}}|l_{1}/\bigl(r_{1}c^{2} \bigr). $$

(5)

The $Q$-factor of the equivalent electric circuit is

$$ Q = \frac{1}{cR(I_{0})}\sqrt{L/C(I_{0})}, $$

(6)

and can be quite high because of the high inductance and comparatively low resistance. Introducing the dimensionless time $\tau = 2\pi \nu_{\mathrm{RLC}}t$, we can write Equation 3 in the form

$$ \frac{\mathrm{d}^{2}y}{\mathrm{d}\tau^{2}} - \varepsilon \bigl( \delta - 2y - y^{2} \bigr) \frac{\mathrm{d}y}{\mathrm{d}\tau} + \biggl( 1 + \frac{3}{2}y + \frac{1}{2}y^{2} \biggr)y = 0, $$

(7)

where $\varepsilon = 1/Q,\delta = [ (|V_{ {r}}|l_{1})/c^{2}r_{1}R(I_{0}) ] - 1$. The small parameter $\varepsilon \ll 1$ in Equation 7 makes it possible to apply the Van der Pol method to solve the equation; under the steady-state condition, the solution has the form (Zaitsev, Stepanov, and Kaufmann 2014)

$$ y = \frac{I(t) - I_{0}}{I_{0}} = 2\sqrt{\delta} \cos \biggl[ 2\pi \nu_{\mathrm{RLC}} \biggl(1 + \frac{3}{4}\delta \biggr)t \biggr]. $$

(8)

Thus, the nonlinearity in Equation 3 leads to the establishment of a finite amplitude of oscillations, as well as to a small shift in the oscillation frequency in comparison with the linear case. The magnitude of the electric current oscillations in the steady-state regime is determined by the excess of the negative resistance of the photospheric EMF located in the coronal loop footpoints over the resistance of the RLC-circuit. Kaufmann et al. (2009) observed the high-$Q$ pulsations of sub-THz radiation (212 and 405 GHz) in the solar flare on 4 November, 2003 which was interpreted by Zaitsev, Stepanov, and Kaufmann (2014) as the effect of modulation of the emission volume by eigenoscillations of the current-currying loop. These authors showed that the amplitude of pulsations of sub-THz radiation is proportional to the amplitude of the electric current variations in the magnetic loop, since the modulation of the flux of energetic electrons accelerated by the induction electric field (Equation 2) depends on the amplitude of electric current variations. This dependence makes it possible to determine the amplitude of the electric current oscillations in the coronal magnetic loop for the flare on 4 November 2003 using the data on high-$Q$ pulsations of sub-THz radiation, $\Delta I/I_{0} = 2\sqrt{\delta} \approx (5 - 8) \times 10^{ - 2}$, as well as the magnitude of the accelerating electric field, $E_{z}(r) \approx (0.2 - 0.3)\nu_{\mathrm{RLC}}I_{0} ( r/r_{0} )^{2}c^{ - 2}$. From Equations 1 and 2 we have that $E_{z}(r)$ depends quadratically on the electric current in the loop and increases from the axis to the surface of the loop.

2.2 Energization Rate and Energy of the Accelerated Electrons

The induced electric field (Equation 2) accelerates some part of the electron population to a velocity exceeding $V > (E_{\mathrm{D}}/E_{z})^{1/2}V_{\mathrm{Te}}$, where $V_{\mathrm{Te}} = (k_{\mathrm{B}}T/m_{\mathrm{e}})^{1/2}$ is the electron thermal velocity, $E_{\mathrm{D}} = e\Lambda \omega_{\mathrm{p}}^{2}/V_{\mathrm{Te}}^{2}$ is the Driecer field, $\Lambda$ is the Coulomb logarithm, and $\omega_{\mathrm{p}}$ is the Langmuir frequency. In the case of a sub-Dreicer field, i.e. $x = E_{\mathrm{D}}/E_{z} \gg 1$, the kinetic theory yields the number of runaway electrons per second accelerated by a DC-electric field (Knoepfel and Spong 1979):

$$ \dot{N}_{\mathrm{S}} = 0.35n\nu_{\mathrm{ei}} V_{\mathrm{a}}x^{3/8} \exp \biggl( - \sqrt{2x} - \frac{x}{4}\biggr), $$

(9)

where $\nu_{\mathrm{ei}} = 5.5n\Lambda /T^{3/2}$ is the effective frequency of electron–ion collisions, $n$ is the thermal electron density, $T$ is the plasma temperature, and $V_{\mathrm{a}}$ is the volume of the acceleration region. From Equations 2 and 9 it follows that in the case of a sub-Dreicer electric field, the flux of accelerated electrons reaches its maximum near the surface of the magnetic flux tube in a layer with thickness

$$\begin{aligned} \Delta r \approx \frac{r_{0}}{\sqrt{2x_{\mathrm{m}}} + \frac{x_{\mathrm{m}}}{2}}, \end{aligned}$$

(10)

where $x_{\mathrm{m}} = E_{\mathrm{D}}/E_{\max}$.

To estimate the acceleration rate and the energy of accelerated electrons, we consider two solar events with quasi-periodic type III bursts.

i) The flare on 23 – 24 September 2011 studied by Kumar, Nakariakov, and Cho (2016) reveals 180 s quasi-periodic pulsations observed in the meter and decimeter radio wavelengths as repetitive groups of type III bursts with negative frequency drift. This means that the acceleration region is located below the level at which the Langmuir frequency $\omega_{\mathrm{p}}/2\pi \approx 600~\mbox{MHz}$. Assuming for the coronal loop $n =10^{10}~\mbox{cm}^{-3}$, $T = 10^{6}~\mbox{K}$, $l = 10^{10}~\mbox{cm}$, and $r _{0} = 10^{8}~\mbox{cm}$, with an electric current $I _{0} = 2\times 10^{9}~\mbox{A}$, we can estimate the eigenfrequency of the current-carrying loop from Equation 1, $\nu_{\mathrm{RLC}} \approx 5.54 \times 10^{-3}~\mbox{Hz}$. Thus, the period of RLC-oscillations is 180 s, equal to the period observed in the repetitive group of type III bursts on 23 – 24 September 2011 (see Figure 1(d – f) in Kumar, Nakariakov, and Cho 2016). Taking a small modulation magnitude, $\Delta I/I_{0} = 10^{ - 3}$, we obtain from Equation 2 the mean value of the electric field along the loop radius: $\overline{E}\approx 1.5\times {10}^{-5}\text{V}{\text{cm}}^{-1}$. Electrons can be accelerated by this electric field at a distance $\Delta l = 2 \times 10^{9}~\mbox{cm}$ up to an energy $\varepsilon \approx 30~\mbox{keV}$, which is the typical energy of electrons responsible for type III bursts. The Driecer field is $E _{\mathrm{D}} = 6\times 10^{-8} n/T = 6\times 10^{-4}~\mbox{V}\,\mbox{cm}^{-1}$, and the ratio $x=E_{\mathrm{D}}/\overline{E}\approx 40\gg 1$. Assuming the acceleration volume $V _{\mathrm{a}} = 6\times 10^{25}~\mbox{cm}^{3}$, from Equation 9 we estimate the energization rate $\dot{N}_{\mathrm{s}} \approx 3 \times 10^{30}~\mbox{s}^{ - 1}$, which is about four times higher than in the pulsating type III event on 25 October 1994 (Zlotnik et al. 2003), but 4 – 6 orders of magnitude lower than the electron acceleration rate in powerful flares.

For this estimate, we used the mean value of the induced electric field along the loop radius $\overline{E}$. The maximum value $E_{\max}$ (Equation 2) is reached near the loop surface and the maximum fluxes of accelerated electrons occur near the surface of the magnetic flux tube in a layer with thickness (Equation 10) $\Delta r = 0.14r_{0} \approx 3 \times 10^{7}~\mbox{cm}$. As the induced electric field depends quadratically on the electric current, a part of the electron population accelerated near the loop surface can reach an energy of about 1 MeV. Moreover, some fraction of energetic electrons can propagate along the open magnetic field lines as type III bursts as a result of diffusion across the magnetic field or of the coalescence between closed and open magnetic field lines (see e.g. Figure 1 in Zlotnik et al. 2003).

An important peculiarity of the RLC-oscillation of coronal magnetic loops is the high $Q$-factor (Equation 6), which is consistent with the idea of an acceleration of electrons by the electric current oscillations. Indeed, using expressions for $L$ and $C(I _{0})$ and taking the threshold value of $R(I _{0})$ in Equation 3 with $|V _{{r}}| = 5\times 10^{4}~\mbox{cm}\,\mbox{s}^{-1}$, $l _{1} = 10^{8}~\mbox{cm}$, and $r _{1} = 5 \times 10^{7}~\mbox{cm}$, we obtain the above parameter $Q \approx 10^{4} \gg 1$ for the plasma loop.

ii) In the flare on 19 July 2012, the set of type III bursts displays in-phase oscillations with a period of 270 s and a positive frequency drift within the range of 0.7 – 3 GHz (Huang et al. 2016). The positive frequency drift indicates that the electron acceleration region is located near the loop top and the beams of energetic electrons are directed downward. The Dreicer electric field reaches its minimum in this region of the loop, which favors the acceleration process. Taking $n=6\times 10^{9}~\mbox{cm}^{-3}$, $T = 10^{6}~\mbox{K}$, $l = 1.5 \times 10 ^{10}~\mbox{cm}$, $r _{0} = 2 \times 10^{8}~\mbox{cm}$, and $I _{0} = 4 \times 10^{9}~\mbox{A}$, we obtain the eigenfrequency of RLC-oscillations from Equation 1, $\nu_{\mathrm{RLC}} \approx 3.76\times 10^{-3}~\mbox{Hz}$. The oscillation period (266 s) is close to the observed period. The mean value of the electric field for $\Delta I/I_{0} = 10^{ - 3}$ is $\overline{E}\approx 2\times {10}^{-5}\text{V}{\text{cm}}^{-1}$, and $E _{\mathrm{D}} \approx 4\times 10^{-4}~\mbox{V}\,\mbox{cm}^{-1}$, and thus $x \approx 20$. Assuming the acceleration volume $V _{\mathrm{a}} = 10^{26}~\mbox{cm}^{3}$ from Equation 9, we can derive an effective energization rate $\dot{N}_{\mathrm{s}} \approx 3 \times 10^{33}~\mbox{s}^{ - 1}$. This is compatible with the energization rate obtained from RHESSI data (Holman et al. 2011). The energy gain for $\overline{E}\approx 2\times {10}^{-5}\text{V}{\text{cm}}^{-1}$ at the distance $\Delta l = 10^{9}~\mbox{cm}$ is approximately $\varepsilon \approx 20~\mbox{keV}$.

Huang et al. (2016) suggested that the acceleration site of electrons producing type III bursts is located above the loop top. In our interpretation, the acceleration site is located at the minimum of the Dreicer field, i.e. at the loop top. Note also that the lumped circuit approach applied here and the suggestion that $\nu _{\mathrm{RLC}} < V _{\mathrm{A}}/l \approx 10^{-2}~\mbox{Hz}$ is satisfied for both the considered events.

2.3 Electron Acceleration and Storage in Ultracool Stars

The idea of energetic electrons stored in magnetic loops in the course of electric current oscillations was also applied to the explanation of very long-lived (several days) intense ratio emission from ultracool dwarfs. Zaitsev and Stepanov (2017) used the example of TVLM 513-46546, a young radio-active M8.5V dwarf with $M_{ *} = 0.07M_{\odot}$, $R_{ *} \approx 0.1R_{\odot}$, and an effective temperature $T_{\mathrm{eff}} \approx 2200~\mbox{K}$, to show that photospheric convection results in the formation of thin magnetic flux tubes with a typical radius ${\approx}\, 10^{7}~\mbox{cm}$ and with an electric current $I_{0} \approx 10^{10}~\mbox{A}$. Dissipation of the current leads to heating of the plasma and to evaporation of the thin “pressed-down” atmosphere of the star. Hence a hot dense coronae in magnetic loops is formed, and the induced electric field driven by the electric current oscillations supplies the energetic electrons responsible for the radio emission. The frequency of high-$Q$ oscillations for TVLM 513-46546 was estimated as $\nu _{\mathrm{RLC}} \approx 8\times 10^{-3}~\mbox{Hz}$ (period ${\approx}\,130~\mbox{s}$) and the electric field is ${\overline{E}}_z\approx 8\times {10}^{-4}\text{V}{\text{cm}}^{-1}$. With this electric field, electrons can be accelerated to an energy ${\approx}\, 800~\mbox{keV}$ at a distance of about $10^{9}~\mbox{cm}$. Estimations have shown that the energization rate in the flare on TVLM 513-46546 for $x = 10$ can be as high as $\dot{N}_{\mathrm{s}} \approx 10^{34}~\mbox{s}^{ - 1}$. With this energization rate, a quite high level of HXR emission from brown dwarfs is expected.

3 Discussion

In this section we discuss the efficiency of the electron acceleration mechanism suggested here in comparison with the electron acceleration driven by five-minute oscillations of the photosphere (Zaitsev and Kislyakov 2006), and the acceleration due to the Rayleigh–Taylor instability (Zaitsev and Stepanov 2015).

3.1 Acceleration Driven by Five-Minute Oscillations of the Photosphere Convection Velocity

It is known that the photospheric convection displays a broad spectrum of velocity oscillations with a maximum of about five minutes. These oscillations belong to the acoustic mode, but they do not propagate in the chromosphere and corona, being reflected from the temperature minimum region. Thereby, the five-minute oscillations cannot directly affect the entire coronal magnetic loop. Nevertheless, acoustic oscillations modulate the electric currents in the coronal loops through the “intermeshing” of the convective flows of photospheric plasma and the magnetic fields at the loop footpoints. The modulation of the electric current in turn leads to periodic changes in the electric field directed along the axis of the flux tube.

Let us assume that the radial component of the convection velocity is modulated by five-minute photosphere oscillations according to the law $\vert V_{{r}} \vert = V_{0} + V_{\sim} \sin (\omega_{5}t)$, where $V_{0} \gg V_{\sim}$. Slow variations of the electric current in the loop on a timescale longer than the eigenoscillation period of the loop as an equivalent electric circuit are described by the equation (Zaitsev, Kislyakov, and Urpo 2003)

$$ \frac{L}{c^{2}}\frac{\partial I_{z}}{\partial t} + R(I_{z})I_{z} = \Xi ( I_{z} ). $$

(11)

Here the EMF generating the current flow along the loop is connected with the velocity of photospheric convection through the relation $\Xi (I_{z}) \approx |V_{{r}}|l_{1}I_{z}r_{1}^{ - 1}c^{ - 2}$. The height interval extends from the lower layers of the photosphere to the transition region between the solar photosphere and chromosphere and is roughly equal to $l_{1} = 500\,\mbox{--}\,1000~\mbox{km}$. The oscillations in the velocity of photospheric convection $V_{\sim}$ are connected with the oscillations of the electric current in the loop, $I_{z} = I_{0} + I_{\sim}$, and for $I _{\sim}$ we have the equation

$$ \frac{\partial I_{\sim}}{\partial t} + \frac{2R(I_{0}) c^{2}}{L}I_{\sim} = \frac{V_{\sim} l_{1} I_{0}}{r_{1}L}\sin \omega_{5}t. $$

(12)

This equation has a forced periodic solution for a current that varies with the frequency of the photospheric oscillations $\omega_{5}$ and displays a relative amplitude of oscillations $I_{\sim}^{\mathrm{m}}/I_{0} \approx l_{1}V_{\sim} /\omega_{5}Lr_{1}$ (Zaitsev and Kislyakov 2006). By analogy with Equation 2, we obtain the expressions for the accelerating electric field

$$E_z(r)=\frac{4r^2{\nu }_5{I}_0}{c^2{r}_0^2}\frac{I_{\sim }^{\mathrm{m}}}{I_0},E_{max}=\frac{4{\nu }_5{I}_0}{c^2}\frac{I_{\sim }^{\mathrm{m}}}{I_0},\overline{E}=\frac{4}{3}\frac{{\nu }_5{I}_0}{c^2}\frac{I_{\sim }^{\mathrm{m}}}{I_0},$$

(13)

where $\nu_{5} = \omega_{5}/2\pi$. The upper panel in Figure 1 shows two solar radio bursts observed at 37 GHz with the Metsähovi radio telescope on 28 August 1990, and the lower panel presents the modulation of eigenoscillations of the loop as an RLC circuit by the five-minute photospheric oscillations obtained with the Wigner–Wille method. The latter transform reveals a higher frequency-time resolution. It can be seen that the relative variations of the frequency of the eigenoscillations of the RLC circuit caused by the current oscillations have a value on the order of $\Delta \nu_{\mathrm{LRC}}/\nu_{\mathrm{LRC}} \approx I_{\sim}^{\mathrm{m}}/I_{0} \approx (1 - 2) \times 10^{ - 2}$, which coincides with the above estimate for pulsations of sub-THz radiation (Zaitsev, Stepanov, and Kaufmann 2014). This means that the five-minute photospheric oscillations induce approximately the same electric fields in the coronal magnetic loops as the eigenoscillations of the loops.

Figure 1

Modulation of microwave radiation at 37 GHz by the five-minute photospheric oscillations in the flare on 28 August 1990 (Zaitsev, Kislyakov, and Urpo 2003). The upper panel shows light curves of two solar radio bursts. The lower panel presents the dynamic spectrum of the low-frequency modulation of the microwave emission flux obtained by the Wigner–Wille transform.

3.2 Acceleration Associated with the Rayleigh–Taylor Instability

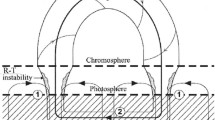
It is also possible that intense electric fields in the magnetic loops are generated as a result of the magnetic Rayleigh–Taylor (R–T) instability in the chromospheric legs of the loops. This instability provokes the penetration of external chromospheric plasma with $\beta = 8\pi p/B ^{2} \leq 1$ into a magnetic flux tube, where $\beta \ll 1$, and where $p$ is the plasma gas pressure. As a result, the magnetic field of the loop is deformed and amplifies the electrical current. Directly in the loop legs, where the R–T instability develops, the induced electric field $\boldsymbol{E} = -(1/c)[ \boldsymbol{V} \times \boldsymbol{B} ]$ is perpendicular to the magnetic field, and therefore this electric field is not able to accelerate electrons. However, for the Alfvén time $\tau _{\mathrm{A}} \approx \Delta l/V _{\mathrm{A}} \approx 1\,\mbox{--}\,10~\mbox{s}$, where $\Delta l \approx (1 - 5) \times 10^{7}~\mbox{cm}$ is the scale of the chromospheric plasma tongue invading the magnetic flux tube, and $V _{\mathrm{A}} \leq 10^{7}~\mbox{cm}\,\mbox{s}^{-1}$ is Alfvén velocity in the chromosphere, a pulse of tension in the magnetic field $B_{\varphi}^{2}(r,t)/8\pi$ leaves the R–T instability region along the loop axis as a pulse of longitudinal electric current (Zaitsev, Kronshtadtov, and Stepanov 2016). In the case of strong electric current, $B_{\varphi}^{2} \gg 8\pi p$, an induced electric field directed along the magnetic field of a loop $B_{{z}0}$ arises (Zaitsev and Stepanov 2015),

$$ \frac{\partial E_{z}}{\partial r} = - \frac{1}{c}\frac{B_{\varphi}^{2}}{4\pi \rho V_{\mathrm{A}}^{2}}\frac{\partial B_{\varphi}}{\partial t}. $$

(14)

The reason is that for $B_{\varphi}^{2} \gg 8\pi p$, the magnetic field perturbations are not compensated for by the gas pressure gradient as they are for the linear Alfvén pulse. Velocity perturbations along the flux tube radius and along $B_{{z}0}$ appear, which generate an electric field along the magnetic loop axis that is nonlinear with respect to the $B _{\varphi}$ component. The maximum of the longitudinal electric field is reached at $r = r_{0}$, and its ratio to the Dreicer field is

$$ \frac{E_{{z\mathrm{m}}}}{E_{\mathrm{D}}} = 2.2 \times 10^{8}\frac{TI_{0}^{3}(A)}{r_{0}^{2}B_{{z}0}n^{3/2}\Delta \xi}, $$

(15)

where $\Delta \xi$ is the scale of the electric current pulse propagating in a coronal magnetic loop along $B_{{z}0}$. Equation 15 suggest that the induced electric field $E_{z}$ depends on the current as $E_{z} \propto I_{0}^{3}$ and for $I _{0} > 10^{10}~\mbox{A}$ exceeds the Dreicer field (Zaitsev, Kronshtadtov, and Stepanov 2016). Hence, the acceleration driven by the R–T instability is the most efficient mechanism because at sufficiently high values of the electric current, the inductive electric field in the chromosphere can be on the order of or even greater than the Dreicer electric field, greatly increasing the number of accelerated electrons. However, it requires quite high electric currents, $I _{0} >10^{10}~\mbox{A}$, and the typical time of the R–T acceleration cannot explain the long-lived radio events.

4 Conclusions

Several models have been suggested to interpret the quasi-periodic electron acceleration and storage of energetic particles in coronal magnetic loops. Quasi-periodic acceleration may be associated with the bursty regime of spontaneous magnetic reconnection, such as that in the case of the current sheet tearing that is associated with the formation of multiple plasmoids (Kliem, Karlický, and Benz 2000). Kumar, Nakariakov, and Cho (2016) also suggest that the periodic reconnection at a magnetic null point most likely causes the repetitive particle acceleration. Nevertheless, all the reconnection regimes cannot explain the quite high $Q$-factor of the observed events. Indeed, numerical simulations of the coalescence of current-carrying loops show that the energy of electrostatic and inductive fields decreases by an order of magnitude just after the first few oscillations (Tajima et al. 1987). The magnetohydrodynamic (MHD) oscillation of flare loops could be a possible option to explain the features in question. However, the sausage and kink MHD modes are not capable of providing synchronous pulsations in a wide frequency interval and have a quite low $Q$-factor.

The mechanism of acceleration and storage of electrons driven by the electric current oscillations in a loop as an equivalent RLC-circuit was first suggested by Zlotnik et al. (2003). Here, we developed this idea for periodic groups of type III bursts. By this, the individual type III bursts forming the periodic groups can be triggered by the bursty regime of magnetic reconnection in the fine loop structure, the thin flux tubes with a cross-section area of about $10^{14}\,\mbox{--}\,10^{15}~\mbox{cm}^{2}$, and/or by the sausage-mode pulsations of these fine structures. The proposed model is similar to that of electron acceleration initiated by the five-minute velocity oscillations of the photosphere (Zaitsev and Kislyakov 2006). Acceleration in the super-Dreicer electric field driven by the R–T instability in the chromospheric legs of the magnetic loops is more efficient (Zaitsev and Stepanov 2015), but it requires high electric currents, $I _{0} >10^{10}~\mbox{A}$, and the typical time of this process does not match the long-lived events. The model developed here can explain the electron acceleration in the long-lived type IV radio continuum with the fine structures such as type III bursts, zebra patterns, and sudden reductions and/or a set of type III bursts without type IV continuum background. The starting point of the type III bursts at 700 MHz described by Huang et al. (2016) suggests that the acceleration site is located near the loop top and the beams of electrons directed toward the 3 GHz plasma frequency level. Moreover, the proposed model can also explain the peculiarities of radio emission from flaring red dwarfs and ultracool stars. Note that if $\nu _{\mathrm{RLC}}$ coincides with the frequency of the loop MHD oscillations, the ratio $\Delta I/I_{0}$ grows and the acceleration and storage processes can be even more effective.